Abstract
Tortuosity is an important geometric vessel parameter and among the first microvascular alterations observed in various retinopathies. In the current study, a quantitative vessel tortuosity index (VTI) based on a combination of local and global centerline features is presented. Performance of VTI and previously established tortuosity indices were compared against human observers’ evaluation of tortuosity. An image-processing pipeline was developed for application of VTI in retinal vessels imaged by optical coherence tomography angiography (OCTA) in perifoveal (6 mm × 6 mm) and parafoveal (3 mm × 3 mm) regions centered on the fovea. Forty-one subjects (12 healthy control (NC) and 29 sickle cell retinopathy (SCR)) and 10 subjects (5 NC and 5 SCR) were imaged in the perifoveal and parafoveal regions, respectively. The relationship between VTI and age was examined in the perifoveal regions in NC subjects. VTI was measured from the OCTA images and compared between NC and SCR subjects using generalized least square regression with and without adjusting for age and race. VTI was found to correlate better than the 4 previous indices with performance of human observers. In the perifoveal region, a significant correlation was observed between VTI and age (r = −0.4, P<0.001, N = 12). VTI was higher in SCR than NC subjects in perifoveal and parafoveal regions (P≤0.001). The results demonstrate that the proposed method shows promise for detection of increased tortuosity in vessels due to retinal disorders.
OCIS codes: (100.2000) Digital image processing, (110.4500) Optical coherence tomography, (170.3880) Medical and biological imaging, (170.4470) Ophthalmology, Tortuosity, Vessel, Retina, Sickle cell retinopathy
1. Introduction
Sickle cell disease (SCD) is a genetic life-long chronic illness [1], characterized by formation of sickle shape erythrocytes [2]. Sickle cell retinopathy (SCR) is a major complication of SCD which is known to affect peripheral and macular retinal vascular beds and can lead to vision loss in the progressed stages due to formation of new vessels [3, 4]. Furthermore, frequent presence of retinal neovascularization, hemorrhages, schisis cavities, and black sunbursts have been reported to be associated with SCR [3, 4].
Fluorescein angiography (FA) has been used as a gold standard in the past decades for clinical evaluation of microvasculopathy due to SCR [5]. However, FA has been mainly performed for advanced proliferative stages of SCR and is known to be non-quantitative and invasive with limited applicability for subjects with small pupil [6]. Previous studies using spectral domain optical coherence tomography (SD-OCT) in SCR showed temporal and central macular thinning [7, 8], and indeed macular thinning was found to be associated with proliferative SCR [8]. Lately, optical coherence tomography angiography (OCTA) became available and offered an alternative to FA by providing high-resolution non-invasive imaging of capillary network in different retinal layers [9–11]. Recent studies in SCR using OCTA in parafoveal regions showed microvasculopathies such as decreased superficial and deep retinal capillary density [5, 12, 13], enlarged foveal avascular zone (FAZ) [5, 13, 14], capillary non-perfused areas [5, 15] and disruption of the perifoveal anastomotic capillary arcade [5].
Tortuosity is an important geometric vessel parameter which has been considered as a risk factor of multiple retinal pathologies [16], and increased vessel tortuosity is known to be among the first microvascular alterations due to many retinopathies such as diabetic retinopathy [17]. In SCR, increased retinal vessels tortuosity has been observed, but not considered as a pathognomonic sign. Non-specific increased tortuosity has been reported in more than 32% of SCR subjects by qualitative analysis of large retinal vessels [18]. Furthermore, increased tortuosity of major retinal vessels has been commonly observed in a majority of SCR subjects with HbS/HbS (SS) genotype [3, 12]. Finally, a recent analysis of OCTA images of parafoveal regions showed vessel tortuosity is more sensitive than thickness for SCR detection [13].
There is no widely accepted mathematical definition for tortuosity [19], and tortuosity evaluation has been mainly performed subjectively by clinicians. However, sensitivity and repeatability of visual tortuosity evaluation is limited due to high inter-observer variability [20], and indeed qualitative evaluation is inefficient for large studies. Quantitative assessment of tortuosity alterations has been reported in various retinal pathologies [17, 21–23], using one or combination of distance measure (DM) (i.e. the ratio of vessel length to its chord length) [13, 17, 21, 23], curvature or integral of curvature [16, 22, 24, 25], and number of inflection points [26, 27]. However, these methods are limited since they cannot always accurately estimate vessel tortuosity [13, 16, 17, 21–24, 26, 28–30], or are scale-dependent [25, 27]. More recently, a measure of tortuosity based on slope chain coding (SCC) was proposed which is invariant to rigid transformations [31]. However, as suggested in [32], SCC depends on length of linear elements which needs to be carefully selected for accurate tortuosity quantification.
In the current study, a method for assessment of retinal vessel touristy is proposed and shown to be invariant to rigid transformations and perform better than previous tortuosity metrics when compared with the evaluation of human observers. VTI does not require any parameter tuning, is computationally efficient, and more sensitive to changes in vessel curvature than methods that rely only on DM. Additionally, OCTA images in both parafoveal and perifoveal regions were analyzed for detection of alterations in retinal vessel tortuosity due to SCR.
2. Subjects
The study was approved by an institutional review board at University of Illinois at Chicago. Informed consents were obtained from subjects in accordance to the tenets of Declaration of Helsinki. The study was performed in 2 cohorts of subjects based on size of the imaged retinal region (i.e. 6 mm × 6 mm (perifoveal); 3 mm × 3 mm (parafoveal)). Perifoveal comprised 41 subjects (13 males and 28 females) with ages ranging from 15 to 62 years. Parafoveal comprised 10 subjects (5 males and 5 females) with ages ranging from 27 to 56 years. Based on a complete clinical history and ocular examination, subjects were categorized into 2 groups of healthy control (NC, N = 12; 7 OD and 5 OS) or sickle cell retinopathy (SCR, N = 29; 15 OD and 14 OS) in perifoveal region, and NC (N = 5; 1 OD and 4 OS) or SCR (N = 5; 3 OD and 2 OS) in parafoveal region. Three NC and 2 SCR subjects were in both cohorts. Subjects demographics and clinical data has been shown in Table 2. Exclusion criteria were inability to give informed consent or participate in the study, diabetes mellitus, glaucoma, or any other retinal disease. Each subject contributed data to the study by one eye with the best image quality.
3. Image acquisition
Imaging was performed by a commercially available OCTA instrument (Optovue Inc, Fremont, California, USA). The laser wavelength was 840 ± 45 nm with an axial scan rate and axial scan depth resolution of 70 KHz and 5 µm, respectively. B scans were acquired from identical retinal locations to generate blood flow map based on motion of red blood cells. Each B-scan was comprised of 304 A scans. Images of the superficial retinal vessels and capillary network were generated in perifoveal (6 mm × 6 mm) and parafoveal (3 mm × 3 mm) regions centered on the fovea. The superficial layer was defined by the Optovue software and displayed the retinal vasculature in the nerve fiber and ganglion cell layers with minimal flow projection and shading effects.
4. Image processing and analysis
Assessment of superficial retinal vessel tortuosity was performed using several image-processing steps as shown in Fig. 1. The algorithms were developed in MATLAB (Release 2015b, MathWorks, Inc., Natick, MA, USA) with image processing toolbox version 9.0.
Fig. 1.
Flow chart depicting steps for VTI assessment in retinal vessels in OCTA.
4.1 Vessel segmentation
Segmentation of vessels in the perifoveal and the perifoveal regions in OCTA was performed using a k-means clustering algorithm [33], similar to a previous study in which human observers performed the classification based on Horton-Strahler schemes [34]. K-means clustering is an iterative classification algorithm that divides data into k clusters where k is a positive integer. Clusters were found to minimize the least square error as shown in Eq. (1).
| (1) |
where E is the error, x is intensity value of pixels, and µ is the centroid of clusters. The algorithm starts with K randomly selected initial centroids. The distance between intensity value of each pixel to the centroids was computed to assign the pixel to a cluster with the closest centroid. A new set of clusters were computed in the next iteration based on assignment of pixels to the clusters in the previous one. This process was repeated to the point that the centroids were not changed between 2 consecutive iterations. The k-means clustering algorithm was used in the current study with k equals to 2 for classifying pixels either as vessel or background pixels to generate a binary image.
The binary image obtained from the k-means clustering was enhanced by a series of morphological operations. Filling was performed to eliminate any hole within the vessels, thickening was performed to bridge between separated vessel branches, objects smaller than 100 pixels, computed by counting the number of pixels in each binary object, were removed to eliminate noise and capillaries. Finally, dilation was performed using a disk shape structuring element to smooth vessel walls. Vessel centerlines between each pair of bifurcation points were extracted using distance transform through manual endpoint selection. The vessel endpoints were selected by simultaneous visualization of the grayscale and binary images in 2 separate windows. The grayscale image was used to identify bifurcations and the binary image was used to more accurately locate them with respect to the vessel boundaries and centerline. Cubic smoothing spline was utilized with a regularization parameter of 0.01 to obtain an adequate centerline and avoid aliasing. Vessel tortuosity index (VTI) was then computed for each of the centerlines as described in the following section.
4.2 Vessel tortuosity assessment
The most frequent tortuosity measures found in the literature were based on DM which is the ratio of arch length to chord length of a vessel segment [17, 21–23]. Despite the fact that DM is a simple and quick approach for vessel tortuosity quantification, there are circumstances where it fails to accurately determine the tortuosity due to its simplicity [29]. A tortuosity measure by combination of DM and number of inflection points was suggested by Bulliet et al. [26], which was shown not always match with visual perception of tortuosity [27]. Additionally, tortuosity density index (DT) defined as multiplication of number of inflection points with sum of DM determined between points of changes in centerline curvature was proposed by Grisan et al. [27]. The main drawback of this method was scale dependency.
Tortuosity measures based on curvature or integral of curvature have been proposed and applied in various pathologies [16, 24, 30]. Hart et al. showed that the sum of squared curvatures along retinal vessel centerline perfectly match with tortuosity perception of experts for classifying their data set into tortuous and non-tortuous blood vessels [16]. However, these methods can lead to misrepresentation of vessel tortuosity without considering changes in the sign of the curve, which is an important parameter used by clinicians for tortuosity evaluation [27].
Tortuosity assessment based on local angle changes was proposed previously [35–37]. Grisan et al. showed limitation of these methods which computed the same tortuosity for a semi-circumference and a curve obtained by juxtaposition of its two arcs. The two have the same mean angle changes but different tortuosity.
A method based on SD of distribution of vessel centerline incremental lateral displacement was proposed earlier by Wenn et al. [38]. Nevertheless, their method does not consider the magnitude of the curve, which plays an important role in clinical evaluation of vessel tortuosity.
Recently, Lisowaka et al. compared performance of 5 different retinal vessel tortuosity measures against sampling rates of vessel centerlines on a public data set [32]. Performance comparison of DM [16], DT [27], SCC [32], and 2 curvature based measures [16] showed that the overall performance of DT was good, but not always the best. They suggested that attention to numerical details and standardization is essential before choosing a tortuosity index. Further details on available tortuosity measures is beyond the scope of the current study and can be found elsewhere [27, 29].
Comparatively little work has been conducted for quantitative assessment of retinal vessel tortuosity in OCTA. The VTI presented in the current study is sensitive to small changes in tortuosity, and hence is suitable for detecting tortuosity alterations in retinal vessels in OCTA. For each point along the centerline, the angle (θ) between a line tangent to the centerline and a reference axis was determined. SD of absolute θ values (SDθ) along each centerline was computed, representing variation of local angle changes. The number of critical points at which the first derivative of centerlines vanishes (N) was quantified for each centerline based on frequency of changes in sign of the slope of the tangent lines. The N value was set to 1 for centerlines with no critical point to avoid zero tortuosity due to the lack of critical points. Inflection points at which the second derivative of centerlines vanishes (Ip) along the centerline were identified by detecting changes in the sign of curvature (k) where k was calculated using Eq. (2). Magnitude of vessel centerline (M) was estimated as mean ratio of arch length (LA) to cord length (LC) between pairs of inflection points including centerline end points as shown in Eq. (3).
| (2) |
| (3) |
The tortuosity index was multiplied by vessel length (LA) since LA increases with tortuosity, and was normalized by vessel chord length (Lc) to allow comparison of vessel segments with variable chord length. The mathematical derivation and visual demonstration of VTI is given in Eq. (4), and Fig. 2, respectively.
Fig. 2.
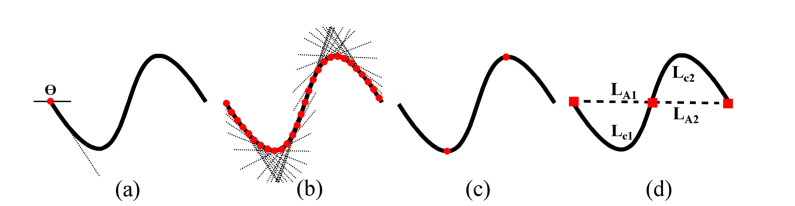
Visual demonstration of parameters extracted from a vessel centerline for VTI computation. (a) Angle between a line tangent to the centerline and a reference axis for the first centerline point. (b) Tangent lines for points along the centerline. SD of angles between each tangent line and the reference axis was computed. (c) Critical points (red circles) were determined based on changes in sign of slope of the tangent lines. (d) Magnitude of curve as ratio of arch length (LA) to the chord length (LC) between pairs of inflection points including centerline end points (red squares).
| (4) |
VTI is unitless similar to previous tortuosity metrics [16, 27, 32]. The minimum value for VTI is equal to 0 for an ideal straight line with zero SD of local angle changes. In theory, there is no maximum value for VTI since it increases with higher variation in angles, number of critical points, and the magnitude of curve. However, VTI in OCTA was generally lower than 1. NC and SCR example of perifoveal OCTA, vessel segmentation, and extracted centerlines for tortuosity analysis are shown in Fig. 3.
Fig. 3.
(a) OCTA images acquired in a NC (top row) and SCR (bottom row) subject in perifoveal regions. Example of a vessel segment endpoints is shown with red arrows (a; top row) (b) Vessel segmentation using k-means clustering. Example of a vessel segment endpoints selected on the binary image for centerline extraction are shown by red dots (b; top row). (c) Vessel endpoints (yellow circles) and centerlines (red lines) for VTI assessment. Mean VTI in the perifoveal region in the NC and SCR subjects were 0.41 and 0.71, respectively.
4.3 VTI validation
VTI was validated by (i) using sinusoidal curves with variable magnitudes and angular frequencies, and (ii) by quantitative comparison against performance of human observers (MS, WO and MK).
Two sets of sinusoidal curves were generated, the first set had constant angular frequency (1.25 rad/sec) and variable magnitudes between 0 and 6. The second set had constant magnitude of 1 and variable angular frequencies between 0 rad/sec and 6.3 rad/sec. A dependable tortuosity index should rise with increasing magnitude and increasing angular frequency coequal with visual perception of tortuosity.
Quantitative comparison of VTI and human observers’ grading was performed using a set of 25 sinusoidal curves generated from randomly selected magnitudes between 0.1 and 5, and randomly selected angular frequencies between 0.6 rad/sec and 4 rad/sec. The random magnitudes and frequencies were generated using Mersenne Twister pseudo-random number generator [39]. VTI and 4 previously established tortuosity indices, namely DI, Tnl [40], DM, and integral of absolute curvature (Tc) were computed for the curves and sorted in an ascending order. Similarly, human observers visually evaluated the curves and arranged them in an ascending order.
5. Statistical analysis
Statistical analysis was performed using SPSS (version 22, SPSS, Chicago, IL, USA) and statistical analysis codes written in MATLAB applied separately to data from the perifoveal and parafoveal regions. The association between VTI and performance of the human observers was determined using Spearman’s rank correlation. Subjects’ demographics were compared using Chi-square or t-test. Correlation between VTI and age in NC subjects was assessed using weighted Pearson’s correlation analysis. Finally, generalized least squares (GLS) was used to determine the effect of disease (NC and SCR) on VTI with and without adjusting for covariates (age (continuous) and race (categorical)). Statistical significance was accepted at P≤0.05.
6. Results
6.1 VTI validation
The validation tests using sinusoidal curves showed that VTI increased exponentially with increasing magnitudes and angular frequencies. The Spearman’s rank correlation statistics for comparison of VTI and the 4 previous methods with performance of human observers is shown in Table 1. VTI was correlated better with all human observers’ evaluations than tortuosity indices derived from previously established methods.
Table 1. Pearson’s rank correlation of human observes vs 5 tortuosity measures from a set of 25 randomly generated sinusoidal curves. VTI (vessel tortuosity index), density index (DI), non-linear curvature (Tnl), distance measure (DM), and integral of absolute curvature (Tc).
| Tortuosity Measure | Observer 1 | Observer 2 | Observer 3 |
|---|---|---|---|
| VTI | 0.89 | 0.91 | 0.93 |
| DI | 0.88 | 0.91 | 0.91 |
| Tnl | 0.88 | 0.86 | 0.90 |
| DM | 0.82 | 0.77 | 0.80 |
| Tc | 0.74 | 0.77 | 0.81 |
6.2 Demographic data
Subjects’ demographics are summarized in Table 2. In perifoveal region, age and eye examined were not different among NC and SCR subjects (P≥0.3), while sex and race were different (P<0.03). In parafoveal, age, sex and eye examined were not different among NC and SCR subjects (P≥0.2), while race was different (P = 0.008).
Table 2. Subject’s demographics. M and F are abbreviations for male and female, respectively. W, AA and A stand for White, African American and Asian, respectively. OD and OS are right and left eye, respectively. SS, SC, and Sβ are abbreviations for sickle cell genotype HbS/HbS, HbS/HbC, and HbS/beta thalassemia, respectively. Bold indicates statistical significance.
| Perifoveal | Parafoveal | |||||
|---|---|---|---|---|---|---|
| NC (N=12) | SCR (N=29) | P-value | NC (N=5) | SCR (N=5) | P-value | |
| Sex (M/F) | 7/5 | 6/23 | 0.03a | 3/2 | 2/3 | 0.9a |
| Race (W/AA/A) | 11/0/1 | 0/29/0 | <0.001a | 4/0/1 | 0/5/0 | 0.008a |
| Eye (OD/OS) | 7/5 | 15/14 | 0.7a | 1/4 | 3/2 | 0.5a |
| Age (years) | 37±12 | 35±14 | 0.3b | 41±10 | 48±12 | 0.2b |
| SCR Type (SS/SC/Sβ) | 17/9/3 | 2/2/1 | ||||
| SCD Stage (O/I/II/III/IV) | 1/1/19/7/1 | 0/0/3/1/1 | ||||
P value determined by Chi-square (a) or t-test (b).
6.3 VTI in perifoveal and parafoveal region
In the perifoveal region, VTI was assessed in 1026 and 2444 vessel segments in NC and SCR subjects, respectively. Mean VTI per subject ranged from 0.25 to 0.9 in perifoveal region. There was a negative correlation between VTI and age in NC subjects (r = −0.4, P<0.001, N = 12). Finally, VTI was significantly higher in SCR (0.61 ± 0.11) than NC (0.31 ± 0.04) subjects with or without age and race adjustment (P<0.001).
In the parafoveal region, VTI was assessed in 181 and 154 vessel segments in NC and SCR subjects, respectively. Mean VTI per subject ranged from 0.34 to 0.88 in parafoveal region. Finally, VTI was significantly higher in SCR (0.69 ± 0.18) than NC (0.40 ± 0.04) subjects with or without age and race adjustment (P≤0.001).
7. Discussion and conclusion
In the current study, a quantitative vessel tortuosity index was formulated by extracting multiple parameters from vessel centerline. This method is similar to human observer’s evaluation because variation of local angle changes, number of critical points, and magnitude of curve, each contribute to visual perception of tortuosity and were included in VTI formula. The method was applied to OCTA images obtained in perifoveal and parafoveal retinal regions and tortuosity alterations in superficial retinal vessels due to SCR were demonstrated.
VTI increased exponentially with higher magnitude and angular frequency of sinusoidal curves, consistent with visual perception of tortuosity. More importantly, VTI was shown to match with visual perception of tortuosity and its performance was better than other commonly used methods such as DI and DM. Furthermore, VTI has several advantages for assessment of retinal microvasculature. First, it is invariant to rigid transformations such as translation, rotation, and scaling because these transformations have no influence on any of its components (SDθ, N, M, LA/Lc). This is important since rigid transformations are common in clinical applications in which different instruments with variable setting are used for image acquisition. Second, VTI was normalized with respect to chord length which is necessary for detection of tortuosity alterations in retinal tissue which is densely vascularized and contains vessels with variable lengths. Third, VTI incorporates vessel length which can contribute to tortuosity. In fact, retinal vessels can become tortuous due to longitudinal stretching or shortening of distance between their tethering points [16, 41]. Although the pathophysiology of vascular stretching is not well established, the assumption is that the tone of smooth vascular muscles which determines vessel length and consequently tortuosity can be altered by mediators, blood gas, and metabolism due to pathology [42].
The proposed and many previously established methods do not account for the influence of vessel caliber on tortuosity. Therefore, the findings may misrepresent tortuosity of the entire network since small caliber and highly tortuous vessels can increase the overall tortuosity of the network. Attempts have been made to consider vessel width information in retinal tortuosity quantification [25], and to detect type of tortuosity alteration in 3D models of intracerebral vessels [26]. However, large clinical studies are required to determine the effect of vessel size on clinical perception of tortuosity to provide a deterministic weight factor to aggregate the impact of vessel size on tortuosity of the network. Although the effect of vessel caliber was not considered in the VTI formula, the k-mean clustering algorithm used in the current study automatically eliminated capillaries with diameter smaller than 20 µm, and hence tortuosity was assessed in relatively larger size vessels within the network which are mainly evaluated by clinicians for detection of tortuosity alterations.
In the current study, increased retinal vessel tortuosity due to SCR was reported in perifoveal and parafoveal regions. This finding is in agreement with previous qualitative [3, 12, 18] and quantitative [13] reports of increased retinal vessels tortuosity in SCR. Despite the report of a moderate increase (17%) in tortuosity of parafoveal vessels [13], we found a marked increase in tortuosity in both the perifoveal (98%) and parafoveal (70%) regions. The difference in findings can be attributable to differences in techniques.
Retinal vessels tortuosity in the perifoveal region was negatively correlated with age in NC subjects, consistent with a previous study [43] that quantified tortuosity in major retinal arterioles and venules. This finding suggests that age has an independent effect on retinal vessel tortuosity and needs to be matched in future studies for detection of retinal tortuosity alterations.
There were some limitations in the current study. Accurate junction point (i.e. bifurcation and crossover) detection in retinal images is crucial for tortuosity evaluation since they define vessel course and their misdetection can result in inaccurate tortuosity measure. In the current study, a human observer (MK) visually inspected images and selected junction points. Despite FA and FP where bifurcation points can be more easily detected as shown in [44, 45], presence of numerous junction points and a dense capillary network in OCTA increases complexity and decreases reliability of automatic junction point detection. Future research is warranted for developing methods for automatic junction point detection in OCTA which can improve the efficiency and increase repeatability of tortuosity assessment. Retinal arteries and veins were not separated since there is no reliable method to distinguish between them in OCTA. In fact, previous studies have shown that there is a difference in tortuosity of arteries and veins [43]. Nevertheless, tortuosity measurements were averaged per subject in the current study to reduce variability due to vessel type. Additionally, we assumed the parameters used in the VTI formula had equal weight toward tortuosity and indeed the strong correlation between VTI and initiative perception of tortuosity further confirmed this hypothesis. Nevertheless, large clinical studies are useful to determine the effect of each parameter on visual perception of tortuosity and make adjustment if necessary. In the current study, the feasibility of application of the method was demonstrated in a relatively uniform population of subjects, predominately with SS genotype and stage II retinopathy. Future studies in larger cohorts of subjects are needed to investigate the effect of genotype and stage of SCR on tortuosity alterations. Additionally, future studies would be useful to investigate the relation of blood vessel tortuosity alterations with other retinal vascular and anatomical abnormalities detected by multimodal imaging [46].
Assessment of retinal vessel tortuosity alterations shows promise for clinical diagnostic evaluation and longitudinal monitoring of microvasculopathies due to SCR. Furthermore, the method presented in the current study can be potentially applied to microvascular images of other tissues for quantitative assessment of vessel tortuosity.
Disclosures
The authors declare that there is no conflict of interest related to this article.
Funding
NIH research grants DK104393, EY001792, Senior Scientific Investigator Award (MS) and departmental award from Research to Prevent Blindness.
References and links
- 1.Serjeant G. R., Serjeant B. E., Sickle Cell Disease (Oxford University Press; New York, 1992), Vol. 3. [Google Scholar]
- 2.Lei H., Karniadakis G. E., “Quantifying the rheological and hemodynamic characteristics of sickle cell anemia,” Biophys. J. 102(2), 185–194 (2012). 10.1016/j.bpj.2011.12.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Welch R. B., Goldberg M. F., “Sickle-cell hemoglobin and its relation to fundus abnormality,” Arch. Ophthalmol. 75(3), 353–362 (1966). 10.1001/archopht.1966.00970050355008 [DOI] [PubMed] [Google Scholar]
- 4.Fadugbagbe A. O., Gurgel R. Q., Mendonça C. Q., Cipolotti R., dos Santos A. M., Cuevas L. E., “Ocular manifestations of sickle cell disease,” Ann. Trop. Paediatr. 30(1), 19–26 (2010). 10.1179/146532810X12637745451870 [DOI] [PubMed] [Google Scholar]
- 5.Minvielle W., Caillaux V., Cohen S. Y., Chasset F., Zambrowski O., Miere A., Souied E. H., “Macular microangiopathy in sickle cell disease using optical coherence tomography angiography,” Am. J. Ophthalmol. 164, 137–144 (2016). [DOI] [PubMed] [Google Scholar]
- 6.Spaide R. F., Klancnik J. M., Jr, Cooney M. J., “Retinal vascular layers imaged by fluorescein angiography and optical coherence tomography angiography,” JAMA Ophthalmol. 133(1), 45–50 (2015). 10.1001/jamaophthalmol.2014.3616 [DOI] [PubMed] [Google Scholar]
- 7.Hoang Q. V., Chau F. Y., Shahidi M., Lim J. I., “Central macular splaying and outer retinal thinning in asymptomatic sickle cell patients by spectral-domain optical coherence tomography,” Am. J. Ophthalmol. 151, 990–994 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murthy R. K., Grover S., Chalam K. V., “Temporal macular thinning on spectral-domain optical coherence tomography in proliferative sickle cell retinopathy,” Arch. Ophthalmol. 129(2), 247–249 (2011). 10.1001/archophthalmol.2010.357 [DOI] [PubMed] [Google Scholar]
- 9.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nagiel A., Sadda S. R., Sarraf D., “A promising future for optical coherence tomography angiography,” JAMA Ophthalmol. 133(6), 629–630 (2015). 10.1001/jamaophthalmol.2015.0668 [DOI] [PubMed] [Google Scholar]
- 11.Lumbroso B., Huang D., Jia Y., Chen C. J., Rispoli M., Romano A., Waheed N. K., Clinical OCT Angiography Atlas (JP Medical Ltd, 2015). [Google Scholar]
- 12.Han I. C., Tadarati M., Scott A. W., “Macular vascular abnormalities identified by optical coherence tomographic angiography in patients with sickle cell disease,” JAMA Ophthalmol. 133(11), 1337–1340 (2015). 10.1001/jamaophthalmol.2015.2824 [DOI] [PubMed] [Google Scholar]
- 13.Alam M., Thapa D., Lim J. I., Cao D., Yao X., “Quantitative characteristics of sickle cell retinopathy in optical coherence tomography angiography,” Biomed. Opt. Express 8(3), 1741–1753 (2017). 10.1364/BOE.8.001741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sanfilippo C. J., Klufas M. A., Sarraf D., Tsui I., “Optical coherence tomography angiography of sickle cell maculopathy,” Retin. Cases Brief Rep. 9(4), 360–362 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Chalam K. V., Sambhav K., “Optical coherence tomography angiography in retinal diseases,” J. Ophthalmic Vis. Res. 11(1), 84–92 (2016). 10.4103/2008-322X.180709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hart W. E., Goldbaum M., Côté B., Kube P., Nelson M. R., “Measurement and classification of retinal vascular tortuosity,” Int. J. Med. Inform. 53(2-3), 239–252 (1999). 10.1016/S1386-5056(98)00163-4 [DOI] [PubMed] [Google Scholar]
- 17.Sasongko M. B., Wong T. Y., Nguyen T. T., Cheung C. Y., Shaw J. E., Wang J. J., “Retinal vascular tortuosity in persons with diabetes and diabetic retinopathy,” Diabetologia 54(9), 2409–2416 (2011). 10.1007/s00125-011-2200-y [DOI] [PubMed] [Google Scholar]
- 18.Emerson G. G., Lutty G. A., “Effects of sickle cell disease on the eye: clinical features and treatment,” Hematol. Oncol. Clin. North Am. 19(5), 957–973 (2005). 10.1016/j.hoc.2005.07.005 [DOI] [PubMed] [Google Scholar]
- 19.Annunziata R., Kheirkhah A., Aggarwal S., Hamrah P., Trucco E., “A fully automated tortuosity quantification system with application to corneal nerve fibres in confocal microscopy images,” Med. Image Anal. 32, 216–232 (2016). 10.1016/j.media.2016.04.006 [DOI] [PubMed] [Google Scholar]
- 20.Kagan A., Aureli E., Dobree J., “A note on signs in the fundus oculi and arterial hypertension: conventional assessment and significance,” Bull. World Health Organ. 34(6), 955–960 (1966). [PMC free article] [PubMed] [Google Scholar]
- 21.Koreen S., Gelman R., Martinez-Perez M. E., Jiang L., Berrocal A. M., Hess D. J., Flynn J. T., Chiang M. F., “Evaluation of a computer-based system for plus disease diagnosis in retinopathy of prematurity,” Ophthalmology 114(12), e59–e67 (2007). 10.1016/j.ophtha.2007.10.006 [DOI] [PubMed] [Google Scholar]
- 22.Hughes A. D., Martinez-Perez E., Jabbar A.-S., Hassan A., Witt N. W., Mistry P. D., Chapman N., Stanton A. V., Beevers G., Pedrinelli R., Parker K. H., Thom S. A., “Quantification of topological changes in retinal vascular architecture in essential and malignant hypertension,” J. Hypertens. 24(5), 889–894 (2006). 10.1097/01.hjh.0000222759.61735.98 [DOI] [PubMed] [Google Scholar]
- 23.Gelman R., Martinez-Perez M. E., Vanderveen D. K., Moskowitz A., Fulton A. B., “Diagnosis of plus disease in retinopathy of prematurity using Retinal Image multiScale Analysis,” Invest. Ophthalmol. Vis. Sci. 46(12), 4734–4738 (2005). 10.1167/iovs.05-0646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Smedby O., Högman N., Nilsson S., Erikson U., Olsson A. G., Walldius G., “Two-dimensional tortuosity of the superficial femoral artery in early atherosclerosis,” J. Vasc. Res. 30(4), 181–191 (1993). 10.1159/000158993 [DOI] [PubMed] [Google Scholar]
- 25.Bhuiyan A., Nath B., Ramamohanarao K., Kawasaki R., Wong T. Y., “Automated analysis of retinal vascular tortuosity on color retinal images,” J. Med. Syst. 36(2), 689–697 (2012). 10.1007/s10916-010-9536-6 [DOI] [PubMed] [Google Scholar]
- 26.Bullitt E., Gerig G., Pizer S. M., Lin W., Aylward S. R., “Measuring tortuosity of the intracerebral vasculature from MRA images,” IEEE Trans. Med. Imaging 22(9), 1163–1171 (2003). 10.1109/TMI.2003.816964 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grisan E., Foracchia M., Ruggeri A., “A novel method for the automatic grading of retinal vessel tortuosity,” IEEE Trans. Med. Imaging 27(3), 310–319 (2008). 10.1109/TMI.2007.904657 [DOI] [PubMed] [Google Scholar]
- 28.Wolffsohn J. S., Napper G. A., Ho S. M., Jaworski A., Pollard T. L., “Improving the description of the retinal vasculature and patient history taking for monitoring systemic hypertension,” Ophthalmic Physiol. Opt. 21(6), 441–449 (2001). 10.1046/j.1475-1313.2001.00616.x [DOI] [PubMed] [Google Scholar]
- 29.Kalitzeos A. A., Lip G. Y., Heitmar R., “Retinal vessel tortuosity measures and their applications,” Exp. Eye Res. 106, 40–46 (2013). 10.1016/j.exer.2012.10.015 [DOI] [PubMed] [Google Scholar]
- 30.Hart W. E., Goldbaum M., Cote B., Kube P., Nelson M. R., “Automated measurement of retinal vascular tortuosity,” in Proceedings of the AMIA Annual Fall Symposium, (American Medical Informatics Association, 1997), 459. [PMC free article] [PubMed] [Google Scholar]
- 31.Bribiesca E., “A measure of tortuosity based on chain coding,” Pattern Recognit. 46(3), 716–724 (2013). 10.1016/j.patcog.2012.09.017 [DOI] [Google Scholar]
- 32.A. Lisowska, R. Annunziata, G. K. Loh, D. Karl, and E. Trucco, “An experimental assessment of five indices of retinal vessel tortuosity with the RET-TORT public dataset,” in Engineering in Medicine and Biology Society (EMBC), 2014 36th Annual International Conference of the IEEE, (IEEE, 2014), 5414–5417. 10.1109/EMBC.2014.6944850 [DOI] [PubMed] [Google Scholar]
- 33.Hartigan J. A., Clustering algorithms (1975).
- 34.Wang Q., Chan S., Yang J. Y., You B., Wang Y. X., Jonas J. B., Wei W. B., “Vascular density in retina and choriocapillaris as measured by optical coherence tomography angiography,” Am. J. Ophthalmol. 168, 95–109 (2016). 10.1016/j.ajo.2016.05.005 [DOI] [PubMed] [Google Scholar]
- 35.Chandrinos K., Pilu M., Fisher R., Trahanias P., Image Processing Techniques for the Quantification of Atherosclerotic Changes (Department of Artificial Intelligence, University of Edinburgh, 1998). [Google Scholar]
- 36.Kheng G., “An automatic diabetic retinal image screening system book chapter in medical data mining and knowledge discovery,” Edited by Cios Krzysztof. 29, 181–210 (2001). [Google Scholar]
- 37.Eze C. U., Gupta R., Newman D. L., “A comparison of quantitative measures of arterial tortuosity using sine wave simulations and 3D wire models,” Phys. Med. Biol. 45(9), 2593–2599 (2000). 10.1088/0031-9155/45/9/312 [DOI] [PubMed] [Google Scholar]
- 38.Wenn C. M., Newman D. L., “Arterial tortuosity,” Australas. Phys. Eng. Sci. Med. 13(2), 67–70 (1990). [PubMed] [Google Scholar]
- 39.Matsumoto M., Nishimura T., “Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator,” ACM Trans. Model. Comput. Simul. 8(1), 3–30 (1998). 10.1145/272991.272995 [DOI] [Google Scholar]
- 40.Aghamohamadian-Sharbaf M., Pourreza H. R., Banaee T., “A novel curvature-based algorithm for automatic grading of retinal blood vessel tortuosity,” IEEE J. Biomed. Health Inform. 20(2), 586–595 (2016). 10.1109/JBHI.2015.2396198 [DOI] [PubMed] [Google Scholar]
- 41.Dougherty G., Varro J., “A quantitative index for the measurement of the tortuosity of blood vessels,” Med. Eng. Phys. 22(8), 567–574 (2000). 10.1016/S1350-4533(00)00074-6 [DOI] [PubMed] [Google Scholar]
- 42.Bracher D., “Changes in peripapillary tortuosity of the central retinal arteries in newborns. A phenomenon whose underlying mechanisms need clarification,” Graefes Arch. Clin. Exp. Ophthalmol. 218(4), 211–217 (1982). 10.1007/BF02150097 [DOI] [PubMed] [Google Scholar]
- 43.Cheung C. Y., Zheng Y., Hsu W., Lee M. L., Lau Q. P., Mitchell P., Wang J. J., Klein R., Wong T. Y., “Retinal vascular tortuosity, blood pressure, and cardiovascular risk factors,” Ophthalmology 118(5), 812–818 (2011). 10.1016/j.ophtha.2010.08.045 [DOI] [PubMed] [Google Scholar]
- 44.Calvo D., Ortega M., Penedo M. G., Rouco J., “Automatic detection and characterisation of retinal vessel tree bifurcations and crossovers in eye fundus images,” Comput. Methods Programs Biomed. 103(1), 28–38 (2011). 10.1016/j.cmpb.2010.06.002 [DOI] [PubMed] [Google Scholar]
- 45.Tavakoli M., Shahri R. P., Pourreza H., Mehdizadeh A., Banaee T., Toosi M. H. B., “A complementary method for automated detection of microaneurysms in fluorescein angiography fundus images to assess diabetic retinopathy,” Pattern Recognit. 46(10), 2740–2753 (2013). 10.1016/j.patcog.2013.03.011 [DOI] [Google Scholar]
- 46.Ghasemi Falavarjani K., Scott A. W., Wang K., Han I. C., Chen X., Klufas M., Hubschman J.-P., Schwartz S. D., Sadda S. R., Sarraf D., Tsui I., “Correlation Of Multimodal Imaging In Sickle Cell Retinopathy,” Retina 36(Suppl 1), S111–S117 (2016). 10.1097/IAE.0000000000001230 [DOI] [PubMed] [Google Scholar]