Abstract
For the prognosis of complex diseases, beyond the main effects of genetic (G) and environmental (E) factors, gene-environment (G-E) interactions also play an important role. Many approaches have been developed for detecting important G-E interactions, most of which assume that measurements are complete. In practical data analysis, missingness in E measurements are not uncommon, and failing to properly accommodate such missingness leads to biased estimation and false marker identification. In this study, we conduct G-E interaction analysis with prognosis data under an accelerated failure time (AFT) model. To accommodate missingness in E measurements, we adopt a nonparametric kernel-based data augmentation approach. With a well-designed weighting scheme, a nice “byproduct” is that the proposed approach enjoys a certain robustness property. A penalization approach, which respects the “main effects, interactions” hierarchy, is adopted for selection (of important interactions and main effects) and regularized estimation. The proposed approach has sound interpretations and a solid statistical basis. It outperforms multiple alternatives in simulation. The analysis of TCGA data on lung cancer and melanoma leads to interesting findings and models with superior prediction.
Keywords: G-E interaction, Missing data, Prognosis, Data augmentation, Penalized estimation
1 Introduction
For the outcomes and phenotypes of complex diseases, it is increasingly recognized that gene-environment (G-E) interactions have independent contributions beyond the main genetic (G) and environmental (E) effects. A large number of studies have been conducted, collecting and analyzing data and searching for important G-E interactions. The literature is too vast to be reviewed here. For relevant discussions, we refer to Hunter (2005), Thomas (2010), and many others. In this study, we consider G-E interaction analysis with a prognosis outcome. Compared to binary (categorical) and continuous outcomes, research on prognosis outcomes is relatively limited, partly because of the extra complexity brought by censoring in prognosis analysis. However, for many complex diseases, prognosis is at least as important as (categorical) risk and (continuous) biomarkers. In recent literature, G-E interaction analysis with a prognosis outcome includes Lee et al. (2012), Sharafeldin et al. (2015), Liu et al. (2013), and a few others.
Most of the existing G-E interaction analysis methods assume that measurements are complete without missingness. In practice, with the fast development of profiling techniques, missingness in G measurements is posing a diminishing concern. However, with limitations in data collection, missingness in E measurements is not uncommon – such a problem has been routinely encountered in epidemiological studies. For example, in the lung adenocarcinoma data collected by TCGA (The Cancer Genome Atlas), which is recent and has a high quality, about 30% of the measurements on “smoking pack years”, a major risk factor for lung cancer, is missing. In the analysis of low-dimensional biomedical data, it has been proved both statistically and numerically that failing to properly accommodate missingness leads to biased estimation and false identification of important markers (Little and Rubin, 2002).
Compared to that in “classic” low-dimensional biomedical studies, research on missingness in high-dimensional genetic data analysis is much limited. When the percentage of records with missing measurements is low, some studies have conducted the simple complete-case-only analysis. In some other data analyses, simple imputations (for example using means of observed measurements) have been conducted. However, research with low-dimensional data suggests that such simple approaches are in general insufficient. More serious effort has also been made to accommodate missingness in genetic data analysis. For example, a family of approaches is based on imputation, and a representative example is the BPCA approach in Oba et al. (2003). Our literature review suggests that such approaches have been mostly developed for accommodating missingness in G measurements and applied to main effects. Another family is likelihood-based and uses the EM (expectation maximization) technique. One example is Spinka et al. (2005), which conducts G-E interaction analysis for case-control data and accommodates missingness in G measurements. Another example is Hu et al. (2010) which also accommodates missingness in G measurements but for prognosis data. It is noted that both Spinka et al. (2005) and Hu et al. (2010) conduct hypothesis testing, analyze a small number of G variables at a time, but cannot accommodate the joint effects of a large number of G variables.
In this study, we consider G-E interaction analysis with a prognosis outcome. Of special interest is to accommodate missingness in E measurements. To achieve that, a novel data augmentation approach is developed. This study complements the existing literature in the following aspects and is hence warranted. First, it is concerned with missingness in E measurements, which is a very practical problem but has been rarely investigated. The fast development in profiling techniques makes missingness in G measurements a diminishing problem. However, the missingness problem in E measurements is expected to last. Second, a novel data augmentation strategy is adopted. Multiple strategies/approaches are potentially applicable to the present problem, including for example the BPCA and other imputations, the IPW (inverse probability weighting; Robins and Rotnitzky, 1995), and others, although we note that they have not been effectively applied in the present context. Our numerical study shows that the proposed approach can outperform state-of-the-art alternatives and provides a practically useful venue. In addition, with a well-designed weighting scheme, a nice “byproduct” is a certain robustness property not shared by the alternatives. Third, prognosis data is analyzed, which is more complicated than categorical and continuous data. It is noted that the analysis of continuous outcome data can be viewed as a special case of the proposed analysis (with zero censoring). In addition, we consider the joint effects of a large number of G measurements and respect the “main effects, interactions” hierarchy, making the analysis more informative than marginal analysis and those that neglect the hierarchy.
2 Methods
2.1 Data and model settings
Consider a prognosis study with N subjects. First consider the scenario without missingness. For the ith subject, let Ti be the survival time of interest, and Xi = (Xi1, ⋯, Xiq)′ and Zi = (Zi1, ⋯, Zip)′ be the q- and p-vectors of E and G measurements, respectively. Consider a model with all G and E effects and their interactions, which makes the proposed analysis more informative than marginal analysis that considers one or a few G measurements at a time. For modeling prognosis, we consider the AFT (accelerated failure time) model, where
| (1) |
Here α0 is the intercept, bj = (βj, γj1, ⋯, γjq)′, Wij = (Zij, ZijXi1, ⋯, ZijXiq)′, and εi is the random error with an unknown distribution. Use Θ = {αk, bj, k = 1, ⋯, q, j = 1, ⋯, p} to denote the regression coefficients for all main effects and interactions.
For subject i, denote Ci as the censoring time. We observe (Yi = log(min(Ti, Ci)), δi = I(Ti ≤ Ci)). Assume that the data {(Xi, Zi, Yi, δi), i = 1, …, N} have been sorted according to Yi from the smallest to the largest. The Kaplan-Meier weights can be computed as
| (2) |
Following Stute (1996), the unknown parameters α0 and Θ can be estimated by minimizing
| (3) |
The analysis of data with a censored survival outcome and high-dimensional covariates has attracted extensive attention in recent research. The adopted models include the AFT (Hu and Chai, 2013; Khan and Shaw, 2016), Cox (He et al., 2016; Ternes et al., 2016), and others. In “classic” survival analysis with low-dimensional covariates, the Cox model is more popular. Under high-dimensional settings, the AFT model may preferred with lucent interpretations. More importantly, with the least squared loss function, it has the lowest computational cost, which is especially desirable with high-dimensional data. In addition, numerical studies in Huang et al. (2006), Zhu et al. (2014), and others suggest that it has satisfactory properties with genetic data. The Stute's estimation is adopted also because of computational cost consideration. With low-dimensional data, it has been suggested that this estimation approach is comparable to the alternatives (rank-based, Buckley-James, etc.). To accommodate the high dimensionality, regularization is usually needed (Xia et al. 2016). In the literature, most of the existing studies have been on the main G and/or E effects, with relatively less attention to G-E interactions.
We next consider the scenario with missingness in E measurements. Our approach consists of two steps. In the next subsection, we first develop a strategy/loss function to accommodate missingness. Then we adopt a penalization approach for regularized estimation and selection of important interactions and main effects.
2.2 Accommodating missingness with data augmentation
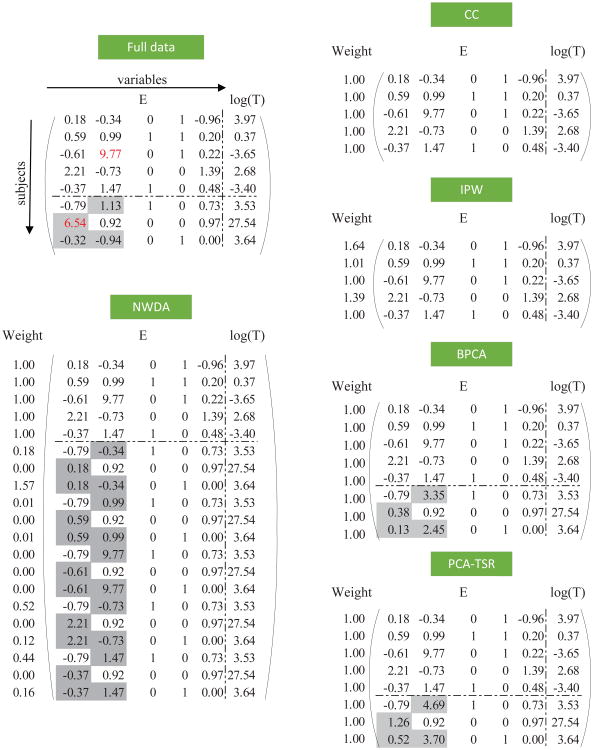
Our methodological development has been motivated by very practical settings, for example data analyzed in this article. Extension to other settings will be briefly discussed. As in quite a few published studies, we take a loose definition of E variables to also include demographic and clinical variables, that is, all “non-G” variables. Some E variables, such as age and gender, are easy to collect, and their measurements are usually available for all subjects, whereas some other E variables may have missing measurements. A schematic example is provided in Figure 1. Among the five E variables, three have measurements available for all subjects, and two have missing measurements. Consider the partition X = {X(o), X(m)}, where the index set o contains E variables whose measurements are available for all subjects, and the index set m contains E variables with missingness for some subjects. For subject i, let ζi be the missingness indicator defined as
Figure 1.
A small example: data analyzed under different approaches. Grey squares represent missing measurements and their augmented/imputed values. The numbers highlighted in red deviate from the majority of the observations (“outliers”).
Then is the number of subjects with complete measurements. In the example in Figure 1, N=8 and Nc=5. Assume missing at random, that is, . For simplicity of notation, rearrange data so that ζi = 1 for i = 1, …, Nc.
We propose using a Nonparametric Weighted Data Augmentation (NWDA) approach to accommodate missingness. First for subject i(= Nc + 1, …, N), denote m̃i and õi as the index sets of missing and observed E variables. For example, in the example in Figure 1, m̃6 = {2} and õ6 = {1, 3, 4, 5}. For subject i(= Nc + 1, …, N), we generate Nc augmented observations, which have G measurements and outcome values equal to those of subject i and with E measurements equal to
That is, for the observed measurements, we keep their values. For the missing measurements, we use those from the Nc complete records.
Next for subject i(= Nc + 1, …, N), we assign a weight to each of the Nc augmented data points, with the consideration that they are not equally likely. Specifically, for l = 1, …, Nc, if subjects l and i are closer to each other as measured by X(o) and outcome, then the augmented data point with { , } should have a higher weight. More specifically, for l = 1, ⋯, Nc and i = Nc + 1, ⋯, N, we first define the Nadaraya-Watson type weight as
| (4) |
where { , log(Tl) − log(Ti)} is the vector composed of and log(Tl) − log(Ti), K(·; h) is a kernel function and h is the bandwidth. The input to the kernel function is multidimensional. To simplify computation, we take
The assumed multiplicative structure may not be efficient (as correlation is not accounted for) but is effective. In many kernel-based studies, it has been suggested that the choice of the kernel function is not too crucial. In our numerical study, the Gaussian kernel is adopted for continuous variables, and the following kernel (Racine and Li, 2005) is adopted for discrete variables:
| (5) |
These two kernel functions have been extensively adopted in the literature and shown to have satisfactory statistical and numerical properties. In our numerical study, the bandwidth hj is chosen using cross-validation. In the definition of wNW, log(T) is used. For a subject with δ = 1, this value is directly available. For subject l with δl = 0, we compute log(Tl) as E(log(Tl)|log(Tl) > Yl) based on the nonparametric Kaplan-Meier estimation. Finally, for l = 1, ⋯, Nc and i = Nc + 1, ⋯, N, the weight for the augmented observation with { , } is
| (6) |
This normalization ensures that, when censoring is not considered, the Nc × (N − Nc) augmented observations have an overall weight of N − Nc.
Note that in this subsection, for notational simplicity, we have rearranged data so that the first Nc subjects have complete measurements. With a slight abuse of notation, still use to denote the Kaplan-Meier weight for the ith subject in the rearranged data. Taking both censoring and missingness into consideration, we extend (3) and propose the new loss function as
| (7) |
2.2.1 Remarks
We accommodate missingness using data augmentation, which has also been referred to as data imputation in some studies. Under missing at random, we are able to augment data from the observed empirical distribution. The proposed augmentation procedure is nonparametric and does not depend on specific models/parameters, making it less restrictive. The weights are fixed, making the proposed approach different from some alternatives. In the literature, some data imputation approaches conduct imputation multiple times. With the proposed approach, one augmentation step is conducted. There are several strong reasons for this. First, conducting imputation multiple times is mostly for inference consideration, whereas in this study we focus on estimation. Second, for each observation with missing measurements, Nc augmented observations are generated. All information on the fully observed subjects has been used. This makes the proposed procedure, in a sense, equivalent to multiple imputations. Third, with high-dimensional data, computation cost is of concern, and thus it is sensible to reduce the number of iterations.
The nonparametric kernel-based weights have been partly motivated by the study on low-dimensional data in Creemers et al. (2012), which suggests that a nonparametric approach can outperform the popular IPW approach and doubly robust approach. There is a vast literature on kernel approaches. Here our adaption is relatively standard. We refer to Creemers et al. (2012) and others for relevant discussions. When generating weights, we take into account both the outcome variable and fully observed E variables. Here it is assumed that the missingness in E variables does not depend on G variables, which is reasonable under many scenarios. The multiplicative structure is adopted to reduce computational cost and improve stability and shown to be effective. For censored subjects, as their event times are not directly available, we use their expected values computed based on the nonparametric Kaplan-Meier estimator.
A nice “byproduct” of our weighting scheme is a certain robustness property. Consider the example in Figure 1. Subject 3 has a “larger than normal” value of the second E variable, while subject 7 has a “larger than normal” value of the first E variable (note that this value is missing in the observed data). For subject 7, caused by the first E variable, its log(T) value is very large compared to those of the first five subjects, making it “far away” from them. Thus, all five augmented observations for subject 7 have small weights, which effectively down-weighs the impact of the outlier in the first E variable. What happens to subject 3 is similar: the augmented observations corresponding to subject 3 have small weights. This robustness property is easily achieved as a byproduct and not shared by the alternatives described in simulation study.
With both censoring and missingness, the proposed loss function contains two sets of weights. It is noted that this loss function has not been considered even for low-dimensional data and thus has independent value beyond this G-E interaction analysis.
2.2.2 An extension to accommodate high missing rates
When a subject has multiple missing measurements, the proposed NWDA imputes their values together using the Nc observations with complete measurements. This ensures that the correlation structure of E measurements is kept. However, a byproduct drawback is that it demands that Nc cannot be too small (otherwise the information used would be limited). When missing rates are high and Nc is small, we propose conducting a minor modification/extension of the proposed NWDA and filling in missing measurements one at a time. Consider for example the 8th subject in the example in Figure 1. With the NWDA, the first five complete measurements are used for imputing the two missing measurements. To use more information, we extend the NWDA and propose imputing the two missing measurements separately. When imputing for the first missing measurement, there are six observations with measurements available, and thus more information is used. A similar procedure can then be applied to the second missing measurement. As two augmentation procedures are conducted, two sets of weights are generated, which need to be multiplied together to generate the final weights.
2.3 Penalized estimation and selection
The number of unknown parameters in (7) can be much larger than the sample size. In addition, among all of the candidate main effects and interactions, only a very small subset is expected to be associated with prognosis. Thus, regularized estimation and marker selection are needed. For this purpose, we adopt penalization, which has been the choice of several recent studies (Liu et al. 2013; Zhu et al. 2014). Consider the penalized estimate
| (8) |
For penalty, we adopt the sparse group MCP, which has been adopted by Liu et al. (2013) under a simpler setting. Specifically,
where is the minimax concave penalty (MCP), λ1 and λ2 are data-dependent tuning parameters, ξ is the regularization parameter, and bjk is the kth element of bj. The nonzero components of Θ̂ correspond to important main effects and interactions that are associated with prognosis.
Adopting this penalty has been motivated by the following considerations. Since E variables are usually pre-selected and have a low dimension, selection is not conducted on E variables. The sparse group penalty respects the “main effects, interactions” hierarchy. That is, if a G-E interaction is selected, the corresponding main G effect is automatically selected. As discussed in Bien et al. (2013) and followup studies, violating this hierarchy causes problems in both estimation and interpretation. This penalty is built on MCP, which has been shown to have satisfactory performance. We also refer to Liu et al. (2013) for relevant discussions.
2.4 Computation
The proposed analysis consists of two steps. The augmentation step involves only simple calculations and does not need special algorithms. For describing the algorithm of penalized estimation, we slightly simplify notations and consider the penalized problem with loss function
| (9) |
Center Yi, Xi, and Wi using their weighted means , , and , respectively. That is,
Then loss function (9) can be rewritten as
| (10) |
where Y is the N-vector composed of Yi's, X and W are the matrices composed of Xi's and Wi's, respectively, and α and b are vectors composed of αk's and bj's, respectively.
Consider the following iterative algorithm: (i) Initialize b̂ = 0; (ii) Compute α̂ = (X′X)−1(X′(Y− Wb̂)); (iii) Compute b̂ by minimizing (10) with α fixed at α̂ using a group coordinate descent (GCD) algorithm; (iv) Iterate Step (ii) and (iii) until convergence. Details on the GCD algorithm is provided in Appendix. In the literature, the GCD technique has been well investigated (Huang et al. 2012; Liu et al., 2013; Zhao et al., 2015) and shown to have satisfactory performance. The specific GCD algorithm for (9) has been developed in Liu et al. (2013) and shown to have satisfactory convergence and numerical properties. R code is available at http://works.bepress.com/shuangge/42/. In numerical study, we use the l2-norm of the difference between two consecutive estimates smaller than 10−5 as the convergence criterion. Convergence is achieved in all of our numerical studies within 30 overall iterations.
The adopted penalty has three parameters. Published studies suggest setting ξ as fixed or examining a small number of values. In our numerical study, we follow the literature and set ξ = 6. As the loss function has a (weighted) least squared form, we adopt the EBIC (extended Bayesian Information Criteria; Chen and Chen, 2008) to choose λ1 and λ2.
3 Simulation
Simulation is conducted to assess performance of the proposed NWDA and compare with competing alternatives. Specifically, the following state-of-the-art alternatives are considered, whose analysis schemes are also shown in Figure 1: (a) Full, which is the ideal approach without missingness. (b) CC, which is a complete-case analysis and based on subjects with complete measurements only. (c) IPW (inverse probability weighting) analysis. This approach, as shown in Figure 1, assigns a weight to each record with complete measurements where the weight is computed using a nonparametric kernel method. This is one of the most commonly adopted missing data techniques (Little and Rubin, 2002). (d) BPCA, which is an imputation method. It is based on the principal component regression, and a probabilistic model and latent variables are estimated simultaneously within the Bayesian inference framework. Oba et al. (2003) and other studies show that it outperforms many competing alternatives, including for example those based on singular value decomposition and K-nearest neighbors. (e) BPCA-TSR, which is a recent imputation method. It constructs a regression model based on the trimmed scores matrix which corresponds to only the observed variables and their associated PCA loadings. Folch-Fortuny et al. (2015) shows that it performs extremely well under a variety of data structures and missingness percentages and outperforms many alternatives such as CC and partial least squares. As shown in Figure 1, the BPCA and BPCA-TSR methods fill in missing measurements, and then all data records are analyzed on the same ground (equal weights). Among the above methods, CC and IPW are perhaps the most popular missing data methods. BPCA and BPCA-TSR are considered since they also take a data imputation strategy and have been shown to outperform many competing alternatives. For all the alternatives, we impose the same penalty as for the proposed approach for comparability. The same tuning parameter selection technique is also applied. It is noted that although may have a certain robustness property, the proposed approach is not originally designed as a robust one. In addition, robust G-E interaction analysis that can accommodate high-dimensional joint effects has been very limited. Thus, we do not pursue comparison with robust methods.
For the first set of simulation, the summary of settings is presented in Table A.1 (Appendix). Under all scenarios, we set N = 150, q = 5, and p = 1, 000. There are thus a total of 1,005 main effects and 5,000 interactions. (a) Four overall settings are considered. Under setting N1, we first simulate the E variables to have a multivariate normal distribution with marginal mean 0 and variance 1. We simulate a compound symmetry correlation structure with correlation coefficient 0.5. As the proposed approach has a certain robustness property, we also consider the following settings with some measurements deviating from the rest majority. Under setting O1.1, 20% of the measurements in X(m) are multiplied by N(0, 10). Under setting O1.2, 20% of the measurements in X(o) are multiplied by N(0, 10). Under setting O.2, the random errors (to be specified below) have a higher variance, which may lead to outliers in the response variable. (b) Beyond the setting described above with five continuous E variables (denoted as “5 continuous” in Table A.1), we also dichotomize two E measurements at 0 and create two binary variable (denoted as “3 continuous + 2 categorical” in Table A.1). (c) The G variables are simulated from a multivariate normal distribution with marginal means 0 and marginal variances 1. Two correlation structures are considered. The first is an AR (auto-regressive) structure where the jth and kth G variables have correlation coefficient 0.3|j–k|. The second is a Band (banded) structure where the jth and kth G variables have correlation coefficient 0.33 if |j – k| = 1 and 0 otherwise. (d) There are five main E effects, eight main G effects, and six G-E interactions that have nonzero coefficients randomly generated from Uniform(0.6, 1). (e) Under Settings N.1, O1.1, and O1.2, ε ∼ N(0, 1), and under Setting O.2, ε ∼ N(0, 4). (f) The log event times are computed from the AFT model, and the censoring times are randomly generated. The censoring rates are about 20%. For missingness, we consider two scenarios. Under Missing M1, one E variable has missing measurements, whereas under Missing M2, two E variables have missing measurements. The missingness probability satisfies a logistic regression model and depends on X(o) and T. Parameters of the logistic model are adjusted so that the overall missing rate is about 15%.
Simulation suggests that the proposed analysis is computationally affordable. For a simulation replicate, the data augmentation step can be accomplished within ten seconds using a desktop with standard configurations. The penalized estimation step can be accomplished within ten minutes.
When evaluating performance, main effects and interactions are considered separately. Measures adopted for evaluation include (a) TP20, which is the number of true positives when overall 20 effects (including both main and interaction) are selected. TP40 is defined in a similar manner. (b) TP.EBIC, which is the number of true positives when the tuning parameters λ1 and λ2 are selected using EBIC. FP.EBIC is the corresponding number of false positives. (c) SSE.EBIC, which is the sum of squared errors and assesses parameter estimation performance at the EBIC-selected tunings. There are a total of sixteen simulation scenarios. Under each scenario, we simulate 200 replicates and compute summary statistics.
Summary results for Scenarios 1 and 2 are shown in Tables 1 and 2, respectively. The rest of the results are shown in Appendix. Note that under the ideal approach Full, all observations are available, and thus the results for Missing M1 and Missing M2 are the same. It is observed that across all simulation scenarios, the proposed NWDA has competitive performance. For example in Table 1 under Missing M2, the proposed approach has TP20=4.4 for interactions, compared to 2.5 (CC), 2.7 (IPW), 3.7 (BPCA), and 4.0 (PCA-TSR). It can also more accurately identify important main effects. For example under Missing M1, it has TP20=6.7 for main effects, compared to 4.8 (CC), 4.5 (IPW), 6.4 (BPCA), and 6.3 (PCA-TSR). In addition, it has satisfactory estimation performance. In general, under overall Setting N1, BPCA and PCA-TSR also have good performance. However, when there are measurements that deviate from the rest majority, the advantage of the proposed approach over BPCA and PCA-TSR gets more prominent. For example in Table 2 under Missing M2, the proposed approach has TP20=4.4 for interactions, compared to 3.4 (CC), 3.5 (IPW), 1.7 (BPCA), and 1.8 (PCA-TSR). For the estimation of main effects, the proposed approach has SSE.EBIC=5.33, compared to 5.99 (CC), 9.11 (IPW), 10.82 (BPCA), and 13.65 (PCA-TSR). It is observed that the models selected by EBIC may be overly conservative (sizes too small), although we do note that the proposed approach also systematically outperforms the alternatives under EBIC. We have explored some other tuning parameter selection techniques but have not found one that is significantly better.
Table 1.
Simulation scenario 1. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.3(0.9) | 4.8(1.2) | 4.5(1.0) | 6.4(1.5) | 6.3(1.3) | 6.7(1.3) |
| TP40 | 7.7(0.8) | 6.6(1.6) | 6.7(1.5) | 7.4(1.0) | 7.4(0.7) | 7.5(1.0) | |
| TP.EBIC | 7.3(0.9) | 5.0(2.0) | 5.2(1.9) | 5.8(2.0) | 6.0(2.0) | 6.6(1.7) | |
| FP.EBIC | 1.4(2.2) | 31.2(24.2) | 28.4(24.2) | 4.0(3.0) | 3.6(3.1) | 3.6(2.8) | |
| SSE.EBIC | 0.96(0.99) | 4.30(3.04) | 4.24(2.97) | 2.58(2.78) | 1.99(1.47) | 1.89(1.66) | |
| Interaction | TP20 | 5.1(1.6) | 2.2(1.9) | 2.3(1.7) | 4.2(2.0) | 4.2(2.0) | 4.6(2.0) |
| TP40 | 5.7(0.8) | 4.7(1.9) | 4.7(1.9) | 5.2(1.7) | 5.4(1.0) | 5.5(1.8) | |
| TP.EBIC | 5.1(1.6) | 2.0(2.4) | 1.9(2.5) | 3.4(2.5) | 3.5(2.5) | 4.2(2.2) | |
| FP.EBIC | 3.7(2.6) | 2.0(3.5) | 1.2(2.6) | 2.7(1.8) | 2.7(2.1) | 2.5(1.1) | |
| SSE.EBIC | 1.01(1.00) | 2.92(1.39) | 2.90(1.48) | 2.19(1.79) | 2.03(1.51) | 2.06(1.65) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.0(1.6) | 5.1(1.7) | 6.2(1.2) | 6.5(1.2) | 7.0(1.0) | |
| TP40 | 5.9(1.4) | 6.4(1.5) | 7.0(1.1) | 7.1(1.1) | 7.5(1.1) | ||
| TP.EBIC | 4.7(1.9) | 5.0(2.1) | 6.5(1.5) | 6.4(1.5) | 6.6(1.5) | ||
| FP.EBIC | 30.2(25.4) | 28.2(24.0) | 4.8(3.3) | 4.0(2.6) | 3.3(2.3) | ||
| SSE.EBIC | 4.60(3.06) | 4.18(3.35) | 1.73(1.34) | 1.65(1.24) | 1.71(1.31) | ||
| Interaction | TP20 | 2.5(2.1) | 2.7(2.3) | 3.7(2.2) | 4.0(2.1) | 4.4(1.5) | |
| TP40 | 3.9(2.2) | 4.2(2.1) | 5.5(0.9) | 5.5(0.9) | 6.0(1.4) | ||
| TP.EBIC | 2.0(2.0) | 2.5(2.5) | 3.9(2.3) | 3.9(2.3) | 4.4(2.4) | ||
| FP.EBIC | 1.6(2.1) | 1.7(2.1) | 2.6(2.8) | 2.7(2.5) | 2.9(2.7) | ||
| SSE.EBIC | 2.91(1.25) | 2.70(1.76) | 1.68(1.47) | 1.72(1.46) | 1.75(1.45) | ||
Table 2.
Simulation scenario 2. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.3(1.7) | 4.3(2.7) | 4.4(2.6) | 2.6(1.5) | 2.6(1.4) | 5.7(2.3) |
| TP40 | 7.5(1.5) | 5.9(2.3) | 5.9(2.4) | 3.5(1.7) | 3.2(1.7) | 6.6(2.2) | |
| TP.EBIC | 7.0(2.1) | 5.0(2.8) | 4.9(2.9) | 2.3(1.6) | 2.2(1.5) | 5.4(2.7) | |
| FP.EBIC | 2.7(3.5) | 15.9(19.8) | 15.0(19.9) | 21.1(13.1) | 25.0(14.7) | 4.9(3.9) | |
| SSE.EBIC | 3.38(13.62) | 9.10(14.55) | 8.77(13.95) | 11.80(12.81) | 13.40(11.46) | 5.06(9.30) | |
| Interaction | TP20 | 5.3(1.6) | 3.5(2.4) | 3.3(2.4) | 1.9(1.8) | 2.2(2.0) | 4.1(2.3) |
| TP40 | 5.3(1.6) | 3.5(2.6) | 3.6(2.6) | 2.2(2.0) | 2.4(2.2) | 4.8(2.3) | |
| TP.EBIC | 4.9(1.7) | 3.1(2.5) | 3.1(2.6) | 1.2(1.5) | 1.0(1.5) | 3.7(2.3) | |
| FP.EBIC | 2.5(2.0) | 2.2(2.5) | 2.1(2.4) | 3.0(3.8) | 2.0(2.9) | 2.2(2.7) | |
| SSE.EBIC | 0.87(1.10) | 2.34(1.98) | 2.25(2.02) | 5.26(3.55) | 5.03(3.50) | 2.88(2.29) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 4.1(2.6) | 4.2(2.7) | 2.8(1.8) | 2.8(1.8) | 5.8(2.1) | |
| TP40 | 5.9(2.3) | 5.1(2.3) | 3.4(1.9) | 3.4(1.9) | 6.7(2.1) | ||
| TP.EBIC | 5.1(2.7) | 5.1(2.9) | 2.5(1.6) | 2.4(1.7) | 5.4(2.6) | ||
| FP.EBIC | 12.5(17.9) | 18.0(22.1) | 16.1(13.3) | 17.3(11.1) | 5.7(6.2) | ||
| SSE.EBIC | 5.99(10.02) | 9.11(14.24) | 10.82(6.04) | 13.65(9.56) | 5.33(9.61) | ||
| Interaction | TP20 | 3.4(2.5) | 3.5(2.4) | 1.7(2.0) | 1.8(2.0) | 4.4(2.3) | |
| TP40 | 3.5(2.6) | 3.5(2.6) | 2.3(2.3) | 2.1(2.3) | 5.0(2.3) | ||
| TP.EBIC | 3.2(2.6) | 3.1(2.6) | 0.9(1.3) | 0.7(1.1) | 3.1(2.2) | ||
| FP.EBIC | 2.9(3.2) | 2.4(3.9) | 1.4(2.6) | 1.6(3.0) | 2.2(3.6) | ||
| SSE.EBIC | 2.48(2.24) | 2.25(1.93) | 4.38(2.47) | 5.06(4.04) | 2.65(2.07) | ||
In the second set of simulation, we evaluate whether the superiority of the proposed method depends on sample size, censoring rate, and signal level. The simulation settings are described in Table A.16 (Appendix), and the results are provided in Appendix. It can be seen that all methods can have better performance with a larger sample size, a lower censoring rate, and a higher signal level. Such results are as expected. Similar to under the previous simulation set, the proposed NWDA is observed to have superior or comparable performance.
In the last section, we describe an extension of the NWDA to accommodate high missing rates. In the third set of simulation, we evaluate its performance and compare with the alternatives. The simulation settings are similar to Scenarios 1 and 2 described in Table A.1. One difference is that there are two E variables with missing rate 50%. Beyond q = 5, we also consider a higher dimensional case with q = 10. The results are summarized in Table A.20. We see that CC and IPW have especially inferior performance as only a small number of completely observed samples are available. The proposed NWDA is again observed to have favorable performance. For example, under Scenario 2 with q = 10, the TP40 values for interactions are 1.2 (CC), 2.0 (IPW), 1.0 (BPCA), 1.8 (PCA-TSR), and 3.4 (proposed). For the estimation of main effects, the SSE.EBIC values are 16.84 (CC), 19.39 (IPW), 12.50 (BPCA), 16.44 (PCA-TSR), and 6.26 (proposed).
4 Data analysis
We analyze the TCGA (https://tcgadata.nci.nih.gov/tcga/) data on lung adenocarcinoma and cutaneous melanoma and search for important G-E interactions (and main G and E effects) associated with overall survival. The TCGA data have been recently collected and have a high quality. Although they have been analyzed in multiple studies, our analysis takes a different angle, emphasizes accommodating missingness in the E variables, and complements the literature. We analyze the processed level 3 data, which are downloaded from TCGA Provisional using the R package CGDS.
4.1 Lung adenocarcinoma (LUAD) data
In analysis, we focus on primary tumor samples of the Whites. Data records with missing overall survival time are removed. We consider four E variables: gender, age, AJCC tumor pathologic stage, and smoking pack years, all of which have been suggested as potentially associated with lung cancer prognosis (Westcott et al. 2015). Among them, age and gender have complete measurements, and AJCC tumor pathologic stage has a very low missing rate (about 1%). The analyzed data contains 388 subjects, among which 32% have missing measurements on smoking pack years. There are 144 deaths during follow-up, with survival times ranging from 0.13 to 238.11 months (median 21.39 months). For G variables, we consider mRNA gene expressions, which are collected using the IlluminaHiseq RNAseq V2 platform and have been lowess-normalized, log-transformed, and median-centered. Data are available on 18,893 Z-scores. As the number of relevant gene expressions is not expected to be large, to improve stability, we conduct a simple prescreening via marginal analysis and select the top 2,500 gene expressions for downstream analysis.
The analysis results using the proposed approach are presented in Table 3. All four E variables have negative coefficients, indicating that higher levels are associated with shorter survival, which is consistent with the literature (Westcott et al. 2015). Our analysis identifies 42 important main G effects and 30 G-E interactions. Most of the identified interactions are with smoking pack years, “re-confirming” the special importance of smoking in lung cancer prognosis. A few interactions with age and gender are also identified. Literature search suggests that the identified genes may have important implications. For example, gene ABHD11 has been suggested as a biomarker for lung carcinoma and exhibits a higher activity in the majority of malignant tissues. Gene NRBP1 is a conserved regulator of cell fate and plays an important role in tumor suppression. A low NRBP1 expression level is associated with a poorer prognosis of lung adenocarcinomas (Wilson 2012). Gene RAP1B is a key suppressor of neutrophil migration and lung inflammation, and a reduced RAP1B prenylation has been detected in lung cancer cell lines. A low or undetectable level of S100PBP has been found in lung squamous cell carcinoma compared with their normal counterparts. Published interaction analysis has also suggested that gene SH3RF1 interacts with smoking to contribute to lung cancer. Over expression of SLC15A2 (hPepT2) has been observed in pneumocytes, bronchial epithelium, and endothelium of the lung small arteries, and this gene has been suggested as a potential target for treatment development. Gene SPON2 encodes a secreted protein homologous to the Mindin/F-spondin family and has been observed to have low expressions in lung cancer cells relative to normal lung cells. Gene TPM2 exhibits an expression profile that is typical for carcinoma-associated fibroblasts, indicating a fundamental reprogramming of normal lung fibroblasts. The interaction between WDR46 and smoking has been suggested as influencing lung development of the young, which may contribute to lung cancer development later in life.
Table 3.
Analysis of lung adenocarcinoma data using NWDA: identified main effects and interactions.
| Main:G | Age | Gender | Stage | Smoking pack years | |
|---|---|---|---|---|---|
| Main:E | -0.012 | -0.076 | -0.063 | -0.041 | |
| ABHD11 | 0.052 | 0.013 | 0.018 | -0.003 | |
| ABI2 | -0.142 | -0.073 | |||
| ANK3 | -0.018 | ||||
| ANP32D | 0.034 | ||||
| APOA2 | 0.020 | -0.003 | |||
| BAIAP3 | 0.055 | -0.002 | 0.018 | -0.003 | |
| BCAR1 | 0.006 | -0.009 | -0.025 | -0.005 | |
| BORCS6 | -0.213 | ||||
| C2ORF50 | -0.009 | ||||
| C5ORF34 | -0.008 | 0.001 | |||
| CCDC170 | -0.017 | ||||
| CCDC173 | -0.033 | ||||
| CCDC30 | -0.007 | ||||
| CCDC63 | -0.117 | -0.015 | -0.002 | ||
| CMPK2 | -0.082 | ||||
| DCP1A | -0.042 | ||||
| FASTKD3 | 0.069 | -0.001 | -0.006 | 0.002 | |
| FKBP4 | -0.340 | ||||
| GFRAL | -0.025 | 0.003 | |||
| GRPEL1 | -0.069 | ||||
| IGSF22 | -0.115 | -0.066 | -0.008 | ||
| ISOC1 | -0.215 | 0.150 | -0.015 | ||
| LDLRAD3 | -0.057 | ||||
| LINC00112 | -0.133 | ||||
| MAPKAPK5 | -0.104 | ||||
| MCL1 | 0.046 | ||||
| NAV3 | -0.070 | ||||
| NRBP1 | 0.003 | ||||
| PRKCE | -0.021 | ||||
| PSMD9 | -0.007 | ||||
| RAP1B | -0.109 | 0.017 | |||
| ROPN1B | -0.161 | ||||
| S100PBP | -0.366 | -0.127 | 0.021 | ||
| SAFB | -0.040 | ||||
| SCARF2 | -0.081 | ||||
| SH3RF1 | -0.052 | -0.088 | |||
| SLC15A2 | -0.033 | ||||
| SPICE1 | 0.044 | ||||
| SPON2 | -0.025 | ||||
| TMEM63C | -0.015 | ||||
| TPM2 | -0.052 | -0.005 | -0.032 | 0.009 | |
| WDR46 | -0.131 | 0.043 |
Beyond the proposed approach, data is also analyzed using the four alternatives. Note that with real data, the approach Full is not feasible. The summary comparison results are provided in Table A.21 (Appendix). Detailed estimation results under the alternative approaches are available from the authors and omitted here. It is observed that different approaches identify significantly different sets of G-E interactions and main effects. To better comprehend their difference/similarity, we compute the RV-coefficients between the identified gene sets of two approaches. The RV-coefficient (Smilde et al., 2009) measures the common information of two matrices (data matrices of genes identified by two different approaches in our case), with a larger value indicating higher similarity. The results are shown in Figure A.1, where we observe that different sets of genes have moderate to small overlapping information. To provide an indirect support to the identification analysis, we conduct a resampling-based prediction evaluation (Huang and Ma, 2010), which has been extensively adopted in the literature. As the outcome is prognosis, the logrank statistic is adopted as the evaluation statistic, with a larger value suggesting better prediction. The prediction logrank statistic of the proposed approach is 5.60 (p-value 0.018), compared to 3.54 (CC), 3.60 (IPW), 3.37 (BPCA), and 3.91 (PCA-TSR). The superior prediction partly supports validity of the proposed approach. In the second evaluation, we examine stability and compute the observed occurrence index (OOI; Huang and Ma, 2010). With a resampling approach, the OOI quantifies the probability of a specific effect (interaction or main) being identified, with a larger value indicating higher stability. For the NWDA identified effects (both interactions and main), the average OOI is 0.48, compared to 0.21 (CC), 0.24 (IPW), 0.40 (BPCA), and 0.38 (PCA-TSR), suggesting better stability of the proposed approach.
4.2 Cutaneous melanoma (SKCM) data
We focus on metastatic samples of the Whites. In analysis, E variables include gender, age, AJCC tumor pathologic stage, Breslow thickness at diagnosis, and Clark level, all of which have been extensively examined in published studies. Among them, gender, age, and AJCC tumor pathologic stage have complete measurements. Among the 321 subjects, 29% have missing measurements for Breslow thickness and/or Clark level. 174 subjects died during followup, with survival times ranging from 0.33 to 369.65 months (median 53.15 months). The G variables are 18,934 gene expression levels. With simple preprocessing, 2,500 gene expressions are kept for downstream analysis.
The analysis results using the proposed approach are presented in Table 4. All five E variables have negative coefficients, which matches observations in the literature. The proposed approach identifies 44 main G effects and 30 G-E interactions. There are ten interactions with Breslow thickness, seven with Clark level, and thirteen with age, gender, and stage. Literature search suggests that the findings may have important implications. For example, the suppression of gene HMGCL has been shown to attenuate the proliferation and tumor growth potential of human melanoma cells expressing BRAF V600E. IFITM2 has been previously reported as deregulated in melanoma and involved in stem cells gene expression. Gene MYB has been suggested as playing an important role in the growth of some melanomas and also as a potential target for treatment development. Mutations in gene NF2 have been reported in a number of cancers including approximately 30% of melanomas. NUDT21 has been identified as a sex-specific genomic marker for cutaneous melanoma. FAM46A belongs to the FAM46 family which may play a critical role during cell differentiation and be involved in the pathogenesis of various cancers including skin cutaneous melanoma. SOCS3 immunoreactivity has been detected in cutaneous melanomas with certain Clark levels, which suggests an interaction. TPM2 has been found to be expressed in human epidermal melanocyte and consistently repressed in melanoma cell lines with complete methylation. Gene WDR34 has been previously suggested as a diagnostic marker. Analysis is also conducted using the four alternatives, and the summary comparison results are shown in Table A.21 (Appendix). The proposed approach has findings different from the alternatives. As in the previous subsection, we use the RV-coefficients to evaluate the similarity of findings. The results are shown in Figure A.1 in Appendix. It is observed that the degree of similarity is much higher. It is noted that different genes may have similar biological functions and correlated expressions. Thus seemingly quite different gene sets can contain similar information. Prediction evaluation is also conducted. The logrank statistic of the proposed approach is 6.96 (p-value 0.0083), compared to 4.52 (CC), 4.73 (IPW), 5.50 (BPCA), and 4.01 (PCA-TSR). The proposed approach again has the best prediction performance, which may suggest the superiority of identification. Stability is evaluated in the same way as in the previous subsection. The average OOI values of the proposed approach is 0.45, compared to 0.28 (CC), 0.29 (IPW), 0.38 (BPCA), and 0.37 (PCA-TSR), indicating the ability of the proposed method to identify more stable effects.
Table 4.
Analysis of cutaneous melanoma data using NWDA: identified main effects and interactions.
| Main:G | Age | Gender | Stage | Breslow thickness | Clark level | |
|---|---|---|---|---|---|---|
| Main:E | -0.171 | -0.085 | -0.044 | -0.063 | -0.282 | |
| CCDC90B | -0.111 | |||||
| CEP120 | -0.062 | |||||
| CLN6 | -0.026 | |||||
| CTSA | 0.004 | |||||
| DNAJC6 | 0.007 | |||||
| ELF1 | 0.029 | 0.054 | 0.098 | -0.028 | -0.012 | |
| ELP6 | -0.028 | |||||
| EPHX1 | -0.044 | |||||
| EVPLL | 0.049 | 0.014 | -0.012 | 0.007 | ||
| FAM46A | -0.061 | |||||
| FNDC8 | -0.053 | |||||
| FYTTD1 | -0.075 | |||||
| GAGE2A | -0.047 | |||||
| GNG2 | -0.011 | |||||
| GPATCH11 | -0.033 | |||||
| GSX1 | -0.092 | |||||
| HIPK3 | -0.043 | 0.112 | -0.011 | -0.020 | ||
| HMGCL | -0.053 | |||||
| HMX2 | -0.098 | |||||
| IFITM2 | -0.254 | |||||
| KIAA0319L | 0.095 | |||||
| MMS22L | -0.091 | 0.009 | 0.009 | 0.002 | ||
| MYB | -0.063 | |||||
| NF2 | 0.033 | |||||
| NPHP4 | -0.033 | |||||
| NUDT21 | -0.029 | -0.001 | -0.012 | 0.003 | -0.003 | |
| PHF23 | -0.044 | |||||
| POMGNT1 | 0.094 | 0.008 | ||||
| PRRT4 | -0.120 | |||||
| QSOX2 | 0.085 | |||||
| RAB5A | 0.009 | |||||
| RNF14 | -0.008 | |||||
| SENP6 | -0.075 | |||||
| SOCS3 | 0.014 | -0.001 | 0.002 | -0.008 | 0.004 | 0.002 |
| STMN3 | -0.027 | 0.009 | ||||
| SUCO | -0.080 | |||||
| TP53TG3B | -0.024 | 0.001 | ||||
| TPMT | -0.148 | 0.009 | ||||
| TPM2 | -0.070 | -0.001 | -0.002 | 0.004 | -0.003 | |
| TROVE2 | 0.110 | |||||
| USP46 | -0.007 | |||||
| USPL1 | -0.082 | |||||
| VEPH1 | -0.023 | |||||
| WDR34 | 0.088 |
4.3 Simulation based on TCGA data
In the previous simulations, the G and E measurements have been generated from parametric distributions. It is recognized that compared to what is practically observed, such settings may be overly simplified. To tackle this problem, we further conduct simulation based on the analyzed TCGA data. Specifically, we use the observed G and E measurements. To simulate the event times, complete measurements are needed. We first conduct a simple imputation of the missing E measurements using the knnimpute approach (Troyanskaya et al., 2001). Note that this step of imputation is for data generation, and there is no need for sophisticated methods. There are 15 main G effects and 10 G-E interactions, with their regression coefficients randomly generated from Uniform(1.2, 1.6). Two random error distributions are considered, namely N(0, 1) and N(0, 4). The event times are then computed from the AFT model. Censoring times are randomly generated and adjusted, so that the censoring rates are the same as observed (LUAD: 62.8% and SKCM: 45.8%). We then remove the imputed values which are missing in the original data and accommodate using the proposed and alternative methods. The results are provided in Table A.22. With a higher dimensionality of the G measurements, higher censoring rates, and complex correlation structures, this set of simulation is more challenging than the previous ones. However, the proposed method is still observed to have favorable performance. For example, for the simulation based on the LUAD data with random error distribution N(0, 1), the proposed method has TP20 equal to 4.0 for interaction identification, compared to 0.2(CC), 0.3(IPW), 3.1(BPCA), and 3.1(PCA-TSR). It also has competitive estimation performance. For the simulation based on the SKCM data with random error distribution N(0, 1), it has SSE.EBIC=17.34 for main effects, compared to 34.00(CC), 35.34(IPW), 20.32(BPCA), and 28.99(PCA-TSR). To better comprehend the difference/similarity of analysis results observed in the previous two subsections (presented in Table A.21 and Figure A.1), for one simulated replicate, we compute the overlaps of findings and the RV-coefficients in the same manner as in data analysis. The results are presented in Table A.23 and Figure A.3 in Appendix. The observed patterns are very similar to those in Table A.21 and Figure A.1. We have examined a few other replicates and drawn similar conclusions. The similar observations and superiority of the proposed method observed in this set of simulation provide a certain confidence to the data analysis results.
5 Discussion
G-E interaction analysis has been widely conducted. Complementing the literature, this study has been focused on accommodating missingness in E measurements, which is not uncommon in practice but has not been well studied. An effective statistical approach has been developed, which has a data augmentation component to accommodate missingness and a penalized selection/estimation component. The proposed approach is based on solid statistical principles and can be effectively realized. In simulation, it outperforms the benchmark CC, popular IPW, and state-of-the-art imputation approaches. Although not “intentionally designed”, the novel weighting scheme leads to a nice robustness property, which is not shared by the alternatives and well demonstrated in simulation. In data analysis, the proposed approach leads to different, biologically sensible findings. The superior prediction and stability performance provides an indirect support to the validity of the proposed approach. Overall, the proposed approach provides a practically useful way for accommodating missing E measurements in G-E interaction analysis.
This study can be potentially extended in multiple aspects. We have focused on data with a prognosis outcome. As briefly mentioned, data with a continuous outcome under a linear regression model can be viewed as a special case of our analysis (and so be directly tackled). With categorical outcomes under generalized linear models, modifications to the weights are needed. The other components of the proposed approach can be directly applied. An AFT model has been adopted for its lucid interpretation and low computational cost. With minor modifications, the proposed approach can be extended to other survival models (although with a higher computational cost). We have focused on the scenario with missingness in E variables. When missingness also happens to G variables and/or outcome, the proposed “nonparametric augmentation + weighting + penalized identification” strategy may still be applicable. However, modifications will be needed. With the proposed augmentation, it is assumed that if two subjects have X(o) and T values close, their X(m) values are also close. This assumption can be reasonable for many practical scenarios. However, to be prudent, in practical analysis, it may be of interest to consider and compare with alternative assumptions. A sparse group penalization technique is adopted for estimation and selection. As the proposed loss function is relatively “independent” of the estimation/selection technique, alternative techniques can also be adopted. In simulation, we have considered continuous G variables which mimic gene expression data later analyzed. In principle, the proposed approach can also be applied to categorical G data (for example SNPs). More extensive numerical studies and comparisons will be conducted in the future.
In this study, we have mostly focused on methodological development and implementation. Components of the proposed method have sound statistical basis. When covariates are low-dimensional (and hence penalization is not needed in estimation) and only main effects are considered, Creemers et al. (2012) shows that the nonparametric weight-based method can provide consistent parameter estimates. Under different contexts and with main effects only, Zhang et al. (2016) establishes that the sparse group MCP is estimation and selection consistent under the AFT model. It is thus reasonable to conjecture that the proposed approach may also have satisfactory statistical properties. However, it is expected that theoretical development can be very challenging. Quite a few recent high-dimensional studies with missing measurements have also focused on methodological and numerical development only (He and Belin, 2014; Zhao and Long, 2016). We postpone theoretical investigation to future research.
Acknowledgments
We thank the associate editor and two reviewers for careful review and insightful comments, which have led to a significant improvement of the manuscript. This study has been partly supported by NIH/NCI awards R21CA191383, R01CA204120, and P50CA121974, and NFSC awards 61402276.
Appendix
This file contains the GCD algorithm and additional numerical results.
The GCD algorithm With a fixed α̂, consider the objective function
| (A.1) |
For j = 1, …, p, the GCD algorithm optimizes the objective function with respect to bj while fixing the other parameters bl(l ≠ j) at their current estimates b̂l Specifically, consider the following simplified objective function
| (A.2) |
where Wj is the submatrix of W corresponding to bj, and . Without loss of generality, assume that each Wj has been orthogonalized such that , which can be achieved by the Cholesky decomposition. Then, the first order derivative of (A.2) is
| (A.3) |
where
and sign(·) is the sign function. By setting the first order derivative equal to zero, we have
| (A.4) |
where and
| (A.5) |
Let ujk be the kth element of uj and ĝ be the value of g(bj) where bj is fixed at the current estimate b̂j. The solution to equation (A.4) is
| (A.6) |
where . Based on (A.6), let υ̂j1 = bj1ĝ = uj1 and , j = 2, ⋯, q + 1. Then according to (A.5), we have
| (A.7) |
Solving the above equation, the final estimate of bj is
| (A.8) |
Figure A.1.
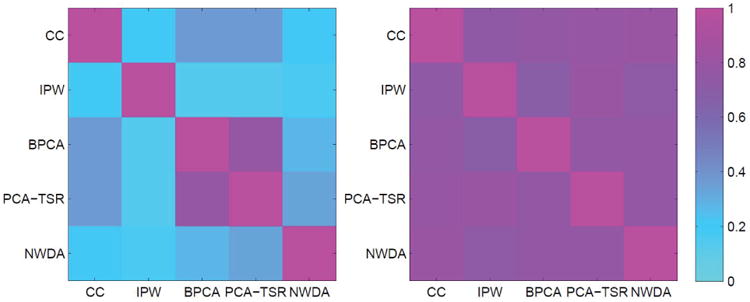
Data analysis: the modified RV-coefficients between different approaches. Left: LUAD; Right: SKCM.
Figure A.2.
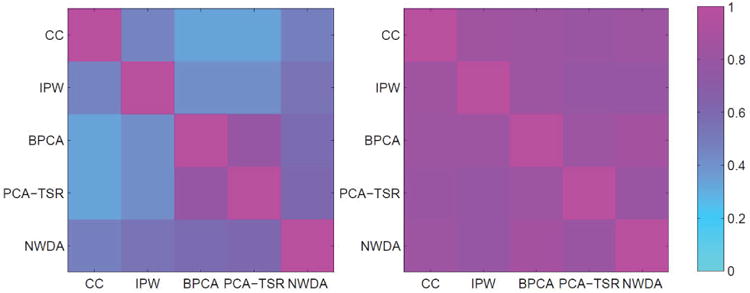
Analysis of one simulation replicate based on the LUAD (left) and SKCM (right) data: the modified RV-coefficients between different approaches.
Table A.1.
Summary of settings for the first set of simulation. Table: Table number of the results; Setting: overall setting; Distribution: distribution of E variables; Correlation: correlation structure of G variables.
| Scenario | Table | Setting | Distribution | Correlation |
|---|---|---|---|---|
| 1 | 1 | N1 | 5 continuous | AR |
| 2 | 2 | O1.1 | 5 continuous | AR |
| 3 | A.2 | O1.2 | 5 continuous | AR |
| 4 | A.3 | O2 | 5 continuous | AR |
| 5 | A.4 | N1 | 5 continuous | Band |
| 6 | A.5 | O1.1 | 5 continuous | Band |
| 7 | A.6 | O1.2 | 5 continuous | Band |
| 8 | A.7 | O2 | 5 continuous | Band |
| 9 | A.8 | N1 | 3 continuous + 2 categorical | AR |
| 10 | A.9 | O1.1 | 3 continuous + 2 categorical | AR |
| 11 | A.10 | O1.2 | 3 continuous + 2 categorical | AR |
| 12 | A.11 | O2 | 3 continuous + 2 categorical | AR |
| 13 | A.12 | N1 | 3 continuous + 2 categorical | Band |
| 14 | A.13 | O1.1 | 3 continuous + 2 categorical | Band |
| 15 | A.14 | O1.2 | 3 continuous + 2 categorical | Band |
| 16 | A.15 | O2 | 3 continuous + 2 categorical | Band |
Table A.2.
Simulation scenario 3. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 6.9(1.9) | 5.3(2.0) | 5.5(1.8) | 5.9(1.9) | 6.0(1.9) | 6.5(1.9) |
| TP40 | 7.2(1.6) | 6.2(1.7) | 6.3(1.8) | 6.4(1.6) | 6.6(1.6) | 7.2(1.5) | |
| TP.EBIC | 6.7(2.3) | 4.8(2.2) | 4.9(2.2) | 6.2(2.1) | 6.4(2.2) | 6.7(2.1) | |
| FP.EBIC | 2.5(8.4) | 12.1(18.5) | 18.6(22.5) | 1.8(2.3) | 1.7(2.5) | 1.8(9.0) | |
| SSE.EBIC | 2.77(10.42) | 6.10(8.03) | 8.07(9.84) | 1.71(1.47) | 1.59(1.54) | 1.53(3.06) | |
| Interaction | TP20 | 5.1(1.8) | 3.1(1.9) | 3.1(2.0) | 4.4(1.8) | 4.2(1.8) | 4.8(1.8) |
| TP40 | 5.2(1.8) | 4.1(2.1) | 4.1(2.1) | 5.0(1.6) | 5.0(1.6) | 5.2(1.8) | |
| TP.EBIC | 4.8(1.9) | 2.7(2.2) | 2.4(2.4) | 4.2(1.8) | 4.3(2.0) | 4.6(2.0) | |
| FP.EBIC | 3.7(2.1) | 3.0(2.3) | 2.3(2.0) | 3.8(1.9) | 4.2(2.3) | 3.5(1.9) | |
| SSE.EBIC | 1.54(2.16) | 2.91(1.69) | 3.03(1.69) | 2.27(2.42) | 2.18(2.75) | 2.24(1.71) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.3(2.1) | 5.6(2.0) | 6.1(1.8) | 6.0(1.9) | 6.7(2.0) | |
| TP40 | 6.2(1.9) | 6.3(1.7) | 6.7(1.7) | 6.8(1.6) | 7.1(1.6) | ||
| TP.EBIC | 4.9(2.3) | 5.3(2.3) | 5.7(2.2) | 5.7(2.1) | 6.3(2.5) | ||
| FP.EBIC | 13.3(17.9) | 11.2(16.0) | 4.6(6.7) | 4.1(7.8) | 3.9(6.8) | ||
| SSE.EBIC | 5.75(6.74) | 5.12(6.72) | 3.08(4.57) | 3.75(4.93) | 2.43(1.76) | ||
| Interaction | TP20 | 3.5(2.2) | 3.6(2.3) | 4.0(1.9) | 4.0(1.9) | 4.5(2.2) | |
| TP40 | 4.0(2.2) | 4.1(2.1) | 4.9(1.8) | 4.8(1.9) | 5.3(2.0) | ||
| TP.EBIC | 2.8(2.4) | 3.1(2.5) | 3.6(2.1) | 3.6(2.1) | 4.4(2.2) | ||
| FP.EBIC | 3.1(2.4) | 2.7(1.8) | 4.2(1.9) | 4.1(2.2) | 4.0(2.8) | ||
| SSE.EBIC | 2.98(2.29) | 2.60(2.08) | 3.27(3.92) | 2.89(2.19) | 2.65(2.19) | ||
Table A.3.
Simulation scenario 4. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 4.8(1.4) | 3.7(1.4) | 3.5(1.4) | 3.9(1.4) | 3.9(1.4) | 4.6(1.5) |
| TP40 | 6.8(1.6) | 4.5(1.5) | 4.5(1.4) | 4.7(1.4) | 4.4(1.4) | 6.5(1.3) | |
| TP.EBIC | 4.4(1.5) | 3.3(1.4) | 3.3(1.4) | 3.7(1.6) | 3.5(1.6) | 5.3(1.5) | |
| FP.EBIC | 6.5(4.7) | 28.4(17.7) | 36.1(20.1) | 9.2(4.7) | 9.2(4.1) | 7.6(3.7) | |
| SSE.EBIC | 5.87(4.62) | 10.25(6.93) | 10.64(5.98) | 6.06(4.74) | 5.75(4.08) | 4.63(1.23) | |
| Interaction | TP20 | 3.3(1.8) | 2.0(2.1) | 2.3(1.8) | 2.2(1.8) | 2.0(1.7) | 3.9(1.6) |
| TP40 | 4.7(1.7) | 3.1(2.2) | 3.3(1.9) | 3.1(2.0) | 3.3(2.1) | 4.3(1.9) | |
| TP.EBIC | 2.9(1.4) | 0.6(1.2) | 0.4(1.2) | 0.8(1.3) | 0.7(1.2) | 2.4(1.0) | |
| FP.EBIC | 0.8(1.9) | 0.5(1.7) | 0.1(0.4) | 0.7(1.5) | 0.3(1.1) | 1.2(2.5) | |
| SSE.EBIC | 2.87(1.29) | 4.07(0.94) | 3.93(0.73) | 3.90(0.76) | 3.63(0.66) | 2.67(0.77) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 3.3(1.2) | 3.3(1.4) | 3.7(1.4) | 3.7(1.3) | 4.8(1.3) | |
| TP40 | 4.0(1.2) | 4.0(1.4) | 4.6(1.2) | 4.3(1.2) | 6.3(1.4) | ||
| TP.EBIC | 3.2(1.1) | 3.3(1.2) | 3.3(1.4) | 3.7(1.4) | 5.3(1.7) | ||
| FP.EBIC | 23.7(22.8) | 34.1(19.0) | 9.1(4.7) | 10.3(5.3) | 7.5(2.1) | ||
| SSE.EBIC | 7.90(5.39) | 10.07(4.05) | 5.23(4.32) | 6.98(6.06) | 3.45(1.17) | ||
| Interaction | TP20 | 1.9(1.8) | 2.3(1.8) | 1.7(1.4) | 1.8(1.5) | 3.6(1.7) | |
| TP40 | 3.3(2.0) | 3.6(1.9) | 2.7(2.3) | 3.0(2.2) | 4.0(1.7) | ||
| TP.EBIC | 0.7(1.2) | 0.7(1.2) | 0.4(1.3) | 0.6(1.4) | 2.3(0.9) | ||
| FP.EBIC | 0.7(1.4) | 0.2(0.9) | 0.6(1.7) | 0.3(1.2) | 1.0(2.6) | ||
| SSE.EBIC | 3.81(0.62) | 3.83(0.62) | 3.83(0.62) | 3.93(0.67) | 2.14(1.51) | ||
Table A.4.
Simulation scenario 5. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.0(1.1) | 4.8(2.0) | 4.5(2.1) | 6.0(1.6) | 6.0(1.6) | 6.5(1.7) |
| TP40 | 7.6(0.9) | 6.0(1.8) | 6.0(1.8) | 7.2(1.2) | 7.1(1.4) | 7.4(1.8) | |
| TP.EBIC | 7.2(1.6) | 4.5(2.4) | 4.8(2.6) | 5.8(1.9) | 6.2(1.7) | 6.6(2.4) | |
| FP.EBIC | 3.5(3.2) | 29.8(23.1) | 30.1(22.9) | 5.7(4.1) | 5.3(3.9) | 5.0(3.1) | |
| SSE.EBIC | 1.03(0.94) | 4.73(3.01) | 4.19(2.74) | 2.50(1.92) | 2.43(2.18) | 2.70(1.66) | |
| Interaction | TP20 | 4.8(1.8) | 2.8(2.2) | 2.8(2.2) | 4.0(1.8) | 4.0(1.8) | 4.5(1.9) |
| TP40 | 5.6(0.8) | 3.9(2.2) | 4.0(2.2) | 5.0(1.3) | 4.7(1.7) | 5.6(1.7) | |
| TP.EBIC | 5.1(1.6) | 1.7(2.3) | 2.3(2.6) | 3.6(2.1) | 3.8(2.1) | 4.1(2.6) | |
| FP.EBIC | 3.5(1.9) | 1.1(2.2) | 1.6(2.3) | 1.9(2.1) | 1.9(2.0) | 1.7(2.0) | |
| SSE.EBIC | 0.87(0.98) | 3.10(1.64) | 2.72(1.76) | 1.91(1.30) | 1.82(1.29) | 2.04(1.56) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 4.4(1.8) | 4.6(1.7) | 5.7(1.7) | 5.9(1.6) | 6.3(1.4) | |
| TP40 | 5.5(1.4) | 5.5(1.5) | 6.8(1.6) | 6.8(1.6) | 7.1(1.5) | ||
| TP.EBIC | 4.4(1.5) | 4.3(1.3) | 5.8(2.2) | 5.8(2.2) | 6.1(1.9) | ||
| FP.EBIC | 30.4(23.5) | 35.3(20.3) | 5.4(3.9) | 6.5(8.3) | 6.4(3.1) | ||
| SSE.EBIC | 5.74(3.05) | 5.85(2.43) | 2.01(1.60) | 2.15(1.64) | 2.19(1.94) | ||
| Interaction | TP20 | 2.3(1.8) | 2.5(1.8) | 3.8(1.7) | 4.0(1.8) | 3.9(1.8) | |
| TP40 | 3.3(1.8) | 3.3(2.1) | 5.2(1.0) | 5.3(0.9) | 5.8(1.2) | ||
| TP.EBIC | 1.2(1.9) | 0.8(1.7) | 3.8(2.4) | 3.6(2.5) | 3.8(2.0) | ||
| FP.EBIC | 1.1(1.8) | 0.4(1.0) | 3.9(3.3) | 3.0(2.4) | 2.1(2.5) | ||
| SSE.EBIC | 3.18(1.08) | 3.28(1.01) | 1.70(1.40) | 1.69(1.40) | 1.70(1.20) | ||
Table A.5.
Simulation scenario 6. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.2(1.7) | 4.0(2.7) | 4.4(2.6) | 1.9(1.1) | 1.9(1.1) | 5.2(2.3) |
| TP40 | 7.5(1.5) | 5.5(2.5) | 5.6(2.3) | 2.6(1.4) | 2.8(1.4) | 6.1(2.1) | |
| TP.EBIC | 7.1(1.9) | 4.6(2.9) | 4.4(2.9) | 1.6(1.3) | 1.6(1.2) | 5.8(2.4) | |
| FP.EBIC | 5.0(3.3) | 13.5(19.3) | 14.6(20.7) | 20.2(14.5) | 21.5(15.6) | 5.0(5.1) | |
| SSE.EBIC | 4.92(17.69) | 9.32(17.79) | 7.99(10.10) | 14.85(11.02) | 16.90(11.52) | 5.32(9.79) | |
| Interaction | TP20 | 5.1(1.6) | 3.3(2.3) | 3.0(2.4) | 2.0(2.0) | 2.3(2.0) | 4.4(2.0) |
| TP40 | 5.4(1.5) | 3.8(2.3) | 3.6(2.5) | 2.3(2.0) | 2.3(2.0) | 4.9(2.2) | |
| TP.EBIC | 5.0(1.7) | 2.9(2.5) | 2.7(2.5) | 0.8(1.1) | 0.8(1.3) | 4.2(2.1) | |
| FP.EBIC | 2.7(2.4) | 2.5(2.3) | 2.4(2.4) | 2.0(2.5) | 2.1(2.9) | 2.0(3.2) | |
| SSE.EBIC | 0.87(1.36) | 3.14(3.24) | 3.35(3.28) | 4.15(1.07) | 4.32(1.80) | 2.90(2.24) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 4.0(2.7) | 4.7(2.6) | 2.1(1.4) | 2.0(1.3) | 5.7(2.3) | |
| TP40 | 5.1(2.5) | 5.7(2.5) | 2.8(1.4) | 2.9(1.5) | 6.5(2.2) | ||
| TP.EBIC | 4.8(2.9) | 4.6(2.7) | 2.0(1.3) | 1.9(1.3) | 5.3(2.5) | ||
| FP.EBIC | 14.1(17.9) | 20.5(23.5) | 20.1(15.9) | 22.8(13.0) | 4.1(3.4) | ||
| SSE.EBIC | 6.61(7.95) | 11.93(18.58) | 16.41(14.32) | 17.55(13.67) | 3.54(1.90) | ||
| Interaction | TP20 | 3.4(2.4) | 3.4(2.4) | 2.0(2.0) | 2.0(1.9) | 4.0(2.3) | |
| TP40 | 4.0(2.3) | 3.9(2.5) | 2.5(2.1) | 2.4(2.0) | 4.6(2.3) | ||
| TP.EBIC | 3.0(2.4) | 2.6(2.5) | 1.1(1.5) | 1.0(1.5) | 3.5(2.1) | ||
| FP.EBIC | 2.2(2.4) | 1.7(2.4) | 2.5(3.3) | 2.2(3.1) | 2.7(2.8) | ||
| SSE.EBIC | 2.96(2.64) | 2.69(2.04) | 4.63(1.95) | 4.38(1.77) | 2.60(3.02) | ||
Table A.6.
Simulation scenario 7. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 6.8(1.6) | 5.3(2.0) | 5.4(2.1) | 6.1(1.6) | 6.2(1.5) | 6.7(1.9) |
| TP40 | 7.1(1.3) | 6.1(1.9) | 6.2(1.9) | 6.5(1.5) | 6.7(1.5) | 7.1(1.6) | |
| TP.EBIC | 6.4(1.9) | 5.0(2.5) | 4.8(2.5) | 6.1(2.0) | 6.1(2.0) | 6.7(2.3) | |
| FP.EBIC | 1.5(2.0) | 10.3(17.4) | 11.1(18.7) | 2.0(2.0) | 1.8(2.0) | 1.7(1.2) | |
| SSE.EBIC | 1.55(1.28) | 4.56(5.76) | 4.39(4.74) | 1.72(1.30) | 1.77(1.30) | 1.18(1.97) | |
| Interaction | TP20 | 5.1(1.5) | 3.5(2.1) | 3.5(2.3) | 4.7(1.6) | 4.7(1.5) | 5.0(2.0) |
| TP40 | 5.2(1.5) | 4.3(2.2) | 4.4(2.2) | 5.0(1.5) | 5.1(1.4) | 5.2(1.8) | |
| TP.EBIC | 4.6(1.8) | 3.2(2.5) | 3.0(2.6) | 4.2(1.9) | 4.3(1.7) | 4.6(2.3) | |
| FP.EBIC | 3.9(1.4) | 3.4(2.5) | 3.0(2.2) | 3.9(1.7) | 3.8(1.4) | 3.3(1.6) | |
| SSE.EBIC | 1.82(2.21) | 2.86(2.47) | 2.90(2.25) | 2.29(2.13) | 2.10(1.80) | 2.06(1.97) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.5(2.1) | 5.5(2.0) | 5.9(1.7) | 6.0(1.7) | 6.6(1.9) | |
| TP40 | 6.0(2.0) | 6.1(2.0) | 6.6(1.6) | 6.7(1.6) | 7.1(1.7) | ||
| TP.EBIC | 5.2(2.4) | 5.2(2.6) | 5.3(2.0) | 5.4(2.0) | 6.2(2.5) | ||
| FP.EBIC | 7.1(12.7) | 10.7(18.2) | 2.2(2.4) | 1.8(1.9) | 2.4(2.9) | ||
| SSE.EBIC | 3.48(4.81) | 4.88(7.63) | 2.43(1.40) | 2.35(1.29) | 2.41(1.64) | ||
| Interaction | TP20 | 4.1(2.3) | 4.1(2.2) | 4.4(1.6) | 4.5(1.6) | 4.9(2.2) | |
| TP40 | 4.4(2.2) | 4.4(2.2) | 5.0(1.6) | 5.0(1.6) | 5.3(2.3) | ||
| TP.EBIC | 3.4(2.4) | 3.4(2.5) | 3.8(1.8) | 3.7(1.8) | 4.5(2.3) | ||
| FP.EBIC | 3.2(1.5) | 3.3(2.1) | 3.4(0.9) | 3.6(1.3) | 3.0(0.1) | ||
| SSE.EBIC | 2.69(2.34) | 2.70(2.47) | 2.88(2.60) | 2.84(2.48) | 2.40(2.12) | ||
Table A.7.
Simulation scenario 8. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 4.7(1.3) | 3.3(1.3) | 3.4(1.3) | 3.7(1.2) | 3.7(1.2) | 4.5(1.1) |
| TP40 | 6.9(1.4) | 4.0(1.4) | 4.1(1.3) | 4.7(1.4) | 4.7(1.4) | 6.5(1.0) | |
| TP.EBIC | 5.2(1.3) | 2.9(1.6) | 3.0(1.3) | 2.9(1.4) | 2.8(1.4) | 4.8(1.5) | |
| FP.EBIC | 6.9(6.7) | 29.0(20.6) | 37.5(19.8) | 7.6(6.9) | 8.0(7.1) | 6.7(5.0) | |
| SSE.EBIC | 4.43(3.58) | 9.21(4.89) | 10.62(4.69) | 6.10(3.46) | 6.15(4.57) | 4.37(1.04) | |
| Interaction | TP20 | 3.33(1.5) | 2.3(1.6) | 2.6(1.7) | 2.7(1.4) | 2.8(1.5) | 3.5(1.5) |
| TP40 | 4.4(1.8) | 3.2(1.6) | 3.3(1.6) | 3.5(1.7) | 3.6(1.7) | 4.4(1.8) | |
| TP.EBIC | 2.3(1.4) | 0.7(1.2) | 0.9(1.4) | 1.4(1.5) | 1.2(1.6) | 2.1(1.5) | |
| FP.EBIC | 2.5(3.0) | 0.8(2.2) | 0.8(1.7) | 2.0(2.7) | 3.1(2.9) | 2.5(3.5) | |
| SSE.EBIC | 2.56(1.21) | 3.85(1.38) | 3.70(1.04) | 3.72(1.34) | 3.63(0.99) | 2.98(1.97) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 3.3(1.3) | 3.3(1.4) | 3.5(1.2) | 3.7(1.3) | 4.4(1.2) | |
| TP40 | 4.3(1.5) | 4.5(1.3) | 4.7(1.4) | 4.7(1.3) | 6.5(1.3) | ||
| TP.EBIC | 2.8(1.5) | 3.0(1.4) | 2.9(1.5) | 3.0(1.3) | 5.8(1.6) | ||
| FP.EBIC | 29.4(19.1) | 31.3(21.3) | 10.1(6.5) | 11.4(7.7) | 7.7(6.2) | ||
| SSE.EBIC | 9.84(5.51) | 9.87(5.59) | 8.46(5.59) | 7.25(5.31) | 4.68(1.56) | ||
| Interaction | TP20 | 2.3(1.5) | 2.5(1.6) | 2.7(1.0) | 2.5(1.3) | 3.9(1.4) | |
| TP40 | 3.0(1.8) | 3.0(1.8) | 3.4(1.8) | 3.4(1.9) | 4.1(1.9) | ||
| TP.EBIC | 0.8(1.4) | 1.0(1.5) | 0.8(1.3) | 0.9(1.4) | 2.6(1.2) | ||
| FP.EBIC | 0.7(1.8) | 0.4(1.3) | 1.9(3.2) | 1.6(2.9) | 1.5(2.9) | ||
| SSE.EBIC | 3.64(0.98) | 3.37(0.87) | 4.31(2.06) | 3.96(1.60) | 2.69(0.85) | ||
Table A.8.
Simulation scenario 9. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.4(1.1) | 5.9(1.8) | 5.8(2.0) | 7.0(1.2) | 7.0(1.1) | 7.4(2.0) |
| TP40 | 7.7(0.7) | 6.8(1.7) | 6.9(1.3) | 7.6(0.9) | 7.7(0.7) | 7.7(0.9) | |
| TP.EBIC | 7.5(1.0) | 6.1(2.1) | 6.3(1.7) | 7.3(1.1) | 7.3(1.1) | 7.4(1.7) | |
| FP.EBIC | 2.2(2.3) | 26.3(21.8) | 28.9(23.9) | 6.3(5.2) | 6.5(5.6) | 5.3(3.8) | |
| SSE.EBIC | 1.10(1.03) | 3.32(2.14) | 3.52(2.26) | 1.47(1.11) | 1.35(1.09) | 1.59(1.23) | |
| Interaction | TP20 | 5.0(1.4) | 2.9(2.1) | 3.3(2.2) | 4.7(1.8) | 4.8(1.5) | 4.9(2.3) |
| TP40 | 5.7(0.7) | 4.3(1.6) | 4.3(1.8) | 5.8(0.6) | 5.8(0.5) | 6.0(1.0) | |
| TP.EBIC | 4.7(1.8) | 2.0(2.2) | 1.9(2.2) | 4.2(2.0) | 4.3(2.1) | 4.9(2.6) | |
| FP.EBIC | 3.5(2.1) | 1.0(1.6) | 0.9(2.0) | 2.9(2.9) | 2.9(2.8) | 2.4(2.8) | |
| SSE.EBIC | 1.64(0.97) | 3.08(1.17) | 3.16(1.09) | 1.97(1.28) | 1.94(1.21) | 2.11(1.42) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.7(1.8) | 5.8(1.7) | 7.1(1.2) | 7.0(1.2) | 7.4(1.5) | |
| TP40 | 6.9(1.3) | 6.8(1.1) | 7.5(0.9) | 7.5(0.8) | 7.7(0.7) | ||
| TP.EBIC | 6.0(1.7) | 6.1(1.8) | 7.0(1.2) | 7.2(1.3) | 7.4(0.9) | ||
| FP.EBIC | 25.3(23.5) | 29.6(24.0) | 3.4(4.9) | 3.6(3.1) | 3.1(3.0) | ||
| SSE.EBIC | 3.5(2.4) | 3.4(2.1) | 1.7(0.9) | 1.4(0.9) | 1.3(0.9) | ||
| Interaction | TP20 | 3.2(1.8) | 3.0(1.9) | 4.1(2.1) | 4.3(2.2) | 4.7(1.8) | |
| TP40 | 4.3(2.1) | 4.5(1.9) | 5.8(0.5) | 5.8(0.5) | 6.0(0.9) | ||
| TP.EBIC | 1.6(2.0) | 2.0(2.2) | 3.3(2.3) | 3.6(2.3) | 4.6(2.0) | ||
| FP.EBIC | 1.0(1.7) | 1.4(2.1) | 2.0(2.6) | 2.9(3.1) | 2.9(2.3) | ||
| SSE.EBIC | 3.07(1.17) | 3.08(1.39) | 2.65(1.25) | 2.37(1.33) | 1.92(1.26) | ||
Table A.9.
Simulation scenario 10. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.3(1.5) | 5.9(2.2) | 6.0(1.8) | 3.4(2.0) | 3.4(2.1) | 6.7(1.8) |
| TP40 | 7.4(1.3) | 6.3(2.2) | 6.4(1.8) | 3.5(1.9) | 3.5(1.9) | 7.0(1.7) | |
| TP.EBIC | 7.2(1.5) | 5.9(2.3) | 6.1(2.4) | 2.7(2.0) | 2.7(1.9) | 6.9(2.1) | |
| FP.EBIC | 3.3(8.8) | 14.8(19.9) | 12.9(20.5) | 22.7(14.9) | 29.8(16.9) | 3.4(2.9) | |
| SSE.EBIC | 2.20(4.83) | 7.14(12.19) | 7.60(15.46) | 11.98(16.94) | 13.99(16.38) | 3.13(2.39) | |
| Interaction | TP20 | 4.7(1.6) | 2.9(2.2) | 3.3(2.1) | 2.2(1.8) | 2.3(1.8) | 3.4(1.6) |
| TP40 | 5.1(1.8) | 3.5(2.2) | 3.9(2.2) | 2.8(2.1) | 2.8(2.0) | 4.2(1.7) | |
| TP.EBIC | 4.2(1.9) | 2.2(1.9) | 2.9(2.0) | 1.3(1.4) | 1.4(1.5) | 2.2(1.5) | |
| FP.EBIC | 2.5(1.8) | 2.0(2.6) | 2.1(2.3) | 1.1(1.8) | 1.3(2.0) | 1.8(2.5) | |
| SSE.EBIC | 1.76(1.39) | 3.55(2.99) | 2.85(2.49) | 6.39(6.75) | 5.83(5.95) | 4.32(6.10) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 6.0(2.2) | 6.0(2.0) | 3.2(2.0) | 3.4(2.0) | 6.9(1.9) | |
| TP40 | 6.1(2.0) | 6.1(2.0) | 3.7(1.8) | 3.7(1.9) | 7.0(1.9) | ||
| TP.EBIC | 5.2(2.4) | 5.4(2.4) | 2.7(1.8) | 2.7(1.9) | 6.2(2.0) | ||
| FP.EBIC | 11.8(17.6) | 12.0(17.9) | 16.4(13.6) | 16.5(15.0) | 4.6(3.6) | ||
| SSE.EBIC | 7.76(14.65) | 7.25(14.46) | 11.71(13.23) | 14.53(15.36) | 3.16(2.33) | ||
| Interaction | TP20 | 3.0(2.1) | 3.5(2.2) | 2.0(1.6) | 2.0(1.6) | 4.2(1.8) | |
| TP40 | 3.8(2.2) | 3.9(2.0) | 2.5(2.0) | 2.5(1.9) | 4.9(1.9) | ||
| TP.EBIC | 2.6(2.0) | 2.5(1.8) | 1.0(1.4) | 1.1(1.5) | 3.0(1.7) | ||
| FP.EBIC | 2.4(3.1) | 1.8(1.9) | 0.7(1.7) | 1.0(1.9) | 1.2(1.7) | ||
| SSE.EBIC | 3.01(1.72) | 3.04(1.65) | 4.99(5.43) | 4.81(3.14) | 3.00(5.11) | ||
Table A.10.
Simulation scenario 11. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.4(1.0) | 6.2(1.9) | 6.4(1.9) | 6.7(1.1) | 6.8(1.1) | 7.3(1.8) |
| TP40 | 7.6(0.8) | 6.8(1.6) | 6.9(1.6) | 7.0(0.9) | 7.0(0.9) | 7.3(1.3) | |
| TP.EBIC | 7.3(1.1) | 6.1(2.1) | 6.2(2.0) | 6.8(1.5) | 6.7(1.5) | 7.2(1.8) | |
| FP.EBIC | 2.3(2.9) | 10.2(16.9) | 10.4(17.4) | 2.6(1.4) | 2.7(1.5) | 2.6(2.2) | |
| SSE.EBIC | 1.24(1.48) | 4.24(5.42) | 3.73(3.84) | 1.91(1.54) | 1.96(1.56) | 1.32(1.15) | |
| Interaction | TP20 | 4.8(1.2) | 3.5(1.6) | 3.5(1.6) | 4.0(1.6) | 4.0(1.5) | 4.6(1.5) |
| TP40 | 5.3(1.1) | 4.1(1.4) | 4.2(1.4) | 5.0(1.4) | 5.1(1.4) | 5.2(1.4) | |
| TP.EBIC | 3.9(1.7) | 2.9(1.9) | 2.9(1.8) | 3.5(1.9) | 3.6(1.9) | 3.6(1.9) | |
| FP.EBIC | 3.4(0.8) | 3.2(1.5) | 3.3(1.6) | 3.6(1.3) | 3.5(1.1) | 3.1(1.9) | |
| SSE.EBIC | 3.10(2.30) | 4.99(7.43) | 4.85(6.11) | 4.21(5.70) | 4.11(5.76) | 3.39(6.30) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 6.5(1.8) | 6.3(2.0) | 6.6(1.2) | 6.7(1.3) | 7.2(1.7) | |
| TP40 | 6.9(1.7) | 7.0(1.7) | 7.5(1.0) | 7.5(1.1) | 7.5(1.5) | ||
| TP.EBIC | 6.1(2.4) | 6.4(2.0) | 7.1(1.1) | 7.0(1.4) | 7.2(1.7) | ||
| FP.EBIC | 8.4(16.2) | 10.1(15.8) | 2.2(1.9) | 1.7(1.5) | 1.6(1.5) | ||
| SSE.EBIC | 3.37(5.42) | 4.59(7.27) | 1.85(1.46) | 1.92(1.97) | 1.88(1.89) | ||
| Interaction | TP20 | 4.2(1.7) | 4.3(1.7) | 4.6(1.4) | 4.7(1.3) | 4.9(1.5) | |
| TP40 | 4.93(1.6) | 4.8(1.7) | 5.4(1.2) | 5.4(1.1) | 5.5(1.4) | ||
| TP.EBIC | 3.3(1.8) | 3.3(2.0) | 3.6(1.9) | 3.6(1.8) | 4.3(1.7) | ||
| FP.EBIC | 3.5(1.4) | 2.9(1.2) | 3.3(0.8) | 3.2(0.6) | 3.7(1.8) | ||
| SSE.EBIC | 3.66(3.34) | 3.30(2.13) | 4.52(3.16) | 3.75(3.31) | 2.75(2.29) | ||
Table A.11.
Simulation scenario 12. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 5.7(1.4) | 3.8(1.1) | 4.1(1.2) | 4.8(1.2) | 4.8(1.2) | 5.7(1.4) |
| TP40 | 6.5(1.4) | 4.8(1.2) | 4.8(1.1) | 5.5(1.4) | 5.6(1.3) | 6.8(1.4) | |
| TP.EBIC | 6.9(1.1) | 3.9(1.6) | 4.6(1.8) | 4.8(1.2) | 5.0(1.2) | 6.3(1.5) | |
| FP.EBIC | 4.2(4.1) | 25.1(21.6) | 27.1(19.0) | 6.3(6.8) | 6.1(6.9) | 4.0(5.9) | |
| SSE.EBIC | 4.30(2.11) | 8.06(3.99) | 8.55(4.78) | 6.78(5.15) | 6.14(4.07) | 4.47(2.25) | |
| Interaction | TP20 | 4.4(1.7) | 3.7(1.4) | 3.5(1.2) | 3.1(1.5) | 3.1(1.5) | 4.5(1.7) |
| TP40 | 5.6(1.5) | 3.5(1.8) | 3.9(1.4) | 4.4(1.3) | 4.3(1.3) | 5.6(1.5) | |
| TP.EBIC | 2.8(1.0) | 0.6(0.9) | 0.7(1.0) | 0.8(1.1) | 1.0(1.4) | 2.7(1.1) | |
| FP.EBIC | 0.8(1.7) | 0.9(2.2) | 0.6(1.5) | 0.4(1.2) | 0.6(1.3) | 0.6(1.6) | |
| SSE.EBIC | 3.52(1.91) | 4.86(2.88) | 4.78(2.94) | 4.47(1.71) | 4.37(1.77) | 3.37(2.07) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 4.1(1.3) | 3.7(1.2) | 4.6(1.5) | 4.6(1.5) | 5.6(1.4) | |
| TP40 | 4.7(1.4) | 4.6(1.4) | 5.3(1.2) | 5.5(1.2) | 6.2(1.5) | ||
| TP.EBIC | 3.6(1.4) | 4.2(1.5) | 4.9(1.3) | 4.7(1.3) | 6.8(1.6) | ||
| FP.EBIC | 23.5(20.5) | 34.7(19.3) | 7.5(5.7) | 8.2(6.5) | 5.8(3.0) | ||
| SSE.EBIC | 7.35(3.24) | 10.41(6.04) | 6.69(2.93) | 5.03(2.77) | 4.06(1.05) | ||
| Interaction | TP20 | 2.94(2.0) | 3.3(1.8) | 3.3(1.9) | 3.5(1.7) | 4.0(1.8) | |
| TP40 | 3.6(2.0) | 4.1(1.7) | 4.2(1.5) | 4.3(1.1) | 5.8(1.5) | ||
| TP.EBIC | 1.0(1.3) | 0.7(1.1) | 1.2(1.7) | 1.0(1.3) | 2.0(1.3) | ||
| FP.EBIC | 1.8(2.7) | 0.8(2.4) | 1.3(2.4) | 1.1(2.3) | 1.8(3.2) | ||
| SSE.EBIC | 5.89(4.10) | 6.06(6.40) | 4.10(1.14) | 4.17(0.98) | 3.41(3.73) | ||
Table A.12.
Simulation scenario 13. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.2(0.9) | 4.8(2.1) | 5.0(1.9) | 6.1(1.9) | 6.1(1.8) | 6.6(1.5) |
| TP40 | 7.5(0.7) | 6.0(1.5) | 5.8(1.3) | 7.3(0.9) | 7.2(0.9) | 7.4(1.1) | |
| TP.EBIC | 7.2(1.0) | 5.3(2.0) | 5.4(1.9) | 5.8(1.7) | 5.8(1.6) | 6.0(2.3) | |
| FP.EBIC | 3.9(3.0) | 28.0(23.6) | 32.8(23.2) | 3.6(2.7) | 5.2(8.6) | 3.5(3.3) | |
| SSE.EBIC | 1.28(0.83) | 3.65(2.23) | 4.00(2.41) | 2.30(1.08) | 2.53(1.44) | 2.42(1.34) | |
| Interaction | TP20 | 4.5(1.2) | 3.5(1.9) | 3.1(2.1) | 4.2(1.2) | 4.3(1.2) | 4.9(1.8) |
| TP40 | 5.6(0.6) | 4.5(1.7) | 4.3(2.0) | 5.5(0.8) | 5.5(0.7) | 5.9(1.2) | |
| TP.EBIC | 4.0(1.8) | 1.3(2.1) | 1.3(1.8) | 2.8(1.8) | 2.7(1.8) | 3.3(1.9) | |
| FP.EBIC | 2.4(1.9) | 0.3(0.9) | 0.8(2.1) | 1.6(2.0) | 1.3(1.8) | 1.5(2.8) | |
| SSE.EBIC | 1.89(0.89) | 3.22(1.05) | 3.11(0.96) | 2.97(1.00) | 3.03(0.98) | 2.80(1.19) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.3(2.2) | 5.5(2.0) | 6.4(1.6) | 6.5(1.6) | 6.8(1.5) | |
| TP40 | 6.4(1.6) | 6.3(1.8) | 7.1(1.0) | 7.2(1.0) | 7.4(0.8) | ||
| TP.EBIC | 5.4(2.0) | 5.5(1.7) | 6.3(1.3) | 6.2(1.3) | 6.8(1.8) | ||
| FP.EBIC | 24.4(21.9) | 22.9(22.2) | 4.6(3.5) | 4.8(3.2) | 4.4(3.3) | ||
| SSE.EBIC | 3.74(2.47) | 3.43(2.36) | 2.02(0.97) | 2.09(0.99) | 2.00(1.44) | ||
| Interaction | TP20 | 3.5(1.5) | 3.6(1.6) | 4.0(1.3) | 3.9(1.3) | 4.0(1.4) | |
| TP40 | 4.6(1.4) | 4.7(1.2) | 5.3(0.8) | 5.5(0.7) | 5.7(1.1) | ||
| TP.EBIC | 1.8(1.8) | 2.0(2.0) | 2.5(1.8) | 2.4(1.8) | 3.4(2.1) | ||
| FP.EBIC | 1.6(2.0) | 1.1(1.7) | 1.3(1.8) | 1.1(1.5) | 1.0(1.5) | ||
| SSE.EBIC | 3.48(1.44) | 3.31(1.63) | 2.65(1.01) | 2.70(0.98) | 2.74(1.09) | ||
Table A.13.
Simulation scenario 14. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.2(1.3) | 5.1(2.4) | 5.6(2.2) | 2.3(1.3) | 2.4(1.2) | 6.1(2.1) |
| TP40 | 7.5(0.8) | 6.2(2.2) | 6.3(2.1) | 3.1(1.6) | 3.2(1.5) | 7.0(2.1) | |
| TP.EBIC | 7.0(1.4) | 5.1(2.2) | 5.1(2.2) | 1.9(1.5) | 1.9(1.4) | 6.1(2.0) | |
| FP.EBIC | 1.6(2.1) | 14.6(20.5) | 12.2(18.5) | 17.9(14.5) | 18.3(14.6) | 3.1(4.6) | |
| SSE.EBIC | 1.72(1.28) | 7.64(12.70) | 9.72(18.86) | 12.84(11.64) | 13.71(12.46) | 2.53(3.61) | |
| Interaction | TP20 | 4.9(1.1) | 3.3(2.0) | 3.6(2.0) | 2.2(2.1) | 2.2(2.0) | 4.3(2.1) |
| TP40 | 5.1(1.3) | 3.8(2.1) | 4.1(2.0) | 2.3(2.0) | 2.2(1.9) | 4.7(2.3) | |
| TP.EBIC | 3.6(1.6) | 2.5(1.8) | 2.5(1.9) | 1.0(1.4) | 1.1(1.5) | 3.0(1.7) | |
| FP.EBIC | 1.9(2.0) | 1.3(1.5) | 1.3(1.6) | 1.8(2.9) | 1.6(2.6) | 1.3(1.8) | |
| SSE.EBIC | 2.09(1.42) | 2.68(1.25) | 2.53(1.18) | 6.22(4.51) | 5.44(4.86) | 2.21(2.08) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.0(2.5) | 5.6(2.5) | 2.1(1.3) | 2.2(1.3) | 6.1(2.1) | |
| TP40 | 6.1(2.5) | 6.3(2.3) | 3.1(1.5) | 3.0(1.6) | 7.1(2.2) | ||
| TP.EBIC | 5.4(2.3) | 5.5(2.3) | 2.0(1.3) | 2.2(1.4) | 6.1(2.3) | ||
| FP.EBIC | 11.0(16.8) | 14.8(20.5) | 21.3(14.2) | 22.9(13.5) | 4.5(4.0) | ||
| SSE.EBIC | 11.72(27.37) | 11.68(23.33) | 15.44(17.97) | 16.30(15.37) | 4.37(7.30) | ||
| Interaction | TP20 | 2.6(2.0) | 2.9(2.1) | 1.9(2.0) | 1.9(1.9) | 3.0(2.2) | |
| TP40 | 3.5(2.4) | 3.7(2.3) | 2.22(2.1) | 2.25(2.1) | 4.0(2.4) | ||
| TP.EBIC | 2.1(1.7) | 2.3(1.8) | 0.8(1.1) | 0.8(1.1) | 3.2(1.6) | ||
| FP.EBIC | 0.9(1.4) | 1.4(1.8) | 1.3(2.8) | 1.0(2.0) | 0.9(1.8) | ||
| SSE.EBIC | 2.95(1.36) | 2.84(1.35) | 6.65(5.08) | 5.09(4.99) | 3.46(3.04) | ||
Table A.14.
Simulation scenario 15. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 7.0(1.3) | 5.6(2.1) | 6.0(2.0) | 6.6(1.6) | 6.6(1.6) | 6.9(1.7) |
| TP40 | 7.1(1.2) | 6.2(1.9) | 6.3(1.8) | 6.9(1.3) | 6.5(1.3) | 7.1(1.5) | |
| TP.EBIC | 6.8(1.5) | 5.7(2.0) | 5.8(1.9) | 6.1(1.4) | 6.1(1.4) | 6.9(2.0) | |
| FP.EBIC | 1.1(1.5) | 10.3(17.1) | 9.8(16.2) | 2.2(2.4) | 2.1(1.8) | 2.1(1.4) | |
| SSE.EBIC | 1.98(1.76) | 6.11(8.91) | 6.34(10.27) | 2.11(1.94) | 2.19(1.9) | 2.03(1.78) | |
| Interaction | TP20 | 4.8(1.2) | 3.5(2.0) | 3.5(1.8) | 4.1(1.1) | 4.2(1.1) | 4.9(1.9) |
| TP40 | 5.3(1.3) | 3.9(2.1) | 4.0(2.0) | 5.1(1.3) | 5.0(1.3) | 5.4(2.2) | |
| TP.EBIC | 4.0(1.6) | 2.5(2.0) | 2.7(1.9) | 3.1(1.7) | 3.1(1.7) | 3.4(1.9) | |
| FP.EBIC | 3.5(1.0) | 2.6(1.7) | 2.5(1.6) | 3.6(1.7) | 3.7(1.9) | 3.5(1.9) | |
| SSE.EBIC | 3.71(4.18) | 4.37(3.98) | 4.17(3.61) | 4.32(5.00) | 4.32(5.03) | 3.89(5.74) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 5.8(1.9) | 5.9(1.9) | 6.1(1.5) | 6.1(1.6) | 6.3(1.6) | |
| TP40 | 6.5(1.6) | 6.5(1.7) | 7.0(1.4) | 7.1(1.3) | 7.1(1.6) | ||
| TP.EBIC | 5.7(2.0) | 5.9(2.1) | 6.2(1.7) | 6.3(1.6) | 6.7(1.9) | ||
| FP.EBIC | 10.2(16.9) | 7.6(14.0) | 2.1(2.0) | 2.1(2.4) | 2.0(2.4) | ||
| SSE.EBIC | 5.41(10.85) | 5.27(11.21) | 2.72(3.29) | 2.53(2.98) | 2.37(2.04) | ||
| Interaction | TP20 | 3.7(1.8) | 3.8(1.7) | 4.1(1.3) | 4.1(1.3) | 4.2(1.7) | |
| TP40 | 4.1(2.0) | 4.4(1.9) | 5.2(1.4) | 5.1(1.5) | 5.9(1.8) | ||
| TP.EBIC | 2.6(1.9) | 3.0(1.9) | 3.5(1.6) | 3.6(1.7) | 3.9(1.9) | ||
| FP.EBIC | 2.8(1.4) | 3.4(2.0) | 3.4(1.2) | 3.8(2.2) | 3.3(2.1) | ||
| SSE.EBIC | 4.28(3.49) | 3.87(3.17) | 4.99(2.65) | 5.21(2.6) | 3.23(1.89) | ||
Table A.15.
Simulation scenario 16. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| Missing M1 | |||||||
| Main | TP20 | 5.1(1.2) | 3.7(1.7) | 3.9(1.8) | 4.2(1.4) | 4.2(1.4) | 5.0(1.5) |
| TP40 | 6.3(0.9) | 4.6(1.4) | 4.8(1.4) | 5.2(1.3) | 5.2(1.2) | 6.4(1.3) | |
| TP.EBIC | 5.5(1.2) | 4.1(0.9) | 4.5(1.1) | 4.0(1.7) | 4.0(1.6) | 5.8(2.0) | |
| FP.EBIC | 4.7(3.8) | 34.1(18.5) | 28.8(16.9) | 9.2(5.0) | 9.6(6.3) | 6.7(4.8) | |
| SSE.EBIC | 5.55(4.09) | 9.89(4.18) | 8.27(3.97) | 7.82(4.38) | 7.03(5.53) | 4.32(1.72) | |
| Interaction | TP20 | 4.2(1.7) | 2.3(2.2) | 2.3(2.1) | 2.9(2.2) | 2.9(2.2) | 4.4(2.0) |
| TP40 | 5.0(1.7) | 3.3(2.0) | 3.5(1.6) | 3.8(1.9) | 3.8(1.9) | 5.2(2.2) | |
| TP.EBIC | 2.5(1.8) | 0.2(0.8) | 0.5(0.9) | 0.8(1.6) | 1.0(1.7) | 2.1(1.4) | |
| FP.EBIC | 1.3(2.0) | 0.2(0.7) | 0.2(0.7) | 0.8(2.4) | 1.1(2.5) | 1.2(1.2) | |
| SSE.EBIC | 2.02(1.27) | 4.35(1.92) | 4.16(1.89) | 3.96(0.83) | 3.95(0.78) | 2.71(5.92) | |
|
| |||||||
| Missing M2 | |||||||
| Main | TP20 | 4.1(1.9) | 4.1(1.9) | 4.2(1.2) | 4.2(1.2) | 5.7(1.6) | |
| TP40 | 5.1(1.6) | 4.8(1.3) | 5.1(1.4) | 4.8(1.4) | 6.1(1.4) | ||
| TP.EBIC | 4.0(1.6) | 4.1(1.5) | 4.1(1.5) | 4.0(1.4) | 5.5(1.7) | ||
| FP.EBIC | 26.7(17.6) | 36.0(13.7) | 9.3(7.9) | 10.9(8.4) | 7.2(2.5) | ||
| SSE.EBIC | 8.29(4.45) | 9.82(3.74) | 6.71(4.44) | 6.54(5.59) | 4.22(1.33) | ||
| Interaction | TP20 | 2.4(2.0) | 2.6(1.9) | 2.8(1.9) | 2.8(2.0) | 4.6(1.9) | |
| TP40 | 3.6(1.8) | 3.7(1.9) | 4.1(1.8) | 4.1(1.9) | 5.6(1.9) | ||
| TP.EBIC | 0.6(1.0) | 0.6(0.8) | 1.0(1.7) | 1.0(1.5) | 2.6(0.9) | ||
| FP.EBIC | 0.8(2.4) | 0.3(1.4) | 0.6(1.2) | 0.7(1.4) | 0.6(1.7) | ||
| SSE.EBIC | 4.18(1.19) | 4.26(0.94) | 4.08(1.53) | 3.63(0.56) | 2.23(1.60) | ||
Table A.16.
Summary of settings for the second set of simulation. Table: Table number of the results; N: sample size; Censoring: censoring rate; Signal: Distribution of the nonzero coefficients. Other settings: 5 continuous E variables, AR correlation for G variables, and 2 missing variables (missing M2) with missing rate 15%.
| Scenario | Table | N | Censoring | Signal |
|---|---|---|---|---|
| 17 | A.17 | 150 | 40% | Uniform(0.6,1) |
| 18 | A.18 | 200 | 40% | Uniform(0.6,1) |
| 19 | A.19 | 150 | 20% | Uniform(1.2,1.6) |
Table A.17.
Simulation scenario 17. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| N1 | |||||||
| Main | TP20 | 4.6(1.5) | 2.9(1.8) | 3.1(1.6) | 4.2(1.5) | 4.2(1.6) | 4.4(1.8) |
| TP40 | 5.6(1.8) | 3.2(1.8) | 3.3(1.7) | 4.7(1.6) | 5.0(1.6) | 5.2(1.6) | |
| TP.EBIC | 3.4(1.8) | 2.1(1.9) | 2.3(1.9) | 2.7(1.6) | 2.2(1.4) | 2.9(1.4) | |
| FP.EBIC | 4.5(3.8) | 31.0(3.7) | 29.5(6.4) | 12.5(13.4) | 12.2(13.7) | 5.7(4.5) | |
| SSE.EBIC | 4.81(3.17) | 11.42(3.48) | 10.70(3.48) | 6.29(3.65) | 6.29(4.01) | 4.76(1.10) | |
| Interaction | TP20 | 3.0(2.0) | 1.7(1.8) | 1.8(1.9) | 2.1(1.8) | 2.1(1.8) | 2.4(1.9) |
| TP40 | 3.4(2.0) | 2.1(1.9) | 2.0(1.9) | 2.8(1.9) | 2.9(1.9) | 3.3(2.2) | |
| TP.EBIC | 2.1(2.1) | 0.4(1.2) | 0.6(1.5) | 0.9(1.5) | 0.7(1.4) | 1.3(1.0) | |
| FP.EBIC | 1.2(2.5) | 0.1(0.2) | 0.1(0.3) | 2.1(3.3) | 2.3(3.5) | 2.1(3.9) | |
| SSE.EBIC | 3.06(1.66) | 3.61(0.95) | 3.68(1.01) | 3.76(0.93) | 4.11(1.75) | 3.68(1.41) | |
|
| |||||||
| O1.1 | |||||||
| Main | TP20 | 5.7(4.0) | 4.3(2.6) | 4.5(2.6) | 2.3(1.5) | 2.3(1.5) | 5.4(1.7) |
| TP40 | 5.7(4.0) | 4.6(2.6) | 4.9(2.6) | 2.3(1.5) | 2.3(1.5) | 5.7(2.1) | |
| TP.EBIC | 5.3(4.6) | 3.1(3.1) | 3.5(3.1) | 0.7(0.6) | 0.7(0.6) | 4.3(2.5) | |
| FP.EBIC | 3.7(6.4) | 12.7(4.6) | 14.3(3.8) | 1.3(0.6) | 1.3(0.6) | 2.7(3.0) | |
| SSE.EBIC | 7.90(6.45) | 13.20(10.85) | 12.87(10.79) | 16.66(4.00) | 15.80(2.47) | 8.76(7.23) | |
| Interaction | TP20 | 4.0(3.5) | 2.7(3.1) | 3.1(2.3) | 0.3(0.6) | 0.3(0.6) | 3.7(2.5) |
| TP40 | 4.0(3.5) | 3.1(2.1) | 3.2(2.1) | 0.3(0.6) | 0.3(0.6) | 3.7(2.1) | |
| TP.EBIC | 4.0(3.5) | 2.6(3.1) | 2.7(3.1) | 0.7(1.2) | 0.7(1.2) | 3.1(2.5) | |
| FP.EBIC | 2.0(1.7) | 3.7(3.1) | 3.7(1.2) | 9.0(1.0) | 9.0(1.0) | 3.7(3.1) | |
| SSE.EBIC | 4.01(6.41) | 8.65(7.47) | 7.71(7.08) | 20.42(7.06) | 20.58(6.96) | 6.67(5.25) | |
|
| |||||||
| O1.2 | |||||||
| Main | TP20 | 4.5(2.1) | 2.7(1.5) | 2.7(1.5) | 3.7(1.0) | 4.1(1.5) | 4.3(1.2) |
| TP40 | 4.7(1.5) | 3.3(0.6) | 3.3(0.6) | 4.1(0.6) | 4.3(1.7) | 4.6(1.2) | |
| TP.EBIC | 3.0(0.0) | 1.7(1.0) | 2.2(0.6) | 3.0(0.0) | 2.7(0.6) | 3.0(2.0) | |
| FP.EBIC | 2.0(2.0) | 12.3(3.2) | 16.7(1.2) | 2.3(2.5) | 2.0(3.5) | 0.7(1.2) | |
| SSE.EBIC | 7.04(1.85) | 13.53(2.24) | 13.21(1.83) | 12.27(0.65) | 12.56(1.06) | 10.55(3.04) | |
| Interaction | TP20 | 3.7(1.2) | 1.7(1.5) | 1.7(1.5) | 3.0(0.0) | 3.3(0.6) | 3.4(2.0) |
| TP40 | 3.7(1.2) | 1.0(1.7) | 1.0(1.7) | 3.5(1.0) | 3.3(0.6) | 3.6(2.0) | |
| TP.EBIC | 2.3(0.6) | 1.7(1.5) | 0.0(0.0) | 1.7(1.5) | 2.3(2.1) | 2.7(2.1) | |
| FP.EBIC | 4.3(2.1) | 5.7(1.5) | 2.7(2.3) | 4.3(0.6) | 5.0(1.0) | 4.3(1.2) | |
| SSE.EBIC | 10.89(6.06) | 18.09(4.33) | 18.00(4.28) | 16.24(5.69) | 14.45(8.22) | 13.68(9.93) | |
|
| |||||||
| O2 | |||||||
| Main | TP20 | 3.1(1.0) | 2.7(0.8) | 2.9(0.9) | 2.9(1.0) | 2.9(1.0) | 3.0(1.1) |
| TP40 | 4.1(1.2) | 3.0(1.0) | 3.1(1.0) | 3.5(1.1) | 3.5(1.1) | 3.7(0.9) | |
| TP.EBIC | 2.7(1.0) | 1.8(1.1) | 1.9(1.1) | 2.0(1.3) | 2.2(1.1) | 2.5(1.6) | |
| FP.EBIC | 7.1(12.6) | 27.0(10.5) | 30.9(8.1) | 10.1(12.1) | 17.0(15.3) | 7.5(5.6) | |
| SSE.EBIC | 10.25(11.14) | 20.18(10.09) | 21.82(9.09) | 8.74(10.22) | 13.75(12.22) | 7.08(7.80) | |
| Interaction | TP20 | 2.5(1.6) | 2.3(1.6) | 2.1(1.4) | 2.1(1.3) | 2.3(1.6) | 2.8(1.4) |
| TP40 | 3.3(1.6) | 2.5(1.7) | 2.3(1.5) | 2.5(1.5) | 2.7(1.7) | 2.9(1.6) | |
| TP.EBIC | 0.8(1.5) | 0.4(0.9) | 0.3(0.7) | 0.3(0.7) | 0.1(0.5) | 0.7(0.9) | |
| FP.EBIC | 0.4(1.1) | 0.0(0.0) | 0.0(0.0) | 2.7(4.1) | 1.7(3.5) | 2.1(3.9) | |
| SSE.EBIC | 3.71(0.60) | 3.77(0.49) | 3.67(0.56) | 4.18(1.72) | 3.90(1.12) | 3.67(1.99) | |
Table A.18.
Simulation scenario 18. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| N1 | |||||||
| Main | TP20 | 7.2(1.1) | 5.3(2.1) | 5.3(2.2) | 6.2(1.8) | 6.1(1.9) | 6.3(1.9) |
| TP40 | 7.8(0.4) | 5.8(2.1) | 6.5(1.8) | 7.3(1.0) | 7.3(1.0) | 7.5(1.5) | |
| TP.EBIC | 6.9(1.6) | 4.1(1.9) | 4.3(2.0) | 5.6(2.4) | 5.9(1.9) | 6.3(2.2) | |
| FP.EBIC | 2.2(2.0) | 14.4(3.7) | 14.4(3.6) | 2.3(2.8) | 2.7(3.2) | 2.9(3.7) | |
| SSE.EBIC | 1.39(1.25) | 3.30(1.43) | 3.20(1.49) | 2.43(1.70) | 2.25(1.53) | 2.07(1.40) | |
| Interaction | TP20 | 5.0(1.1) | 2.8(2.5) | 3.0(2.3) | 4.3(1.6) | 4.4(1.7) | 4.6(2.1) |
| TP40 | 5.8(0.6) | 3.8(2.2) | 4.0(2.1) | 5.3(1.1) | 5.3(1.1) | 5.4(1.4) | |
| TP.EBIC | 4.2(2.1) | 1.5(2.2) | 1.8(2.3) | 2.9(2.6) | 3.1(2.6) | 3.0(2.1) | |
| FP.EBIC | 2.3(2.6) | 2.0(2.4) | 1.6(2.4) | 2.3(2.7) | 1.6(1.7) | 2.0(3.5) | |
| SSE.EBIC | 1.45(1.40) | 3.37(1.61) | 3.40(1.68) | 2.64(1.77) | 2.46(1.63) | 2.48(1.48) | |
|
| |||||||
| O1.1 | |||||||
| Main | TP20 | 6.5(2.5) | 4.3(2.7) | 4.7(2.8) | 2.5(1.7) | 2.6(1.6) | 5.3(3.1) |
| TP40 | 6.8(2.0) | 4.9(2.8) | 5.1(2.8) | 3.0(1.7) | 3.0(1.7) | 5.9(2.7) | |
| TP.EBIC | 5.7(2.9) | 4.2(2.9) | 4.3(3.0) | 1.5(1.4) | 1.4(1.2) | 4.6(3.0) | |
| FP.EBIC | 1.3(2.8) | 16.0(9.5) | 15.4(9.9) | 3.9(3.9) | 4.0(3.9) | 4.0(4.4) | |
| SSE.EBIC | 1.93(1.99) | 6.50(3.64) | 7.04(13.25) | 5.77(2.00) | 5.81(1.95) | 3.39(2.09) | |
| Interaction | TP20 | 4.6(2.1) | 3.1(2.4) | 3.2(2.4) | 2.5(2.3) | 2.7(2.3) | 3.9(2.5) |
| TP40 | 4.8(2.1) | 3.7(2.4) | 3.7(2.4) | 3.1(2.5) | 3.1(2.5) | 3.8(2.7) | |
| TP.EBIC | 4.3(2.3) | 3.0(2.4) | 3.0(2.4) | 1.5(1.9) | 1.5(1.9) | 3.6(2.3) | |
| FP.EBIC | 2.5(2.8) | 1.6(1.9) | 1.6(1.9) | 4.4(4.1) | 4.3(4.1) | 1.1(1.4) | |
| SSE.EBIC | 1.62(1.99) | 3.82(3.82) | 3.56(3.29) | 4.84(2.38) | 4.83(2.39) | 2.07(1.72) | |
|
| |||||||
| O1.2 | |||||||
| Main | TP20 | 7.4(0.9) | 5.2(1.8) | 5.5(1.7) | 6.1(1.1) | 6.3(1.1) | 6.5(2.1) |
| TP40 | 7.5(0.9) | 5.8(1.6) | 6.1(1.5) | 6.6(1.0) | 6.9(1.1) | 7.4(1.9) | |
| TP.EBIC | 6.8(1.8) | 4.3(2.3) | 5.0(1.9) | 5.3(1.4) | 5.3(1.4) | 5.9(2.2) | |
| FP.EBIC | 0.4(0.7) | 14.7(10.2) | 11.8(2.7) | 3.0(1.3) | 3.9(1.3) | 3.0(2.9) | |
| SSE.EBIC | 1.25(1.26) | 4.55(3.63) | 3.78(1.60) | 2.34(0.96) | 2.32(0.95) | 2.22(1.63) | |
| Interaction | TP20 | 5.0(1.3) | 3.3(2.3) | 3.4(2.0) | 4.1(1.8) | 4.3(1.5) | 4.2(1.9) |
| TP40 | 5.3(1.1) | 3.9(2.2) | 4.1(2.1) | 5.2(1.1) | 5.1(1.1) | 5.2(2.2) | |
| TP.EBIC | 4.7(1.7) | 2.5(2.3) | 2.8(2.1) | 3.2(1.9) | 3.4(1.8) | 3.6(1.9) | |
| FP.EBIC | 3.3(1.2) | 3.4(2.6) | 3.2(1.7) | 3.0(0.0) | 3.2(0.6) | 3.3(2.1) | |
| SSE.EBIC | 1.81(2.15) | 3.74(2.76) | 3.96(3.91) | 3.14(1.98) | 2.78(1.57) | 2.03(1.12) | |
|
| |||||||
| O2 | |||||||
| Main | TP20 | 4.1(1.3) | 3.1(1.3) | 3.2(1.5) | 3.4(1.4) | 3.6(1.5) | 3.8(1.2) |
| TP40 | 5.2(0.9) | 3.8(1.3) | 4.1(1.3) | 4.6(1.1) | 4.4(1.2) | 4.9(1.2) | |
| TP.EBIC | 4.9(1.4) | 2.2(1.6) | 2.8(1.4) | 3.0(1.3) | 2.8(1.5) | 3.9(1.3) | |
| FP.EBIC | 4.1(3.8) | 10.2(11.1) | 17.9(7.7) | 6.5(3.0) | 5.3(3.5) | 4.3(3.9) | |
| SSE.EBIC | 4.28(0.64) | 7.03(5.07) | 6.65(3.25) | 4.40(0.82) | 4.37(0.69) | 4.03(0.71) | |
| Interaction | TP20 | 3.5(1.9) | 2.1(1.8) | 2.1(1.8) | 3.2(1.4) | 3.1(1.4) | 3.5(1.1) |
| TP40 | 3.6(1.2) | 3.3(1.5) | 3.4(1.6) | 3.7(1.2) | 3.6(1.4) | 3.6(1.2) | |
| TP.EBIC | 3.1(2.0) | 1.6(1.5) | 1.6(1.5) | 1.8(1.2) | 2.0(1.3) | 2.1(1.7) | |
| FP.EBIC | 4.5(2.6) | 4.3(3.2) | 3.8(3.0) | 1.0(2.3) | 2.1(2.9) | 1.3(2.5) | |
| SSE.EBIC | 3.83(1.45) | 4.26(1.66) | 3.95(0.98) | 4.49(1.36) | 4.30(1.42) | 3.92(0.76) | |
Table A.19.
Simulation scenario 19. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|---|
| N1 | |||||||
| Main | TP20 | 8.0(0.0) | 6.1(2.3) | 6.3(2.2) | 7.6(0.9) | 7.4(1.1) | 7.7(1.9) |
| TP40 | 8.0(0.0) | 6.2(2.2) | 6.4(2.4) | 7.9(0.1) | 8.0(0.0) | 7.9(0.1) | |
| TP.EBIC | 8.0(0.0) | 5.8(2.9) | 6.3(2.7) | 6.8(2.3) | 7.0(2.3) | 6.9(2.4) | |
| FP.EBIC | 0.0(0.0) | 12.9(3.9) | 12.0(3.4) | 1.0(1.9) | 0.4(0.7) | 1.1(0.9) | |
| SSE.EBIC | 0.21(0.09) | 5.68(6.67) | 4.50(6.55) | 3.91(5.33) | 3.27(5.04) | 3.45(5.75) | |
| Interaction | TP20 | 6.0(0.0) | 3.7(2.9) | 4.0(3.0) | 5.0(2.1) | 5.2(1.3) | 5.1(2.6) |
| TP40 | 6.0(0.0) | 4.0(3.0) | 4.2(2.7) | 6.0(0.0) | 6.0(0.0) | 6.0(0.0) | |
| TP.EBIC | 6.0(0.0) | 3.3(3.2) | 4.0(3.0) | 5.2(1.3) | 5.4(1.0) | 5.6(2.6) | |
| FP.EBIC | 3.0(0.0) | 2.8(3.1) | 3.0(2.6) | 2.9(1.9) | 3.7(2.2) | 2.7(2.2) | |
| SSE.EBIC | 0.31(0.12) | 6.46(7.68) | 5.27(7.78) | 3.17(3.87) | 2.37(3.15) | 2.55(4.93) | |
|
| |||||||
| O1.1 | |||||||
| Main | TP20 | 5.3(3.1) | 3.3(2.3) | 3.2(2.4) | 2.3(2.1) | 2.3(2.1) | 4.6(2.5) |
| TP40 | 5.3(3.1) | 4.1(2.1) | 4.2(2.2) | 2.8(2.1) | 2.7(2.0) | 4.9(2.2) | |
| TP.EBIC | 4.8(3.6) | 3.3(3.1) | 3.7(2.8) | 1.6(1.7) | 1.7(1.7) | 4.1(2.4) | |
| FP.EBIC | 3.8(4.6) | 14.2(4.2) | 16.8(5.2) | 3.4(3.1) | 2.9(2.9) | 3.1(3.2) | |
| SSE.EBIC | 8.02(10.96) | 16.53(17.16) | 20.65(28.69) | 17.02(6.07) | 16.54(5.87) | 11.25(9.79) | |
| Interaction | TP20 | 3.4(2.9) | 1.9(2.6) | 2.1(2.6) | 1.0(1.7) | 1.0(1.7) | 2.9(2.5) |
| TP40 | 3.4(2.9) | 2.3(2.5) | 2.3(2.5) | 1.2(2.0) | 1.2(2.0) | 3.1(2.4) | |
| TP.EBIC | 3.1(2.9) | 1.8(2.6) | 1.8(2.6) | 0.8(1.4) | 1.0(1.5) | 2.6(1.6) | |
| FP.EBIC | 2.3(2.5) | 3.5(3.5) | 1.3(1.1) | 5.7(4.4) | 6.3(3.9) | 2.0(3.4) | |
| SSE.EBIC | 6.32(5.90) | 12.90(10.64) | 10.49(7.12) | 29.14(29.60) | 30.65(29.36) | 9.01(4.65) | |
|
| |||||||
| O1.2 | |||||||
| Main | TP20 | 6.2(2.2) | 3.7(2.2) | 3.5(2.1) | 5.5(2.2) | 5.8(2.2) | 5.4(2.4) |
| TP40 | 6.5(1.7) | 4.3(1.9) | 4.1(2.1) | 6.3(1.6) | 6.8(1.6) | 6.8(2.2) | |
| TP.EBIC | 5.6(2.4) | 2.8(2.1) | 3.1(2.1) | 4.4(1.8) | 4.9(2.0) | 5.1(2.5) | |
| FP.EBIC | 1.1(1.7) | 16.1(10.4) | 17.2(9.9) | 1.7(1.8) | 1.3(1.9) | 1.9(2.6) | |
| SSE.EBIC | 7.52(6.63) | 14.86(9.48) | 14.49(10.63) | 10.18(4.98) | 9.98(5.45) | 8.64(5.66) | |
| Interaction | TP20 | 4.8(1.4) | 2.0(2.0) | 2.0(2.0) | 4.0(1.6) | 4.3(1.2) | 4.5(2.3) |
| TP40 | 4.9(1.3) | 1.8(2.1) | 2.3(2.2) | 4.4(1.6) | 4.8(1.3) | 4.8(2.3) | |
| TP.EBIC | 3.8(2.2) | 1.6(1.8) | 1.4(2.2) | 2.3(2.0) | 3.0(2.1) | 3.6(2.1) | |
| FP.EBIC | 3.4(1.1) | 3.8(2.4) | 3.5(2.5) | 4.0(1.2) | 4.0(1.0) | 3.5(1.8) | |
| SSE.EBIC | 9.24(8.50) | 12.45(5.00) | 11.93(5.48) | 12.52(6.18) | 10.61(6.96) | 9.87(5.81) | |
|
| |||||||
| O2 | |||||||
| Main | TP20 | 6.2(1.3) | 4.3(1.8) | 4.8(1.9) | 4.9(1.6) | 4.8(1.5) | 5.1(1.8) |
| TP40 | 6.4(1.6) | 5.4(1.7) | 5.5(1.7) | 6.1(1.2) | 6.1(1.3) | 6.4(1.4) | |
| TP.EBIC | 4.5(1.7) | 3.7(1.5) | 4.4(1.7) | 4.0(2.0) | 4.3(1.4) | 4.4(1.7) | |
| FP.EBIC | 4.3(3.8) | 9.3(3.2) | 9.7(2.9) | 3.7(3.3) | 4.4(3.4) | 4.3(3.9) | |
| SSE.EBIC | 9.22(3.65) | 11.47(3.08) | 9.89(3.35) | 9.80(3.45) | 9.54(3.19) | 9.60(3.43) | |
| Interaction | TP20 | 3.3(1.7) | 2.3(2.1) | 2.4(2.1) | 2.5(2.5) | 2.6(2.5) | 3.6(2.0) |
| TP40 | 4.1(1.9) | 3.2(1.9) | 3.1(1.8) | 4.2(2.1) | 4.3(2.0) | 4.4(1.7) | |
| TP.EBIC | 2.8(2.1) | 1.3(1.8) | 2.0(2.0) | 1.6(2.2) | 1.6(2.2) | 2.9(1.9) | |
| FP.EBIC | 1.6(2.7) | 1.5(2.7) | 2.3(3.6) | 2.7(3.4) | 1.8(2.9) | 1.1(2.2) | |
| SSE.EBIC | 9.61(3.70) | 11.24(2.22) | 10.19(3.77) | 10.99(3.50) | 9.79(3.31) | 10.06(3.01) | |
Table A.20.
Simulation with the extended NWDA. In each cell, mean (sd) based on 200 replicates.
| Full | CC | IPW | BPCA | PCA-TSR | ENWDA | ||
|---|---|---|---|---|---|---|---|
| Scenario 1, q = 5 | |||||||
| Main | TP20 | 7.3(1.0) | 1.9(1.2) | 1.6(1.1) | 4.4(1.7) | 4.6(1.5) | 4.7(1.2) |
| TP40 | 7.9(0.3) | 2.1(1.1) | 1.9(1.1) | 6.2(1.5) | 6.3(1.0) | 6.8(1.0) | |
| TP.EBIC | 7.0(1.5) | 1.1(1.1) | 0.9(0.9) | 4.1(1.6) | 3.6(1.8) | 3.9(1.3) | |
| FP.EBIC | 2.5(2.8) | 22.4(3.2) | 22.4(2.6) | 5.8(3.1) | 4.8(3.2) | 4.9(3.3) | |
| SSE.EBIC | 1.32(1.05) | 10.51(2.40) | 10.78(2.20) | 3.60(0.84) | 3.77(0.93) | 3.27(0.85) | |
| Interaction | TP20 | 5.4(1.3) | 0.6(1.2) | 0.9(1.3) | 3.2(1.6) | 3.2(1.6) | 3.4(1.9) |
| TP40 | 6.0(0.0) | 0.8(1.2) | 1.3(1.7) | 4.5(1.1) | 4.3(1.3) | 4.4(2.1) | |
| TP.EBIC | 4.2(2.6) | 0.0(0.0) | 0.0(0.0) | 2.8(1.1) | 2.9(1.3) | 2.8(1.5) | |
| FP.EBIC | 2.0(1.5) | 0.1(0.5) | 0.1(0.2) | 4.9(1.9) | 4.9(2.8) | 3.2(3.2) | |
| SSE.EBIC | 1.46(1.54) | 4.24(1.32) | 3.95(0.42) | 3.77(0.46) | 3.74(0.43) | 3.64(0.48) | |
|
| |||||||
| Scenario 2, q = 5 | |||||||
| Main | TP20 | 7.1(2.4) | 1.7(1.0) | 1.8(1.3) | 1.7(0.8) | 1.5(0.8) | 3.9(1.3) |
| TP40 | 7.3(2.1) | 1.8(1.1) | 1.9(1.3) | 2.1(1.0) | 2.1(1.0) | 4.1(1.4) | |
| TP.EBIC | 6.8(3.0) | 1.1(1.1) | 1.2(1.1) | 0.9(0.7) | 0.7(0.7) | 3.7(1.2) | |
| FP.EBIC | 3.8(3.2) | 18.7(4.3) | 14.9(6.1) | 19.2(7.0) | 16.0(3.6) | 5.9(4.2) | |
| SSE.EBIC | 3.15(2.89) | 38.23(17.67) | 20.20(19.32) | 10.88(12.17) | 10.65(12.18) | 5.63(0.77) | |
| Interaction | TP20 | 4.8(2.4) | 1.1(1.8) | 0.9(1.3) | 1.1(1.8) | 0.9(1.5) | 3.2(1.5) |
| TP40 | 5.1(2.6) | 1.4(1.8) | 1.0(1.5) | 1.1(1.8) | 1.2(1.8) | 3.7(1.8) | |
| TP.EBIC | 4.5(2.4) | 0.2(0.4) | 0.2(0.4) | 0.6(1.4) | 0.4(0.9) | 3.1(1.0) | |
| FP.EBIC | 2.1(1.6) | 0.3(0.5) | 0.6(1.3) | 3.6(3.3) | 4.6(4.5) | 1.7(2.2) | |
| SSE.EBIC | 1.33(2.12) | 4.24(1.39) | 4.90(2.45) | 5.28(3.22) | 6.17(3.76) | 4.33(0.90) | |
|
| |||||||
| Scenario 1, q = 10 | |||||||
| Main | TP20 | 6.6(1.6) | 1.4(1.0) | 1.2(1.1) | 5.1(1.7) | 4.9(2.0) | 5.3(1.4) |
| TP40 | 7.5(1.0) | 1.4(1.0) | 1.1(0.9) | 5.8(1.7) | 5.8(1.7) | 6.1(1.5) | |
| TP.EBIC | 5.9(2.0) | 0.6(0.6) | 0.5(0.6) | 4.5(2.1) | 4.2(2.3) | 4.2(1.0) | |
| FP.EBIC | 3.9(2.6) | 19.3(1.8) | 19.2(2.1) | 6.4(2.4) | 5.4(3.2) | 5.1(2.7) | |
| SSE.EBIC | 2.22(1.54) | 10.98(3.19) | 10.72(2.08) | 3.60(0.89) | 3.78(1.06) | 3.76(1.03) | |
| Interaction | TP20 | 4.3(1.6) | 0.5(1.4) | 0.6(1.4) | 2.4(2.0) | 2.4(1.8) | 2.3(0.8) |
| TP40 | 5.5(1.0) | 0.6(1.4) | 0.8(1.4) | 3.8(1.8) | 3.7(1.8) | 3.8(1.8) | |
| TP.EBIC | 3.1(2.5) | 0.2(0.8) | 0.3(0.2) | 2.2(0.8) | 2.3(0.9) | 2.3(0.9) | |
| FP.EBIC | 1.8(1.7) | 0.4(0.1) | 0.5(0.3) | 4.8(2.6) | 4.8(3.4) | 3.8(2.9) | |
| SSE.EBIC | 2.27(1.71) | 4.85(0.53) | 4.91(0.59) | 3.94(0.65) | 3.86(0.73) | 3.16(0.98) | |
|
| |||||||
| Scenario 2, q = 10 | |||||||
| Main | TP20 | 6.0(3.1) | 1.6(0.5) | 1.6(0.5) | 1.6(1.5) | 1.4(1.3) | 3.4(1.9) |
| TP40 | 7.6(0.9) | 1.6(0.5) | 1.6(0.5) | 2.2(1.3) | 1.8(1.5) | 4.2(1.4) | |
| TP.EBIC | 6.2(1.3) | 1.0(1.0) | 0.6(0.9) | 1.0(1.4) | 0.8(1.3) | 3.1(1.2) | |
| FP.EBIC | 2.2(3.9) | 16.4(5.0) | 19.6(5.2) | 19.8(14.9) | 13.0(3.5) | 4.0(4.6) | |
| SSE.EBIC | 1.31(1.07) | 16.84(12.74) | 19.39(18.05) | 12.50(10.55) | 16.44(7.70) | 6.26(1.21) | |
| Interaction | TP20 | 4.4(1.8) | 1.2(2.2) | 1.2(2.2) | 1.0(1.2) | 1.0(1.7) | 2.8(2.5) |
| TP40 | 5.2(1.8) | 1.2(2.2) | 2.0(2.0) | 1.0(1.2) | 1.8(2.5) | 3.4(2.5) | |
| TP.EBIC | 4.8(1.6) | 0.6(0.9) | 0.4(0.9) | 0.4(0.5) | 0.2(0.4) | 3.2(0.4) | |
| FP.EBIC | 2.2(2.9) | 0.2(0.4) | 0.2(0.4) | 3.2(0.4) | 4.4(4.0) | 2.2(2.2) | |
| SSE.EBIC | 1.32(1.31) | 3.81(0.46) | 3.95(0.55) | 9.20(5.58) | 11.40(14.70) | 4.19(0.61) | |
Table A.21.
Data analysis: main effects and interactions identified by different approaches and their overlaps.
| LUAD | Main | Interaction | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||
| CC | IPW | BPCA | PCA-TSR | NWDA | CC | IPW | BPCA | PCA-TSR | NWDA | |
| CC | 33 | 2 | 5 | 4 | 4 | 12 | 1 | 0 | 0 | 2 |
| IPW | 30 | 1 | 2 | 4 | 12 | 0 | 0 | 0 | ||
| BPCA | 58 | 17 | 8 | 19 | 9 | 1 | ||||
| PCA-TSR | 51 | 7 | 21 | 0 | ||||||
| NWDA | 42 | 30 | ||||||||
|
| ||||||||||
| SKCM | Main | Interaction | ||||||||
|
|
|
|||||||||
| CC | IPW | BPCA | PCA-TSR | NWDA | CC | IPW | BPCA | PCA-TSR | NWDA | |
|
| ||||||||||
| CC | 46 | 12 | 9 | 10 | 11 | 9 | 2 | 0 | 0 | 3 |
| IPW | 50 | 3 | 10 | 9 | 13 | 0 | 0 | 6 | ||
| BPCA | 93 | 14 | 11 | 10 | 0 | 0 | ||||
| PCA-TSR | 71 | 10 | 17 | 2 | ||||||
| NWDA | 44 | 30 | ||||||||
Table A.22.
Simulations for LUAD and SKCM. In each cell, mean (sd) based on 200 replicates.
| CC | IPW | BPCA | PCA-TSR | NWDA | ||
|---|---|---|---|---|---|---|
| LUAD: N(0, 1) | ||||||
| Main | TP20 | 9.7(1.5) | 9.7(1.5) | 11.7(1.5) | 11.7(1.5) | 12.6(0.6) |
| TP40 | 9.7(1.5) | 9.7(1.5) | 14.0(1.0) | 14.0(1.0) | 14.3(1.2) | |
| TP.EBIC | 9.3(1.2) | 9.3(1.2) | 10.7(1.2) | 10.7(1.2) | 10.7(1.2) | |
| FP.EBIC | 13.7(5.5) | 13.3(2.1) | 12.3(3.5) | 12.3(3.5) | 7.3(5.1) | |
| SSE.EBIC | 22.09(7.68) | 22.48(7.71) | 19.55(3.34) | 19.52(3.38) | 15.68(2.56) | |
| Interaction | TP20 | 0.2(0.5) | 0.3(0.6) | 3.1(1.2) | 3.1(1.2) | 4.0(1.7) |
| TP40 | 0.7(1.2) | 1.0(1.0) | 5.0(1.7) | 5.0(1.7) | 6.3(1.5) | |
| TP.EBIC | 0.1(0.6) | 0.1(0.6) | 0.4(0.1) | 1.0(0.5) | 3.7(1.5) | |
| FP.EBIC | 4.2(3.4) | 3.0(2.1) | 4.6(4.6) | 2.4(1.9) | 4.0(4.9) | |
| SSE.EBIC | 20.71(3.39) | 19.48(5.94) | 19.54(4.36) | 20.54(5.44) | 17.76(2.53) | |
|
| ||||||
| LUAD: N(0, 4) | ||||||
| Main | TP20 | 5.1(1.4) | 5.1(1.8) | 6.4(1.6) | 6.4(1.6) | 7.3(1.9) |
| TP40 | 5.4(1.5) | 5.6(1.6) | 6.5(1.6) | 6.7(1.6) | 7.9(2.1) | |
| TP.EBIC | 5.1(1.3) | 5.0(1.6) | 6.0(1.7) | 6.0(1.7) | 6.9(2.1) | |
| FP.EBIC | 14.6(5.9) | 13.2(6.7) | 15.2(6.5) | 14.9(6.2) | 13.6(6.5) | |
| SSE.EBIC | 26.88(9.82) | 25.25(11.97) | 20.23(9.01) | 24.08(9.12) | 19.51(9.88) | |
| Interaction | TP20 | 0.2(0.8) | 0.4(0.9) | 1.1(0.4) | 1.1(0.4) | 2.1(0.4) |
| TP40 | 0.4(0.9) | 0.6(1.0) | 2.9(1.2) | 2.6(1.2) | 3.1(1.3) | |
| TP.EBIC | 0.1(0.3) | 0.2(0.8) | 0.2(0.6) | 0.2(0.6) | 1.9(0.4) | |
| FP.EBIC | 1.1(4.3) | 1.5(5.6) | 2.1(5.9) | 2.1(5.9) | 1.1(2.4) | |
| SSE.EBIC | 19.62(0.96) | 19.56(0.92) | 19.40(0.99) | 19.40(0.98) | 19.11(0.97) | |
|
| ||||||
| SKCM: N(0, 1) | ||||||
| Main | TP20 | 4.4(1.1) | 4.5(0.9) | 7.5(1.4) | 7.3(1.7) | 7.9(1.5) |
| TP40 | 4.4(0.9) | 4.6(1.7) | 9.1(1.6) | 8.6(1.2) | 9.8(1.2) | |
| TP.EBIC | 4.5(0.9) | 4.3(0.7) | 7.3(1.5) | 7.3(1.3) | 8.1(1.1) | |
| FP.EBIC | 11.3(6.1) | 8.5(2.4) | 9.3(5.1) | 8.6(4.9) | 8.4(4.1) | |
| SSE.EBIC | 34.00(17.49) | 35.34(15.77) | 20.32(12.49) | 28.99(9.82) | 17.34(9.81) | |
| Interaction | TP20 | 1.8(1.7) | 1.4(1.5) | 3.5(0.8) | 3.8(1.5) | 3.9(0.9) |
| TP40 | 2.9(1.1) | 3.6(1.4) | 6.5(1.9) | 5.5(1.9) | 6.9(1.9) | |
| TP.EBIC | 1.0(1.2) | 0.6(0.7) | 2.9(1.2) | 2.6(1.2) | 3.1(0.9) | |
| FP.EBIC | 6.6(5.9) | 7.1(7.4) | 5.8(8.6) | 4.9(9.1) | 3.8(6.0) | |
| SSE.EBIC | 21.51(4.64) | 19.98(1.60) | 17.48(0.72) | 19.72(1.08) | 16.22(1.45) | |
|
| ||||||
| SKCM: N(0, 4) | ||||||
| Main | TP20 | 3.9(1.1) | 4.0(0.9) | 5.5(1.5) | 5.6(1.6) | 6.6(1.7) |
| TP40 | 4.9(1.2) | 4.6(1.1) | 6.4(1.8) | 6.4(1.7) | 7.5(1.2) | |
| TP.EBIC | 3.0(1.2) | 3.9(1.2) | 5.3(1.8) | 5.1(1.6) | 6.3(1.8) | |
| FP.EBIC | 13.0(7.4) | 9.3(3.4) | 9.4(6.9) | 10.6(6.2) | 9.1(4.3) | |
| SSE.EBIC | 39.12(14.18) | 23.59(16.72) | 23.11(9.80) | 22.70(10.18) | 18.52(11.25) | |
| Interaction | TP20 | 0.6(1.1) | 1.1(1.1) | 2.0(0.8) | 1.9(1.0) | 2.9(0.8) |
| TP40 | 1.8(1.2) | 1.9(1.6) | 3.6(1.4) | 3.6(0.9) | 4.1(1.4) | |
| TP.EBIC | 0.3(0.5) | 0.1(0.4) | 1.6(0.7) | 1.1(0.4) | 2.5(0.8) | |
| FP.EBIC | 4.5(6.5) | 4.0(5.6) | 8.9(9.9) | 4.0(5.7) | 6.4(9.4) | |
| SSE.EBIC | 20.30(1.83) | 20.34(1.68) | 20.42(2.23) | 19.74(1.08) | 18.24(1.90) | |
Table A.23.
Analysis of one simulation replicate based on the LUAD and SKCM data: main effects and interactions identified by different approaches and their overlaps.
| LUAD | Main | Interaction | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||
| CC | IPW | BPCA | PCA-TSR | NWDA | CC | IPW | BPCA | PCA-TSR | NWDA | |
| CC | 31 | 9 | 7 | 7 | 8 | 13 | 2 | 0 | 0 | 0 |
| IPW | 48 | 7 | 9 | 9 | 12 | 2 | 2 | 1 | ||
| BPCA | 62 | 29 | 11 | 10 | 6 | 1 | ||||
| PCA-TSR | 53 | 13 | 10 | 4 | ||||||
| NWDA | 67 | 9 | ||||||||
|
| ||||||||||
| SKCM | Main | Interaction | ||||||||
|
|
|
|||||||||
| CC | IPW | BPCA | PCA-TSR | NWDA | CC | IPW | BPCA | PCA-TSR | NWDA | |
|
| ||||||||||
| CC | 37 | 7 | 5 | 5 | 8 | 15 | 4 | 4 | 2 | 2 |
| IPW | 36 | 6 | 7 | 5 | 10 | 4 | 0 | 0 | ||
| BPCA | 48 | 14 | 11 | 19 | 3 | 3 | ||||
| PCA-TSR | 35 | 12 | 29 | 5 | ||||||
| NWDA | 50 | 16 | ||||||||
References
- Bien J, Taylor J, Tibshirani R. A lasso for hierarchical interactions. Annals of Statistics. 2013;41:1111–1141. doi: 10.1214/13-AOS1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J, Chen Z. Extended Bayesian information criteria for model selection with large model spaces. Biometrika. 2008;95(3):759–771. [Google Scholar]
- Creemers A, Aerts M, Hens N, Molenberghs G. A nonparametric approach to weighted estimating equations for regression analysis with missing covariates. Computational Statistics & Data Analysis. 2012;56(1):100–113. [Google Scholar]
- Folch-Fortuny A, Arteaga F, Ferrer A. PCA model building with missing data: New proposals and a comparative study. Chemometrics & Intelligent Laboratory Systems. 2015;146:77–88. [Google Scholar]
- He K, Li Y, Zhu J, Liu H, Lee JE, Amos CI, Li Y. Component-wise gradient boosting and false discovery control in survival analysis with high-dimensional covariates. Bioinformatics. 2016;32(1):50–57. doi: 10.1093/bioinformatics/btv517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He R, Belin T. Multiple imputation for high-dimensional mixed incomplete continuous and binary data. Statistics in Medicine. 2014;33(13):2251–2262. doi: 10.1002/sim.6107. [DOI] [PubMed] [Google Scholar]
- Hu YJ, Lin DY, Zeng D. A general framework for studying genetic effects and gene-environment interactions with missing data. Biostatistics. 2010;11(4):583–598. doi: 10.1093/biostatistics/kxq015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J, Chai H. Adjusted regularized estimation in the accelerated failure time model with high dimensional covariates. Journal of Multivariate Analysis. 2013;122:96–114. [Google Scholar]
- Huang J, Ma S. Variable selection in the accelerated failure time model via the bridge method. Lifetime Data Analysis. 2010;16(2):176–195. doi: 10.1007/s10985-009-9144-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J, Ma S, Xie H. Regularized estimation in the accelerated failure time model with high-dimensional covariates. Biometrics. 2006;62(3):813–20. doi: 10.1111/j.1541-0420.2006.00562.x. [DOI] [PubMed] [Google Scholar]
- Huang J, Breheny P, Ma S. A selective review of group selection in high-dimensional models. Statistical Science: a Review Journal of the Institute of Mathematical Statistics. 2012;27(4) doi: 10.1214/12-STS392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter DJ. Gene-environment interactions in human diseases. Nature Reviews Genetics. 2005;6:287–298. doi: 10.1038/nrg1578. [DOI] [PubMed] [Google Scholar]
- Khan MHR, Shaw JEH. Variable selection for survival data with a class of adaptive elastic net techniques. Statistics and Computing. 2016;26(3):725–741. [Google Scholar]
- Lee S, Kwon MS, Oh JM, Park T. Gene-gene interaction analysis for the survival phenotype based on the Cox model. Bioinformatics. 2012;28(18):i582–i588. doi: 10.1093/bioinformatics/bts415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. Wiley-Interscience; 2002. [Google Scholar]
- Liu J, Huang J, Zhang Y, Lan Q, Rothman N, Zheng T, Ma S. Identification of gene-environment interactions in cancer studies using penalization. Genomics. 2013;102:189–194. doi: 10.1016/j.ygeno.2013.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oba S, Sato MA, Takemasa I, Monden M, Tsubara K, Ishii S. A bayesian missing value estimation method for gene expression profile data. Bioinformatics. 2003;19:2088–2096. doi: 10.1093/bioinformatics/btg287. [DOI] [PubMed] [Google Scholar]
- Racine J, Li Q. Nonparametric estimation of regression functions with both categorical and continuous data. Journal of Econometrics. 2005;119(1):99–130. [Google Scholar]
- Robins J, Rotnitzky A. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90:122–129. [Google Scholar]
- Sharafeldin N, Slattery ML, Liu Q, Franco-Villalobos C, Caan BJ, Potter JD, Yasui Y. A candidate-pathway approach to identify gene-environment interactions: analyses of colon cancer risk and survival. Journal of the National Cancer Institute. 2015;107(9):djv160. doi: 10.1093/jnci/djv160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smilde AK, Kiers HAL, Bijlsma S, Rubingh CM, Van Erk MJ. Matrix correlations for high-dimensional data: the modified RV-coefficient. Bioinformatics. 2009;25(3):401–405. doi: 10.1093/bioinformatics/btn634. [DOI] [PubMed] [Google Scholar]
- Spinka C, Carroll RJ, Chatterjee N. Analysis of case-control studies of genetic and environmental factors with missing genetic information and haplotype-phase ambiguity. Genetic Epidemiology. 2005;29(2):108–127. doi: 10.1002/gepi.20085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stute W. Distributional convergence under random censorship when covariables are present. Candinavian Journal of Statistics. 1996;23:461–471. [Google Scholar]
- Thomas D. Gene-environment-wide association studies: emerging approaches. Nature Reviews Genetics. 2010;11:259–272. doi: 10.1038/nrg2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Altman RB. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17(6):520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- Ternes N, Rotolo F, Michiels S. Empirical extensions of the lasso penalty to reduce the false discovery rate in high-dimensional Cox regression models. Statistics in Medicine. 2016;35(15):2561–2573. doi: 10.1002/sim.6927. [DOI] [PubMed] [Google Scholar]
- Westcott PMK, Halliwill KD, To MD, et al. The mutational landscapes of genetic and chemical models of Kras-driven lung cancer. Nature. 2015;517(7535):489–492. doi: 10.1038/nature13898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CH, Crombie C, van der Weyden L, et al. Nuclear receptor binding protein 1 regulates intestinal progenitor cell homeostasis and tumour formation. The EMBO Journal. 2012;31(11):2486–2497. doi: 10.1038/emboj.2012.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia X, Jiang B, Li J, Zhang W. Low-dimensional confounder adjustment and high-dimensional penalized estimation for survival analysis. Lifetime Data Analysis. 2016;22:547–567. doi: 10.1007/s10985-015-9350-z. [DOI] [PubMed] [Google Scholar]
- Zhang Q, Zhang S, Liu J, Huang J, Ma S. Penalized integrative analysis under the accelerated failure time model. Statistica Sinica. 2016;26:493–508. [Google Scholar]
- Zhao Q, Shi X, Huang J, Liu J, Li Y, Ma S. Integrative analysis of omics data using penalty functions. Wiley Interdisciplinary Reviews: Computational Statistics. 2015;7(1):99–108. doi: 10.1002/wics.1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Long Q. Multiple imputation in the presence of high-dimensional data. Statistical Methods in Medical Research. 2016;25(5):2021–2035. doi: 10.1177/0962280213511027. [DOI] [PubMed] [Google Scholar]
- Zhu R, Zhao H, Ma S. Identifying gene-environment and gene-gene interactions using a progressive penalization approach. Genet Epidemiology. 2014;38(4):353–68. doi: 10.1002/gepi.21807. [DOI] [PMC free article] [PubMed] [Google Scholar]