Cell Surface as a Fractal: Normal and Cancerous Cervical Cells Demonstrate Different Fractal Behavior of Surface Adhesion Maps at the Nanoscale

Abstract

Here we show that the surface of human cervical epithelial cells demonstrates substantially different fractal behavior when the cell becomes cancerous. Analyzing the adhesion maps of individual cervical cells, which were obtained using the atomic force microscopy operating in the HarmoniX mode, we found that cancerous cells demonstrate simple fractal behavior, whereas normal cells can only be approximated at best as multifractal. Tested on ~300 cells collected from 12 humans, the fractal dimensionality of cancerous cells is found to be unambiguously higher than that for normal cells.

Fractals [1] are “self-similar” irregular curves or shapes that repeat their pattern when zoomed in or out. These complex disorderly patterns are typically formed under far-from-equilibrium conditions [2], or emerge from chaos [3]. Examples of fractal shape range from the large-scale structure of the Universe [4] to forms of continental coastlines [5], trees [6], grain structures of many metals, ceramics and minerals [7], clouds [8], and even some artistic creations [9]. Some biological tissues [10] show fractal patterns. Recently a fractal structure of chromatin has been used to show how the cell’s nucleus holds molecules that manage nuclear DNA in the right location [11].

There has been a long-standing hypothesis that a misbalance of various biochemical reactions, which is typically associated with cancer, could result in chaos and the associated fractal behavior [12] of cancer. Cancer-specific fractal behavior of tumors at the macroscale was found when analyzing the tumor perimeters [10,13]. Similar analysis of one-dimensional perimeter of cross-sections of individual cells did not show the transition to fractal behavior when cells become cancerous. Both cancer and normal cells demonstrated good fractal behavior, although with different fractal dimensionality (FD) [14,15]. Moreover, the previous works were descriptive in nature; they were based on the analysis of the previously well-known morphometric features of the cell boundary (pseudopodia) and did not provide any noticeable improvement in identification of cancer cells [16].

Here we show that the cell surface can indeed develop fractal behavior when cells become cancerous. Our analysis shows that this can only be seen at the nanoscale, when analyzing the distribution of adhesive properties over the two-dimensional surface of biological cells. We show this for human cervical epithelial cells that were imaged with atomic force microscopy (AFM). The AFM technique has been previously used to study cells [17,18], including cervical cells [19,20]. The recently proposed new AFM mode, HarmoniX [21] allows not only imaging cell surfaces but also obtaining maps of surface distribution of the rigidity modulus, dissipation energy, and adhesion.

Cancer-specific features of the surface brush were recently found on cervical cells [20]. Furthermore, the difference between physical adhesion of micron silica beads to cancer and normal cervical cells was reported [19,22]. Thus, at first glance, we expected to see differences in the HarmoniX images. However, the results reported here turned out to be substantially different from the expectations. First, there was no significant difference in the regular (topographical) images of the cell surface. Moreover, we found that only one parameter characterizing the surface (out of more than 30), FD (fractal dimensionality) of only adhesion maps showed a substantial difference. The difference observed is virtually 100% (as measured on ~300 cells derived from 12 humans). Because of the known intrinsic variability of cancer cells [18], it is surprising to find an invariant feature that is so specific to cancerous transformation.

To avoid the problem of handling viable cells, to simplify the imaging procedure, and to mimic prescreening medical tests for cervical cancer, cells were fixed, and then freeze dried before imaging. Representative examples of topography and adhesion maps are shown in Figs. 1(a), 1(b), 1(e), and 1(f) for both cancer and normal cells. Fractal analysis of both topographical images and adhesion maps was done with the help of the Fourier analysis [23,24]. 2D Fourier magnitude F(u, ν) of the AFM images is given by

FIG. 1.

(color online). Representative AFM HarmoniX images and Fourier spectra of cancer and normal cells. Panels (a), (b) show topographical images whereas (e),(f) demonstrate the adhesion maps of cell surface. The corresponding Fourier spectra (the magnitude) as a function of reciprocal space are shown in (c),(d) and (g),(h) for topography and adhesion, respectively. The fractal behavior corresponds to straight (shown dashed) lines. The left (right) panels show the data for cancerous (normal) cells.

$$F(u,v)=\frac{1}{N_x{N}_y}\sum _{x=0}^{N_x-1}\sum _{y=0}^{N_y-1}z(x,y)e^{-i2\pi (ux/N_x+vy/N_y)},$$ (1)

where N_x, N_y are the number of pixels in the x, y directions, u, v are discrete Fourier indices = 0, 1, 2, … N_x−1, and v = 0, 1, 2 … N_y−1. z(x, y) is the value of the image at point (x, y); it can be either height or the adhesion force F_adh(x, y).

The magnitude was then considered in polar coordinates and averaged on all angles. Figures 1(c) and 1(d) show representative angle-averaged radial spectral magnitudes A as a function of reciprocal space Q (inverse lateral size of the geometrical features on the map, L) for the topographical images of Figs. 1(a) and 1(b). Figures 1(g) and 1(h) show the similar spectra for the adhesion maps of Figs. 1(e) and 1(f). Linear behavior of A(Q) in the log-log scale is a basic feature of fractals. An important parameter of fractals is the FD α, which can be found as α = 2 − b, where b is the slope of the linear log-log dependence A(Q) ~ Q^b. Such a definition of FD gives α = 2 for flat and α = 3 for infinitely rough surfaces.

It should be noted that the fractal behavior analyzed here has natural limitations [25] due to the finite size of data and digitalization or pixelization of any digital image. It implies that the fractal behavior cannot be well defined for the size of geometrical features L that are either greater than the size of the recorded image or smaller than the lateral size of each pixel. For example, if the analyzed AFM images of 5 × 5 μm² is recorded with 256 × 256 pixels, the fractal behavior can be analyzed for L ranging between ~5 μm and 5 μm/256 (~ 20 nm).

One can see in Fig. 1(g) that the adhesion maps of cancer cells demonstrate a fractal (linear) behavior in the entire range of L. Intriguingly, normal cells can be described as a fractal just approximately; they show so-called multifractal scaling behavior (the log-log Fourier spectra can be approximated with several straight lines shown in Fig. 1) [25,26]. As one can see from Figs. 1(g) and 1(h), the most distinctive feature of cancer cells is the FD defined on the range of features L ~ 40–300 nm size (corresponding reciprocal range of Q is 3–25 μm⁻¹). Figures 1(c) and 1(d) show that topography of both cancer and normal cells behave as a simple fractal. Statistical comparison of FD of the topographical images showed no significant difference between cancer and normal cells (not shown).

Figure 2 shows the distribution histogram of the FD of the adhesion maps as defined above, on the range of features L ~ 40–300 nm size. The data are presented for approximately 300 cells derived from biopsies obtained from 6 cancer patients and 6 normal individuals without cancer. The error of calculation of the FD in Fig. 2 is about 2% for each spot analyzed on cancerous (0.0028) and 3% for normal cells (0.0035). It is small enough to ignore in the histograms presented. One can see a virtually 100% discrimination in the fractal dimension between cancerous and normal cells.

FIG. 2.

(color online). Distributions of fractal dimensionality (FD) for adhesion maps of cancer and normal cells calculated on the range of features L ~ 40–300 nm size. Each value shown corresponds to a single cell, which was found as an average of the fractal dimensionalities calculated on several square micron maps collected over 4 areas on each cell (the variation of the FD between the areas was less than 3% over each cell).

It is worth mentioning for further development of practical applications that the FD parameter is very robust. It is virtually independent of a particular geometry of the AFM probe, scanning conditions, etc. (will be published elsewhere [27]).

To understand the biological nature of the observed difference, it is important to note the scale of the analyzed features. The cell surface is covered with microvilli, glycocalyx, filopodia, etc. The FD reported here was found on the areas free of filopodia fibers [27]. Thus, the difference reported here comes from physical irregularity of the cell membrane at the nanometer level, coming from the intrinsic membrane roughness (cortical layer of cytoskeleton), small microvilli, and/or glycocalyx on the cell surface (“surface brush”, hereafter). Chaotic misbalance of processes responsible for formation of the brush due to malignant transformations in cells is presumably the mechanism explaining the observed difference in the fractal behavior.

Let us now analyze the physical nature of the observed difference. At first glance, the difference in the surface brush of cancerous cells previously observed [20] is unlikely to be the reason responsible for the difference in the FD. Two cancerous cells out of 16 analyzed in [20] showed the averaged brush similar to normal, whereas here the observed FD difference of adhesion shows not even a single overlap among about 300 cells tested. In addition, the topographical images of the cell surface studied here demonstrated no difference in the FD when cells become cancerous. However, the adhesion does depend on topography. Let us demonstrate that the observed fractal difference can be explained by the difference in the cell geometry at the nanoscale, which was not seen in [20]. The adhesion force that occurs due to a contact interaction can be estimated [28] as

$$F_{\text{adh}}=2\pi W{R}_1{R}_2/(R_1+R_2),$$ (2)

where R₁ is radius of the AFM probe, R₂ is the radius of curvature of the surface at the point of contact, W is the adhesion energy per unit area between a flat contact of two materials of the probe and surface. This equation is applied here since the probe-cell force curves show simple adhesion behavior, typical for physical interaction.

Processing the adhesion maps through Eq. (2) and using a known R₁ = 10 nm), one can derive the radius of curvature of the surface features at each point of the image R₂ = F_adhR₁/(2πR₁W − F_adh); see [27] for more detail. These derived radii turned out to be within single nm. To resolve such radii in topological mode, one would need the lateral resolution of subnanometers. This is presently impossible to obtain on soft samples due to the deformation of the surface. Thus, it is impractical to record the radii information in the topography or height mode to obtain the radii comparable with the derived from the adhesion. To amplify, the topography of the cell surface plays an important role in the adhesion, and consequently, the observed FD of the adhesion maps. However, it cannot be derived from the height images due to the intrinsic limitation of spatial resolution of AFM.

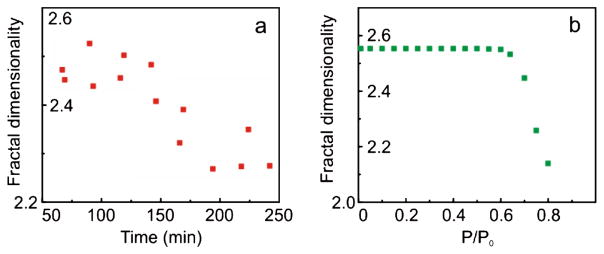
Let us further demonstrate that the hypothesis that the nanometer features of cell topography define the measured FD is plausible. We will show that the behavior of FD on cells imaged under different humidity is in well agreement with this hypothesis. Moisture adsorbed from air plays an important role in the observed adhesion. We observed that FD did not change noticeably when imaging was done in relative humidity less than ~50%–60%, but it starts altering considerably for humidity higher than ~70%. Figure 3(a) shows an example of measurements of FD on cells in air with humidity ~70%. The cells were imaged at various times after extracting from a desiccator, in which they were stored after freeze drying. Right after extracting from the desiccator, the cells are dry and effectively adsorb moisture, creating a relatively dry environment on the scanning interface. Figure 3(a) shows the decrease of FD with time, which corresponds to the equilibration of moisture content of the initially dried cells with the humidity of the environment.

FIG. 3.

(color online). (a) An example of the dependence of fractal dimensionality (FD) of cancer cell surface maps of adhesion on time lapsed after extracting the cells from a desiccator. The imaging was done in humidity of ~70%. (b) Modeling of FD as a function of humidity.

Let us see how such behavior can be explained just by using the surface features at the nanoscale. The dependence of FD on humidity can be found with the help of Eq. (2). In addition to the adhesion described by the contact interaction of Eq. (2), adsorbed moisture creates an additional capillary force [29,30]

$$F_c=\pi {\gamma }_L{R}_{1}sin{\beta }_1\left[2sin({\mathrm{\Theta }}_1+{\beta }_1)+R_{1}sin{\beta }_1\left(\frac{1}{r}-\frac{1}{l}\right)\right].$$ (3)

here γ_L is the interfacial tensions between liquid and vapor (0.072 N/m), Θ₁ is the contact angle between water and AFM probe (Θ₁ ~ 0 since the probe surface is quite hydrophilic),

$$\begin{array}{l}r=-\frac{{\lambda }_K}{ln(P/P_0)},\\ l=R_{1}sin{\beta }_1-r[1-sin({\mathrm{\Theta }}_1+{\beta }_1)],\\ {\beta }_1=arccos\left(\frac{{(R_2+r)}^2-{(R_1+r)}^2-{(R_1+R_2)}^2}{-2(R_1+r)(R_1+R_2)}\right),\end{array}$$

where λ_K is so-called Kelvin length (0.52 nm for water) [29,30] and P/P₀ is the relative humidity. Here the radii of contact R₂ are defined by Eq. (2), when processing the data obtained in low (“zero”) humidity.

Combining Eq. (2) and (3), we restore the map of adhesion for a given humidity P/P₀. FD of such maps are shown in Fig. 3(b). One can clearly see the experimentally observed change of FD when humidity exceeds 60%–70%, which is in very good agreement with the observations. Thus, based on the above results, it is plausible to claim that the observed difference in the fractal behavior comes from the difference in nanoscale topographical features of the cell surface (further development of subnanometers imaging of soft samples will help to confirm this explicitly). Unusually strong dependence of fractal dimensionality on cell malignancy is still a puzzle when compared to all other parameters used for the surface characterization. This will be addressed in future works.