Accounting for measurement error in biomarker data and misclassification of subtypes in the analysis of tumor data

Abstract

A common paradigm in dealing with heterogeneity across tumors in cancer analysis is to cluster the tumors into subtypes using marker data on the tumor, and then to analyze each of the clusters separately. A more specific target is to investigate the association between risk factors and specific subtypes and to use the results for personalized preventive treatment. This task is usually carried out in two steps–clustering and risk factor assessment. However, two sources of measurement error arise in these problems. The first is the measurement error in the biomarker values. The second is the misclassification error when assigning observations to clusters. We consider the case with a specified set of relevant markers and propose a unified single-likelihood approach for normally distributed biomarkers. As an alternative, we consider a two-step procedure with the tumor type misclassification error taken into account in the second-step risk factor analysis. We describe our method for binary data and also for survival analysis data using a modified version of the Cox model. We present asymptotic theory for the proposed estimators. Simulation results indicate that our methods significantly lower the bias with a small price being paid in terms of variance. We present an analysis of breast cancer data from the Nurses’ Health Study to demonstrate the utility of our method.

1. Introduction

Within a given type of cancer, substantial heterogeneity often exists among tumors at the molecular level. This heterogeneity can reflect the existence of disease subtypes representing distinct biological entities. A common approach is to cluster tumors into subtypes (or clusters) based on biomarker data. Breast cancer is one example. In the 1970s, estrogen receptors (ER) status and tumor grade were identified as important prognostic factors. More recently, in the early 2000s, four major breast cancer molecular subtypes were identified: luminal A-like, luminal B-like, HER2+ type, and triple negative (or basal-like). It has been found that different breast cancer subtypes are associated with different etiologies, risk factors, clinical outcomes, and treatment options.

In particular, heterogeneity among tumors at the molecular level is often associated with the effects of risk factors. With tumors clustered into subtypes as described previously, risk factor effects can be examined for each subtype separately. In the case of breast cancer, for example, the effect of Body Mass Index (BMI) on tumor incidence varies according to the levels of ER and progesterone receptors (PR) [1–3]. However, tumor biomarker levels exhibit substantial biological variation. In addition, the measured biomarker levels are often subject to substantial measurement error. Failing to account for these sources of variability may lead to biased estimators of parameters such as the cluster means and to bias in the assessment of risk factor effects. Thus, in analyzing etiological heterogeneity across tumor subtypes, it is necessary to account for variation in observed biomarker levels within tumor subtypes.

A natural approach to carrying this out is to model the distribution of the vector of biomarker levels as a mixture of a family of distributions, e.g., multivariate Gaussians, with parameters varying across the mixture components. Mixture models are reasonable and popular approach for the analysis of heterogeneous data and have been studied extensively. See, for example, [4]. In [5], this approach is described for the analysis of microarray expression data. This paper also suggested a mixture of factor analyzers model to reduce the dimensionality of the model. In [6], the variable selection problem is recast as a model selection problem, and a greedy search algorithm is suggested. This algorithm compares nested models using BIC-based approximation of Bayes factors.

There is a growing literature on how to choose which markers should be used out to identify subtype membership of each observation. The current discussion in the research community centers in the case the number of measured biommarkers is larger than the number of available samples, and hence, a sparse statistical model is needed, e.g., [7–10]. See also [11] for a recent survey of model-based clustering for high-dimensional data. An alternative to model-based clustering is to use a more heuristic approach, and to avoid of assuming a statistical model. One possible heuristic approach is to search for a subspace which describes well the observed heterogeneity in the data. See [12] for a review of subspace clustering methods and [13] for more recent review that also includes additional methods.

This paper has a different focus. We assume the set of relevant biomarkers for defining the disease subtypes (clusters) is given, and we focus on the inter-relationship between the process of characterizing each subtype, i.e., estimating relevant distribution parameters (which may vary across the subtypes) and the process of estimating risk factor effects for each subtype. In assessing the risk factor effects, our proposed methods account for the uncertainty in subtyping each given disease case that arises from the variation in the tumor biomarker levels within each subtype. This variation includes not only the biologic mechanics of the human body, but also error in the measured biomarker level because of the measurement process itself. Although the Gaussian mixture model we use for characterizing the subtypes is well-established, the inter-relationship between characterizing disease subtypes and estimating risk factor effects for each subtype has not, to our knowledge, been previously investigated.

We consider two settings. In the first, the information on each subject includes a binary disease (tumor) indicator, a risk factor vector, and the measured tumor biomarker levels. The latter is only observed for patients with the disease. However, their disease subtype is unknown. Therefore, while the observed outcome is binary, the underlying model is of a multinomial nature. The second scenario involves survival data. Subjects are followed until the occurrence of either an event or censoring. However, when an event is observed, it is unknown which subtype it is.

The rest of the paper is organized as follows. Section 2 introduces the notation and problem setting. Section 3 first presents an latent multinomial model for observed binary outcomes, then proceeds to describe various two-step methods for estimating the parameters of interest, and finally describes an asymptotically efficient unified likelihood approach. Section 4 presents a simulation study comparing the different methods. In Section 5, a model is developed for survival data, and a partial likelihood is constructed and used to obtain consistent and asymptotically normally distributed estimators. Section 6 presents simulation results for the survival data setting. In Section 7, the partial likelihood approach is applied to breast cancer data in the Nurses’ Health Study (NHS) [2]. Section 8 provides a brief discussion.

2. Notation and problem setting

Let X denote the vector of true expression levels of p markers in a tumor sample. We assume that X is distributed according to a K-component multivariate normal mixture, with the mixture components representing biologically distinct tumor subtypes. We denote by μ_k the mean marker vector in Cluster k (k = 1, …, K), by Γ_k the corresponding covariance matrix, and by π₁,…, π_K the mixture probabilities (Σ π_k = 1). The vector X is not observed directly. Instead, we observe W = X + U with U being a measurement error vector, independent of X, that follows a multivariate normal distribution with mean zero and a covariance matrix Ω. Here, we treat Ω as known. If Ω is unknown, it can be estimated using a validation study or replicate measurements of W in the main study itself, as in the analysis in Section 7 of breast cancer data from the NHS. We call the unknown parameters

$$\mathit{\nu }=\{\mathit{\pi },\mathit{\mu },\mathbf{\Gamma }\}≔\{{\pi }_1,\dots ,{\pi }_K,{\mathit{\mu }}_1,\dots ,{\mathit{\mu }}_K,{\mathbf{\Gamma }}_1,\dots ,{\mathbf{\Gamma }}_K\}$$

the clustering parameters. We also denote Σ_k = Γ_k + Ω, and note that W is distributed according a K-component normal mixture with the components being N(μ_k, Σ_k), k = 1, …, K, with the same mixture probabilities as X.

A vector of risk factors Q is measured without error, and the analysis is conditioned on the value Q takes. We denote the tumor subtype (or disease subtype) by Y, where Y equals 0 for no disease, and equals k for disease of type k. We also denote D = 𝕀_{Y>0} for the indicator of disease occurrence, regardless of the subtype. We use the notation of C for the subtype (cluster) membership of an observation with D = 1. We also assume that given C, W and Q are independent. That is, given the subtype membership, the biomarker levels and the risk factors are independent.

3. Multinomial logistic model

In the binary data scenario where the outcome variable is the binary variable D, the triplet (W_i, D_i, Q_i) is observed for each subject i where W_i is considered to be missing if D_i = 0. However, the assumed underlying cluster structure implies a multinomial model for Y. Let p_k(q) ≔ Pr(Y = k|Q = q) be the probability function of Y given Q. In this paper, we consider the logistic model

$$p_k(\mathbf{q})=\frac{\text{exp}({\alpha }_k+{\mathit{\beta }}_k^T\mathbf{q})}{1+{\sum }_{j=1}^K\text{ exp }({\alpha }_j+{\mathit{\beta }}_j^T\mathbf{q})}$$ (1)

for k = 1, …, K, and p₀(q) is simply $1-\sum _{k=1}^K{p}_k(\mathbf{q})$. We refer to the parameters φ = {α, β} ≔ {α₁, …, α_K, β₁, …, β_K} as the risk parameters. Our problem is not a covariate measurement error problem; rather, the challenge here is addressing misclassification of the outcome, which is due in part to natural variation in the biomarkers and in part to measurement error in the biomarkers.

We now present a series of methods for estimating the risk factor parameters. We begin by presenting, as benchmarks, two approaches commonly used in practice, which we call the naive K-means approach and the hard thresholding approach. These approaches take a two-step form, involving an initial clustering step followed by a risk assessment step, where the risk assessment step disregards the possibility of assigning a disease case to the wrong cluster as a result of natural variation in the biomarker levels and measurement error in the observed biomarker levels. We then present our proposed methods, which are designed to take into account this misclassfication. We begin with a relatively simple two-step method, which we call the Semi-hard method. We then present a more sophisticated two-step method, which we call the soft method. Finally, we present a unified likelihood method in which the clustering parameters and risk factor parameters are estimated in a single step.

3.1. Benchmark approaches

In the approach, we call the naive K-means method, the analysis begins by applying the well-known K-means clustering algorithm [14] to the biomarker data (W) to assign each of the observations with D = 1 to a cluster. We let ${\hat{Y}}_i^{\mathit{\text{NV}}}$ be subject i’s assigned cluster if D_i = 1, with ${\hat{Y}}_i^{\mathit{\text{NV}}}=0$ if D_i = 0.With the clusters thus formed, the clustering parameters are estimated as described in Section 4. The risk assessment step involves estimation of the parameters in the risk factor model by maximizing the multinomial likelihood

$$L_{\mathit{\text{NV}}}(\mathit{\phi })=\prod _{i=1}^n{p}_{{\hat{Y}}_i^{\mathit{\text{NV}}}}({\mathbf{q}}_i).$$

In this naive K-means method, the clustering step is carried heuristically rather than within a formal statistical framework.

In the approach, we call the hard thresholding method, the analysis begins, as with the K-means method, with a clustering step where each of the observations with D_i = 1 is assigned to a cluster ${\hat{Y}}_i^{\mathit{\text{HT}}}$, but now the clustering step is carried out within a formal statistical framework. Estimates of the clustering parameters are obtained as the maximizers of the normal mixture (NM) likelihood

$$L_{\mathit{\text{NM}}}=\prod _{\{i:D_i=1\}}\left[\sum _{k=1}^K{\pi }_k\text{ det}{({\mathbf{\sum }}_k)}^{-1/2}\varphi \right({\mathbf{\sum }}_k^{-1/2}({\mathbf{W}}_i-{\mathit{\mu }}_k)\left)\right]$$ (2)

with ϕ(·) being the standard p-variate normal density. We note here some details about the maximization process, which will carry over to our proposed methods.

Recall that Σ_k = Γ_k+Ω where Ω is a known positive definite matrix. We use a Cholesky decomposition for the parametrization of Γ_k, namely ${\mathbf{\Gamma }}_k={\mathbf{P}}_k{\mathbf{P}}_k^T$ where P_k is a lower diagonal matrix with positive elements on the diagonal. This approach has good performance both computationally and statistically as described in [15].

In order to ensure identifiability of the model, we assume without loss of generality that μ_k’s satisfy the constraint μ₁₁ ≤ μ₂₁ ≤ … ≤ μ_K1, where μ_ki is the i-th entry in μ_k, the mean vector in cluster k. A second family of linear constraints are 0 < π_k < 1 for all k and ${\sum }_{k=1}^K{\pi }_k=1$ to ensure that the vector π = (π₁ π₂ … π_K) is indeed a vector of mixture probabilities. Finally, we impose additional linear constraints so the diagonal elements of Γ_k are strictly positive for all k, thereby ensuring that the estimate of Γ_k (the covariance matrix of X in Cluster k) is a positive definite matrix. Initial values are obtained using the K-means cluster assignments. We can then use any algorithm for linearly constrained maximization. Details are given in Section 4.

A common problem in normal mixture likelihood maximization is the unboundedness of the likelihood function for unwanted solutions. To address this problem, further nonlinear constraints are usually added, and local maximizers have to be carefully examined. See [4], particularly Sections 3.8.1 and 3.9.1. However, because in our case Σ_k = Γ_k + Ω and Ω is a known positive definite matrix, we have a lower positive bound for det(Σ_k) and hence, L_NM is bounded as a function of {π_k, μ_k, Γ_k}. See Lemma 1 in Web Appendix A for the details.

A popular tool for the maximization of a mixture model likelihood is the EM algorithm [16], or one of its many variants. However, our experience in the present context is that there is no real gain in terms of computation or performance compared with the direct (constrained) maximization approach, and therefore, we use the latter.

The clustering parameters having been estimated, each disease case is assigned to a cluster in the following manner. Let $Z_i^{(k)}$ denote the probability that subject i belongs to cluster k, given the observed biomarker data on subject i, and define ${\mathbf{Z}}_i=(Z_i^{(1)}{Z}_i^{(2)}\dots Z_i^{(K)})$. That is,

$$Z_i^{(k)}=\mathit{\text{Pr}}(C_i=k|{\mathbf{W}}_i,D_i=1)=\frac{{\pi }_k\text{ det}{({\mathbf{\sum }}_k)}^{-1/2}\varphi ({\mathbf{\sum }}_k^{-1/2}({\mathbf{W}}_i-{\mathit{\mu }}_k))}{\sum _{j=1}^K\left[{\pi }_j\text{ det}{({\mathbf{\sum }}_j)}^{-1/2}\varphi \right({\mathbf{\sum }}_j^{-1/2}({\mathbf{W}}_i-{\mathit{\mu }}_j)\left)\right]}$$ (3)

with Z_i is taken to be missing if D_i = 0. The quantity Z_i depends of the cluster parameters ν, but we will often suppress this dependence from the notation. Let ${\stackrel{\sim }{Y}}_i^{\mathit{\text{HT}}}={\stackrel{\sim }{Y}}_i^{\mathit{\text{HT}}}(\mathit{\nu })={\text{argmax}}_k{Z}_i^{(k)}$ be the cluster subject i is most likely belongs to, given his biomarker level vector (and given D_i = 1). For observations with D_i = 0 put ${\stackrel{\sim }{Y}}_i^{\mathit{\text{HT}}}=0$. Let Ẑ_i and ${\hat{Y}}_i^{\mathit{\text{HT}}}$ be the corresponding quantities using the estimates ν̂ of the clustering parameters obtained in the clustering step by the maximization of L_NM. The quantity ${\hat{Y}}_i^{\mathit{\text{HT}}}$ is the final cluster assignment for observation i.

Moving on to the risk factor assessment step, with the final cluster assignments having been made as described previously, estimates of the risk parameters φ are obtained as the maximizers of

$$L_{\mathit{\text{HT}}}=\prod _{i=1}^n{p}_{{\hat{Y}}_i^{\mathit{\text{HT}}}}({\mathbf{q}}_i).$$

In this hard threshold approach, a statistical model is used in the clustering step, but misclassification in the assignment of tumors to clusters is ignored in the risk factor step.

3.2. Semi-hard method

One way to address misclassification is to incorporate the probability of assigning an observation to Cluster k, while it actually belongs to Cluster k′. Denote this quantity by ${\psi }_i(k\prime ,k)≔\mathit{\text{Pr }}({\hat{Y}}_i^{\mathit{\text{HT}}}=k\prime |C_i=k)$. In the semi-hard method, the clustering step is the same as for the hard thresholding method, while the risk assessment step is carried out by maximizing

$$L_{\mathit{\text{SH}}}=\prod _{i=1}^n{(1-\sum _{k=1}^K{p}_k({\mathbf{q}}_i))}^{1-d_i}{(\sum _{k=1}^K{p}_k({\mathbf{q}}_i){\psi }_i({\hat{Y}}_i^{\mathit{\text{HT}}},k))}^{d_i}.$$ (4)

Note that, unlike in the two methods previously presented, here, the biomarker values are used in the risk assessment step and each observation may contribute to the estimator of the risk parameters in more than one cluster.

If only two clusters are considered, ψ_i(k′, k) can be simplified. For example, ${\psi }_i(2,1)=\mathit{\text{Pr }}(Z_i^{(2)}>0.5|C=1)$ for k′ = 2 and k = 1. Note that in this case $Z_i^{(1)}=1-Z_i^{(2)}$. For K = 2, the distribution of $Z_i^{(2)}$ can be derived as a transformation of a linear combination of independent χ² random variables. Technical details are provided in Web Appendix B. If K > 2, the distribution of Ŷ^HT can be approximated using simple simulations, given the clustering parameters.

3.3. Soft method

This method works with the actual value of each Z_i. The clustering step is carried out in the same way as for the two previous methods. Let g_k(z) be the (multivariate) density of the first K − 1 components of Z_i given Y_i = k. We then replace ${\psi }_i({\hat{Y}}_i^{\mathit{\text{HT}}},k)$ in (4) with g_k(z_i) and get

$$L_S=\prod _{i=1}^n{(1-\sum _{k=1}^K{p}_k({\mathbf{q}}_i))}^{1-d_i}{(\sum _{k=1}^K{p}_k({\mathbf{q}}_i)g_k({\mathbf{z}}_i))}^{d_i}.$$

This choice allows an observation to contribute more for the estimation of the risk parameters in a cluster if it is more likely to belong to it. The semi-hard method can be seen as discretized version of this method. Under this method, there is no definite assignment of observations to a specific cluster. This approach resembles the concept of fuzzy clustering (s[17]).

3.4. Unified likelihood

We now turn to a unified likelihood approach. This is a one-step procedure for the estimation of all the parameters in the model at once. It can be viewed as a fully Bayesian method for our model with uninformative priors for the model parameters. Recalling that given the subtype membership, the risk factors and the biomarker levels are independent, the full likelihood of the entire data is

$$L=\prod _{i=1}^n{\mathit{\text{Pr}}(D_i=0|{\mathbf{Q}}_i={\mathbf{q}}_i))}^{1-d_i}{(\mathit{\text{Pr}}(D_i=1,{\mathbf{W}}_i={\mathbf{w}}_i|{\mathbf{Q}}_i={\mathbf{q}}_i))}^{d_i}=\prod _{i=1}^n{(1-\sum _{k=1}^K{p}_k({\mathbf{q}}_i))}^{1-d_i}{(\sum _{k=1}^K\mathit{\text{Pr}}(Y_i=k|{\mathbf{Q}}_i={\mathbf{q}}_i)\mathit{\text{Pr}}({\mathbf{W}}_i={\mathbf{w}}_i|Y_i=k))}^{d_i}=\prod _{i=1}^n{(1-\sum _{k=1}^K{p}_k({\mathbf{q}}_i))}^{1-d_i}{(\sum _{k=1}^K{p}_k({\mathbf{q}}_i)f_k({\mathbf{w}}_i))}^{d_i}$$ (5)

where f_k(w) = f(w; μ_k, Γ_k, Ω) is the multivariate normal density with mean μ_k and covariance matrix Σ_k = Γ_k + Ω. In this model, π is no longer a free parameter but a function of α, β and the distribution of Q. As described in Section 3.1, we use a Cholesky decomposition for Γ_k. Maximum likelihood estimators are obtained by the implementation of a linear-constrained maximization algorithm where the linear constrains are the same as in Section 3.1 with the exception of the conditions on π which are no longer needed.

3.5. Remarks

The methods we have presented exploit the assumption that the biomarkers and the risk factors are conditionally independent given the subtype. We further discuss the plausibility of this assumption in Section 8. We also consider the robustness of the methods with respect to this assumption as part of the simulations presented in Section 4 and in the breast cancer data example in Section 7.

Throughout this section we treated K, the number of subtypes, as known. In practice, this is not necessarily the case. A likelihood-based model selection procedure, e.g., based on AIC [18] or BIC [19], can be applied to determine the appropriate number of subtypes. We recommend BIC, as our goal is to identify the true clusters, that is, to select the true model, and BIC is more suited to this goal than AIC, which is more geared to optimal prediction [20].

Because (5) is a regular likelihood function (recall Lemma 1, Web Appendix A), standard likelihood theory implies that the unified likelihood estimators are consistent, asymptotically normal, and asymptotically efficient. We cannot expect all these properties to hold for the other methods under consideration. In particular, methods that involve hard assignment of observations to clusters are bound to be biased and inconsistent as long as there is a non-negligible probability of misclassification. The semi-hard and the soft methods eliminate the bias but are expected to have a larger asymptotic variance than the unified likelihood estimator. The simulation results presented in the next section bear out these statements.

We now expand on the asymptotic properties of the soft method. If ν were known, then the analogue L̃_S of L_S using the true ν is the conditional likelihood of Y_i given D_i, Z_i(ν), and Q_i. The estimate of φ that we would get using L̃_S would therefore be consistent, by standard likelihood theory. Accordingly, the estimate φ̂ based on L_S is a consistent estimator of φ. An outline derivation of the asymptotic distribution of the estimate is provided in Web Appendix C.

Although the soft method is not optimally asymptotically efficient, it offers some advantages. In the soft method, the risk factor assessment process deals only with the K − 1 numbers $Z_i^{(k)}$, k = 1, …, K − 1 and not with the entire p-vector of observed biomarker levels. This is an advantage when the number of markers is substantially greater than the number of clusters, as will often be the case. In particular, when p is substantially greater than K, it can be computationally more practicable to carry out the clustering step and the risk factor step separately rather than using the unified likelihood. In addition, with the soft method, a variety of risk factor models can be explored without redefining the cluster structure each time.

4. Simulation results for binary outcome

We present here results of a simulation study involving all the methods described in the preceding section, for the case of K = 2 subtypes. The number of markers is taken to be p = 2, 3, 5, or 10. We take μ₁ = 0e_p, μ₂ = 2.5e_p, and Γ₁ = Γ₂ = I_p where e_p is a vector of length p all of whose elements are equal to 1, and I_p is the identity matrix with dimension p. While we take Γ₁ = Γ₂ in generating the simulation data, our estimation procedure does not assume that this equality holds. The measurement error covariance Ω is taken to be a known diagonal matrix with equal values ω along the diagonal. This was performed for simplicity of presentation. In practice, Ω can have non-zero off-diagonal elements with no effect on the theoretical development. Furthermore, the assumption of known Ω can be relaxed to allow for estimation of Ω from a validation study or a design with replicate biomarker measurements. We considered ω = 0.25, 0.50, 0.75, 1.5, 2, 3 which implies correlation between X_j and W_j, for each component j, of 0.89,0.82,0.76,0.63,0.58,0.50, respectively. Regarding the risk parameters, we consider a single binary risk factor Q, and we take Pr(Q = 1) = 0.4, α₁ = α₂ = −2.079, β₁ = 0.405 (= log 1.5), and β₂ = 1.609 (= log 5). The resulting mixture probabilities are π = (1/3, 2/3) (π is a function of the other model parameters).We take n = 1000 observations per dataset. The design outlined previously results in about 300 tumors per dataset. The number of simulation replications was 1000.

For the naive K-means approach, the cluster parameters are estimated in the following way. Following the assignments of each observation with D_i = 1 to a cluster, means are estimated using the sample mean in each cluster. Regarding the covariance matrix Γ_k of the true biomarker levels, let ${\hat{\mathbf{\sum }}}_k^{\mathit{\text{NV}}}$ be the sample covariance matrix of the observed biomarker levels for subjects assigned to cluster k and let ${\hat{\mathbf{\sum }}}_k^{\mathit{\text{NV}}}={\hat{\mathbf{V}}}_k{\hat{\mathbf{\Lambda }}}_k{\hat{\mathbf{V}}}_k^T$ be the usual spectral decomposition of Σ̂_k with V̂_k being a matrix that contains the eigenvectors of Σ̂_k and Λ̂_k being a diagonal matrix with the eigenvalues of Σ̂_k as its diagonal. We then estimate Γ_k using ${\hat{\mathbf{\Gamma }}}_k^{\mathit{\text{NV}}}={\hat{\mathbf{V}}}_k({\hat{\mathbf{\Lambda }}}_k-\mathbf{\Omega }){\hat{\mathbf{V}}}_k^T$ and replace negative or near-zero entries in the diagonal of Λ̂_k−Ω with an arbitrary small number. The obtained estimates from the naive K-means are used as initial values for the rest of the methods examined.

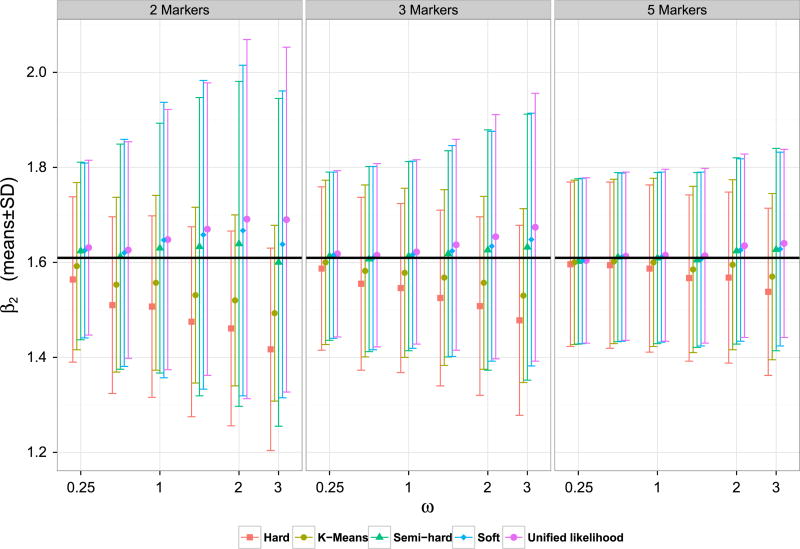
The simulations results are presented in Web Tables I and II in Web Appendix D. Figures 1 and 2 present the mean and the standard deviations in the estimation of β₁ and β₂, respectively, under the various methods. The results indicate that the methods that do not carry out a hard assignment of each observation to a specific cluster have significantly lower bias, with a small price being paid in terms of variance. While the unified likelihood approach is theoretically more efficient than the soft and the semi-hard method, in the finite sample cases, we considered the three methods performed comparably.

Figure 1.

Means and standard deviations of β₁ estimates in simulated data. The black solid horizontal line represents the true value β₁ = 0.405.

Figure 2.

Means and standard deviations of β₂ estimates in simulated data. The black solid horizontal line represents the true value β₂ = 1.609.

In the simulation results we have presented, we have excluded outlier simulations, defined as simulations in which |β̂_j| > 5 for j = 1, j = 2 or both, or simulations where optimization failed. The percentage of outliers is generally small, but for the combination of a low number of markers (2) and large measurement error (ω > 1.5) the percentage of outliers is more substantial. See Web Appendix E for more details. The methods we have presented assume that the biomarker vector X follows a multivariate normal distribution. While this assumption may be plausible in practice, the robustness of our methods to this assumption is of interest. Web Tables 6 and 7 of Web Appendix F present simulation results for our methods when the assumed distribution of the biomarkers is multivariate normal, but the correctly-measured biomarker vector actually follows a multivariate t distribution, while the other model components, including the normal measurement error, are left unchanged. A marginal increase, if at all, was observed for the bias while a minor increase of about 5% was observed in the standard deviations. In practice, the assumed multivariate distribution can be replaced by another parametric distribution, where a notable change is that f_k(w) becomes a convolution of the assumed distribution for X with the normal distribution of the measurement error. While the distribution of Z in the case of two clusters is not as shown in Web Appendix B, the associated density can be computed by simulation.

As discussed before, the robustness of the methods to the assumption of conditional independence of the biomarkers and the risk factors is also of interest. We thus considered the following two scenarios where this assumption does not hold. In the first scenario, we increased the mean of all biomarkers by 0.1 whenever Q = 1, and for both clusters. For example, for an observation belonging to Cluster 2, with Q = 1, the mean was taken to be 2.6 for all biomarkers. In the second scenario, we increased the value of the first biomarker only by 0.5 whenever Q = 1, and for both clusters. The results, presented in Web Tables 8–11 of Web Appendix F suggest that for a small number of biomarkers and more than minimal measurement error, the added bias is substantial. The increased bias was greater for the unified likelihood approach than for the soft method. For both scenarios, the bias was greatly reduced as the number of biomarkers grew. We further consider this assumption and its plausibility in Sections 7 and 8.

5. Survival data model

The proposed unified likelihood approach can be extended to models other than the one described in Section 3. In this section, we present a partial likelihood approach for survival data subject to right censoring and left truncation. The proposed partial likelihood is of a form similar to the Cox partial likelihood [21] and is derived using a similar argument. In what follows, we first recall relevant notation from Section 2, with adjustments made for the survival data case. We then present our unified partial likelihood approach. A similar extension can be carried out for the the soft approach.

As before, denote the true biomarker level by X and the observed level by W, where W = X + U and U is measurement error vector independent of X with the multivariate normal distribution N_p(0, Ω). The vector X again follows a mixture distribution with components N(μ_k, Γ_k). Recall that Y = 0 for no disease and Y = k for disease of subtype k.

The observed data for each individual i is (T_i, 𝔻_i, Q_i, W_i) where T_i is the observed follow-up time, 𝔻_i is the event indicator, Q_i is the value of a risk factor vector, possibly time-dependent (and then, it is denoted by Q_i(t)), and W_i is the marker levels vector, observed if 𝔻_i = 1 and otherwise regarded as missing. Note that because an event of only one type can occur for each subject, we have a competing risk model. See [22] for a basic introduction to competing risk models.

Let λ_k(t, q(t)) be the crude cause-specific hazard function for the k−th cluster when Q(t) = q(t), that is,

$${\lambda }_k(t,\mathbf{q}(t))=\underset{\mathrm{\Delta }\downarrow 0}{\text{lim}}\text{ Pr}(T\in [t,t+\mathrm{\Delta }],Y=k|T\ge t,\mathbf{Q}(t)=\mathbf{q}(t)).$$

We use a proportional hazard model for the crude hazard function for each subtype k,

$${\lambda }_k(t,\mathbf{q}(t))={\lambda }_{0k}(t)\text{ exp }({\mathit{\beta }}_k^T\mathbf{q}(t)).$$ (6)

This is the model discussed in Section 3.3.1 of [22]. We write the cause-specific baseline hazard function as λ_0k(t) = λ_0K(t)h_k(t), where h_k(t) = λ_0k(t)/λ_0K(t) is the baseline hazard ratio for Cluster k relative to Cluster K and with h_K(t) = 1. We work with a parametric model for h_k(t); i.e., we take h_k(t) = h(t; η_k) for a vector of unknown parameters η_k (k = 1, …, K − 1). We leave λ_0K(t) unspecified, as in the classical proportional hazard model. Similar to Cox’s partial likelihood, λ_0K(t) cancels out of our partial likelihood; the hazard ratio functions h_k(t), however, do not. Our formulation is more flexible than assuming a parametric model for all of the baseline hazard functions ${\lambda }_{0k}^{\mathit{\eta }}(t)$, k = 1, …, K.

The density function for W_i given that subject i belongs to Cluster k is denoted by f (w; ν_k), where ν_k is a vector containing the parameters of the relevant normal distribution. That is, $f(\mathbf{w};{\mathit{\nu }}_k)={\mathbf{\sum }}_k^{-1/2}\varphi ({\mathbf{\sum }}_k^{-1/2}(\mathbf{w}-{\mathit{\mu }}_k))$. Let β = (β₁, …, β_K), η = (η₁, …, η_K), and ν = (ν₁, …, ν_K). Finally, denote the vector of all unknown parameters by θ = (η, β, ν).

Let ξ_i(t) be equal 1 if person i is at risk at time t and 0 otherwise, and define the event counting process in the usual way: N_i(t) = 𝔻_i𝕀_{Ti≤t}. Let W_i(t) be the process defined as W_i if N_i(t) = 1, and arbitrarily defined as some constant when N_i(t) = 0. We introduce the filtration ℱ_t = σ(ξ_i(u), Q_i(u), N_i(u), W_i(u), i = 1, …, n, u ∈ [0, t]). We denote the maximum follow-up time by τ and use the notation ℱ to denote the filtration as a whole, i.e., ℱ = {ℱ_t, t ∈ [0, τ]}.

We now construct our partial likelihood. Consider a small interval of time [t − Δ, t], where Δ is small. Let ℰ(t, Δ) denote the set of study realizations in which an event of some type occurred to some individual in [t − Δ, t], and let 𝒪(t, Δ, i, k, w) denote the subset of ℰ(t, Δ) in which subject i is the one who suffered the event, the event is of type k, and the ensuing biomarker vector is w. That is, 𝒪(t, Δ, i, k, w) = {T_i ∈ [t − Δ, t], Y_i = k, W_i = w}, and $ℰ(t,\mathrm{\Delta })={\cup }_{i=1}^n{\cup }_{k=1}^K𝒪(t,\mathrm{\Delta },i,k,\mathbf{w})$. Similar to the derivation of the Cox partial likelihood [21], we work with the conditional likelihood of 𝒪(t, Δ, i, k, w) given ℱ_t−Δ and ℰ(t, Δ). We can write

$$\text{Pr}(𝒪(t,\mathrm{\Delta },i,k,\mathbf{w})|{ℱ}_{t-\mathrm{\Delta }})\doteq {\xi }_i(t-\mathrm{\Delta }){\lambda }_{0k}^{\mathit{\eta }}(t-\mathrm{\Delta })\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_i(t-\mathrm{\Delta }))f_k(\mathbf{w})\mathrm{\Delta }.$$

where the joint distribution of (T_i, Y_i, Wi) given the history was expressed in terms of the joint distribution of (T_i, Y_i) given the history and the distribution of W_i given Y_i, exploiting the assumption of conditional independence of the biomarkers with other quantities. Accordingly,

$$\text{Pr}(ℰ(t,\mathrm{\Delta })|{ℱ}_{t-\mathrm{\Delta }})\doteq [\sum _{j=1}^n{\xi }_j(t-\mathrm{\Delta })\sum _{k=1}^K{\lambda }_{0k}^{\mathit{\eta }}(t-\mathrm{\Delta })\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_j(t-\mathrm{\Delta }))]\mathrm{\Delta }.$$

Thus,

$$\text{Pr}(𝒪(t,\mathrm{\Delta },i,k,\mathbf{w})|{ℱ}_{t-\mathrm{\Delta }},ℰ(t-\mathrm{\Delta }))\doteq \frac{{\xi }_i(t-\mathrm{\Delta }){\lambda }_{0k}(t-\mathrm{\Delta })\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_i(t-\mathrm{\Delta }))f_k(\mathbf{w})}{{\sum }_{j=1}^n{\xi }_j(t-\mathrm{\Delta }){\sum }_{k\prime =1}^K{\lambda }_{0k\prime }^{\mathit{\eta }}(t-\mathrm{\Delta })\text{ exp }({\mathit{\beta }}_k^{\prime T}{\mathbf{Q}}_j(t-\mathrm{\Delta }))}=\frac{{\xi }_i(t-\mathrm{\Delta })h(t-\mathrm{\Delta };{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_i(t-\mathrm{\Delta }))f_k(\mathbf{w})}{{\sum }_{j=1}^n{\xi }_j(t-\mathrm{\Delta }){\sum }_{k\prime =1}^{K}h(t-\mathrm{\Delta };{\mathit{\eta }}_{k\prime })\text{ exp }({\mathit{\beta }}_{k\prime }^T{\mathbf{Q}}_j(t-\mathrm{\Delta }))}$$

Now, let $T_r^{\ast }$, r = 1, …, R denote the ordered observed event times, H_r the index of the person who suffered the event at time $T_r^{\ast },Y_r^{\ast }$ be the (unobserved) cluster index for the event that occurred at time $T_r^{\ast }$, and ${\mathbf{W}}_r^{\ast }$ the biomarker vector for the event that occurred at time $T_r^{\ast }$. Let ℰ_r represent the occurrence of an event of some type at time $T_r^{\ast }$. From the calculations previously, we obtain (letting Δ go to 0)

$$\text{Pr }(H_r={\kappa }_r,{\mathbf{W}}_r^{\ast }={\mathbf{w}}_r^{\ast }|{ℱ}_{T_r^{\ast -}},{ℰ}_r)=\frac{{\sum }_{k=1}^K\text{Pr }(Y_r^{\ast }=k,H_r={\kappa }_r,{\mathbf{W}}_r^{\ast }={\mathbf{w}}_r^{\ast }|{ℱ}_{T_r^{\ast -}},{ℰ}_r)}{{\sum }_{j=1}^n{\xi }_j(T_r^{\ast }){\sum }_{k=1}^K\text{Pr }(Y_r^{\ast }=k,H_r=j|{ℱ}_{T_r^{\ast -}},{ℰ}_r)}=\frac{{\sum }_{k=1}^{K}h(T_r^{\ast };{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_{h_r}(T_r^{\ast }))f_k({\mathbf{w}}_r^{\ast })}{{\sum }_{j=1}^n{\xi }_j(T_r^{\ast }){\sum }_{k=1}^{K}h(T_r^{\ast };{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_j(T_r^{\ast }))}$$

and the partial likelihood is then

$$L(\mathit{\theta })=\prod _{r=1}^R\frac{{\sum }_{k=1}^{K}h(T_r^{\ast };{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_{h_r}(T_r^{\ast }))f_k({\mathbf{W}}_r^{\ast })}{{\sum }_{j=1}^n{\xi }_j(T_r^{\ast }){\sum }_{k=1}^{K}h(T_r^{\ast };{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_j(T_r^{\ast }))}.$$ (7)

We can write L in the following alternate form:

$$L(\mathit{\theta })=\prod _{i=1}^n{\left[\frac{{\sum }_{k=1}^{K}h(T_i;{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_i(T_i))f_k({\mathbf{W}}_i)}{{\sum }_{j=1}^n{\xi }_j(T_i){\sum }_{k=1}^{K}h(T_i;{\mathit{\eta }}_k)\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_j(T_i))}\right]}^{{𝔻}_i}.$$ (8)

Maximum (partial) likelihood estimator for θ is obtained by maximizing (8) under the same linear constraints as described in Section 3. In particular, the constraints impose model identifiability and positive definiteness of the covariance matrix estimates Γ̂_k, k = 1, …, K. Generalizing the hard, semi-hard and soft method to the time-to-event design is straightforward. The clustering step utilizes L_NM, defined in (2), and is identical to the binary data case, and the risk assessment is carried out by replacing f_k(W_i) in the denominator of (8) with the appropriate g_k(Z_i) and then maximizing the resulting expression as a function of the risk parameters.

Under suitable regularity conditions, the maximum (partial) likelihood estimator using either the unified likelihood or the soft methods are consistent and asymptotically normally distributed with covariance matrix that can be estimated from the data. Consistency is shown by noting that the score vector u(θ) corresponding to ℓ(θ) = log L(θ) converges to a limit u*(θ) which is equal to zero at the true value of θ. Asymptotic normality is shown by an argument along the lines of [23]. Proofs are provided in Web Appendix G. For the extension of the soft method of Subsection 3.3 to the survival setting, the asymptotic properties can be established by combining the argument in Web Appendix G with the asymptotic argument made for the soft method in Web Appendix C.

In the next section, we present simulation results for the unified partial likelihood approach and the soft method and compare them with a naive K-means approach for survival data. And then, in Section 7, we present a case study involving breast cancer data from the NHS.

6. Simulation results for survival data

For the simulation design, we take p = 3 markers, K = 2 subtypes and the same clustering parameters, μ₁, μ₂, Γ₁, and Γ₂, as in the simulation for the binary data. The matrix Ω is again a diagonal matrix with equal values ω along the diagonal. Q is taken to be a single binary covariate with Pr(Q = 1) = 0.4. Regarding the risk factor effects, we take β₁ = 0.405 (= log 1.5) and β₂ = 1.609 (= log 5).

We take the baseline hazard for each subtype k to be of parametric form, and more specifically Weibull with parameters m_k and γ_k. That is,

$${\lambda }_{0k}(t)=\frac{m_k}{{\gamma }_k}{\left(\frac{t}{{\gamma }_k}\right)}^{m_k-1}$$

which implies that h(t, η) = η₁t^η₂ with the appropriate η₁ and η₂. For creating the dataset, we take the values γ₁ = 175, γ₂ = 110, m₁ = 1.5, and m₂ = 2.5 and accordingly η₁ ≈ 0.03 and η₂ = 1. We also add an exponential right-censoring to the data (mean=50) and censor all observation at t = 90 if no event or censoring has occurred before. In total, we take 1000 observations per dataset. The design outlined previously results in about 300 events per data set, 100 for k = 1 and 200 for k = 2. For each of the datasets created, we estimate the parameters using the naive K-means approach and using the maximum partial likelihood described in Section 5, as well as the soft method appropriately modified for survival data. The number of simulation replications was 1000.

In implementing the naive K-means method, we first used the K-means algorithm to cluster observations with 𝔻 = 1 into two clusters. With the clusters thus formed, the means in each cluster (μ_k) were estimated using the within-cluster sample means, and the covariance matrices were estimated in the same way as described in Section 4 for the binary data case. The risk assessment step was then carried out by fitting a Weibull regression model to a modified version of the data using the ‘phreg’ function in the ‘eha’ package in R [24]. For each subtype k, observations with Ŷ^NV ≠ k were taken to be censored and estimates for γ_k, m_k and β_k were obtained using a Weibull regression model for censored data. Thereafter, estimates for η₁ and η₂ were calculated by substituting in the estimates for γ₁, γ₂, m₁ and m₂.

The partial likelihood estimates were obtained by maximizing (7) under linear constraints similar to those described for the binary data. The identifiability constraints (after reparameterization) and the constraint η₁ > 0 are simply lower bounds for the model parameters. Therefore, a standard quasi-Newton optimization algorithm can be implemented. We used the ‘constrOptim’ function in R. In cases the algorithm did not converge, the slower Nelder-Mead algorithm was used instead (about 5% of cases). We eliminated less than 5% of the original 1000 iterations per simulation scenario (per ω value), according to the following criteria: The Nelder-Mead algorithm did not converge; Weibull fitting failed to converge. See Web Appendix E for more details. Simulation results are presented in Web Table III of Web Appendix D for the unified (partial) likelihood, the soft and the naive K-means methods. Both the unified (partial) likelihood and the soft methods appear to outperform the naive K-means approach in terms of bias. The unified (partial) likelihood seems to have much better performance in terms of bias comparing with the soft method, especially for large measurement error. The bias when using the soft method should vanish as the sample size grows.

7. Analysis of nurses’ health study data

We applied the methods we have described on data from the NHS [2]. The NHS began in 1976 when 121,700 female nurses aged 30–55 returned a questionnaire about their lifestyle and their health. Participants answered a biennial questionnaire and their answers identified the occurrence of various clinical events and formed the vector of time dependent covariates. The clinical event we considered here is incidence of breast cancer. Tumor tissue was stored, and later several biomarker levels were measured. In our analysis, we considered the following tumor biomarkers: ER, PR, and Ki67 protein. Previous research identified breast cancer subtypes using these biomarkers (cf. [3]). The biomarkers were assessed using the Definiens software as the proportion of nuclei that fell above the Immunohistochemistry marker threshold for positive cells on the tumor core of the total number of nuclei detected.

Some individuals have two or three repeated measurements of at least one biomarker. Measurement error arises here from two sources. The first source is tumor tissue heterogeneity, because the repeated measures were taken from different tumor cores located in different places in the tumor. The second source is the technical laboratory error of the measurement. However, we model the pooled measurement error arising from both sources as a single source.

Because breast cancer exhibits different properties depending on whether it occurs pre-menopause or post-menopause, we restricted our analysis to post-menopausal records only. The risk factor we considered was BMI, expressed in terms of three categories: Normal or Low weight (BMI < 25), Overweight (BMI between 25 and 29) and Obesity (BMI > 29). We also include various known confounders in the model. In the succeeding discussion, we list these confounders, and their definitions.

• Parity and Age at 1st Birth: Categorical variable describing parity and age at first birth. Reference category is ‘Nulliparous’; the rest of the categories are crossproduct of parity and age at first birth categories.

• Age at Menar: Categorical variable, age at menarche (‘<= 12’, ‘= 13’, ‘>= 14’). Reference category ‘<= 12’.

• Alcohol: Binary variable, alcohol drinking.

• Postmenopausal hormon use: Categorical variable, postmenopausal hormon use (‘never used’, ‘current user’, ‘past user’). Reference category is ‘never used’.

We used the missing-indicator method for categorical variables. We used records from the first eight questionnaire cycles. In total, our analysis included 556,472 records, representing 93,104 distinct individuals. This cohort includes 683 breast cancer cases.

In order to improve the fit of the normal model to the biomarker data, we applied an arcsine-root transformation for the biomarkers’ values. This transformation is helpful when the observed values are between 0 and 1, and are relatively concentrated in the edges, as appeared to be the case here. After the transformation, the biomarker measurements were normalized to have mean 0 and standard deviation 1. The measurement error covariance matrix Ω was assumed to be diagonal, and was estimated by running a random effects anova model on the replicate biomarker data (using the R package ‘nmle’[25]). The resulting estimated measurement error variances were 0.20 for ER, 0.10 for PR, and 0.21 for Ki67. Because we have replicate measurements of the biomarker levels, the model described in Section 5 is slightly modified. However, no additional parameters are introduced, and the technical changes, given in Web Appendix H, apply only to f_k(w).

We considered a model with two clusters. Initial estimates for the parameters were obtained using the naive K-means approach. The implementation of the K-means algorithm on the biomarkers values led to partition of the 683 cases into two groups, with 311 cases in Cluster 1 and 372 cases in Cluster 2. Means and covariance matrices were then estimated as described in Section 4.

In constructing the partial likelihood for the risk factor model, we stratified by questionnaire cycle (S = 1, …, 8). The unified partial likelihood (8) then becomes

$$L(\mathit{\theta })=\prod _{s=1}^S\prod _{i=1}^{n_s}{\left[\frac{{\sum }_{k=1}^2{h}_s(T_{\mathit{\text{si}}};{\mathit{\eta }}_{\mathit{\text{sk}}})\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_{\mathit{\text{si}}}(T_{\mathit{\text{si}}}))f_k({\mathbf{W}}_{\mathit{\text{si}}})}{{\sum }_{j=1}^{n_s}{\xi }_{\mathit{\text{sj}}}(T_{\mathit{\text{si}}}){\sum }_{k=1}^{2}h(T_{\mathit{\text{si}}};{\mathit{\eta }}_{\mathit{\text{sk}}})\text{ exp }({\mathit{\beta }}_k^T{\mathbf{Q}}_{\mathit{\text{sj}}}(T_{\mathit{\text{si}}}))}\right]}^{{𝔻}_{\mathit{\text{si}}}}$$ (9)

with stratum-specific definitions for all relevant quantities (parameters, random variables, and values). For the baseline hazard ratio, we took h_s(t) = h_s, that is, a different constant for each stratum.

Initial estimates for h_s, s = 1, …, 8 and for the vectors β₁ and β₂ were obtained as follows. We temporarily converted all events in Cluster 2 to censored records, while events from Cluster 1 and non-event records were left untouched. We then ran a stratified exponential regression under the counting process framework taking the Cluster 1 cases as events. We then carried out a similar exponential regression analysis with the roles of the clusters reversed, so that Cluster 2 cases were regarded as events and Cluster 1 cases were regarded as censored observations. Initial estimates for β₁ and β₂ were obtained from these exponential regression analyses. Initial estimates for h_s were obtained by taking the ratio of the estimated constant baseline hazard ratio in each regression, for each stratum separately.

We first implemented the procedure we just described on a sample of the data, containing all 683 cases and a stratified sample of 7,000 non cases. For this sampled data, the naive K-means estimates were taken as initial values in an optimization algorithm aimed at maximizing the partial likelihood (9) under linear constraints that ensure identifiability of the model and positive definitiveness of Γ̂₁ and Γ̂₂. We also considered at this point the option of more than two clusters. Using this sample of 7,683 individuals, BIC directed us to the model with two clusters (BIC values of 16,295, 16,644, and 16,956 for K = 2, K = 3 and K = 4, respectively). We then took estimates obtained and used them as initial values for optimization using the full data. In the succeeding discussions, we compare between results obtained by the naive K-means and the unified partial likelihood approaches, both implemented for the full data.

Table I presents medians and interquartile ranges (IQRs) in the markers original scales. Looking at this table, we see that PR median estimates obtained using our method are smaller. IQR estimates using our method are larger for ER and PR in Cluster 1 and for PR in Cluster 2. Table II displays Kendell’s τ for each pair of biomarkers. We use Kendall’s τ correlation because it is invariant to transformations. Our results implies moderate correlation between PR and ER in both clusters, while correlations using K-means estimates are negative for cluster 2 (−0.27) and positive in Cluster 1 (0.25). There are also apparent differences in the PR/Ki67 correlation estimates. Inference for β_k in the naive K-means methods was carried out under the standard exponential regression model, ignoring the possibility of misclassification. The partial likelihood estimators are consistent and normally distributed (Web Appendix G). The variance of β̂ was estimated using an extension of the sandwich formula given in Web Appendix G that allows for repeated measurements of biomarkers and a stratified hazard model.

Table I.

Estimated medians and IQRs.

		Cluster 1			Cluster 2
		ER	PR	Ki67	ER	PR	Ki67
Naive K-means	Median	0.42	0.10	0.07	0.53	0.68	0.07
	IQR	0.72	0.58	0.21	0.70	0.64	0.22
Unified partial likelihood	Median	0.46	0.06	0.09	0.61	0.62	0.06
	IQR	0.78	0.56	0.26	0.69	0.71	0.19

IQR An asymptotic theory for linear model selections, interquartile ranges; ER, estrogen receptors; PR, progesterone receptors.

Table II.

Estimated Kendall’s τ.

		Cluster 1	Cluster 2
Naive K-means	ER/PR	0.25	−0.27
	ER/Ki67	−0.06	0.09
	PR/Ki67	−0.11	−0.08
Unified partial likelihood	ER/PR	0.44	0.42
	ER/Ki67	0.04	0.10
	PR/Ki67	0.19	0.12

ER, estrogen receptors; PR, progesterone receptors.

Table III presents β estimates using both methods. Our main concern here is the BMI effect. In Cluster 1, BMI did not have a significant effect (hazard ratios 0.94 and 0.85, p-values 0.94 and 0.41, respectively) and in Cluster 2, Overweight increases this risk (hazard ratio 1.39, p-value < 0.01) while Obesity did not have a significant effect (hazard ratio 1.06, p-value 0.68).

Table III.

β estimates when using naive K-means and unified partial-likelihood methods.

		Naive K-means			Unified partial-likelihood
		Estimate(exp)	p	CI(95%)	Estimate(exp)	p	CI(95%)
Cluster 1	Parity 1–4 & AgeAt1stBirth < 25	−0.22 (0.80)	0.37	(−0.70, 0.26)	−0.22 (0.80)	0.43	(−0.77, 0.33)
	Parity 1–4 & AgeAt1stBirth 25 – 30	−0.02 (0.98)	0.93	(−0.51, 0.46)	−0.09 (0.91)	0.74	(−0.63, 0.45)
	Parity 1–4 & AgeAt1stBirth > 30	0.17 (1.19)	0.54	(−0.37, 0.72)	0.03 (1.03)	0.94	(−0.59, 0.64)
	Parity > 4 & AgeAt1stBirth	−0.05 (0.95)	0.87	(−0.61, 0.51)	−0.19 (0.83)	0.56	(−0.84, 0.46)
	Parity > 4 & AgeAt1stBirth > 25	0.23 (1.26)	0.45	(−0.34, 0.82)	−0.05 (0.95)	0.89	(−0.74, 0.65)
	Parity or AgeAt1stBirth missing	−0.03 (0.97)	0.95	(−0.89, 0.83)	0.11 (1.11)	0.82	(−0.83, 1.05)
	AgeAtMenar = 13	0.10 (1.11)	0.44	(−0.16, 0.36)	0.22 (1.24)	0.15	(−0.08, 0.52)
	AgeAtMenar >= 14	0.06 (1.06)	0.70	(−0.23, 0.35)	0.03 (1.03)	0.85	(−0.31, 0.38)
	AgeAtMenar missing	0.21 (1.24)	0.71	(−0.93, 1.36)	0.43 (1.54)	0.46	(−0.72, 1.59)
	BMI 25 – 29	0.10 (1.11)	0.42	(−0.15, 0.35)	−0.01 (0.94)	0.94	(−0.32, 0.30)
	BMI > 29	−0.26 (0.77)	0.13	(−0.59,−0.08)	−0.16 (0.85)	0.41	(−0.53, 0.22)
	Alcohol	0.07 (1.07)	0.64	(−0.21, 0.34)	0.06 (1.06)	0.72	(−0.26, 0.38)
	Alcohol missing	−0.18 (0.84)	0.42	(−0.62, 0.26)	−0.19 (0.82)	0.45	(−0.70, 0.31)
	PMHuse: past	−0.12 (0.89)	0.46	(−0.44, 0.20)	−0.20 (0.82)	0.28	(−0.56, 0.16)
	PMHuse: current	0.06 (1.07)	0.65	(−0.21, 0.34)	−0.13 (0.88)	0.46	(−0.48, 0.22)
	PMHuse missing	−0.17 (0.84)	0.37	(−0.54, 0.20)	−0.19 (0.83)	0.37	(−0.61, 0.23)
Cluster 2	Parity 1–4 & AgeAt1stBirth < 25	−0.13 (0.87)	0.56	(−0.58, 0.31)	0.01 (1.01)	0.96	(−0.43, 0.45)
	Parity 1–4 & AgeAt1stBirth 25 – 30	0.05 (1.05)	0.84	(−0.40, 0.49)	0.07 (1.08)	0.75	(−0.37, 0.51)
	Parity 1–4 & AgeAt1stBirth > 30	0.35 (1.41)	0.17	(−0.15, 0.84)	0.30 (1.35)	0.22	(−0.18, 0.78)
	Parity > 4 & AgeAt1stBirth < 25	−0.42 (0.65)	0.14	(−0.99, 0.14)	−0.20 (0.82)	0.46	(−0.73, 0.33)
	Parity > 4 & AgeAt1stBirth > 25	−0.09 (0.91)	0.77	(−0.68, 0.50)	0.01 (1.01)	0.98	(−0.56, 0.58)
	Parity or AgeAt1stBirth missing	0.21 (1.23)	0.59	(−0.54, 0.95)	0.15 (1.16)	0.71	(−0.62, 0.92)
	AgeAtMenar = 13	−0.13 (0.88)	0.29	(−0.36, 0.11)	−0.19 (0.82)	0.10	(−0.42, 0.04)
	AgeAtMenar >= 14’	−0.23 (0.79)	0.10	(−0.51, 0.05)	−0.25 (0.78)	0.06	(−0.51, 0.01)
	AgeAtMenar: missing	−0.08 (0.92)	0.89	(−1.22, 1.06)	−0.25 (0.78)	0.67	(−1.39, 0.89)
	BMI 25 – 29	0.32 (1.38)	0.01	(0.10, 0.55)	0.33 (1.39)	<0.01	(0.11, 0.54)
	BMI > 29	0.16 (1.17)	0.29	(−0.13, 0.44)	0.06 (1.06)	0.68	(−0.22, 0.34)
	Alcohol	0.10 (1.10)	0.45	(−0.15, 0.34)	0.12 (1.13)	0.32	(−0.12, 0.36)
	Alcohol missing	−0.46 (0.63)	0.04	(−0.91,−0.02)	−0.41 (0.67)	0.07	(−0.84, 0.03)
	PMHuse past	0.00 (1.0)	0.99	(−0.28, 0.28)	−0.17 (0.84)	0.23	(−0.44, 0.10)
	PMHuse current	−0.13 (0.87)	0.31	(−0.39, 0.12)	0.02 (1.02)	0.85	(−0.22, 0.27)
	PMHuse missing	−0.37 (0.69)	0.04	(−0.73,−0.01)	−0.48 (0.62)	0.01	(−0.84,−0.12)

In this data analysis example, we have assumed that the biomarkers are conditionally independent of the risk factors, given the true subtypes. As a sensitivity analysis, we redid the analysis three additional times, each time allowing the mean of a different biomarker (ER, PR, or Ki67) to depend not only on the subtype, but also on the categorical variable of interest, BMI. The covariance matrix was kept the same for all three BMI levels. The sensitivity analyses were carried out by replacing f_k(w) in (9) with f_k,q(w), where q is the BMI level (1,2, or 3), and f_k,q(w) is the multivariate normal density with mean μ_k,q and covariance matrix Σ_k. In each reanalysis, we allowed the mean of a different biomarker to depend on the BMI level by setting the j−th component of μ_k,q to be equal to μ_kj+ϱ_q, for k = 1, 2 and q = 1, 2, 3. We took ϱ₁ equal to zero for identifiability. When we carried out this modification, most estimates did not change substantially. In particular, the coefficients for the effect of Overweight and Obesity originally estimated as {−0.01, 0.16} in Cluster 1, were estimated as {0.03, −0.16}, {0.09, −0.15}, and {−0.01, −0.16} when allowed the mean of ER, PR, and Ki67, respectively, to depend on BMI. In Cluster 2, the corresponding original estimates {0.33, 0.06} were slightly changed to {0.31, 0.06}, {0.28, 0.06}, and {0.33, 0.06} when we allowed the mean of ER, PR, and Ki67, respectively, to depend on BMI.

8. Discussion

We have developed a new approach to risk factor analysis of cancer data when the risk factor effects can vary across tumor subtypes. Although the subtypes are not known a priori, measured biomarker levels aid the researcher in identifying the subtypes, with the parameters of the biomarker distribution depending on the subtype. Here, it was assumed the biomarker level vector is multivariate normal.

A common practice is to carry out a hard classification of observations to clusters and then estimate risk factor effects in each cluster separately. However, because of misclassification, this approach yields inconsistent estimators. Under a multinomial logistic model for the risk factor effects on the tumor subtypes, we described a unified likelihood approach that accounts for the natural biological variability and measurement error in the biomarker data. We also considered two intermediate two-step methods that provide consistent estimators, a semi-hard method that carries out a hard classification but incorporates misclassification probabilities into the parameter estimation, and a soft method that avoids a hard classification and instead works with cluster membership probabilities (fuzzy clustering). Simulation results indicated that, in comparison with the common approach taken in practice, our proposed approaches lead to estimates with greatly reduced bias, with a small price being paid in terms of variance.

As between the two consistent two-stage estimators, the semi-hard and soft estimators, the soft method makes more precise use of the data and is therefore generally to be preferred.

By standard likelihood theory, the unified likelihood method is asymptotically optimally efficient, whereas the soft method is not. On the other hand, the soft method offers some advantages, as we described in Section 3.5. In light of our simulation results, the soft method should be preferred over the unified likelihood method, when the sample size is low to moderate and the measurement error is small. The soft method could also be used to provide initial values for the unified likelihood method. When the measurement error is large, the soft method can be used as an approximate method in order to investigate expeditiously certain questions of interest, for example covariate selection for the regression model.

Our methods rely on the assumption that given the subtype membership, the risk factors are not informative regarding the biomarker. While we think this assumption is often plausible, its soundness should be assessed in a specific application. As we demonstrated in the breast cancer data example, the unified likelihood method can be extended to cover this dependence, although it may be impractical to fit more complicated models because of the large number of parameters needed. If the non-informativeness assumption is violated, then any method that attempts to incorporate dependence between the biomarkers and the risk factors is bound to be complicated and to include a large number of parameters. Regarding the suggested two-stage methods, namely semi-hard and soft methods, these methods cannot be extended directly to cover this dependence, because of the separation of the cluster step and the risk factor step. If one suspects that a specific side variable is related to both the biomarker and the risk factor, a practical approach is to adjust the biomarker for the side variable prior to the clustering step and then to add the side variable as a background covariate in the risk factor step.

We also considered a survival data model (for right-censored and left-truncated survival data) in which the cluster-specific crude hazard functions are taken to be of proportional hazards form. We developed a unified partial likelihood approach with an appropriately-defined partial likelihood function. This partial likelihood approach allows for time-dependent covariates. We also presented the appropriate implementation of the soft method for survival data. The resulting estimators were shown to be consistent and asymptotically normal. Simulation results yielded the same conclusions as in the multinomial case. In the analysis of the NHS breast cancer data, we have shown how the partial likelihood approach can be applied to estimate risk factor effects in different cancer subtypes. A possible extension of our approach would be to combine our method with variable selection procedure in order to identify new subtypes when many biomarkers are available.