Abstract
Jamming, or dynamical arrest, is a transition at which many particles stop moving in a collective manner. In nature it is brought about by, for example, increasing the packing density, changing the interactions between particles, or otherwise restricting the local motion of the elements of the system. The onset of collectivity occurs because, when one particle is blocked, it may lead to the blocking of a neighbor. That particle may then block one of its neighbors, these effects propagating across some typical domain of size named the dynamical correlation length. When this length diverges, the system becomes immobile. Even where it is finite but large the dynamics is dramatically slowed. Such phenomena lead to glasses, gels, and other very long-lived nonequilibrium solids. The bootstrap percolation models are the simplest examples describing these spatio-temporal correlations. We have been able to solve one such model in two dimensions exactly, exhibiting the precise evolution of the jamming correlations on approach to arrest. We believe that the nature of these correlations and the method we devise to solve the problem are quite general. Both should be of considerable help in further developing this field.
There exists within nature a whole class of systems that exhibit a geometrical percolation transition at which they become spanned by a single infinite cluster extending across the whole system (1–3). Such transitions may be observed, for example, by randomly occupying lattice sites at some prescribed density. Spatio-temporal particle correlations implied by simple dynamical models may also be studied by using percolation ideas. Indeed, since its introduction (4, 5), the potential of the bootstrap percolation problem (6, 7) to analyze the dynamics of a system of highly coupled and locally interacting units has been recognized. The range of applications has continued to grow (8–12).
This problem is of particular interest because of a growing focus on, and appreciation of, the unifying role of dynamical arrest (13–17) or jamming (18) in the formation of complex condensed states of matter. Despite many advances, there is as yet no complete and fundamental conceptual framework to describe the phenomena. In comparable situations it has been an important lesson of critical phenomena (19, 20) that an exact solution, even of a 2D model system, can be of great assistance in broader efforts to understand the issues. Thus, an exact closed solution of one bootstrap problem (with all of the implications of strong packing-induced coupling and divergent correlated domains) would represent, even without direct access to transport coefficients, a solution of a nontrivial (and non-mean field) jamming or arrest scenario. We will present such a solution in this article.
That such a treatment is possible must be considered surprising, for there have been no prior indications of such simplification, to our knowledge.
The connection of the bootstrap percolation problem to jamming phenomena is clear. Thus, particles, processors, or members of a competing population are considered to become inactive (or blocked) depending on the state of their immediate environment. The relationship of the bootstrap process to dynamics is as follows. Beginning with a lattice occupied according to the steady-state (usually random) distribution of particles of the underlying dynamical model, units not blocked (i.e. movable) are iteratively removed. Those remaining are blocked irrespective of the arrangements of the movable ones in the configuration. Onset of extended mutual blocking (in which one unit is prevented from moving by its neighbors and also contributes to the blocking† of some of those neighbors) manifests itself by a sharp change in the occupancy of the lattice after the bootstrap process. Percolation occurs when, after the iterative procedure finishes, the blocked clusters extend across the whole system. Even on approach to such a transition, single-particle movement requires a long sequential and contingent string of changes in surrounding units. In the underlying dynamics this long string implies a growing correlation length and accompanying time scale, both determined by mutual blocking effects. This (dynamical) length scale is named the bootstrap length. Apart from those errors introduced by removal (rather than movement, and subsequent averaging) of particles, this is the characteristic blocking or jamming length over which motions can occur only by rare and cooperative motions. Beyond it, motion is diffusive.
Methods
Bootstrap percolation transitions are believed to fall into two broad universality classes (21), depending on the dimensionality d and on the local rule c, and we might expect this to be reflected in the classes of jamming. The first type is a continuous transition in which the blocked domain size diverges as a power law in system size and density. The second type, when d ≤ c < 2d – 1, displays discontinuous transitions with different essential singularities. Specifically, the case c = d (5, 22, 23) is believed to be more relevant to particle jamming, and there the bootstrap length ξ diverges as ξ = expo(d–1) (A/(1 – ρ)) (24) [here expo(d–1) is the exponential function iterated d – 1 times]. For the 2D square lattice (c = 2),† theoretical calculations based on a set of bounds (25) have resulted in an elegant outcome; essentially exact asymptotic results, 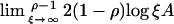 , where A = π2/9 and π2/3 for conventional and modified bootstrap,† respectively. It transpires that at high packing this length is also the typical distance between increasingly rare voids (later named connected holes) in the configuration (26), providing a key connection between the spatio-temporal correlations, and the packing of particle configurations that determine them.
, where A = π2/9 and π2/3 for conventional and modified bootstrap,† respectively. It transpires that at high packing this length is also the typical distance between increasingly rare voids (later named connected holes) in the configuration (26), providing a key connection between the spatio-temporal correlations, and the packing of particle configurations that determine them.
A striking aspect of this arena of research is that all attempts (27, 28) (including some of the most extensive calculations to have been applied in statistical mechanics) to obtain agreement between simulations and known exact asymptotic results have so far failed. Indeed, the bootstrap problem has generated topical interest (29) because of the notorious (apparent) lack of agreement between simulation (27, 28) and theoretical (24, 25, 30–32) developments.
In our study we introduce holes or dynamically available volume (22, 33), these being empty sites on the lattice into which at least one neighboring particle can move. A hole is termed connected or disconnected, respectively, if the lattice can (or cannot) be vacated by sequentially removing particles by using it as an origin in the bootstrap process. In the underlying dynamics, connected holes typically initiate a sequence of moves that will mobilize every particle in the system. They are therefore the mediators of transport in the system and the order parameter of arrest. For a system to bootstrap (and therefore not be jammed) it must contain at least one connected hole. We identify ν as being the connected hole density (average frequency of such occurrences in the lattice). In the high-density regime, the bootstrap length may therefore be calculated from ξ = 1/ν1/d (26), the particles within this distance being movable only via the restricted motions made available by a single connected hole.
Disconnected holes in the modified bootstrap problem (for d = 2, c = 2-modified†) are found to be enclosed by a single continuous rectangular boundary or cage of particles, none of which can be moved by any particle rearrangements inside the boundary. They cannot be formed for edge lengths much larger than lc [the cut-off size, lc ∼ 1/(1 – ρ)] for then there is typically an intervening vacancy. We can therefore sample particle removal paths around holes directly in simulations (26). If particle domains much larger than lc can be removed, the hole may be identified as connected, rendering the simulation very efficient. Thus, the points (°) in Fig. 1 are hole densities one would obtain for systems sizes up to L = 220,000. They constitute the largest simulations to have been carried out, to our knowledge, on a 2D bootstrap problem.
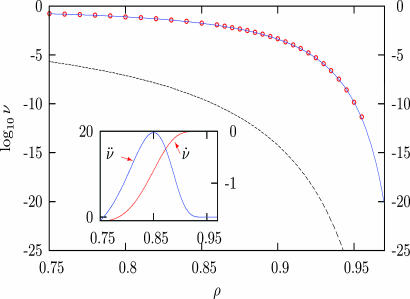
Fig. 1.
Connected hole density in the modified bootstrap model. Open circles represent the total hole density from simulations (26), the last point being equivalent to a system of size 220,000, the current limit of computer simulation. The solid line represents the result of our exact theory. These are compared with the asymptotic result exp(–π2/3(1 – ρ)) (dashed line) (25). We recall that results for the total connected hole density ν coincide with 1/ξ2 at high density (26), where ξ is the bootstrap percolation correlation length. (Inset) ∂ν/∂ρ (red) and ∂2ν/∂ρ2 (blue) against density in the same range. ∂ν/∂ρ increases sharply from –1.73 to approximately zero with an inflexion signalled by the peak in ∂2ν/∂ρ2 at ρ = 0.85.
The bootstrap problem is an example of strong (packing-induced) coupling, so theoretical developments, including simple extensions of previous approaches (25) involving asymptotic bounds, invariably fail. Instead we define intermediate states that imply bootstrap-type (i.e. spatio-temporal) correlations. Transitions between them may then be composed into sequences or particle removal paths whose steps are decorrelated, and transition coefficients [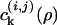 ] from state to state are then easily calculated from the random ensemble. These intermediate states are rectangular regions (of size k by k + s, see Fig. 2). They are, irrespective of their orientation in space, completely empty, or empty save for one, two (adjacent) or three edges occupied entirely by particles. The probabilities that such rectangles are visited during the emptying process are
] from state to state are then easily calculated from the random ensemble. These intermediate states are rectangular regions (of size k by k + s, see Fig. 2). They are, irrespective of their orientation in space, completely empty, or empty save for one, two (adjacent) or three edges occupied entirely by particles. The probabilities that such rectangles are visited during the emptying process are 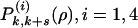 [the states
[the states 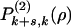 and
and 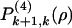 are also defined, these bearing the same meaning as
are also defined, these bearing the same meaning as 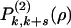 and
and 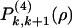 , but for the orientation of the occupied lines with respect to the direction of the elongation]. In defining the transitions between them, only certain directions (illustrated by arrows in Fig. 2) of the removal paths are permitted.‡ For example, if the path leads to a state 1 [probability
, but for the orientation of the occupied lines with respect to the direction of the elongation]. In defining the transitions between them, only certain directions (illustrated by arrows in Fig. 2) of the removal paths are permitted.‡ For example, if the path leads to a state 1 [probability 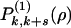 ] the next attempt to grow the vacated rectangle will be via either of the two long directions, thus requiring removal of particles along one or other of those directions. These directions are chosen randomly, with equal probability.
] the next attempt to grow the vacated rectangle will be via either of the two long directions, thus requiring removal of particles along one or other of those directions. These directions are chosen randomly, with equal probability.
Fig. 2.
Intermediate states. Intermediate local configurations surrounding a candidate hole required in evaluation of the sum over particle removal paths that are used to empty the lattice (k = 4 and s = 3 in the example). The white circles are sites that have been emptied in previous steps, and the red disks are temporarily blocked particles along the perimeter edges. For each configuration, the arrows indicate allowed transitions (to be selected at random) involving the growth of one boundary line by one step. This process restores that local configuration to another intermediate state [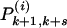 or
or 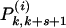 ] with the indices k, s suitably revised. The process terminates (as a disconnected hole) when the local configuration makes a transition from
] with the indices k, s suitably revised. The process terminates (as a disconnected hole) when the local configuration makes a transition from 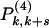 outside of the class
outside of the class 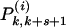 .
.
The next intermediate state will be a k + 1 by k + s rectangle, either in state 1 or in state 2, since these represent the only outcome of that transition. The transition (jump) rates for these two choices are (1 – ρk+s) and ρk+s, and they define 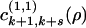 and
and 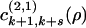 , respectively.
, respectively.
We reiterate these choices. In essence, a highly correlated bootstrap process becomes uncorrelated within the subset of intermediate states, leading to an exact method to identify connected holes by random sampling of a constrained set of states. For connected holes we remain within the closed set of rectangular states with the indices suitably modified after each step. Disconnected holes, being bounded by a rectangular contour of particles, are identified by a transition outside of this set of states. No transition between states involves more than one attempt to remove a group of particles, and the transition rates may be calculated from the random ensemble. The equations of the bootstrap probabilities, if one recalls that in the bootstrap problem movable and removable particles are analogous, represent a map of dynamics at one scale onto the next largest scale, with the packing correlations automatically accommodated.
These features constitute the key elements of the methodological advances described in this article, and similar treatments may be attempted for other such problems in the future (26).
The exact equations representing the process may be written in closed form,
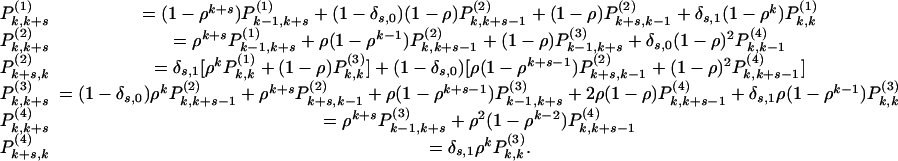 |
[1] |
Here s ≥ 0 and the equations are solved numerically subject to the initial conditions, 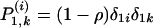 . These equations converge numerically for k » lc and 0 < s/k < 1. The connected hole density, the probability to bootstrap a square of indefinite size, is then given by the expression,
. These equations converge numerically for k » lc and 0 < s/k < 1. The connected hole density, the probability to bootstrap a square of indefinite size, is then given by the expression,
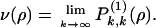 |
[2] |
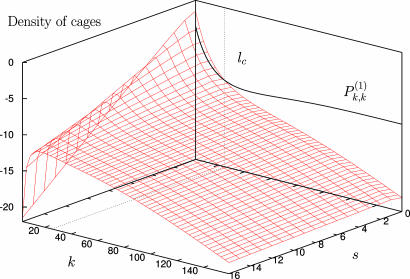
Because of the cut-off in cage size, these equations converge very rapidly and there are no practical limitations on the density range that can be studied by computer, as already discussed (26). Based on exact asymptotic analysis, the quantity –2(1 – ρ) log ξ + π 2/3 = f(ρ) would be predicted to be positive and vanishing in the asymptotic limit (ρ → 1). Now we have numerically calculated the solution for the modified model up to the largest sizes allowed by the precision of the computer, and indeed this quantity does decrease monotonically when ρ approaches 1. However, at ρ ∼ 0.9965, f(ρ) is still of order unity, rather too large to be neglected. Suffice it to say that the true exact bootstrap length for this density is ξ ∼ 10150. Thus in reality, for large but finite systems one sees ξ = exp[–f(ρ)/2(1 – ρ)] exp[π 2/6(1 – ρ)], f(ρ) being a decreasing but always finite function of (1 – ρ). Eq. 1 may also be solved asymptotically. We illustrate in Fig. 3 the density of cages (dimension k by k + s) at particle density ρ = 0.95 and the probability for vacated square-like regions 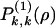 . There we see that cages become rare somewhat beyond the critical size lc.§ The reduction of cages, capable of preventing bootstrapping, leads to the dominance of
. There we see that cages become rare somewhat beyond the critical size lc.§ The reduction of cages, capable of preventing bootstrapping, leads to the dominance of 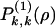 and
and 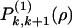 beyond the critical core size.
beyond the critical core size.
Fig. 3.
Cages. Particle density ρ = 0.95. Illustrative calculation in the metastable or droplet state is shown. The red surface represents the probability (in log10 scale) that a rectangular cage surrounding a vacant site is first found at size k by k + s. The probability density of cages is plotted against k (core size) and s (asymmetry degree) and decreases monotonically in k. High degrees of asymmetry are very rare. The probability of finding an empty square of size k is also plotted for a comparison. The intersection with the corresponding cage size distribution is at lc = 25,§ indicating that cages become statistically irrelevant (i.e. extremely rare) already at sizes much smaller than ξ ∼ 105.
Results
The results for connected hole density, the full curve in Fig. 1, or equivalently the bootstrap length, settle a longstanding mystery, the theory now being in precise agreement with simulation where the latter is applicable. They permit us to explore the nature of the problem all the way from lower density to the asymptotic form, as solutions to a single closed set of equations. It is now clear that there has never been any inconsistency between the simulations and asymptotic results. They were both correct, but direct comparison is not appropriate for any range of density appropriate to computer simulation. The numerical results (and associated asymptotic analysis) from these same equations are sufficient to show that the previously reported exponential asymptotic form (25) occurs for such high density (and large length scales) that systems of physical interest will never reach this regime. As noted in the previous paragraph, even at system sizes of ξ ∼ 10150 there remains a singular model-dependent prefactor to the leading exponential. Formulae purporting to describe the behavior for finite systems (or systems at finite density) in terms of a simple exponential are effective fits and possess no fundamental significance.
The real paradoxes lie in the physics. As we now show, this physics turns out to be much richer than had been supposed until now. In discussing these issues we have in mind primarily the clarification of the model system, though the results may relate to recent experimental observations and could help to clarify these issues also. We give only pointers to these directions.
Recall that the connected hole density in a region characterizes the ease of long-ranged movement of particles in that region, these being the empty spaces on the lattice that permit sustained motion. Given this, the Fig. 1 Inset is striking. There we show both the first (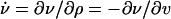 ) and second derivatives (
) and second derivatives (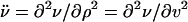 ) of the connected hole density with respect to particle (or vacancy, υ) density. The former is the long-wavelength limit of the response of dynamical processes in the system to small changes in particle density. We observe a transition in the response of the dynamics to small changes in particle density. For densities lower than ρ = 0.85 (the unstable regime¶) a small local decrease of density leads to many new connected holes, and thereby opens up many new transport pathways. For particle densities higher than this (the metastable regime) the response of dynamical properties to a density fluctuation is vanishingly small.
) of the connected hole density with respect to particle (or vacancy, υ) density. The former is the long-wavelength limit of the response of dynamical processes in the system to small changes in particle density. We observe a transition in the response of the dynamics to small changes in particle density. For densities lower than ρ = 0.85 (the unstable regime¶) a small local decrease of density leads to many new connected holes, and thereby opens up many new transport pathways. For particle densities higher than this (the metastable regime) the response of dynamical properties to a density fluctuation is vanishingly small.
Albeit in this context of near-arrested systems, these ideas make contact with early prescient remarks (30) in which it was suggested that bootstrap models might offer an explanation for the decay of the metastable state and (by extension) the spinodal transition to unstable state decay. Indeed, the two regimes of connected hole density reflect the relaxation of particle configurations by two characteristic means. At low density, configurations are intrinsically unstable to small spatial variations of density, these leading to dynamical pathways reminiscent of spinodal waves that enable efficient relaxation of quite dense particle configurations. Beyond the peak at ρ = 0.85 the state develops metastability, this being reflected also in the characteristic exponentially small connected hole density there, and the decay of such configurations becomes much more difficult. Fig. 4 illustrates these ideas in a more visual manner. Thus, Fig. 4A represents a configuration at density ρ = 0.79. There we see the development of spinodal-like patterns of empty space as particles are removed from the unstable state. Fig. 4B, at ρ = 0.915, exhibits the classical appearance of decay of the metastable state, including growing empty droplets, with smaller subcritical droplets failing to grow any further. These analogies will prove deeply helpful in future formulations of quantitative laws for dynamical arrest also (34).
Fig. 4.
The two regimes. Shown are configurations (L = 400) after partial removal of particles via parallel updating. The two examples refer to the unstable regime (A) and the metastable regime (B), lying respectively to the left and right of the peak in the Fig. 1 Inset. The process is stopped after removal of 50% of the particles (black) (the gray scale representing the time during the process when the particles were removed).
The peak of the second derivative in Fig. 1 defines a transition between two near-jammed regimes, the first unstable regime where spatial density heterogeneities produce large heterogeneities also in the dynamics, the second metastable regime where the response is much weaker. This observation may well be related to recent ideas derived from simulations (35, 36) and experiments (37–39) where dynamically heterogeneous processes have been viewed as intrinsic to the arrest process. The size of these domains in our bootstrap calculation (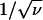 ) in the unstable regime reaches a maximum value of ld = 8 at ρ = 0.85. Thereafter the dynamically heterogeneous processes change their nature to droplets of movement and the system continues to slow further, as the number of connected holes decreases. Thus, the dynamical (here bootstrap) correlation length continues to diverge, but no longer has the same quality of dynamical heterogeneity.
) in the unstable regime reaches a maximum value of ld = 8 at ρ = 0.85. Thereafter the dynamically heterogeneous processes change their nature to droplets of movement and the system continues to slow further, as the number of connected holes decreases. Thus, the dynamical (here bootstrap) correlation length continues to diverge, but no longer has the same quality of dynamical heterogeneity.
That there exists two such regimes, with a clearly defined transition between them has not been previously clarified in the scientific literature, to our knowledge. There is inferential evidence from simulations and experiment that dynamical heterogeneities near arrest (36) might change as the system further progresses toward complete arrest. However, the broader implication of this discussion is that dynamical heterogeneities, and the metastable state, could be formulated into a theoretical approach via these response functions in available volume. It is encouraging to note that, with the advent of new microscopy tools (37, 38), there has emerged the possibility to directly measure these more appropriate order parameters and response functions by using direct optical imaging.
We do not here deal with the issue in detail, but note that, associated with the two regimes of the response function, the transport coefficients governing these two regimes should be quite different. This observation might also point to a resolution of another long-standing controversy about the nature of the dynamical laws (power law or `exponential') near arrest.¶
Discussion
In summary, this approach to treating strong jamming correlations by using random paths between appropriately selected states means that the 2D bootstrap model can now be solved exactly. This advance allows us to explore phenomena far beyond the reach of simulations with modern computers and provides us with a complete picture of the onset of arrest.∥ The conclusions of the study are intriguing and resolve long-standing apparent conflicts between theoretical and simulation treatment of these problems.
True arrest occurs only as a limit of a metastable state when the system is dense-packed on the lattice. Thus, even the smallest amounts of available volume means that motion is still possible, albeit at enormously long time scales. The finite size dependence of this regime is barely appreciable, but nevertheless persists up to the fully packed limit and means that neither simulations, nor nature, can ever access length scales where simple asymptotic results in terms of density are valid.** However, the results written in terms of connected hole density, or dynamically available volume, are simple. This has deep implications for the way in which experiments (indeed the whole study of dynamical arrest) might be framed in the future (22, 33).
Finally, and important to the general arena of dynamical arrest, we have shown how the conceptual infrastructure of order parameters, dynamically available volumes, spatio-temporal correlation lengths, and equations to represent them, may be framed into a closed theory, from which rational approximations emerge. However, it is our belief that these principles governing treatment of the bootstrap are close to those required to frame a comparable dynamical theory, from which one would obtain the transport coefficients in systems that are dynamically slowed.
Understanding and ultimately calculating these transport coefficients in dynamically slowed systems from a fundamental theoretical basis, and comparing them to results from carefully designed experiments, constitutes one of the outstanding challenges of those interested in the field of dynamical arrest.
Acknowledgments
We acknowledge fruitful interactions with A. van Enter, E. Marinari, M. Mezard, G. Parisi, A. Robledo, M. Sellitto, D. Stauffer, and P. Tartaglia.
This paper was submitted directly (Track II) to the PNAS office.
Footnotes
In conventional bootstrap percolation, particles are removed if they are surrounded by c or fewer particles. In modified bootstrap percolation, an additional condition requires the neighboring vacant sites to be second neighbors to each other.
These movements tend to restore the symmetric empty square, except for the state represented by 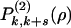 .
.
The threshold value lc in (Fig. 3) can be understood as that size at which, with equal probability, the droplet can either grow or find a cage in the next step.
The low-density near-arrest regime has a hole density that is well fitted to power laws (ρc – ρ)μ with ρc and μ suitably defined in the range of interest, whereas the high-density regime is well fitted to the exponential law exp[f(ρ)/(1 – ρ)]exp[–π2/3(1 – ρ)].
It is possible to show that more complicated jamming scenarios may also be exactly solved in two dimensions, providing the defining constraints on particle movement remain short-ranged on the lattice.
This issue deserves some comment. There is as yet not settled opinion on where, for continuum systems, true dynamical arrest occurs. The continuum analogue of the lattice arrest transitions would likely be random close packing for hard spheres, or the Kautzmann condition for systems with finite energy repulsions.
References
- 1.Shante, V. K. S. & Kirkpatrick, S. (1971) Adv. Phys. 30, 325–357. [Google Scholar]
- 2.Reynolds, P. J., Klein, W. & Stanley, H. E. (1977) J. Phys. C 10, L167–L172. [Google Scholar]
- 3.Stauffer, D. & Aharony, A. (1992) Introduction to Percolation Theory (Taylor and Francis).
- 4.Pollak, M. & Reiss, I. (1975) Phys. Status Solidi b 69, K15–K18. [Google Scholar]
- 5.Kogut, P. M. & Leath, P. L. (1981) J. Phys. C. 14, 3187–3194. [Google Scholar]
- 6.Ertel, W., Frobröse, K. & Jäckle, J. (1988) J. Chem. Phys. 88, 5027–5034. [Google Scholar]
- 7.Jäckle, J. & Krönig, A. (1994) J. Phys. Condens. Matter 6, 7633–7653. [Google Scholar]
- 8.Kirkpatrick, S., Wilcke, W., Garner, R. & Huels, H. (2002) Physica A 314, 220–229. [Google Scholar]
- 9.Ritort, F. & Sollich, P. (2003) Adv. Phys. 52, 219–342. [Google Scholar]
- 10.Toninelli, C. & Biroli, G. (2004) J. Stat. Phys. 117, 27–54. [Google Scholar]
- 11.Pan, A. C., Garrahan, J. P. & Chandler, D. (2004) e-Print Archive, http://xxx.lanl.gov/abs/cond-mat/0410525.
- 12.Schwarz, J. M., Liu, A. J. & Chayes, L. Q. (2004) e-Print Archive, http://xxx.lanl.gov/abs/cond-mat/0410595.
- 13.Dawson, K. A. (2000) Curr. Opin. Coll. Int. Sci. 7, 218–227. [Google Scholar]
- 14.Kirkpatrick, T. R., Thirumalai, D. & Wolynes, P. G. (1989) Phys. Rev. A 40, 1045–1054. [DOI] [PubMed] [Google Scholar]
- 15.Mezard, M. & Parisi, G. (2000) J. Phys. Condens. Matter 12, 6655–6673. [Google Scholar]
- 16.Debenedetti, P. G. & Stillinger, F. H. (2001) Nature 410, 259–267. [DOI] [PubMed] [Google Scholar]
- 17.Götze, W. (1991) in Freezing and Glass Transition, eds. Hansen, J. P., Levesque, D. & Zinn-Justin, J. (North–Holland, Amsterdam), pp. 287–343.
- 18.Liu, A. J. & Nagel, S. R. (1998) Nature 396, 21–22. [Google Scholar]
- 19.Onsager, L. (1944) Phys. Rev. 65, 117–149. [Google Scholar]
- 20.Widom, B. (1974) Physica 73, 107–118. [Google Scholar]
- 21.Adler, J. (1991) Physica A 171, 453–470. [Google Scholar]
- 22.Lawlor, A., Reagan, D., McCullagh, G. D., De Gregorio, P., Tartaglia, P. & Dawson, K. A. (2002) Phys. Rev. Lett. 89, 245503. [DOI] [PubMed] [Google Scholar]
- 23.Toninelli, C., Biroli, G. & Fisher, D. (2004) Phys. Rev. Lett. 92, 185504. [DOI] [PubMed] [Google Scholar]
- 24.Cerf, R. & Manzo, F. (2002) Stochastic Processes Appli. 101, 69–82. [Google Scholar]
- 25.Holroyd, A. (2003) Probability Theor Related Fields 125, 195–226. [Google Scholar]
- 26.De Gregorio, P., Lawlor, A., Bradley, P. & Dawson, K. A. (2004) Phys. Rev. Lett. 93, 025501. [DOI] [PubMed] [Google Scholar]
- 27.Kurtsiefer, D. (2003) Int. J. Mod. Phys. C 14, 529–536. [Google Scholar]
- 28.Adler, J. & Lev, U. (2003) Brazilian J. Phys. 33, 641–644. [Google Scholar]
- 29.Gray, L. (2003) Notices Am. Math. Soc. 50, 200–211. [Google Scholar]
- 30.Aizenman, M. & Lebowitz, J. L. (1988) J. Phys. A Math. Gen. 21, 3801–3813. [Google Scholar]
- 31.van Enter, A. C. D., Adler, J. & Duarte, J. A. M. S. (1990) J. Stat. Phys. 60, 323–332. [Google Scholar]
- 32.Schonmann, R. (1992) Ann. Probab. 20, 174–193. [Google Scholar]
- 33.Dawson, K. A., Lawlor, A., De Gregorio, P., McCullagh, G. D., Zaccarelli, E., Foffi, G. & Tartaglia, P. (2003) Faraday Discuss. 123, 13–26. [DOI] [PubMed] [Google Scholar]
- 34.Lawlor, A., De Gregorio, P., Bradley, P., Sellitto, M. & Dawson, K. A. (2005) e-Print Archive, http://xxx.lanl.gov/abscond-mat/0503089. [DOI] [PubMed]
- 35.Franz, S. & Parisi, G. (2000) J. Phys. Condens. Matter 12, 6335–6342. [Google Scholar]
- 36.Glotzer, S. C., Novikov, V. N. & Schroeder, T. B. (2000) J. Chem. Phys. 112, 509–512. [Google Scholar]
- 37.Weeks, E. R., Crocker, J. C., Levitt, A. C., Schofield, A. & Weitz, D. A. (2000) Science 287, 627–631. [DOI] [PubMed] [Google Scholar]
- 38.Kegel, W. K. & van Blaaderen, A. (2000) Science 287, 290–293. [DOI] [PubMed] [Google Scholar]
- 39.Cipelletti, L., Bissig, H., Trappe, V., Ballesta, P. & Mazoyer, S. (2003) J. Phys. Condens. Matter 15, S57–S64. [Google Scholar]