Architectural and synaptic mechanisms underlying coherent spontaneous activity in V1

Abstract

To investigate the existence and the characteristics of possible cortical operating points of the primary visual cortex, as manifested by the coherent spontaneous ongoing activity revealed by real-time optical imaging based on voltage-sensitive dyes, we studied numerically a very large-scale (≈5 × 10⁵) conductance-based, integrate-and-fire neuronal network model of an ≈16-mm² patch of 64 orientation hypercolumns, which incorporates both isotropic local couplings and lateral orientation-specific long-range connections with a slow NMDA component. A dynamic scenario of an intermittent desuppressed state (IDS) is identified in the computational model, which is a dynamic state of (i) high conductance, (ii) strong inhibition, and (iii) large fluctuations that arise from intermittent spiking events that are strongly correlated in time as well as in orientation domains, with the correlation time of the fluctuations controlled by the NMDA decay time scale. Our simulation results demonstrate that the IDS state captures numerically many aspects of experimental observation related to spontaneous ongoing activity, and the specific network mechanism of the IDS may suggest cortical mechanisms and the cortical operating point underlying observed spontaneous activity.

Traditional views of cortical information processing have emphasized the activity of single neurons. Alternatively, in population coding, spontaneous cortical activity of single neurons is often regarded as mere noise that carries no functional significance and, as a consequence, should be averaged out by pooling to yield signal (1–3). However, recent experimental evidence has revealed interesting structure in these spontaneous cortical fluctuations and implies that response variability arises from nonrandom, correlated interactions and that spontaneous activity has a significant impact on neuronal responses (4–7). Advances in real-time optical imaging based on voltage-sensitive dyes (VSD) (8, 9) have opened up new opportunities for exploring population activity (10). With high spatial and temporal resolutions, the real-time optical imaging using VSD has made it possible to capture activity in neuronal dendrites that cannot be easily explored by single unit recordings. Experimental results such as provided by the VSD optical imaging in combination with single unit recordings are particularly powerful in unravelling the neuronal network mechanisms because, together, they strongly constrain network dynamics. These measurements provide both spatial and temporal information in concert with individual neuron activity, and thereby can help to discriminate sharply between competing neuronal network mechanisms. The real-time optical imaging of the cat primary visual cortex by using VSD has revealed beautiful, coherent spatiotemporal structures of ongoing spontaneous activity of neuronal ensembles over imaged areas of approximately millimeter sizes (12, 13). It is found that the ongoing activity exhibits a high degree of synchrony over approximately millimeter scales, and that the spatial structures of cortical states associated with evoked activity are strongly correlated with those of spontaneous activity.

The observed spontaneous ongoing activity suggests an intriguing possibility that spontaneous cortical states possess strong functional significances by providing a cortical operating point, in interaction with external stimuli, for sensory information processing (11). Because spontaneous activity is in the absence of external stimulation, theoretical emphasis can be focused on a purely cortical model, with less modeling complications arising from processes related to retina or LGN. Two mechanisms or operating points have been hypothesized: (i) The ongoing spontaneous activity reflects the system wandering through a set of intrinsic cortical states which are closely related to orientation maps (4, 8, 12–14). In this view, the intrinsic cortical states are localized, broken-symmetry states that can be locked to a weakly tuned drive. (ii) The second view is single-state hypothesis, that is, the spontaneous ongoing activity is merely the dynamics of a single background state, driven by cortical noise (14). In ref. 14, these two models are contrasted, but simulations in ref. 14 are inconclusive in differentiating which mechanism is in operation.

In this article, by using a very large-scale computational model of V1, we have (i) identified a distinct operating point in which the model reproduces recent experimental observations (12, 13) of spontaneous ongoing activity obtained by real-time VSD optical imaging; and (ii) identified precisely the mechanisms by which the model operates in this cortical state. Our fast algorithm for large scale, integrate-and-fire conductance-based neuronal networks (developed and described elsewhere) enables us to integrate a network with sufficient lateral extent to capture spontaneous cortical activity, namely, a network of ≈5 × 10⁵ neurons, covering an ≈16-mm² cortical patch, with 64 orientation hypercolumns. By incorporating lateral, orientation specific long-range (LR) connections, together with the slow time scale of NMDA receptors, our simulations show that when the model cortex is in a cortical operating state of intermittent desuppression (described in Discussion), it exhibits spatiotemporal coherent ongoing activity that captures the experimental observations. As discussed below, this intermittent desuppressed state (IDS) is a dynamical state of the model cortex of (i) high conductance and (ii) strong inhibition, which operates in a regime driven by (iii) strong temporal fluctuations. These specific network mechanisms in the model cortex in turn suggest cortical mechanisms underlying the observed spontaneous activity in anesthetized cat.

Methods

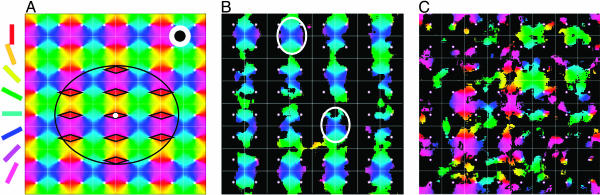
A patch (≈16 mm²) of primary visual cortex is modelled by a network of ≈5 × 10⁵ coupled, conductance-based, integrate-and-fire neurons, composed of 75% excitatory and 25% inhibitory cells, which are distributed uniformly over a two-dimensional lattice with periodic boundary conditions. This patch is tiled with 64 orientation hypercolumns with an orientation preference singularity at their centers (pinwheels; Fig. 1 A) (15–17). The dynamics of our network is governed by

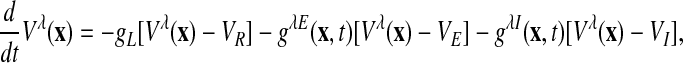[1]

where x indexes the spatial location of the neuron on the cortex, λ = E, I labels excitatory or inhibitory neurons. When the voltage of a cell reaches the threshold of –55 mV, the spike time T is recorded and the voltage is reset to the reset potential –70 mV with a refractory period τ_ref = 2 ms. We use normalized units, in which the voltage threshold becomes V_T = 1; the reset potential becomes V_reset = 0; and the reversal potentials become V_R = 0, V_E = 14/3, and V_I =–2/3, for the leak, excitatory, and inhibitory conductance, respectively, g^–1 = 20 ms (for conversion to physiological units, see ref. 18). ^LThe conductances have the form

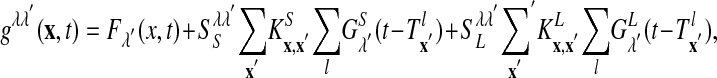where λ, λ′ = E, I and 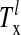is the lth spike of the neuron located at x. The second term models the isotropic local connections: 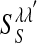is the local coupling strength; and 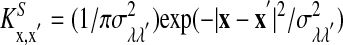, with σ_λE and σ_λI being the excitatory and inhibitory spatial scales, respectively (σ_λE, σ_λI ∼ 100–300 μm.) The time course of the synaptic conductance, 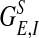, is an α function with rise time 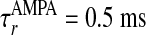, 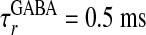and decay time 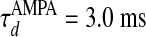, 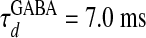for α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and GABA_A type, respectively. The third term models the anisotropic, orientation-specific LR connections, which are solely excitatory, (hence, 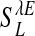is the LR coupling strength and is 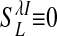) and are taken to project onto both excitatory and inhibitory cells (15, 19–21). 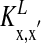takes an elliptical Gaussian form with spatial scale σ_L ∼ 1500 μm, suitably modified to account for the eccentricity of the LR patch connection (22). The coordinate x of a neuron also encodes the preferred orientation θ_op(x) of the neuron because pinwheels are overlaid on the lattice. The primed summation denotes that LR connections to x involve only cells at locations x′ of similar orientation preference (within the angular spread ±Δθ_LR to θ_op(x), Δθ_LR ≃ 7.5° and excluding its own hypercolumn of x). The conductance time course has the form 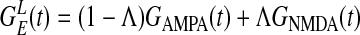, where Λ denotes the percentage of NMDA receptor contribution to the total LR conductance (23–27), G_AMPA(t) is the same as 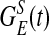, and the NMDA time course is given by 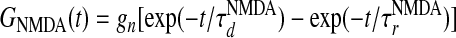, with 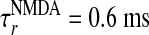, , 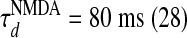where g_n is a constant (29, 30). Both 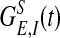and G_NMDA(t) are normalized to have unit integral. F_λ^′′(x, t) models the input to cortex due to spikes from the LGN driven by external stimulus and from the background noise to V1. In the absence of external stimulus, this input is modeled as independent Poisson spike trains to each cell, with a spatially homogeneous, constant rate to maintain a background firing rate ν_B of approximately two to five spikes per second per neuron. Detailed modeling of effective external stimuli is as described in ref. 31. We note that our network is an effective or “lumped” model of V1 because we do not include the detailed laminar structure of V1 in our modeling, consistent with the fact that the signal of the real-time optical imaging using VSD measures the sum of the membrane potential changes in all the neuronal elements in the imaged area with emphasis on the subthreshold synaptic potentials and dendritic action potentials in neuronal arborizations originating from cells in all cortical layers whose dendrites reach the superficial layers (10). We have developed a fast integrator algorithm in order to solve system 1 with 10⁵–10⁶ neurons.

Fig. 1.

Instantaneous spontaneous activity. (A) Network architecture. Periodic tiling of 64 orientation hypercolumns, with the orientation preference singularity (pinwheel center) indicated by the small white dots. The color at a spatial point labels the orientation preference of the neuron at that location. The isotropic local excitatory coupling length scale is indicated by the radius of the large white disk, which is obscured by the black disk, whose radius indicates the length scale of the local inhibitory coupling. The large ellipse indicates the spatial extent of the lateral LR connections; the rhombuses indicate the orientation domains in which the neurons are connected by the LR coupling to the neurons in the orientation domain marked by the small white circle. (B) Instantaneous spontaneous activity pattern V(x, t). The black mask is obtained by thresholding the level of instantaneous membrane potentials of the model neurons. The black area corresponds to low activity locations, where neurons have low values of membrane potential, whereas the “window” area corresponds to areas of high activity, where neurons have high values of membrane potential. These neurons are further labeled by colors to indicate their preferred orientation as tiled in the numerical cortex (which is the same as the distribution of orientations as shown in A). Two ovals indicate regions over which voltage activity can be highly correlated in time. (C) Another spontaneous activity pattern. A state with two emerging orientation preferences, which occupy mostly separate cortical regions but with a small overlap due to the LR synaptic connections of similar orientations, is shown. (For clarity of visual presentation, we used periodic boundary conditions to shift one hypercolumn down relative to A and B.)

Results

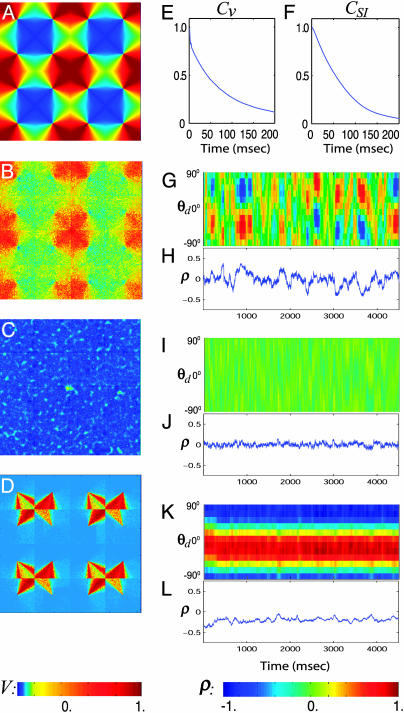
In Fig. 2 A, we display the preferred cortical state (PCS) of a neuron, defined as the spatial pattern of the average voltage V_P(x; θ_op) ≡ Σ_i V(x, tⁱ; θ_op)/N_f, evoked by a strong stimulus at the optimal orientation θ_op of the neuron, where tⁱ is the ith spike time of the neuron and N_f is the total number of spikes, as in the real-time optical-imaging experiments (12, 13). Following the same quantifications of the spontaneous activity patterns as in the experiment described in refs. 12 and 13, we compute (i) the similarity index (SI), which is the spatial correlation coefficient ϱ(θ_op; t) between the PCS V_P (x; θ_op) and the membrane potential V(x, t) of our network (we used an area of 4 × 4 pinwheels to evaluate SI, which conforms with the relevant size used in experiment); and (ii) the spike-triggered spontaneous-activity pattern (SSAP); i.e., V̄ _st(x) ≡ Σ_i V(x, tⁱ)/N_f of the network without stimulus, triggered on the spike times of a neuron with the same preferred orientation θ_op. Our simulation demonstrates that the network exhibits three distinct dynamical regimes for spontaneous activity patterns. The strength of LR synaptic connections determines these regimes, with all remaining parameters fixed.

Fig. 2.

Three dynamical regimes of the network. (A) PCS V_P(x; θ_op) across an area of 4 × 4 hypercolumns in the model. (B–D) SSAP V̄_st(x) across an area of 4 × 4 hypercolumns in the IDS, homogeneous, and locked states, respectively. The value of V in A–D is indicated by the color bar at the bottom of the left column. (E and F) Time correlation of voltage trace V(t) and the SI ϱ, respectively. (G, I, and K) The evolution of SI, ϱ(θ_d; t), for all θ_d, for the IDS, homogeneous, and locked states, respectively. ϱ(θ_d; t) is the correlation coefficient between the instantaneous voltage pattern V(x, t) and the PCS V_P(x; θ_d) evoked by the drive of orientation θ_d.¶ The value of ϱ is indicated by the color bar at the bottom right. (H, J, and L) The time trace of SI, ϱ(θ_d; t), for θ_d =–60°, for the IDS, homogeneous, and locked states, respectively. Note, in particular, the pattern and the time scale of ϱ(θ_d; t) for the IDS state.

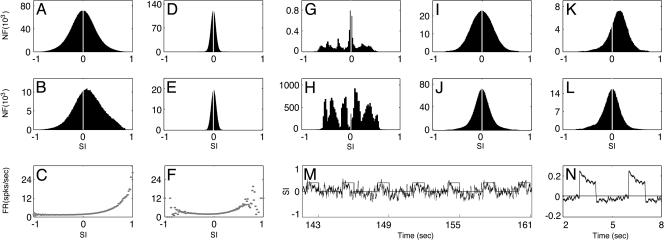
First, an IDS regime, created by a moderately strong LR coupling, giving rise to an SSAP V̄ _st(x) (Fig. 2B) that strongly resembles the PCS V_P (x; θ_op) of the neuron, as seen by comparing Fig. 2 A and B. Fig. 2G shows the evolution of ϱ(θ_d; t), which shows the ongoing activity of emergences of a spontaneous activity pattern of a particular orientation, drifting to neighboring orientations in time and disappearing. Fig. 2 G and H show that the typical duration of smooth transitions between neighboring orientations is ≈80 msec, as further quantified by the decay time in the SI autocorrelation (Fig. 2F). Fig. 3 A and B display the distribution, respectively, of the all-time SI (i.e., computed by using the instantaneous voltage patterns for all times) and of the spike-triggered SI (i.e., computed by using only the instantaneous voltage patterns triggered on the spikes of a neuron). Together, these results clearly show that the spontaneous cortical states in our simulation produce SI behavior similar to that measured in the experiment in terms of distribution and time course of SI (12, 13). Fig. 3C describes the firing rate for the neuron as a function of SI, which reproduces the experimentally observed asymmetry: the more likely the neuron is to fire, the larger the values of the SI. We observe that the time scale τ_ρ of the SI fluctuations is approximately the same as the time scale τ_v of the membrane potential fluctuation, as shown in Fig. 2 E and F. (See a description of the cortical mechanism underlying this dynamic regime in Discussion.)

Fig. 3.

Similarity index of different dynamical regimes. (A, D, and G) The distribution P_A(SI) of the all-time SI for the IDS, homogeneous, and locked states, respectively. The all-time SI was computed by spatially correlating V_P(x; θ_d) for a fixed θ_d with the instantaneous spontaneous voltage pattern frames sampled at the rate ν_S = 1 frame per millisecond for a total duration T = 256 s. (B, E, and H) The distribution P_S(SI) of the spike-triggered SI for the IDS, the homogeneous state, and the locked state, respectively. The spike-triggered SI was computed by spatially correlating V_P(x; θ_d) for the same fixed θ_d as in A, D, and G, with the instantaneous spontaneous voltage patterns sampled only on the spike times of N_SI neurons that have the same orientation preference θ_op = θ_d in a small area for the same duration T = 256 s. (We used the number of neurons N_SI = 64 instead of one neuron here to improve statistics.) (C and F) The firing rate (spikes per second) as the function of the SI for the IDS and the homogeneous state, respectively. This curve is constructed by [(P_S(SI)/N_SI)/P_A(SI)] × ν_S. (I and J) We collected instantaneous voltage pattern frames V(x, t, θ_d) (sampled at the rate ν_S) evoked by drives of all possible orientations, θ_d ∈ [0, π). (I) The ON distribution of SI. The values of SI used to obtain the ON distribution were generated by correlating each V(x, t_on, θ_d) (frames recorded over the stimulus-on intervals) with the PCS V_P(x; θ_op) of a neuron. (J) The OFF distribution of SI, similarly obtained by using V(x, t_off, θ_d) (frames recorded over the stimulus-off intervals). (K and L) We collected instantaneous voltage pattern frames V(x, t, θ_op) (sampled at the rate ν_S) evoked by the drive of fixed θ_d = θ_op of a neuron. (K) The ON distribution of SI. The values of SI used to obtain the ON distribution were generated by correlating each V(x, t_on, θ_op) (frames recorded over the stimulus-on intervals) with the PCS V_P(x; θ_op) of the neuron. (L) The OFF distribution of SI, similarly obtained by using V(x, t_off, θ_op) (frames recorded over the stimulus-off intervals). [The ordinate for A, B, D, E, and G–L is the number of frames (NF).] (M) The time trace of SI, ϱ(θ_op; t), under a periodic drive of orientation θ_d = θ_op, which is on for 1 s and then off for 2 s, as indicated by the teeth. (N) The cycle-averaged trace of the SI evolution in M (two cycles displayed).

Second, a homogeneous regime, created by weak LR couplings, that exhibits a spatially homogeneous cortical state whose SSAP is depicted in Fig. 2C. The pattern is not correlated with the PCS (i.e., it no longer encodes the orientation preference of the neuron), and the evolution (as shown in Fig. 2 I and J)ofthe SI fluctuates around zero with a very small variance of ≈0.06 (as further corroborated by Fig. 3 D and E), which is much smaller than experimentally observed values (12, 13). The firing rate for the neuron vs SI (Fig. 3F) in this regime fails to capture the experimentally observed shape. These results show that our homogeneous regime reproduces in the large-scale neuronal network the behavior of the “homogeneous phase” studied in ref. 14 in idealized mean-field models.

Third, a dynamically locked regime, created by very strong LR couplings, which locks an SSAP to particular orientations that may or may not be the preferred orientation of the neuron. Fig. 2D shows such a locked pattern of nonpreferred orientations, which persists in time for many tens of seconds or longer, as shown in Fig. 2K. When a particular locked pattern is not the same as the PCS, then the SI will be small for the duration of locking (Fig. 2L). In this locked regime, the distribution of the SI (Fig. 3G) reveals that the spontaneous cortical states do not correlate with the PCS for most of the total simulation time of 256 s. In our simulation, the network locks to such a broken-symmetry state (32) of orientation for a long period, then drifts to another broken-symmetry state. Fig. 3H shows that for the total duration of the simulation time of 256 s, the network has only wandered through approximately six of such broken-symmetry states. These results show that the dynamics of this locked regime is similar to that of the marginal phase in ref. 14. As pointed out there, all these features are inconsistent with experiment. We observed that the transition from the fluctuation-dominated IDS regime to the locked regime is rapid: only a small percentage of change in the LR coupling strength 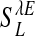switches the network from the IDS to the locked state.

In the IDS regime, we note that any particular pattern of the coherent spontaneous activities can persist, or smoothly transition to neighboring orientations, typically for ≈80 ms and its spatial span can cover the entire extent of the network. Such a dynamic cortical state is shown in Fig. 1B. Here, we see clearly that those spatial patches of high activity lie over the isoorientation domains corresponding to the “blue-green” angles. We note that any two nonoverlapping regions of these orientation domains of high activity (for example, regions marked by two ovals in Fig. 1B) tend to emerge simultaneously or follow each other closely in time as the pattern slowly drifts continuously in space. This phenomenon arises from nearly synchronized voltage over domains of similar orientations over large distances (of scales of many pinwheels) caused by the LR synaptic connections as explained in Discussion. This phenomenon is observed experimentally (13).

It is important to emphasize that not all these patterns have to span the entire network with a single orientation preference. Fig. 1C shows a spontaneous cortical state with two emerging orientation preferences (angles labelled by “green-cyan” and “purple-red,” respectively), which predominantly occupy separate cortical regions with small penetrations into each other's territory because of the LR synaptic connections of similar orientations. Note that, in this particular case, these two orientations (green-cyan vs. purple-red) happen to be orthogonal to each other. The cortical state in Fig. 1C has many instances in which high activity of two orientations, orthogonal (e.g., green-cyan vs. purple-red, or blue vs. yellow) or neighboring (e.g., blue vs. cyan or blue vs. purple) can be present simultaneously in a single pinwheel. Cortical patterns of a multi-preference type are not necessarily fast transient states between two robust patterns of single orientation preferences because they can also persist as fluctuating, long-lived (≈80 ms, not seconds), drifting cortical states in the IDS regime. These features would be difficult to account for by using the notion of marginal phase (12, 14, 32) (see also the discussion of locked regime above).

Next, we turn to evoked cortical states: Here, we fix the LR coupling strength such that our network dynamics is in the IDS regime in the absence of a stimulus. Under the LGN drive of the optimal orientation of a neuron, which is turned on and off periodically, the spike-triggered activity patterns produced in our network look essentially similar to the PCS (data not shown). The time evolution of SI is shown in Fig. 3M, which shows that, when the stimulus is on, the activity patterns tend to rapidly swing into positive values of SI (i.e., to correlate more with the PCS of the neuron for the whole evoked duration), as further corroborated by the positive mean in the SI distribution shown in Fig. 3K and by a cycle-averaged SI time course (Fig. 3N). An important feature of the SI time course (Fig. 3M) is that, when the stimulus is just turned off, the SI tends to quickly swing into negative values of SI and, then, gradually moves back towards zero, as accentuated by the cycle-averaged SI time course (Fig. 3N) and further illustrated by a negative mean in the SI distribution in Fig. 3L. Note that all of these features, including “negative-swing” phenomenon, are observed experimentally (12, 33).

We further describe how the dynamics of the cortical activity states are modulated by the stimulus in this evoked IDS regime. Fig. 3I plots the ON distribution of SI that is computed by using only the instantaneous voltage patterns evoked by drives of all possible orientations θ_d over the stimulus-on intervals, which is then correlated with the PCS of a neuron, whereas Fig. 3J plots a distribution, obtained the same way except over the stimulus-off intervals (which will be referred to as the OFF distribution). Because all drive orientations θ_d are included, these distributions are obviously symmetric. However, the OFF distribution has a much narrower width than the ON distribution, implying that under the modulatory effect of the stimulus, the cortex is driven into a highly correlated/ anticorrelated state much more often over the stimulus-on intervals than the base-line state of the stimulus-off intervals, a fact that is distinct from the marginal phase scenario (12, 14, 32).

Discussion

Next, we turn to a discussion of the underlying mechanisms for the IDS cortical state or operating point. A key feature of IDS is the rapid recruitment of excitatory neurons in an orientation domain. After a short transient, the network dynamics settles into the IDS state, in which the neurons in an orientation domain become nearly synchronized statistically, with a single spontaneous firing of one neuron leading to a recruitment of many nearby neurons, i.e., they all fire within a few milliseconds after one another. This excitatory recruitment event induces desuppression in our strongly inhibited network, immediately recruiting neurons of similar orientation preferences via strong g_NMDA synaptic couplings across the area covered by the LR connection (as shown schematically in Fig. 1 A). The recruitment may spread to almost all similar orientation domains by means of cascading events, giving rise to a near voltage synchronization statistically over these orientation domains and to the voltage spatial pattern statistically resembling the PCS of this orientation (i.e., a higher SI value). (Note that this high SI is also correlated with a higher firing rate because there are more firings in the cascading recruitments. Hence, the asymmetry in Fig. 3C).

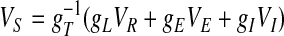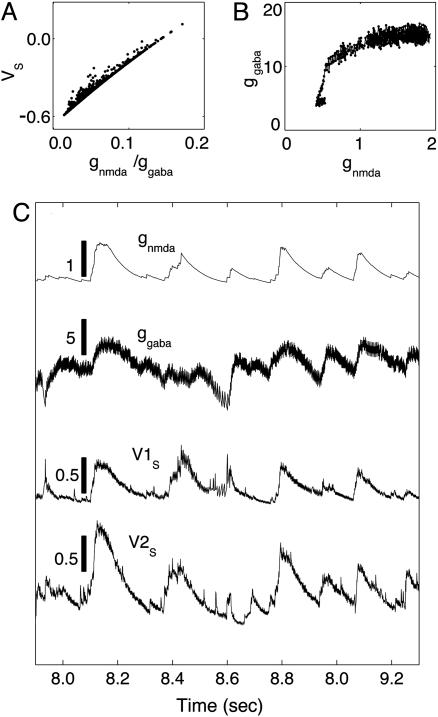
The IDS state can be more completely and thoroughly understood by combining this recruitment mechanism with the “correlation mechanisms” at a strongly inhibited, high conductance state. The governing equation for a single integrate-and-fire neuron in our network can be cast as V̇ =–g_T(V – V_S). g_T = g_L + g_E + g_I, g_E = g_AMPA + g_NMDA, g_I = g_GABA, is the slaving potential. The postanalysis of our network simulation shows that the IDS state operates at a high conductance state; i.e., g_T >> g_L, (with the time scale 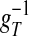much shorter than that of the NMDA synaptic fluctuations) in a strongly inhibited regime (34); i.e., V_S is much below V_T for most of time and g_E/g_I << 1 (g_E/g_I ∼ 0.1–0.2 in our simulation). This state is clearly not any state of a balanced network (35). It is observed that, in the IDS state, g_NMDA >> g_AMPA. Hence, the strong inhibition, g_E/g_I << 1, yields V_S ≈ (g_NMDA/g_I)V_E + V_I, as confirmed in Fig. 4A.§ Therefore, the membrane potential V is slaved to V_S (36) over the time-scale of 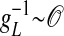(10 ms) (thus, certainly on the NMDA time scale of the predominant synaptic fluctuations) and is strongly correlated with the ratio g_NMDA/g_I. In addition, it is observed that the inhibitory conductance g_I increases sublinearly with the synaptic NMDA input g_NMDA statistically, as shown in Fig. 4B. Therefore, the subthreshold V is positively correlated with the g_NMDA of a neuron in the IDS regime, inducing correlation between the voltage spatial pattern of our network and the NMDA conductance spatial pattern. Thus, in the IDS state, we have a sequence of correlations: V(t) ∼ V_S(t) ≈ (g_NMDA/g_I)V_E + V_I ∼ g_NMDA. These correspondences show, for example, that in the recruitment events, a spontaneous firing of one neuron can be triggered by an increase of its fluctuating synaptic input g_NMDA or by a decrease of its g_I and that a desuppressing recruitment event immediately increases the g_NMDA substantially of the neurons of similar orientation preferences across the area covered by the LR connection and, thus, gives rise to a near voltage synchronization statistically over these orientation domains.

Fig. 4.

Correlation mechanisms. (A) The statistical relationship between V_S and the ratio g_NMDA/g_I, where g_I = g_GABA, which plots V_S(t_s) vs. g_NMDA(t_s)/g_I(t_s) at the same sampling times t_s, which are sampled at a fixed rate, where V_S(t), g_NMDA(t), g_I(t) are typical time traces of slaving voltage, the NMDA conductance, and inhibitory conductance, respectively, from our simulation in the IDS state. (B) The statistical relationship between g_I and g_NMDA, which plots g_I(t_s) vs. g_NMDA(t_s) at the same sampling times t_s, which are sampled at a fixed rate, from typical time traces of g_I(t) and g_NMDA(t) from our simulation in the IDS state. (C) The two upper traces are typical time traces of g_NMDA(t) and g_I(t), which clearly are strongly correlated with a fluctuation time scale of 𝒪 (80 ms) [Note that, obviously, g_I(t) has also a faster time scale of the GABA conductance decay time 𝒪 (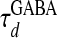).] The vertical bars indicate the relative values of the conductances. Bottom traces show typical time traces of V_S(t) (but with stronger fluctuations than the typical case) for two model neurons in the IDS state that are ≈0.5 mm apart spatially and are not spiking for the duration shown here but with a strong correlated evolution. The vertical bars indicate the value of the voltage in our nondimensional units. Note that the V_S(t)–g_NMDA(t) correlation is clearly observed here.

In addition, the recruitment events simultaneously evoke a strong inhibitory suppression by local connections, extinguishing the recruitment locally, leaving the g_NMDA to decay naturally, thus leading to a gradual decay of the voltage pattern of this angle because of the strong V–g_NMDA correlation. Clearly, the decay time of this voltage activity pattern is controlled by the decay time scale of g_NMDA, on 𝒪 (80 ms). Note that under this decaying g_NMDA, the inhibitory neurons gradually reduce their firing rate over the same time scale. Fig. 4C (upper traces) shows this correlated evolution of g_NMDA and g_GABA with a fluctuation decay time of ≈50–100 ms after each rapid rise, which is induced by intermittent recruitment events. Last, because of the angular spread of the LR connection and a higher recruitment probability arising from a large g_NMDA, the voltage pattern can also drift to a nearby preference, as shown in Fig. 2G.

We point out that our network in the IDS cortical state exhibits additional noteworthy dynamic features that are consistent with experimental observations.

First, the spontaneous fluctuations of the membrane potentials V (t) for neurons located in a small cortical area (less than ≈0.5 mm) in our network can be strongly synchronized even when they are not spiking, thanks to their common synaptic inputs from LR connections. Typical V (t) traces of such two cells are shown in Fig. 4C (two bottom traces). These traces exhibit a strong similarity to the synchronized spontaneous fluctuations reported in ref. 7 of the intracellular recordings, which are not caused by mutual interconnections by spiking. A time correlation function for V (t)isplotted in Fig. 2E, which shows a decay time τ_v of 𝒪 (80 ms), similar to what is observed in intracellular measurements (7). Clearly, τ_ρ ∼ τ_v is directly related to the fluctuation time scale in the synaptic conductance inputs by our mechanism. We note that the correlated spontaneous fluctuations in our network instantiates that the so-called spontaneous noise, usually associated with response variability, should be carefully modeled because a mere pooled averaging may not sharpen signals (4, 6, 7), contrary to the common practice in population coding.

Second, an important aspect of our modeling is that the LR synaptic coupling contains NMDA conductance. In our IDS regime, the persistence time scale τ_ρ of an activity pattern is controlled by the NMDA conductance decay time scale. A shorter (or longer) 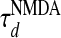will produce a shorter (or longer) τ_ρ. This NMDA-mediated spontaneous activity is consistent with experimental observations that blocking NMDA receptors with the antagonist APV in vivo can substantially reduce random, spontaneous activity of cells in the cat visual cortex (24, 27). Although the ratio Λ of the NMDA contribution can be as small as 5% to obtain all the IDS features by adjusting the LR coupling strength, it cannot be set at zero; i.e., the LR connection cannot be purely AMPA. Blocking the NMDA, the dynamics of our network can be readjusted, by strengthening AMPA, into an IDS regime to exhibit similar distributions of SI and similar spatial activity patterns (data not shown) to the PCS. However, the persistence time scale of the pattern fluctuations is too short: only ≈20 ms (data not shown), which is not consistent with experiment (7, 13) either in terms of patterns drifting (13) or the time scale of spontaneous fluctuations (6, 7).

Third, the negative-swing of SI (Fig. 3 M and N) observed in our network in the evoked IDS regime is consistent with the scenario of disinhibition from cross-orientation sites, i.e. cells in cat visual cortex show increase in response to nonoptimal orientations during inactivation of a laterally remote, cross-orientation site (37, 38). The optimal isoorientation domains in our entire network, with the presence of strong NMDA conductance, have excitatory recruitment enhancements when the stimulus is on. In turn, these recruitment events induce more firings of inhibitory cells, thus enhancing suppression of activities in the surrounding domains of other orientations. Hence, more frequent positive large values of SI during the stimulus-on period (Fig. 3N). As soon as the stimulus is switched off, this inhibition is reduced, giving rise to a potential increase in activity in nearby domains. Because the domains with the orthogonal orientation were the least inhibited, the disinhibition induces a quick excitatory recruitment, generating high activity there, in turn suppressing other domains. Therefore, this process produces a spatial activity pattern that is anti-correlated with the PCS after the stimulus is switched off. Hence, the negative-swing in SI (Fig. 3N). These positive and negative swings were observed experimentally (12, 33), as commented above. We note that, in our network, the effective spatial scale of cross-orientation inhibition, which is transmitted by the LR NMDA coupling, can be over several millimeters, therefore, involving many pinwheels.

It is worthwhile to comment about some additional important model characteristics in our network. (i) We do not invoke structured feedback from higher cortical regions or a correlated LGN background firing to produce the spontaneous fluctuating cortical states, because the background inputs to our network have no spatial nor temporal structure; they are merely independent Poisson spike inputs to every neuron with the same constant rate. (ii) In our network, there are two types of cells (i.e., simple and complex cells) of an equal proportion. They are modeled by different strengths of their short range connections: Complex cells have a stronger cortico-cortical interaction and weaker or no inputs from the background. The spike-triggered SI distribution (Fig. 3B) can be viewed as the sum of two Gaussian-like contributions from these two types of cells, with a larger shift in mean towards positive, high SI values by the complex population. If there were a continuous diversity among complex/simple types (31), then the net effect by complex cells is merely to shift the mean, without the clear separation of two populations.

Last, we address the robustness of our results. Over wide ranges of network architectural parameters, the dynamic features observed in the IDS regime can be obtained, by readjusting coupling strengths. Thus, the IDS persists for (i) the ratio Λ of NMDA to the total conductance of the LR connection ranging from ≈5% to 100%; (ii) the LR coupling eccentricity (22), characterized by the ratio of major axis to the minor, ranging from ≈1 to 2; (iii) the ratio σ_λE/σ_λI of the spatial scales of excitatory to inhibitory cells, ranging from ≈0.5 to ≈2; (iv) a synaptic release probability (28) for cortico-cortical connections, ranging from 100% to ≤50%; (v) the background firing rate ν_B from 2 to 20 spikes per second; (vi) the orientation spread projected by the LR couplings, ±Δθ_LR from ±5° to ±11°. Adding synaptic depression and spike frequency adaptation to our modeling was shown in our simulations to have little effects because of the very low spontaneous firing rate of the cortex (data not shown).