Abstract
Background:
Cancer is one of the most common causes of human mortality, with about 14 million new cases and 8.2 million deaths reported in in 2012. Early diagnosis of cancer through screening allows interventions to reduce mortality. Fractal analysis of medical images may be useful for this purpose.
Materials and Methods:
In this study, we examined magnetic resonance (MR) images of healthy livers and livers containing metastases from colorectal cancer. The fractal dimension and the Hurst exponent were chosen as diagnostic features for tomographic imaging using Image J software package for image processings FracLac for applied for fractal analysis with a 120x150 pixel area. Calculations of the fractal dimensions of pathological and healthy tissue samples were performed using the box-counting method.
Results:
In pathological cases (foci formation), the Hurst exponent was less than 0.5 (the region of unstable statistical characteristics). For healthy tissue, the Hurst index is greater than 0.5 (the zone of stable characteristics).
Conclusions:
The study indicated the possibility of employing fractal rapid analysis for the detection of focal lesions of the liver. The Hurst exponent can be used as an important diagnostic characteristic for analysis of medical images.
Keywords: Computer aided diagnosis, cancer, fractal analysis, data set, screening, machine learning
Introduction
Due to its high incidence and poor long-term results to treatment, Cancer remains the one of the most important problems in medicine. According to the International Agency for Research on Cancer, oncological diseases are a major cause of morbidity and mortality throughout the world - in 2012 was about 14 million new cases and 8.2 million deaths associated with cancer (Stewart et al., 2016). It is expected that over the next 20 years the number of new cases will increase by about 70%. The problem of improving the immediate and long-term results of treatment is in the closest relationship with the resolution of the question of early detection of cancer (Ng et al., 2013).
The presence of clinical manifestations in cancer often shows a significant prevalence of pathological process.
Therefore, expanding the range of diagnostic procedures during the asymptomatic cancer seems the obvious solution, primarily due to the improvement of the forms of screening.For example, in the US, the development of early diagnostic methods has increased the survival of patients from 1 in 69 to 1 in 22 cases (Arteaga et al., 2014). Diagnostic methods for screening in terms of economy and security may be less accurate than the clinical diagnosis (Tsuda and Moore, 2001). Computer-aided diagnostics and analysis of MR images could be some of the most useful methods of screening because of their ability to improve the processing efficiency of the relatively large amounts of information (Podolsky et al., 2016; Alharbi et al., 2016)
The authors have experience in the study of MRI image processing, as well as methods of mathematical analysis (Flegontov et al., 2009).
At present, the allocation of small objects, which have a random arrangement or fuzzy contours on medical images, is large enough complexity (Marusina et al., 2015). Such objects, inter alia, may be the formation of small foci. Therefore, the use of fractal analysis can be important for determining the presence of small focal lesions in the medical images (Mohammadzadeh et al., 2015).
Modern research shows that many natural objects characterized by fractal structure, such a structure have the bronchial tree and the arterial tree (Ishida et al., 1993). The development of fractal analysis technology allows using for the detection and description of the structure of focal lesions, in particular making it possible to assess the development of cancer. This was first noted by Landini and Rippin (1993). However, only in recent years, has attentions been paid to the advantages of using fractal geometry in medicine, particularly in cardiology and radiology. For example, Hemsley (2009) proposed a classification method for focal lesions using multifractal analysis. Several studies have shown the potential of fractal analysis as the morphological characteristic of irregular structures of focal lesions, based on the fact that fractal geometry is the theoretical basis for the study and modeling of irregular structures (Mandelbrot, 1983). For example, fractal characteristics have been used to represent complex changes in the density and structure of the breast tissue that are used to highlight atypical areas on the mammograms (Caldwell et al., 1990; Guo et al., 2005).
The objective of this study is to evaluate the applicability of fractal analysis for the detection of focal lesions on MR images.
Materials and Methods
Materials
In the study, we used ImageJ software package (Rasband W., National Institutes of Health, USA, ver. 1.50d, URL: https://imagej.nih.gov/ij) for image processing and special application FracLac (Karperien A., Charles Sturt University, Australia, ver. 2.5., URL: https://imagej.nih.gov/ij/plugins/fraclac/FLHelp/Introduction.htm) for fractal analysis. This software package allows you to analyze, edit, process, 8-, 16- and 32-bit images of various formats - including the DICOM format, which is especially important in this work, as this format is a recognized standard for the preservation of radiological studies and in particular is widely used for screening. Moreover, the complex supports image processing functions such as logic and arithmetic operations between images, change the contrast and sharpness, convolution, smoothing, edge detection, Fourier analysis. Conveniently that it was made possible in one of the program as the process images (select areas of different sizes, change their settings, etc.) and to carry out fractal analysis.
Methods
The fractal dimension of the image and the Hurst exponent were chosen as diagnostic features for tomographic imaging.
Fractal dimension for regular fractals describes the repeatability of geometry, and for irregular it describes repeatability of statistical characteristics when zooming.
One of the most widely used methods of determining the fractal dimension is the box-counting method. Its popularity is proven by fairly simple mathematical calculations, empirical evaluation and application of the same efficiency for point sets, linear objects, areas and volumes (Falconer et al., 1990; Li et al., 2009). In this method, the area containing a fractal A is divided into square cells with ε size at each step (at each stage of iteration the size ε is different from the previous one). Then, count the number of cells required to cover every case. Obtained values are substituted in ratio
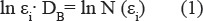
or plotted ln N (εi), from the cell size ln εi, where the tangent of the angle of the line is a cell dimension D. Calculated cell dimension D is an estimate of the fractal dimension D.
The Hurst exponent is a measure of self-similarity. The value of this parameter for most signals in the range 0 < H < 1 and for the two-dimensional signal defined by the ratio
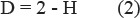
The closer the Hurst exponent to 1, the more pronounced the fractal properties. Thus, the value of the Hurst exponent, which lies within the 0.7 < H < 0.9 indicates self-similar process with the long-term dependence, while at H < 0.5 process is unstable (antipersistent), and at H = 0.5 – random process.
The research was conducted in several stages
1) MR images of the abdominal cavity in a *.dcm format, containing abnormal changes, as well as unmodified liver parenchyma were opened in the ImageJ.
2) With the command “Image-Crop” an area size of 120 x 150 pixels was allocated.
3) FracLac application perform calculations of fractal dimension DB for healthy and pathologic tissues using the Box-counting method. The Hurst exponent was calculated by the expression (2).
4) Parameters WW (Window Width) и WL (Window Level) were adjusted in order to increase the contrast of the researched areas. To study the images with modified parameters WW and WL, correct levels for the whole series of tomograms were selected in the program RadiAnt DICOM Viewer. For existing research, the WW and WL range is 290-450 and 240-250 respectively. After that, selected sections were opened in ImageJ package, where required parameters were set using command Image - Adjust - Window / Level. The Hurst exponent was also calculated by the expression (2).
-
For the obtained values, the average value of the Hurst exponent and standard deviation were calculated in accordance with formulas:

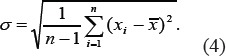
5) In order to establish the optimum size of the researched area, images of liver tissue were analyzed in several sections using frames of various sizes. Selected sections are shown in Figure 3. The sections were also analyzed with with optimal values of WW and WL, some examples of researched areas are shown in Figure 4 and Figure 5.
Figure 1.
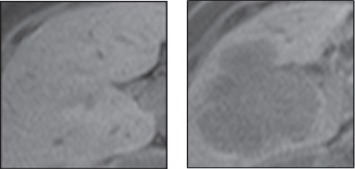
Samples of Healthy Liver Tissue (on the Left Picture) and Liver Tissue Containing Metastatic Colorectal Cancer (on the Left Picture)
Figure 2.
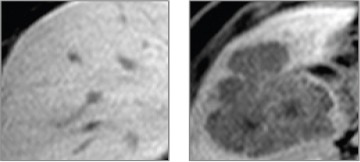
Samples of Healthy Liver Tissue (on the Left Picture) and Liver Tissue Containing Metastatic Colorectal Cancer (on the Left Picture) with Adjusted Parameters WW=290 and WL= 240
Figure 3.
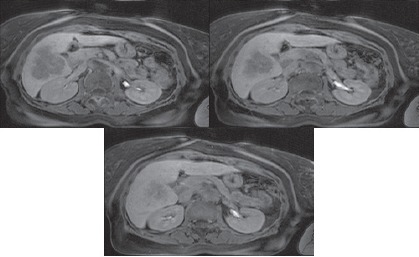
Sections Selected to Determine the Optimum Size of the Researched Area
Figure 4.
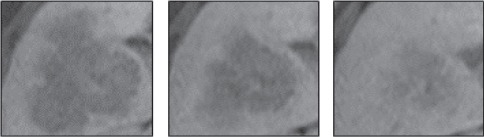
Examples of Researched Areas Size of 110x110 Pixels
Figure 5.

Examples of Researched Areas Size of 80x80 Pixels
Results
Results show that in the case of a pathology (foci formation), the exponent is less than 0.5 (the region of unstable statistical characteristics), and for the healthy tissue, the Hurst index is greater than 0.5 (the zone of stable characteristics).
By calculating the mean and standard deviation for the Hurst exponent for obtained values, it was found that in case of pathology HP = 0.43 ± 0.06 and in case of healthy tissue HN = 0.8 ± 0.10”. For results obtained DB with optimal values of WW and WL HP = 0.42 ± 0.05, HN = 0.81 ± 0.10.
Thus, for section 1, the value of the Hurst exponent indicating pathology (<0.5) has been established through all samples except for the sample sizes of 80x80; for section 2, pathology was detected in all samples; and for cut 3, the pathology was indicated only in the sample size of 50x50.
The same steps were performed for these sections with the optimal values of WW and WL, equal to 290 and 240 respectively.
Table 1.
The Results Obtained for Images Size of 120x150 Pixels
| N | Fractal dimension (DB) | Hurst exponent (H) | ||
|---|---|---|---|---|
| pathology | norm | pathology | norm | |
| 1 | 1.6 | 1.3 | 0.4 | 0.7 |
| 2 | 1.6 | 1.0 | 0.4 | 1.0 |
| 3 | 1.6 | 1.2 | 0.4 | 0.8 |
| 4 | 1.5 | 1.1 | 0.5 | 0.9 |
| 5 | 1.5 | 1.2 | 0.5 | 0.8 |
| 6 | 1.5 | 1.2 | 0.5 | 0.8 |
| 7 | 1.5 | 1.3 | 0.5 | 0.7 |
| 8 | 1.6 | 1.1 | 0.4 | 0.9 |
| 9 | 1.6 | 1.1 | 0.4 | 0.9 |
| 10 | 1.5 | 1.2 | 0.5 | 0.8 |
| 11 | 1.6 | 1.3 | 0.4 | 0.7 |
| 12 | 1.7 | 1.3 | 0.3 | 0.7 |
Table 2.
The Results Obtained for Images with Optimal Values of WW and WL
| N | Fractal dimension (DB) | Hurst exponent (H) | ||
|---|---|---|---|---|
| pathology | norm | pathology | norm | |
| 1 | 1.5 | 1.1 | 0.5 | 0.9 |
| 2 | 1.5 | 1.1 | 0.5 | 0.9 |
| 3 | 1.5 | 1.1 | 0.5 | 0.9 |
| 4 | 1.6 | 1.1 | 0.4 | 0.9 |
| 5 | 1.6 | 1.2 | 0.4 | 0.8 |
| 6 | 1.6 | 1.2 | 0.4 | 0.8 |
| 7 | 1.6 | 1.4 | 0.4 | 0.6 |
| 8 | 1.6 | 1.2 | 0.4 | 0.8 |
| 9 | 1.6 | 1.2 | 0.4 | 0.8 |
| 10 | 1.6 | 1.2 | 0.4 | 0.8 |
| 11 | 1.6 | 1.2 | 0.5 | 0.8 |
| 12 | 1.7 | 1.4 | 0.3 | 0.7 |
Although the values obtained for the fractal dimension and the Hurst exponent are different for the section 1 and section 2, these values show that there is no fundamental difference between the original and the processed images, whereas for section 3, these values have changed somewhat in the direction of the pathological values.
Table 3.
Dependence of DB and H from Size of Researched Area
| Size of area | Section 1 | Section 2 | Section 3 | |||
|---|---|---|---|---|---|---|
| DB | H | DB | H | DB | H | |
| 120х150 | 1.6 | 0.4 | 1.5 | 0.5 | 1.3 | 0.7 |
| 110х130 | 1.6 | 0.4 | 1.5 | 0.5 | 1.3 | 0.7 |
| 110х110 | 1.6 | 0.4 | 1.5 | 0.5 | 1.2 | 0.8 |
| 100х100 | 1.6 | 0.5 | 1.5 | 0.5 | 1.4 | 0.6 |
| 80х80 | 1.4 | 0.6 | 1.5 | 0.5 | 1.5 | 0.5 |
| 50х50 | 1.6 | 0.4 | 1.6 | 0.4 | 1.6 | 0.5 |
Table 4.
The Results Obtained for Images with Optimal Values of WW and WL
| Size of area | Section 1 | Section 2 | Section 3 | |||
|---|---|---|---|---|---|---|
| DB | H | DB | H | DB | H | |
| 120х150 | 1.5 | 0.5 | 1.6 | 0.4 | 1.5 | 0.5 |
| 110х130 | 1.5 | 0.5 | 1.6 | 0.4 | 1.5 | 0.5 |
| 110х110 | 1.5 | 0.5 | 1.6 | 0.5 | 1.5 | 0.5 |
| 100х100 | 1.5 | 0.5 | 1.6 | 0.4 | 1.5 | 0.5 |
| 80х80 | 1.4 | 0.6 | 1.4 | 0.6 | 1.5 | 0.5 |
| 50х50 | 1.6 | 0.4 | 1.6 | 0.4 | 1.5 | 0.5 |
Discussion
Based on these results, the following recommendations for the use of fractal analysis to assess the presence of foci formation can be formed:
1) The analysis window must be quite large. In this study, the most acceptable results were obtained for the window size of 120x150 pixels.
2) In the analysis window, healthy tissue should occupy a larger area than the tissue that contains foci formation.
In the analysis of tissue, healthy tissue should occupy a larger volume than the tissue containing foci formation. This is due to the fact that the abnormal tissue structure can also be sufficiently homogeneous, and the situation with a large volume homogeneous pathological tissue than healthy lead to the opposite result - healthy tissue is perceived as abnormal, but the result of the analysis lie in the normal range.
3) It is better if the tomogram will be pre-processed, i.e. selected values WW and WL parameters such that there will be a significant difference in the contrast between pathological and healthy tissue. In the study, values lie within WW 290-450 and WL - 240-250.
4) Due to the fact that in determining the fractal dimension of the box-counting method is used, the threshold image processing, less contrasting pathology cannot be taken into account. However, when selecting the optimum contrast of the tissue, if the contrast abnormality differs from the norm in any case, then the study should be seen by a medical specialist.
The study examined the possibility of creating a fractal rapid analysis for the presence of focal lesions of the liver and recommendations for its use. Results of the study indicate significant differences of the fractal dimension and the Hurst exponent between the areas of healthy liver tissue and areas containing foci formations. Consequently, the Hurst exponent can be used as an important diagnostic feature.
Obtained data confirm Lopez et al.’s (2009) findings which showed that for images of pathologic brain tissue of animals with epilepsy, the Hurst exponent was less than 0.5 while for images of the healthy tissue, the Hurst exponent was greater than 0.5.
This leads to the conclusion about the prospects of the fractal analysis of medical images in screening programs. The main advantage of fractal analysis in this application is the possibility to create a fully automatic system of selection of medical images, because it uses a fully programmatic method. This will save time for medical staff inspecting the pictures manually, as well as improve the effectiveness of screening programs, which will cover a larger number of people.
Acknowledgements
This paper is sponsored by the Ministry of Education and Science (Minobrnauka) of the Russian Federation within the project RFMEFI57814X0008.
References
- Alharbi A, Tchier F, Rashidi M. Using a geneticfuzzy algorithm as a computer aided breast cancer diagnostic tool. Asian Pac J Cancer Prev. 2016;17:3651–3651. [PubMed] [Google Scholar]
- Arteaga C, Adamson C, Engelman J, et al. AACR cancer progress report 2014. Clin Cancer Res. 2014;20:1–1. doi: 10.1158/1078-0432.CCR-14-2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caldwell C, Stapleton S, Holdsworth D, et al. Characterisation of mammographic parenchymal pattern by fractal dimension. Phys Med Biol. 1990;35:235–235. doi: 10.1088/0031-9155/35/2/004. [DOI] [PubMed] [Google Scholar]
- Falconer K. Fractal geometry:mathematical foundations and applications. John Wiley and Sons. 2004 [Google Scholar]
- Flegontov A, Marusina M. The comparison method of physical quantity dimensionalities. In International Workshop on Computer Algebra in Scientific Computing. 2009:81–8. [Google Scholar]
- Guo Q, Ruiz V, Shao J, Guo F. A novel approach to mass abnormality detection in mammographic images. In Proceedings of the IASTED International Conference on Biomedical Engineering. 2005:180–5. [Google Scholar]
- Hemsley A, Mukundan R. Multifractal measures for tissue image classification and retrieval. In Proceedings of the 11th IEEE International Symposium on Multimedia. 2009:618–23. [Google Scholar]
- Ishida T, Yamashita K, Takigawa A, Kariya K, Itoh H. Trabecular pattern analysis using fractal dimension. Jpn J App Phys. 1993;32:1867–1867. [Google Scholar]
- Landini G, Rippin J. Fractal dimensions of the epithelial-connective tissue interfaces in premalignant and malignant epithelial lesions of the floor of the mouth. Anal Quat Cytol Histol. 1993;15:144–144. [PubMed] [Google Scholar]
- Li J, Du Q, Sun C. An improved box-counting method for image fractal dimension estimation Pattern Recognit. 2009;42:2460–9. [Google Scholar]
- Lopez T, Manjarrez J, Plascencia N, et al. Fractal analysis of EEG signal in the brain of epileptic rats, with and without biocompatible implanted neuroreservoirs. Appl Mech and Mat. 2009;15:127–127. [Google Scholar]
- Mandelbrot B. The fractal geometry of nature. Macmillan. 1983;173:250–250. [Google Scholar]
- Marusina M, Sizikov V, Volgareva A. Noise suppression in the task of distinguishing the contours and segmentation of tomographic images. J Opt Technol. 2015;82:673–673. [Google Scholar]
- Mohammadzadeh Z, Safdari R, Ghazisaeidi M, Davoodi S, Azadmanjir Z. Advances in optimal detection of cancer by image processing;experience with lung and breast cancers. Asian Pac J Cancer Prev. 2015;16:5613–5613. doi: 10.7314/apjcp.2015.16.14.5613. [DOI] [PubMed] [Google Scholar]
- Ng S, Wong S. Colorectal cancer screening in Asia. Br Med Bull. 2013;105:29–29. doi: 10.1093/bmb/lds040. [DOI] [PubMed] [Google Scholar]
- Podolsky M, Barchuk A, Kuznetcov V, et al. Evaluation of machine learning algorithm utilization for lung cancer classification based on gene expression levels. Asian Pac J Cancer Prev. 2016;17:835–835. doi: 10.7314/apjcp.2016.17.2.835. [DOI] [PubMed] [Google Scholar]
- Stewart B, Wild C. World cancer report 2014 World. 2016 [Google Scholar]
- Tsuda H, Moore M. Cancer screening:A review with particular attention to areas for future international research efforts. Asian Pac J Cancer Prev. 2001;3:99–99. [PubMed] [Google Scholar]


