Abstract
Simulations of the passage of eukaryotic cells through a constricted channel aid in studying the properties of cancer cells and their transport in the bloodstream. Compound capsules, which explicitly model the outer cell membrane and nuclear lamina, have the potential to improve computational model fidelity. However, general simulations of compound capsules transiting a constricted microchannel have not been conducted and the influence of the compound capsule model on computational performance is not well known. In this study, we extend a parallel hemodynamics application to simulate the fluid-structure interaction between compound capsules and fluid. With this framework, we compare the deformation of simple and compound capsules in constricted microchannels, and explore how deformation depends on the capillary number and on the volume fraction of the inner membrane. The computational framework’s parallel performance in this setting is evaluated and future development lessons are discussed.
Keywords: lattice Boltzmann, parallel computing, capsules, fluid-structure interaction
1 Introduction
The passage of eukaryotic cells flowing through a constriction has several applications, including the study of cancer cells. Microfluidic devices with constricted channels are used to study how single or clustered cancer cells pass through narrow capillaries in blood flow [1]. Similar microfluidic devices are used to study the properties of cancer cells themselves [2]. Finally, the process by which cancer cells extravisate from the blood stream includes passage through narrow intercellular openings in the endothelial layer [28]. Numerical simulations of all three applications have the potential to complement and extend in vitro studies, by clarifying the role of a single physical parameter in a complex process or exploring regions of the parameter space that are otherwise difficult to access.
Computational studies of cell deformation have generally focused on red blood cells and other non-eukaryotic models. A common paradigm, developed for red blood cells, has modeled cells as fluid-filled capsules surround by a single zero-thickness [13, 7] or finite thickness [6] membrane. Simulations of red blood cells passing through a constricted microchannel have been validated [20] and extensively studied (e.g., [14]). However, the discoidal shape, lack of a nucleus, and high membrane incompressibility of red blood cells may preclude the direct extension of their behaviour in constricted microchannels to eukaryotic cells.
Single membrane models have also been used to model eukaryotic cells [18, 12]. Recent studies have sought to improve model fidelity for eukaryotes by explicitly including the nucleus with a compound capsule model. In a compound capsule, the outer cell membrane and nuclear lamina are modeled with two separate membranes. As opposed to the simple (single) capsule used for red blood cells, the two membranes are uncoupled and may be modeled with different physical properties. Luo et al used a front-tracking method to simulate the deformation of an elastic compound capsule in shear flow [16]. These results were extended from initially spherical to ellipsoidal compound capsules, the dynamics of which were investigated in depth [15]. Similar compound models have been developed for vesicles [26, 11] and droplets [25, 29].
Initial applications have used compound capsules to simulate the passage of a eukaryote through a constricted microchannel. Using dissipative particle dynamics, Xiao et al. showed that a stiff inner membrane can preclude the passage of a compound capsule through a constriction [28]. Casquero et al. performed a two-dimensional simulation and observed deformation of the inner membrane to be highest at the exit of the narrowed region [3]. However, only a single, proof-of-concept compound capsule simulation was conducted in these studies.
Further, it is not well understood how the addition of a second membrane representing the nucleus alters the computational cost or parallel performance of the fluid-structure interaction (FSI) simulation, as previous performance studies have focused on red blood cells (e.g., [5, 23, 17]). Intuitively, the addition of a second membrane may increase FSI- and capsule-related computation by as much as 100%. Further, compound capsules seem to require higher fluid grid resolutions than simple capsules, even in shear flow [16]. These potential increases in computational expense underscore the importance of efficient parallel codes for FSI.
HARVEY is a massively parallel computational fluid dynamics solver, focused on hemodynamics and based on the lattice Boltzmann method [21, 22]. In this paper, we integrate HARVEY with FSI-functionality, using the immersed boundary method to couple a finite element model for deformable capsules to the fluid model. We discuss how the parallelization strategy for the FSI framework builds on existing HARVEY parallelism. The code is used to simulate passage of simple and compound capsules through a constricted microchannel, comparing results from simulations with and without an inner membrane to quantify the influence of the ‘nucleus’ on capsule deformation during transit of the constriction. We study the dependence of compound capsule deformation on the capillary number and on the inner capsule’s volume fraction. Finally, we evaluate the parallel performance of the FSI solver in this setting.
2 Methodology
2.1 Lattice Boltzmann
The lattice Boltzmann method (LBM) is a deterministic, mesoscopic approach to numerically solve the Navier-Stokes equations [4]. The fluid is represented as a particle distribution function fi(x, t), which denotes the number of particles at grid point x at time t with discrete velocity ci. The evolution of distribution f is governed by the lattice Boltzmann equation,
| (1) |
for timestep δt, Maxwell-Boltzmann equilibrium distribution function , collision operator Ω, and the distribution F corresponding to external force g being applied to the fluid. HARVEY employs a standard implementation, with the D3Q19 discretization of velocity space, BGK collision operator , and kinematic viscosity with lattice speed of sound . The halfway bounce-back boundary condition enforces the no-slip condition on the geometry surface. Flow at the inlet and outlet of the geometry is governed by Zou-He boundary conditions, with a fixed velocity profile at the inlet and a fixed pressure at the outlet [9].
We extend the collision kernel in previous HARVEY implementations to include an external force distribution F derived from an external force g [8]. The external force is used in the immersed boundary method to couple fluid and capsule dynamics, as discussed below. The hydrodynamic moments, density ρ and momentum ρv, in this kernel are computed as
| (2) |
The components Fi external force distribution are computed from the v and g by the relation
| (3) |
The velocity v is also used to compute the Maxwell-Boltzmann equilibrium distribution.
2.2 Capsule finite element model
Following the approach described by Luo et al. [16, 15], a cell with a nucleus is represented as a compound capsule, with two zero-thickness membranes to represent the outer cell membrane and nuclear lamina. The triangulated grid for each membrane is created by taking successive subdivisions of an icosahedron, which produces favorable regularity and isotropy, and projecting onto the capsule’s initially spherical shape [13]. The shear and dilational elastic responses to strain of each membrane are governed by a Skalak constitutive law,
| (4) |
for strain invariants I1, I2, shear elastic modulus G, and the ratio of dilational to shear elastic moduli C = 1 [27]. A simple C0 finite element model is used to compute the membrane forces G from the strain energy function [24]. In this study, we assume that modulus G is identical for the inner and outer membranes. For compound capsules, the size of the inner membrane is described by the volume fraction ϕ, equal to the volume ratio of the inner membrane to the outer membrane. A penalty force fp is applied to enforce a constant capsule volume; the resulting volume variation is less than 1% for either membrane during all subsequent simulations.
2.3 Immersed boundary
The immersed boundary method (IBM) handles the FSI of the capsule and fluid by coupling the finite element model for the capsule (defined on a Lagrangian grid) with the lattice Boltzmann method (defined on an Eulerian grid) [19]. Using a discrete delta function δ to transfer physical values between the two grids, IBM approximately enforces the no-slip condition on the capsule surface and allows the capsule to exert a force on the surrounding fluid. In our implementation, there are three components of the IBM: spreading, interpolation, and updating.
The force G defined on the capsule vertex X is spread onto the fluid grid by the equation
| (5) |
and fluid velocity v is updated with the lattice Boltzmann algorithm. In the interpolation step, the updated velocity V of the capsule vertex X is computed at time t + δt with the sum
| (6) |
Finally, the position of the capsule vertex is updated using the no-slip condition:
| (7) |
In this implementation, the discrete delta function is defined by the one-dimensional delta function
| (8) |
using the spatial step δx of the fluid grid. A general discussion of the coupling of LBM and finite element methods with IBM may be found in [13].
2.4 Parallelism
The lattice Boltzmann algorithm is parallelized in HARVEY with MPI, with the simulation domain decomposed into bounding boxes belonging to each task. Communication between tasks occurs on the overlapping halo around each task’s bounding box. Data is transferred on these halo regions between neighboring tasks using non-blocking MPI calls. Indirect addressing is used to limit the required memory, as vascular geometries often occupy a small percentage of their bounding box volume. Global communication is not required and the lattice Boltzmann algorithm in HARVEY scales up to 1.5 million tasks [21, 22].
We extend this parallel paradigm to the coupled LBM-IBM-FEM framework for FSI. The overlapping halo is set to half of the support of the delta function (2 grid points). The capsule workload is distributed on two levels, by capsule and by vertex, similar to the approach in [17]. First, each capsule is owned by the task to which its center belongs and this task is responsible for computing forces from the finite element model on the capsule. Second, each vertex X belongs to the task in which it is located and this task interpolates the velocity V of the vertex. The other immersed boundary functions, updating and spreading, are not fully parallelized, in order to minimize communication. MPI communication is used to collect velocities V from all tasks owning vertices X of a capsule to the task which owns the capsule, and to send force G at each vertex from the task owning the capsule to the tasks owning each vertex. We do not alter the load balancing methodology in HARVEY to account for FSI; it remains based on the fluid grid alone, as described in [22].
3 Results and discussion
3.1 Validation
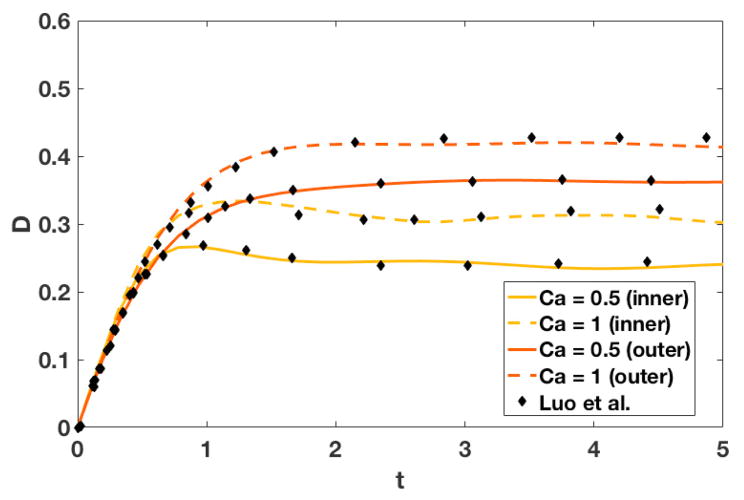
To validate our FSI framework, the deformation of an initially spherical compound capsule in an abruptly started simple shear flow is compared with the method of Luo et al. [16]. Deformation is measured with the Taylor deformation parameter D, defined as using the major and minor axes L and B, respectively, of the ellipsoid with the same moment of inertia. Figure 1 shows the deformation in time of compound capsules with volume fraction ϕ = 0.05 and capillary numbers Ca = 0.5 and 1. For shear flow, the capillary number is defined as , for shear rate γ and outer membrane radius R. Inner and outer capsules are each composed of 5120 triangular elements. The Eulerian fluid grid resolution is set such that the radius of the undeformed outer sphere is equal to 12 grid spacings and simulations are compared with results from [16] at the same fluid grid resolution. Our results generally agree well and show the slight transient fluctuations reported by [16].
Figure 1.
Compound capsules in shear flow with ϕ = 0.05.
3.2 Constriction passage
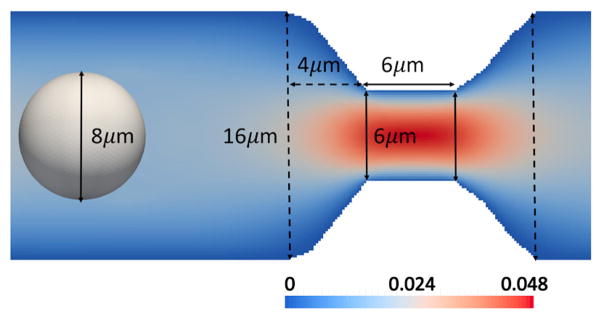
We study the transit of a compound capsule through a microchannel constriction. A range of constriction geometries exist in the literature, with varied cross-sectional shapes [30] and with lengths ranging from 2 to more than 50μms [28, 12]. For this study, the constricted channel is rectangular and the 6μm length is comparable to the 8μm capsule diameter. Depicted in profile in figure 2, the channel is 16μm high, the transverse direction (not shown) is 16μm deep, and the constriction height is 6μm. Further, the channel has a 4μm slope in the axial direction between the regular and constricted heights, and the sides of the microchannel are assumed to be no-slip. Initially spherical capsules with a diameter of 8μm must deform to transit the constriction. The fixed inflow is 2.21 × 10−6 mL/s, corresponding to a parabolic flow with a maximum velocity u0 = 0.025m/s at the inlet. The fluid is characterized by Reynolds number Re = 0.1, dynamic viscosity μ = 1cP, and LBM relaxation time τ = 1. The capillary number is defined as .
Figure 2.
Central region of constricted microchannel. Vertical lines indicate the boundary of the constriction (solid) and narrrowed region (dotted). Shaded by fluid velocity in m/s.
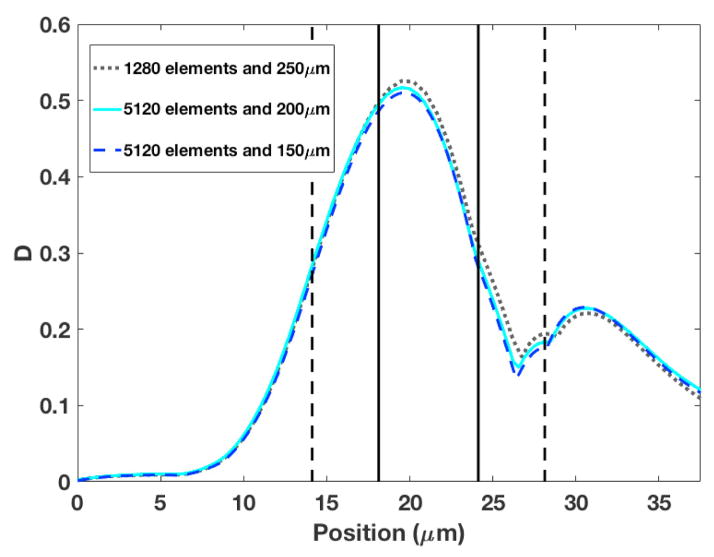
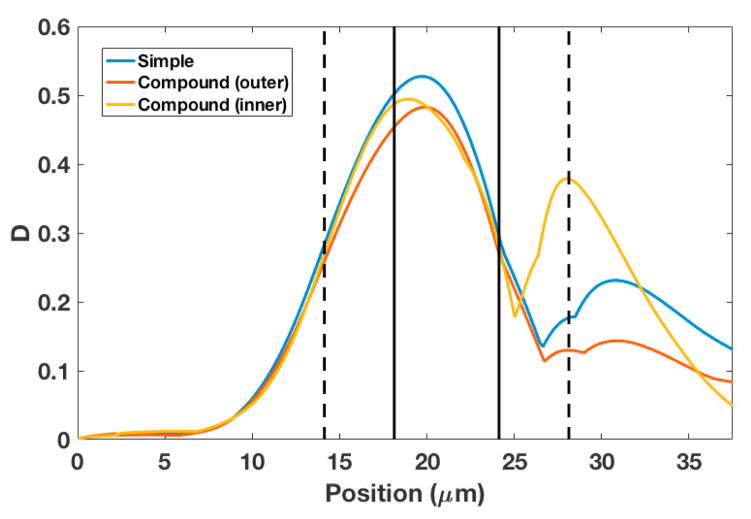
To determine the appropriate simulation resolution, figure 3 shows the deformation D of a simple capsule with Ca = 0.5. Corresponding images of the capsule are illustrated in figure 4. Simulations with Eulerian fluid grid resolutions of 150μm and 200μm agree well over the course of the passage, while 5120 triangular elements for the capsule grid resolve the higher curvature regions in the constriction. Subsequent simulations are conducted at 150μm fluid grid resolution with 5120 elements to represent each capsule membrane.
Figure 3.
Deformation D as a function of axial position z of the capsule center; Ca = 0.5.
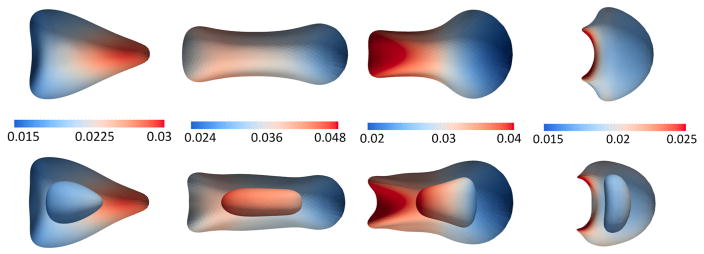
Figure 4.
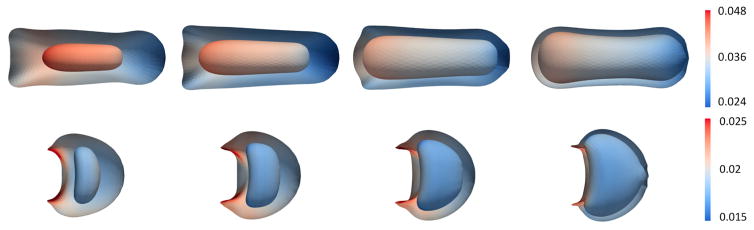
Shapes during constriction passage (from left to right): entering, transiting, exiting, and returning to the full channel, for simple (top) and compound (bottom) capsules. Parameters are Ca= 0.5 and ϕ = 0.125. Colored by membrane velocity in m/s.
Figure 4 compares simple and a compound capsules (ϕ = 0.125) with Ca = 0.5. Starting from a spherical shape, the simple capsule begins to develop a protrusion on the leading side during the entry into the narrowing. Within the constriction, the capsule shape is heavily deformed and becomes approximately discoidal with a bulbous leading side. The bulbous region continues to expand upon exit of the constriction, before recovering the familiar ‘parachute’-like shape. These qualitative aspects for simple capsules are consistent with simulations in a shorter constriction [28].
At this relatively high capillary number, the shape of the outer membrane in a compound capsule remains similar to simple capsules, except for the indentation at the trailing side in the constriction. The outer and inner membranes deform similarly during the entrance and transit phases, but take on very different shapes in the exit phase. The outer membrane become nearly spherical on the leading side, while indentation on the trailing side becomes more pronounced. Meanwhile, the inner membrane deforms to a more discoidal shape, inclined perpendicular to the direction of flow. The resulting shape of the inner membrane leads to a second peak in D, as shown in figure 5 for Ca = 0.5. Simulations at lower Ca indicate that maximum deformation of the inner membrane occured near the exit of the narrowing, but a second peak in deformation was not discussed [3]. After passing the narrowed region, the deformation D of the two membranes in the compound capsule becomes similar again.
Figure 5.
Deformation of simple and compound capsules with Ca = 0.5 and ϕ = 0.125.
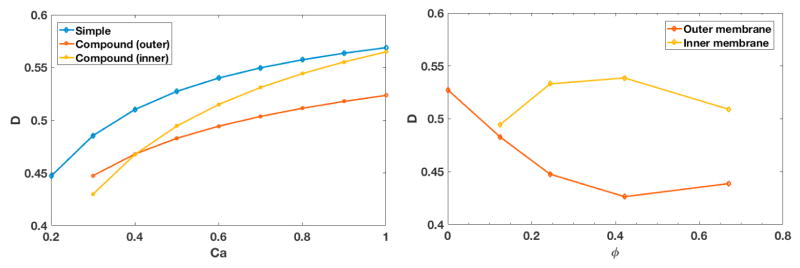
The deformation of a given capsule in the constriction depends on the capillary number Ca. In figure 6, maximum capsule deformation is plotted as a function of Ca for simple and compound capsules with volume fraction ϕ = 0.125. The outer membrane of the compound capsule deforms less than the corresponding simple capsule over the entire range of Ca considered, as previously observed for compound capsules in shear flow [16] and optical tweezing simulations [10]. The outer membrane deforms more than the inner membrane at Ca = 0.3, but this relationship reverses at higher Ca. Indeed, the deformation of the inner membrane approaches the corresponding simple capsule as Ca → 1. This ‘crossover’ point between larger inner and outer membrane deformation is remarkably consistent with results from shear flow at a similar volume fraction [16].
Figure 6.
Maximum deformation D in the constriction as a function of Ca (left) and ϕ (right).
The passage of the compound capsule through the constriction also depends on volume fraction ϕ. For Ca = 0.5, we consider inner membranes with radii of 2, 2.5, 3.0, and 3.5μm, corresponding to ϕ = 0.125, 0.244, 0.422, and 0.67. The maximum deformation of the inner and outer membranes in the constriction are shown in figure 6, while the corresponding capsule images at this location are depicted in figure 7. While membrane deformation is similar at ϕ = 0.125, the inner membrane is more heavily deformed at higher ϕ. However, as ϕ becomes large, the flow field between the two membranes is not sufficient to cause further deformation of the outer membrane, and inner membrane deformation becomes intuitively limited. Overall, we find that both the shape and deformation of inner and outer membranes depends significantly on the volume fraction.
Figure 7.
Shapes in constriction (top) and returning to full channel (bottom) with Ca = 0.5. From left to right, ϕ = 0.125, 0.244, 0.422, and 0.67. Colored by membrane velocity in m/s.
3.3 Influence on computational profile
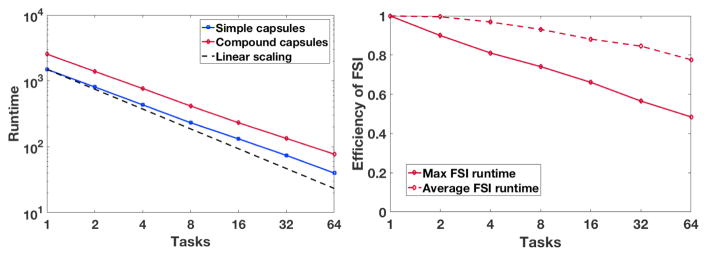
The simulation of compound, rather than simple, capsules requires additional computational expense. To assess our parallel framework, we study the strong scaling of simple and compound capsules in the constricted microchannel. To emphasize FSI components, we simulate 81 capsules with 4μm outer membrane diameters spread throughout the geometry, at the same numerical capsule and fluid resolutions discussed above. While the problem size is too small for large-scale computation, performance in this setting is nonetheless of interest. Results are presented in figure 8 up to 64 cores on the IBM Blue Gene/Q system Vulcan at Lawrence Livermore National Laboratory. Total runtime scales somewhat better for simple capsules, performing at 81% parallel efficiency at 8 cores and 58% at 64 cores, versus 77% and 51% for compound capsules at the same core counts.
Figure 8.
(left) Strong scaling of simulations with simple and compound capsules. (right) Maximum and average task efficiency for FSI-related computation with compound capsules.
The performance loss with capsules is primarily due to two factors: the load imbalance of the FSI-related computation and the small problem size. We define FSI-related computation as the contributions of the immersed boundary and finite element models, along with the related MPI communication. Load balance challenges have been discussed in previous FSI frameworks, such as [5] and [17]. Figure 8 shows that average FSI-related computation for compound capsules remains at 80% efficiency at 64 processors. However, this work is not well-distributed and the overall FSI-related efficiency is reduced to approximately 48%. However, as simple capsules require approximately half the FSI-related computation of compound capsules, they have slightly better strong scaling. Additionally, the small problem size limits parallel performance: at 64 cores, every capsule is shared by multiple tasks and the parallel overhead becomes large relative to the computation time. In contrast, [17] demonstrated superior strong scaling over a much larger problem size.
4 Conclusion
In this study, we present a framework for conducting FSI simulations of cells in flow. This framework builds on a massively parallel hemodynamics application, HARVEY, and is based on the lattice Boltzmann and immersed boundary methods. Eukaryotic cells are represented as compound capsules with a standard finite element model. The parallelization scheme for the FSI-related computation builds on existing HARVEY parallelism.
We apply the resulting computational framework to simulate deformation of simple and compound capsules through a constricted microchannel. Results are consistent with the extensive study by Luo et al. [16] in shear flow: (1) at a given capillary number, the maximum deformation of a simple capsule is higher than that of the compound capsule’s outer membrane and (2) the volume fraction of the inner membrane has a strong influence on the shape and deformation of the outer membrane. Further, we observe that the inner membrane undergoes two deformations to discoidal shapes: first, aligned with the direction of flow in the constriction and, second, perpendicular to the flow direction at the exit of the channel narrowing.
In a strong scaling test of the computational framework, we observe that the additional membrane in compound capsules reduces parallel performance, due to the more limited parallelism and load balance of the FSI model. In future work, we aim to improve performance with static and dynamic load balancing of FSI-related computation to solve large-scale problems.
Acknowledgments
Support was provided by the Department of Veterans Affairs’ Big Data-Scientist Training Enhancement Program. Research reported in this publication was supported by the Office of the Director of the National Institutes of Health under Award Number DP5OD019876. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Computing support for this work came from Lawrence Livermore National Laboratory’s Institutional Computing Grand Challenge program.
References
- 1.Au SH, Storey BD, Moore JC, Tang Q, Chen YL, Javaid S, Sarioglu AF, Sullivan R, Madden MW, OKeefe R, et al. Clusters of circulating tumor cells traverse capillary-sized vessels. Proc Natl Acad Sci USA. 2016;113(18):4947–4952. doi: 10.1073/pnas.1524448113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Byun S, Son S, Amodei D, Cermak N, Shaw J, Kang JH, Hecht VC, Winslow MM, Jacks T, Mallick P, et al. Characterizing deformability and surface friction of cancer cells. Proc Natl Acad Sci USA. 2013;110(19):7580–7585. doi: 10.1073/pnas.1218806110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Casquero H, Bona-Casas C, Gomez H. NURBS-based numerical proxies for red blood cells and circulating tumor cells in microscale blood flow. Comput Methods Appl Mech Eng. 2016 [Google Scholar]
- 4.Chen S, Doolen GD. Lattice Boltzmann method for fluid flows. Ann Rev Fluid Mech. 1998;30(1):329–364. [Google Scholar]
- 5.Clausen JR, Reasor DA, Aidun CK. Parallel performance of a lattice-Boltzmann/finite element cellular blood flow solver on the IBM Blue Gene/P architecture. Comput Phys Comm. 2010;181(6):1013–1020. [Google Scholar]
- 6.Fai TG, Griffith BE, Mori Y, Peskin CS. Immersed boundary method for variable viscosity and variable density problems using fast constant-coefficient linear solvers I: Numerical method and results. SIAM J Sci Comput. 2013;35(5):B1132–B1161. [Google Scholar]
- 7.Gounley J, Peng Y. Computational modeling of membrane viscosity of red blood cells. Comm Comp Phys. 2015;17(04):1073–1087. [Google Scholar]
- 8.Guo Z, Zheng C, Shi B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys Rev E. 2002;65(4) doi: 10.1103/PhysRevE.65.046308. [DOI] [PubMed] [Google Scholar]
- 9.Hecht M, Harting J. Implementation of on-site velocity boundary conditions for D3Q19 lattice Boltzmann simulations. J Stat Mech. 2010;(01):2010. [Google Scholar]
- 10.Hosseini SM, Feng JJ. How malaria parasites reduce the deformability of infected red blood cells. Biophys J. 2012;103(1):1–10. doi: 10.1016/j.bpj.2012.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kaoui B, Krüger T, Harting J. Complex dynamics of a bilamellar vesicle as a simple model for leukocytes. Soft Matter. 2013;9(33):8057–8061. [Google Scholar]
- 12.Kojić N, Milošević M, Petrović D, Isailović V, Sarioglu AF, Haber DA, Kojić M, Toner M. A computational study of circulating large tumor cells traversing microvessels. Comput Biol Med. 2015;63:187–195. doi: 10.1016/j.compbiomed.2015.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Krüger T, Varnik F, Raabe D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput Math Appl. 2011;61(12):3485–3505. [Google Scholar]
- 14.Li X, Peng Z, Lei H, Dao M, Karniadakis GE. Probing red blood cell mechanics, rheology and dynamics with a two-component multi-scale model. Phil Trans R Soc A. 2014;372(2021) doi: 10.1098/rsta.2013.0389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Luo ZY, Bai BF. Dynamics of nonspherical compound capsules in simple shear flow. Phys Fluids. 2016;28(10) [Google Scholar]
- 16.Luo ZY, He L, Bai BF. Deformation of spherical compound capsules in simple shear flow. J Fluid Mech. 2015;775:77–104. [Google Scholar]
- 17.Mountrakis L, Lorenz E, Malaspinas O, Alowayyed S, Chopard B, Hoekstra AG. Parallel performance of an IB-LBM suspension simulation framework. J Comp Sci. 2015;9:45–50. [Google Scholar]
- 18.Pappu V, Bagchi P. 3D computational modeling and simulation of leukocyte rolling adhesion and deformation. Comput Biol Med. 2008;38(6):738–753. doi: 10.1016/j.compbiomed.2008.04.002. [DOI] [PubMed] [Google Scholar]
- 19.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- 20.Quinn DJ, Pivkin I, Wong SY, Chiam K-H, Dao M, Karniadakis GE, Suresh S. Combined simulation and experimental study of large deformation of red blood cells in microfluidic systems. Ann Biomed Eng. 2011;39(3):1041–1050. doi: 10.1007/s10439-010-0232-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Randles A, Draeger EW, Bailey PE. Massively parallel simulations of hemodynamics in the primary large arteries of the human vasculature. J Comp Sci. 2015;9:70–75. doi: 10.1016/j.jocs.2015.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Randles A, Draeger EW, Oppelstrup T, Krauss L, Gunnels JA. Massively parallel models of the human circulatory system. Proc. International Conference for High Performance Computing, Networking, Storage and Analysis; ACM; 2015. p. 1. [Google Scholar]
- 23.Reasor DA, Clausen JR, Aidun CK. Coupling the lattice-Boltzmann and spectrin-link methods for the direct numerical simulation of cellular blood flow. Int J Numer Meth Fluids. 2012;68(6):767–781. [Google Scholar]
- 24.Shrivastava S, Tang J. Large deformation finite element analysis of non-linear viscoelastic membranes with reference to thermoforming. J Strain Anal Eng. 1993;28(1):31–51. [Google Scholar]
- 25.Stone H, Leal L. Breakup of concentric double emulsion droplets in linear flows. J Fluid Mech. 1990;211:123–156. [Google Scholar]
- 26.Veerapaneni SK, Young Y-N, Vlahovska PM, Bławzdziewicz J. Dynamics of a compound vesicle in shear flow. Phys Rev Lett. 2011;106(15) doi: 10.1103/PhysRevLett.106.158103. [DOI] [PubMed] [Google Scholar]
- 27.Walter J, Salsac A-V, Barthès-Biesel D, Le Tallec P. Coupling of finite element and boundary integral methods for a capsule in a Stokes flow. Int J Numer Meth Eng. 2010;83(7):829–850. [Google Scholar]
- 28.Xiao L, Liu Y, Chen S, Fu B. Numerical simulation of a single cell passing through a narrow slit. Biomech Model Mechanobiol. 2016:1–13. doi: 10.1007/s10237-016-0789-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhang Z, Xu J, Chen X. Int Mech Eng Congress Expo. American Society of Mechanical Engineers; 2015. Compound droplet modelling of circulating tumor cell microfiltration. [Google Scholar]
- 30.Zhang Z, Xu J, Hong B, Chen X. The effects of 3D channel geometry on ctc passing pressure–towards deformability-based cancer cell separation. Lab Chip. 2014;14(14):2576–2584. doi: 10.1039/c4lc00301b. [DOI] [PubMed] [Google Scholar]