Wave-CAIPI for Highly Accelerated MP-RAGE Imaging

Abstract

Purpose

We introduce a highly accelerated T1-weighted MP-RAGE acquisition that utilizes Wave-CAIPI encoding to retain high image quality.

Methods

Significant acceleration of the MP-RAGE sequence is demonstrated using the Wave-CAIPI technique. Here, sinusoidal waveforms are used to spread aliasing in all three directions in order to improve the g-factor. Combined with a rapid 2 sec coil sensitivity acquisition and data-driven trajectory calibration, we propose an online integrated acquisition-reconstruction pipeline for highly efficient MP-RAGE imaging.

Results

The 9-fold accelerated MP-RAGE acquisition can be performed in 71 sec, with maximum and average g-factor of g_max = 1.27 and g_avg = 1.06 at 3T. Compared to the state-of-the-art 2D-CAIPIRINHA method, this is a factor of 4.6/1.4 improvement in g_max/g_avg. In addition, we demonstrate a 57 sec acquisition at 7T with 12-fold acceleration. This acquisition has a g-factor performance of g_max = 1.15 and g_avg = 1.04.

Conclusion

Wave encoding overcomes the g-factor noise amplification penalty and allows for an order of magnitude acceleration of MP-RAGE acquisitions.

Introduction

In 1990 Mugler et al. demonstrated that MP-RAGE (Magnetization Prepared RApid Gradient Echo) provides high resolution structural images with detailed contrast between gray matter (GM), white matter (GW) and cerebrospinal fluid (CSF) [1]. Numerous applications of MP-RAGE, mainly in neuroimaging, have been introduced. MP-RAGE serves as a precise anatomical reference for T2* weighted functional MRI data [2]. It has proven to be a powerful tool to investigate psychiatric and neurodegenerative disorders by applying brain volumetry [3], segmentation and cortical surface reconstruction [4]. This has enabled measures such as cortical thickness to be accurately obtained [5]. To achieve T1 weighted contrast, MP-RAGE utilizes a magnetization preparation period followed by a gradient echo readout train and a recovery period [1]. These sequence features lead to long scan times of over 10 min without acceleration for whole-brain coverage at 1 mm isotropic resolution. This poses several problems for the clinical use of MP-RAGE where long scans increase susceptibility to patient motion, reduce patient comfort and compliance, and may necessitate sedation of pediatric patients.

The speed of conventional Cartesian imaging is mainly limited by contrast preparation and the encoding of a large number of k-space lines. Parallel imaging methods, such as SENSE [6] and GRAPPA [7] can be employed to reduce the number of phase encoding steps through the use of coil sensitivity encoding from multichannel receiver arrays. Further improvement in image reconstruction quality at higher accelerations can be achieved by applying Controlled Aliasing In Parallel Imaging Results IN Higher Acceleration (2D-CAIPIRINHA, or 2D-CAIPI) [8]. Recently, Brenner et al. combined 2D-CAIPI and elliptical scanning for MP-RAGE acquisition and demonstrated R=6 acceleration with comparable results to R=4 GRAPPA reconstruction [9]. This has allowed an MP-RAGE acquisition at 1 mm isotropic resolution in approximately 2 min.

To provide further improvement and achieve an order of magnitude acceleration, we propose Wave-CAIPI MP-RAGE, which reduces the scan time to below 1 min while providing high quality imaging with only a small g-factor noise penalty. Wave-CAIPI modifies the conventional gradient echo readout by playing sinusoidal waveforms on the G_y and G_z gradients during the sampling period, which produces voxel spreading in the x (readout) axis [10]. As the amount of readout spreading is dependent on the y and z spatial positions, Wave encoding improves the coil sensitivity variation in the collapsed voxels for accelerated acquisitions. In addition to Wave-CAIPI, our MP-RAGE acquisition also employs a novel reordering scheme to gain further speed up from inner loop acceleration, as conventional undersampling in partition direction reduces blurring without decreasing the scan time [11]. Since the actual waveforms played on the gradients deviate from the theoretical sinusoidal functions, the experimental corkscrew k-space trajectory needs to be estimated for improved image quality. As opposed to prior work that relied on extra calibration acquisitions [10], here we estimate the gradient waveforms in an entirely data-driven fashion [12].

Methods

We implemented MP-RAGE using Wave-CAIPI for the Siemens IDEA environment. At 3T, we aimed for R=9-fold acceleration (R=R_y×R_z) and ~1 min scan time, as we have previously shown low g-factor and high quality imaging for Wave GRE [10] at this acceleration factor. We created an online acquisition/reconstruction framework (Siemens ICE environment) with rapid coil sensitivity acquisition (2 sec) and data driven trajectory estimation. In addition, we employed SVD coil compression [13], [14] for efficient reconstruction (see Supporting Material for details) and a novel MP-RAGE sampling scheme (detailed below) to achieve the desired scan time. In order to provide image quality comparison, we also acquired data at R=3×3 2D-CAIPI (reconstructed offline using MATLAB) and R=4×1 GRAPPA acceleration (Siemens product reconstruction). Optimal parameters for coil compression, CAIPI shift and Wave gradient strength were obtained from additional g-factor simulations.

In order to assess the feasibility of higher acceleration, acquisitions were also performed at 7T sensitivity variation helped mitigate the inherent $\sqrt{R}$ SNR penalty and the g-factor noise amplification. Since 7T scanners are mainly used for neuroscientific research, we have not yet implemented an online reconstruction for this platform. Nevertheless, our results serve as a proof of concept.

Novel MP-RAGE reordering

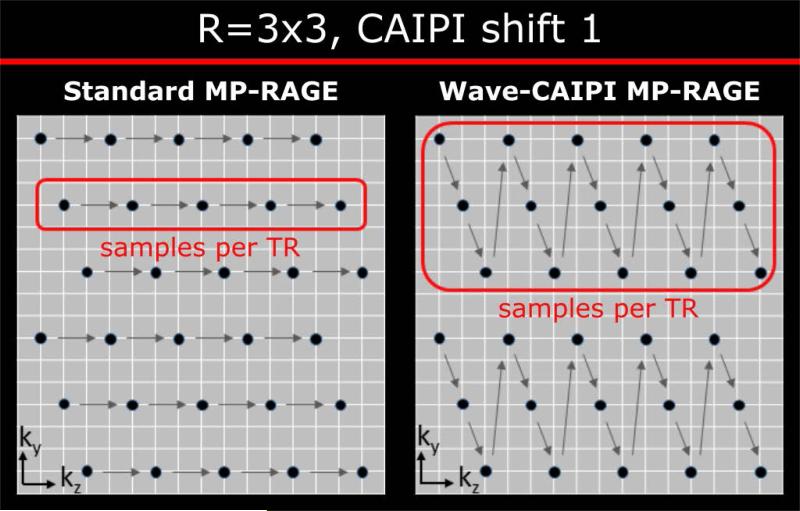
Magnetization preparation (P), rapid gradient echo acquisition (A) of a k_x-k_z plane (k_x: RO, k_y: PE, k_z: PAR) and subsequent recovery period (R) form the inner loop of MP-RAGE. To acquire full k-space, the P-A-R cycle has to be repeated for all k_y locations, i.e. the outer loop [1]. Whereas acceleration in the outer loop decreases the number of P-A-R cycles and hence reduces the overall scan time, acceleration in the partition encoding shortens only the echo train length of the gradient echo readout without affecting the acquisition time. This procedure is useful for high resolution imaging, as it minimizes blurring induced by relaxation and recovery effects during the inner loop which cause windowing of the k-space data and lead to a loss of spatial resolution [11]. Figure 1 (left) depicts the acquisition scheme for acceleration factor R=3×3 and CAIPI shift 1.

Figure 1.

(left) Standard k-space sampling for R=3×3 acceleration using CAIPI shift 1. Per TR one k_x-k_z plane is acquired, the blurring in partition encoding direction is reduced, however the overall scan time is only affected by the acceleration in phase encoding direction (Ry = 3). (Right) Three k_x-k_z planes are merged to form one P-A-R cycle, which shortens the scan time by a factor of 9. The reordering enforces the k-space center of each plane to be acquired at inversion time TI, preserving the MP-RAGE contrast.

As blurring is not significant at 1 mm isotropic resolution (see Supporting Figure S2 for details), we propose a reordering scheme (Figure 1, right), that takes advantage of both inner and outer loop acceleration to reduce the scan time by a factor of R. Specifically, R_z planes of k_x-k_z k-space are merged in an interleaved fashion to ensure that the k-space center of each plane is acquired close to the inversion time (TI), which will preserve the known MP-RAGE contrast. It is important to note that the echo train length is equal to an R_z=1 scan. Also the amount of blurring remains unchanged compared to an MP-RAGE scan without inner loop acceleration (R_z=1). More information can be obtained from Supporting Figure S2.

Data-driven PSF calibration

System imperfections can cause deviations from the theoretical k-space trajectory corresponding to the oscillating wave gradients. As precise knowledge of the underlying PSF is critical for image reconstruction, calibration scans on a phantom can be used to characterize the gradients accurately [10]. However, these additional scans are time consuming and specific to a certain parameter set, e.g. they need to be repeated if the wave parameters or acquisition bandwidth changes. Instead, here we use an integrated data-driven approach for trajectory calibration as presented in [12]. Without system imperfections, the PSF can be described using a single coefficient a₁ of the Fourier series, corresponding to the desired number of sinusoidal wave cycles. In our approach, we add four additional Fourier terms a_2...5 at adjacent frequencies to help describe the gradient imperfections along with two linear coefficients b_1,2 to correct for spatial mismatch between the coil sensitivity map and the acquisition. To characterize both G_y and G_z gradient imperfections, two sets of the coefficients a_i and b_i are required and summarized as vector t. Since the correction terms are not known a priori, an initial guess of the PSF based on the theoretical wave trajectory is constructed first. Next, the cost function

$$\underset{t}{\min }\underset{m}{\min }{\Vert M\cdot {\mathcal{F}}_x^{-1}\left(\mathrm{Psf}\left(\mathrm{t}\right)\cdot {\mathcal{F}}_x(C\cdot m)\right)-w\Vert }_2$$

is minimized with respect to the PSF coefficients t. Here M denotes a matrix that sums over the collapsing voxel indices, ${\mathcal{F}}_x$ the discrete Fourier transform along the readout axis, Psf the point-spread function in hybrid space, C the coil sensitivity profiles, m the underlying magnetization and w the collapsed wave image.

By using only a few representative test locations in forming m (five readout lines evenly spaced around the center of the collapsed image), the optimization problem requires significantly less computational effort while still yielding accurate results. Once the gradient trajectory is known, the optimized PSF is used to reconstruct the complete data set. The online reconstruction at 3T is implemented in the Siemens ICE environment and parallelized (12 CPUs) to ensure rapid processing (recon time approx. 3 min for 1mm isotropic whole brain coverage).

Comparing R=3×3 Wave-CAIPI with 2D-CAIPI at 3T

A female, healthy volunteer was scanned on a 3T Skyra scanner in compliance with IRB requirements. The protocol was chosen in accordance with van der Kouwe et al. to maximize contrast between GM, WM and CSF [20]: FOV=240 × 240 × 192 mm³; voxel size=1 × 1 × 1 mm³; 32 channel Siemens product receive coil; acceleration R=3×3; optimal CAIPI shift 1 (as detailed in Supporting Material); wave amplitude = 8.8 mT/m using 11 sinusoidal cycles per readout. The acquisition time was 69 sec with TE/TR/TI = 3.8/2500/1100 ms, echo spacing = 7.9 ms and bandwidth = 200 Hz/pixel. Siemens standard adiabatic inversion pulse was used in all acquisitions. The flip angle was chosen to be 9°. An additional low resolution (24×24 lines) gradient echo sequence was acquired prior to the MP-RAGE scan to compute coil sensitivities using ESPIRiT [15]. The parameters for this 1.8 sec calibration scan were: TE/TR = 2.0/3.2 ms, bandwidth=1000 Hz/pixel and flip angle = 5°.

As a benchmark for comparison, a 2D-CAIPI scan including the novel reordering but without wave gradients was acquired. To improve the computational efficiency of the ESPIRiT coil sensitivity computation, 20-channel SVD coil compression (see Supporting Figure S2 for details) was applied to both data sets. The undersampled Wave-CAIPI data was reconstructed online, while the 2D-CAIPI scan was processed offline using MATLAB. G-factor maps according to reference [6] were computed to quantify noise amplification.

Comparing time matched R=3×3 Wave-CAIPI with R=4×1 GRAPPA at 3T

To assess the quality of Wave-CAIPI in comparison to techniques routinely used in clinical settings, we acquired three averages of Wave-CAIPI using the protocol described above (total scan time 3 min 23 sec) and a R=4×1 GRAPPA measurement of similar duration (3 min 14 sec including 24 integrated ACS lines). The standard Siemens MP-RAGE sequence was reconstructed using GRAPPA with the following protocol parameters: FOV=256 × 240 × 192 mm³; voxel size=1 × 1 × 1 mm³; 32-channel product receive coil; outer loop acceleration R=4×1 including 24 integrated ACS lines; TE/TR/TI = 3.3/2500/1100 ms; bandwidth 200 Hz/pixel. The reconstruction and averaging of Wave-CAIPI were performed offline using MATLAB, while the Siemens online GRAPPA reconstruction was used for the standard clinical acquisition. Both scans were performed on the same female volunteer as described above.

Gray matter segmentation

As a further benchmark of comparison segmentation using the FSL software package (version 5.0.7) [16] was applied to the 2D-CAIPI, Wave-CAIPI and GRAPPA datasets. The processing pipeline consisted of the functions robustfov (identifying and cropping the brain FOV), bet (brain masking with threshold=0.2 [17]) and fast (segmentation with bias field correction [18]).

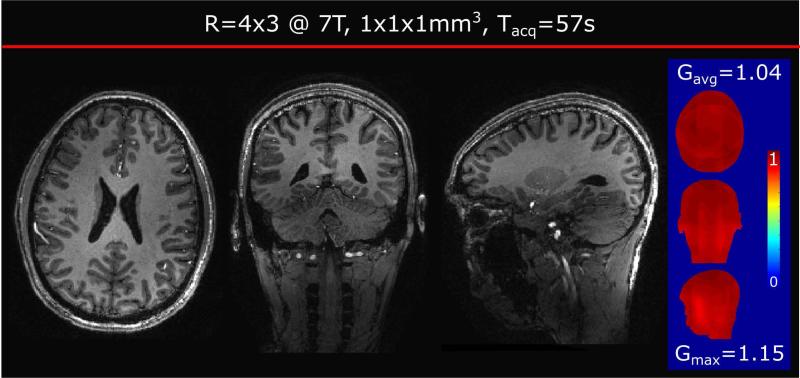
R=4×3 Wave-CAIPI at 7T

To allow for even higher acceleration, a healthy male volunteer was scanned on a Siemens Magnetom 7T scanner at acceleration R=4×3 resulting in a scan time of 57 sec. The protocol parameters were: FOV=256 × 256 × 192 mm³; voxel size=1 × 1 × 1 mm³; custom phased-array (31ch) and birdcage Tx coil [19]; acceleration R=4×3; CAIPI shift 1; wave amplitude 16,1 mT/m using 9 sinusoidal cycles per readout to reduce the maximum gradient slew rate and avoid physiological nerve stimulation; bandwidth 200 Hz/pixel; TE/TR/TI = 3.8/2500/1100 ms and flip angle 7°. In addition, a low resolution GRE (24×24 lines, TE/TR = 1.5/3.4 ms, BW=1030 Hz/px, T_acq=2.0 s, flig angle 9°) was acquired prior to the scan for computation of ESPIRiT coil sensitivities. Image reconstruction and g-factor calculation were performed offline using MATLAB.

Results

Comparing R=3×3 Wave-CAIPI with 2D-CAIPI at 3T

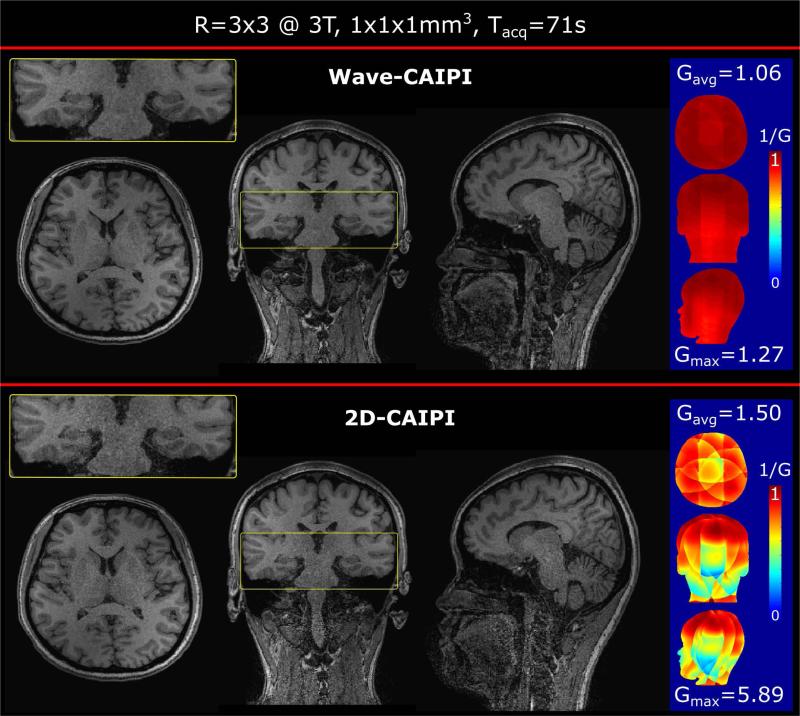
Figure 2 shows reconstructions of whole brain Wave-CAIPI and 2D-CAIPI acquisitions at 1 mm isotropic resolution and R=3×3 acceleration. Compared to Wave-CAIPI, the zoomed-in view of the 2D-CAIPI result shows significant noise amplification particularly in the brain stem. This is also reflected in the g-factor maps (displayed 1/g-factor to keep the scale within [0,1]). In comparison, the g-factor of Wave-CAIPI is very close to 1 over the entire volume (g_min=1.06, g_max=1.27). The 2D-CAIPI scan shows severe SNR loss particularly in the center of the brain and the lower half of the head (g_min=1.50, g_max=5.89).

Figure 2.

R=3×3 accelerated acquisitions of Wave-CAIPI and 2D-CAIPI are compared at 3T (scan time 71 sec). Zoom-in (yellow) shows significant noise amplification for 2D-CAIPI. The panel on the right, demonstrates inverse g-factor maps and reports average and maximum g-factor values for Wave-CAIPI and 2D-CAIPI.

Comparing time matched R=3×3 Wave-CAIPI to R=4×1 GRAPPA at 3T

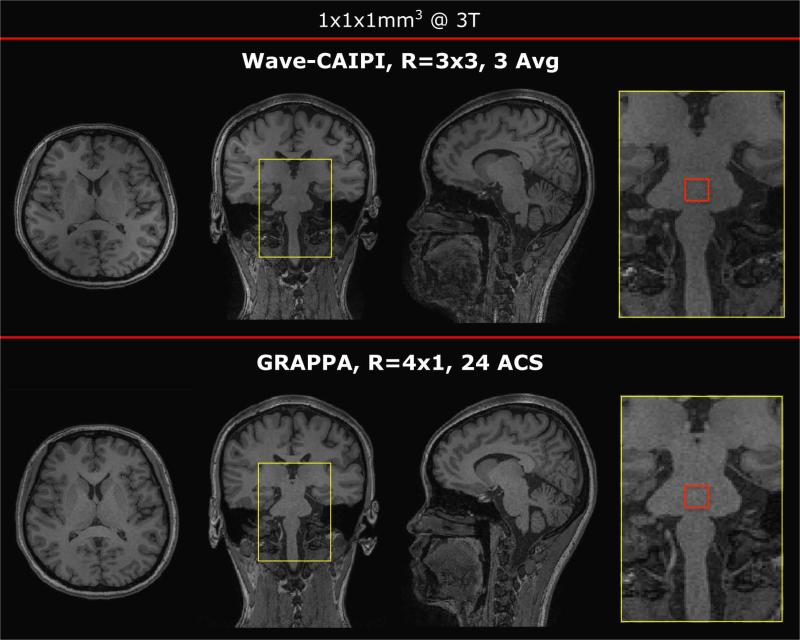
A time matched R=4×1 GRAPPA scan (Siemens product sequence) is compared to three averages of R=3×3 Wave-CAIPI MP-RAGE in Figure 3. GRAPPA and Wave-CAIPI reconstructions show comparable image quality and T1 weighted contrast in all three orthogonal views. Mean value over standard deviation calculated for the area surrounded by the red square was found to be 14.7 for Wave and 13.6 for GRAPPA. This further underlines that both methods provide similar SNR.

Figure 3.

Comparison three averages of R=3×3 accelerated Wave-CAIPI (scan time 3 min 23 sec) vs. R=4×1 GRAPPA (scan time 3 min 14 sec) at 3T. All three views show comparable image quality and negligible artifacts. The red square was used for a quantitative SNR comparison.

Gray matter segmentation

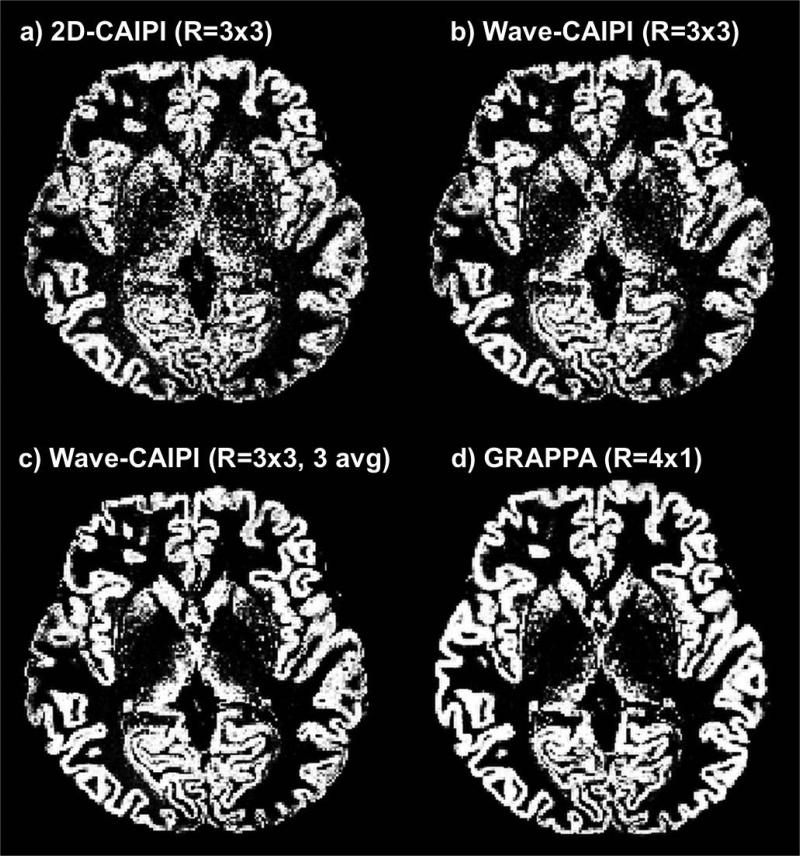
Figure 4 (a,b) shows the segmentation results of the R=3×3 accelerated 2D-CAIPI and Wave-CAIPI datasets. Improved gray matter segmentation was achieved by the Wave-CAIPI scan particularly in the center of the brain where wave encoding provided superior g-factor and minimal noise amplification compared to conventional 2D-CAIPI. Three averages of R=3×3 Wave-CAIPI and R=4×1 GRAPPA provided similar segmentation results with hardly noticeable differences, as demonstrated in Fig. 4 (c,d).

Figure 4.

Gray matter segmentation using FSL for (a) R=3×3 2D-CAIPI, (b) R=3×3 Wave-CAIPI, (c) 3 averages of R=3×3 Wave-CAIPI and (d) R=4×1 GRAPPA.

R=4×3 Wave-CAIPI at 7T

Shorter scan time in accelerated 3D sequences comes at a cost of intrinsic $\sqrt{R}$ SNR penalty. To overcome this issue, we examined an acquisition at 7T. Figure 5 shows MP-RAGE at 12-fold acceleration (R=4×3), corresponding to just below one minute of acquisition time (T_acq=57 sec). Despite the significant loss of SNR ($\sqrt{\mathrm{R}}=3.46$) due to the intrinsic $\sqrt{\mathrm{R}}$ penalty, all three views show detailed contrast and high image quality. The g-factor performance was found to be close to 1 as depicted in the side panel (g_avg = 1.04, g_max= 1.15). The average and maximum g-factor of 2D-CAIPI at R=4×3 acceleration (CAIPI shift 1) was also calculated (g_avg=1.6, g_max=9.4). In comparison, for g-factor hotspots Wave-CAIPI provides 9 times increased SNR.

Figure 5.

R=4×3 accelerated Wave-CAIPI acquisition at 7T (scan time 57 sec). Inverse g-factor and average/maximum g-factor values depicted in the blue panel on the right.

Discussion

We have demonstrated highly accelerated MP-RAGE imaging using the Wave-CAIPI technique at 3T and 7T. A comparison against the established 2D-CAIPI method revealed almost 5-fold improvement in maximum g-factor and enhanced noise mitigation over the entire imaging volume. However, Wave-CAIPI requires a more computationally intensive reconstruction when compared to the standard 2D-CAIPI or GRAPPA methods. Nonetheless, the separability of the Wave-CAIPI reconstruction allowed for images to be made available within less than 3 minutes using a parallelized, online ICE reconstruction [12] on 12 CPUs. A significant speed up is further anticipated from migration to graphics processing units (GPU). As described in the Supporting Material section, SVD coil compression to 20 channels is utilized to further accelerate the ESPIRiT sensitivity estimation, while preserving high reconstruction quality with negligible impact on g-factor performance.

We have demonstrated 9-fold accelerated Wave-CAIPI MP-RAGE imaging at 3T in just over one minute with a negligible g-factor penalty. While conventional 2D-CAIPI acquisitions suffer from severe and localized SNR losses, Wave-CAIPI is only limited by the intrinsic $\sqrt{\mathrm{R}}$ penalty on SNR. To increase SNR, three averages of Wave-CAIPI were obtained and compared to a time matched and clinically available R=4×1 GRAPPA acquisition. While both sequences demonstrated comparable image quality, contrast and SNR, it is anticipated that the Wave-CAIPI approach will provide increased robustness to patient motion. Specifically, Wave-CAIPI permits each average to be acquired within a shorter time frame, thus reducing the overall motion susceptibility. This also allows discarding motion-corrupted averages, which is not possible with the single average R=4×1 GRAPPA scan. However, the susceptibility to motion within a single Wave-CAIPI measurement needs to be studied in a future investigation and is outside the scope of this work.

Since the intrinsic SNR penalty impedes achieving beyond an order of magnitude acceleration at 3T, we have also implemented Wave-CAIPI MP-RAGE at 7T. Higher magnetic field strength, a tight-fitting custom 32-channel receive array [19], and increased wave amplitude and slew rate provided sufficient SNR to push the scan time below one minute using 12-fold acceleration. Despite such a high acceleration factor, the obtained results provided sharp and detailed contrast. As 7T scanners are used mainly for neuroscientific research, 12-fold acceleration can also be leveraged for higher resolution imaging and reduced blurring, however at the cost of longer scan times. To this end, the 3-fold inner loop acceleration could potentially be used to reduce the T1 blurring in the partition encoding direction (as mentioned in Method section) at the cost of increased acquisition time. The 4-fold outer loop acceleration will provide scan time reduction, e.g. making a 0.75 mm isotropic MP-RAGE acquisition possible in 3:30 minutes. Multiple averages can be acquired and then co-registered for increased SNR. This should enable ultra-high resolution imaging with low blurring and reduced motion susceptibility. Multi echo version of MP-RAGE (ME-MPRAGE) [20] mitigates distortions due to B0 inhomogeneity by increasing the readout bandwidth while sampling multiple echoes during each excitation to help retain the SNR. Future work includes extending Wave-CAIPI MP-RAGE to sample multiple echoes, and enable highly accelerated imaging while suppressing B0 artifacts. Since ME-MPRAGE involves higher bandwidth (e.g. 650Hz/px) [20], and a smaller readout duration respectively, the number of sinusoidal wave cycles needs to be reduced to meet the slew rate limitations of the system. In Supporting Figure S1 the wave parameter space was investigated and corresponding g-factor maps reported. It is seen that 3 cycles at 10 mT/m gradient amplitude (respectively 37.4 mT/m/ms slew rate) yield sufficient g-factor (g_avg = 1.06, g_max = 1.22) and indicate feasibility of higher bandwidth acquisitions.

Conclusion

We have introduced the Wave-CAIPI MP-RAGE sequence with a novel reordered sampling scheme that allows up to an order of magnitude acceleration with negligible g-factor penalty. Also, we have provided an integrated acquisition-reconstruction pipeline that combined with ESPIRiT coil sensitivity estimation from a 2 sec scan and auto-calibrated trajectory estimation allows for rapid online image reconstruction. This fast sequence is expected to benefit clinical and research applications that routinely employ MP-RAGE for T1 weighted imaging with high contrast and quality.