Identifying Treatment Effect Heterogeneity in Clinical Trials Using Subpopulations of Events: STEPP

Abstract

Background

Investigators conducting randomized clinical trials (RCTs) often explore treatment effect heterogeneity to assess whether treatment efficacy varies according to patient characteristics. Identifying heterogeneity is central to making informed personalized health care decisions. Treatment effect heterogeneity can be investigated using subpopulation treatment effect pattern plot (STEPP), a non-parametric graphical approach that constructs overlapping patient subpopulations with varying values of a characteristic. Procedures for statistical testing using STEPP when the endpoint of interest is survival remain an area of active investigation.

Motivating Data

A STEPP analysis was used to explore patterns of absolute and relative treatment effects for varying levels of a breast cancer biomarker, Ki-67, in the phase III BIG (Breast International Group) 1-98 RCT, comparing letrozole to tamoxifen as adjuvant therapy for postmenopausal women with hormone receptor-positive breast cancer. Absolute treatment effects were measured by differences in 4-year cumulative incidence of breast cancer recurrence, while relative effects were measured by the subdistribution hazard ratio in the presence of competing risks using O − E (observed-minus-expected) methodology, an intuitive non-parametric method. While estimation of hazard ratio values based on O − E methodology has been shown, a similar development for the subdistribution hazard ratio has not. Furthermore, we observed that the STEPP analysis, may not produce results, even with 100 patients within each subpopulation.

After further investigation through simulation studies, we observed inflation of the type I error rate of the traditional test statistic and sometimes singular variance-covariance matrix estimates that may lead to results not being produced. This is due to the lack of a sufficient number of events within the subpopulations, which we refer to as instability of a STEPP analysis.

Methods

We introduce methodology designed to improve stability of a STEPP analysis and generalize O − E methodology to the competing risks setting. Simulation studies were designed to assess the type I error rate of the tests for a variety of treatment effect measures, including subdistribution hazard ratio based on O − E estimation. This STEPP methodology and standard regression modeling were used to evaluate heterogeneity of Ki-67 in the BIG 1-98 RCT.

Results

We developed methodology that improves stability of a STEPP analysis by pre-specifying the number of events across subpopulations while controlling the type I error rate. STEPP analysis of the BIG 1-98 RCT showed that patients with high Ki-67 percentages may benefit most from letrozole, while heterogeneity was not detected using standard regression modeling.

Conclusions

STEPP methodology can be used to study complex patterns of treatment effect heterogeneity, as illustrated in the BIG 1-98 RCT. For a STEPP analysis, we recommend a minimum of twenty events within each subpopulation.

A. Introduction

Patients and their doctors often make treatment decisions without knowing how a treatment will affect them. Because real-world treatment choices often depend on individual patient characteristics (e.g., age, biological markers), it is important to show how the same treatment can have different effects on different patients. We refer to this phenomenon as treatment effect heterogeneity or, more simply, heterogeneity. Identifying heterogeneity is central to helping patients and their doctors make informed personalized health care decisions.^{1, 2}

Typically, heterogeneity is investigated using subgroup analysis, where patients are divided (often arbitrarily) into subgroups based on a patient characteristic (aka, covariate). Treatment comparisons are then performed within each subgroup (e.g., low vs. high biomarker Ki-67 levels) to identify heterogeneity. However, there are many problems with subgroup analysis. First, categorizing patients into subgroups has been attributed to a loss of critical patient care information by diminishing the effect of the baseline characteristic as a predictor of treatment effectiveness.³ Second, while randomization ensures that prognosis in the different treatment groups is balanced at baseline, such balance cannot be assumed in subgroups unless randomization was stratified by the patient characteristic or the size of the subgroup is sufficiently large with at least 100 patients per subgroup.⁴ Third, subgroup analysis often leads to chance findings since the presence of a treatment effect is separately tested in each subgroup.^{1, 5} For example, testing the hypothesis that there is no treatment effect for high biomarker Ki-67 levels, and then testing it separately in patients with low biomarker Ki-67 levels does not address whether treatment differences vary according to Ki-67 levels.

Guidelines for heterogeneity evaluation recommend introducing an interaction term between treatment and covariate in a regression model.^{1, 6} Traditional regression models, however, require specifying the functional form of the relationship between the outcome and covariate. This can distill a complex interaction effect to the p-value of a regression parameter and may not address the potential issue of subgroup imbalance that results in treatment group incomparability.

A non-parametric alternative is subpopulation treatment effect pattern plots (STEPP) which graphically illustrates complex patterns of heterogeneity.^7-10 STEPP constructs overlapping subpopulations along the continuum of the covariate, thus improving the precision of the estimated treatment effects.⁷ The construction of the subpopulations depends on two parameters, r1, maximum number of patients overlapping across subpopulations and r2, minimum number of patients in a subpopulation. The STEPP methodology for survival outcomes was recently extended to include a variety of treatment effect measures, including observed-minus-expected (O − E) estimation of the hazard ratio.¹⁰ This O − E estimation requires no assumptions about the underlying distribution of survival times, and it is more easily explained to non-statisticians than standard regression modeling approaches. The primary advantage of STEPP over other methods is that STEPP can detect patterns of heterogeneity while making no or few assumptions.

However, the traditional test in STEPP can be sensitive to the choices of r1 and r2. Specifically, for smaller number of patients in each subpopulation, the test results became less stable, with the analysis consistently detecting heterogeneity when at least 15% of patients were included in each subpopulation, but failing to detect it with fewer patients.⁸ After further investigation through simulation studies, we observed an inflation of the type I error rate of the traditional test statistic and sometimes singular variance-covariance matrix estimates that may lead to results not being produced. This is due to the lack of a sufficient number of events within the subpopulations, which we refer to as instability of a STEPP analysis.

We introduce methodology to improve the stability of STEPP analyses while controlling type I error rate of the interaction tests. This methodology pre-specifies the number of events across treatment groups and within subpopulations to reduce the chance of treatment group incomparability.^{4, 11} To our knowledge, no other treatment effect heterogeneity approach has been designed to pre-specify the number of events within subpopulations. Furthermore, we show how O − E methodology can be used to estimate the subdistribution hazard ratio in the presence of competing risks. While estimation of hazard ratio values based on O − E methodology has already been shown,¹² a similar development for the subdistribution hazard ratio has not.

This article is organized as follows. In Section B, we use STEPP methodology to analyze data from the BIG 1-98 RCT. In Section C, we propose methodology to improve stability of a STEPP analysis. We then generalize O − E methodology to the competing risks setting. A simulation study of STEPP interaction tests, including a new interaction test for a variety of endpoints including O − E estimation of subdistribution hazard ratio, and its results are presented in Section D. Results of the analysis of the BIG 1-98 RCT are also provided in this section. The discussion is in Section E.

B. A Motivating Example

BIG (Breast International Group) 1-98 is an international, double-blind, phase III RCT of 8,010 postmenopausal women with hormone-receptor positive early invasive breast cancer. Patients were randomly assigned to receive one of four adjuvant endocrine therapy groups: letrozole, tamoxifen, or sequences of letrozole to tamoxifen or tamoxifen to letrozole. A previous BIG 1-98 trial report presented overall study results indicating that letrozole significantly reduced the cumulative incidence of breast cancer recurrence as compared with tamoxifen in the presence of two competing risks, 2^nd non-breast primary event and death prior to breast cancer recurrence.^{13, 14}

A potentially important predictor of breast cancer prognosis is the biomarker Ki-67, an indicator of tumor proliferation, which is associated with chemotherapy effectiveness.^15,16 Of the 4,922 patients who were randomized to receive 5 years of tamoxifen or letrozole in the BIG 1-98 trial, 2,685 patients had tumors with centrally confirmed estrogen receptor expression and tumor material available for Ki-67 determination in a central laboratory. The median follow-up was 51 months.¹⁷

The objective of the STEPP analysis used as an example in this paper was to investigate potential patterns of treatment effect for varying levels of the biomarker Ki-67 in the BIG 1-98 RCT. Breast cancer recurrence was the primary outcome of interest in the competing risks setting, where non-breast second malignancies and deaths without recurrence were considered competing risks.

The STEPP approach examined heterogeneity by estimating absolute and relative treatment effects within overlapping subpopulations defined by increasing values of Ki-67. Absolute treatment effects were measured by differences in 4-year cumulative incidence of breast cancer recurrence, while relative effects were measured by the subdistribution hazard ratio. The 4-year time-point was selected to coincide with the time-point used in previous analyses of BIG 1-98 data. The total number of recurrence events was 123 with 58 competing events (181 total events) for tamoxifen, and 73 events with 49 competing events (122 total events) for letrozole. STEPP analysis was performed using R (package: stepp, function: analyze.CumInc.stepp).¹⁸

While one-hundred patients has been recommended⁴ for each subpopulation to ensure comparability across treatment groups, there were simply not enough events to perform a traditional STEPP analysis. Our initial STEPP analysis generated 21 possibly overlapping intervals of Ki-67 values. Each interval defines a subpopulation of patients having those Ki-67 values. Even with one-hundred patients in each subpopulation, seven subpopulations had fewer than 10 events (breast cancer recurrence or competing) and one included only three events (two events for letrozole and one event for tamoxifen).

Similar results were produced in a simulation study, particularly for small sample sizes and low event rates, such as when survival at 4 years was 90% or when the sample size was less than 500. Sparse events within subpopulations and imbalance of events across treatment subpopulations caused instability of the traditional STEPP analyses and inflation of the type I error rate of the test statistic. To solve this instability problem of the traditional STEPP approach, we propose methodology in Section C that pre-specifies the number of events within each subpopulation.

C. Methods

C.1 Subpopulations

The goals of the proposed methodology are to ensure that every subpopulation contains enough events to assess heterogeneity and that there are an adequate number of subpopulations to provide good resolution over the range of the covariate (e.g., Ki-67). This will be achieved by pre-specifying the number of events, e1 and e2, in a STEPP analysis, where e1 is the largest number of events in common (overlapping) among consecutive subpopulations of each treatment group and e2 is the minimum number of events in each treatment group of each subpopulation (e2 > e1). The overlapping subpopulations are constructed, as follows.

Patients are ordered from the lowest to highest value of the covariate. The first subpopulation consists of patients with at least e2 events within each treatment group with the lowest covariate values. The next subpopulation is formed by removing patients with e2 minus e1 events with the lowest covariate values from the current subpopulation and replacing them with the next set of patients with e2 minus e1 events in the ordered list. This process continues until all patients have been included in at least one subpopulation, and each subpopulation has at least e2 events. When the last subpopulation does not meet the e2 criterion, it will be combined with the previous subpopulation. In the competing risks setting, e2 and e1 denote the event of the cause of interest. We call this this ‘sliding window event STEPP’.

C.2 Treatment effects

After the overlapping subpopulations are constructed, both absolute and relative treatment effects can be estimated. The treatment effect for the lth subpopulation, θˆ_l, can be estimated by the absolute difference between two survival curves at a fixed time-point using the Kaplan-Meier product limit estimate¹⁹ or the cumulative incidence estimate.²⁰

Alternatively, θˆ_l can be obtained by estimating the relative difference between two survival curves using hazard ratio values based on the “O − E” methodology.^{21, 22} The log hazard ratio, θˆ_l, is estimated by a first order approximation of the partial likelihood (L), as described in Section A of the Supplementary Materials. To our knowledge, a similar approach when using the subdistribution hazard ratio has not been studied. By reformulating Fine and Gray's²³ score based on the competing risks regression model as a Cox-like score structure, we show in Section B of the Supplementary Materials how a log rank type of test statistic in the form of O − E can be obtained for the following three cases: (1) no censoring; (2) complete censoring; and (3) randomly censored data.

C.3 Inference

After treatment effects are estimated within each subpopulation, results are then shown graphically, allowing for an exploration of treatment effect heterogeneity. This STEPP plot presents the estimated treatment effects, θˆ_l, for g subpopulations P_l, (l = 1, …, g) with associated pointwise confidence intervals or confidence bands by the median value of the covariate Z within each subpopulation.

To complement these graphical displays, a formal test for heterogeneity is performed. The null hypothesis, Ho, is: θ₁ = θ₂ = ⋯ = θ_g. We use θ to denote the g-dimensional vector of subpopulation specific treatment effects.

The ability to detect heterogeneity both graphically and via statistical testing may depend on the type of endpoint selected (absolute vs. relative endpoints).^{24, 25} For example, patterns of heterogeneity may be detected between a covariate and treatment effect measured on the absolute scale (e.g., using 4-year absolute difference in cumulative incidence), but may not be present (or detected) on the relative scale (e.g., using sub distribution hazard ratio).

Detection of heterogeneity may also depend on the choice of test statistic. We propose an interaction test statistic, denoted as ${\chi }_1^2$, that evaluates the size of the deviations of subpopulations from the overall treatment effect. This test statistic is:

$${\chi }_1^2={(\widehat{\theta }-{\widehat{\theta }}_{\mathit{\text{All}}})}^T{\widehat{\sum }}_1^{-1}(\widehat{\theta }-{\widehat{\theta }}_{\mathit{\text{All}}}),$$

where θˆ denotes the g-dimensional vector of subpopulation treatment effect estimates θˆ₁, …, θˆ_g, and θˆ_All denotes the g-dimensional vector with all elements equal to the estimated overall treatment effect θˆ_All. Let Σˆ₁ denote an empirical variance-covariance matrix of (θˆ − θˆ_All) and σˆ_l denote the estimated standard deviation of (θˆ_l − θˆ_All), i.e., σˆ_l is the square root of the lth diagonal term of Σˆ₁.

This proposed ${\chi }_1^2$ test has not been studied in STEPP. Nor has the traditional STEPP test, known as the supremum (T_max), been studied for absolute and relative end points, including hazard ratio and subdistribution hazard ratio based on O − E estimation, where:

$$\begin{array}{cc}{T}_{\mathit{max}}=\mathit{max}\left\{\frac{\left|{\widehat{\theta }}_l-{\widehat{\theta }}_{\mathit{\text{All}}}\right|}{{\widehat{\sigma }}_l}\right\},& l=1\dots g.\end{array}$$

Statistical significance is assessed using a permutation approach. Each of the permutation datasets are independently drawn by rearranging the values of a covariate within a treatment group. Let C represent the number of unique values of the covariate of interest and n_jk denote the total number of patients on treatment k (k = 1,2) with covariate value j (j = 1, …, C), where we assume n_jk ≥ 1. Thus, there are

${\prod }_{k=1}^2\left[\stackrel{\left({\sum }_{j=1}^C{n}_{jk}\right)!}{}/\underset{({\prod }_{j=1}^C{n}_{jk}!)}{}\right]$ permutations, and a random sample is extracted from them. The test statistics, T_max and ${\chi }_1^2$, are calculated from the observed and permuted datasets, where the variance-covariance matrices are estimated from the permuted samples. The significance level is defined as the fraction of sampled permutations in which the test statistic exceeds the test statistic calculated from the observed data.

Given a large number of permutations, k, the estimator of the p-value is approximately normally distributed with mean p and variance p(1 − p)/(k). The choice of k was based on the interval within which the estimated significance value will be 99% of the time for a given significance level.²⁶ We used 2500 permutations for the BIG 1-98 analysis so that if the true p-value is 0.01, 0.05 or 0.10 then these 99% intervals would be (0.00, 0.02), (0.04, 0.06), (0.08, 0.12), respectively.

C. 4 Simulation study

Through simulation studies, we evaluated the performance of two STEPP interaction tests, T_max and ${\chi }_1^2$ using the new STEPP methodology. We studied the accuracy in the recovery of the type I error probability (α) under the null hypothesis of no treatment effect heterogeneity of the tests for both absolute and relative endpoints. Calculations were performed using R.¹⁸

The simulation studies were designed as follows. Under the null hypothesis of no treatment effect, patient survival times were randomly generated from an exponential distribution, such that the survival function at 4 was S(t*=4)=0.1, 0.5 and 0.9. The data for the competing risks analyses were generated by assuming existence of two failure types, such that time without failure for each type followed an exponential distribution. Patients were assumed to have failed from the type of event that occurred earliest.

For every simulated dataset regardless of the type of endpoint (absolute v. relative), it was assumed that the patients entered the study uniformly over five years, with two additional years of follow up. Administrative censoring was applied to survival times seven years from the opening of accrual. For each patient, one of two treatment groups (A, B) was randomly assigned with a 1:1 ratio and a continuous covariate, where Z∼N(55,7). For each of the 300 simulations of sample size n (from 200 to 1000), overlapping subpopulations were constructed using the parameters e1 and e2.

After the overlapping subpopulations were constructed, we considered both absolute and relative treatment effects. Survival based on the Kaplan-Meier product limit and cumulative incidence was calculated at 4 years for each treatment group within each subpopulation and across all subpopulations within each treatment group. The relative endpoints, hazard ratio and subdistribution hazard ratio based on O − E estimation, were calculated within each subpopulation and across all subpopulations.

For each of the 300 datasets, 2500 permutation datasets were sampled by randomly rearranging the values of the covariate within treatment groups. The interaction test statistics, T_max or ${\chi }_1^2$, were calculated from observed and permutation datasets, and the critical value for rejection, for example at the 0.05 level, is the 95^th percentile of the 2500 test statistics. The p-value for the test was then calculated as the proportion of the 2500 test statistics greater than the value of the test statistic observed on the simulated data set. For comparability, the seed was set at the same place for every simulation.

D. Results

D.1 Simulation Results

For standard survival endpoints (see Figure 1) and for competing risks endpoints (Figure 2), in most scenarios of the simulation studies, the alpha level of the test for interaction was recovered quite accurately. However, for standard survival endpoints (Figure 1) and competing risks endpoints when a constant treatment effect was assumed (Figure 3), with sample sizes less than 200, this recovery of alpha was often quite conservative, and this may have implications on statistical power to detect treatment effect heterogeneity. For the cumulative incidence endpoint (Figure 2), T_max recovered the alpha level accurately, even for most cases with small sample sizes and low event rates. Though, both test statistics were quite conservative when the treatment effect was subdistribution hazard ratio (Figure 2), even when a constant treatment effect was assumed (Figure 3). The recovery of the type I error rate appeared adequate regardless of the number of subpopulations. Though some of the simulations had fewer than four subpopulations, we recommend at least four.

Figure 1.

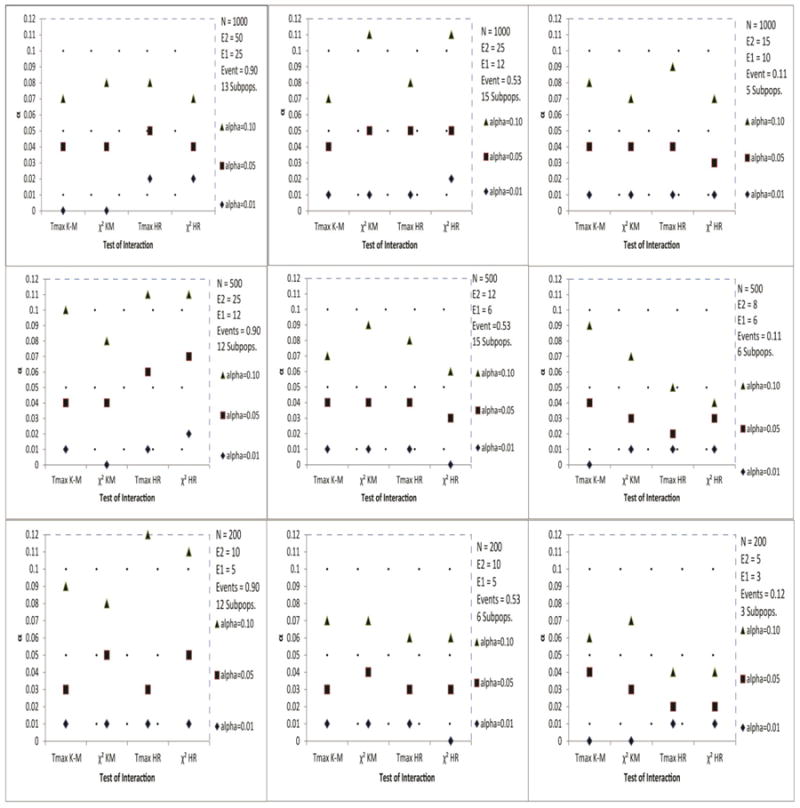
Estimated α level of the test for interaction based on the T_max and ${\chi }_1^2$ statistics of STEPP survival endpoints: Kaplan-Meier (K-M) and Hazard Ratio (HR^O-E) based on O − E estimation.

The 99% interval for permutation probability value 0.01, 0.05 and 0.10 are (0.00, 0.02), (0.04, 0.06) and (0.08, 0.12), respectively.

Events represents the average proportion of observed events.

Subpops. represents the average number of subpopulations.

The results were based on 300 simulations of sample size N.

Figure 2.

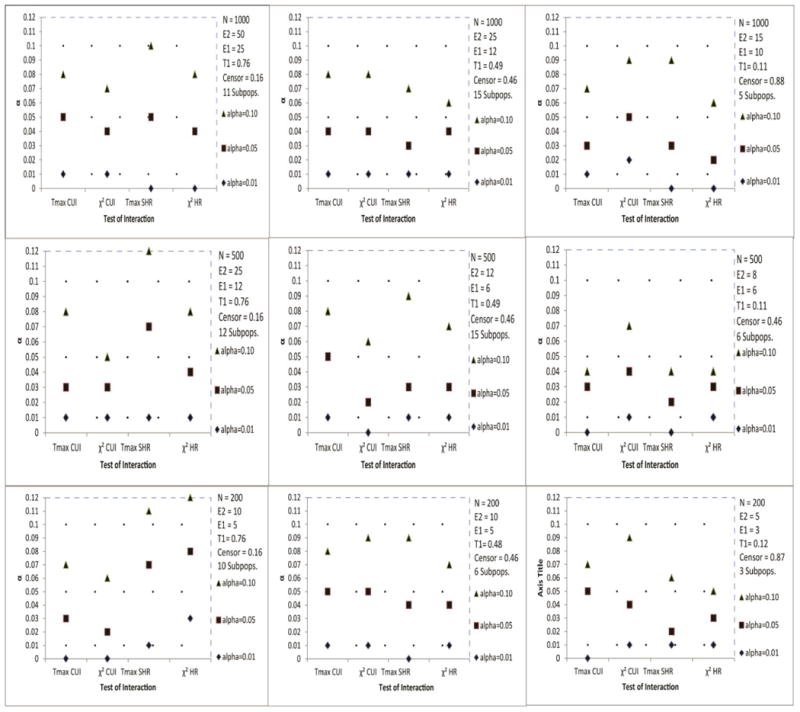
Estimated α level of the test for interaction based on the T_max and ${\chi }_1^2$ statistics of STEPP competing risks endpoints: Cumulative Incidence (CUI) and Subdistribution Hazard Ratio (SHR^O-E) based on O − E estimation.

The 99% interval for permutation probability value 0.01, 0.05 and 0.10 are (0.00, 0.02), (0.04, 0.06) and (0.08, 0.12), respectively.

T1 represents the observed average proportion of events of interest, and Censor represents the observed average proportion censored.

Subpops. represents the average number of subpopulations.

The results were based on 300 simulations of sample size N.

Figure 3.

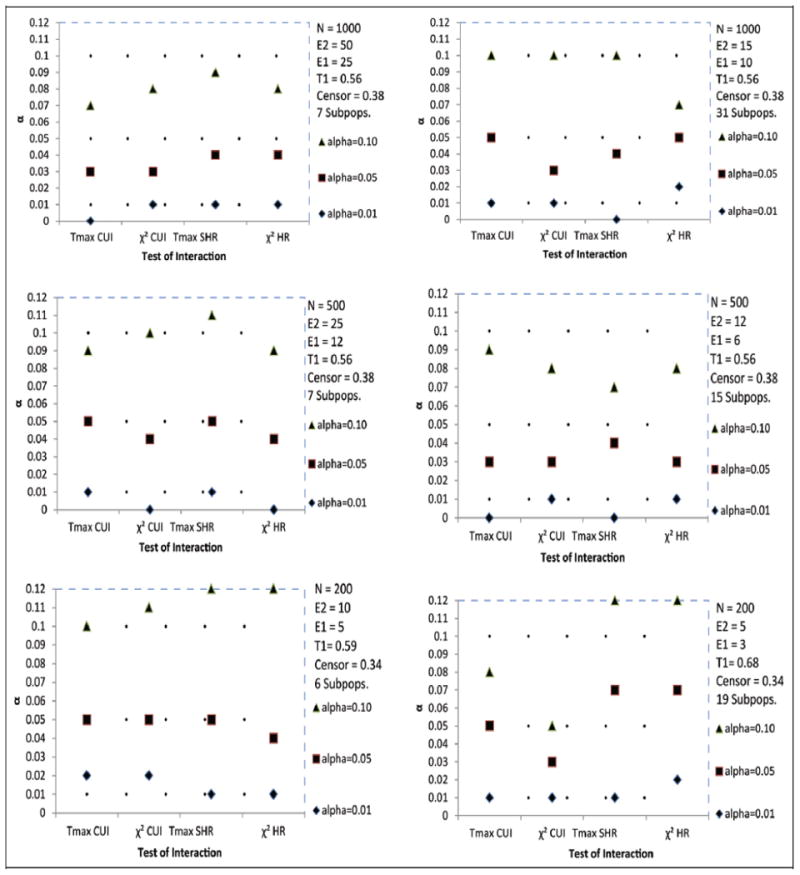
Estimated α level of the test for interaction based on the T_max and ${\chi }_1^2$ statistics of STEPP competing risks endpoints in the presence of constant treatment effect: Cumulative Incidence (CUI) and Subdistribution Hazard Ratio (SHR^O-E) based on O − E estimation.

The 99% interval for permutation probability value 0.01, 0.05 and 0.10 are (0.00, 0.02), (0.04, 0.06) and (0.08, 0.12), respectively.T1 represents the observed average proportion of events of interest, and Censor represents the observed average proportion censored.

Subpops. represents the average number of subpopulations. The results were based on 300 simulations of sample size N.

We should stress that the recovery of the type I error rate was liberal when we did not pre-specify the number of events across treatment groups within each subpopulation. It is therefore important to ensure an adequate number of events across treatment group subpopulations.

While recovery of the alpha level in nearly all scenarios was adequate, we found that some permutation datasets were discarded since fewer than two events per subpopulation were observed. This occurred for datasets with few events (i.e., 20 events total). As the total number of events in the subpopulation increased, as did the sample size, the total number of discarded permutation datasets decreased to zero. We therefore recommend that the results be interpreted with caution for datasets with fewer than 20 events. We also recommend that each subpopulation include at least 20 events (i.e., e2 = 10).

D.2 BIG 1-98 Analysis

Using the new STEPP methodology proposed in Section C, we can now explore patterns of treatment effect for varying levels of the biomarker Ki-67 in the BIG 1-98 RCT, described in Section B. Figure 4A summarizes the STEPP analysis of 4-year cumulative incidence of breast cancer recurrence. Five overlapping subpopulations of Ki-67 (median Ki-67 values of each subpopulation: 4, 9, 14, 20, 28) were generated, and subpopulations with high Ki-67 values had the greatest magnitude of treatment difference, indicating benefit for letrozole compared to tamoxifen. Figure 4B displays the difference in 4-year cumulative incidence of breast cancer recurrence (letrozole minus tamoxifen; differences < zero favor letrozole). Although these analyses suggested presence of treatment effect heterogeneity, no statistically significant heterogeneity was detected (P=0.10 based on ${\chi }_1^2$; P=0.08 based on T_max, Fig 4A;Fig 4B).

Figure 4.

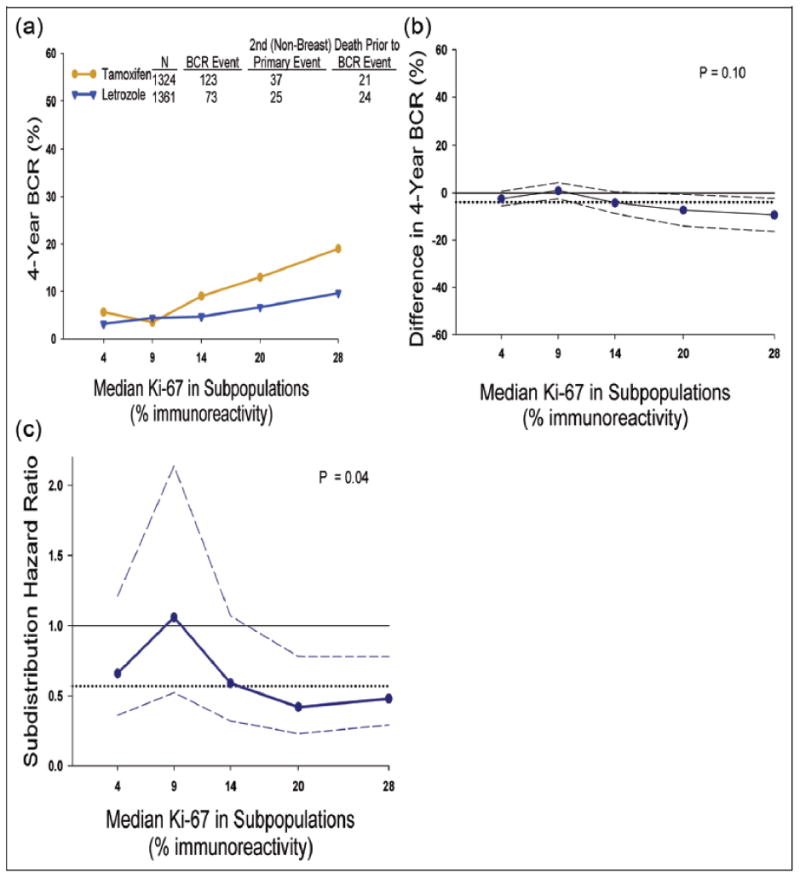
Subpopulation treatment effect pattern plot analysis of the treatment effect of letrozole vs. tamoxifen as measured by: (A) 4-year cumulative incidence of breast cancer recurrence (BCR), (B) difference in 4-year cumulative incidence of BCR (letrozole minus tamoxifen, less than zero suggested letrozole better, otherwise tamoxifen better), and (C) subdistribution hazard ratio (letrozole v tamoxifen; less than one suggested letrozole better; otherwise tamoxifen better) with corresponding point-wise 95% confidence intervals (dashed lines). The x-axes indicate median percentage of Ki-67 for patients in each of the overlapping subpopulations. To construct the overlapping subpopulations, we set e2 = 15 events as the number of events of each subpopulation in each treatment group, thus totaling at least 30 events within each subpopulation, and e1 = 5 as the number of events within consecutive overlapping subpopulations within each treatment group, thus totaling a maximum of 10 overlapping events. Solid grey line indicates no effect, and black dotted line indicates overall effect.

We also explored patterns of relative treatment effectiveness based on O − E estimation of subdistribution hazard ratio. The estimated ratio for breast cancer recurrence tended to be less than 1.0, showing benefit of letrozole relative to tamoxifen. STEPP analysis provides evidence of heterogeneity (P=0.04 based on ${\chi }_1^2$; P=0.07 based on T_max). As a sensitivity analysis, we evaluated the consistency of the STEPP results by varying the number of subpopulations from 3 to 6 overlapping subpopulations of Ki-67 values. We found consistent evidence of heterogeneity on the absolute scale (P>0.05 based on ${\chi }_1^2$ and T_max) and relative scale (P<0.05 based on ${\chi }_1^2$; P>0.05 based on T_max) showing benefit of letrozole over tamoxifen.

As an alternative to STEPP, we used Fine and Gray's²³ subdistribution hazard ratio regression modeling to evaluate heterogeneity of Ki-67 in the BIG 1-98 RCT. Three models were considered to evaluate different forms of the covariate effect. First, we used the median cutoff from Ki-67 distribution to dichotomize levels of Ki-67 as high (>10% with 62 breast cancer recurrence events) or low (≤ 10% with 134 breast cancer recurrence events). The treatment-by-covariate interaction was not statistically significant (P=0.21). We then used quartiles of the Ki-67 distribution to construct four patient subpopulations: high (19% to 90% with 79 recurrence events), medium-high (11% to 18% with 55 recurrence events), low-medium (6% to 10% with 37 recurrence events) and low (0% to 5% with 25 recurrence events [reference category]). The interaction test did not provide statistically significant results (P=0.91, P=0.46 and P=0.39, respectively), and the overall p-value was P=0.61. Finally, we used Ki-67 percentage as a continuous covariate in the Fine-Gray model, and the interaction term was again not statistically significant (P=0.10).

E. Discussion

We proposed methodology that improves stability of a STEPP analysis by pre-specifying the number of events across treatment group subpopulations. While additional investigation is needed to determine the optimal number of events per subpopulation, based on the results from the simulation study, we recommend a minimum of 20 events (or e2 = 10 with 10 events in each treatment group of each subpopulation) within each subpopulation and at least four subpopulations. Certainly more events are almost always preferable since they improve the precision of the treatment effects within subpopulations.

STEPP methodology was used to analyze competing risks data from the Breast International Group (BIG) 1-98 RCT. This STEPP analysis provided evidence of relative (non-monotonic) treatment effect heterogeneity related to the value of Ki-67. The monotonic effects that have been observed using traditional regression approaches might be an artifact of the modeling procedure since most heterogeneity results of Ki-67 are generated from a linear model that assumes a linear effect of Ki-67 on relative efficacy. Further investigation is needed to understand and confirm the biological underpinnings of this finding.

While relative effects are useful for measuring treatment effectiveness relative to a control group, in this case tamoxifen, in the general population, absolute effects are more clinically useful than relative effects for treatment decision making in individual patients for ‘personalized medicine’ (aka precision health). Relative effects, however, are more easily obtained using standard software and are often claimed as being ‘less heterogeneous’ than absolute effects.²⁷ Therefore, detecting heterogeneity on the relative scale may be of greater importance than detecting heterogeneity on the absolute scale since it provides understanding about the biological underpinnings.

The STEPP results from the BIG 1-98 trial provided evidence of heterogeneity on the relative scale and were suggestive of heterogeneity on the absolute scale. The treatment effectiveness patterns showed that patients with high Ki-67 percentages may benefit most from letrozole treatment. This benefit of letrozole treatment compared with tamoxifen may be explained by the reduced residual circulating estrogen levels in patients receiving aromatase inhibitors, such as letrozole. Despite the biological plausibility of the observed results, the complex role of potentially important patient characteristics, as the Ki-67 biomarker in the BIG 1-98 trial, needs extensive validation studies before the results from these analyses can be applied to clinical practice. Certainly the potential to target therapies to subpopulations most likely (or least likely) to benefit from a certain treatment is very attractive.

Other approaches have been designed to identify whether certain subpopulations are more or less likely to benefit from a certain treatment. This includes a tail-oriented version of STEPP, which is often used with risk index covariates. While the instability issues may be more limited in that case (since large subpopulations are used), here we focus on the sliding window approach due to its widespread use. To implement this alternative sliding window STEPP approach using subpopulations of events, software will be available at google (see sites.google.com/site/stepprpackage) and R.¹⁸

An alternative approach to STEPP that relies on evaluating interaction terms from a regression model to assess heterogeneity is known as multivariable fractional polynomial interaction (MFPI).²⁸ An advantage of MFPI is that it does not require pre-specification of the functional form of the regression parameters. Another approach is based on Bayesian methodology introduced by Simon, Dixon and Friedlin²⁹ (see also Simon³⁰). This Bayesian method avoids many of the problems associated with subgroup analysis because it does not allow separate analysis of subgroups. Another alternative is splines, including regression and smoothing splines. The most commonly used approach to evaluate heterogeneity is, however, regression modeling, such as the Fine-Gray modeling approach.

To compare the results from the new STEPP method, we also evaluated heterogeneity using the standard Fine-Gray regression model that often uses dichotomized covariates measured on a continuous scale. Certainly categorizing baseline characteristics measured on a continuous scale can fail to identify the value of a baseline characteristic as a predictor of treatment effectiveness, as illustrated in the BIG 1-98 example. Associations between biomarker Ki-67 expression level and treatment effect did not appear to follow a linear pattern, and therefore was not detected using standard modeling.

In this article, we described simulation studies to assess the type I error rate of STEPP test statistics for a variety of endpoints, but not statistical power. This emphasis is motivated by the fact that making a type I error has severe consequences on clinical practice. This is not to say that type II errors are not important, especially since heterogeneity tests for interaction are generally underpowered. Based on the simulation studies it appeared that in some situations the tests were very conservative, and this may have implications on the statistical power to detect heterogeneity. Future work is needed to compare the statistical power of this new STEPP method with the standard heterogeneity regression approach, especially in the competing risks setting.