Revised time scales of RNA virus evolution based on spatial information

Abstract

The time scales of pathogen evolution are of major concern in the context of public and veterinary health, epidemiology and evolutionary biology. Dating the emergence of a pathogen often relies on estimates of evolutionary rates derived from nucleotide sequence data. For many viruses, this has yielded estimates of evolutionary origins only a few hundred years in the past. Here we demonstrate through the incorporation of geographical information from virus sampling that evolutionary age estimates of two European hantaviruses are severely underestimated because of pervasive mutational saturation of nucleotide sequences. We detected very strong relationships between spatial distance and genetic divergence for both Puumala and Tula hantavirus—irrespective of whether nucleotide or derived amino acid sequences were analysed. Extrapolations from these relationships dated the emergence of these viruses most conservatively to at least 3700 and 2500 years ago, respectively. Our minimum estimates for the age of these hantaviruses are ten to a hundred times older than results from current non-spatial methods, and in much better accordance with the biogeography of these viruses and their respective hosts. Spatial information can thus provide valuable insights on the deeper time scales of pathogen evolution and improve our understanding of disease emergence.

1. Introduction

Rapidly evolving pathogens cause a majority of emerging diseases in humans and livestock. There is often little consensus about their origin and evolutionary history [1,2], but understanding the process of disease emergence and spread is crucial for the development of preventive strategies and to combat epidemics. Important information such as the time of emergence and evolutionary rates can be derived from time-calibrated phylogenies of pathogen sequences using the dates of sample collection during an outbreak [3–5]. For example, for recent epidemics of Ebola virus, influenza virus, human immunodeficiency virus (HIV) and others, the combination of nucleotide sequence data of the pathogens with epidemiological reports has enabled detailed reconstructions of spatial and temporal transmission patterns of the infectious agents [4,6,7].

Serially sampled sequence data are often also used to infer the dates of much older events in the evolutionary history [8], but the absolute age of many pathogens remains contentious due to the lack of fossils, ancient DNA or other information that could provide support for the accuracy of estimated time scales [9]. Moreover, estimates based on heterochronous sequences (tip-dating sensu [10]) are often in conflict with biogeographic evidence or the evolutionary history of co-evolving host species. For example, tip-dated phylogenies of simian immunodeficiency viruses—which gave rise to HIV—indicated an emergence less than 2000 years ago [11]. By contrast, the biogeography of these ubiquitously distributed viruses of African non-human primates and their association with the host phylogeny clearly revealed an ancient history of co-divergence over tens of thousands of years [12].

Temporal reconstruction of virus evolutionary history based on heterochronous sequence data has been questioned on grounds of insufficient temporal structure in phylogenetic trees [13] and underestimated genetic divergence due to mutational saturation [14]. The latter is a consequence of the high evolutionary rates of many pathogen species where multiple substitutions can occur at the same sequence position already over relatively short absolute time scales [15]. Sophisticated models of sequence evolution are designed to consider multiple substitutions at the same position, but the full extent of divergence in rapidly evolving sequences might still not be captured [16].

In this study, we exploit spatial distance as a hitherto unused source of information about genetic divergence of rapidly evolving pathogens and their time scales of emergence. We capitalize on the long-established realization that genetic similarity representing evolutionary divergence tends to be higher among spatially close organisms in systems with low dispersal, a pattern called isolation by distance (IBD) in population genetics [17,18]. With this correlation, the spatial distance between individuals can be informative about their genetic divergence. Over larger distances, this relationship is more likely to be affected by intrinsic (e.g. mutational saturation) and extrinsic factors (e.g. habitat availability, colonization history). A pattern of IBD at short spatial distances that decays over larger distances is thus indicative of such factors impacting on genetic divergence estimates. IBD has been detected in many organisms, including humans [19,20], with only relatively few formal reports from viruses [21–25]. However, many studies report the spatial clustering of nucleotide sequences in phylogenetic trees [26–30] which might indicate an IBD pattern.

Here we revise evolutionary time scales by incorporating spatial data for the case of hantaviruses (family Hantaviridae)—RNA viruses with often enigmatic evolutionary history and phenology [31]. Tip-dated phylogenies indicated the origin of rodent-borne hantaviruses sampled across North America, Asia and Europe only 849 [32] or 1915 years ago [33]. Such a recent emergence is unlikely in the light of, for example, the separation of the American and the Eurasian continent by the Bering Sea preventing rodent migration for more than 10 000 years [34,35]. Further, the specialization of hantaviruses to different widely co-distributed rodent hosts (e.g. in Europe Puumala virus, PUUV—Myodes glareolus; Tula virus, TULV—Microtus arvalis; Dobrava-Belgrade virus—Apodemus spec.) would have taken place within very short time. By stark contrast, studies focusing on the association of hantaviruses with their mostly Muroidea hosts place their origin millions of years ago based on phylogenetic relationships of the hosts dated with molecular and fossil data [36–38], but the actual phylogenetic evidence from virus data suggesting long-time coevolution is debated [39,40]. We focus our analyses on the hantaviruses PUUV and TULV because large-sequence datasets with initial evidence of spatial clustering are available, and their mostly European distribution range is relatively well covered [41–44]. Furthermore, their sedentary arvicoline rodent hosts display evidence of IBD at larger geographical scales [45–47]. We demonstrate that time estimates of hantavirus origins can be strongly biased by excessive mutational saturation in divergent sequence data, which can be detected and improved by taking spatial information about virus sampling locations into account.

2. Material and methods

(a). Phylogenetic analysis

Nucleotide sequence data from the PUUV and TULV nucleocapsid protein-encoding region of the small genomic segment (S-segment) and from complete PUUV genomes were collected from GenBank. Sequences of short overlap in the alignment, those originating from humans or cell lines instead of rodent hosts or with unknown place or date of sampling, as well as identical sequences from the same location, were excluded. Final alignments consisted for PUUV S-segment of 97 sequences of 504 bp length and for TULV of 115 sequences of 543 bp length. Sampling dates ranged between 1987 and 2012 for PUUV, and between 1987 and 2013 for TULV. The PUUV full genome alignment contained concatenated coding sequences from all three genomic segments (total: 11 228 bp). While PUUV sampling localities were heterogeneously distributed over a large region of Europe, TULV sequences mainly originated from Central Europe (figure 1a,b). Both datasets contained additional distant sequences from Russia and Kazakhstan (figure 1c). For phylogenetic inference, TULV was used as outgroup for PUUV and vice versa. Bayesian reconstruction of phylogenetic relationships was done with MrBayes v. 3.2.2 [48] on the CIPRES platform [49]. Nucleotide data were partitioned into two groups: combined 1st + 2nd and 3rd codon position, with the evolutionary rate unlinked across partitions. Reversible-jump sampling across the entire general time-reversible (GTR) substitution model space was implemented for each partition [50]. Metropolis-coupled Markov chain Monte Carlo (MCMC) sampling was performed for 10⁷ generations in four independent runs of four chains for all datasets. A sample was recorded every 10³ generation with a burn-in fraction of 25%. For amino acid sequence analyses, nucleotide sequences were translated in MrBayes using the protein substitution model. MCMC analyses were run as described above implementing a mixed amino acid model prior to averaging over different amino acid rate matrices. FigTree v. 1.4.2 [51] was used to draw consensus trees.

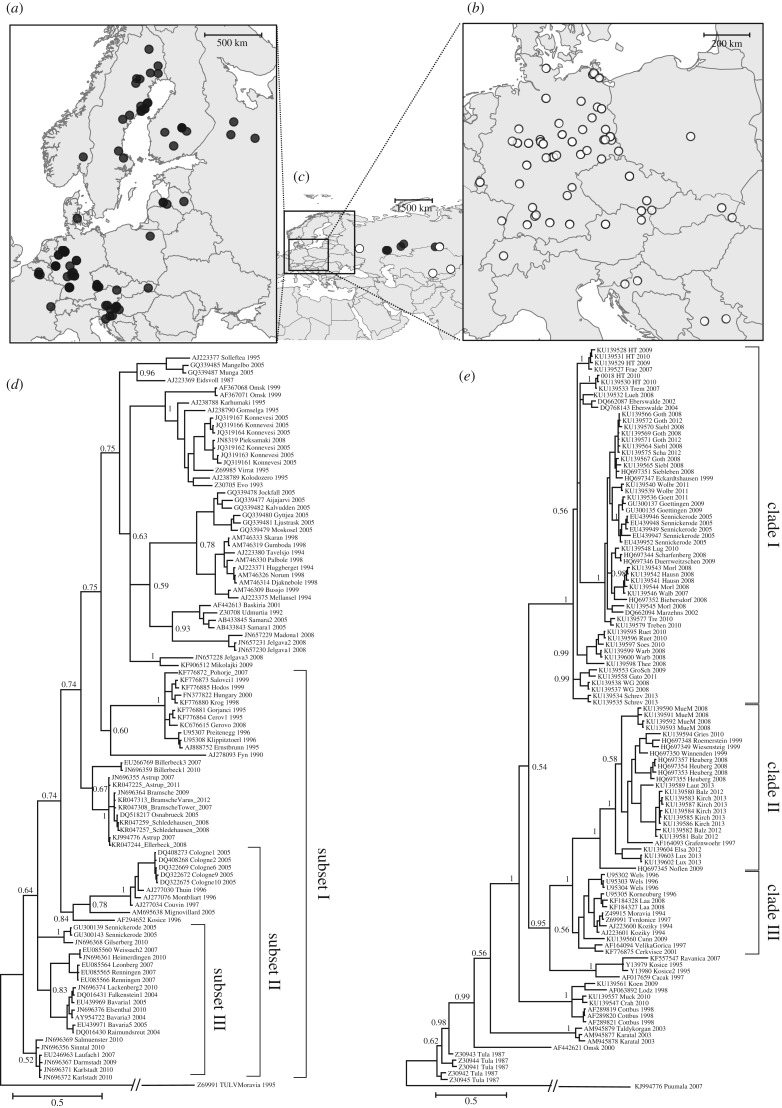
Figure 1.

Geographical origin and phylogenetic relationships of Puumala (PUUV) and Tula (TULV) hantavirus sequences. (a,b) Maps show European sampling locations of (a) PUUV and (b) TULV sequence data (note the difference in scale). (c) Additional distant sampling locations in Russia and Kazakhstan are indicated by black and white symbols for PUUV and TULV sequence origins, respectively. (d,e) Maximum clade credibility phylogenetic trees based on partial S-segment sequences of (d) PUUV and (e) TULV with posterior node probabilities shown for major branches only. Subsets of different evolutionary levels in PUUV and evolutionary clades in TULV (see text) are indicated with brackets. Leaves are labelled with GenBank sequence accession number, sampling location and year of sample collection.

(b). Association between geographical distance and genetic divergence

Information on the geographical origin of virus sequences was obtained from the original publications or their authors. Geographic Distance Matrix Generator [52] was used to calculate pairwise Euclidean geographical distances between localities of origin. A GTR model with four substitution classes, among-site rate variation and proportion of invariable sites (TIM2 + G + I) was the best model of nucleotide substitution for all datasets according to Bayesian information criterion inferred with jModelTest v. 2.1.6 [53]. Pairwise genetic divergence was calculated in MEGA 6 [54] as (i) p-distance (percentage of variable sites) and (ii) under the Tamura and Nei (TrN + G + I) model [55], as it best corresponds to TIM2 + I + G. From the Bayesian phylogenetic analyses described above, trees with highest likelihood scores were used to infer (iii) pairwise genetic distance along branches (sum of branch lengths) between samples, representing phylogenetically interdependent divergence estimates [16]. For amino acid sequences, p-distance and tree distance was inferred analogously. Statistical significance of the correlation between the matrices of geographical distance and genetic divergence was determined with a Mantel test using 10⁵ permutations performed in Arlequin v. 3.5.1.3 [56].

(c). Testing for mutational saturation

To examine mutational saturation, we plotted pairwise transition to transversion ratios (Ti/Tv) against genetic divergence estimated with the TrN + I + G model. Saturation at synonymous and non-synonymous sites was analysed by plotting pairwise genetic divergence based on the combined 1st + 2nd and the separated 3rd codon positions against geographical distance. Signals of mutational saturation among different evolutionary levels were investigated following Duchêne et al. [16] by removing basal sequences from the fixed topology of a phylogenetic tree to obtain sequence subsets of reduced evolutionary age. Tree topologies for this saturation test were estimated with Maximum-likelihood (ML) in GARLI [57] on CIPRES. For the PUUV dataset, basal branches of the ML topology were removed to form an initial subset 1, and younger subsets 2 and 3 were obtained by further removing basal branches (electronic supplementary material, figure S1). For TULV, the evolutionary clades described in [44] were defined as reduced-age subsets if represented by at least ten sequences in our dataset (figure 1e). For all trees and subsets, we calculated Ti/Tv, which is expected to decay with evolutionary time when divergence is underrepresented by the evolutionary model [58]. Analogously, we inferred the ratio of non-synonymous to synonymous substitutions (dN/dS), the GC contents and the shape parameter of a gamma-distributed among-site rate variation (α) to examine potential effects of natural selection and base composition on Ti/Tv. α is expected to scale negatively with increasing divergence when mutational saturation is accurately accounted for [16]. All parameters were estimated using CODEML implemented in PAML v. 4.8 [59].

(d). Virus divergence and age estimates

We used the observed correlation between genetic divergence and geographical distance among hantavirus sequences to deduce the per-distance increase of genetic divergence (slope). While mutational saturation among spatially distant sequences is expected to weaken this correlation (and flatten the slope), for recently diverged sequence pairs, the impact of mutational saturation on genetic divergence is low because the overall number of accumulated mutations during short time spans is small. To infer slopes mostly from sequence data at short distances that were less affected by mutational saturation, two different approaches were applied. (i) We simultaneously fitted two linear regressions with minimal overall residuals on either side of a separation point to the relationships between geographical distance and genetic divergence using R [60]. This resulted in a short-distance partition of more recently diverged sequence pairs of low mutational saturation characterized by a positive slope, and a partition at longer geographical distances representing a plateau of saturated sequence pairs (see Results). (ii) We first determined the saturation growth rate (SGR) model (y = ax/(b + x)) with CurveExpert v. 1.3 [61] as the best single model with regard to parametrization and standard error to fit the geographical distance to genetic divergence relationships of all data points. Then, we calculated the slope as the derivation for zero geographical distance where no effect of mutational saturation on the SGR curve is expected and determined confidence intervals with 1000 bootstrap replicates.

The inferred slopes from both approaches were then applied to linear models of unsaturated growth to provide estimates of revised genetic divergence across the full distribution range of virus species and clades. The minimum age of PUUV and TULV was assessed by dividing the expected unsaturated genetic divergence at maximum geographical distance by twice the substitution rate. We used a median substitution rate of 2.70 × 10⁻⁴ substitutions per site per year as assessed on recently diverged PUUV sequences sampled over eight years from the same geographical region [43] so that effects of mutational saturation should be insignificant. To compare our estimates incorporating geographical information with results of frequently used time-calibrated phylogenetic methods, we ran analyses in BEAST v. 2.3.0 [62] on CIPRES. Bayesian model averaging was performed using the bModelTest package [63] on partitioned data as described above. A Bayesian skyline coalescent tree prior with relaxed lognormal molecular clock was implemented in MCMC sampling of 10⁸ generations with samples recorded every 5000 generations. TempEst v. 1.5 [64] showed that the temporal signal in our sequence datasets was very low as indicated by weak correlations of sampling dates with root-to-tip distances for both viruses (PUUV: R² = 0.00022 and TULV: R² = 0.053). The resulting age estimates are thus given for comparative purposes only.

3. Results

(a). Phylogeographic structure of PUUV and TULV

We detected very high sequence variability in both hantaviruses across their large distribution ranges (PUUV S-segment: 44.2% variable sites; PUUV full genomes: 32.7%; TULV S-segment: 43.5%), but all phylogenies were informative about the geographical origin of sequences irrespective of the year of sample collection (figure 1). Local phylogeographic clusters were highly supported in both viruses despite exclusion of identical sequences, whereas posterior probabilities of basal tree relationships were generally lower (figure 1d,e). For PUUV sequences from a large geographical area with heterogeneously distributed sampling localities, no deep phylogeographic structure could be determined (figure 1a,d), while TULV formed geographically segregated genetic clades (figure 1b,e).

(b). Association of geographical distance, divergence and mutational saturation

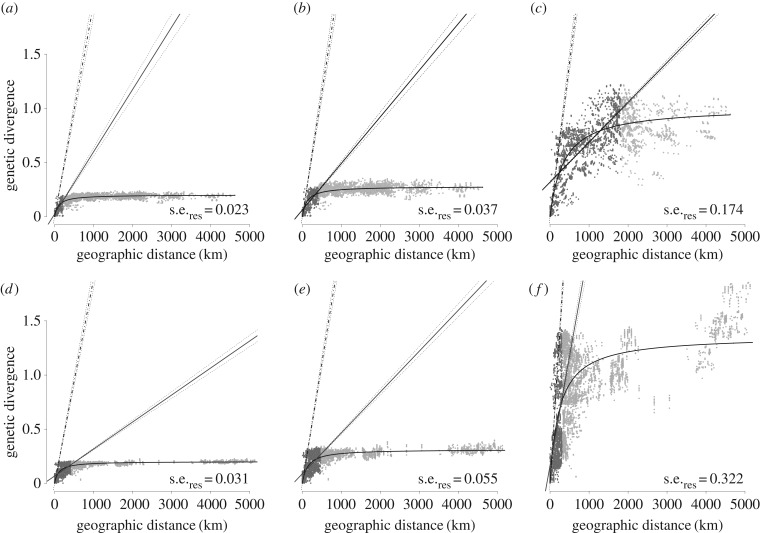
For both hantaviruses, we found an extremely strong association between geographical distance and genetic divergence (all p < 0.001; figure 2), irrespective of the estimator of divergence used for S-segment, full genome (in PUUV; electronic supplementary material, figure S2) or amino acid sequences (electronic supplementary material, figure S3). There were strong positive relationships at local scale and all slopes flattened at larger geographical distances, demonstrating strong mutational saturation for synonymous and non-synonymous codon positions likewise (electronic supplementary material, figure S4). This evidence of mutational saturation was corroborated by a clear negative correlation between Ti/Tv and genetic divergence (electronic supplementary material, figure S5) as well as between Ti/Tv and evolutionary age of phylogenetic relationships (table 1). dN/dS, α and GC contents remained constant among evolutionary levels, providing no evidence for influences on the decay of Ti/Tv other than mutational saturation (table 1). As expected under mutational saturation, pairwise genetic divergence based on p-distances was lower than estimated with the TrN + I + G model, which accounts for multiple substitutions per site (figure 2a,b,d,e; electronic supplementary material, table S1). Tree distances—representing branch lengths extracted from Bayesian analyses—were considerably larger than both pairwise sequence divergence estimates. Branch lengths in trees were sensitive to branch length priors, but the pattern of mutational saturation at larger geographical distances was unaffected (figure 2c,f; electronic supplementary material, table S1).

Figure 2.

Relationships between geographical distance and genetic divergence among European hantaviruses. For PUUV (a–c) and TULV (d–f) genetic divergence is inferred either as p-distance (a,d), under the TrN + I + G model of nucleotide evolution (b,e), or as branch lengths in the Bayesian tree reconstruction (figure 1) (c,f). Dark grey points and the solid line (dotted lines: 95% CIs) represent the linear regression over the short-distance partition derived from fitting two linear regressions simultaneously (see text). Light grey data points represent the long distance partition with flat slope. Curves represent the saturation growth rate model (SGR; see text) with residual standard errors (s.e._res). The slope of the derivation of the SGR at zero distance is indicated by the hatched line with 1% and 99% quantiles from 1000 bootstraps.

Table 1.

Sample sizes and substitution parameters determined for PUUV and TULV S-segment phylogenies and several subsets or clades of different evolutionary age (see text). n, number of sequences; Ti/Tv, transition/transversion ratio; dN/dS, ratio of non-synonymous to synonymous substitutions per site; GC, GC-content; α, shape parameter of the gamma distribution of among-site rate variation.

	n	Ti/Tv	dN/dS	GC	α
PUUV full tree	97	5.570	0.019	0.405	3.010
subset I	55	6.055	0.018	0.405	2.455
subset II	30	7.908	0.017	0.407	2.275
subset III	21	9.885	0.023	0.406	3.369
TULV full tree	115	6.025	0.010	0.426	2.237
clade I	56	8.987	0.007	0.428	2.365
clade II	26	9.263	0.005	0.422	1.804
clade III	13	13.033	0.009	0.424	1.830

Extrapolation of genetic divergence at maximum geographical distance in our datasets (PUUV: 4623 km; TULV: 5296 km) led to 16- to 52-fold higher estimates based on the derivation of the SGR curve compared with the fitted SGR curve (figure 2; electronic supplementary material, table S1). Extrapolation from the regression slope over short geographical distances resulted in two to 14 times higher genetic divergence at maximum geographical distance compared with the SGR curve (figure 2; electronic supplementary material, table S1). For PUUV, slopes of the short-distance regressions and SGR curves were consistent no matter how genetic divergence was inferred (figure 2a–c; electronic supplementary material, table S1). Phylogenetic clades in TULV (figure 1e) appear to affect the slope most noticeably for tree distances (figure 2d–f; electronic supplementary material, table S1) as highly diverged sequences from different clades can be found at short geographical distances.

(c). Hantavirus emergence dating using spatial information

Age estimates of both hantaviruses were considerably older based on spatially informed genetic divergence than those from tip-dated phylogenies. Analyses with BEAST estimated the age of PUUV overall as 346 years (95% highest posterior density interval, HPD: 201–571 years) and for TULV as 254 years (95% HPD: 145–392 years) (table 2; electronic supplementary material, figure S6). Geographically coherent sequence clusters in both viruses spanning vast areas of Europe were estimated to be very young. For example, the time to the most recent common ancestor (TMRCA) of PUUV subset I covering much of Central and Eastern Europe was estimated to 296 years (95% HPD: 177–487 years; electronic supplementary material, figures S1, S6). Similarly, the TMRCA of TULV clade III with sequences from Germany, Czech Republic, Slovakia, Austria, Slovenia and Croatia was 73 years (95% HPD: 45–109 years), and the split between clades II and III covering the area from Luxembourg to Croatia was estimated to only 126 years (95% HPD: 74–194 years) (figure 1b; electronic supplementary material, S6). By contrast, divergence time estimates based on linear regression slopes suggested a minimum evolutionary age of PUUV overall between 3700 and 5000 years, and of TULV between 2600 and 20 100 years (table 2). The minimum age estimates based on derivations from SGR slopes ranged between 16 800 and 24 300 years for the full PUUV dataset and 18 600–55 000 years for all TULV sequences. Based on Bayesian branch lengths, PUUV subset I was at least 6500 years and TULV clade III at least 6200 years old (table 2). When we alternatively applied the extremely high substitution rates inferred with BEAST (9.38 × 10⁻⁴ substitutions per site per year for PUUV and 1.51 × 10⁻³ substitutions per site per year for TULV), our age estimates incorporating spatial information were still 2 to 38 times higher than the tip-dated estimates (electronic supplementary material, table S2).

Table 2.

Minimum age estimates in years for full PUUV and TULV S-segment datasets and for several subsets or clades of younger evolutionary age. Calculations are based on extrapolation of linear regression slopes over short-distance data or derived slopes from the fitted saturation growth rate (SGR) curve. Both methods were applied on data with genetic distances calculated as p-distance, applying the TrN + I + G model of nucleotide substitution or as sum of branch lengths in a phylogenetic tree (tree). Numbers in brackets indicate 95% CIs. The last column contains results of the tip-dating analysis in BEAST with 95% highest posterior density (HPD) intervals indicated.

	extrapolation linear			extrapolation SGR
	p-distance	TrN + I + G	tree	p-distance	TrN + I + G	tree	phylogenetics dating
PUUV
full dataset	4966 (4610–5320)	3795 (3591–3998)	3741 (3665–3815)	16 841 (15 582–18 372)	19 697 (17 912–21 892)	24 354 (22 592–26 175)	346 (201–571)
subset I	1360 (1270–1447)	1098 (1049–1143)	1432 (1417–1444)	4501 (4165–4910)	5264 (4787–5851)	6509 (6038–6996)	296 (177–487)
subset II	781 (734–825)	664 (641–685)	1061 (1048–1072)	2519 (2331–2748)	2946 (2679–3274)	3643 (3379–3915)	209 (119–341)
subset III	469 (445–490)	431 (420–440)	861 (846–875)	1451 (1342–1583)	1698 (1544–1887)	2099 (1947–2256)	130 (475–217)
TULV
full dataset	2569 (2465–2673)	3865 (3716–4014)	20 102 (18 600–21 603)	18 551 (17 364–19 671)	21 808 (20 551–23 086)	54 969 (51 349–58 574)	254 (145–392)
clade I	338 (333–343)	486 (478–492)	2026 (1936–2107)	1612 (1509–1709)	1895 (1786–2006)	4776 (4462–5090)	81 (46–128)
clade II	338 (332–342)	485 (477–490)	2022 (1929–2099)	1608 (1505–1704)	1890 (1781–2000)	4763 (4450–5076)	89 (51–138)
clade III	403 (395–410)	584 (572–593)	2551 (2420–2670)	2103 (1969–2230)	2473 (2330–2618)	6233 (5822–6642)	73 (45–109)

4. Discussion

Consistent spatial structure in PUUV and TULV allows for the first time to describe the extent of mutational saturation in two RNA virus species. We showed that models of sequence evolution severely underestimate the genetic divergence in our datasets (electronic supplementary material, table S1), which corroborates concerns about the accuracy of evolutionary time scales inferred with time-calibrated phylogenies for many rapidly evolving pathogen species [15,16]. For two RNA viruses, we demonstrated that combining sequence data with spatial information can lead to highly improved age estimates. The strong correlation between geographical distance and genetic divergence in PUUV and TULV makes the sampling locations informative about evolutionary differences even in highly saturated sequence data. While local disturbance of the IBD pattern is expected (e.g. through geographical barriers like larger water bodies), the general association between spatial distance and genetic divergence in these hantaviruses remains relatively unaffected. Our approach relies on predictable geographical structuring that may not necessarily be found among far-dispersing pathogens or may break down with extensive host migration. These factors differ widely between different study systems, but it is generally straightforward to test for IBD patterns in a sequence dataset and fit a saturation model. In more complex systems, simple spatial distances are unlikely to describe evolutionary relationships sufficiently well, but it might be possible to characterize pathogen diffusion patterns, for example through network connections [65]. The use of network distances that consider host mobility, migration history [66] and landscape factors [12] could thus potentially enable distance-based divergence estimation even for highly dispersed infectious agents.

We found that phylogenetic relationships of serially sampled PUUV and TULV sequences are determined rather by spatial proximity (figure 1) than by the time-points of sample collection. This suggests a long-lasting stationary presence of both hantaviruses across Europe, where genetic divergence between sequences is rather the result of long-term IBD than due to the collection of samples through time. The observed loss of phylogeographic resolution even for whole-genome and amino acid sequences over geographical distances of less than 1000 km due to strong mutational saturation (figure 2; electronic supplementary material, S2, S3) supports a scenario of ancient colonization and low dispersal for both hantaviruses. Ancient emergence times as inferred in this study (table 2) are therefore in much better accordance with phylogeographic insights than results of tip-dated analyses [32,33], and they are in line with hypotheses of virus–host co-divergence at least in recent evolutionary periods [36–38]. Still, our results represent minimum estimates for the emergence of these hantaviruses, and their true age might be even higher: the data analysed here may not cover the full spatial distribution of PUUV and TULV and larger geographical distances would indicate higher overall evolutionary divergence. Higher divergence estimates deduced from the derivation of the SGR curve might be closer to true values than the ones from linear regressions because slopes over short-distance data are expected to be affected by gradually increasing mutational saturation (figure 2). While the variance of evolutionary time scales of hantaviruses inferred in this study remains large, all estimates are decisively older than tip-dated results (table 2).

Unlike in recent virus outbreaks, where the place of origin and direction of spread could be recovered from serially sampled sequence data [21,23,28], high mutational saturation probably impedes better temporal calibration of PUUV and TULV phylogenies using the dates of sample collection [13]. We found strong signals of mutational saturation at different levels of genetic divergence indicated by a clear decline in Ti/Tv ratios towards more diverged evolutionary levels (table 1). We tested for the influence of other factors on phylogenetic dating studying further evolutionary parameters, namely time-dependency of evolutionary rates [67]. Recently diverged sequences may contain slightly deleterious non-synonymous mutations, which have not yet been removed by purifying selection. Substitution rates of younger evolutionary groups would therefore appear to be higher than those of groups that have diverged a long time ago. Rates inferred for recently diverged sequences may thus not be applicable to subsequently date deeper phylogenetic relationships. However, we did not find evidence for changes in the evolutionary rates over time [10,68] as dN/dS ratios were consistently low among evolutionary levels (table 1). The number of pairwise synonymous and non-synonymous substitutions both increased with spatial distance and displayed mutational saturation over large distances (electronic supplementary material, figure S4). While we cannot exclude some effects of rate variability, our results demonstrate that for highly diverged hantavirus sequences, mutational saturation is the predominant cause of biases in molecular clock dating.

5. Conclusion

Evolutionary models, time-calibrated phylogenies and sampling data provide valuable information on pathogen transmission dynamics and instant processes of sequence change during disease outbreaks. However, the investigation of deeper evolutionary processes in rapidly evolving pathogens benefits also from taking spatial information into account. With a better understanding of the particular ecology of a pathogen–host system, it might be possible to define more reliably evolutionary time scales and reconstruct key processes of host jumps and long-term adaptive change. Learning about the evolutionary past of rapidly evolving pathogens is crucial to understand their fundamental biology, and to prevent and control future disease outbreaks.

Data accessibility

Sequence alignments including accession numbers, sampling dates and geographical coordinates were submitted to Dryad (http://dx.doi.org/10.5061/dryad.dc770) [69].

Authors' contributions

G.H. conceived the study. M.S. and V.W.d.M. collected and analysed the data guided by G.H. R.G.U. provided advice and discussion. M.S. and G.H. wrote the manuscript that was revised and approved by all authors.

Competing interests

We declare no competing interests.

Funding

This study was supported by a grant from the Swiss National Science Foundation (31003A-149585) to G.H. and Deutsche Forschungsgemeinschaft (SPP 1596 ‘Ecology and Species Barriers in Emerging Viral Diseases’, UL 405/1-1) to R.G.U.