Performance trade-offs and ageing in the ‘world's greatest athletes’

Abstract

The mechanistic foundations of performance trade-offs are clear: because body size and shape constrains movement, and muscles vary in strength and fibre type, certain physical traits should act in opposition with others (e.g. sprint versus endurance). Yet performance trade-offs are rarely detected, and traits are often positively correlated. A potential resolution to this conundrum is that within-individual performance trade-offs can be masked by among-individual variation in ‘quality’. Although there is a current debate on how to unambiguously define and account for quality, no previous studies have partitioned trait correlations at the within- and among-individual levels. Here, we evaluate performance trade-offs among and within 1369 elite athletes that performed in a total of 6418 combined-events competitions (decathlon and heptathlon). Controlling for age, experience and wind conditions, we detected strong trade-offs between groups of functionally similar events (throwing versus jumping versus running) occurring at the among-individual level. We further modelled individual (co)variation in age-related plasticity of performance and found previously unseen trade-offs in throwing versus running performance that manifest through ageing. Our results verify that human performance is limited by fundamental genetic, environmental and ageing constraints that preclude the simultaneous improvement of performance in multiple dimensions. Identifying these constraints is fundamental to understanding performance trade-offs and predicting the ageing of motor function.

1. Introduction

The concept of trade-off is key to many research fields, such as evolutionary organismal biology, physiology, behavioural ecology and functional morphology [1–3]. Performance trade-offs occur when characteristics that enhance one aspect of performance decrease another type of performance. The mechanistic basis of many performance trade-offs is well described and accepted [4–7]. For example, greater proportions of slow-twitch oxidative muscle fibres should enhance stamina, whereas more fast-twitch glycolytic fibres would facilitate sprinting abilities. However, current empirical evidence is weak for performance trade-offs at the whole-animal level [8–13]. Indeed, most studies exploring trade-offs in non-human animals find that high performers in one task are also high performers in other tasks, or find no trade-off between tasks at all [11–14]. Given the intuitive physiological basis of many performance trade-offs, the paucity of studies showing them suggests that whole-organism performance is composed of many components that can counteract each other to obfuscate predicted functional trade-offs.

Performance trade-offs should be especially overt in elite athletes competing in multi-events sports like the decathlon (male) and heptathlon (female). Male decathletes compete in 10 different track and field events over 2 consecutive days, comprising throws (shot put, discus, javelin), jumps (high jump, long jump, pole vault) and runs (110 m hurdles, 100 m, 400 m, 1500 m). Similarly, female heptathletes compete in seven events (shot put, javelin, high jump, long jump, 100 m hurdles, 200 m, 800 m) over 2 consecutive days. In both decathlon and heptathlon, the winner is determined by a points system based on the combined performance across all events. Given the demanding nature of performing in track and field, and the apparent difficulty with attaining excellence across all or even multiple events, the winner of the Olympic decathlon is traditionally given the title of ‘world's greatest athlete’.

Well-established physiological and biomechanical theory predicts the occurrence of trade-offs between groups of functionally similar events (throwing, jumping, running). Simply comparing the morphology of athletes specialized in shot put versus high jump should be enough to realize that improving performance in one should negatively affect performance in the other (e.g. having high upper body muscle mass will help in shot put, but hinder high jump). Yet, like many studies on non-human animals [11–14], performance trade-offs have proven hard to detect in decathletes. Indeed, past studies report mostly positive or non-significant correlations among performances in the 10 events of the decathlon [15–18]. How can we explain these counterintuitive results [15–18]?

Some suggest among-individual variation in overall ‘quality’ can obscure performance trade-offs [15,19] in a similar way to the ‘big houses, big cars’ scenario relevant to life-history trade-offs [20]. In this classic model of life-history evolution, a trade-off occurs within individuals because they need to allocate a finite resource to competing demands, but this trade-off may not be detectable because individuals vary in the amount of resource available to them [21]. For example, females with small abdominal cavities may lay few small eggs, whereas females with large abdominal cavities may lay many large eggs, thus creating a positive correlation in a situation where a trade-off is expected between egg quantity and size. Applying the same reasoning to performance, some decathletes may have morphological or physiological properties that enhance performance in all events, thus generating positive correlations among throwing, jumping and running performance. Decathletes may also differ in the time they spend training, which would generate positive correlations among athletes. Yet decathletes do not have access to infinite time for training, thus they ultimately face a trade-off in the allocation of training time across events. Given this situation, it has been argued that within-individual trade-offs emerge after statistically adjusting for among-individual variation in ‘quality’ [15,19]. However, this is currently debated on conceptual and statistical bases [16], even though performance trade-offs have never been properly partitioned at the among- versus within-individual levels [22].

One potential issue with previous studies of performance trade-offs in decathletes (and many studies on animals) is that statistical analyses are based on maximal performances for each individual. In other words, the ‘personal best’ for each athlete in each event was retained for the analysis, irrespective of whether personal bests for different events were achieved in different competitions or under different conditions. However, retaining individual maxima can bias the correlations due to the undesirable properties of the sampling distribution of extreme values [23]. This bias is especially large when individuals differ in their total number of repeated measures [22], as typical in datasets on decathletes. Moreover, past studies do not account for the multiple intrinsic and extrinsic factors that can introduce variation into measures of performance. Factors like age, experience and wind assistance [24] should be taken into account when testing for the occurrence of trade-offs in decathletes and heptathletes, otherwise these sources of within-individual variation will attenuate correlations at the among-individual level [25]. Although quite evident from a purely statistical perspective, the problems related with attenuation and the use of ‘personal best’ are not fully recognized in the literature on performance trade-offs.

Here, we use data on decathletes and heptathletes to illustrate the problems associated with using personal best and the insights that can be gained by considering all repeated observations to partition performance trade-offs at the among- versus within-individual levels. We compiled 18 years of data on 1369 elite athletes that performed in a total of 6418 combined-events competitions. First, we show that the bias introduced by using personal best is so strong it can generate spurious positive correlations. Second, we show that strong trade-offs can be revealed—without the need to correct for ‘quality’—by partitioning correlations at the among- and within-individual levels. Finally, we adopted a multivariate reaction norm perspective and reveal previously undetected trade-offs between throwing and running performance during ageing.

2. Material and methods

(a). Source of data

Each step described below (data extraction and analysis) was repeated twice (once for decathlon and once for heptathlon). Data were compiled from the website of the International Association of Athletics Federations (IAAF; iaaf.org) on 26 April 2017. Data were extracted from the ‘top list’ of each year (1999–2016) and combined into a single dataset, leaving a total of 2830 observations on 636 decathletes and 3588 observations on 733 heptathletes (electronic supplementary material, figure S1). The data include the date and location of the competition, some background information on competitors (name, date of birth, nationality), results in all events (in seconds, metres), and final score (points). The data also include wind assistance (in m s⁻¹) for the events in which it is recorded (hurdles, 100 m, 200 m and long jump). Date of birth was missing for six decathletes and nine heptathletes. Athletes with only year of birth (but not day or month) were assumed to be born on 1 January of that year (three decathletes and 17 heptathletes). Wind assistance was missing for 168 (decathlon) and 311 (heptathlon) observations. Data for one or more events were missing for 13 (decathlon) and 39 (heptathlon) observations. We assume that these data were missing at random and did not bias parameter estimates. Overall, 2625 (decathlon) and 3266 (heptathlon) observations had complete information for the variables of interest, which represents 94% and 91% of the datasets, respectively.

We first calculated age as the number of days elapsed between date of birth and date of the competition. We also calculated experience for each athlete as their cumulative number of participations. To facilitate interpretation, we multiplied times for running events (100 m, 200 m, 400 m, 800 m, 1500 m and hurdles) by −1 such that larger values indicate better performance. Finally, we standardized (mean = 0, s.d. = 1) and organized performance into groups of functionally similar events (throwing, jumping, running). For simplicity, performances in the different events are referred to below as ‘traits’ (10 for decathlon and 7 for heptathlon) and multiple records for each athlete are referred to as ‘repeated measures’. All data and R codes were made available to editors and reviewers upon initial submission.

(b). Personal-best and personal-average values

We extracted personal-best and personal-average values and estimated phenotypic correlations (r_P) between all traits by fitting multivariate models using the asreml() function in ASReml-R [26]. All traits were included as dependent variables and we fitted an unstructured (co)variance matrix at the residual level (see electronic supplementary material, appendix S1 for model equations). Since these models did not include any fixed effect (other than a separate intercept for each trait), the residual correlations provide the raw r_P between each trait. However, these correlation estimates should be biased because athletes greatly vary in the number of competitions in which they participated [22,27]. In this case, personal best values are not comparable among athletes because the expected value of a maximum increases with the number of repeated measures (n_trial). Athletes who participated in less than five competitions are much less likely to express their true maximal performance in each event than athletes who participated in more than 20 competitions. Thus, positive correlations could be potentially generated by the fact that athletes with many repeated measures expressed their true maxima in all events whereas athletes with few repeated measures had fewer chances to perform at their best in each event. To show the extent of the bias introduced by using individual maximum values when individuals differ in their n_trial, we included athlete's n_trial as a fixed effect and recalculated r_P based on the unstructured (co)variance matrix at the residual level. Thus, the resulting r_P are conditioned on each athlete's total number of repeated measures (n_trial) from which their personal best values were extracted. Note that n_trial is not the same as experience as included in the models below (in fact, for a given athlete, n_trial and experience are the same only at the last competition of that athlete).

(c). Effects of extrinsic and intrinsic factors

To estimate the effects of various extrinsic and intrinsic factors, we used all repeated measures from all athletes and ran a series of univariate mixed models with lmer() function in R package lme4 [28]. We included as fixed effects the year and Julian day of the competition, age and experience of the athlete, and wind assistance (only for events in which it is recorded; see above). We used the sim() function of the package arm [29] to simulate values of the posterior distribution of the model parameters and extracted the modes and the 95% credible intervals (CI) based on 1000 simulations [30]. Effects were considered to be important when the 95% CI did not overlap with 0. We used visreg() function in R package visreg [31] to independently visualize the effect of age, experience, and wind assistance, while conditioning on all other variables in the model (partial residuals).

All mixed models included a random effect for individual identity. Therefore, the phenotypic variance (V_P) not accounted for by fixed effects was partitioned into components of among-individual variance (V_ind) and residual variance (V_e), which allowed calculating repeatability as the ratio of V_ind/(V_ind + V_e). We used the rpt() function in R package rptR [32] to calculate the 95% CI around repeatability estimates.

(d). Among- and within-individual correlations

We used the asreml() function in ASReml-R [26] to fit multivariate mixed models that included all traits as response variables and year, Julian day, wind assistance, age, and experience fitted as fixed effects separately for each trait (see electronic supplementary material, appendix S1 for model equations). This allowed us to partition r_P into two distinct levels—the among-individual correlation (r_ind) and the residual correlation (r_e; see equations (10) and (11) in electronic supplementary material, appendix S1). Accordingly, each multivariate model included two fully unstructured (co)variance matrices: one for the random effect of individual identity to model all V_ind and among-individual covariance (COV_ind), and one for the residuals to model all V_e and within-individual or residual covariance (COV_e). For each pair of traits, we calculated r_ind and r_e by dividing the COV_ind or COV_e term of interest by the square root of the product of the V_ind or V_e, respectively. We used the proLik() function in nadiv [33] to calculate the approximate 95% CI of all r_ind and r_e using profile likelihoods. We also used nadiv [33] to calculate repeatability (±s.e.) using estimates from the multivariate mixed models.

The r_ind indicates consistent association between individual mean values for different traits over the time span within which the measures were taken [34]. The r_ind is influenced by two main sources of among-individual covariance between traits: genetic and permanent environmental effects, both of which are likely to occur in the data. Indeed, the dataset includes athletes from over 60 different countries showing large differences in environmental, cultural and socioeconomic factors that may generate consistent among-individual differences in performance. If one or more environmental factors consistently affect performance in more than one event, this would cause correlations at the among-individual level. Genetic correlations can also contribute to consistent covariation among traits through pleiotropy and linkage disequilibrium. If one or more genes affect performance in more than one event, this would cause correlations at the among-individual level.

The r_e indicates whether an athlete's change in performance in one event between time period t and t + 1 is correlated with its change in another event over the same period [34]. One source of covariance at the residual level comes from correlated measurement error. For example, if a biased chronometer or measuring tape was used to measure performance in multiple events within a competition, then this would cause all observations for that competition to be biased. Similarly, tracks may differ in length and inclination by a small amount, which would also contribute to a positive r_e among sprint performance within a competition. However, given the precision of photo-finish systems and linear measurements in IAAF facilities (to the nearest whole mm) and competitions [35], we consider correlated measurement error to be a negligible source of covariance.

An r_e can also arise from combined, reversible changes between traits occurring within an athlete due to correlated phenotypic plasticity. This would occur if, for example, athletes change their performance in multiple events as a function of an unidentified covariate (e.g. training regime). Whenever there is a significant r_e, it is worthwhile to test whether correlated phenotypic plasticity can be modelled separately from the residuals using a multivariate random regression [36,37].

(e). Multivariate reaction norms

We used the asreml() function in ASReml-R [26] to fit multivariate random regression models (see electronic supplementary material, appendix S1 for model equations). In random regression, each trait is modelled as a reaction norm with an intercept (mean performance) and a slope (change in performance over time). This allows testing if athletes differ in how their performance changed as they gained experience in competition and through ageing (both z-transformed). We fitted multivariate random regression models that included a fully unstructured covariance matrix between intercepts (V_ind, as above) and slopes (V_slp) of all traits. Multivariate random regression models also included a fully unstructured covariance matrix for the residuals (COV_e). We were mostly interested in the correlations between the slopes of the reaction norms for different traits. In these models, the heterogeneity in the residuals is now reduced to measurement error (presumably negligible, see above) and any unidentified variable influencing performance in various events.

3. Results

(a). Personal-best and personal-average values

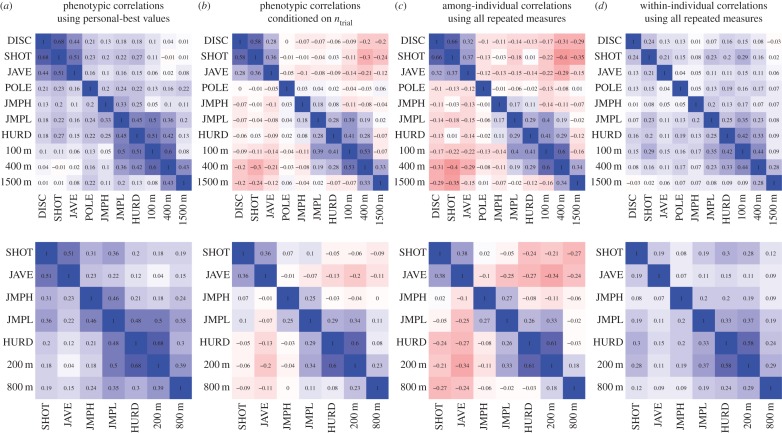
Like past studies [15–18], we failed to detect trade-offs among performance traits when restricting the data to personal-best values, as it yielded positive r_Ps among all performance traits in both the decathlon and heptathlon (figure 1a). However, these correlation estimates should be biased because athletes greatly vary in the number of competitions in which they participated (n_trial; range: 1–41, median = 6–8; electronic supplementary material, figure S1), such that their personal bests are not comparable. Accordingly, recalculating all r_P, this time after conditioning on each athlete's n_trial, revealed the expected pattern: mostly negative correlations among functional groups (throwing, jumping, running) and clusters of positive correlations within throws, jumps and runs (figure 1b). The difference in figure 1a versus figure 1b shows the extent of the bias introduced by using personal best values. Note, however, that there is a positive correlation between n_trial and the athletes average score (decathlon: r₆₃₄ = 0.68; heptathlon: r₇₃₁ = 0.67), such that controlling for n_trial may also partially control for ‘quality’ [15,16].

Figure 1.

Performance trade-offs in elite athletes competing in combined-events sports. ‘Heat maps’ display the sign and magnitude of the correlations among performance in the 10 decathlon events (top row; n = 636) and the seven heptathlon events (bottom row; n = 733). Shown are the phenotypic correlations based on personal-best values (a) before and (b) after correcting for the total number of repeated measures (n_trial; see electronic supplementary material, figure S1). Comparing (a) versus (b) shows the extent of the bias related to the use of ‘personal bests’ when individuals differ in n_trial. Clearly, (b) shows performance trade-offs and clusters of positive correlations along the main diagonal, which correspond to functional groups (throwing, jumping, running). Correlations at the (c) among- and (d) within-individual levels using all repeated performances (n = 2830 decathlons and 3588 heptathlons) and controlling for effects of year, Julian day, wind assistance, age, and experience. Comparing panels (b) versus (c) shows that stronger trade-offs and functional clustering emerge after factoring out sources of within-individual correlations (d). Events: discus (DISC), shot put (SHOT), javelin (JAVE), pole vault (POLE), high jump (JMPH), long jump (JMPL) and hurdles (HURD). Times for running events were multiplied by −1 such that larger values indicate better performance.

(b). Effects of extrinsic and intrinsic factors

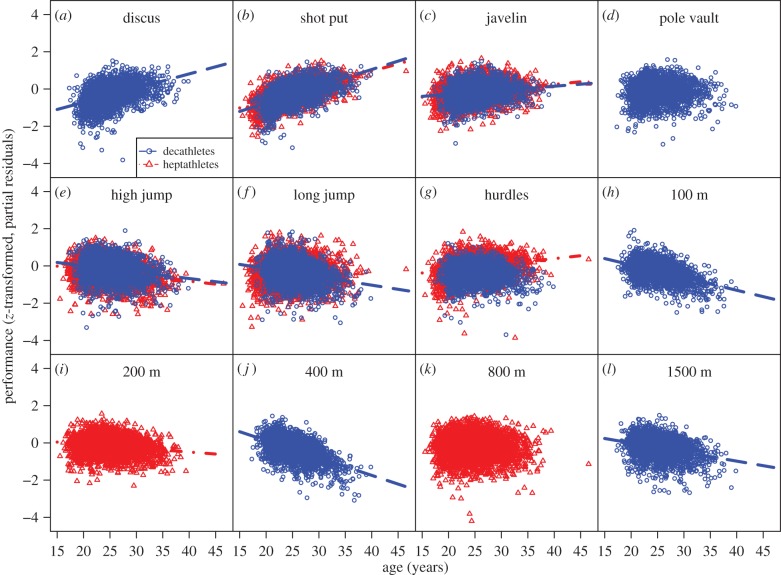
Across the two datasets, wind assistance varied from −4.8 to +5.8 m s⁻¹ and had, as expected, a positive effect on performance (electronic supplementary material, table S1 and figure S2). Age and experience varied considerably both among and within athletes (electronic supplementary material, figure S3). Performance considerably increased with experience in all but three events of the decathlon and all events of the heptathlon (electronic supplementary material, table S1). Interestingly, age showed contrasting effects on arm- versus leg-based events in both decathletes and heptathletes (figure 2; electronic supplementary material, table S1). While performance in all arm-based events increased through ageing (figure 2a–c), performance in most leg-based events decreased through ageing (figure 2e–l).

Figure 2.

Ageing effects on performance. Shown are partial residuals as function of age (years) in decathletes (blue) and heptathletes (red), after controlling for year, Julian day, experience and wind assistance. This figure shows that while performance in all arm-based events increases with age (a–c; discus, shot put, and javelin), performance in most leg-based events deceases with age (e–l; high jump, long jump, 100 m, 200 m, 400 m, and 1500 m). Lines are provided only if 95% credible intervals for the age effect did not overlap with zero (see electronic supplementary material, table S1 for estimates from the linear mixed-effect models). Times for running events were multiplied by −1 such that larger values indicate better performance and all traits were standardized (mean = 0, variance = 1).

(c). Among- and within-individual (co)variance

After accounting for the effects of wind, age and experience, the average repeatability of performance in the various events are 0.69 (range = 0.56–0.74) for the decathlon and 0.67 (range = 0.53–0.76) for the heptathlon (electronic supplementary material, table S2). Repeatability estimates obtained from multivariate mixed models were all within 2% of the univariate estimates (electronic supplementary material, table S2). Multivariate mixed models revealed strong trade-offs at the among-individual level (figure 1c) and mostly positive correlations at the within-individual level (figure 1d). In decathletes, all r_ind > |0.07| were significantly different from zero (electronic supplementary material, table S3a). In heptathletes, all r_ind > |0.08| were significantly different from zero (electronic supplementary material, table S4a). The negative r_ind indicates that athletes that are consistently better than average in a given functional group (e.g. throwing) tend to consistently perform more poorly than average in other functional groups (e.g. running). By contrast, the r_e values were mostly positive (figure 1d) and significantly different from zero in decathletes (electronic supplementary material, table S3b). In heptathletes, all the r_e were positive and significantly different from zero (electronic supplementary material, table S4b). This indicates that an athlete performing better than its average in an event on a given competition will tend to perform better than its average in all other events of that same competition.

(d). Multivariate reaction norms

Having identified contrasting ageing effects on arm- versus leg-based events at the population level (figure 2), we verified whether athletes differed in how their performance changed through ageing and whether these changes were correlated. Multivariate random regressions revealed significant negative correlations between the slopes of the performance–age reaction norms for some throwing versus running events (figure 3). The negative slope–slope correlations in figure 3d indicate that decathletes who increased throwing performance through ageing (relative to the positive average trend; figure 2a–c) decreased their performance in the 400 and 1500 m through ageing (relative to the negative average trend; figure 2j,k). Similar negative slope–slope correlations were observed in heptathletes, except that it involved only one of the throwing event (i.e. javelin; figure 3h). By contrast, slopes of the performance-experience reaction norms were mostly positively correlated (electronic supplementary material, figure S4), suggesting the trade-offs mostly occur through ageing affects.

Figure 3.

Performance–age reaction norms in elite athletes. This figure shows previously undetected ageing trade-offs in decathletes (top row) and heptathletes (bottom row). Performance in (a) discus and (b) 1500 m as function of age, showing individual reaction norms of all athletes (thin black lines) and two illustrative individuals with contrasting slopes for discus and 1500 m (blue line and triangles versus red line and dots). (c) Relationship between individual slope estimates for discus and 1500 m (red and blue symbols denote same individuals as in (a) and (b)). (d) Heat map showing all slope-slope correlations estimated by the multivariate random regression model. Thus, (c) illustrates one of the many slope–slope correlations in (d) (the correlation depicted is identified by a green frame). Performance in (e) javelin and (f) 200 m as function of age, showing individual reaction norms of all athletes (thin black lines) and two illustrative individuals (blue and red lines). (g) Relationship between individual slope estimates for javelin and 200 m (red and blue symbols denote same individuals as in (e) and (f)). (h) Heat map showing all slope–slope correlations estimated by the multivariate random regression model. Times for running events were multiplied by −1 such that larger values indicate better performance and all traits were standardized (mean = 0, variance = 1).

4. Discussion

Physiological and biomechanical theory predicts the occurrence of trade-offs among certain underlying components of performance, yet trade-offs are rarely detected at the whole-organism level [8–14]. It has been suggested that performance trade-offs emerge as expected after statistically adjusting for among-individual variation in ‘quality’ [15,19]. However, recent work has shown that performance trade-offs are not always detected when ‘quality’—in whatever ambiguous form it can take—is accounted for [16]. Here, we showed the severity of the bias in correlations based on personal bests values [23,38], which calls into question the relevance of the debate on the need to control for ‘quality’ [15,16,19]. Indeed, it seems like positive correlations were partly generated by among-individual variation in the total number of competitions in which athletes participated (compare figure 1a versus figure 1b). When extracting personal-best values, the true maximum of each athlete will be differentially underestimated according to the sample size for that athlete [27,38]. Given that using personal-best values is common practice in organismal performance studies [27], our results may explain why performance trade-offs are rarely detected.

As previously suggested in studies of performance [38], the simplest solution to reduce bias is to calculate personal-average values. Accordingly, in both decathlon and heptathlon datasets, analysing personal-average values revealed the expected pattern: clusters of positive correlations among events within functional groups (throwing, jumping, running) and mostly negative correlations among functional groups (electronic supplementary material, figure S5a). However, phenotypic correlations based on mean values can still be attenuated by within-individual variance [25], which include measurement error and the effect of various intrinsic and extrinsic variables that influence performance such as age, experience and wind assistance [24] (see electronic supplementary material, table S1). When left unaccounted for, these effects will statistically appear as measurement error and will cause correlation estimates to be, on average, attenuated (i.e. biased towards zero). Although it is possible to detect trade-offs without controlling for any fixed effect (electronic supplementary material, figure S5b), the among-individual correlations are markedly stronger when including fixed effects like year, Julian day and wind assistance (electronic supplementary material, figure S5c). Obviously, it is desirable to control for as many sources of within-individual variation as possible when testing for performance trade-offs.

Although experience had positive effects on performance in most events (electronic supplementary material, table S1), age had a strikingly different effect on performance in arm- versus leg-based events (figure 2). One potential explanation for this difference is the clear effects of ageing on the elasticity of tendons. In contrast to throwing performance, which relies on muscle power and technique, running and jumping performances are reliant on the elasticity of tendons. The gastrocnemius—and its associated tendon—facilitates a catapult mechanism from the ankle that delivers a burst of mechanical power during walking, running and jumping in both humans and non-human animals [39]. Deficits in muscles that surround the ankle joint can mediate age-related declines in the walking performance of humans [40]. Potentially the most important biomechanical change with ageing is the disruption of the catapult mechanism from the muscle-tendon associated with gastrocnemius during the propulsive ‘push-off’ phase [41]. Despite this mechanism, it remains unclear how age-related changes in the properties of the Achilles tendon and its associated muscle are directly linked to declines in running and jumping performance with age in elite athletes. Nevertheless, it offers a potential explanation to the differential ageing effects on performance in arm- versus leg-based events.

Using all repeated records and controlling for wind, age, and experience, we found relatively strong trade-offs occurring at the among-individual level and mostly positive correlations at the within-individual level (figure 2c,d; electronic supplementary material, tables S3 and S4). It is intuitive to expect trade-offs to occur within individuals because decathletes and heptathletes need to allocate their limited energy and time to train for multiple events. However, we found that trade-offs occurred among individuals. Individuals consistently differ in many morphological (e.g. gear ratio) and physiological (muscle fibre types) traits that enhance their performance in certain tasks (e.g. speed), while hindering performance in others (e.g. endurance), which should generate negative correlations among performance traits at the among-individual level. We note, however, the correlations revealed may depend on the studied population. Our analysis was restricted to a highly selected subpopulation (elite generalist athletes), but of course adding data on non-elite athletes would generate positive among-individual correlations due to larger variation in athletic capacities, motivation and total time spent training. Still, if we knew all of the relevant variables (such as body mass, height and time spent training), then controlling for these variables should allow detection of trade-offs at the among-individual level.

Performance trade-offs may also occur at the within-individual level. In the case of decathletes and heptathletes, the most obvious reason is that they perform in all events over 2 consecutive days. In this case, negative r_e values may emerge if, for example, athletes performing harder than usual on the first events of a given day would compromise their performance in events later on the same day (or among days within a competition). This scenario is not supported, however, given the positive r_es we obtained (figure 1d; electronic supplementary material, tables S3b and 4b). In other words, when an athlete performs better than usual in an event of a given competition, it tends to perform better than usual in all other events of the same competition. This suggests that within-individual variance may reflect changes in general physical condition, which could in turn positively affect all performance traits. Although we accounted for age, experience and wind assistance, there are many unidentified variables that could have potentially influenced performance in various events within a competition. Accounting for additional factors like altitude, temperature and training regime should reduce r_e closer to zero [36,37].

Individual (co)variation in phenotypic plasticity can also contribute to within-individual correlations. Correlated plasticity describes the situation in which two or more traits change simultaneously along an identified covariate. Using multivariate random regressions, we captured correlated plasticity and found relatively strong trade-offs between throwing and running performance occurring through ageing. As far as we know, these ageing trade-offs were previously undetected. At the start of their professional career, athletes may naturally perform better in a given functional group of traits (e.g. throwing) compared with other functional groups (e.g. jumping and running). Athletes could thus train harder to improve performance in their weakest functional group, which may compromise their progression in performance in their naturally strong functional group. Irrespective of the mechanism underlying age-related correlated plasticity, it remains clear that elite athletes competing in combined-event sports need to optimize their training regimes to account for a multitude of effects, including ageing. Ageing-mediated trade-offs may also occur in wild animals as they migrate, capture prey, escape predators, defend territories and acquire mates throughout their lives. These various complex tasks involve a wide range of different performances (biting, jumping, climbing, sprinting, stamina) that should trade off with each other.

5. Conclusion

Using multivariate mixed models, we (i) controlled for extrinsic and intrinsic factors and (ii) partitioned correlations at the among- and within-individual levels to (iii) unambiguously show the presence of relatively strong performance trade-offs occurring not only among individuals, but also within individuals as they age. Because correlations at the among-individual level are generated by correlated genetic and/or permanent environmental effects, our results indicate that performance is limited by genetic, environmental and ageing constraints that preclude the simultaneous improvement of all dimensions of physical capabilities. The next step will be to determine the relative contribution of genetic versus environmental constraints underlying performance trade-offs [42–44]. Ultimately, identifying these constraints is fundamental to our understanding of the evolution of performance trade-offs, and perhaps will help enhance athletic performance. While there is nothing we can do about genetic effects (at least ethically), identifying the environmental sources of constraints generating performance trade-offs may be useful for designing better training regimes and rehabilitation programmes.

Data accessibility

The data used for this study have been deposited in Dryad as http://datadryad.org/resource/doi:10.5061/dryad.c9p98.

Authors' contributions

V.C. compiled and analysed the data. Both authors were involved in interpreting the results and contributed to writing the manuscript.

Competing interests

We have no competing interests.

Funding

This project was supported by grants from Natural Science and Engineering Research Council to V.C. R.S.W. is supported an Australian Research Council fellowship (FT150100492).