A passive cold storage device economic model to evaluate selected immunization location scenarios

Abstract

Background

The challenge of keeping vaccines cold at health posts given the unreliability of power sources in many low- and middle-income countries and the expense and maintenance requirements of solar refrigerators has motivated the development of passive cold storage devices (PCDs), containers that keep vaccines cold without using an active energy source. With different PCDs under development, manufacturers, policymakers and funders need guidance on how varying different PCD characteristics may affect the devices’ cost and utility.

Methods

We developed an economic spreadsheet model representing the lowest two levels of a typical Expanded Program on Immunization (EPI) vaccine supply chain: a district store, the immunization locations that the district store serves, and the transport vehicles that operate between the district store and the immunization locations. The model compares the use of three vaccine storage device options [(1) portable PCDs, (2) stationary PCDs, or (3) solar refrigerators] and allows the user to vary different device (e.g., size and cost) and scenario characteristics (e.g., catchment area population size and vaccine schedule).

Results

For a sample set of select scenarios and equipment specification, we found the portable PCD to generally be better suited to populations of 5,000 or less. The stationary PCD replenished once per month can be a robust design especially with a 35L capacity and a cost of $2,500 or less. The solar device was generally a reasonable alternative for most of the scenarios explored if the cost was $2,100 or less (including installation). No one device type dominated over all explored circumstances. Therefore, the best device may vary from country-to-country and location-to-location within a country.

Conclusions

This study introduces a quantitative model to help guide PCD development. Although our selected set of explored scenarios and device designs was not exhaustive, future explorations can further alter model input values to represent additional scenarios and device designs.

1. Introduction

Cold storage is critical in vaccine supply chains because most vaccines consist of proteins that may rapidly break down and become ineffective when exposed to higher temperatures, necessitating their storage in either refrigerators or freezers until administration [1,2]. However, power source and maintenance unreliability in many low- and middle-income countries hinders the use of traditional refrigerators and freezers. Solar refrigerators can overcome these limitations but can be quite costly, require more complicated installation and maintenance, and for models with batteries, have varying battery lifetimes [3–10].

This situation has motivated the development of another alternative, passive cold storage devices (PCDs), containers that keep vaccines cold without needing an active energy source [11,12]. PCDs are composed of materials and designs that minimize heat leakage and provide space to carry vaccines and a cooling medium (i.e., a phase-changing material such as ice) keeping temperatures low. Without incorporated machinery, PCDs may require much less maintenance than refrigerators and freezers. Other benefits depend on the PCD design; for example, smaller and lighter PCDs may be portable but, unlike standard vaccine carriers or cold boxes, may store vaccines for extended periods of time (i.e., several days up to one month) [13,14].

With different PCDs currently under development, manufacturers, policymakers and funders need guidance on how varying different PCD characteristics may affect the device’s cost and use. Therefore, we developed an economic spreadsheet model representing the lowest two levels of a vaccine supply chain: a district store, the immunization locations that the district store serves, and the transport vehicles that operate between the district store and the immunization locations. The model compares the use of three vaccine storage device options to support health post vaccination [(1) portable PCDs, (2) stationary PCDs, or (3) solar refrigerators] and allows the user to vary different device characteristics (e.g., size and cost) and scenario characteristics (e.g., population and vaccine schedule). The model can help delineate a PCD target product profile (TPP) (i.e., a menu of desirable characteristics to guide PCD development), and potential PCD use cases (i.e., the roles, situations, and circumstances under which a PCD would be favorable) [14,15]. Here, we employ our model to evaluate a sample set of selected scenarios and device designs.

2. Methods

2.1. Model structure

Our equation-based spreadsheet model developed in Microsoft Excel (Microsoft Corporation, Redmond, WA) represents a typical district store, the immunization locations that it serves, the catchment areas served by each immunization location, transport vehicles, transport and storage devices, and all associated costs.

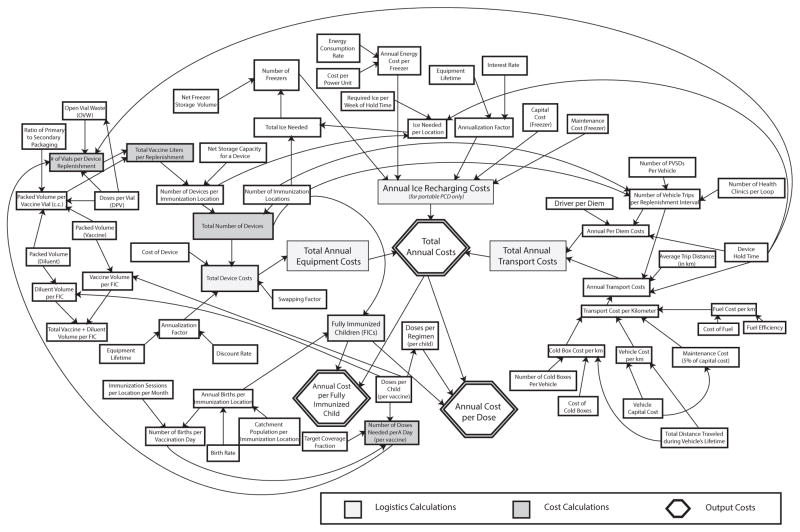
The influence diagram in Fig. 1 depicts the model’s cost relationships for a portable PCD. The models for the stationary PCD (with only minor changes to the transport section, since the stationary PCD assumes that only vaccines and ice, not PCDs, are transported) and a solar refrigerator (which does not use ice) are similar. All three models assume that district store-based trucks will serve immunization locations in a transport loop, visiting several immunization locations per outing.

Fig. 1.

Schematic diagram of the relationships between variables in the model.

2.2. Model inputs and parameters

Table 1 lists all model parameters and their evaluated ranges [16–18]. (The model is available on our website: hermes.psc.edu.) The device hold time (HT) is the duration between ice and vaccine replenishment shipments. The swapping factor is the ratio of extra PCDs needed, in the case of portable PCDs, to swap in fully loaded PCDs (i.e., with vaccines and ice) and swap out depleted PCDs. For example, if 10 PCDs are required across an entire district and the swapping factor is 1.2, then an extra 2 PCDs (for a total of 12 = 10 × 1.2) will be needed to exchange full and empty PCDs.

Table 1.

Inputs for the model.

User inputs	Units	Value for initial experiments
Cold storage device characteristics
Passive cold device (PCD)
Portable PCD
Device capital cost	$US	700, 1000, 1300
Net storage capacity	Liters	4–8
Device hold time	Days	28
Required ice per week of hold time	kg	1
Swapping factor		1.2
Equipment lifetime	Years	10
Stationary PCD
Device capital cost	$US	1750, 2500, 3250
Net storage capacity	Liters	20–50
Device hold time	Days	28, 84
Required ice per week of hold time	kg	1.8
Equipment lifetime	Years	10
Freezerb
Capital cost	$US	570
Net storage capacity	Liters	72
Equipment life	Years	10
Annual maintenance cost (default 5% capital cost)	$US	29
Energy consumption rate	kWh/hr	0.11
Cost per power unit	$US/kWh	0.1123
Solar refrigeratora
Capital cost	$US	2100, 3000
Net storage capacity	Liters	19.5
Annual maintenance cost	$US	150
Shipping interval	Days	28
Equipment life	Years	10
Demand
Catchment population per immunization location	Individuals	1000–30,000
Birth rate	Per 1000 persons	35.0
Immunization locations served	Number of locations	24
Immunization sessions per location per month	Number of sessions	28
Transport route
Average one way distance to IHC	km	30c
IHCs per loop	Number of locations	4
Vehicles
Vehicle capital cost	$US	40,000
Total distance traveled during vehicle lifetime	km	300,000
Maintenance cost (% of vehicle capital cost/km)	%	15%
Fuel
Fuel efficiency	km/Liter	5
Cost of fuel	$US/Liter	1.3
Total $/km	$US	0.45
Driver
Driver per diem	$US	15
Vehicle storage capacity
Number of PCDs	Devices	8
Number of cold boxes	Devices	6
Cold boxesd
Net capacity per cold box	Liters	20
Cost per cold box	$US	700
Economic
Discount rate	%	3%

^aThe freezer used at the district level is based on the Dometic TFW 800 model [18].

^bBased on Vestfrost MKS 044 model and solar costs obtained from EPI Logistics Forecasting Tool [17,21].

^cA representative value based on district to clinic distances.

^dCold box costs were based on Dometic RCW-25 costs [16].

2.3. Logistics calculations

The following steps compute the number of devices needed:

• Step 1: Number of doses administered per vaccination day for each vaccine equals the product of births per vaccination day, the vaccine’s target coverage, and number of doses needed to complete the vaccine’s regimen.

• Step 2: Number of vials per device replenishment equals the number of doses administered per day (Step 1) multiplied by days between vaccine and ice replenishment shipments divided by doses per vial. For relevant vaccines (e.g., lyophilized vaccines such as measles), an open vial wastage (OVW) term further augments this number, assuming a Poisson client arrival process (see [19,20] for details). All vial volumes are increased by 25%, following the WHO recommendation [21].

• Step 3: Number of total vaccine liters per replenishment equals the sum of the following product across all vaccines: vials per replenishment (Step 2) times packaged vial volume for each vaccine.

• Step 4: Total number of devices for all immunization locations within a district equals devices per immunization location multiplied by immunization locations per district, where devices per immunization location equals vaccine liters required per replenishment (Step 3) divided by device net storage capacity.

2.4. Cost calculations

The following steps transformed input data, along with the logistics calculations, into costs:

• Step 1: Total device cost per district equals the product of the number of devices required for all the district’s immunization locations (from Logistics Calculations Step 4), the swapping factor where applicable, and an annualization factor (amortization of device cost assuming a 3% discount rate and 10-year device lifetime).

• Step 2: Total annual ice recharging cost is the number of freezers needed to satisfy ice requirements for all the district’s storage devices times the sum of the freezer’s annual amortization, maintenance, and energy costs [22].

• Step 3: Total transport cost equals annual driver per diem cost plus annual transport cost. Annual per diem cost equals the per diem rate times trips per replenishment and replenishments per year. Number of vehicle trips per replenishment is the greater of: (i) number of immunization locations divided by maximum number of immunization locations served by one loop; or (ii) number of immunization locations served based on the vehicle’s vaccine carrying capacity. Therefore annual transport cost is trips per replenishment times average trip distance (km), cost per kilometer and replenishments per year.

2.5. Outputs

For each scenario and cold device type, the model generated:

• Total annual cost for each type of device is the sum of equipment, transportation, and ice recharging costs (when a PCD is used).

• Cost per dose administered for each type of device equals total annual cost divided by total number of doses administered.

• Cost per fully immunized child (FIC) is total annual cost divided by the number of fully-immunized children.

2.6. Experiments

The experiments compared the use of the three specific conceptual device options: (1) a solar refrigerator, (2) a portable PCD, and (3) a stationary PCD (with PCD design parameters drawn from existing PCDs [23,24]) under a specific set of potential scenarios/conditions/assumptions. To reflect variation in population sizes served by each immunization location, we varied the immunization location catchment population from 1000 to 30,000 with the birth cohort being 3.5% of the catchment population. The vaccine schedule includes the first seven Expanded Program on Immunization (EPI) vaccines in Table 2, along with either the large or small rotavirus presentation [21]. The total packaged size of the complete vaccine schedule is 134.6 cc (when including the small rotavirus presentation) and 238.1 cc (with the large rotavirus presentation).

Table 2.

Vaccine types and sizes [21].

Vaccine type	Number of doses	Packaged volumea (cc)
Tuberculosis (BCG)	1	1.9
Tetanus (TT)	2	6.0
Measles (M)	1	6.6
Polio (OPV)	4	4
Yellow Fever (YF)	1	6.6
DTP-HepB-Hib	3	39.3
PCV-13	3	36.0
Small Rotavirus (SR)	2	34.2
Big Rotavirus (BR)	3	137.7

^aRepresents the packaged volume for all doses required (including diluent if needed).

Table 3 shows the device characteristics tested (boldface represents baseline values). The portable PCD’s (PortD) intended use is for hold times ranging from a few days up to one month; therefore, a 28-day hold time (28-day HT PortD) was tested. Because the stationary PCD (StatD) could be used for a hold time of a few days up to a few months, it is analyzed for both a 28-day (28-day HT StatD) and a 84-day (84-day HT StatD) hold time to evaluate a one-month (used in many countries we have worked with) and three-month (under consideration for smaller, more difficult to access locations) hold time scenario, respectively. Sensitivity analyses explored the effects of varying the size of the portable and stationary storage devices, device costs, and vaccine complement.

Table 3.

Device characteristics.

Device	Device characteristics
	Net storage capacity (L)	Hold time (days)	Price ($US)
Solar	19.5a	28	2100; 3000
Portable PCD	4, 6, 8	28	700; 1000; 1300
Stationary PCD	20, 35, 50	28	1750; 2500; 3250
Stationary PCD	20, 35, 50	84	1750; 2500; 3250

^aValues in boldface represent baseline values.

3. Results

3.1. Baseline scenario

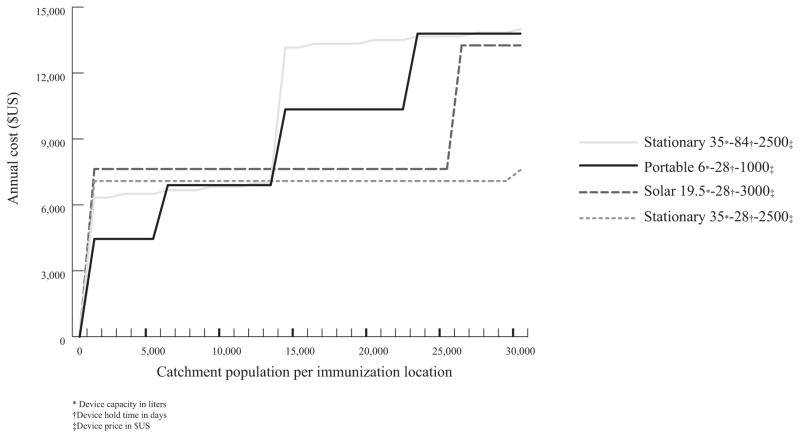
Fig. 2 shows a graph of the annual cost (US$) per clinic for each of the different cold storage devices corresponding to its baseline scenario (values listed in Table 3).

Fig. 2.

Annual cost for baseline designs.

• The 6 L, $1000, 28-day HT PortD is the least expensive design for clinic catchment populations of 5000 or less and between 12,000 and 13,000 (mean: $2.87/FIC (range: $0.95–7.95)).

• The 35 L, $2500, 84-day HT StatD is least costly for populations of 6000–11,000 ($1.48/FIC ($1.11–1.98)).

• The 35 L, $2500, 28-day HT StatD is least costly for populations of 14,000 and larger ($0.61/FIC ($0.44–0.90)).

• Solar is never the least expensive option.

Thus, the optimal device type differs for different population sizes. If a single device type is needed across all population sizes, a stationary PCD with a 28-day hold time is the most robust and costs on average 11% more than the total cost for the best solution for each individual population size.

3.2. Device size sensitivity analysis

Varying portable device size between 4 L and 8 L, while maintaining the same cost and hold time as the baseline (6 L) device, yielded the following results:

• A 4 L, 28-day HT PortD is the least costly only for populations ≤4000 [$4.14/FIC ($1.99–7.95)].

• However, an 8 L, 28-day HT PortD is the least costly option for populations ≤8000 and between 12,000 and 19,000 [$1.76/FIC ($0.65–7.95)].

Maintaining the same cost and hold times, while changing the size of the 28-day HT StatD and the 84-day HT StatD simultaneously from 35 L to either 20 L or 50 L, yielded the following:

• A 20 L, 28-day HT StatD is the lowest cost option for populations of 14,000–30,000 [$0.71/FIC ($0.51–90)].

• Reducing the 84-day HT StatD to 20 L increases costs significantly, making it the least costly option for a 6000-person population ($1.98/FIC).

• If increased to 50 L in size, then the 28-day HT StatD is least costly for populations ≥15,000 [$0.59/FIC ($0.44–0.84)].

• Increasing the size to 50 L makes the 84-day HT StatD the least costly option for populations of 6000–11,000 and 14,000 [$1.39/FIC ($0.89–1.98)].

3.3. Device cost sensitivity analysis

Ranging the price of the PCDs by ±30%, while reducing solar refrigerator costs by 30% ($3000–2100), revealed the following:

• A $700, 28-day HT PortD would be the least costly option for populations ≤13,000 [$1.87/FIC ($0.76–6.74)].

• A $1300, 28-day HT PortD is the least expensive option only for populations ≤5000 [$4.18/FIC ($1.83–9.15)].

• A $1750, 28-day HT StatD is the least costly alternative for populations ≥14,000 [$0.49/FIC ($0.35–0.72)].

• A $1750, 84-day HT StatD is the cheapest option for populations between 6,000 and 13,000[$1.08/FIC ($0.77–1.57)].

• A $3250, 28-day HT StatD is the least costly solution for populations between 26,000–30,000 [$0.55/FIC ($0.52–0.58)].

• A $3250, 84-day HT StatD is never the least costly option.

• Finally, a $2100 solar refrigerator is the least costly option for populations of 6000–25,000 [$0.81/FIC ($0.42–1.77)].

3.4. Change in the vaccine schedule

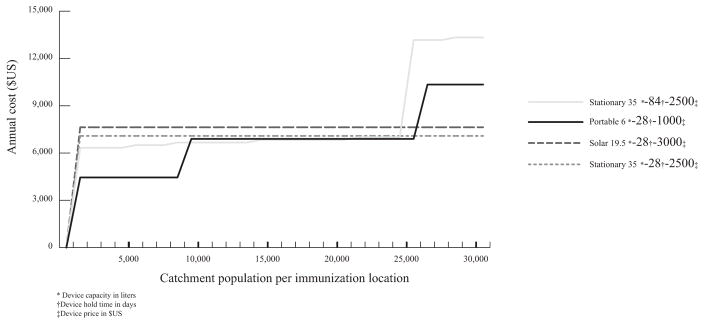
Changes in total vaccine schedule volume could arise from vaccine presentation changes or vaccine addition/removal. The smaller (vs. larger) rotavirus presentation makes the portable device more attractive and the 84-day HT StatD an effective strategy for several use cases (Fig. 3):

Fig. 3.

Annual cost of baseline designs for vaccine schedule with smallest rotavirus presentation.

• The 28-day HT PortD is the lowest cost option for populations ≤ 8000 and 21,000–25,000 [$1.87/FIC ($0.49–7.95)].

• The 84-day HT StatD is the lowest cost option for populations of 9000–20,000 [$0.88/FIC ($0.61–1.32)].

• The 28-day HT StatD is the lowest cost option for populations of 26,000–30,000 [$0.45/FIC ($0.42–0.49)].

The 28-day HT PortD is most robust to vaccine regimen changes and, on average, costs only 8.5% more than the least costly solution for each population size.

4. Discussion

Since each device’s value depends heavily on device characteristics and ambient circumstances, funders, manufacturers, and policy makers could benefit from guidance. Our model can help delineate designs that funders should invest in, manufactures should aim for, and policy makers should support. In essence, our model can help various decision makers establish different device TPPs and show which factors (in our sample study population size, total vaccine regimen volume, device cost) have greatest influence on cost.

As our initial study showed a single device does not dominate under all conditions, the solution within a given country may be different devices for different locations or circumstances rather than a single device for all locations. For the range of designs/circumstances studied here, portable PCDs were generally better suited to populations ≤5000. Decreasing portable PCD cost or increasing its storage capacity increased this population threshold to 10,000 or even 15,000. A 4 L storage capacity device had limited applicability for clinics. The 28-day hold time stationary PCD was generally the most robust design. The solar device was generally a reasonable alternative, and if its cost can be reduced to ≤$2100, became an attractive alternative for population sizes from 1,000 to 30,000.

Initiatives have emerged to both fund and develop a PCD for vaccines. In 2009, PATH issued a call, “Long-term Cold Storage Containers and Carriers for Heat/Freeze-sensitive Vaccines: Target Performance Criteria” [25], for designs for passive cold storage devices having a cold life of between 7–30 days and vaccine capacities of up to 5 liters or a larger device with capacity of up to 60 L. Over the past several years, designs have emerged from Georgia Tech [26], the University of Maryland [27] and Intellectual Ventures [11,23,28]. Examples of commercially-manufactured PCDs described by PATH [12] include the SAVSU Nano-Q 14 [24] and the Air Container Package System [29]. Based on these current design samples, the range of qualities that is being considered includes hold times ranging from 7–90 days and sizes ranging from 2–3 L up to 50 L.

Although it is unclear which device developers currently utilize models to guide design, without models, design could rely more on experiential guidance, and trial and error, costing considerable time, effort, and resources [13]. Even if developers use models, more open sharing of such models would promote knowledge exchange to improve designs [30].

5. Limitations

Models, by definition, simplify real life and therefore cannot capture every possible factor, relationship, or outcome [31–33]. Constructing our model involved substantial data collection from a variety of sources. Transportation capacity per vehicle, vehicle purchase prices, and operating costs can vary greatly across countries and even within a single country, and we have assumed a single value for each.

Specific use case costs link tightly to our sample set of baseline design values. There are discrete system cost jumps when populations become just large enough to exceed a location’s storage capacity threshold and require an additional device. Therefore, looking at the behavior of different devices across a range of population sizes is more important than focusing on specific population sizes.

While our study focused on cost, other factors may be key in selecting cold storage devices. For example, the current study does not explicitly consider outreach or campaigns, which exhibit considerable variability in how they are practiced; however, our model can readily incorporate both concepts and add necessary inventory requirements to the locations conducting such activities. For instance, a solar refrigerator or freezer can make, and the PCD can store, ice for outreach vaccine carriers [4]. This ice in turn could occupy substantial space in the PCDs by either occupying space in the vaccine compartment, if the ice is properly conditioned, or by requiring the size of the ice compartment to increase and thereby reducing the size of the vaccine compartment, reducing the amount of available space for vaccines per PCD. A small enough mobile PCD could replace the use of vaccine carriers for outreach. Large campaigns can also occupy large amounts of available storage capacity. Future explorations with our model can analyze these situations.

The current analysis assumes proper conditioning of ice and cold packs and does not evaluate vaccine freezing risk for different devices, which can be difficult to estimate and vary greatly with training and operational procedures in different settings. We also assume no problems with supply disruptions (resulting in shortages independent of the device selection), maintenance, breakdowns, and repairs. Additionally, to maintain consistency of transport equipment across device types/scenarios, our study assumed 4 × 4 trucks for all transport. Future analyses with our model can consider different transport devices.

It may be possible to obtain ice from sources local to the clinic, which would eliminate the need to have additional freezer capacity at the district level for the PCDs, thereby reducing the transport and energy requirements. However, these savings would have to balance against the cost of obtaining the ice locally.

Also, note that this study’s purpose is to introduce the model and present its application to a selected sample set of scenarios and device designs. These are by no means exhaustive. Companies continue to develop different PCD designs with each having different ice requirements, capacities, and costs. Therefore, this study aims to show the model capabilities and some trends among our sample scenario set rather than evaluate every possible circumstance and device design. The model has flexibility to use different inputs. Future studies could explore these variations. If there are changes in the assumptions and data that are input into the cost analysis, then the conclusions about the most cost-effective device for different population sizes may change.

6. Conclusion

As we have demonstrated for a selected sample set of scenarios and device designs, our model can identify the combinations of device characteristics (e.g., size and cost) and circumstances (e.g., population size and vaccine schedule) under which the different device options (portable PCD, stationary PCD, or solar refrigerator) would be the least costly option to support health post vaccination. Among the scenarios and designs explored, one type of device does not dominate over all circumstances. Therefore, the best device may vary from country to country and location to location within a country. Our model can help guide the funding, development, and implementation of the different devices. Future explorations can utilize the model to evaluate additional scenarios and device designs.