Asymptotics of empirical eigenstructure for high dimensional spiked covariance

Abstract

We derive the asymptotic distributions of the spiked eigenvalues and eigenvectors under a generalized and unified asymptotic regime, which takes into account the magnitude of spiked eigenvalues, sample size, and dimensionality. This regime allows high dimensionality and diverging eigenvalues and provides new insights into the roles that the leading eigenvalues, sample size, and dimensionality play in principal component analysis. Our results are a natural extension of those in Paul (2007) to a more general setting and solve the rates of convergence problems in Shen et al. (2013). They also reveal the biases of estimating leading eigenvalues and eigenvectors by using principal component analysis, and lead to a new covariance estimator for the approximate factor model, called shrinkage principal orthogonal complement thresholding (S-POET), that corrects the biases. Our results are successfully applied to outstanding problems in estimation of risks of large portfolios and false discovery proportions for dependent test statistics and are illustrated by simulation studies.

1. Introduction

Principal Component Analysis (PCA) is a powerful tool for dimensionality reduction and data visualization. Its theoretical properties such as consistency and asymptotic distributions of the empirical eigenvalues and eigenvectors are challenging especially in high dimensional regime. For the past half century, substantial amount of efforts have been devoted to understanding empirical eigen-structure. An early effort came from Anderson (1963) who established the asymptotic normality of sample eigenvalues and eigenvectors under the classical regime with large sample size n and fixed dimension p. However, when dimensionality diverges at the same rate as the sample size, sample covariance matrix is a notoriously bad estimator with dramatically different eigen-structure from the population one. A lot of recent literature makes the endeavor to understand the behavior of the empirical eigenvalues and eigenvectors under high dimensional regime where both n and p go to infinity. See for example Baik, Ben Arous and Péché (2005); Bai (1999); Paul (2007); Johnstone and Lu (2009); Onatski (2012); Shen et al. (2013) and many related papers. For additional developments and references, see Bai and Silverstein (2009).

Among different structures of population covariance, the spiked covariance model is of great interest. It typically assumes several eigenvalues larger than the remaining, and focuses on recovering only these leading eigenvalues and their associated eigenvectors. The spiked part is of importance, as we are usually interested in the directions that explain the most variations of the data. In this paper, we consider a high dimensional spiked covariance model with the leading eigenvalues larger than the rest. We provide new understanding on how the spiked empirical eigenvalues and eigenvectors fluctuate around their theoretical counterparts and what their asymptotic biases are. Three quantities play an essential role in determining the asymptotic behavior of empirical eigen-structure: the sample size n, the dimension p, and the magnitude of leading eigenvalues ${\{{\lambda }_j\}}_{j=1}^m$. The natural question to ask is how the asymptotics of empirical engen-structure depends on the interplay of those quantities. We will give a unified answer to this important question in the principal component analysis. Theoretical properties of PCA have been investigated from three different perspectives: (i) random matrix theories, (ii) sparse PCA and (iii) approximate factor model.

The first angle to analyze PCA is through random matrix theories, where it is typically assumed p/n → γ ∈ (0, ∞) with bounded spike sizes. It is well known that if the true covariance matrix is identity, the empirical spectral distribution converges almost surely to the Marcenko-Pastur distribution (Bai, 1999) and when γ < 1 the largest and smallest eigenvalues converge almost surely to ${(1+\sqrt{\gamma })}^2$ and ${(1-\sqrt{\gamma })}^2$ respectively (Bai and Yin, 1993; Johnstone, 2001). If the true covariance structure takes the form of a spiked matrix, Baik, Ben Arous and Péché (2005) showed that the asymptotic distribution of the top empirical eigenvalue exhibits an n^2/3 scaling when the eigenvalue lies below a threshold $1+\sqrt{\gamma }$, and an n^1/2 scaling when it is above the threshold (named BBP phase transition after the authors). The phase transition is further studied by Benaych-Georges and Nadakuditi (2011) and Bai and Yao (2012) under more general assumptions. For the case where we have the regular scaling, Paul (2007) investigated the asymptotic behavior of the corresponding empirical eigenvectors and showed that the major part of an eigenvector is normally distributed with a regular scaling n^1/2. The convergence of principal component scores under this regime was considered by Lee, Zou and Wright (2010). The same random matrix regime has also been considered by Onatski (2012) in studying the principal component estimator for high-dimensional factor models. More recently, Koltchinskii and Lounici (2014a,b) revealed a profound link of concentration bounds of empirical eigen-structure with the effective rank defined as r̄ = tr(Σ)/λ₁ (Vershynin, 2010). Their results extend the regime of bounded eigenvalues to a more general setting, although the asymptotic results in most cases still rely on the assumption r̄ = o(n), which essentially requires a low dimensionality, i.e. p/n → 0, if λ₁ is bounded. In this paper, we consider the general regime of bounded p/(nλ₁), which implies r̄ = O(n) and allows diverging λ₁. More discussions will be given in Section 3.

A second line of efforts is through sparse PCA. According to Johnstone and Lu (2009), PCA does not generate consistent estimators for leading eigenvectors if p/n → γ ∈ (0, 1) with bounded eigenvalues. This motivates the development of sparse PCA, which leverages the extra assumption on the sparsity of eigenvectors. A large amount of literature has contributed to the topic of sparse PCA, for example Amini and Wainwright (2008); Vu and Lei (2012); Birnbaum et al. (2013); Berthet and Rigollet (2013); Ma (2013). Specifically, Vu and Lei (2012) derived optimal bound for the minimax estimation error of the first sparse leading eigenvector, while Cai, Ma and Wu (2015) conducted a more thorough study on the minimax optimal rates for estimating top eigenvalues and eigenvectors of spiked covariance matrices with jointly k-sparse eigenvectors. This type of work assumes bounded eigenvalues, which ignore the contributions of the strong signals from the data in many real applications. To make the problem solvable, sparsity assumptions on the eigenvectors are imposed. In contrast, driven by applications such as genomics, economics, and finance, this paper studies the contributions of the diverging eigenvalues (signals) to the estimation of their associated eigenvectors, without relying on sparsity assumptions on the eigenvectors.

In order to illustrate the third perspective, let us briefly review the approximate factor model (Bai, 2003; Fan, Liao and Mincheva, 2013) and see how the spiked eigenvalues arise naturally from the model. Consider the following data generating model:

$${\mathbf{y}}_t=\mathbf{B}{\mathbf{f}}_t+{\mathit{\epsilon }}_t,\text{ for }t=1,\dots ,T,$$

where y_t is a p-dimensional vector observed at time t, f_t ∈ ℝ^m is the vector of latent factors that drive the cross-sectional dependence at time t, B is the matrix of the corresponding loading coefficients, and ε_t is the idiosyncratic part that can not be explained by the factors. Assume without loss of generality that var(f_t) = I_m, the m × m identity matrix. Then, the model implies Σ = var(y_t) = BB′ + Σ_ε, where Σ_ε = var(ε). It admits a low-rank plus sparse structure, when Σ_ε is assumed to be sparse (Fan, Fan and Lv, 2008; Fan, Liao and Mincheva, 2013). The recovery of the low-rank and sparse matrices was considered thoroughly by Candès et al. (2011) and Chandrasekaran et al. (2011) under the incoherence condition in the noise-less setting and by Agarwal, Negahban and Wainwright (2012) in the noisy case. If the factor loadings {b_i}_i≤p (the transpose of rows of B) are i.i.d. samples from a population with mean zero and covariance Σ_b [this is a pervasive assumption commonly used in the factor models (Fan, Liao and Mincheva, 2013)], then by the law of large numbers, $p^{-1}\mathbf{B}\prime \mathbf{B}=p^{-1}{\sum }_{i=1}^p{\mathbf{b}}_i{\mathbf{b}}_i^{\prime }\to {\mathbf{\Sigma }}_b$, as p → ∞. In other words, the eigenvalues of BB′ are approximately

$$p{\lambda }_1({\mathbf{\Sigma }}_b)(1+o(1)),\cdots ,p{\lambda }_m({\mathbf{\Sigma }}_b)(1+o(1)),0,\cdots ,0,$$

where λ_j(Σ_b) is the j^th eigenvalue of Σ_b. Then, by Weyl’s theorem, we conclude that the eigenvalues of Σ

$${\lambda }_j=p{\lambda }_j({\mathbf{\Sigma }}_b)(1+o(1)),\text{ for }j=1,\cdots ,m,$$ (1.1)

and the remaining are bounded, if ‖Σ_ε‖ is bounded. Therefore, the factor model implies a spiked covariance with diverging leading eigenvalues. Fan, Liao and Mincheva (2013) showed that if the leading eigenvalues grow linearly with the dimension, then the corresponding eigenvectors can be consistently estimated as long as sample size goes to infinity. See Section 4 for more details.

Deviating from the classical random matrix and sparse PCA literature, we consider the high dimensional regime, allowing p/n → ∞. To take into account the contributions of the signals for PCA, we allow λ_j → ∞ for the first m leading eigenvalues. This leads to the third perspective for understanding PCA from this high dimensional setting. Shen et al. (2013) adopted this point of view and considered the regime of p/(nλ_j) → γ_j where 0 ≤ γ_j < ∞ for leading eigenvalues. This is more general than the bounded eigenvalue condition. Specifically if eigenvalues are bounded, we require the ratio p/n converges to a bounded constant as in the random matrix regime. On the other hand, if the dimension is much larger than the sample size, we offset the dimensionality by assuming increased signals or sample size, without additional sparse eigenvector assumption as in sparse PCA regime. In particular, as shown in (1.1), the strong (or pervasive) factors considered in financial applications corresponds to γ_j = 0 with the leading eigenvalues λ_j ≍ p; see for example Stock and Watson (2002); Bai (2003); Bai and Ng (2002); Fan, Liao and Mincheva (2013); Fan, Liao and Wang (2016). The weak or semi-strong factors considered by De Mol, Giannone and Reichlin (2008) and Onatski (2012) also imply bounded p/(nλ₁), with p/n bounded and λ_j ≍ p^θ for some θ ∈ [0, 1).

Hall, Marron and Neeman (2005); Jung and Marron (2009) started the research of high dimension low sample size (HDLSS) regime. With n fixed, Jung and Marron (2009) concluded that consistency of leading eigenvalues and eigenvectors is granted if λ_j ≍ p^θ for θ > 1, which also corresponds to γ_j = 0. Shen et al. (2013) revealed an interesting fact that when γ_j ≠ 0, spiked sample eigenvalues almost surely converge to a biased quantity of the true eigenvalues; furthermore the corresponding sample eigenvectors show an asymptotic conical structure. However, their work focuses only on the consistency problem. In this study, we will consider the same regime as theirs, but focus more on the rates of convergence and the asymptotic distributions of the empirical eigen-structure, and under more relaxed conditions. Our results can be viewed as a natural extension of Paul (2007) to the high dimensional setting.

We would like to emphasize more on the scope and importance of our contributions here. Firstly, the regime we consider in this paper is p/(nλ_j) → γ_j ∈ [0, ∞) for j ≤ m, which permits high dimensionality p/n → ∞ and diverging eigenvalues without specifying their divergence rates. As we have argued, this encompasses many situations considered in the existing literature. It puts into the same framework of the typical random matrix regime with bounded eigenvalues and HDLSS analysis with fixed sample size. Secondly, the contributions of diverging eigenvalues are indeed recognized and accounted for in our theoretical developments. This avoids the restrictive assumptions on sparse eigenvectors. PCA without sparsity assumptions has been widely used in the diverging fields such as population association study (Yamaguchi-Kabata et al., 2008), genome-wide association study (Ringnér, 2008), microarray data (Landgrebe, Wurst and Welzl, 2002; Price et al., 2006), fMRI data (Thomas, Harshman and Menon, 2002), and financial returns (Chen and Shimerda, 1981; Chamberlain and Rothschild, 1983). Our efforts contribute to theoretical understanding why such a plain PCA works in these diverse fields. Finally, by allowing certain generality, we gain theoretical insights into how n, p and signal strength λ_j interplay.

The results are useful in two ways. On the one hand, they help quantify the biases of empirical eigen-structure and explain where they come from. Specifically, in Theorem 3.1, the bias of the j^th sample eigenvalue (j ≤ m) is quantified by p/(nλ_j), which is also showed by Yata and Aoshima (2012, 2013) under different assumptions of the spiked covariance model. Our novel contribution lies in Theorem 3.2, revealing the bias of the j^th sample eigenvector (j ≤ m). In (3.7), we provide a decomposition of each empirical eigenvector into a spiked part, which converges to the true eigenvector with a deflation factor also quantified by p/(nλ_j), and a non-spiked part, which creates a random bias distributed uniformly on an ellipse. More details will be presented in Section 3. On the other hand, the theoretical results provide new technical tools for analyzing factor models, which motivate the study. As we have seen, although it is natural to assume eigenvalues grow linearly with dimension, the assumption imposes a strong signal. Note that when p/(nλ_j) → 0, no biases will occur. So in Section 4, we consider to relax the order of spikes to slightly faster than $\sqrt{p}$. By correcting the biases, we propose a new method called Shrinkage Principal Orthogonal complEment Thresholding (S-POET) and employ it to two applications: risk assessment of large portfolios (Pesaran and Zaffaroni, 2008; Fan, Liao and Shi, 2015) and false discovery proportion estimation for dependent test statistics (Leek and Storey, 2008; Fan, Han and Gu, 2012). Existing methodologies for those two problems reply on rather strong signal level, but we are able to relax it with the help of S-POET.

The paper is organized as follows. Section 2 introduces the notations, assumptions, and an important fact which serves as basis of our proofs. Sections 3.1 and 3.2 devote to the theoretical results for the sample eigenvalues and eigenvectors of the spiked covariance matrix. In Section 4, we discuss several applications of the theories in the previous section. Simulations are conducted in Section 5 to demonstrate the theoretical results at the finite sample and the performance of S-POET. Section 6 provides concluding remarks. The proofs for Section 3 are provided in the appendix and those for Section 4 are relegated to the supplementary material.

2. Assumptions and a simple fact

Assume that ${\{{\mathbf{Y}}_i\}}_{i=1}^n$ is a sequence of i.i.d. random variables with zero mean and covariance matrix Σ_p×p. Let λ₁, …, λ_p be the eigenvalues of Σ in descending order. We consider the spiked covariance model as follows.

Assumption 2.1

λ₁ > λ₂ > ⋯ > λ_m > λ_m+1 ≥ ⋯ ≥ λ_p > 0, where the non-spiked eigenvalues are bounded, i.e. c₀ ≤ λ_j ≤ C₀, j > m for constants c₀, C₀ > 0 and the spiked eigenvalues are well separated, i.e. ∃ δ₀ > 0 such that min_j≤m(λ_j − λ_j+1)/λ_j ≥ δ₀.

The eigenvalues are divided into the spiked ones and bounded non-spiked ones. We do not need to specify the order of the leading eigenvalues nor require them to diverge. Thus, our results in Section 3 are applicable to both bounded and diverging leading eigenvalues. For simplicity, we only consider distinguishable eigenvalues (multiplicity 1) for the largest m eigenvalues and a fixed number m, independent of n and p.

The factor model y = Bf + ε with pervasive factors considered in Fan, Liao and Mincheva (2013) implies a spiked covariance model with λ_j ≍ p in (1.1) and satisfies the above assumption. For the interplay of the sample size n, dimension p and the spikes λ_j ’s, the following relationship is assumed as in Shen et al. (2013).

Assumption 2.2

Assume p > n. For the spiked part 1 ≤ j ≤ m, c_j = p/(nλ_j) is bounded, and for the non-spiked part, ${(p-m)}^{-1}{\sum }_{j=m+1}^p{\lambda }_j=\overline{c}+o(n^{-1/2})$.

We allow p/n → ∞ in any manner, though λ_j also needs to grow fast enough to ensure bounded c_j. In particular, c_j = o(1) is allowed as in the factor model. We do not assume the non-spiked eigenvalues are identical, as in most spiked covariance model literature (e.g. Paul (2007); Johnstone and Lu (2009)).

By spectral decomposition, Σ = ΓΛΓ′, where the orthonormal matrix Γ is constructed by the eigenvectors of Σ and Λ = diag(λ₁, …, λ_p). Let X_i = Γ′Y_i. Since the empirical eigenvalues are invariant and the empirical eigenvectors are equivariant under an orthonormal transformation, we focus the analysis on the transformed domain of X_i and then translate the results into those of the original data. Note that var(X_i) = Λ. Let Z_i = Λ^−1/2X_i be the elementwise standardized random vector.

Assumption 2.3

${\{{\mathbf{Z}}_i\}}_{i=1}^n$ are i.i.d copies of Z. The standardized random vector Z = (Z₁, …, Z_p) is sub-Gaussian with independent entries of mean zero and variance one. The sub-Gaussian norms of all components are uniformly bounded: max_j ‖Z_j‖_ψ2 ≤ C₀, where ‖Z_j‖_ψ2 = sup_q≥1 q^−1/2(E|Z_j|^q)^1/q.

Since Var(X_i) = diag(λ₁, λ₂, …, λ_p), the first m population eigenvectors are simply unit vectors e₁, e₂, …, e_m with only one nonvanishing element. Denote the n by p transformed data matrix by X = (X₁, X₂, …, X_n)′. Then the sample covariance matrix is

$${\hat{\mathbf{\Sigma }}}_{p\times p}=\frac{1}{n}\mathbf{X}\prime \mathbf{X}=\frac{1}{n}\sum _{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{\prime },$$

whose eigenvalues are denoted as λ̂₁, λ̂₂, …, λ̂_p (λ̂_j = 0 for j > n) with corresponding eigenvectors ξ̂₁, ξ̂₂, …, ξ̂_p. Note that the empirical eigenvectors of data Y_i’s are ${\hat{\mathit{\xi }}}_j^{(Y)}=\mathbf{\Gamma }{\hat{\mathit{\xi }}}_j$.

Let Z_j be the j^th column of the standardized X. Then each Z_j has i.i.d sub-Gaussian entries with zero mean and unit variance. Exchanging the roles of rows and columns, we get the n by n Gram matrix

$${\tilde{\mathbf{\Sigma }}}_{n\times n}=\frac{1}{n}\mathbf{X}\mathbf{X}\prime =\frac{1}{n}\sum _{j=1}^p{\lambda }_j{\mathbf{Z}}_j{\mathbf{Z}}_j^{\prime },$$

with the same nonzero eigenvalues λ̂₁, λ̂₂, …, λ̂_n as Σ̂ and the corresponding eigenvectors u₁, u₂, …, u_n. It is well known that for i = 1, 2, …, n

$${\hat{\mathit{\xi }}}_i={(n{\hat{\lambda }}_i)}^{-1/2}\mathbf{X}\prime {\mathbf{u}}_i\text{ and }{\mathbf{u}}_i={(n{\hat{\lambda }}_i)}^{-1/2}\mathbf{X}{\hat{\mathit{\xi }}}_i,$$ (2.1)

while the other eigenvectors of Σ̂ constitute a (p−n)-dimensional orthogonal complement of ξ̂₁, …, ξ̂_n.

By using this simple fact, for the specific case with c₀ = C₀ = 1 in Assumption 2.1, λ_j = 1 for j > m in Assumption 2.2, and Gaussian data in Assumption 2.3, Shen et al. (2013) showed that

$$\frac{{\hat{\lambda }}_j}{{\lambda }_j}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }1+c_j,1\le j\le m;$$

and

$$|\langle {\hat{\mathit{\xi }}}_j,{\mathbf{e}}_j\rangle |\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{(1+c_j)}^{-\frac{1}{2}},$$

where 〈a, b〉 denotes the inner product of two vectors. However, they fail to establish any results on convergence rates or asymptotic distributions of the empirical eigen-structure. This motivates the current paper.

The aim of this paper is to establish the asymptotic normality of the empirical eigenvalues and eigenvectors under more relaxed conditions. Our results are a natural extension of Paul (2007) to a more general setting with new insights, where the asymptotic normality of sample eigenvectors is derived using complicated random matrix techniques for Gaussian data under the regime of p/n → γ ∈ [0, 1). In comparison, our proof, based on the relationship (2.1), is much simpler and insightful for understanding the behavior of high dimensional PCA.

Here are some notations that we will use in the paper. For a general matrix M, we denote its matrix entry-wise max norm as ‖M‖_max = max_i,j{|M_i,j|} and define the quantities $\Vert \mathbf{M}\Vert ={\lambda }_{\text{max}}^{1/2}(\mathbf{M}\prime \mathbf{M}),{\Vert \mathbf{M}\Vert }_F={({\sum }_{i,j}{M}_{i,j}^2)}^{1/2}$, ‖M‖_∞ = max_i ∑_j |M_i,j| to be its spectral, Frobenius and induced ℓ_∞ norms. If M is symmetric, we define λ_j(M) to be the j^th largest eigenvalue of M and λ_max(M), λ_min(M) to be the maximal and minimal eigenvalues respectively. We denote tr(M) as the trace of M. For any vector v, its ℓ₂ norm is represented by ‖v‖ while ℓ₁ norm is written as ‖v‖₁. We use diag(v) to denote the diagonal matrix with the same diagonal entries as v. For two random vectors a, b of the same length, we say a = b+O_P(δ) if ‖a−b‖ = O_P(δ) and a = b + o_P(δ) if ‖a − b‖ = o_P(δ). We denote $\mathbf{a}\stackrel{d}{\Rightarrow }ℒ$ for some distribution ℒ if there exists b ~ ℒ such that a = b + o_P(1). Throughout the paper, C is a generic constant that may differ from line to line.

3. Asymptotic behavior of empirical eigen-structure

3.1. Asymptotic normality of empirical eigenvalues

Let us first study the behavior of the leading m empirical eigenvalues of Σ̂. Denote by λ_j(A) the j^th largest eigenvalue of matrix A and recall that λ̂_j = λ_j(Σ̂). We have the following asymptotic normality of λ̂_j.

Theorem 3.1

Under Assumptions 2.1 – 2.3, ${\{{\hat{\lambda }}_j\}}_{j=1}^m$’s have independent limiting distributions. In addition,

$$\sqrt{n}\{\frac{{\hat{\lambda }}_j}{{\lambda }_j}-(1+\overline{c}{c}_j+O_P({\lambda }_j^{-1}\sqrt{p/n})\left)\right\}\stackrel{d}{\Rightarrow }N(0,{\kappa }_j-1),$$ (3.1)

where κ_j is the kurtosis of X_j.

The theorem shows that the bias of λ̂_j/λ_j is $\overline{c}{c}_j+O_P({\lambda }_j^{-1}\sqrt{p/n})$. The second term is dominated by the first term since p > n and it is of order o_P(n^−1/2) if $\sqrt{p}=o({\lambda }_j)$. The latter assumption is satisfied by the strong factor model in Fan, Liao and Mincheva (2013) and a part of weak or semi-strong factor model in Onatski (2012). The theorem reveals the bias is controlled by a term of rate p/(nλ_j). To get the asymptotically unbiased estimate, it requires c_j = p/(nλ_j) → 0 for j ≤ m. This result is more general than that of Shen et al. (2013) and sheds a similar light to that of Koltchinskii and Lounici (2014a,b) i.e. ‖Σ̂ − Σ‖/‖Σ‖ → 0 almost surely if and only if the effective rank r̄ = tr(Σ)/λ₁ is of order o(n), which is true when c₁ = o(1). Our result here holds for each individual spike. Yata and Aoshima (2012, 2013) employed a similar technical trick and gave a comprehensive study on the asymptotic consistency and distributions of the eigenvalues. They got similar results under different conditions from ours. Our framework is more general here. If c_j ↛ 0, bias reduction can also be made; see Section 4.2, where an estimator for c̄ is proposed. Under the bounded spiked covariance model considered in Baik, Ben Arous and Péché (2005), Johnstone and Lu (2009) and Paul (2007), it is assumed λ_j = c₀ = C₀, j > m so that c̄ = c₀, the minimum eigenvalue of the population covariance matrix. Our result is also consistent with Anderson (1963)’s result that

$$\sqrt{n}({\hat{\lambda }}_j-{\lambda }_j)\stackrel{d}{\Rightarrow }N(0,2{\lambda }_j^2),$$

for Gaussian data and fixed p and λ_j’s, where the non-spiked part does not exist and thus the bias $O_P({\lambda }_j^{-1}\sqrt{p/n})$ disappears. The proof is relegated to the appendix.

3.2. Behavior of empirical eigenvectors

Let us consider the asymptotic distribution of the empirical eigenvectors ξ̂_j’s corresponding to λ̂_j, j = 1, 2, …, m. As in Paul (2007), each ξ̂_j is divided into two parts corresponding to the spiked and non-spiked components, i.e. ${\hat{\mathit{\xi }}}_j=({\hat{\mathit{\xi }}}_{jA}^{\prime },{\hat{\mathit{\xi }}}_{jB}^{\prime })\prime$ where ξ̂_jA is of length m.

Theorem 3.2

Under Assumptions 2.1 – 2.3, we have

1. For the spiked part, if m = 1,

   $$\frac{2(1+\overline{c}{c}_1)}{\overline{c}{c}_1}\sqrt{n}(\sqrt{1+\overline{c}{c}_1}{\hat{\xi }}_{1A}-1+O_P(\sqrt{\frac{p}{n{\lambda }_1^2}}\left)\right)\stackrel{d}{\Rightarrow }N(0,{\kappa }_1-1),$$ (3.2)

   while if m > 1,

   $$\sqrt{n}(\frac{{\hat{\mathit{\xi }}}_{jA}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }-{\mathbf{e}}_{jA}+O_P(\sqrt{\frac{p}{n{\lambda }_j^2}}\left)\right)\stackrel{d}{\Rightarrow }{N}_m(\mathbf{0},{\mathbf{\Sigma }}_{\mathbf{j}}),$$ (3.3)

   for j = 1, 2, …, m, with

   $${\mathbf{\Sigma }}_j={\sum }_{k\in [m]\backslash j}{a}_{jk}^2{\mathbf{e}}_{kA}{\mathbf{e}}_{kA}^{\prime },$$

   where [m] = {1, ⋯, m}, e_kA is the first m elements of the unit vector e_k, and $a_{jk}={\text{lim}}_{{\lambda }_j,{\lambda }_k\to \infty }\sqrt{{\lambda }_j{\lambda }_k}/({\lambda }_j-{\lambda }_k)$, which is assumed to exist.
2. For the non-spiked part, if we further assume the data is Gaussian, there exists p − m dimensional vector h₀ ~ Unif (B_p−m(1)) such that

   $$\Vert {\mathbf{D}}_0\frac{{\hat{\mathit{\xi }}}_{jB}}{\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }-{\mathbf{h}}_0\Vert =O_P\left(\sqrt{\frac{n}{p}}\right)+o_P\left(\frac{1}{\sqrt{n}}\right),$$ (3.4)

   where ${\mathbf{D}}_0=\text{diag}(\sqrt{\overline{c}/{\lambda }_{m+1}},\dots ,\sqrt{\overline{c}/{\lambda }_p})$ is a diagonal matrix and Unif (B_k(r)) denotes the uniform distribution over the centered sphere of radius r. In addition, the max norm of ξ̂_jB satisfies

   $${\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }_{\text{max}}=O_P(p/(n{\lambda }_j^{3/2})+\sqrt{\text{log }p/(n{\lambda }_j)}).$$ (3.5)
3. Furthermore, $\Vert {\hat{\mathit{\xi }}}_{jA}\Vert ={(1+\overline{c}{c}_j)}^{-1/2}+O_P({\lambda }_j^{-1}\sqrt{p/n}+p/(n^{3/2}{\lambda }_j))$ and $\Vert {\hat{\mathit{\xi }}}_{jB}\Vert ={(\frac{\overline{c}{c}_j}{1+\overline{c}{c}_j})}^{1/2}+O_P(\sqrt{1/{\lambda }_j}+\sqrt{p/(n^2{\lambda }_j)})$. Together with (i), this implies the inner product between empirical eigenvector and the population one converges to (1 + c̄c_j)^−1/2 in probability and

   $$\langle {\hat{\mathit{\xi }}}_j,{\mathbf{e}}_j\rangle -\frac{1}{\sqrt{1+\overline{c}{c}_j}}=O_P({\lambda }_j^{-1}\sqrt{p/n}+p/(n^{3/2}{\lambda }_j))+O_P(n^{-1})I_{\{m>1\}}.$$ (3.6)

In the above theory, we assume $a_{jk}={\text{lim}}_{{\lambda }_j,{\lambda }_k\to \infty }\frac{\sqrt{{\lambda }_j{\lambda }_k}}{{\lambda }_j-{\lambda }_k}$ exists. This is not restrictive if eigenvalues are well separated i.e. min_j≠k≤m |λ_j − λ_k|/λ_j ≥ δ₀ from assumption 2.1. The assumption obviously holds for the pervasive factor model, in which $a_{jk}=\sqrt{{\lambda }_j({\mathbf{\Sigma }}_b){\lambda }_k({\mathbf{\Sigma }}_b)}/({\lambda }_k({\mathbf{\Sigma }}_b)-{\lambda }_j({\mathbf{\Sigma }}_b))$.

Theorem 3.2 is an extension of random matrix results into high dimensional regime. Its proof sheds light on how to use the smaller n × n matrix Σ̃ as a tool to understand the behavior of the larger p × p covariance matrix Σ̂. Specifically, we start from Σ̃u_j = λ̂_ju_j or identity (A.3) and then use the simple fact (2.1) to get a relationship (A.4) of eigenvector ξ̂_j. Then (A.4) is rearranged as (A.6) which gives a clear separation of the dominating term, that is asymptotically normal, and the error term. This makes the whole proof much simpler in comparison with Paul (2007) who showed a similar type of result through a complicated representation of ξ̂_j and λ̂_j under more restricted assumptions. From this simple trick, we can understand deeply how some important high and low dimensional quantities link together and differ from each other.

Several remarks are in order. Firstly, since ${\hat{\mathit{\xi }}}_j^{(\mathbf{Y})}=\mathbf{\Gamma }{\hat{\mathit{\xi }}}_j$ is the j^th empirical eigenvector based on observed data Y, we have decomposition

$${\hat{\mathit{\xi }}}_j^{(\mathbf{Y})}={\mathbf{\Gamma }}_A{\hat{\mathit{\xi }}}_{jA}+{\mathbf{\Gamma }}_B{\hat{\mathit{\xi }}}_{jB},$$ (3.7)

where Γ = (Γ_A, Γ_B). Note that Γ_Aξ̂_jA converges to the true eigenvector deflated by a factor of $\sqrt{1+\overline{c}{c}_j}$ with the convergence rate $O_P(\sqrt{p/(n{\lambda }_j^2)}+p/(n^{3/2}{\lambda }_j)+n^{-1/2})$ while Γ_Bξ̂_jB creates a random bias, which is distributed uniformly on an ellipse of (p − m) dimension and projected into the p dimensional space spaned by Γ_B. The two parts intertwine in such a way that correction for the biases of estimating eigenvectors is almost impossible. More details are discussed in Section 4 for the factor models. Secondly, it is clearly as in the eigenvalue case, the bias term ${\lambda }_j^{-1}\sqrt{p/n}$ Theorem 3.2 (i) disappears when $\sqrt{p}=o({\lambda }_j)$. In particular, for the stronger factor given by (1.1), ${\hat{\mathit{\xi }}}_j^{(\mathbf{Y})}$ is a consistent estimator. Thirdly, the situations m = 1 and m > 1 have slight difference in that multiple spikes could interact with each other. Especially this is reflected in the convergence of the angle between the empirical eigenvector and its population counterpart: the angle converges to (1 + c̄c_j)^−1/2 with an extra rate O_P(1/n) which stems from estimating ξ̂_jk for j ≠ k ≤ m (see proof of Theorem 3.2 (iii)). The difference will only be seen when the spike magnitude is higher than the order $\sqrt{pn}\vee p{n}^{-1/2}$. We will verify this by a simple simulation in Section 5. Finally, it is the first time that the max norm bound of the non-spiked part is derived. This bound will be useful for analyzing factor models in Section 4.

Theorem 3.2 again implies the results of Shen et al. (2013). It also generalizes the asymptotic distribution of non-spiked part from pure orthogonal invariant case of Paul (2007) to a more general setting. In particular, when p/n → ∞, the asymptotic distribution of the normalized non-spiked component is not uniform over a sphere any more, but over an ellipse. In addition, our result can be compared with the low dimensional case, where Anderson (1963) showed that

$$\sqrt{n}({\hat{\mathit{\xi }}}_j-{\mathbf{e}}_j)\stackrel{d}{\Rightarrow }{N}_p(\mathbf{0},\sum _{k\in [m]\backslash j}\frac{{\lambda }_j{\lambda }_k}{{({\lambda }_j-{\lambda }_k)}^2}{\mathbf{e}}_k{\mathbf{e}}_k^{\prime }),$$ (3.8)

for fixed p and λ_j’s. Under our assumptions, since the spiked eigenvalues may go to infinity, the constants in the asymptotic covariance matrix are replaced by the limits a_jk’s. Similar to the behavior of eigenvalues, the spiked part ξ̂_jA preserves the normality property except for a bias factor 1/(1+ c̄c_j) caused by the high dimensionality. Also, recent work of Koltchinskii and Lounici (2014b) provides general asymptotic results for the empirical eigenvectors from a spectral projector point of view, but they mainly focus on the regime of p/nλ_j → 0 or r̄ = o(n). Last but not least, it has been shown by Johnstone and Lu (2009) that PCA generates consistent eigenvector estimation if and only if p/n → 0 when the spike sizes are fixed. This motivates the study of sparse PCA. We take the spike magnitude into account and provide additional insights by showing that PCA consistently estimate eigenvalues and eigenvectors if and only if p/(nλ_j) → 0. This explains why Fan, Liao and Mincheva (2013) can consistently estimate the eigenvalues and eigenvectors while Johnstone and Lu (2009) can not.

4. Applications to factor models

In this section, we propose a method named Shrinkage Principal Orthogonal complEment Thresholding (S-POET) for estimating large covariance matrices induced by the approximate factor models. The estimator is based on correction of the bias of the empirical eigenvalues as specified in (3.1). We derive for the first time the bound for the relative estimation errors of covariance matrices under the spectral norm. The results are then applied to assessing large portfolio risks and estimating false discovery proportions, where the conditions in existing literature are significantly relaxed.

4.1. Approximate factor models

Factor models have been widely used in various disciplines. For example, it is used to extract information from financial market for sufficient forecasting of other time series (Stock and Watson, 2002; Fan, Xue and Yao, 2015) and to adjust heterogeneity for biological data aggregation of multiple sources (Leek et al., 2010; Fan et al., 2016). Consider the approximate factor model

$$y_{it}={\mathbf{b}}_i^{\prime }{\mathbf{f}}_t+u_{it},$$ (4.1)

where y_it is the observed data for the i^th (i = 1, …, p) individual (e.g. returns of stocks) or component (e.g. expressions of genes) at time t = 1, …, T; f_t is an m × 1 vector of latent common factors and b_i is the factor loadings for the i^th individual or component; u_it is the idiosyncratic error, uncorrelated with the common factors. In genomics application, t can also index repeated experiments. For simplicity we assume there is no time dependency.

The factor model can be written into a matrix form as follows:

$$\mathbf{Y}=\mathbf{B}\mathbf{F}\prime +\mathbf{U},$$ (4.2)

where Y_p×T, B_p×m, F_T×m, U_p×T are respectively the matrix form of the observed data, the factor loading matrix, the factor matrix, and the error matrix. For identifiability, we impose the condition that cov(f_t) = I. Thus, the covariance matrix is given by

$$\mathbf{\Sigma }=\mathbf{B}\mathbf{B}\prime +{\mathbf{\Sigma }}_u,$$ (4.3)

where Σ_u is the covariance matrix of the idiosyncratic error at any time t.

Under the assumption that Σ_u = (σ_u,ij)_i,j≤p is sparse with its eigenvalues bounded away from zero and infinity, the population covariance exhibits a “low-rank plus sparse” structure. The sparsity is measured by the following quantity

$$m_p=\underset{i\le p}{\text{max}}\sum _{j\le p}{|{\sigma }_{u,ij}|}^q,$$

for some q ∈ [0, 1] (Bickel and Levina, 2008). In particular, with q = 0, m_p equals the maximum number of nonzero elements in each row of Σ_u.

In order to estimate the true covariance matrix with the above factor structure, Fan, Liao and Mincheva (2013) proposed a method called “POET” to recover the unknown factor matrix as well as the factor loadings. The idea is simply to first decompose the sample covariance matrix into the spiked and non-spiked part and estimate them separately. Specifically, recall Σ̂ = T⁻¹YY′ and let {λ̂_j} and {ξ̂_j} be its corresponding eigenvalues and eigenvectors. They define

$${\hat{\mathbf{\Sigma }}}^{\top }=\sum _{j=1}^m{\hat{\lambda }}_j{\hat{\mathit{\xi }}}_j{\hat{\mathit{\xi }}}_j^{\prime }+{\hat{\mathbf{\Sigma }}}_u^{\top },$$ (4.4)

where ${\hat{\mathbf{\Sigma }}}_u^{\top }$ is the matrix after applying thresholding method (Bickel and Levina, 2008) to ${\hat{\mathbf{\Sigma }}}_u=\hat{\mathbf{\Sigma }}-{\sum }_{j=1}^m{\hat{\lambda }}_j{\hat{\mathit{\xi }}}_j{\hat{\mathit{\xi }}}_j^{\prime }$.

They showed that the above estimation procedure is equivalent to the least square approach that minimizes

$$(\hat{\mathbf{B}},\hat{\mathbf{F}})=\text{arg }\underset{\mathbf{B},\mathbf{F}}{\text{min}}{\Vert \mathbf{Y}-\mathbf{B}\mathbf{F}\prime \Vert }_F^2\mathrm{s}.\mathrm{t}.\frac{1}{T}\mathbf{F}\prime \mathbf{F}={\mathbf{I}}_m,\mathbf{B}\prime \mathbf{B}\text{ is diagonal}.$$ (4.5)

The columns of $\hat{\mathbf{F}}/\sqrt{T}$ are the eigenvectors corresponding to the m largest eigenvalues of the T × T matrix T⁻¹Y′Y and B̂ = T⁻¹YF̂. After B and F are estimated, the sample covariance of Û = Y − B̂F̂′ can be formed: Σ̂_u = T⁻¹ÛÛ′. Finally thresholding is applied to Σ̂_u to generate ${\hat{\mathbf{\Sigma }}}_u^{\top }={({\hat{\sigma }}_{u,ij}^{\top })}_{p\times p}$, where

$${\hat{\sigma }}_{u,ij}^{\top }\{\begin{array}{cc}{\hat{\sigma }}_{u,ij},\hfill & i=j;\hfill \\ s_{ij}({\hat{\sigma }}_{u,ij})I(|{\hat{\sigma }}_{u,ij}|\ge {\tau }_{ij}),\hfill & i\ne j.\hfill \end{array}$$ (4.6)

Here s_ij(·) is the generalized shrinkage function (Antoniadis and Fan, 2001; Rothman, Levina and Zhu, 2009) and τ_ij = τ(σ̂_u,iiσ̂_u,jj)^1/2 is the entry-dependent threshold. The above adaptive threshold corresponds to applying thresholding with parameter τ to the correlation matrix of Σ̂_u. The positive parameter τ will be determined later.

Fan, Liao and Mincheva (2013) showed that under Assumptions ?? - ?? listed in Appendix ?? in the supplementary material (Wang and Fan, 2015),

$${\Vert {\hat{\mathbf{\Sigma }}}^{\top }-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma },F}=O_P(\frac{\sqrt{p}\text{ log }p}{T}+m_p{(\frac{\text{log }p}{T}+\frac{1}{p})}^{(1-q)/2}),$$ (4.7)

where ‖A‖_Σ,F = p^−1/2‖Σ^−1/2AΣ^−1/2‖_F and ‖ · ‖_F is the Frobenius norm. Note that

$${\Vert {\hat{\mathbf{\Sigma }}}^{\top }-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma },F}=p^{-1/2}{\Vert {\mathbf{\Sigma }}^{-1/2}{\hat{\mathbf{\Sigma }}}^{\top }{\mathbf{\Sigma }}^{-1/2}-{\mathbf{I}}_p\Vert }_F,$$

which measures the relative error in Frobenius norm. A more natural metric is relative error under the operator norm ‖A‖_Σ = ‖Σ^−1/2AΣ^−1/2‖, which can not be obtained by using the technical device of Fan, Liao and Mincheva (2013). Note ‖A‖_Σ,F ≤ ‖A‖_Σ. Via our new results in the last section, we will establish a result under those two relative norms, under weaker conditions than their pervasiveness assumption. Note that the relative error convergence is particularly meaningful for spiked covariance matrix, as eigenvalues are in different scales.

4.2. Shrinkage POET under relative spectral norm

The discussion above reveals several drawbacks of POET. First, the spike size has to be of order p which rules out relatively weak factors. Second, it is well known that the empirical eigenvalues are inconsistent if the spiked eigenvalues do not significantly dominate the non-spiked part. Therefore, a proper correction or shrinkage is needed. See a recent paper by Donoho, Gavish and Johnstone (2014) for optimal shrinkage of eigenvalues.

Regarding to the first drawback, we relax the assumption ‖p⁻¹B′B − Ω₀‖ = o(1) in Assumption ?? to the following weaker assumption.

Assumption 4.1

$\Vert {\mathbf{\Lambda }}_A^{-1/2}\mathbf{B}\prime \mathbf{B}{\mathbf{\Lambda }}_A^{-1/2}-{\mathbf{\Omega }}_0\Vert =o(1)$ for some Ω₀ with eigenvalues bounded from above and below, where Λ_A = diag(λ₁, …, λ_m). In addition, we assume λ_m → ∞, λ₁/λ_m is bounded from above and below.

This assumption does not require the first m eigenvalues of Σ to take on any specific rate. They can still be much smaller than p, although for simplicity we require them to diverge and share the same diverging rate. Since ‖Σ_u‖ is assumed to be bounded, the assumption λ_m → ∞ is also imposed to avoid the issue of identifiability. When λ_m does not diverge, more sophisticated condition is needed for identifiability (Chandrasekaran et al., 2011).

In order to handle the second drawback, we propose the Shrinkage POET (S-POET) method. Inspired by (3.1), the shrinkage POET modifies the first part in POET estimator (4.4) as follows:

$${\hat{\mathbf{\Sigma }}}^S=\sum _{j=1}^m{\hat{\lambda }}_j^S{\hat{\mathit{\xi }}}_j{\hat{\mathit{\xi }}}_j^{\prime }+{\hat{\mathbf{\Sigma }}}_u^{\top },$$ (4.8)

where ${\hat{\lambda }}_j^S=\text{max}\{{\hat{\lambda }}_j-\overline{c}p/n,0\}$, a simple soft thresholding correction. Obviously if λ̂_j is sufficiently large, ${\hat{\lambda }}_j^S/{\lambda }_j={\hat{\lambda }}_j/{\lambda }_j-\overline{c}{c}_j=1+o_P(1)$. Since c̄ is unknown, a natural estimator ĉ is such that the total of the eigenvalues remains unchanged:

$$\text{tr}(\hat{\mathbf{\Sigma }})=\sum _{j=1}^m({\hat{\lambda }}_j-ĉp/n)+(p-m)ĉ$$

or $ĉ=(\text{tr}(\hat{\mathbf{\Sigma }})-{\sum }_{j=1}^m{\hat{\lambda }}_j)/(p-m-pm/n)$. It has been shown by Lemma 7 of Yata and Aoshima (2012) that

$$(ĉ-\overline{c})\frac{p}{n{\lambda }_j}=O_P(\frac{\text{tr}(\hat{\mathbf{\Sigma }})-{\sum }_{j=1}^m{\hat{\lambda }}_j}{(n-m){\lambda }_m}-\frac{\overline{c}p}{n{\lambda }_m})=O_P(n^{-1}).$$

Thus, replacing c̄ by ĉ, we have ${\hat{\lambda }}_j^S/{\lambda }_j-1=O_P({\lambda }_j^{-1}\sqrt{p/n}+n^{-1/2})$, i.e. the estimation error in ĉ is negligible. From Lemma 3.1, we can easily obtain the asymptotic normality, $\sqrt{n}({\hat{\lambda }}_j^S/{\lambda }_j-1)\stackrel{d}{\Rightarrow }N(0,{\kappa }_j-1)$ if $\sqrt{p}=o({\lambda }_j)$.

To get the convergence of relative errors under the operator norm, we also need the following additional assumptions:

Assumption 4.2

1. {u_t, f_t}_t≥1 are independently and identically distributed with 𝔼[u_it] = 𝔼[u_itf_jt] = 0 for all i ≤ p, j ≤ m and t ≤ T.

2. There exist positive constants c₁ and c₂ such that λ_min(Σ_u) > c₁, ‖Σ_u‖_∞ < c₂, and min_i,j Var(u_itu_jt) > c₁.

3. There exist positive constants r₁, r₂, b₁ and b₂ such that for s > 0, i ≤ p, j ≤ m,

   $$\mathbb{P}(|u_{it}|>s)\le \mathit{\text{exp}}(-{(s/b_1)}^{r_1})\mathit{\text{ and }}\mathbb{P}(|f_{jt}|>s)\le \mathit{\text{exp}}(-{(s/b_2)}^{r_2}).$$

4. There exists M > 0 such that for all i ≤ p, j ≤ m, $|b_{ij}|\le M\sqrt{{\lambda }_j/p}$.

5. $\sqrt{p}{(\text{log }T)}^{1/r_2}=o({\lambda }_m)$.

The first three conditions are common in factor model literature. If we write B = (b̃₁, …, b̃_m), by Weyl’s inequality we have max_1≤j≤m ‖b̃_j‖²/λ_j ≤ 1+‖Σ_u‖/λ_j = 1+o(1). Thus it is reasonable to assume the magnitude |b_ij | of factor loadings is of order $\sqrt{{\lambda }_j/p}$ in the fourth condition. The last condition is imposed to ease technical presentation.

Now we are ready to investigate ‖Σ̂^S −Σ‖_Σ. Suppose the SVD decomposition of Σ,

$$\mathbf{\Sigma }=\left({\mathbf{\Gamma }}_{p\times m}{\mathbf{\Omega }}_{p\times (p-m)}\right)\left(\begin{array}{cc}\hfill {\mathbf{\Lambda }}_{m\times m}\hfill & \hfill \hfill \\ \hfill \hfill & \hfill {\mathbf{\Theta }}_{(p-m)\times (p-m)}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathbf{\Gamma }\prime \hfill \\ \hfill \mathbf{\Omega }\prime \hfill \end{array}\right).$$

Then obviously

$${\Vert {\hat{\mathbf{\Sigma }}}^S-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}\le \Vert {\mathbf{\Sigma }}^{-\frac{1}{2}}(\hat{\mathbf{\Gamma }}{\hat{\mathbf{\Lambda }}}^S\hat{\mathbf{\Gamma }}\prime -\mathbf{B}\mathbf{B}\prime ){\mathbf{\Sigma }}^{-\frac{1}{2}}\Vert +\Vert {\mathbf{\Sigma }}^{-\frac{1}{2}}({\hat{\mathbf{\Sigma }}}_u^{\top }-{\mathbf{\Sigma }}_u){\mathbf{\Sigma }}^{-\frac{1}{2}}\Vert ≕{\mathrm{\Delta }}_L+{\mathrm{\Delta }}_S,$$ (4.9)

and

$${\mathrm{\Delta }}_S\le \Vert {\mathbf{\Sigma }}^{-1}\Vert \Vert {\hat{\mathbf{\Sigma }}}_u^{\top }-{\mathbf{\Sigma }}_u\Vert \le C\Vert {\hat{\mathbf{\Sigma }}}_u^{\top }-{\mathbf{\Sigma }}_u\Vert .$$ (4.10)

It can be shown

$${\mathrm{\Delta }}_L=\Vert \left(\begin{array}{c}\hfill {\mathbf{\Lambda }}^{-\frac{1}{2}}\mathbf{\Gamma }\prime \hfill \\ \hfill {\mathbf{\Theta }}^{-\frac{1}{2}}\mathbf{\Omega }\prime \hfill \end{array}\right)(\hat{\mathbf{\Gamma }}{\hat{\mathbf{\Lambda }}}^S\hat{\mathbf{\Gamma }}\prime -\mathbf{B}\mathbf{B}\prime )\left(\mathbf{\Gamma }{\mathbf{\Lambda }}^{-\frac{1}{2}}\mathbf{\Omega }{\mathbf{\Theta }}^{-\frac{1}{2}}\right)\Vert \le {\mathrm{\Delta }}_{L1}+{\mathrm{\Delta }}_{L2},$$ (4.11)

where ${\mathrm{\Delta }}_{L1}=\Vert {\mathbf{\Lambda }}^{-\frac{1}{2}}\mathbf{\Gamma }\prime (\hat{\mathbf{\Gamma }}{\hat{\mathbf{\Lambda }}}^S\hat{\mathbf{\Gamma }}\prime -\mathbf{B}\mathbf{B}\prime )\mathbf{\Gamma }{\mathbf{\Lambda }}^{-\frac{1}{2}}\Vert$ and ${\mathrm{\Delta }}_{L2}=\Vert {\mathbf{\Theta }}^{-\frac{1}{2}}\mathbf{\Omega }\prime (\hat{\mathbf{\Gamma }}{\hat{\mathbf{\Lambda }}}^S\hat{\mathbf{\Gamma }}\prime -\mathbf{B}\mathbf{B}\prime )\mathbf{\Omega }{\mathbf{\Theta }}^{-\frac{1}{2}}\Vert$. Thus in order to find the convergence rate of relative spectral norm, we need to consider the terms Δ_L1, Δ_L2 and Δ_S separately. Notice that Δ_L1 measures the relative error of the estimated spiked eigenvalues, Δ_L2 reflects the goodness of the estimated eigenvectors, and Δ_S controls the error of estimating the sparse idiosyncratic covariance matrix. To bound the relative Frobenius norm ‖Σ̂_S − Σ‖_Σ,F, we define similar quantities Δ̃_L1, Δ̃_L2, Δ̃_S which replace the spectral norm by Frobenius norm multiplied by p^−1/2. Note that (4.9) – (4.11) also hold for relative Frobenius norm with Δ̃_L1, Δ̃_L2, Δ̃_S. The following theorem reveals the rate of each term. Its proof will be provided in Appendix ?? of the supplementary material (Wang and Fan, 2015).

Theorem 4.1

Under Assumptions 2.1, 2.2, 2.3, 4.1 and 4.2, if p log p > max{T(log T)^4/r₂, T(log(pT))^2/r₁}, we have

$${\tilde{\mathrm{\Delta }}}_{L1}\le {\mathrm{\Delta }}_{L1}=O_P\left(T^{-1/2}\right),{\mathrm{\Delta }}_{L2}=O_P\left(\frac{p}{T}\right),{\tilde{\mathrm{\Delta }}}_{L2}=O_P\left(\frac{\sqrt{p}}{T}\right),$$

and by the applying adaptive thresholding estimator (4.6) with

$${\tau }_{ij}=C{\omega }_T{({\hat{\sigma }}_{u,ii}{\hat{\sigma }}_{u,jj})}^{1/2},\mathit{\text{ and }}{\omega }_T=\sqrt{\text{log }p/T}+\sqrt{1/p},$$

we have

$${\tilde{\mathrm{\Delta }}}_S\le {\mathrm{\Delta }}_S=O_P\left(m_p{\omega }_T^{1-q}\right).$$

Combining the three terms, ${\Vert {\hat{\mathbf{\Sigma }}}^S-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma }}=O_P(p/T+m_p{\omega }_T^{1-q})$ and ${\Vert {\hat{\mathbf{\Sigma }}}^S-\mathbf{\Sigma }\Vert }_{\mathrm{\Sigma },F}=O_P(\sqrt{p}/T+m_p{\omega }_T^{1-q})$.

The relative error convergence characterizes the accuracy of estimation for spiked covariance matrix. In contrast with the result on relative Frobenius norm, this is the first time that the relative rate under spectral norm is derived. As long as λ_m is slightly above $\sqrt{p}$, we reach the same rates of convergence. Therefore, we can conclude S-POET is effective even under a much weaker signal level. Comparing the rate with (4.7), under relative Frobenius norm, we achieve a better rate without the artificial log term, thanks to the new asymptotic results.

4.3. Portfolio risk management

The risk of a given portfolio with allocation weight w is conventionally measured by its variance w′Σw, where Σ is the volatility (covariance) matrix of the returns of underlying assets. To estimate large portfolio’s risks, it needs to estimate a large covariance matrix Σ and factor models are frequently used to reduce the dimensionality. This was the idea of Fan, Liao and Shi (2015) in which they used POET estimator to estimate Σ. However, the basic method for bounding the risk error |w′Σ̂w − w′Σw| in their paper is

$$|\mathbf{w}\prime \hat{\mathbf{\Sigma }}\mathbf{w}-\mathbf{w}\prime \mathbf{\Sigma }\mathbf{w}|\le {\Vert \mathbf{w}\Vert }_1^2{\Vert \hat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}.$$

They assumed that the gross exposure of the portfolio is bounded, i.e. ‖w‖₁ = O(1). Technically, when p is large, w′Σw can be small. What an investor cares mostly is the relative risk error RE(w) = |w′Σw/w′Σw − 1|. Often w is a data-driven investment strategy, which depends on the past data. Regardless of what w is,

$$\underset{\mathbf{w}}{\text{max}}\mathrm{R}\mathrm{E}(\mathbf{w})={\Vert \hat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\mathbf{\Sigma }},$$

which does not converge by Theorem 4.1 for p > T. Thus the question of interest is what kind of portfolio w will make the relative error converge. Decompose w as a linear combination of the eigenvectors of Σ, namely w = (Γ, Ω)η and $\mathit{\eta }=({\mathit{\eta }}_A^{\prime },{\mathit{\eta }}_B^{\prime })\prime$. We have the following useful result for risk management.

Theorem 4.2

Under Assumptions 2.1, 2.2, 4.1,4.2 and the factor model (4.1) with Gaussian noises and factors, if there exists C₁ > 0 such that ‖η_B‖₁ ≤ C₁, and assume λ_j ∝ p^α for j = 1, …, m and T ≥ Cp^β for α > 1/2, 0 < β < 1, α + β > 1, then the relative risk error is of order

$$\mathrm{R}\mathrm{E}(\mathbf{w})=|\frac{\mathbf{w}\prime {\hat{\mathbf{\Sigma }}}^S\mathbf{w}}{\mathbf{w}\prime \mathbf{\Sigma }\mathbf{w}}-1|=O_P(T^{-\text{min}\{\frac{2(\alpha +\beta -1)}{\beta },\frac{1}{2}\}}+m_p{w}_T^{1-q}),$$

for α < 1. If α ≥ 1 or ‖η_A‖ ≥ C₂, $\mathrm{R}\mathrm{E}(\mathbf{w})=O_P(m_p{w}_T^{1-q})$.

The condition ‖η_B‖₁ ≤ C₁ is generally weaker than ‖w‖₁ = O(1). It does not limit the total exposure of investor’s position, but only put constraint on investment of the non-spiked section. Note that under the conditions of Theorem 4.2, p/(Tλ_j) → 0, and S-POET and POET are approximately the same. So the stated result is valid for POET too.

4.4. Estimation of false discovery proportion

Another important application of the factor model is the estimation of false discovery proportion. For simplicity, we assume Gaussian data X_i ~ N(μ, Σ) with an unknown correlation matrix Σ and wish to test which coordinates of μ are nonvanishing. Consider the test statistic $\mathbf{Z}=\sqrt{n}\overline{\mathbf{X}}$ where X̄ is the sample mean of all data. Then Z ~ N(μ*, Σ) with ${\mathit{\mu }}^{*}=\sqrt{n}\mathit{\mu }$. The problem is to test

$$H_{0j}:{\mu }_j^{*}=0\hspace{1em}\mathrm{v}.\mathrm{s}.\hspace{1em}{H}_{1j}:{\mu }_j^{*}\ne 0.$$

Define the number of discoveries R(t) = #{j : P_j ≤ t} and the number of false discoveries V(t) = #{true null : P_j ≤ t}, where P_j is the p-value associated with the j^th test. Note that R(t) is observable while V(t) needs to be estimated. The false discovery proportion (FDP) is defined as FDP(t) = V(t)/R(t).

Fan and Han (2013) proposed to employ the factor structure

$$\mathbf{\Sigma }=\mathbf{B}\mathbf{B}\prime +\mathbf{A},$$ (4.12)

where $\mathbf{B}=(\sqrt{{\lambda }_1}{\mathit{\xi }}_1,\dots ,\sqrt{{\lambda }_m}{\mathit{\xi }}_m)$. λ_j and ξ_j are respectively the j^th eigenvalue and eigenvector of Σ as before. Then Z can be stochastically decomposed as

$$\mathbf{Z}={\mathit{\mu }}^{*}+\mathbf{B}\mathbf{W}+\mathbf{K},$$

where W ~ N(0, I_m) are m common factors and K ~ N(0, A), independent of W, are the idiosyncratic errors. For simplicity, assume the maximal number of nonzero elements of each row of A is bounded. In Fan and Han (2013), they argued that the asymptotic upper bound

$$\mathrm{F}\mathrm{D}{\mathrm{P}}_A(t)=\sum _{i=1}^p[\mathrm{\Phi }(a_i(z_{t/2}+{\eta }_i))+\mathrm{\Phi }(a_i(z_{t/2}-{\eta }_i))]/R(t)$$ (4.13)

of FDP(t) should be a realistic target to estimate for dependence tests, where z_t/2 is the t/2-quantile of the standard normal distribution a_i = (1 − ‖b_i‖²)^−1/2, ${\eta }_i={\mathbf{b}}_i^{\prime }\mathbf{W}$ and ${\mathbf{b}}_i^{\prime }$ is the i^th row of B.

Realized factors W and the loading matrix B are typically unknown. If a generic estimator Σ̂ is provided, then we are able to estimate B and thus b_i from its empirical eigenvalues and eigenvectors λ̂_j’s and ξ̂_j’s. W can be estimated by the least-squares estimate Ŵ = (B̂′B̂)⁻¹B̂′Z. Fan and Han (2013) proposed the following estimator for FDP_A(t):

$${\widehat{\mathrm{F}\mathrm{D}\mathrm{P}}}_U(t)=\sum _{i=1}^p[\mathrm{\Phi }({â}_i(z_{t/2}+{\hat{\eta }}_i))+\mathrm{\Phi }({â}_i(z_{t/2}-{\hat{\eta }}_i))]/R(t),$$ (4.14)

where â_i = (1 − ‖b̂_i‖²)^−1/2 and ${\hat{\eta }}_i={\hat{\mathbf{b}}}_i^{\prime }\mathbf{Ŵ}$. The following assumptions are in their paper.

Assumption 4.3

There exists a constant h > 0 such that (i) R(t)/p > hp^−θ for h > 0 and θ ≥ 0 as p → ∞ and (ii) â_i ≤ h, a_i ≤ h for all i = 1, …, p.

They showed that if Σ̂ is based on the POET estimator with a spike size λ_m ≍ p, under Assumptions ?? - ??, on the event that Assumption 4.3 holds,

$$|{\widehat{\mathrm{F}\mathrm{D}\mathrm{P}}}_{U,POET}(t)-\mathrm{F}\mathrm{D}{\mathrm{P}}_A(t)|=O_P\left(p^{\theta }\right(\sqrt{\frac{\text{log }p}{T}}+\frac{\Vert {\mathit{\mu }}^{*}\Vert }{\sqrt{p}}\left)\right).$$ (4.15)

Again we can relax the assumption on the spike magnitude from order p to much weaker Assumption 4.1. Since Σ is a correlation matrix, λ₁ ≤ tr(Σ) = p. This, together with Assumption 4.1, leads us to consider leading eigenvalues of order p^α for 1/2 < α ≤ 1.

Now we apply the proposed S-POET method to obtain Σ̂^S and use it for FDP estimation. The following theorem shows the estimation error.

Theorem 4.3

If Assumptions 2.1, 2.2, 4.1, and 4.2 are applied to Gaussian independent data X_i ~ N(μ, Σ), and λ_j ∝ p^α for j = 1, …, m, T ≥ Cp^β for 1/2 < α ≤ 1, 0 < β < 1, α + β > 1, on the event that Assumption 4.3 holds, we have

$$|{\widehat{FDP}}_{U,SPOET}(t)-FD{P}_A(t)|=O_P\left(p^{\theta }\right(\Vert {\mathit{\mu }}^{*}\Vert p^{-\frac{1}{2}}+T^{-\text{min}\{\frac{\alpha +\beta -1}{\beta },\frac{1}{2}\}}\left)\right).$$

Comparing the result with (4.15), this convergence rate attained by S-POET is more general than the rate achieved before. The only difference is the second term, which is O(T^−1/2) if $\alpha +\frac{1}{2}\beta \ge 1$ and T^{−(α + β−1)/β} otherwise. So we relax the condition from α = 1 in Fan and Han (2013) to α ∈ (1/2, 1]. This means a weaker signal than order p is actually allowed to obtain a consistent estimate of false discovery proportion.

5. Simulations

We conducted some simulations to demonstrate the finite sample behavior of empirical eigen-structure, the performance of S-POET, and validity of applying it to estimate false discovery proportion.

5.1. Eigen-structure

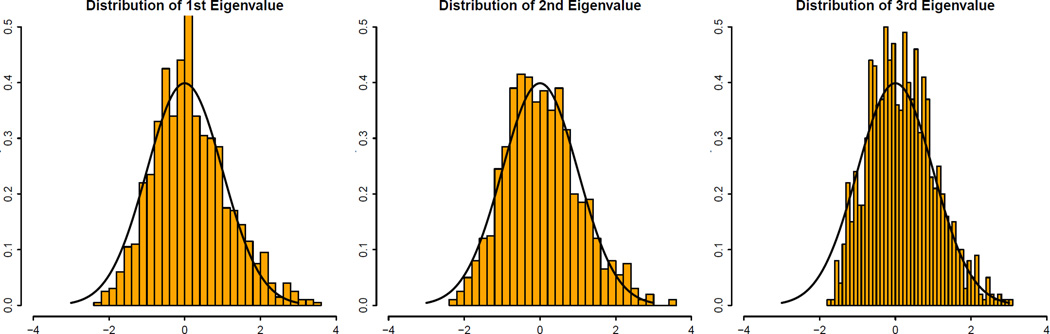
In this simulation, we set n = 50, p = 500 and Σ = diag(50, 20, 10, 1, …, 1), which has three spike eigenvalues (m = 3) λ₁ = 50, λ₂ = 20, λ₃ = 10 and correspondingly c₁ = 0.2, c₂ = 0.5, c₃ = 1. Data was generated from multivariate Gaussian. The number of simulations is 1000. The histograms of the standardized empirical eigenvalues $\sqrt{n/2}({\hat{\lambda }}_j/{\lambda }_j-1-c_j)$, and their associated asymptotic distributions (standard normal) are plotted in Figure 1. The approximations are very good even for this low sample size n = 50.

Fig 1.

Behavior of empirical eigenvalues. The empirical distributions of $\sqrt{n/2}({\hat{\lambda }}_j/{\lambda }_j-1-c_j)$ for j = 1, 2, 3 are compared with their asymptotic distributions N(0, 1).

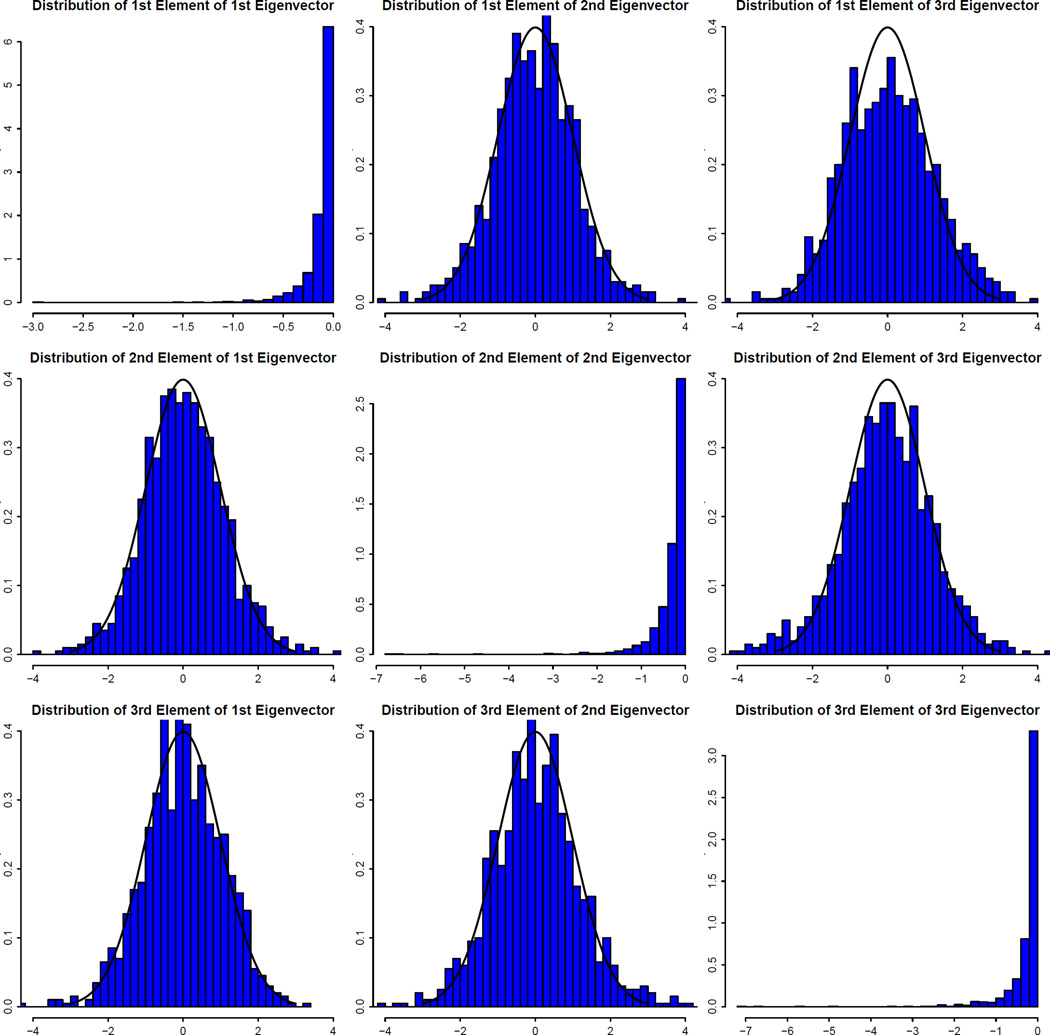
Figure 2 shows the histograms of $\sqrt{n}({\hat{\mathit{\xi }}}_{jA}/\Vert {\hat{\mathit{\xi }}}_{jA}\Vert -{\mathbf{e}}_{jA})$ for the first three elements (the spiked part) of the first three eigenvectors. On the one hand, according to the asymptotic results, the values in the diagonal position should stochastically converge to 0 as observed. On the other hand, plots in the off-diagonal positions should converge in distribution to N(0, 1) for k ≠ j after standardization, which is indeed the case. We also report the correlations between the first three elements for the three eigenvectors based on those 1000 repetitions in Table 1. The correlations are all quite close to 0, which is consistent with the theory.

Fig 2.

Behavior of empirical eigenvectors. The histogram of the k^th element of the j^th empirical vector is depicted in the location (k, j) for k, j ≤ 3. Off-diagonal plots of values $\sqrt{n}{\hat{\xi }}_{jk}/\Vert {\hat{\mathit{\xi }}}_{jA}\Vert /\sqrt{\frac{c_j{c}_k}{{(c_j-c_k)}^2}}$ are compared to their asymptotic distributions N(0, 1) for k ≠ j while diagonal plots of values $\sqrt{n}({\hat{\xi }}_{jj}/\Vert {\hat{\mathit{\xi }}}_{jA}\Vert -1)$ are compared to stochastically 0.

Table 1.

The correlations between the first three elements for each of the three empirical eigenvectors based on 1000 repetitions

	1st & 2nd elements	1st & 3rd elements	2nd & 3rd elements
1st Eigenvector	0.00156	−0.00192	−0.04112
2nd Eigenvector	−0.02318	−0.00403	0.01483
3rd Eigenvector	−0.02529	−0.04004	0.12524

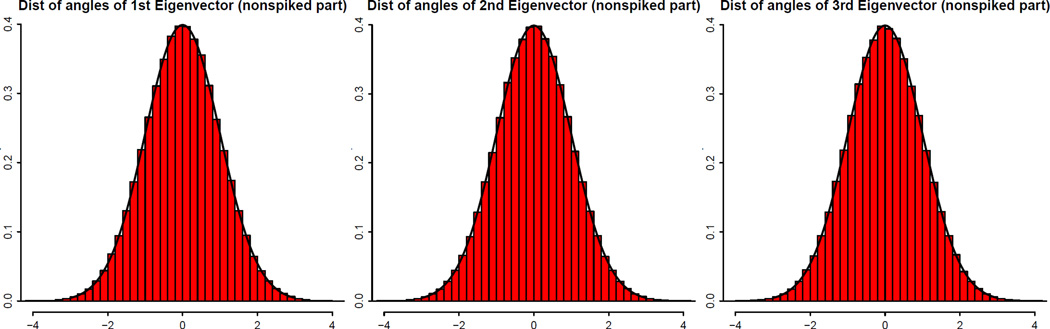
For the normalized non-spiked part ξ̂_jB/‖ξ̂_jB‖, it should be distributed uniformly over the unit sphere. This can be tested by the results of Cai, Fan and Jiang (2013). For any n data points X₁, …, X_n on a p-dimensional sphere, define the normalized empirical distribution of angles of each pair of vectors as

$${\mu }_{n,p}=\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i<j\le n}{\delta }_{\sqrt{p-2}(\pi /2-{\mathrm{\Theta }}_{ij})},$$

where Θ_ij ∈ [0, π] is the angle between vectors X_i and X_j. When the data are generated uniformly from a sphere, μ_n,p converges to the standard normal distribution with probability 1. Figure 3 shows the empirical distributions of all pairwise angles of the realized ξ̂_jB/‖ξ̂_jB‖ (j = 1, 2, 3) in 1000 simulations. Since number of such pairwise angels is $\left(\begin{array}{c}\hfill 1000\hfill \\ \hfill 2\hfill \end{array}\right)$, the empirical distributions and the asymptotic distributions N(0, 1) are almost identical. The normality holds even for a small subset of the angles.

Fig 3.

The empirical distributions of all pairwise angles of the 1000 realized ξ̂_jB/‖ξ̂_jB‖ (j = 1, 2, 3) compared with their asymptotic distributions N(0, 1).

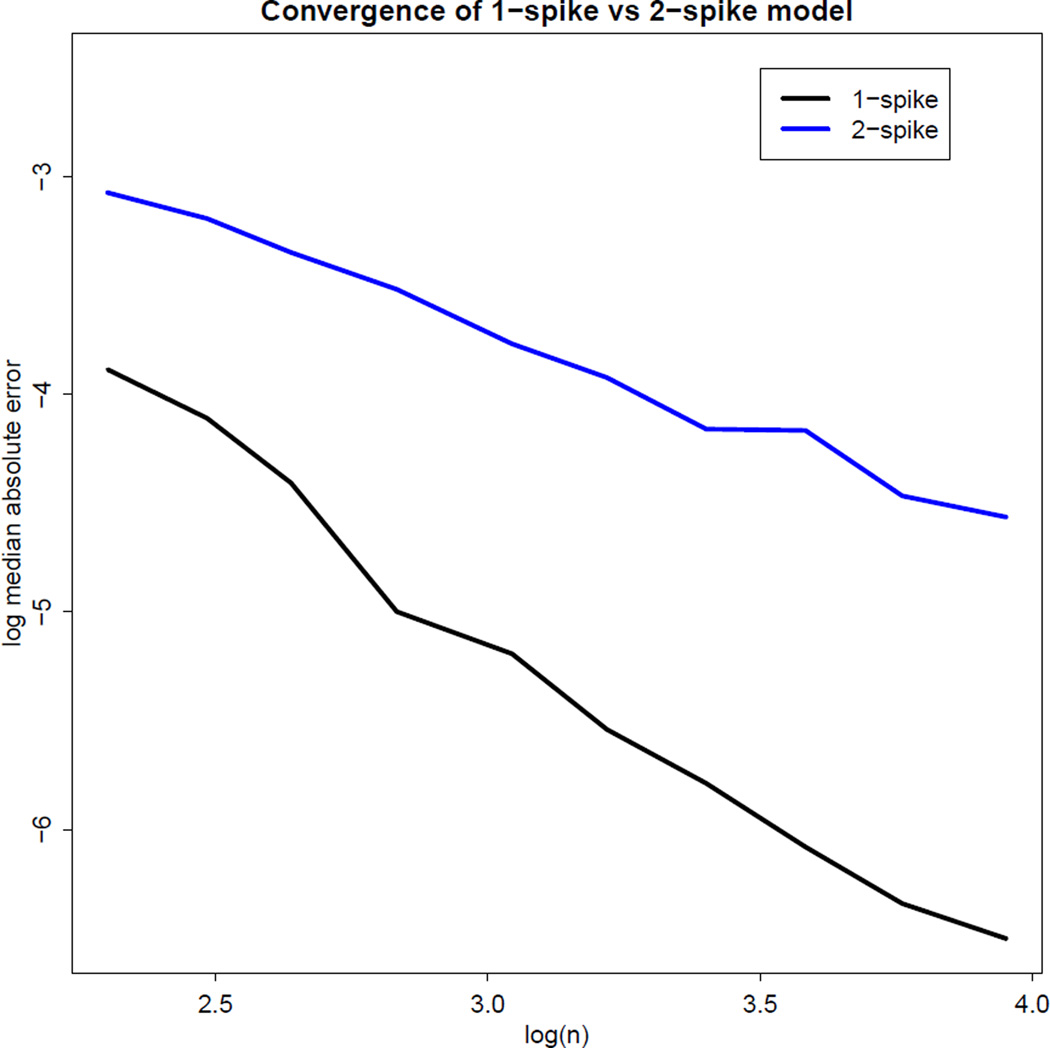
Lastly, we did simulations to verify the rate difference of 〈ξ̂_j, e_j〉 for m = 1 and m > 1, revealed in Theorem 3.2 (iii). We choose n = [10 × 1.2^l] for l = 0, …, 9, p = [n³/100], where [·] represents rounding. We set λ_j = 1 for j ≥ 3 and consider two situations: (1) λ₁ = p, λ₂ = 1, (2) λ₁ = 2λ₂ = p. Under both cases, simulations were carried out 500 times and the corresponding angle of the empirical eigenvector and its truth was calculated for each simulation. The logarithm of the median absolute error of $\langle {\hat{\mathit{\xi }}}_1,{\mathbf{e}}_1\rangle -1/\sqrt{1+c_1}$ was plotted against log(n). Under the two situations, the rates of convergence are O_P(n^−3/2) and O_P(n⁻¹) respectively. Thus the slope of the curves should be −3/2 for a single spike and −1 for two spikes, which is indeed the case as shown in Figure 4.

Fig 4.

Difference of convergence rate of $\langle {\hat{\mathit{\xi }}}_1,{\mathbf{e}}_1\rangle -1/\sqrt{1+c_1}$ for models with a single spike and two spikes. The error should be expected to decrease at the rate of O_P(n^−3/2) and O_P(n⁻¹) respectively.

In short, all the simulation results match well with the theoretical results for the high dimensional regime.

5.2. Performance of S-POET

We demonstrate the effectiveness of S-POET in comparison with POET. A similar setting to the last section is used, i.e. m = 3 and c₁ = 0.2, c₂ = 0.5, c₃ = 1. The sample size T ranges from 50 to 150 and p = [T^3/2]. Note that when T = 150, p ≈ 1800. The spiked eigenvalues are determined from p/(Tλ_j) = c_j so that λ_j is of order $\sqrt{T}$, which is much smaller than p. For each pair of T and p, the following steps are used to generate observed data from the factor model for 200 times.

1. Each row of B is simulated from the standard multivariate normal distribution and the j^th column is normalized to have norm λ_j for j = 1, 2, 3.

2. Each row of F is simulated from standard multivariate normal distribution.

3. Set ${\mathbf{\Sigma }}_u=\text{diag}({\sigma }_1^2,\dots ,{\sigma }_p^2)$ where σ_i’s are generated from Gamma(α, β) with α = β = 100 (mean 1, standard deviation 0.1). The idiosyncratic error U is simulated from N(0, Σ_u).

4. Compute the observed data Y = BF′ + U.

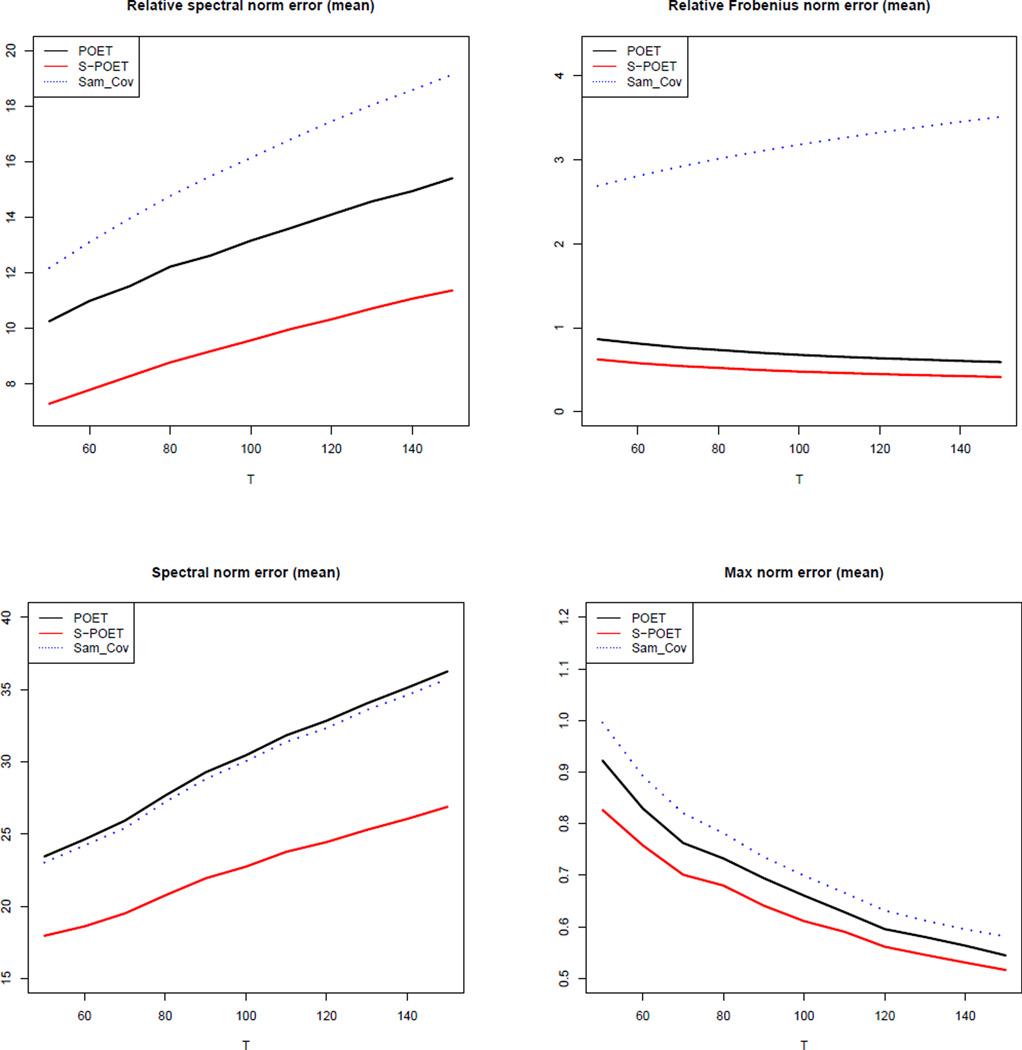
Both S-POET and POET are applied to estimate the covariance matrix Σ = BB′ + Σ_u. Their mean estimation errors over 200 simulations, measured in relative spectral norm ‖Σ̂ − Σ‖_Σ, relative Frobenius norm ‖Σ̂ − Σ‖_Σ,F, spectral norm ‖Σ̂ − Σ‖ and max norm ‖Σ̂ − Σ‖_max, are reported in Figure 5. The errors for sample covariance matrix are also depicted for comparison. First notice that no matter in what norm, S-POET uniformly outperforms POET and the sample covariance. It affirms the claim that shrinkage of spiked eigenvalues is necessary to maintain good performance when the spikes are not sufficiently large. Since the low rank part is not shrunk for POET, its error under the spectral norm is comparable and even slightly larger than that of the sample covariance matrix. The errors under max norm and relative Frobenius norm as expected decrease as T and p increase. However the error under the relative spectral norm does not converge: our theory shows it should increase in the order $p/T=\sqrt{T}$.

Fig 5.

Estimation errors of covariance matrix under relative spectral, relative Frobenius, spectral and max norms using S-POET (red), POET (black) and sample covariance (blue).

5.3. FDP estimation

In this section, we report simulation results on FDP estimation by using both POET and S-POET. The data are simulated in a similar way as in Section 5.2 with p = 1000 and n = 100. The first m = 3 eigenvalues have spike size proportional to $p/\sqrt{n}$ which corresponds to α = β = 2/3 in Theorem 4.3. The true FDP is calculated by using FDP(t) = V (t)/R(t) with t = 0.01. The approximate FDP, FDP_A(t), is calculated as in (4.13) with known B but estimated W given by Ŵ = (BB′)⁻¹B′Z. This FDP_A(t) based on a known covariance matrix serves as a benchmark for our estimated covariance matrix to compare with. We employed POET and S-POET to get ${\widehat{\mathrm{F}\mathrm{D}\mathrm{P}}}_{U,POET}(t)$ and ${\widehat{\mathrm{F}\mathrm{D}\mathrm{P}}}_{U,SPOET}(t)$.

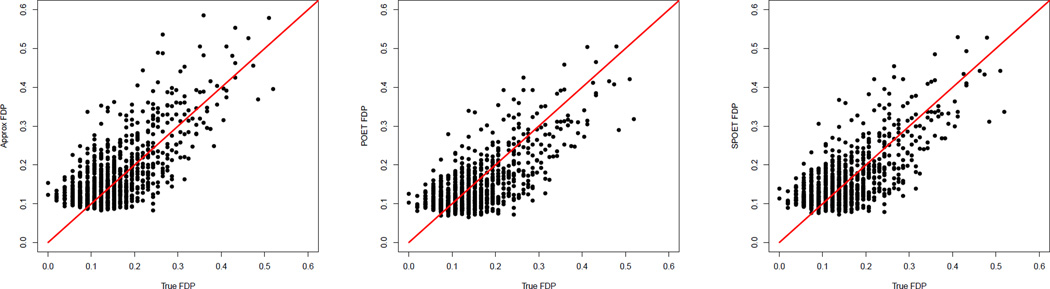
In Figure 6, three scatter plots are drawn to compare FDP_A(t), ${\widehat{\mathrm{F}\mathrm{D}\mathrm{P}}}_{U,POET}(t)$ and ${\widehat{\mathrm{F}\mathrm{D}\mathrm{P}}}_{U,SPOET}(t)$ with the true FDP(t). The points are basically aligned along the 45 degree line, meaning that all of them are quite close to the true FDP. With the semi-strong signal $\lambda \propto p/\sqrt{n}$, although much weaker than order p, POET accomplishes the task as well as S-POET. Both estimators perform as well as if we know the covariance matrix Σ, the benchmark.

Fig 6.

Comparison of estimated FDP’s with true values. The left plot assumes knowledge of B, the middle and right ones are corresponding to POET and S-POET methods respectively. The results are aligned along the 45-degree line, indicating the accuracy of the estimated FDP.

6. Conclusions

In this paper, we studied two closely related problems: the asymptotic behavior of empirical eigenvalues and eigenvectors under a general regime of bounded p/(nλ_j) and the large covariance estimation for factor models with relaxed signal level of $\sqrt{p}=o({\lambda }_j)$.

The first study provides new technical tools for the derivation of error bounds for large covariance estimation under relative Frobenius norm (with better rate) and relative spectral norm (for the first time). The results motivate the new proposed covariance estimator S-POET for the second problem by correcting biases of the estimated leading eigenvalues. S-POET is demonstrated to have better sampling properties than POET, and this is convincingly verified in the simulation study. In addition, we are able to apply S-POET to two important applications, risk management and false discovery control, and relax the required signal to $\sqrt{p}$. Those conclusions shed new lights for applications of factor models.

On the other hand, the second problem is a key motivation for us to study the empirical engen-structure in a more general high dimensional regime. We aim to understand why PCA works for pervasive factor models but fails classical random matrix problems, without sparsity assumptions. What are the fundamental limit for the PCA in high dimension? We clearly showed that for both empirical eigenvalues and vectors, consistency is granted once p/(nλ_j) → 0. Further, our theories give a fine-grained characterization of the asymptotic behavior under the generalized and unified regime, which includes the situation of bounded eigenvalues, HDLSS, and pervasive factor models, especially for empirical eigenvectors. The asymptotic rate of convergence is obtained as long as p/(nλ_j) is bounded, while the asymptotic distribution is fully described when $\sqrt{p}=o({\lambda }_j)$. Some interesting phenomena, such as interaction between multiple spikes, are also revealed in our results. Our proofs are novel in that we clearly identify terms that keep the low-dimensional asymptotic normality and terms that generate the random biases. In sum, our results serve as a necessary complement of the random matrix literature when the signal diverges with dimensionality.

APPENDIX A

PROOFS FOR SECTION 3

A.1. Proof of Theorem 3.1

We first provide three useful lemmas for the proof. Lemma A.1 provides non-asymptotic upper and lower bound for the eigenvalues of weighted Wishart matrix for sub-Gaussian distributions.

Lemma A.1

Let A₁, …, A_n’s be n independent p dimensional sub-Gaussian random vectors with zero mean and identity variance, and the sub-Gaussian norms bounded by a constant C₀. Then for every t ≥ 0, with probability at least 1 − 2 exp(−ct²), one has

$$\overline{w}-\text{max}\{\delta ,{\delta }^2\}\le {\lambda }_p\left(\frac{1}{n}\sum _{i=1}^n{w}_i{\mathbf{A}}_i{\mathbf{A}}_i^{\prime }\right)\le {\lambda }_1\left(\frac{1}{n}\sum _{i=1}^n{w}_i{\mathbf{A}}_i{\mathbf{A}}_i^{\prime }\right)\le \overline{w}+\text{max}\{\delta ,{\delta }^2\}.$$

where $\delta =C\sqrt{p/n}+t/\sqrt{n}$ for constants C, c > 0, depending on C₀. Here |w_i|’s is bounded for all i and $\overline{w}=n^{-1}{\sum }_{i=1}^n{w}_i$.

The above lemma is the extension of the classical Davidson-Szarek bound [Theorem II.7 of Davidson and Szarek (2001)] to the weighted sample co-variance with sub-Gaussian distribution. It was shown by Vershynin (2010) that the conclusion holds with w_i = 1 for all i. With similar techniques to those developed in Vershynin (2010), we can obtain the above lemma for general bounded weights. The details are omitted.

Now in order to prove the theorem, let us define two quantities and treat them separately in the following two lemmas. Let

$$\mathbf{A}=n^{-1}\sum _{j=1}^m{\lambda }_j{\mathbf{Z}}_j{\mathbf{Z}}_j^{\prime },\text{ and }\mathbf{B}=n^{-1}\sum _{j=m+1}^p{\lambda }_j{\mathbf{Z}}_j{\mathbf{Z}}_j^{\prime },$$

where Z_j is columns of $\mathbf{X}{\mathbf{\Lambda }}^{-\frac{1}{2}}$. Then,

$$\tilde{\mathbf{\Sigma }}=\frac{1}{n}\sum _{j=1}^p{\lambda }_j{\mathbf{Z}}_j{\mathbf{Z}}_j^{\prime }=\mathbf{A}+\mathbf{B}.$$ (A.1)

Lemma A.2

Under Assumptions 2.1 – 2.3, as n → ∞,

$$\sqrt{n}({\lambda }_j(\mathbf{A})/{\lambda }_j-1)\stackrel{d}{\Rightarrow }N(0,{\kappa }_j-1),\mathit{\text{ for }}j=1,\dots ,m.$$

In addition, they are asymptotically independent.

Lemma A.3

Under Assumptions 2.1 – 2.3, for j = 1, ⋯, m, we have

$${\lambda }_k(\mathbf{B})/{\lambda }_j=\overline{c}{c}_j+O_P\left({\lambda }_j^{-1}\sqrt{p/n}\right)+o_P(n^{-\frac{1}{2}}),\mathit{\text{ for }}k=1,2,\dots ,n.$$

The proofs of the above two lemmas will be given in Appendix?? in the supplementary material (Wang and Fan, 2015).

Proof of Theorem 3.1

By Wely’s Theorem, λ_j(A) + λ_n(B) ≤ λ̂_j ≤ λ_j(A) + λ₁(B): Therefore from Lemma A.3,

$$\frac{{\hat{\lambda }}_j}{{\lambda }_j}=\frac{{\lambda }_j(\mathbf{A})}{{\lambda }_j}+\overline{c}{c}_j+O_P\left({\lambda }_j^{-1}\sqrt{\frac{p}{n}}\right)+o_P(c_j{n}^{-1/2}),$$

By Lemma A.2 and Slutsky’s theorem, we conclude that $\sqrt{n}({\hat{\lambda }}_j/{\lambda }_j-(1+\overline{c}{c}_j+O_P({\lambda }_j^{-1}\sqrt{p/n)}))$ converges in distribution to N(0, κ_j − 1) and the limiting distributions of the first m eigenvalues are independent.

A.2. Proofs of Theorem 3.2

The proof of Theorem 3.2 is mathematically involved. The basic idea for proving part (i) is outlined in Section 2. We relegate less important technical lemmas A.4 – A.6 to Appendix ?? in the supplementary material (Wang and Fan, 2015) in order not to distract the readers. The proof of part (ii) utilizes the invariance of standard Gaussian distribution under orthogonal transformations.

Proof of Theorem 3.2

(i) Let us start by proving the asymptotic normality of ξ̂_jA for the case m > 1. Write

$$\mathbf{X}=({\mathbf{Z}}_A{\mathbf{\Lambda }}_A^{\frac{1}{2}},{\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}})=(\sqrt{{\lambda }_1}{\mathbf{Z}}_1,\dots ,\sqrt{{\lambda }_m}{\mathbf{Z}}_m,\sqrt{{\lambda }_{m+1}}{\mathbf{Z}}_{m+1},\dots ,\sqrt{{\lambda }_p}{\mathbf{Z}}_p),$$

where each Z_j follows a sub-Gaussian distribution with mean 0 and identity variance I_n. Then by the eigenvalue relationship of equation (2.1), we have

$${\hat{\mathit{\xi }}}_{jA}=\frac{{\mathbf{\Lambda }}_A^{\frac{1}{2}}{\mathbf{Z}}_A^{\prime }{\mathbf{u}}_j}{\sqrt{n{\hat{\lambda }}_j}}\text{ and }{\mathbf{u}}_j=\frac{\mathbf{X}{\hat{\mathit{\xi }}}_j}{\sqrt{n{\hat{\lambda }}_j}}=\frac{{\mathbf{Z}}_A{\mathbf{\Lambda }}_A^{\frac{1}{2}}{\hat{\mathit{\xi }}}_{jA}}{\sqrt{n{\hat{\lambda }}_j}}+\frac{{\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}}{\hat{\mathit{\xi }}}_{jB}}{\sqrt{n{\hat{\lambda }}_j}}.$$ (A.2)

Recall u_j is the eigenvector of the matrix Σ̃, that is, $\frac{1}{n}\mathbf{X}\mathbf{X}\prime {\mathbf{u}}_j={\hat{\lambda }}_j{\mathbf{u}}_j$. Using $\mathbf{X}=({\mathbf{Z}}_A{\mathbf{\Lambda }}_A^{\frac{1}{2}},{\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}})$, we obtain

$$({\mathbf{I}}_n-\frac{1}{n}{\mathbf{Z}}_A\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}{\mathbf{Z}}_A^{\prime }){\mathbf{u}}_j=\mathbf{D}{\mathbf{u}}_j-\mathrm{\Delta }{\mathbf{u}}_j,$$ (A.3)

where we denote $\mathbf{D}={(n{\lambda }_j)}^{-1}{\mathbf{Z}}_B{\mathbf{\Lambda }}_B{\mathbf{Z}}_B^{\prime }-\overline{c}{c}_j{\mathbf{I}}_n$, Δ = λ̂_j/λ_j − (1 + c̄c_j). We then left-multiply equation (A.3) by ${\mathbf{\Lambda }}_A^{\frac{1}{2}}{\mathbf{Z}}_A^{\prime }/\sqrt{n{\hat{\lambda }}_j}$ and employ relationship (A.2) to replace u_j by ξ̂_jA and ξ̂_jB as follows:

$$({\mathbf{I}}_m-\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}){\hat{\mathit{\xi }}}_{jA}=\frac{{\mathbf{\Lambda }}_A^{\frac{1}{2}}(\frac{1}{n}{\mathbf{Z}}_A^{\prime }{\mathbf{Z}}_A-{\mathbf{I}}_m){\mathbf{\Lambda }}_A^{\frac{1}{2}}}{{\lambda }_j}{\hat{\mathit{\xi }}}_{jA}+\frac{{\mathbf{\Lambda }}_A^{\frac{1}{2}}{\mathbf{Z}}_A^{\prime }\mathbf{D}{\mathbf{Z}}_A{\mathbf{\Lambda }}_A^{\frac{1}{2}}}{n{\hat{\lambda }}_j}{\hat{\mathit{\xi }}}_{jA}+\frac{{\mathbf{\Lambda }}_A^{\frac{1}{2}}{\mathbf{Z}}_A^{\prime }\mathbf{D}{\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}}}{n{\hat{\lambda }}_j}{\hat{\mathit{\xi }}}_{jB}-\mathrm{\Delta }{\hat{\mathit{\xi }}}_{jA}.$$ (A.4)

Further define

$$\mathbf{R}=\sum _{k\in [m]\backslash j}\frac{{\lambda }_j}{{\lambda }_j-{\lambda }_k}{\mathbf{e}}_{kA}{\mathbf{e}}_{kA}^{\prime }.$$

Then we have $\mathbf{R}(\mathbf{I}-{\mathbf{\Lambda }}_A/{\lambda }_j)={\mathbf{I}}_m-{\mathbf{e}}_{jA}{\mathbf{e}}_{jA}^{\prime }$. Note that R is only well defined if m > 1. Therefore, by left multiplying R to equation (A.4),

$${\hat{\mathit{\xi }}}_{jA}-\langle {\hat{\mathit{\xi }}}_{jA},{\mathbf{e}}_{jA}\rangle {\mathbf{e}}_{jA}=\mathbf{R}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}\mathbf{K}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}{\hat{\mathit{\xi }}}_{jA}+\mathbf{R}\frac{{\mathbf{\Lambda }}_A^{\frac{1}{2}}{\mathbf{Z}}_A^{\prime }\mathbf{D}{\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}}}{n{\hat{\lambda }}_j}{\hat{\mathit{\xi }}}_{jB}-\mathrm{\Delta }\mathbf{R}{\hat{\mathit{\xi }}}_{jA},$$ (A.5)

where $\mathbf{K}=n^{-1}{\mathbf{Z}}_A^{\prime }{\mathbf{Z}}_A-{\mathbf{I}}_n+{\lambda }_j{(n{\hat{\lambda }}_j)}^{-1}{\mathbf{Z}}_A^{\prime }\mathbf{D}{\mathbf{Z}}_A$. Dividing both side by ‖ξ̂_jA‖, we are able to write

$$\frac{{\hat{\mathit{\xi }}}_{jA}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }-{\mathbf{e}}_{jA}=\mathbf{R}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}\mathbf{K}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}{\mathbf{e}}_{jA}+{\mathbf{r}}_n,$$ (A.6)

where

$${\mathbf{r}}_n=(\langle \frac{{\hat{\mathit{\xi }}}_{jA}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert },{\mathbf{e}}_{jA}\rangle -1){\mathbf{e}}_{jA}+\mathbf{R}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}\mathbf{K}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}(\frac{{\hat{\mathit{\xi }}}_{jA}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }-{\mathbf{e}}_{jA})+\mathbf{R}\frac{{\mathbf{\Lambda }}_A^{\frac{1}{2}}{\mathbf{Z}}_A^{\prime }\mathbf{D}{\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}}}{n{\hat{\lambda }}_j}\frac{{\hat{\mathit{\xi }}}_{jB}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }-\mathrm{\Delta }\mathbf{R}(\frac{{\hat{\mathit{\xi }}}_{jA}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }-{\mathbf{e}}_{jA}).$$ (A.7)

Lemma A.4

As n → ∞, $\Vert {\mathbf{r}}_n\Vert =O_P({\lambda }_j^{-1}\sqrt{p/n}+1/n)$.

By Lemma A.4, r_n is a smaller order term. Since ${({\mathbf{\Lambda }}_A/{\lambda }_j)}^{\frac{1}{2}}{\mathbf{e}}_{jA}={\mathbf{e}}_{jA}$,

$$\sqrt{n}(\frac{{\hat{\mathit{\xi }}}_{jA}}{\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }-{\mathbf{e}}_{jA}+O_P(\sqrt{\frac{p}{n{\lambda }_j^2}}\left)\right)=\sqrt{n}\mathbf{R}{\left(\frac{{\mathrm{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}\mathbf{K}{\mathbf{e}}_{jA}+o_P(1).$$ (A.8)

Now let us derive normality of the right hand side of (A.8). According to the definition of R,

$$\mathbf{R}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}=\sum _{k\in [m]\backslash j}\frac{\sqrt{{\lambda }_j{\lambda }_k}}{{\lambda }_j-{\lambda }_k}{\mathbf{e}}_{kA}{\mathbf{e}}_{kA}^{\prime }\to \sum _{k\in [m]\backslash j}{a}_{jk}{\mathbf{e}}_{kA}{\mathbf{e}}_{kA}^{\prime }.$$ (A.9)

Let $\mathbf{W}=\sqrt{n}\mathbf{K}{\mathbf{e}}_{jA}=(W_1,\dots ,W_m)$ and W^(−j) be the (m − 1)-dimensional vector without the j^th element in W. Since the j^th diagonal element of R is zero, $\mathbf{R}{({\mathbf{\Lambda }}_A/{\lambda }_j)}^{\frac{1}{2}}\mathbf{W}$ depends only on W^(−j).

Lemma A.5

${\mathbf{W}}^{(-j)}+O_P({\lambda }_j^{-1}\sqrt{p/n})\stackrel{d}{\Rightarrow }N(\mathbf{0},{\mathbf{I}}_{\mathbf{m}-\mathbf{1}})$.

Therefore, by Lemma A.5 and Slutsky’s theorem,

$$\sqrt{n}\mathbf{R}{\left(\frac{{\mathbf{\Lambda }}_A}{{\lambda }_j}\right)}^{\frac{1}{2}}\mathbf{K}{\mathbf{e}}_{jA}+O_P\left(\sqrt{\frac{p}{n{\lambda }_j^2}}\right)\stackrel{d}{\Rightarrow }{N}_m(\mathbf{0},\sum _{k\in [m]\backslash j}{a}_{jk}^2{\mathbf{e}}_{kA}{\mathbf{e}}_{kA}^{\prime }).$$

Together with (A.8), we concludes (3.3) for the case m > 1.

Now let us turn to the case of m = 1. Since R is not defined for m = 1, we need to find a different derivation. Equivalently, (A.3) can be written as

$$\frac{1}{n}{\mathbf{Z}}_1{\mathbf{Z}}_1^{\prime }{\mathbf{u}}_1+\frac{1}{n{\lambda }_1}{\mathbf{Z}}_B{\mathbf{\Lambda }}_B{\mathbf{Z}}_B^{\prime }{\mathbf{u}}_1=\frac{{\hat{\lambda }}_1}{{\lambda }_1}{\mathbf{u}}_1.$$

Left-multiplying ${\mathbf{u}}_1^{\prime }$ and using relationship (A.2), we obtain easily

$${\hat{\xi }}_{1A}^2=1-\frac{\overline{c}{c}_1}{{\hat{\lambda }}_1/{\lambda }_1}-\frac{{\lambda }_1}{{\hat{\lambda }}_1}{\mathbf{u}}_1^{\prime }\mathbf{D}{\mathbf{u}}_1=1-\frac{\overline{c}{c}_1}{{\hat{\lambda }}_1/{\lambda }_1}+O_P({\lambda }_1^{-1}\sqrt{p/n}),$$

where D is defined as before and $\Vert \mathbf{D}\Vert =O_P({\lambda }_1^{-1}\sqrt{p/n})$ according to the proof of Lemma A.4. Expanding $\sqrt{1-\overline{c}{c}_1/x}$ at the point of (1 + c̄c₁), we have

$${\hat{\xi }}_{1A}=\frac{1}{\sqrt{1+\overline{c}{c}_1}}+\frac{\overline{c}{c}_1}{2{(1+\overline{c}{c}_1)}^{3/2}}({\hat{\lambda }}_1/{\lambda }_1-(1+\overline{c}{c}_1))+O_P(\sqrt{\frac{p}{n{\lambda }_1^2}}+c_1{n}^{-1}).$$

Note that from Lemmas A.2 and A.3, ${\hat{\lambda }}_1/{\lambda }_1-(1+\overline{c}{c}_1)=({\Vert {\mathbf{Z}}_1\Vert }^2/n-1)+O_P({\lambda }_1^{-1}{(p/n)}^{1/2})+o_P(c_j{n}^{-1/2})$. Therefore due to the fact $\sqrt{n}({\Vert {\mathbf{Z}}_1\Vert }^2/n-1)$ is asymptotically N(0, κ₁ − 1), we conclude

$$\frac{2{(1+\overline{c}{c}_1)}^{3/2}}{\overline{c}{c}_1}\sqrt{n}({\hat{\xi }}_{1A}-\frac{1}{\sqrt{1+\overline{c}{c}_1}}+O_P(\sqrt{\frac{p}{n{\lambda }_1^2}}\left)\right)\stackrel{d}{\Rightarrow }N(0,{\kappa }_1-1).$$

This completes the first part of the proof.

(ii) We now prove the conclusion for the non-spiked part ξ̂_jB. Recall that X_i follows N(0, Λ). Consider ${\mathbf{X}}_i^R=\text{diag}({\mathbf{I}}_m,{\mathbf{D}}_0){\mathbf{X}}_i$ where as defined in the theorem ${\mathbf{D}}_0=\text{diag}(\sqrt{\overline{c}/{\lambda }_{m+1}},\dots ,\sqrt{\overline{c}/{\lambda }_p})$. Here the superscript R indicates rescaled data by diag(I_m, D₀). After rescaling, we have ${\mathbf{X}}_i^R~N(\mathbf{0},\text{diag}({\mathbf{\Lambda }}_A,\overline{c}{\mathbf{I}}_{p-m}))$. Correspondingly, the n × p data matrix X^R = X diag(I_m, D₀) = (X_A, X_BD₀) where ${\mathbf{X}}_A={\mathbf{Z}}_A{\mathbf{\Lambda }}_A^{\frac{1}{2}}$ and ${\mathbf{X}}_B={\mathbf{Z}}_B{\mathbf{\Lambda }}_B^{\frac{1}{2}}$ as the notations before. Assume ${\hat{\mathbf{\xi }}}_j^R$ and ${\mathbf{u}}_j^R$ are eigenvectors given by Σ̂^R and Σ̃^R of the rescaled data X^R and ${\hat{\mathit{\xi }}}_j^R=({\hat{\mathit{\xi }}}_{jA}^R,{\hat{\mathit{\xi }}}_{jB}^R)\prime$. It has been proved by Paul (2007) that ${\mathbf{h}}_0≔{\hat{\mathit{\xi }}}_{jB}^R/\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert$ is distributed uniformly over the unit sphere and is independent of $\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert$ due to the orthogonal invariance of the non-spiked part of ${\hat{\mathit{\xi }}}_{jB}^R$. Hence it only remains to link ξ̂_jB/‖ξ̂_jB‖ with h₀.

Note that Σ̃ = n⁻¹XX′ and Σ̃^R = n⁻¹X^RX^R′, so

$$\Vert \tilde{\mathbf{\Sigma }}-{\tilde{\mathbf{\Sigma }}}^R\Vert =\Vert \frac{1}{n}{\mathbf{X}}_B(\mathbf{I}-{\mathbf{D}}_0^2){\mathbf{X}}_B^{\prime }\Vert =\Vert \frac{1}{n}\sum _{j=m+1}^p({\lambda }_j-\overline{c}){\mathbf{Z}}_j{\mathbf{Z}}_j\Vert ,$$

where the last term is of order $O_P(\sqrt{p/n})$ by Lemma A.1. Thus by the sin θ theorem of Davis and Kahan (1970), $\Vert {\mathbf{u}}_j-{\mathbf{u}}_j^R\Vert =O_P({\lambda }_j^{-1}\sqrt{p/n})$. Next we convert from u_j to ξ̂_jB using the basic relationship (2.1). We have,

$$\Vert {\mathbf{D}}_0\frac{{\hat{\mathit{\xi }}}_{jB}}{\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }-\frac{{\hat{\mathit{\xi }}}_{jB}^R}{\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert }\Vert =\Vert \frac{{\mathbf{D}}_0{\mathbf{X}}_B^{\prime }{\mathbf{u}}_j}{\sqrt{n{\hat{\lambda }}_j}\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }-\frac{{\mathbf{D}}_0{\mathbf{X}}_B\prime {\mathbf{u}}_j^R}{\sqrt{n{\hat{\lambda }}_j^R}\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert }\Vert \le \Vert \frac{{\mathbf{D}}_0{\mathbf{X}}_B^{\prime }{\mathbf{u}}_j}{\sqrt{n{\lambda }_j}}\Vert |\sqrt{\frac{{\lambda }_j}{{\hat{\lambda }}_j{\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }^2}}-\sqrt{\frac{{\lambda }_j}{{\hat{\lambda }}_j^R{\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert }^2}}|+\Vert \frac{{\mathbf{D}}_0{\mathbf{X}}_B^{\prime }}{\sqrt{n{\hat{\lambda }}_j^R}\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert }\Vert \Vert {\mathbf{u}}_j-{\mathbf{u}}_j^R\Vert ≕I+II.$$

First it is not hard to see $II=O_P({\lambda }_j^{-1}\sqrt{p/n})$ since $\Vert {\mathbf{u}}_j-{\mathbf{u}}_j^R\Vert =O_P({\lambda }_j^{-1}\sqrt{p/n}),\Vert {\mathbf{X}}_B^{\prime }/\sqrt{n{\lambda }_j}\Vert =O_P(\sqrt{c_j}),{\lambda }_j/{\hat{\lambda }}_j^R=O_P(1)$ and $1/\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert =O_P(1/\sqrt{c_j})$. The last result is due to the following lemma.

Lemma A.6

$\Vert {\hat{\mathit{\xi }}}_{jA}\Vert ={(1+\overline{c}{c}_j)}^{-1/2}+O_P({\lambda }_j^{-1}\sqrt{p/n}+c_j{n}^{-1/2})$ and $\Vert {\hat{\mathit{\xi }}}_{jB}\Vert ={(\frac{\overline{c}{c}_j}{1+\overline{c}{c}_j})}^{1/2}+O_P(\sqrt{1/{\lambda }_j}+\sqrt{c_j}{n}^{-1/2})$.

We claim $I=O_P(\sqrt{n/p})+o_P(n^{-1/2})$. Actually from the proof of Lemma A.6, we have

$${\hat{\lambda }}_j{\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }^2/{\lambda }_j=\overline{c}{c}_j+O_P({\lambda }_j^{-1}\sqrt{p/n})+o_P(c_j{n}^{-1/2}).$$

Then some elementary calculation gives the rate of I. Therefore, $\Vert {\mathbf{D}}_0{\hat{\mathit{\xi }}}_{jB}/\Vert {\hat{\mathit{\xi }}}_{jB}\Vert -{\mathbf{h}}_0\Vert =O_P(\sqrt{n/p})+o_P(n^{-1/2})$. The conclusion (3.4) follows.

To prove the max norm bound (3.5) of ‖ξ̂_jB‖_max, we first show ${\Vert {\mathbf{h}}_0\Vert }_{\text{max}}=O_P(\sqrt{\text{log }p/p})$. Recall that h₀ is uniformly distributed on the unit sphere of dimension p − m. This follows easily from its normal representation. Let G to be (p − m)-dimensional multivariate standard normal distributed, then ${\mathbf{h}}_0\stackrel{d}{=}\mathbf{G}/\Vert \mathbf{G}\Vert$. It then follows

$${\Vert {\mathbf{h}}_0\Vert }_{\text{max}}=\underset{i\le p-m}{\text{max}}|G_i|/\Vert \mathbf{G}\Vert =O_P(\sqrt{\text{log }p/p}).$$

From the derivation above,

$${\Vert {\hat{\mathit{\xi }}}_{jB}\Vert }_{\text{max}}\le \sqrt{{\hat{\lambda }}_j^R/{\hat{\lambda }}_j}\Vert {\mathbf{D}}_0^{-1}\Vert \Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert (II+{\Vert {\mathbf{h}}_0\Vert }_{\text{max}}),$$

which gives $O_P(\sqrt{c_j}(\sqrt{p/(n{\lambda }_j^2})+\sqrt{\text{log }p/p}))=O_P(p/n{\lambda }_j^{3/2})+\sqrt{\text{log }p/(n{\lambda }_j))}$, given the fact that $\Vert {\hat{\mathit{\xi }}}_{jB}^R\Vert =O_P(\sqrt{c_j})$ by Lemma A.6. Thus we are done with the second part of the proof.

(iii) The proof for the convergence of ‖ξ̂_jA‖ and ‖ξ̂_jB‖ are given in Lemma A.6. If m = 1, the result for ‖ξ̂_jA‖ directly gives (3.6) with the same rate. For m > 1, from Lemma A.6 we have

$${\Vert {\hat{\mathit{\xi }}}_{jA}\Vert }^2={(1+\overline{c}{c}_j)}^{-1}+O_P(\sqrt{p/(n{\lambda }_j^2)}+c_j{n}^{-1/2}).$$

On the other hand, from Theorem 3.2 (i), ${\hat{\xi }}_{jk}^2=O_P(p/(n{\lambda }_j^2)+1/n)$ for k ≠ j ≤ m. So ${\hat{\xi }}_{j1}^2={(1+\overline{c}{c}_j)}^{-1}+O_P(\sqrt{p/(n{\lambda }_j^2)}+c_j{n}^{-1/2}+1/n)$, which implies (3.6).