Synergistic Cytotoxicity from Drugs and Cytokines In Vitro as an Approach to Classify Drugs According to Their Potential to Cause Idiosyncratic Hepatotoxicity: A Proof-of-Concept Study

Abstract

Idiosyncratic drug-induced liver injury (IDILI) typically occurs in a small fraction of patients and has resulted in removal of otherwise efficacious drugs from the market. Current preclinical testing methods are ineffective in predicting which drug candidates have IDILI liability. Recent results suggest that immune mediators such as tumor necrosis factor-α (TNF) and interferon-γ (IFN) interact with drugs that cause IDILI to kill hepatocytes. This proof-of-concept study was designed to test the hypothesis that drugs can be classified according to their ability to cause IDILI in humans using classification modeling with covariates derived from concentration-response relationships that describe cytotoxic interaction with cytokines. Human hepatoma (HepG2) cells were treated with drugs associated with IDILI or with drugs lacking IDILI liability and cotreated with TNF and/or IFN. Detailed concentration-response relationships were determined for calculation of parameters such as the maximal cytotoxic effect, slope, and EC₅₀ for use as covariates for classification modeling using logistic regression. These parameters were incorporated into multiple classification models to identify combinations of covariates that most accurately classified the drugs according to their association with human IDILI. Of 14 drugs associated with IDILI, almost all synergized with TNF to kill HepG2 cells and were successfully classified by statistical modeling. IFN enhanced the toxicity mediated by some IDILI-associated drugs in the presence of TNF. In contrast, of 10 drugs with little or no IDILI liability, none synergized with inflammatory cytokines to kill HepG2 cells and were classified accordingly. The resulting optimal model classified the drugs with extraordinary selectivity and specificity.

Introduction

Idiosyncratic drug-induced liver injury (IDILI) is a typically rare reaction that occurs at drug doses that are safe in the majority of patients. Cases of IDILI can be severe, leading to liver transplantation or death (Ostapowicz et al., 2002). In addition to public health concerns, IDILI is a common cause of removal of drugs from the pharmaceutical market due to the occurrence and severity of these reactions and to the poor ability of standard toxicity tests to identify drug candidates with IDILI liability before they reach the market (Watkins, 2005; Aithal et al., 2011). The causes of IDILI are unknown, but it is thought that genetic and/or environmental factors predispose patients to toxicity from an otherwise safe dose of a drug (Roth and Ganey, 2011). Because these reactions are usually rare, drugs with IDILI potential are often not identified during clinical trials that employ limited numbers of human subjects. More effective preclinical strategies to identify drug candidates with IDILI potential could inform decisions about whether to allow a drug candidate to proceed through the development process. An in vitro approach that uses cells that are readily available and easily grown in culture, requires little compound, employs a single relevant endpoint, and is amenable to high-throughput format would be highly desirable.

Development of such an approach has been challenging due to limited knowledge about mechanisms underlying IDILI. Several attempts have been made based on direct effects of drugs on hepatocellular biochemistry and/or on physical-chemical characteristics of drugs (Usui et al., 2009; Low et al., 2011; Sakatis et al., 2012; Thompson et al., 2012; Chen et al., 2013, 2014; Khetani et al., 2013; Morgan et al., 2013; Aleo et al., 2014; Zhu et al., 2014; Choi et al., 2015; Schadt et al., 2015; Susukida et al., 2015; Ware et al., 2015; Zhang et al., 2016a,b). For the most part, the performance of these (selectivity and/or specificity) has not been ideal. Although it is commonly believed that activation of the immune system underlies IDILI, the results of such activation are typically not considered in the design. Such consideration could lead to an improved approach.

Activation of immune cells culminates in the release of immune mediators such as cytokines. Some recently developed animal models as well as human genetic association studies suggest that adaptive immunity plays a role in the precipitation of IDILI responses to some drugs (Lucena et al., 2011; Chakraborty et al., 2015). Mice that have impaired immune tolerance developed liver injury after several administrations of IDILI-associated drugs such as halothane and amodiaquine (Metushi et al., 2015; Chakraborty et al., 2015). Although these models involving activation of the adaptive immune system resulted in only mild liver injury, they could represent an advance in understanding IDILI pathogenesis. Thus far, very few animal models of IDILI have been developed that recapitulate the severity of hepatocellular injury observed in humans. Most of these are based on the interaction of drugs with an activated innate immune system (Roth and Ganey, 2011). Among the models based on the interaction between drugs and the innate immune system, the inflammatory mediators tumor necrosis factor-α (TNF) and interferon-γ (IFN) were critical to the pathogenesis of liver injury (Hassan et al., 2008; Shaw et al., 2009a,b; Zou et al., 2009; Dugan et al., 2011; Lu et al., 2012).

Both innate and adaptive immune responses culminate in the release of these potentially cytotoxic, proinflammatory cytokines. Findings from the animal studies raised the possibility that IDILI-associated drugs sensitize hepatocytes to cell death signaling from cytokines such as TNF and IFN (Roth and Ganey, 2011). Indeed, using a series of drugs, Cosgrove et al. (2009) found a correlation between IDILI liability and the ability of drugs to synergize with cytokines to kill primary human hepatocytes in vitro. Using a smaller subset of drugs, Cosgrove et al. (2009) also found that their results in primary human hepatocytes could be reproduced using HepG2 cells, suggesting that the latter cells hold promise in classifying drugs according to IDILI liability. These and other studies suggest that IDILI-associated drugs act in part by causing stress to hepatocytes, such that they become susceptible to killing mediated by cytokines (Cosgrove et al., 2009; Zou et al., 2009; Fredriksson et al., 2011, 2014; Beggs et al., 2014, 2015; Maiuri et al., 2015; for review, see Roth et al., 2017).

Using HepG2 cells, we recently studied the cytotoxic interaction of TNF/IFN with a series of nonsteroidal anti-inflammatory drugs (NSAIDs) with various IDILI liabilities and also with an antibiotic, trovafloxacin (Beggs et al., 2014, 2015; Maiuri et al., 2015). In studies presented here, we expand on those findings with a larger set of drugs. Importantly, elucidation of detailed concentration-response relationships permitted calculation of various parameters (e.g., EC₅₀, maximal response, slope, etc.) that we then incorporated into statistical models to evaluate the ability of this approach to classify drugs according to their association with IDILI. The results suggest a highly promising, in vitro approach to predict IDILI liability.

Materials and Methods

Materials

All drugs were purchased from Sigma-Aldrich (St. Louis, MO) or Santa Cruz Biotechnology (Dallas, TX) unless otherwise noted. Recombinant human TNF and IFN were purchased from R&D Systems (Minneapolis, MN) or Millipore (Billerica, MA). Phosphate-buffered saline, Dulbecco’s modified Eagle’s medium, fetal bovine serum, antibiotic-antimycotic, and 0.25% trypsin-EDTA were purchased from Life Technologies (Carlsbad, CA).

Cell Culture

Human hepatoma HepG2 cells (American Type Culture Collection, Manassas, VA) were grown in 25-cm² tissue culture flasks and maintained in Dulbecco’s modified Eagle’s medium supplemented with 10% fetal bovine serum and 1% antibiotic-antimycotic in a humidified incubator at 37°C under 95% air and 5% CO₂. Cells were passed or used for experiments when they reached approximately 80% confluence. Cells were used at passages 6–16; at higher passage numbers, the responses became less consistent and, in some cases, less robust.

IDILI Classification

The 24 drugs evaluated in this study were classified as being associated with (IDILI+) or not associated with (IDILI—) IDILI. Known classification was based on a set of criteria established by Xu et al. (2008). Table 1 lists the drugs evaluated in this study, their maximal plasma concentration (C_max) after pharmacologic dosing in human patients, and their known IDILI classification. The drugs that were used span several therapeutic classes (i.e., antibiotics, NSAIDs, anticancer, antiepileptic, antidiabetic, and anxiolytic/neuroleptic/antidepressant/antipsychotic drugs). Most of the IDILI+ drugs we chose have caused hepatocellular injury in people, although some (flucloxacillin, chlorpromazine, flutamide, and clavulanate) have been associated with mixed or cholestatic liver damage. Some of the IDILI+ drugs (chlorpromazine, diclofenac, and trovafloxacin) produced liver injury in experimental animals when coupled with an inflammatory stimulus (Buchweitz et al., 2002; Deng et al., 2006; Shaw et al., 2009b).

TABLE 1.

IDILI classification, daily dose, C_max, and references from which C_max values were taken

Drug	IDILI Liability	Cmax	Daily Dose	Cmax Reference
		μM	mg
Aspirin	IDILI−	47	1300	Brandon et al., 1986
Azithromycin	IDILI−	0.5	500	Xu et al., 2008
Buspirone	IDILI−	0.005	15	Xu et al., 2008
Idarubicin	IDILI−	0.02	1	Xu et al., 2008
Levofloxacin	IDILI−	15.7	500	Xu et al., 2008
Moxifloxacin	IDILI−	6.2	400	Stass et al., 1998
Pioglitazone	IDILI−	2.67	15	Xu et al., 2008
Promethazine	IDILI−	0.06	25	Xu et al., 2008
Rofecoxib	IDILI−	1	12.5	Gottesdiener et al., 2003
Sertraline	IDILI−	0.06	50	Xu et al., 2008
Bromfenac	IDILI+	13.5	50	Gumbhir-Shah et al., 1997
Chlorpromazine	IDILI+	0.84	200	Xu et al., 2008
Clavulanate	IDILI+	12	125	Hu et al., 2002
Diclofenac	IDILI+	7.44	100	Xu et al., 2008
Doxorubicin	IDILI+	1	1	Barpe et al., 2010
Flucloxacillin	IDILI+	72.6	250	Røder et al., 1995
Flutamide	IDILI+	0.36	750	Xu et al., 2008
Ibuprofen	IDILI+	164	800	Bramlage and Goldis, 2008
Isoniazid	IDILI+	77	300	Xu et al., 2008
Naproxen	IDILI+	300	500	Setiawati et al., 2009
Nimesulide	IDILI+	21.08	200	Xu et al., 2008
Telithromycin	IDILI+	2.77	800	Xu et al., 2008
Trovafloxacin	IDILI+	5	300	Xu et al., 2008
Valproic acid	IDILI+	175	60	Rha et al., 1993

IDILI classification was determined by a set of criteria described in Xu et al. (2008). IDILI− indicates that the drug is not associated with IDILI, whereas IDILI+ indicates that the drug is associated with IDILI.

Cytotoxicity Assessment

HepG2 cells were plated at a density of 4 × 10⁴ cells per well in black-walled, 96-well tissue culture plates and were allowed to attach overnight before being treated with compounds. Drugs were reconstituted in vehicles (VEHs) consisting of sterile water or dimethylsulfoxide (concentration <0.5%). Cells were treated with various concentrations of the drug or its VEH (control) alone or in combination with the cytokines TNF (10 ng/ml) and/or IFN (10 ng/ml) or their phosphate-buffered saline VEH. Cytotoxicity was evaluated as lactate dehydrogenase (LDH) activity released from the cells into culture medium using the Homogeneous Membrane Integrity Assay kit from Promega (Madison, WI). A spectrophotometric method was used to measure the percentage of LDH release in cases in which the drug interfered with the fluorescence-based assay (Vanderlinde, 1985).

Concentration-response curves were generated for 24 drugs, 14 of which are associated with human IDILI and 10 of which are not. Cells were treated with drug concentrations generally ranging from 0 to 100 times the C_max observed in human patients. This range of concentrations is based on scaling factors described in Xu et al. (2008) and accounts for variability in C_max as well as exposure of the liver to greater concentrations. The cytokine concentrations used in this study are within 10-fold of the concentrations found in the serum of human patients undergoing an inflammatory response (Pinsky et al., 1993; Taudorf et al., 2007). If a cytotoxic response was observed but did not reach a plateau by the 100× C_max concentration, further testing was performed with larger concentrations of drug to generate a complete (sigmoidal) concentration-response curve. Typically, the range of drug concentrations included at least two that were without effect, two defining the maximal effect, and two surrounding the EC₅₀. This was necessary because four-parameter logistic modeling used in the statistical analysis requires well defined, sigmoidal concentration-response curves. Cells were exposed to drug/cytokine combinations for 24 hours. This time was chosen based on previous results demonstrating that cytotoxicity from drug/cytokine exposure begins within 24 hours (Beggs et al., 2014; Maiuri et al., 2015). For analysis of drug concentration-response data, concentrations of each drug were expressed as a fraction of its C_max.

Statistical Analysis

The statistical approach used in this study can be divided into three phases: 1) drug concentration-response modeling and covariate development using four-parameter logistic models, 2) classification model development using logistic regression models, and 3) analysis of classification accuracy with receiver operating characteristic (ROC) curves.

Defining Covariates: Four-Parameter Logistic Concentration-Response Model.

In the first phase, variables (potential covariates) for use in the classification analysis were defined from the analysis of drug concentration-response data. Initially, a one-way analysis of variance was used as an omnibus test to determine whether a particular treatment (e.g., drug alone or in combination with TNF and/or IFN) caused a significant change in LDH release relative to baseline (i.e., LDH release in the absence of drug, hereafter designated “min”). The criterion for significance for the analysis of variance was set at α = 0.01. A 1% level of significance was used to rule out more vigorously marginal relationships between concentration and response. For treatments that did not result in a significant change in LDH above min (P > 0.01), the following was assumed for the purpose of concentration-response modeling: the minimum LDH response (min) = the maximum LDH response (max). For drug/cytokine treatment combinations that did result in a statistically significant LDH response, the concentration-response data were modeled using the following four-parameter logistic function:

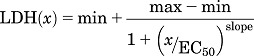where LDH(x) is the percentage of LDH released at a given concentration x, x is [drug]/C_max, min is the percentage of LDH release at 0 drug concentration (i.e., baseline), and max is the maximal LDH response (i.e., maximum percentage of LDH release). From this equation, the drug concentration associated with the 50% maximal response (EC₅₀) and the slope of the concentration-response curve were calculated. The four-parameter logistic models were generated using R statistical software (R package “drc”; R Foundation for Statistical Computing, Vienna, Austria) (R Core Team, 2015; Ritz and Streibig, 2005).

In addition to slope and EC₅₀, several other “base covariates” were calculated from the concentration-response curves for use in further analyses. These were calculated for each of the 96 drug/cytokine treatment combinations evaluated in this study (24 drugs × 4 cytokine combinations) (Supplemental Tables 1–9). Delta was defined as max minus min. In addition to the covariates determined from concentration-response curves, C_max was considered as another base covariate.

Similar to EC₅₀, the covariate EC₁₀ represents the [drug]/C_max value associated with a 10% increase above min relative to max and was determined by the following equation:

where D₁₀ is a categorical variable related to reaching a threshold LDH response above which a drug is classified as positively associated with IDILI. D₁₀ is defined as 0 if delta is < 10% LDH release and as 1 if delta is ≥ 10% LDH release.

The base covariate R₁₀ represents the [drug]/C_max value associated with an increase in 10 LDH percentage points above min for a particular treatment condition and was determined by the following equation:

R₁₀ is considered to be 0 when delta is < 10% LDH (i.e., when D₁₀ = 0).

From the base covariates defined above, several other covariates were derived. These included the EC₅₀ quotient, EC₁₀ quotient, R₁₀ quotient, deltadiff, and TNF change. Each of these “derived” covariates is explained in more detail below.

The EC₅₀ quotient, EC₁₀ quotient, and R₁₀ quotient represent the ratio between the EC₅₀, EC₁₀, or R₁₀ of the drug/cytokine concentration-response curve and the respective value for the drug/VEH concentration-response curve. In some instances, the value derived from this calculation is indeterminate (i.e., when the denominator = 0). To incorporate the quotient values into the classification models described below, the categorical variable “Q” was used to eliminate the possibility of the quotient being indeterminate. Q is defined as 0 if delta VEH and/or delta cytokine is < 10% LDH and 1 if both delta VEH and delta cytokine are ≥ 10% LDH. For the purposes of calculating the EC₅₀ quotient, the following condition was applied: if Q = 0, then the EC₅₀ quotient = 0; if Q = 1, then the EC₅₀ quotient = EC₅₀ VEH/EC₅₀ cytokine. The same condition was applied for calculation of the EC₁₀ quotient and R₁₀ quotient.

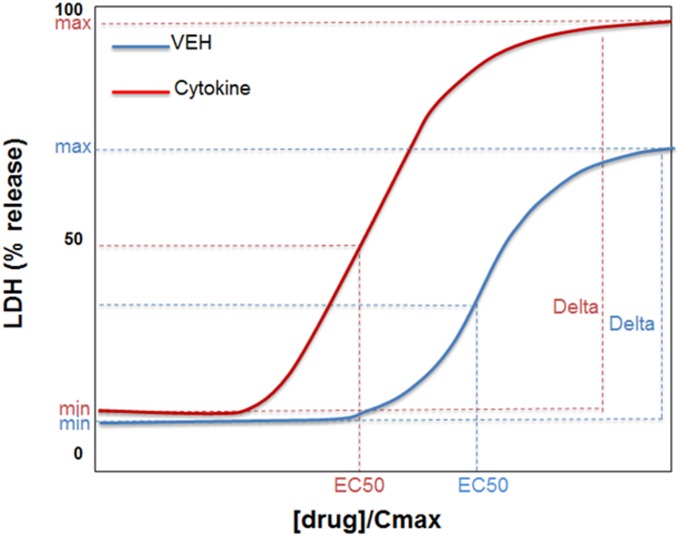
Deltadiff represents the difference between the delta of the drug/cytokine concentration-response curve and the delta of the drug/VEH curve. In other words, deltadiff = (delta cytokine) – (delta VEH). Figure 1 graphically illustrates several of the covariates defined above. Supplemental Tables 1–9 list the values of all of the covariates computed in this study. In addition to the covariates derived from the concentration-response curves, the maximal therapeutic plasma drug concentration (C_max) in human patients was used in some models (Table 1).

Fig. 1.

Depiction of base covariates considered for evaluation. The blue curve represents hypothetical response to drug alone; the red curve represents response to drug in the presence of cytokine. Min is the LDH release in the absence of drug, max is the maximal LDH release. Delta = max(LDH) – min(LDH) for each curve. Although not depicted in the figure, deltadiff = delta cytokine − deltaVEH. EC₅₀ is the [drug]/C_max value at 50% delta. R₁₀ is not depicted but it represents the [drug]/C_max value associated with a 10% increase in LDH release above min(LDH).

TNF change is a categorical variable related to the alteration in the drug-induced cytotoxic response in the presence and absence of TNF, determined as follows:

Recall that D₁₀ is defined as 0 if delta is 10% change in LDH release, and D₁₀ is defined as 1 if delta is > 10% change in LDH release. Accordingly, TNF change = 1 if the TNF curve has a delta > 10% LDH release and the VEH curve has a delta ≤ 10% LDH release; TNF change = 0 in all other situations.

Classification Modeling Using Defined Covariates.

In the second phase of analysis, classification models were developed using logistic regression with covariates as independent variables in the analysis and known IDILI classification as the dependent variable. The ability to classify drugs accurately was evaluated using the known IDILI classifications shown in Table 1. A model selection process was used to determine whether a covariate or set of covariates is associated with IDILI liability. Covariates were first evaluated individually to determine how well a particular covariate classified drugs according to IDILI liability, and then covariates were evaluated in combination. Combinations of covariates were selected to maximize the ability of the model to distinguish between drugs associated or not with IDILI. Specifically, covariates that describe changes in efficacy (delta, deltadiff, etc.) were paired with covariates that describe changes in potency (EC₅₀, EC₁₀, R₁₀, etc.) to find covariate combinations that led to models that most accurately discriminated between drugs that are and are not associated with IDILI. The best-fit logistic regression models were used as classification models to compute a probability that a given drug is associated with IDILI. The logistic regression models use the following equation:

where 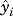is the calculated (predicted) probability that drug i with a vector of covariates x_i is associated with IDILI. The β coefficients (β₀, the regression intercept; and β_i, the regression slopes for model covariates, x_i) were derived from the logistic regression models using 1) combinations of the covariates (x_i) generated by concentration-response modeling for each of the 24 drugs evaluated in this study plus daily dose and C_max, and 2) the known IDILI classification for the dependent variable y_i (i.e., 1 for IDILI+ drugs and 0 for IDILI− drugs). For treatments that did not result in a significant change in LDH above min (P > 0.01), a value of 0 was assigned for covariates derived from EC₅₀ for purposes of calculating β_i. The regression coefficients (β_i) were calculated using Firth’s method, which eliminates bias when estimating the value β_i (Firth, 1993). Firth’s method was necessary since many of the covariates used in this study exhibited quasi-complete separation. This occurs when a covariate almost perfectly separates observations into the appropriate categories. In this study, several covariates almost completely separated drugs according to their IDILI liability. When separation or quasi-complete separation occurs, use of the standard method (i.e., maximum likelihood estimation) provides biased, unreliable estimates of β_i. Firth’s method uses a penalized likelihood regression to rectify this and is an appropriate method to use for estimating β_i when quasi-complete separation of data occurs (Firth, 1993). All logistic regression models were computed using R statistical software (R package “logistf”) (Heinze et al., 2013; R Core Team, 2015).

ROC Analysis.

In the third phase of the statistical approach, the classification models, generated as logistic regression models using single covariates or combinations of covariates, were evaluated by ROC analysis to determine which model and corresponding sets of covariates led to the most accurate classification of drugs according to their potential to cause IDILI. An ROC curve was created for each model by graphing the true positive rate (sensitivity; i.e., proportion of drugs correctly classified as associated with IDILI) against the true negative rate specificity (1 − false positive rate; i.e., proportion of drugs correctly classified as not associated with IDILI) at various probability cutoff thresholds (k). ROC curves were generated using R package pROC (Robin et al., 2011; R Core Team, 2015). An area under the curve (AUC) and confidence interval were computed for each ROC curve (where each logistic regression model has one ROC curve). Plots depicting the AUCs and 95% confidence intervals of the ROC curves were generated for the purpose of comparing multiple logistic regression models using R package Metafor (Viechtbauer, 2010). Corresponding to each ROC curve is an optimal threshold value (k*), the threshold yielding the highest point of accuracy on the curve [i.e., the point nearest the point (1,1) on the curve]. Thus, each ROC curve has a corresponding AUC and an optimal cutoff (k*) that corresponds to the highest point of accuracy on that ROC curve.

Combinations of covariates were strategically selected for evaluation based on what was deemed to lead to the most accurate classification of drugs. ROC curves and corresponding whisker plots were generated to illustrate graphically the ability of each classification model to classify drugs accurately. This allowed for selection of optimal set(s) of covariates for accurate drug classification according to IDILI liability. Our goal was to achieve a classification model and a corresponding set of covariates with an AUC as close to 1 as possible with the narrowest 95% confidence interval. A model that is able to classify drugs perfectly according to their potential to cause IDILI would have an ROC curve with an AUC = 1. DeLong’s method was used to determine whether there were statistically significant differences among ROC curves (DeLong et al., 1988).

A separate classification analysis was also performed to evaluate the ability of C_max to classify a larger set of drugs with known IDILI potential. C_max values were obtained for 272 drugs from a study conducted by Xu et al. (2008) and evaluated using ROC analysis.

Results

Drug/Cytokine Cytotoxicity: Concentration Response In Vitro

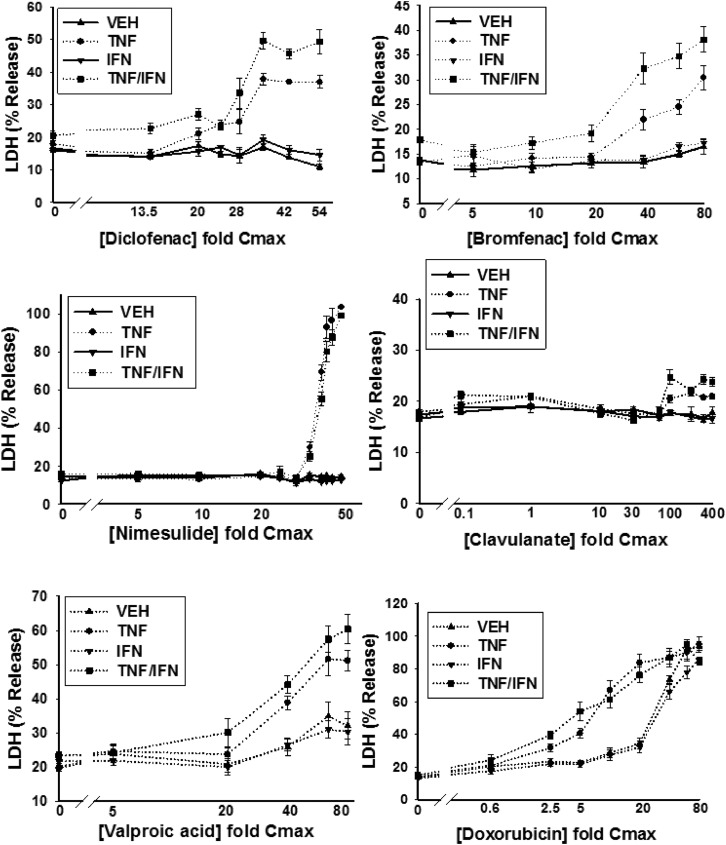
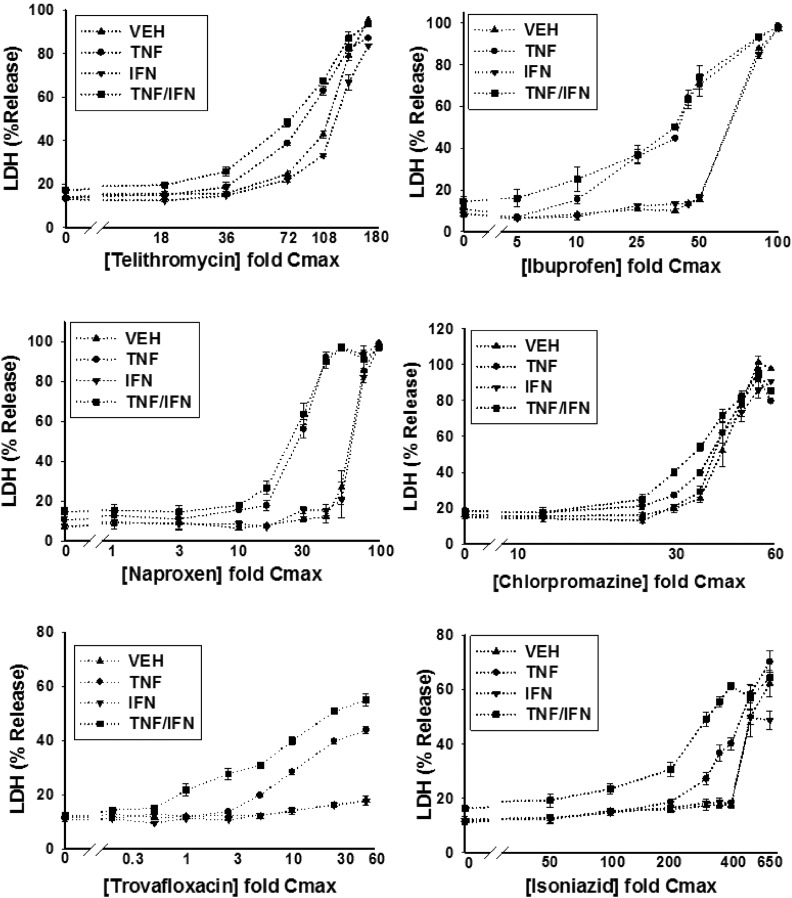
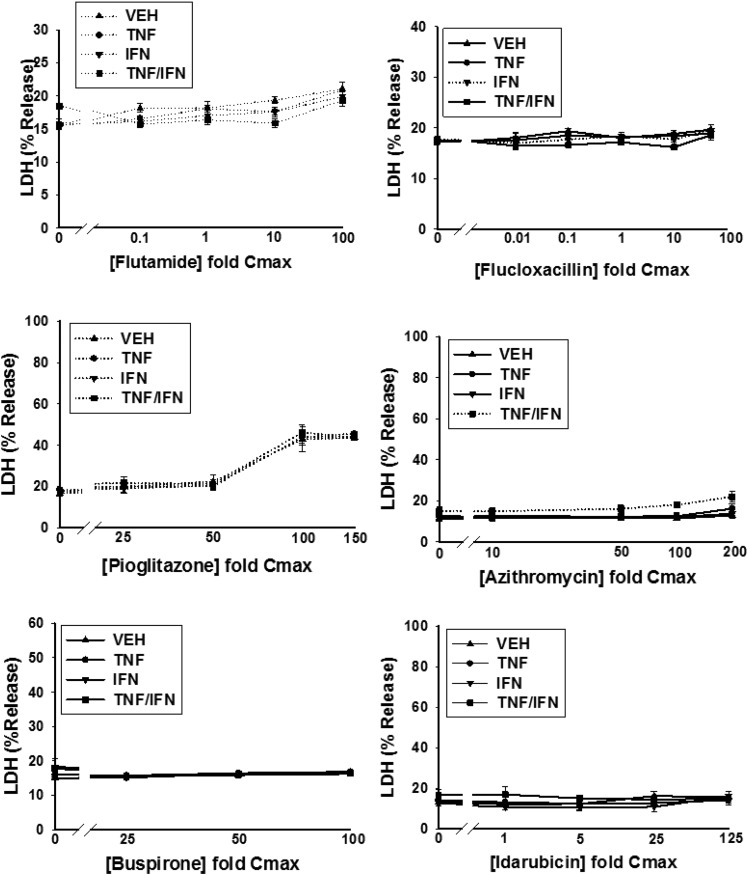
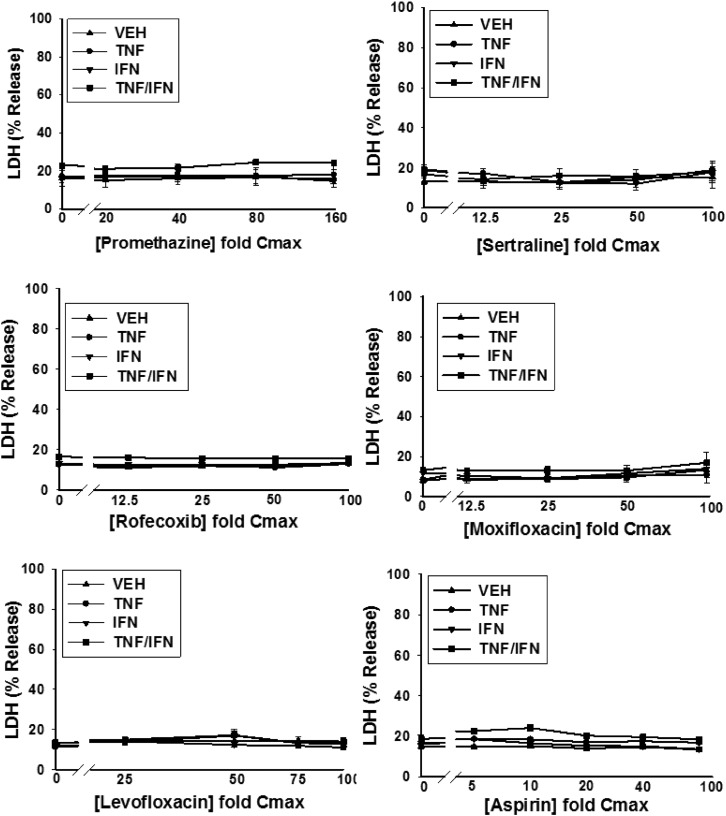
HepG2 cells were treated with various concentrations of a drug alone or in combination with TNF and/or IFN, and cytotoxicity was assessed 24 hours later as increased LDH activity in the culture medium. Detailed cytotoxicity concentration-response curves were generated for 24 drugs (Table 1): 14 drugs that are associated with IDILI and 10 that are not (negative comparators) (Fig. 2; Supplemental Fig. 4). Of the 14 drugs associated with IDILI, almost all synergized with cytokines in causing cell death (Fig. 2). Four of these (diclofenac, bromfenac, nimesulide and clavulanate) caused no cytotoxicity on their own but synergized with TNF to cause cytotoxicity. Nine IDILI-associated drugs led to a statistically significant increase in LDH release (relative to no drug) in the absence of cytokines (valproic acid, doxorubicin, telithromycin, ibuprofen, naproxen, chlorpromazine, flutamide, trovafloxacin, and isoniazid). Interestingly TNF significantly enhanced the cytotoxicity mediated by eight of these drugs (valproic acid, doxorubicin, telithromycin, ibuprofen, naproxen, chlorpromazine, trovafloxacin, and isoniazid). In contrast to TNF, IFN did not interact with any drug to cause cytotoxicity. However, coexposure to IFN enhanced the cytotoxic interaction between TNF and several of the drugs (diclofenac, bromfenac, trovafloxacin, valproic acid, chlorpromazine, telithromycin, and isoniazid). Two of the 14 IDILI-associated drugs (flutamide and flucloxacillin) did not synergize with cytokines to kill HepG2 cells. Of the 10 negative comparators, pioglitazone was the only drug that caused cytotoxicity on its own; however, this effect was not enhanced by the addition of cytokines. With the exception of azithromycin, which was modestly cytotoxic in the presence of TNF/IFN, none of the remaining negative comparator drugs synergized with cytokines to kill HepG2 cells (Fig. 2).

Fig. 2.

Drug/cytokine-induced cytotoxicity: concentration-response. HepG2 cells were treated with 14 drugs associated with IDILI and 10 drugs not associated with IDILI, alone (VEH) and in combination with TNF and/or IFN. Cytotoxicity (% LDH release) was evaluated 24 hours after treatment. The numbers listed on the x-axis represent the concentration of drug relative to C_max (fold C_max). Refer to Table 1 for the C_max information and known IDILI classification for each drug and to the Materials and Methods for the rationale concerning the range of drug concentrations evaluated. Each data point represents the mean ± standard error of the mean (SEM) of at least three separate experiments. The dotted curves indicate that the treatment condition (i.e., VEH, TNF, IFN, or TNF/IFN) resulted in a statistically significant change in LDH from baseline (no drug) at one or more drug concentrations (ANOVA P < 0.01). Solid lines indicate that the treatment condition did not result in a statistically significant change in LDH relative to baseline at any drug concentration (ANOVA P ≥ 0.01). The dotted curves were modeled using a four-parameter logistic function as described in the Materials and Methods to compute parameters describing curve characteristics (minimum cytotoxic effect, maximum cytotoxic effect, EC₅₀, etc.).

Classification Models and ROC Analysis

Data used in the classification models consisted of covariate data generated as described above (i.e., parameters of the concentration-response curves for each of the 24 drugs and additional variables derived from these parameters) in addition to the daily dose and C_max for each drug. Daily dose and C_max values are shown in Table 1. Supplemental Tables 1–9 summarize parameters of the concentration-response curves for each drug and all derived covariates. Numerous logistic regression models were constructed. We began with models employing each covariate alone, then moved onto models populated with combinations of covariates (Supplemental Table 10). All classification models were evaluated for their ability to classify the 24 drugs using ROC analysis. Findings are described below.

C_max Is Moderately Associated with IDILI Potential

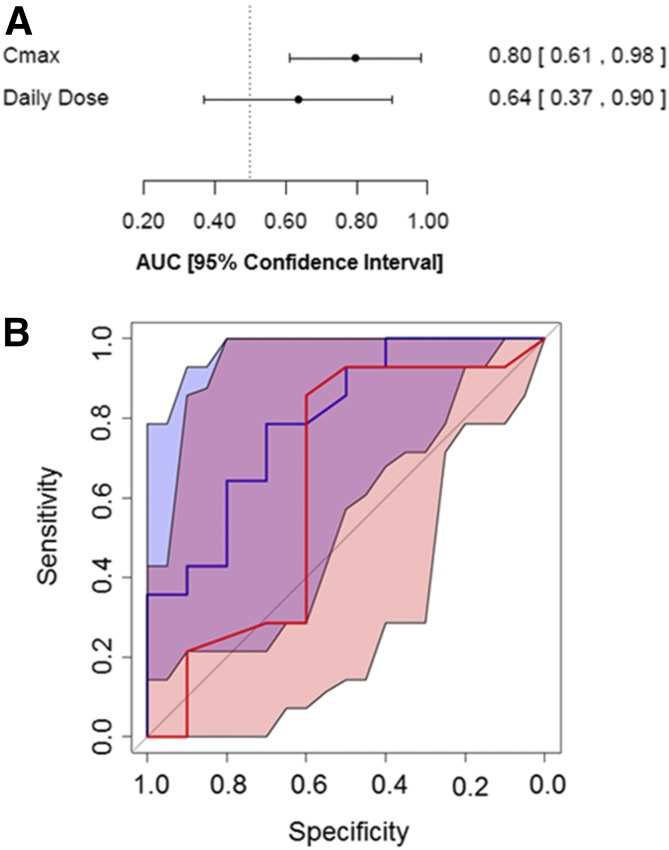
IDILI reactions were once thought not to be dose related; however, the observation that most drugs that have been withdrawn from the market or have received a black box warning due to IDILI were prescribed at doses >50 mg/d suggested that daily dose plays some role in the propensity of a drug to cause IDILI (Uetrecht, 1999). Based on this observation, we evaluated how accurately the daily dose or the C_max of a drug classifies drugs listed in Table 1 according to their potential to cause IDILI. We used logistic regression modeling and ROC analysis as described in the Materials and Methods. The AUC of the ROC curve generated for the model incorporating daily dose was 0.64 (95% confidence interval, 0.37, 0.9) (Fig. 3). Since the 95% confidence interval for the ROC curve from the daily dose model contained the value 0.5, representing no better than random classification, it cannot be concluded that the magnitude of the daily dose is predictive of IDILI for this drug set. A larger set of drugs may be needed to determine whether daily dose can predict IDILI.

Fig. 3.

Comparison of the model incorporating daily dose to that incorporating C_max. (A) AUCs and 95% confidence intervals are depicted for the ROC curves derived from the models incorporating either daily dose or C_max. The covariates are listed on the left, and the AUC for each one is shown on the right next to the 95% confidence interval (shown in brackets). (B) The ROC curves for the model incorporating daily dose and C_max are indicated by red and blue lines, respectively. The 95% confidence intervals for the model incorporating daily dose and C_max are shaded red or blue, respectively. Overlap between the confidence intervals for the two ROC curves appears in violet.

The AUC of the ROC curve generated for the model employing C_max for our set of 24 drugs was 0.80 (95% confidence interval, 0.61, 0.98) (Fig. 3). Similar results were obtained by Shah et al. (2015) for a set of 125 drugs. These results suggest that C_max is associated with IDILI.

To determine whether our set of 24 drugs is representative of a larger set of drugs and to further evaluate the ability of C_max to predict IDILI liability, C_max values were obtained for 272 drugs from a study conducted by Xu et al. (2008) and converted to micromolar units. C_max was significantly associated with IDILI for this larger data set (β_Cmax= 0.044, P < 0.001). The AUC of the ROC curve generated from this larger set of drugs was 0.70 (95% confidence interval, 0.64, 0.76). The ROC curves derived from the set of 24 drugs and from the set of 272 drugs are depicted along with their 95% confidence intervals in Supplemental Fig. 2. The confidence interval corresponding to the ROC curve derived from the set of 272 drugs (shaded red) is contained within the confidence interval for the ROC curve derived from the set of 24 drugs (shaded gray). This suggests that the smaller set of drugs adequately represents the relationship between C_max and IDILI potential seen in a much larger set of drugs.

ROC Analysis of Models Incorporating the Base Covariates

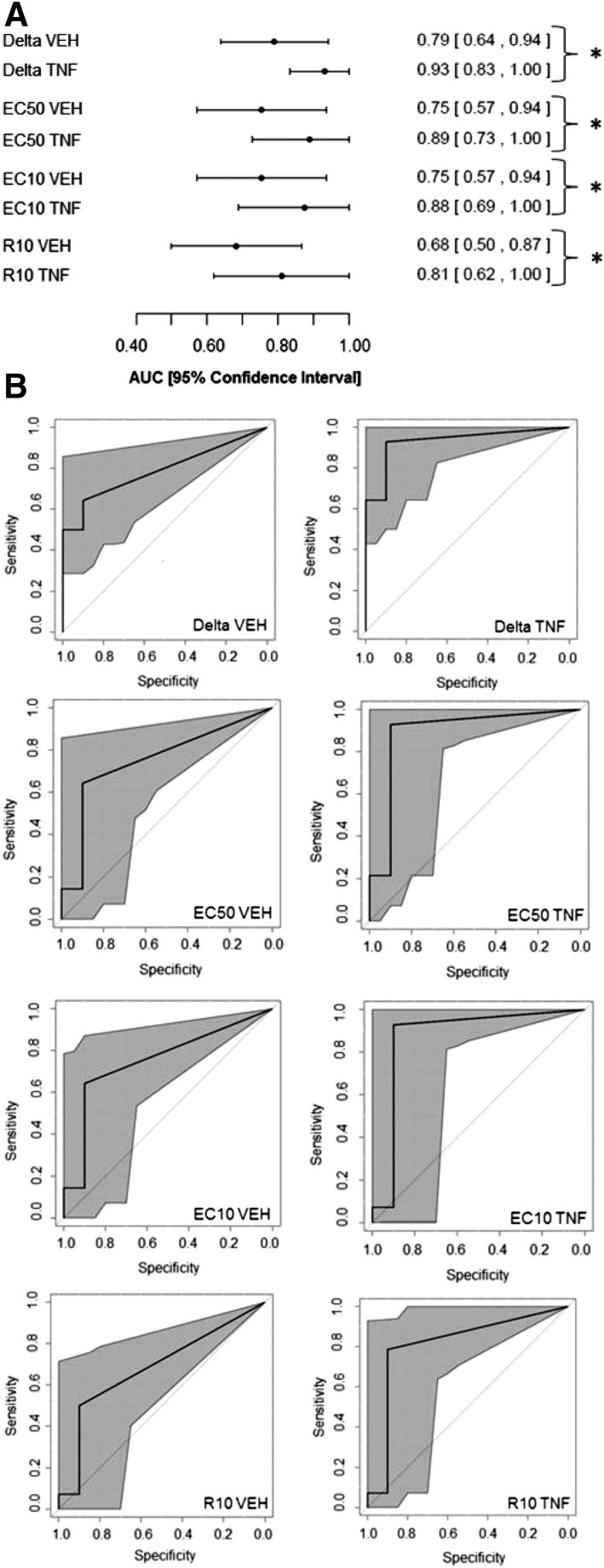
Almost all of the 14 IDILI-associated drugs synergized with TNF to cause death of HepG2 cells, and some of them were cytotoxic by themselves (Fig. 2). These results suggested that cytotoxic synergy with TNF might be associated with IDILI liability. Accordingly, classification models were constructed using base covariates from the concentration-response curves to determine whether the presence of TNF improved a model’s ability to classify drugs according to IDILI liability. The base covariates were modeled for each drug individually; base covariates that were at least moderately associated with IDILI liability included delta VEH, delta TNF, EC₅₀ VEH, EC₅₀ TNF, EC₁₀ VEH, EC₁₀ TNF, R₁₀ VEH, and R₁₀ TNF. AUCs and 95% confidence intervals are shown in Fig. 4A for each of these covariates. It can be seen that the confidence interval for each of these covariates does not contain the value 0.5, indicating a significantly better than random ability to classify the 24 drugs according to IDILI potential. The model incorporating delta TNF produced the ROC curve with the greatest AUC (0.93) and the narrowest 95% confidence interval (0.83, 1.00); this suggesting that of these models, it provided the most accurate classification of the drugs (Fig. 4A). Furthermore, the base covariates that described the response to drug/TNF (labeled “TNF”) led to models that produced ROC curves that had improved AUCs with narrower confidence intervals than those that described the response to drug alone (i.e., labeled “VEH”) (Fig. 4).

Fig. 4.

Evaluation of models incorporating the base covariates. (A) AUCs and 95% confidence intervals are illustrated for the ROC curves derived from the models incorporating the base covariates delta VEH, delta TNF, EC₅₀ VEH, EC₅₀ TNF, EC₁₀ VEH, EC₁₀ TNF, R₁₀ VEH, or R₁₀ TNF. The covariates are listed on the left, and the AUC for each is shown on the right next to the 95% confidence interval (shown in brackets). *P < 0.05 (statistically significant difference between ROC curves as determined by DeLong’s test) (DeLong et al., 1988). (B) ROC curves were generated and indicate for each model the 95% confidence interval shaded in gray. The covariates incorporated in the model are listed on the bottom right corner of each ROC curve.

ROC Analysis of Models Incorporating Derived Covariates

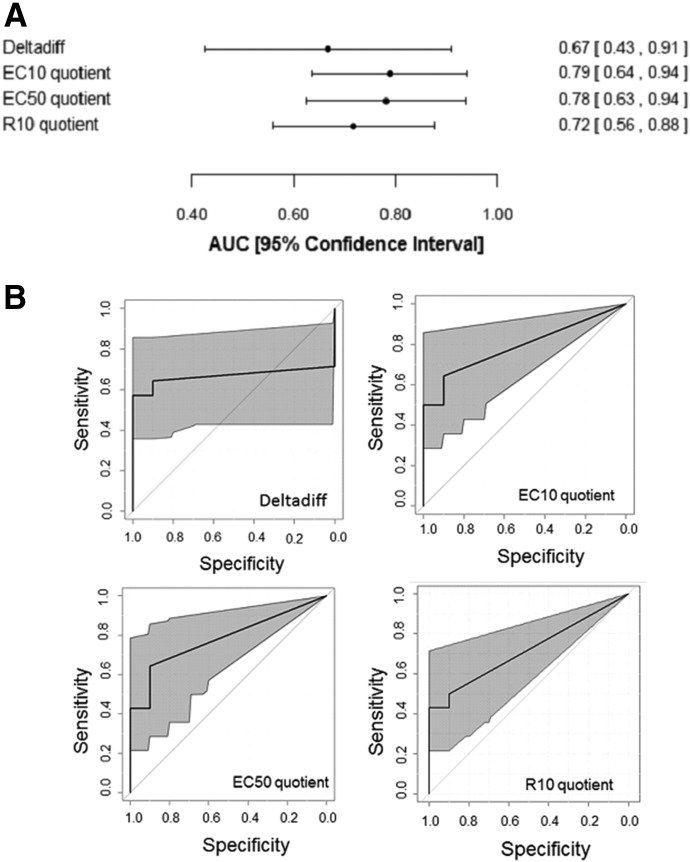
Probability models were also generated using the individual covariates that were derived from the base covariates: EC₅₀ quotient, EC₁₀ quotient, R₁₀ quotient, and deltadiff. In Fig. 5, the EC₅₀, EC₁₀, and R₁₀ quotient covariates represent the ratio of the drug/TNF concentration-response curve to the drug/VEH curve, and deltadiff represents the difference between the deltas from the drug/TNF concentration-response curve and the drug/VEH curve. Each of these covariates (except deltadiff) was moderately associated with IDILI liability (Fig. 5); however, the ROC curves generated based on these models did not have greater AUCs or narrower confidence intervals than the models produced by incorporating the base covariates (compare Figs. 4 and 5).

Fig. 5.

Evaluation of models incorporating the derived covariates. (A) AUCs and 95% confidence intervals for the ROC curves are depicted for the models incorporating the derived covariates individually. The covariates are listed on the left, and the AUC for each is shown on the right next to the 95% confidence interval (shown in brackets). (B) ROC curves were generated and indicate for each model the 95% confidence interval shaded in gray. The covariate incorporated in the model is listed on the bottom-right corner of each ROC curve.

Addition of IFN Data Did Not Improve the Classification of Drugs

None of the drugs synergized with IFN in the absence of TNF to cause cytotoxicity, but several IDILI-associated drugs synergized with IFN in the presence of TNF (Fig. 2). Accordingly, we examined whether incorporation of the TNF/IFN responses would improve the performance of models that employed only TNF responses. The drug/TNF/IFN models tended to have smaller AUCs and larger confidence intervals than the drug/TNF models (Supplemental Fig. 3), indicating that the addition of data describing the IFN response did not enhance the ability of models to classify drugs.

ROC Analysis of Models Incorporating Combinations of the Base and Derived Covariates

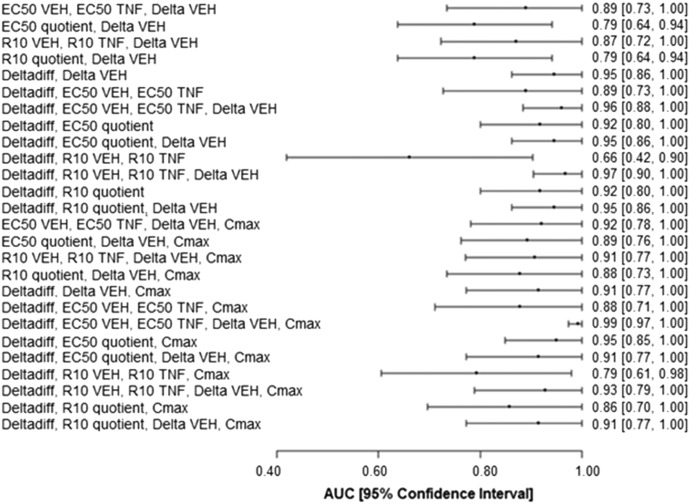
Although it was illustrative to evaluate the base and derived covariates individually, we hypothesized that incorporation of several covariates into a model would lead to more accurate classification of drugs than incorporation of a single covariate. Accordingly, various combinations of the base and derived covariates were evaluated to identify a set of covariates that led to the most accurate drug classification. Combining base and derived covariates led to several models with greater AUCs and narrower confidence intervals than the models incorporating only a single covariate. A representative set including the best-performing models is presented in Fig. 6. Furthermore, when C_max was added as a covariate, it improved the performance (AUC and confidence interval) of some models but not others (Fig. 6). Supplemental Table 10 shows the coefficients (β values) and their P values for the models shown in Fig. 6.

Fig. 6.

Evaluation of models incorporating combinations of the base and derived covariates with and without C_max. AUCs and 95% confidence intervals for the ROC curves are depicted for the models incorporating various combinations of base and derived covariates in the absence (upper half) and presence (lower half) of C_max. The covariates are listed on the left, and the AUC for each is shown on the right next to the 95% confidence interval (shown in brackets).

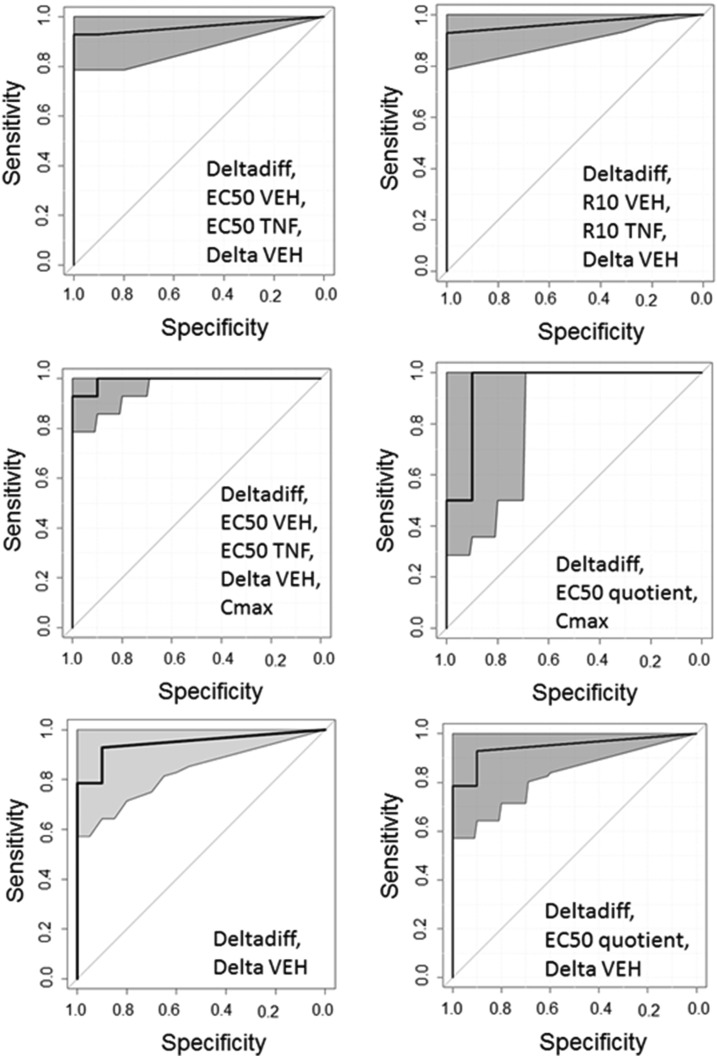
Some of the combination models were associated with remarkably high AUCs, and some of these were associated with small confidence intervals. There were no statistically significant differences among the models with an AUC > 0.95 as determined by DeLong’s method for comparing ROC curves (P > 0.05) (DeLong et al., 1988). The ROC curves that met this criterion (AUC > 0.95) are shown in Fig. 7.

Fig. 7.

ROC curves with an AUC ≥ 0.95. ROC curves for which AUC ≥ 0.95 are depicted. The 95% confidence interval is shaded gray. The covariates incorporated into the model are listed at the bottom-right corner of each ROC curve. The ROC curves shown were not significantly different from each other as determined by DeLong’s test (P > 0.05).

Discussion

The purpose of this proof-of-concept study was to develop and evaluate an in vitro approach combined with statistical modeling to classify drugs according to their potential to cause IDILI. The overall hypothesis tested was that the ability of a drug to synergize with the cytokines TNF and/or IFN to kill HepG2 cells is associated with the drug’s propensity to cause IDILI in humans. Detailed concentration-response curves were generated, and this proved to be critical for development of a statistical classification model with the capacity to classify drugs correctly.

Since it has been suggested that the daily dose of a drug might be associated with its potential to cause IDILI and since dose is often related to C_max, we evaluated how well daily dose or C_max classifies drugs according to their IDILI liability. Daily dose was not effective at classifying the set of 24 drugs according to their potential to cause IDILI (Fig. 3). Plasma drug concentration is used as a surrogate for tissue or intracellular concentration, which is difficult to obtain. The relationship between C_max and the concentration of free drug in liver cells can differ among drugs. The intrahepatocellular concentration of drugs can be affected not only by physicochemical properties of the drug, but also by uptake and efflux mechanisms and metabolism as well as binding to cellular or acellular components (Chu et al., 2013). Accordingly, for some drugs, the intrahepatocellular drug concentration can be many times the plasma concentration. Despite this potential disconnect, C_max was somewhat effective at classifying the set of 24 drugs, suggesting that the magnitude of plasma drug concentration is a contributor to IDILI. However, it is clear that the use of C_max as the sole covariate did not lead to a model with great classification ability (Supplemental Fig. 2).

We then determined whether cytotoxicity induced by treatment with drugs in the absence of cytokines could produce a high-performing model. Models employing only individual base covariates describing cytotoxicity in the absence of TNF performed no better than C_max (compare Figs. 3 and 4). In contrast, the models incorporating TNF performed significantly better in classifying the drugs.

The derived covariates, when evaluated individually, did not produce more desirable ROC curves than the base covariates (compare Fig. 5 with Fig. 4). However, when covariates that account for TNF-induced changes in potency and/or efficacy were combined with those derived from drug alone, much better models resulted (Figs. 6 and 7). Furthermore, incorporating C_max into these models led to the ROC curve with the greatest AUC (0.99) and narrowest confidence interval (0.97, 1) (Figs. 6 and 7). The coefficients and test statistic values for this best-performing classification model, which incorporated deltadiff, EC₅₀ VEH, EC₅₀ TNF, delta VEH, and C_max as covariates, are listed in Table 2. A cutoff value is an estimated probability above which a drug would be classified as associated with IDILI (1 = associated with IDILI) and below which a drug would be classified as not associated with IDILI (0 = not associated with IDILI). The optimal cutoff threshold is the probability cutoff that permits the most accurate classification of drugs according to IDILI liability for a given model [i.e., the point on the ROC curve closest to the coordinate (1, 1)]. Table 3 shows the sensitivity and specificity of the best-performing model when the optimal cutoff threshold was applied. Based on this model, the estimated probability that a specific drug from the set of 24 drugs is associated with IDILI is shown in Table 4. As can be seen in Table 4, this classification model led to almost complete separation between IDILI-associated drugs and drugs that are not associated with IDILI. If this model were to be used in a preclinical safety evaluation setting to predict IDILI potential of a set of drugs, the user could either select the optimal cutoff threshold or choose a cutoff threshold that is either more or less sensitive depending on what false positive rate is deemed acceptable.

TABLE 2.

Logistic regression coefficients and P values for the optimal classification model incorporating the covariates deltadiff, EC₅₀ VEH, EC₅₀ TNF, delta VEH, and C_max

Covariate	β	χ2	P Value
Intercept	−1.924	7.091	0.008
Deltadiff	0.108	2.471	0.116
EC50 VEH	−0.066	6.215	0.013
EC50 TNF	0.050	4.480	0.034
DeltaVEH	0.081	11.038	0.001
Cmax	0.0031	0.129	0.720

The coefficients (β values) were computed using Firth’s approach as described in the Materials and Methods (Firth, 1993). A P value < 0.05 indicates that the covariate contributes significantly to the prediction of outcome (IDILI liability).

TABLE 3.

Sensitivity and specificity for the optimal classification model incorporating the covariates deltadiff, EC₅₀ VEH, EC₅₀ TNF, delta VEH, and C_max

Measure	Value	95% Confidence Interval
Optimal cutoff threshold (k*)	0.46
True negative rate (specificity) using threshold k*	1	(0.7, 1)
True positive rate (sensitivity) using threshold k*	0.93	(0.79, 1)
AUC	0.99	(0.97, 1)

The optimal cutoff threshold (k*) is shown as are the specificity and sensitivity of the model at k*. Also indicated are the area under the ROC curve (AUC) and the 95% confidence intervals for the specificity, sensitivity, and AUC.

TABLE 4.

Estimated probabilities that a drug is associated with IDILI computed from the best-performing logistic regression model employing deltadiff, EC₅₀ VEH, EC₅₀ TNF, delta VEH, and C_max as covariates

Drug	Estimated Probability	True Classification
Buspirone	0.1275	IDILI−
Idarubicin	0.1275	IDILI−
Promethazine	0.1275	IDILI−
Sertraline	0.1275	IDILI−
Azithromycin	0.1276	IDILI−
Rofecoxib	0.1278	IDILI−
Moxifloxacin	0.1296	IDILI−
Levofloxacin	0.1329	IDILI−
Aspirin	0.1445	IDILI−
Flucloxacillin	0.1545	IDILI+
Pioglitazone	0.2935	IDILI−
Telithromycin	0.6685	IDILI+
Flutamide	0.7036	IDILI+
Trovafloxacin	0.7448	IDILI+
Isoniazid	0.7562	IDILI+
Diclofenac	0.8578	IDILI+
Naproxen	0.8589	IDILI+
Doxorubicin	0.8839	IDILI+
Bromfenac	0.9397	IDILI+
Clavulanate	0.9509	IDILI+
Chlorpromazine	0.961	IDILI+
Ibuprofen	0.9733	IDILI+
Valproic acid	0.9909	IDILI+
Nimesulide	1	IDILI+

With regard to the true IDILI classification of drugs, IDILI− indicates that the drug is not associated with IDILI and IDILI + indicates that the drug is associated with IDILI in human patients.

IFN contributed to hepatotoxicity in several animal models of IDILI and was therefore of interest to include in our examination (Hassan et al., 2008; Shaw et al., 2009a; Dugan et al., 2011; Roth et al., 2017). Interestingly, IFN did not synergize with any of the drugs in our study to cause cell death (Fig. 2); however, as we showed previously for diclofenac (Maiuri et al., 2015), IFN enhanced the cytotoxic interaction between several IDILI-associated drugs and TNF. What underlies this pattern of response to IFN is not known; however, IFN can increase expression of TNF receptors (Wang et al., 2006) and, conversely, TNF can increase IFN signaling (Han et al., 1999; Robinson et al., 2003). These actions could explain why IFN had an effect only in the presence of TNF.

We evaluated whether a change in the concentration-response curves due to exposure to IFN could improve the classification of drugs. The classification model developed from the covariates that described the response to drug/TNF/IFN produced ROC curves that were not improved from those incorporating covariates that describe the response to drug/TNF (Supplemental Fig. 3). These results indicate that cytotoxic synergy between IDILI-associated drugs and TNF is sufficient to produce a statistical model that accurately classifies drugs irrespective of the presence of IFN. They also suggest that the cell killing activity of IFN depends on the presence of TNF.

It is worth considering the possibility that other cytokines play a role in the pathogenesis of IDILI, and it would be interesting to examine whether other cytokines could interact with drugs to cause cytotoxicity in vitro and/or synergize with TNF to enhance cytotoxicity. Cosgrove et al. (2009) performed a study examining drug/cytokine interactions in vitro and found that interleukin (IL)-1β in combination with TNF and IFN interacted with some drugs to cause cytotoxicity. It is unclear to what extent IL-1β contributed to this interaction. However, Shaw et al. (2009b) demonstrated that IL-1β levels are elevated in mice cotreated with trovafloxacin and lipopolysaccharide, raising the possibility that IL-β plays a role in the hepatotoxicity observed in these mice. Whether the presence of IL-1β or other immune mediators would improve the ability of the models presented herein to classify drugs is unknown but worth considering in future studies.

We reported recently that IFN-mediated enhancement of NSAID/TNF-induced cytotoxicity occurs with some IDILI-associated NSAIDs but not others, and this effect was related to chemical structure and to the magnitude of clinical concern about IDILI for specific NSAIDs (Maiuri et al., 2015). Specifically, several acetic acid derivatives that are associated with IDILI of greatest clinical concern synergized with TNF to cause HepG2 cell death, and IFN enhanced this effect. In contrast, two propionic acid derivatives, which are associated with IDILI that is of less clinical concern, also synergized with TNF, but IFN was without effect. In the analysis presented here, we were seeking a binary answer (IDILI potential yes or no) and inclusion of IFN did not affect the outcome. It would be interesting if the ability of drugs to sensitize cells to the harmful effects of IFN could distinguish drugs of greater concern clinically for IDILI from those of less concern. Clearly, a larger number of drugs would need to be analyzed to evaluate this.

A potential challenge that might be faced when employing this assay during preclinical safety evaluation is the inability to generate complete concentration-response relationships due to solubility limitations of the drug or other factors. Computing covariates using the four-parameter logistic model requires complete concentration-response curves; however, we defined several covariates that can be computed without the need to generate a complete concentration-response curve. One of these is R₁₀, or the drug concentration at which there is an increase of 10% LDH activity above min. Another covariate that could be computed without the need to generate a complete concentration-response curve we defined as “TNF change.” TNF change identifies those drugs that are only cytotoxic in the presence of TNF without the need for complete concentration-response curves. Interestingly, combining the covariates R₁₀ quotient (i.e., R₁₀ TNF/R₁₀ VEH) and TNF change resulted in an ROC curve with an AUC of 0.88 (95% confidence interval, 0.75, 1) (Supplemental Fig. 1). This suggests that a model that leads to good classification of drugs according to their potential to cause IDILI can be generated without the need to delineate complete concentration-response relationships. This model might be useful for predicting the IDILI potential of drug candidates when availability of compound is limited or when solubility limitation prevents generation of a complete concentration-response curve.

Although HepG2 cells are human derived, their use for drug toxicity evaluation has been criticized because they have limited capacity to bioactivate drugs to toxic metabolites via cytochrome P450–mediated pathways. Despite this potential limitation, Cosgrove et al. (2009) found that HepG2 cells behave similarly to primary human hepatocytes in their cytotoxic responses to drug-cytokine combinations. We have also observed comparable responses in primary murine hepatocytes (Zou et al., 2009; Beggs et al., 2014; Maiuri et al., 2015). These findings suggest either that 1) metabolic activation of drugs by HepG2 cells, although limited, is sufficient to stress cells so that they respond to cytokine exposure by dying or 2) metabolism is not generally needed for the cytotoxic interaction of drugs with cytokines.

Visual inspection of Fig. 2 revealed three IDILI+ drugs for which there was modest (flutamide, clavulanate) or no (flucloxacillin) response. Despite this, statistical modeling classified flutamide and clavulanate as IDILI+. In the case of flucloxacillin, analysis of variance of the concentration-response data determined that there was no statistically significant increase in LDH alone or in the presence of TNF. As a result, covariates were set to zero with the exception of C_max, and the calculated probability for flucloxacillin was low (0.154; see the formula in the Materials and Methods). In contrast, analysis of variance applied to the concentration-response data for flutamide alone and in combination with TNF detected very small but statistically significant increases in LDH release relative to baseline (Fig. 2; Supplemental Fig. 1). Consequently, nonzero covariates were generated from the concentration-response data. Similarly for clavulanate, there was an interaction with TNF that was small but statistically significant, resulting in nonzero covariates. These nonzero covariates led to calculated probabilities that, at the optimal cutoff, identified flutamide and clavulanate correctly as IDILI+. The pronounced reproducibility of even small changes using HepG2 cells and the apparent sensitivity of the model in these two cases may be a strength of this approach to classification.

Flutamide is metabolized in vivo to 2-hydroxyflutamide (C_max, 5.74 μM), which is more potent pharmacologically as an antiandrogen (Brogden and Clissold, 1989) and is thought to contribute to IDILI responses (Ball et al., 2016). To strengthen this proof-of-concept study and to further evaluate the modest cytotoxic effect of flutamide, we investigated the performance of 2-hydroxyflutamide in the assay. Concentration-response curves were generated (Supplemental Fig. 5), and covariates derived from the curves were used in the best-performing classification model. A high probability for association with IDILI was calculated (0.999) for 2-hydroxyflutamide. Furthermore, we replaced the flutamide covariate data in the best-performing model with the 2-hydroxyflutamide covariates. Recalculation of the best-performing classification model yielded coefficients similar to those presented in Table 2 (Supplemental Table 11), the same AUC for the ROC curve, and no change in classification of drugs as IDILI+ or IDILI−. These results strengthen the conclusions based on the modest cytotoxic response to flutamide and support the approach to classifying IDILI-associated drugs.

The observation that flucloxacillin was incorrectly classified as not associated with IDILI suggests that the best-performing model, although seemingly promising, has limitations. It is worth noting that flucloxacillin typically produces liver injury in humans that is classified as cholestatic rather than hepatocellular (Enat et al., 1980; Williams and Malatjalian, 1981; Bengtsson et al., 1985; Moseley, 2013). Clavulanate is also associated predominately with a cholestatic pattern of injury in human patients (Sánchez-Ruiz-Granados et al., 2012; Beraldo et al., 2013) and interacted only weakly with TNF. Accordingly, it is possible that the approach described herein is more robust in classifying drugs that cause hepatocellular rather than cholestatic patterns of injury.

In summary, these results add to evidence that drug-induced stress can sensitize hepatocytes to the killing actions of cytokines such as TNF and IFN (reviewed in Roth et al., 2017). Moreover, this could be requisite for the pathogenesis of IDILI, since numerous IDILI-associated drugs show cytotoxic synergy with cytokines in vitro at drug concentrations near those that occur in patients. Currently, effective assays to screen preclinically for IDILI potential are lacking. A method that accurately identifies drug candidates with the potential to cause IDILI could revolutionize preclinical testing strategies. Our results suggest an in vitro assay that could do just that (i.e., by delineating drug concentration-response curves in the absence and presence of TNF and employing resulting covariates in an appropriate statistical model for classification). One of the strengths of this approach is that the user would have discretion to choose a level of risk tolerance guided by the results of ROC analysis. That choice could depend on a variety of factors, including risk tolerance in the context of the therapeutic use, other drug candidates that are in contention for going forward into development, and so forth. For example, if several potentially effective compounds with no apparent toxicity were identified in early preclinical screens but some returned an “IDILI+” result in a drug-cytokine assay, this might prompt a decision to pursue other candidates for development. The magnitude of interaction with TNF assessed by direct inspection of concentration-response curves (Fig. 2) might also be useful to inform such decisions. Overall, this classification approach is attractive because it 1) uses a cell type that is easily obtained and maintained in culture and yields consistent results, 2) requires minimal amounts of test compound, 3) employs a single, easily and inexpensively measured phenotypic endpoint that is directly relevant to IDILI (hepatocellular death), 4) is based on interaction between drug and a product of immune system activation likely to be relevant to IDILI pathogenesis, and 5) is adaptable to high-throughput technology. Validation of this approach as a screening tool will require the evaluation of additional drugs, but the results presented herein are quite promising.

Abbreviations

AUC

area under the curve

IDILI

idiosyncratic drug-induced liver injury

IFN

interferon-γ

IL

interleukin

LDH

lactate dehydrogenase

NSAID

nonsteroidal anti-inflammatory drug

ROC

receiver operating characteristic

TNF

tumor necrosis factor-α

VEH

vehicle

Authorship Contributions

Participated in research design: Maiuri, Wassink, Hession, Ganey, Roth.

Conducted experiments: Maiuri, Turkus, Breier, Lansdell, Kaur.

Performed data analysis: Maiuri, Wassink, Hession, Ganey, Roth.

Wrote or contributed to the writing of the manuscript: Maiuri, Hession, Ganey, Roth.