Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2017 May 24;119(2):55–63. doi: 10.1038/hdy.2017.26

Comparison of different genetic distances to test isolation by distance between populations

M Séré 1,2,3, S Thévenon 2,3, A M G Belem 4, T De Meeûs 2,3,*
PMCID: PMC5564375  PMID: 28537571

Abstract

Studying isolation by distance can provide useful demographic information. To analyze isolation by distance from molecular data, one can use some kind of genetic distance or coalescent simulations. Molecular markers can often display technical caveats, such as PCR-based amplification failures (null alleles, allelic dropouts). These problems can alter population parameter inferences that can be extracted from molecular data. In this simulation study, we analyze the behavior of different genetic distances in Island (null hypothesis) and stepping stone models displaying varying neighborhood sizes. Impact of null alleles of increasing frequency is also studied. In stepping stone models without null alleles, the best statistic to detect isolation by distance in most situations is the chord distance DCSE. Nevertheless, for markers with genetic diversities HS<0.4–0.5, all statistics tend to display the same statistical power. Marginal sub-populations behave as smaller neighborhoods. Metapopulations composed of small sub-population numbers thus display smaller neighborhood sizes. When null alleles are introduced, the power of detection of isolation by distance is significantly reduced and DCSE remains the most powerful genetic distance. We also show that the proportion of null allelic states interact with the slope of the regression of FST/(1−FST) as a function of geographic distance. This can have important consequences on inferences that can be made from such data. Nevertheless, Chapuis and Estoup’s FreeNA correction for null alleles provides very good results in most situations. We finally use our conclusions for reanalyzing and reinterpreting some published data sets.

Introduction

The ecology of natural populations can conveniently be assessed through the study of spatio-temporal genetic variations of molecular markers with population genetics tools. This is particularly useful for organisms such as parasites and vectors that are difficult to observe directly even with mark–release–recapture methods. Indirect methods offer the possibility to access to rare and past events (Slatkin, 1987), reproductive modes and/or strategies, dispersal, population sizes and pattern of population subdivision (De Meeûs et al., 2007).

Different patterns of population subdivision can occur. The most frequent one probably corresponds to situations where geographic distance is the main factor limiting gene flow and thus allowing local genetic differentiation. This was called isolation by distance by Wright who derived the first model (Wright, 1943). Since then, different patterns of isolations by distance were proposed from the discontinuous stepping stone models, where migration mainly occurs between adjacent populations, to continuous models with different dispersal functions (see (Guillot et al., 2009) and references therein). Empirical studies of isolation by distance generally aim at determining the strength and significance of the relationship between an estimator of subdivision (for example, a genetic distance) and geographic distance between subsamples or individuals. This is typically undertaken with two distance matrices of each kind between which a correlation coefficient is computed. The significant departure from 0 of this coefficient is then tested through a randomization procedure, the Mantel test, because the existing autocorrelation that links the different cells in each matrix prevents using parametric methods (De Meeûs et al., 2007). The rows and columns of one matrix are randomized a great number of times and the P-value of the test is the proportion of times a correlation as big as or bigger than the one observed between the true matrices was obtained during these randomizations.

Several parameters and their estimators exist to measure genetic relationship between different subsamples. Among those, Rousset’s θ/(1−θ) (Rousset, 1997) (FST*), where θ is Weir and Cockerham’s (Weir and Cockerham, 1984) unbiased estimator of Wright’s FST (Wright, 1965) or its equivalent between individuals (Watts et al., 2007), was shown to be linearly related to geographic distances (one-dimension frameworks) or to its log transform (two dimensions) with a slope that is inversely proportional to demographic parameters (effective population density and dispersal). FST is not a genetic distance in the strict sense. It is more a relative inbreeding of subsamples as compared with inbreeding in the total sample. It is thus a direct measure of inbreeding due to subdivision and hence is often considered as a measure of differentiation between subsamples. Nevertheless, θ is known to display undesirable behavior as a distance (Kalinowski, 2002) and is especially unstable (large variance) when measured between population pairs (Balloux and Goudet, 2002). These problems led to several authors advising the use of other genetic distances such as the chord distance (Cavalli-Sforza and Edwards, 1967) (DCSE), which provides more reliable relative measures for tree construction (Takezaki and Nei, 1996; Kalinowski, 2002) or the shared alleles distance (DSA) (Bowcock et al., 1994), which can be preferred in some cases (De Meeûs et al., 2010) but without a formal demonstration of the statistical superiority of these distances.

Another difficulty arises when PCR-based amplification failures affect the genotyping of individuals at some loci (for example, null alleles, allelic dropouts). Null alleles lead to underestimation of genetic diversity and overestimation of population differentiation (Chapuis and Estoup, 2007) and to confusions about reproductive strategy inferences (Séré et al., 2014).

Finding methods that are the most powerful at detecting isolation by distance and the least affected by null alleles thus represents an interesting goal.

In this paper, we propose a simulation approach in order to compare the respective performances of three genetic distances, FST* (using θ and other related FST estimators), DCSE and DSA, in terms of statistical power for detecting isolation by distance and of robustness to the presence of null alleles. We then use the distance that displays the best performances to reanalyze real population genetics data sets and check how the initial interpretations are affected.

Methods

Simulations

Simulations were undertaken with EASYPOP version 2.0.1 (Balloux, 2001). We simulated 25, 36, 49 and 64 sub-populations of N=200 dioecious individuals with even sex ratio, random mating and discrete generations. We studied genetic information at 20 loci following a KAM model of mutation (each mutation event changes an allele into one of the K−1 remaining allelic states) with a mutation rate of u=10−4 and K=99. Each simulation started with all alleles present with balanced frequencies in all sub-populations (maximum diversity) and stopped after 10 000 generations (if not specified otherwise), which was considered enough for reaching mutation-drift equilibrium. Two different models of subdivided populations were explored. Island models (see De Meeûs et al., 2007), where no spatial structure is defined, provided the material for the null hypothesis (no isolation by distance). Two-dimension stepping stone models (see De Meeûs et al., 2007) allowed the evaluation of the performance of the different genetic distances in case of more or less pronounced isolation by distance (alternative hypothesis), without null alleles or with increasing frequencies of those. Three migration rates (m) were used (0.01, 0.2 and 0.5). In Island models, only m=0.01 and m=0.5 were used with 100 replicates for each. For stepping stone simulations, 60 replicates were used (except if specified otherwise). For simulations with 49 and 64 sub-populations, only m=0.5 was used. For 25 sub-populations with m=0.5, for which less significant tests were expected, we undertook 80 replicates. For each replicate, 10 sub-populations with 20 individuals (10 females and 10 males) were sampled. We minimized edge effects by choosing sub-populations with four neighbors, except in the 25 sub-populations case were one sub-population had three neighbors. Coordinates of chosen sub-populations were (row, column): (2,1) (3 neighbors), (2,2), (2,3), (2,4), (3,2), (3,3), (3,4), (4,2), (4,3), (4,4) for 25 sub-populations simulations; (2,2), (2,3), (2,4), (2,5), (3,2), (3,3), (3,4), (3,5), (4,2), (4,3) for 36 sub-populations; (2,2), (2,3), (2,4), (2,5), (2,6), (3,2), (3,3), (3,4), (3,5), (3,6) for 49 sub-populations; and (2,2), (2,3), (2,4), (2,5), (2,6), (2,7), (3,2), (3,3), (3,4), (3,5) for 64 sub-populations. A supplementary 20 replicates set was undertaken with 121 and 400 sub-populations in two-dimension stepping stones to check for the effects of edges and mean number of neighbors per sub-population on slope estimate and its variance. With n sub-populations, the mean number of neighbors for each sub-population is 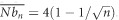Inline graphic. With 400 sub-populations, the mean number of neighbors (3.8) is then reasonably close to the one in a torus (4) and hence the effect of marginal sub-populations becomes more discrete. For n=400, two sample sets were analyzed: central set with sub-populations at coordinates (9,8), (9,9), (9,10), (9,11), (9,12), (10,8), (10,9), (10,10) (10,11) and (10,12); and Marginal set with populations at coordinates (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (1,9) and (1,10). For these 20 replicates, migration rate was m=0.5 and the number of generation only 200, which was enough for reaching equilibrium for FST. Other parameters were the same as for other simulations. Graphic representations of the different sampling designs can be found in Supplementary File S1. The effect of reducing the number of possible alleles was also explored with K=2, u=10−9 (to conform to single-nucleotide polymorphisms) (Séré et al., 2014), n=25 sub-populations and m=0.5. In that case, we used 20 loci to compare with other cases and 200 loci to conform to what could be advised for single-nucleotide polymorphisms. We also undertook some simulations with K=5 and u=10−7, K=10 and u=10−6, K=20 and u=10−5 and K=40 and u=10−4. This was carried out for m=0.5 and n=36 or n=25. Finally, variable sub-population sizes were explored with sub-population sizes alternating between 100 and 200 individuals in the 36 sub-population case (the most discriminating between genetic distances, see below) with the same other parameters as described above.

Null alleles

We define null alleles as alleles that cannot be seen (as it occurs through PCR amplification failure). At a given locus, an individual can thus be homozygous or heterozygous for normal alleles, homozygous for the same null allele or heterozygous for two different null alleles, in which cases the individual corresponds to a missing data (blank) at the corresponding locus. It can be heterozygous for a normal and a null allele, in which case the individual is seen as a homozygous for the normal allele. In simulations, null alleles were generated by recoding the data outputted by EASYPOP. For each locus, alleles 1–10 (10% of null alleles), 1–20 (20%) and 1–50 (50%) were recoded as null alleles. Hence, individuals harboring one of these alleles were recoded as homozygous for the other allele harbored, individuals harboring two of these alleles were recoded as missing data and individuals harboring none of these alleles were not recoded. At the end of each simulation, some alleles are lost by drift. This produces a large variation of null allele frequencies across loci (absence, weak medium or substantial frequency) as it is expected in real data with null alleles (De Meeûs et al., 2007; Séré et al., 2014). These proportions of null alleles (10, 20 and 50%) actually correspond to the proportions of allelic states that are null. For the sake of simplification, we will call these ‘Proportion of null alleles’ or ‘Null allele frequencies’.

Geographic and genetic distances

Geographic distances (DG) between each sub-population pairs were computed with the Euclidian distance using their coordinates as implemented in Genepop version 4.6 kindly provided by F Rousset before online publication (updated from Rousset, 2008).

We have used three genetic distances among the most popular ones: DCSE (Cavalli-Sforza and Edwards, 1967), DSA (Bowcock et al., 1994), and FST*=FST/(1−FST) (Rousset, 1997). Other FST-related measures were also studied in a subset of simulated data sets: GST′ (Meirmans and Hedrick, 2011) and DJ (Jost, 2008), computed with GenAlEx 6.5 (Peakall and Smouse, 2012); Robertson and Hill’s FST_RH and its modified version FST_RH′ (Raufaste and Bonhomme, 2000), computed with Genetix (Belkhir et al., 2004). DCSE and DSA were computed with MSA v3.1 (Dieringer and Schlötterer, 2003). In one instance, MSA could not compute one genetic distance for unknown reasons. This distance was recomputed with FreeNA (Chapuis and Estoup, 2007). We then used Genepop to compute FST*=θ/(1−θ), where θ is Weir and Cockerham’s unbiased estimator of FST (Weir and Cockerham, 1984). In two-dimension isolation by distance, the slope b of the regression FST*=a+b × ln(DG) is inversely proportional to the average neighborhood size of a sub-population: b=1/(4πDeσ2), where De is the effective sub-population density and σ2 is the average squared axial distance between an adult and its parents (dispersal) (Rousset, 1997) and hence σ is half the average adult–parent distance.

Detecting isolation by distance

For each data set, not recoded or recoded for null allele presence, correlation between geographic and genetic distances was computed and tested with a Mantel test with Genepop and 1 000 000 randomizations, as recommended (De Meeûs et al., 2007). The test uses Pearson’s regression coefficient between geographic and genetic distance matrices as the statistics and the P-value of the test corresponds to the proportion of times the randomized regression coefficient is as big as or bigger than the observed one. For the sake of homogeneity, all Mantel tests were undertaken with the ln transform of geographic distances. Even if the P-values obtained with the untransformed distances can be different, this did not affect the proportion of significant tests obtained (not shown). The proportion of significant tests at the 5% level was used to compare performances between the different genetic distances and between data sets with or without null alleles. Genepop also performs an ABC Bootstrap procedure that allows computing a 95% confidence interval (CI) for the regression slope. For each data set, in addition to Mantel tests using genetic distances, we have also recorded when this CI excluded the 0 value as a significant test at the 5% level (95% CI).

For simulations with the Island model (no spatial structure), to check if no >5% significant tests were obtained with each genetic distance, we undertook a unilateral exact binomial test with R version 3.2.1 (R Development Core Team, 2016).

Performance comparisons between genetic distances were carried out with Fisher’s exact tests with R. To account for multiple non-independents testing, the P-values obtained were adjusted with the sequential Bonferroni procedure (for example, De Meeûs, 2014).

The effect of null alleles on the power to detect isolation by distance was assessed with generalized mixed models with a binomial error distribution and a logit link with the package lme4 of R (Bates et al., 2015). The model (command glmer) had the form:

graphic file with name hdy201726e1.jpg

where, for ‘Significance’, a value of 0 was given if P>0.05 and a value of 1 was given if P⩽0.05, ‘GenetDist’ is a factor defining one of the three genetic distances, ‘PropNulls’ is the proportion of null alleles as defined above, ‘m’ is the migration rate, ‘(1|Rep)’ are the random effects of replicates and ‘:’ stands for interaction between two variables.

To check whether collinearity between explanatory variables might explain convergence failure for the model above, significance co-occurrence between statistics (for example, between FST* and DCSE) was measured by recoding the results as 1 (not significant) and 2 (significant) for each statistic and doubling these coding (11 or 22) to build an artificial genotypic data set with four ‘loci’ (the four statistics) with two alleles each (hence if FST* and DCSE gave a significant isolation by distance this would result in genotypes 22 and 22). We then computed Garnier Géré and Dillman correlation coefficient rGGD (Garnier-Géré and Dillmann, 1992) between each ‘locus’ pair. This correlation was computed in Genetix 4.05.2 (Belkhir et al., 2004).

Effects of null alleles on the regression slope of isolation by distance

The effect of null alleles and migration rate on the slope b, of the regression FST*=a+b × ln(DG), was assessed with a linear mixed effect model (lme) (Pinheiro et al., 2014), fitted with the maximum likelihood method, with package nlme of R version 3.0.2 and a model of the type:

graphic file with name hdy201726e2.jpg

where the random effects are the replicates (random=~1|Rep). The variance in each replicate increases as a function of the proportion on null alleles and migration rates. To account for this violation of homoscedasticity, we used the argument ‘weights’ (weights=varIdent(form=~1|PropNulls) or weights=varIdent(form=~1|m)), as recommended in the R documentation (Pinheiro and Bates, 2000). Because the slope (bounded between −1 and +1) cannot strictly follow a normal distribution, we also undertook Spearman correlation tests with the package rcmdr (Fox, 2005) of R for each migration rate separately.

The effect of the proportion of null alleles and migration rate on the variance of the slope of the aforementioned regression was analyzed with a linear regression with R and the model:

graphic file with name hdy201726e3.jpg

The quality of fit of each of aforementioned model was assessed by graphically checking residuals’ normality and homoscedasticity. For each model, the minimal model was looked for with the command ‘drop1’, using the Akaike information criterion (AIC; Akaike, 1974).

Comparative vulnerability of the different genetic distances to null alleles

For each genetic distance, the coefficient of determination (R2, the proportion of variance explained by the model) of the regressions between ln(DG) matrix and genetic distances matrices with null alleles of increasing frequencies (0, 0.1, 0.2 and 0.5) was computed for each replicate of each parameter set. We used rcmdr to compute R2. For each parameter set, in terms of null allele frequency and migration rate, and for each genetic distance, we computed the average R2 (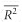Inline graphic) over replicates and used the s.d. 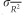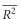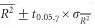of the mean Inline graphic and Student’s t0.05,γ, where γ=Nrep−1 (Nrep=number of replicates of a given simulation), to compute the 95% CIs of each Inline graphic as Inline graphic. We then applied a generalized mixed model to the data, as described above with a random effect of replicates (random=~1|Rep), fitted with the maximum likelihood method (method=‘ML’), adjusted for heteroscedasticity with the argument ‘weights=varIdent(form=~1|PropNulls)’ or ‘weights=varIdent(form=~1|m)’ (model with the lowest AIC was kept). The model explored was:

graphic file with name hdy201726e4.jpg

Here again the function drop1 was used to try selecting the best (minimal) model.

Using corrected estimates

We also checked how far results can be improved using the available correcting option implemented in the software FreeNA (Chapuis and Estoup, 2007). Genetic parameters are estimated from the corrected data set (replacing all missing genotypes by homozygous genotypes for the same null allele labeled 999) only on visible alleles and using the ENA correction method for FST and using the INA correction method for DCSE (Chapuis and Estoup, 2007). We also used these estimations on several simulated data sets with null alleles to check for the effect on the slope and on power of isolation by distance testing with regression approaches.

Real data

Several available data sets using microsatellite markers were reanalyzed to illustrate our results. For all data, we transformed GPS coordinates (Genepop uses coordinates of subsamples or individuals) into UTM so that we get geographic distances in meters. The first data set was on the European vector of Lyme disease, the tick Ixodes ricinus (De Meeûs et al., 2002) where a lot of null alleles are present (frequently 40–50% and up to 60 %). The second concerned the rusa deer Cervus timorensis russa in New-Caledonia (De Garine-Wichatitsky et al., 2009; without null allelles). The third and fourth data came from (Kone et al., 2011) on two tsetse flies (trypanosomosis vectors), Glossina tachinoides and G. palpalis gambiensis in Burkina Faso, where as many as 40–50 % of null alleles can be found and up to 70%. The fifth data concerned another tsetse fly, G. palpalis from Cameroon and from the Democratic Republic of Congo (DRC), (Mélachio et al., 2011) where null allele proportions frequently reach 40–50% and up to 70%. The sixth data set concerned Leishmania guyanensis (a trypanosomatid parasites) from French Guyana (Rougeron et al., 2011) without null alleles. For I. ricinus and tsetse fly data, because some loci are X-linked, we only used females so that FreeNA results are not too biased by male genotypes at these loci. These data sets were all analyzed for isolation by distance using Genepop using FST* and DCSE on raw data and on FreeNA-corrected data. We then compared the P-values obtained and also the neighborhood size as Nb=1/b (b is the slope of the isolation by distance regression) (Rousset, 1997). For L. guyanensis, data could only be analyzed at an individual-based scale. We used the statistic a (Watts et al., 2007) as recommended when the slope b obtained is such that neighborhood Nb=1/b<50. FreeNA cannot compute this statistic so that the effect on the slope could not be assessed here. Three independent samples (2006, 2007 and 2008) were analyzed separately and then the resulting P-values combined with generalized binomial procedure with MultiTest V 1.2 (De Meeûs et al., 2009) setting the threshold number of tests k′=3 as recommended when the total number of tests is <4 (De Meeûs, 2014). Some data sets did not have strong evidence for null alleles (rusa deer and Leishmania) while other displayed strong evidence for null alleles (ticks, tsetse flies) with other problems, such as probable Wahlund effects (ticks and G. palpalis gambiensis) or short allele dominance (ticks). Leishmania were shown to alternate clonal propagation with sexual recombination with a strong tendency for mating between relatives (inbreeding).

Results

For all simulations with 10 000 generations (25–64 sub-populations), the final mean number alleles maintained and unbiased estimate of genetic diversity HS (Nei and Chesser, 1983) varied between 17 and 37 and between 0.58 and 0.84, respectively (see Supplementary File S1), which should provide unbiased estimates of Deσ2 (Leblois et al., 2003). For bigger simulations (121 and 400 sub-populations) that were run for only 1000 and 200 generations only, values obtained are far beyond the limit and are expected to give biased estimates. In fact, only the case with 121 sub-populations provided biased slope estimates (Supplementary File S1, worksheet ‘Compare slopes’).

Detecting isolation by distance under the null hypothesis

In the Island model, where no spatial structure exists, no procedure gave >5% significant isolation by distance signature (all P-values >0.2, exact unilateral binomial tests). With 11 (5.5 %), 7 (3.5 %), 13 (6.5 %) and 8 (4 %) significant tests (out of 200 tests) for 95% CI for the regression slope, FST*, DCSE and DSA respectively, no procedure gave more often significant tests than the other (P-value=0.5047, Fisher exact test; Supplementary File S1). This confirms the robustness of Mantel test. With between 3.5% and 6.5 % significant tests under the null hypothesis, it also highlights that with such data sets Mantel test is not too conservative.

Detecting isolation by distance under the alternative hypothesis

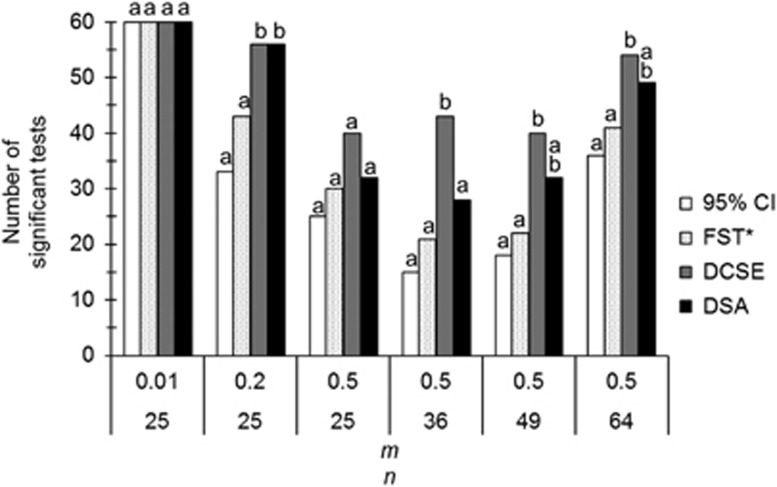
For the stepping stone model, results are presented in Figure 1. Detailed simulation results are available in Supplementary File S1. The best results are observed for DCSE. Globally, summing all significant values across the 380 simulations for all genetic distances, all comparisons are significant after sequential Bonferroni correction. The poorest statistic is the test based on 95% CI of the slope (95% CI) (187 significant tests), followed by FST* (217 significant tests), DSA (257 significant tests) and DCSE (293 significant tests). Except when migration rates are low, where the different statistics tend to perform equally well, difference in performance between the different genetic distances follows the same pattern independently of the number of sub-populations: 95% CI<FST*<DSA<DCSE. We checked this in the most discriminating simulations in stepping stone models of 36 sub-populations. In Supplementary File S1 (worksheet ‘OtherDistances’), it can be seen that the P-values obtained for isolation by distance with GST′ and DJ are almost completely correlated to those obtained with FST* (r>0.889) and thus offer no benefit for isolation by distance detection. Alternatively, FST_RH appears more performant than all other statistics but DCSE, while FST_RH′ appears just above FST*. From the Supplementary File S1, it can be seen that the regression slope (b) obtained with FST_RH is negatively biased as compared with Weir and Cockerham’s based FST* and that this bias increases with FST, while its variance is much smaller one, as expected (Raufaste and Bonhomme, 2000). It can also be seen that FST_RH′ displays a constant positive bias and the highest variance, which explains its poor performances.

Figure 1.

Figure 1

Open in a new tab

Performance comparisons between the different genetic distances to detect isolation by distance in two-dimension stepping stones with different migration rates (m) and sub-population numbers (n). Four different procedures are compared: the 95% CI of the slope obtained by ABC bootstrap (95% CI), mantel tests using FST*, DCSE or DSA. Letters a and b are indicative of significant differences of performance after sequential Bonferroni correction: bars with no letter in common are significantly different. More explanations can be found in the text.

Effect of sub-population number on the slope and its variance

There is a negative, though marginally not significant (P-value=0.0599) relationship between the slope and the number of sub-populations, with a decrease of the positive bias of b (from ~0.003 for n=25 to ~0.002 for n=64) as compared with the expected value be=1/2πNm (Rousset, 1997) (0.00159 when N=200 and m=0.5) with decreasing sub-population number. This may come from the mean number of neighbors per sub-population, which tends to increase with the total number of sub-populations, as the proportion of marginal sub-populations decreases as well. To confirm this, we have studied the slope and its variance in the center and the margin of 20 × 20=400 sub-populations of 200 individuals in a stepping stone with m=0.5 (10 replicates). The mean slope observed for central sub-populations perfectly fits the expected value and is significantly above for marginal sub-populations (Supplementary File S1). At the same time, we can observe a swift decrease of 95% CI with the number of sub-populations. As a consequence, the proportion of significant tests tends to increase with the number of sub-populations n. Nevertheless, the relative performance of each statistic, as compared with the others, remains unchanged and hence DCSE stays the best statistic for detecting isolation by distance.

Reduced number of possible alleles on statistical power

When the number of available alleles is K=2, there is no more significant differences in performances between the different statistics, which all show weak power to detect isolation by distance (only 11% tests are significant with DCSE against 50% when K=99). At the same time, averaged slopes are not affected but the variance doubled (Supplementary File S1). With the more realistic 200 loci, the power to detect isolation by distance and lower variance for slope are restored. Nevertheless, no genetic distance seems better than the other in that configuration (Supplementary File S1).

Effect of variable sub-population size on the power of tests

In that case, DCSE still displays the highest power but is not significantly better than DSA anymore in that respect (Supplementary File S1).

Effect of null alleles on the power to detect a signature of isolation by distance

We have already seen that the number of sub-populations does not influence statistics’ relative performances in detecting isolation by distance. Nevertheless, small sub-population numbers increases the variance of these statistics and hence decreases the power to detect isolation by distance for all them. Consequently, the effect of null alleles was only studied with n=25 stepping stone models. The best model and significance of variables of the generalized linear mixed model are presented in Supplementary Table S1. The model could never converge when 95% CI was included, as a probable result of its collinearity with other statistics as can be measured with Garnier Géré and Dillman rGGD (see Supplementary File S1). We also needed to remove two interaction terms (m:PropNulls and m:GenetDist). After model comparisons with the AIC, the minimum model retained is Significance~PropNulls+m+GenetDist+(1|Rep). The results obtained with the generalized mixed effect model show that FST* has far less power to detect isolation by distance than DCSE, and DSA has slightly less power than DCSE (Supplementary Table S1 and Supplementary File S2). As expected, migration rate has a major negative effect. The power of detection of isolation by distance signatures is strongly negatively correlated with the proportion of null alleles. The interaction between genetic distances and the proportion of null alleles was not important for the model (lower AIC without it) and was thus removed from the model. Hence, the performance differences between all distances do not significantly change with null alleles.

Effect of null alleles on the slope of Rousset’s regression

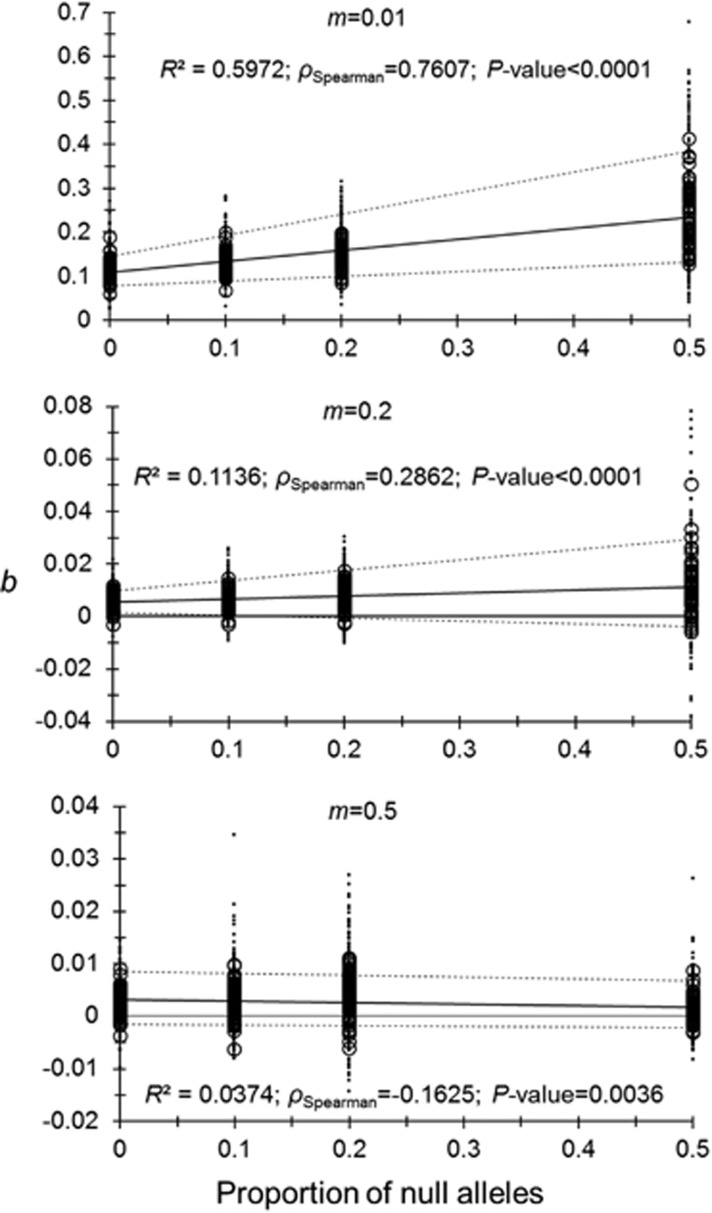
The analysis of this model is presented in Supplementary Table S2 and in Supplementary File S2. Controlling for the increasing variance of the residuals with null allele frequencies or migration rates (weights=varIdent(form=~1|PropNulls) or weights=varIdent(form=~1|m)) provided identical results for the linear mixed effect model, though AIC was smaller with the second model. All parameters and interactions appeared highly significant (Supplementary Table S2). The corresponding results of Spearman correlation (ρ) test results are given in Figure 2. It can be seen that there is a significant positive effect of null allele frequencies on the slope (b) of the regression FST*= a+b × ln(DG) for the smallest neighborhoods (m⩽0.2) and a reverse relationship for the biggest neighborhood (m=0.5) (interaction between m and null allele frequency). The three Spearman’s rank correlation tests (for each migration rate explored) were all highly significant.

Figure 2.

Figure 2

Open in a new tab

Influence of null allele frequencies on the slope of the regression between FST* and ln(DG) for different migration rates (m=0.01, m=0.2 and m=0.5). In each graph, Spearman’s correlation (ρ) and its significance (P-value) are given (bilateral tests). The regression of b (circles) as a function of null allele frequencies is represented with a thick straight line and the corresponding determination coefficient is also given (R2). The 95% CIs of slope values obtained by ABC bootstraps in Genepop (small dots) are also given with their corresponding regression (dotted thin lines). When useful, the 0 line is represented by a thin straight line.

There is also an increase of the variance with null allele frequencies when neighborhoods are small but not for the biggest ones (m=0.5) (Supplementary Table S3 and Figure 2) (see corresponding graphics in Supplementary File S2). The significant interaction between m and the proportion of null alleles makes the effect of m very uneasy to predict and is not significant with the t-test. An analysis of variance does not confirm the significance of null alleles proportion (m becomes significant). Thus the interaction at least is significant (Supplementary Table S3).

Vulnerability of the different genetic distances to null alleles

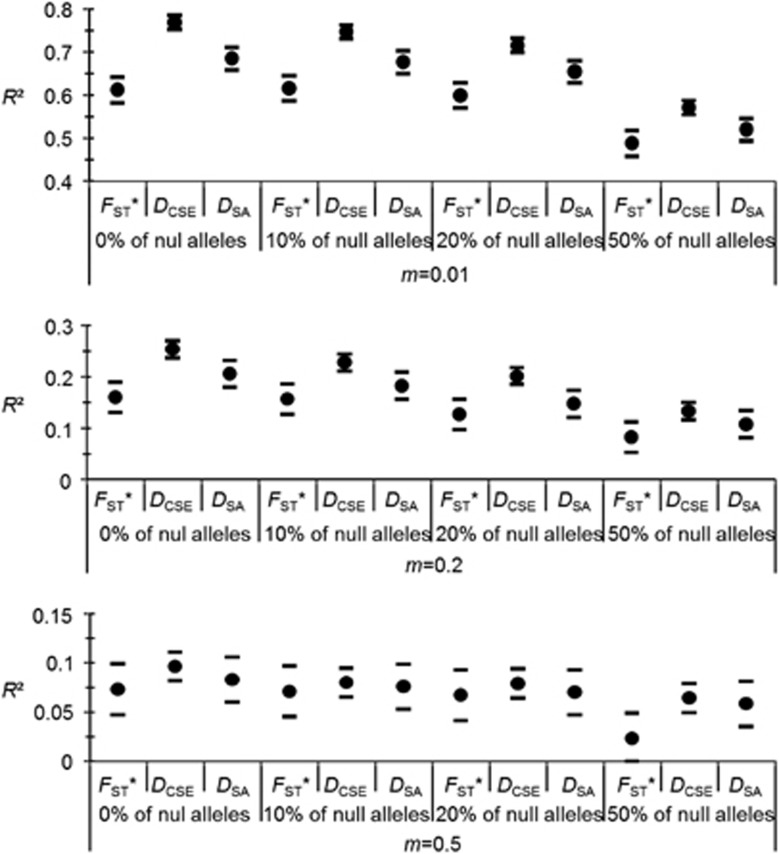
Results of the fixed effect model are given in Supplementary Table S4. The smallest AIC was obtained for the model with weights=varIdent(form=~1|m). Dropping terms lead to remove the interaction between null allele frequencies and genetic distances and all other parameters were highly significant (Supplementary Table S4). The proportion of null alleles and migration rates are the most important factors and DCSE is associated with the highest R2, followed by DSA and then FST*. All parameters significantly interact with m: the difference between genetic distances is the highest for low migration rates and low null allele frequencies and the magnitude of differences tends to drop for highest values (see Figure 3 and Supplementary File S2).

Figure 3.

Figure 3

Open in a new tab

Effects of null allele frequency, migration rate (m) and genetic distances on the determination coefficient (R2) of regressions between the different genetic distances as a function of geographic distances ln(DG). The bigger R2 the better the genetic distances account for the respective geographic location of each sub-population as compared with the others. The mean R2 and 95% CIs across replicates are represented. Note that negative values of lower bounds were replaced by 0.

Using FreeNa corrections

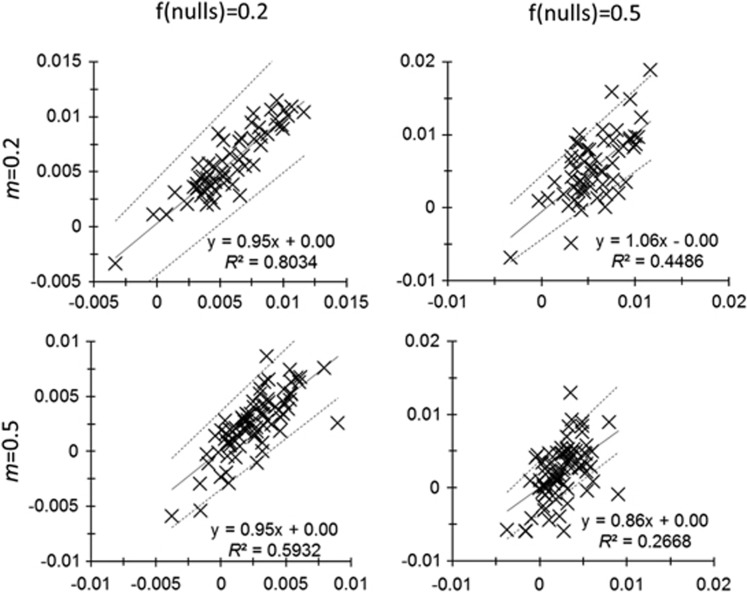
Simulations were revisited with the correction implemented in FreeNA. In the Figure 4 (see also Supplementary File S2), it can be seen that FreeNA provides a very good correction for the slope, except when the proportion of null alleles is too big (50%) and isolation by distance weak (m=0.5), because the variance of estimate becomes very large, thus reducing R2 to a great extent with a slight alteration of slope estimate (Figure 4). A logistic mixed model on the significance obtained with FreeNA-corrected data was undertaken using DCSE. It suggests that using FreeNA-corrected data does not bring more power and even less so (Supplementary Table S5). There is also a small effect of interactions of statistics with the other variables, suggesting that for some migration rates and/or null allele frequencies FreeNA-corrected data may be slightly more powerful, but the effect is obviously weak as compared with the effect of null alleles alone (see also Supplementary File S3).

Figure 4.

Figure 4

Open in a new tab

Regression results between the initial isolation by distance slopes obtained without null alleles (abscissa) and the slopes obtained using FreeNA correction for null alleles (ordinates). Regressions displayed are for different null allele frequencies (f(nulls)) and migration rates (m). Resulting regression formula and corresponding determination coefficient (R2) are given. The slopes and intercepts of these regressions actually measure the average bias of FreeNA-corrected values while R2 measures how FreeNA-corrected slopes fit to initial ones.

Real data

Results are presented in Supplementary File S3. Generally speaking, as for the simulation results, FreeNA does not bring much benefit for the significance of the tests and DCSE from unmodified data provided more power to the tests, except for G. palpalis palpalis from Cameroon and DRC and G. palpalis gambiensis from Burkina-Faso.

For I. ricinus females from Switzerland, even if the drop in P-value is substantial (from 0.241 to 0.088), the use of DCSE leads to a marginally not significant isolation by distance. The use of FreeNA provides a strong effect as it leads to almost halve Nb (from 707 to 444 individuals) (hence in the wrong direction).

For Cervus timorensis russa in New-Caledonia, using DCSE changes the significance level from 0.15 to 0.008 and, as expected with a data set with no or almost no null alleles, neighborhood size is weakly affected when using FreeNA correction (from 104 to 107).

For Glossina tachinoides females in Burkina Faso, the use of DCSE is important (the P-value drops from 0.1 to 0.005) and FreeNA has much effect on Nb that increases from 81 to 1667.

For G. palpalis palpalis from Cameroon and DRC, FST*-based tests provide highly significant results while DCSE-based tests give marginally not significant P-values (0 and 0.146, respectively). The FreeNA-corrected Nb is weakly increased (from 153 to 179).

For Glossina palpalis gambiensis females from Burkina Faso, the smallest P-value is obtained with FST* on FreeNA-adjusted data (0.004) while DCSE does not give a significant result (0.522). Here Nb estimated from FreeNA-corrected data decreases from 249 to 196, instead of increasing.

Finally, in L. guyanensis data from French Guyana, the P-value obtained with a (3 years combined) drops from a slightly significant value with FST* (0.017) to a highly significant value when using DCSE (0.0018).

Discussion

Our Island model simulations have confirmed the robustness of Mantel tests as no >5% significant tests were found in that case.

In two-dimension stepping stone models, the most powerful statistic to detect isolation by distance is DCSE, followed in order of power by FST_RH, DSA, FST_RH′, FST* (together with GST′ and DJ) and the least powerful being the test based on the 95% CI of the slope. The fact that FST_RH provides more powerful tests than the other statistics but DCSE is probably linked to its very low variance for small values (Raufaste and Bonhomme, 2000), which concerns most of our simulations. The greater weight given to the rarest alleles is probably the main cause of this, though unbalanced samplings, which were not fully explored here, might lower the good properties of this statistic in this respect (Goudet et al., 1996). Similar reasons probably explain the greater power of DCSE (Kalinowski, 2002), though its connection with FST-based measures is more complex.

When subdivision is extreme (m=0.01), choice of a genetic distance to detect a significant signature of isolation by distance becomes irrelevant (all statistics behave equally well). The same lack of difference occurs for weakly polymorphic loci as when K=2 where at least 200 loci are required for the sake of statistical power and slope estimate accuracy. This is more than classically advised given our sample sizes (20) (for example, Smouse, 2010). In fact, it can be seen from Supplementary File S5 that DCSE outperforms the other statistics only when genetic diversity outreaches 0.4–0.5 (hence applying to microsatellite markers). The difference of statistical power may thus be related to the way allele frequencies are weighted by each statistic. Nevertheless, it is somehow difficult to understand this when more than two alleles are maintained. It will thus require further theoretical investigations to be fully understood. Performance ranking is not influenced by the number of sub-populations, sub-population size variation or by the proportion of null alleles. The poor performances of FST-based measures is a confirmation of earlier studies where it was shown that its weak statistical performances results from an inflated variance of its unbiased estimator θ especially when measured between paired subsamples (Balloux and Goudet, 2002). Intrinsically, FST is more a measure of inbreeding within subsamples than a genetic distance between subsample pairs.

Another interesting and unexpected result is the influence of marginal sub-populations, located at the edges of the metapopulation. Because these marginal sub-populations receive immigrants from less numerous neighbors, this results in an increase of estimated slope when these marginal sub-populations are included in the sample or at the vicinity of those. Moreover, because in small metapopulations central sub-populations are more closely related to these marginal sub-populations, this slope inflation will also affect the entire mesh. This also increases the heterogeneity between different sub-populations and thus the variance of slope estimates and hence the power of isolation by distance tests. Consequently, sampling at the margins of any metapopulation will result in a reduced neighborhood size as compared with central sub-populations, and sampling small metapopulation (25–64 sub-populations) will also result in reduced effective neighborhood size and decline the power of isolation by distance detection (because of increased variance).

The presence of null alleles disturbs the signature of isolation by distance not only in terms of detection but also in terms of the slope of the regression that can be used for demographic inferences. The decrease of power detection affects each distance equally. More importantly, null alleles generate an inflated estimate of the slope and of its variance. With regard to demographic inferences, null alleles will therefore lead to an underestimate of neighborhood sizes and/or of dispersal but with an inflated uncertainty as well.

Chord distance DCSE is known to better reflect the topology of branching nodes between subsamples or species (Takezaki and Nei, 1996). We confirm here that DCSE also reflects geographic distances more accurately than DSA and FST and is also the most robust genetic distance to null allele interference in that respect.

Null alleles are known to have major effects when differentiation is strong and much weaker effects when it is weak (Chapuis and Estoup, 2007). We confirm this in the isolation by distance case, with an additional interactive effect. Indeed, in case of high migration rate (m=0.5), weak null allele effect on FST* seems to interact strongly with its variance resulting in a decrease of the regression slope of isolation by distance with null allele frequencies, while it increases with those in case of smaller neighborhoods (for example, m=0.2).

FreeNA correction (Chapuis and Estoup, 2007) appears quite satisfactory if not excellent, at least for slope estimates, except for high null allele frequencies and strong migration rates where the variance of estimates might provide unreliable results. Statistically speaking though, this correction brings weak improvements if any. Nevertheless, the underlying hypothesis of FreeNA is that observed heterozygote deficits must be entirely explained by null alleles. Other factors can produce heterozygote deficits as measured by FIS. Wahlund effects and selfing should affect all loci equally in this respect and consequently should theoretically be easy to distinguish from null alleles that affect each locus in a particular way. Nevertheless, null alleles are not specific to panmictic populations and can as well affect selfing species or subsamples experiencing Wahlund effects. Some methods exist for quantifying the relative effects of inbreeding and null alleles (for example, see Campagne et al., 2012 and references therein). In a simulation with the same parameters as described above, with 20% of selfing and m=0.01, the use of FreeNA produced an underestimate of the isolation by distance slope of 6% in average, which is not much and thus validates the usefulness of FreeNA in that case. Wahlund effect might be more detrimental and will require further attention. Indeed, Wahlund effect will decrease identity between individuals in subsamples and can also increase identity between subsamples resulting in an artificial deflation of genetic differentiation between geographically separated groups. Hence, Wahlund effect is likely to decrease the slope of isolation by distance regressions (and hence increase neighborhood estimate). Applying FreeNA might induce an additional decrease of this slope and lead to biased results. Important Wahlund effects are known to occur in I. ricinus tick populations in Europe (Kempf et al., 2010). This might represent a good explanation why DCSE did not produce a significant isolation by ditance. Nevertheless, the fact that FreeNA correction had such a spectacular decreasing effect on the neighborhood estimate in that particular situation remains obscure. Short allele dominance affecting one of the five loci and high null allele frequencies in four loci probably explains these discrepancies. Wahlund effects are also known to occur in G. palpalis gambiensis and might explain the observed lack of improvement when using DCSE. The results obtained for the rusa deer and Leishmania are in total agreement with what was expected: an increased power of isolation by distance test using DCSE, changing the initial rusa deer P-value into a significant one, and for this last, lacking null alleles, an absence of effect of FreeNA correction. For G. palpalis palpalis, for which Wahlund effect has been excluded as a possible explanation, the reason why the reverse result was obtained for significance ranking between FST* and DCSE might be just due to chance. In our simulation, FST*-based tests could rarely, but possibly, give much smaller P-values than DCSE-based ones. Finally, for G. tachinoides, performances of the different statistics are in the expected direction as is FreeNA-corrected neighborhood size estimate, though the decrease is a bit extreme. Wahlund effect was not detected in that species but may be this would require further investigations.

Finally, one-dimension patterns of migration, which are known to structure more than two-dimension ones (Rousset, 1997; Séré et al., 2014), were not studied here but would probably have provided more frequent isolation by distance detection as a whole. Nevertheless, we see no reasons why DCSE would not remain above the others in that respect, even if this might require further investigations. More complex migration models could also have been explored. This would have required the choice of supplementary parameters (distance of dispersal and kurtosis) with little gain in generalization of the results as we see no obvious reason why this would dramatically change the major conclusions of the present study.

Recommandations

With null allele-free data, using DCSE chord distance (Cavalli-Sforza and Edwards, 1967) represent the best strategy in most situations for detecting isolation by distance, except for low polymorphism situations (HS<0.4) where the choice of any statistics seems irrelevant.

To cite a verbal quotation from a lecture: ‘the best way to handle missing data is to have none’ (literally translated from a lecture given by Jean-Dominique Lebreton). However, sometimes the worse is inevitable. In case of null alleles, if these are not too frequent (no >20%) and if one can be confident that null alleles represent the only explanation for observed heterozygote deficits, FreeNA correction will provide an excellent way to correct for slope biases. As null alleles equally affect the statistical power of all genetic distances, DCSE stays the best option in that case.

Finally, when other factors than null alleles might be responsible for observed heterozygote deficits, available amending method will not be always useful. In such situations, one should consider that null alleles, if evidenced from important variance of Wright’s FIS across loci, will produce a reduced probability to find a significant isolation by distance. In that case, resampling at smaller scales (to avoid or limit Wahlund effects) and redesigning primers (to reduce the consequences of null alleles) might be of help.

Data archiving

All simulation results and real data can be found in Supplementary Files S1–S5. All simulated data can be sent upon request to the corresponding author.

Acknowledgments

This study was financed by the AIRD (Agence Inter-établissements de Recherche pour le Développement) as part of a PEERS program (Programme d’Excellence pour l’Enseignement et la Recherche au Sud) TAO (Trypanosomes et tsétsés en Afrique de l’Ouest: apport de la génétique des populations). It was undertaken in the Lamivect (Laboratoire Mixte International sur les maladies à vecteurs de Bobo-Dioulasso), which is supported by the IRD (Institut Recherche pour le Développement). MS is financed by a grant from the AIRD ‘thèse du programme d’appui au renforcement et à la consolidation des potentiels de recherche dans les pays du Sud’ with the cooperation of the Centre de coopération Internationale en Recherche Agronomique pour le Développement (CIRAD). We thank Dr Sophie Ravel, Dr Bruno Bucheton, Dr Christine Chevillon and Dr Frédéric Simard for very useful discussions during PhD committees. A special thank goes to François Rousset and his patience while discussing many different issues regarding some odd results and for kindly providing Genepop version 4.6 before online publication. We also thank Giuliano Cecchi and Jérémy Bouyer for their help during UTM transformation of GPS coordinates from two different UTM zones. We finally thank Heredity’s Editor and four anonymous referees whose comments helped to considerably improve our manuscript.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

The authors declare no conflict of interest.

Supplementary Material

Supplementary Table S1
Click here for additional data file. (19KB, docx)
Supplementary Table S2
Click here for additional data file. (18.8KB, docx)
Supplementary Table S3
Click here for additional data file. (19.3KB, docx)
Supplementary Table S4
Click here for additional data file. (19.4KB, docx)
Supplementary Table S5
Click here for additional data file. (18.8KB, docx)
Supplementary File
Click here for additional data file. (15KB, docx)
Supplementary File S1
Click here for additional data file. (453.4KB, xlsx)
Supplementary File S2
Click here for additional data file. (631.7KB, xlsx)
Supplementary File S3
Click here for additional data file. (11.4KB, xlsx)
Supplementary File S4
Click here for additional data file. (89.7KB, xlsx)
Supplementary File S5
Click here for additional data file. (102.3KB, xlsx)

References

  1. Akaike H. (1974). A new look at the statistical model identification. IEEE Trans Auto Control 19: 716–723. [Google Scholar]
  2. Balloux F. (2001). EASYPOP (version 1.7): a computer program for population genetics simulations. J Hered 92: 301–302. [DOI] [PubMed] [Google Scholar]
  3. Balloux F, Goudet J. (2002). Statistical properties of population differentiation estimators under stepwise mutation in a finite island model. Mol Ecol 11: 771–783. [DOI] [PubMed] [Google Scholar]
  4. Bates D, Maechler M, Bolker B, Walker S. (2015). Fitting linear mixed-effects models using lme4. J Stat Softw 67: 1–48. [Google Scholar]
  5. Belkhir K, Borsa P, Chikhi L, Raufaste N, Bonhomme F. (2004) GENETIX 4.05, Logiciel Sous Windows TM Pour la Génétique des Populations. Laboratoire Génome, Populations, Interactions, CNRS UMR 5000. Université de Montpellier II: Montpellier, France. [Google Scholar]
  6. Bowcock AM, Ruiz-Linares A, Tomfohrde J, Minch E, Kidd JR, Cavalli-Sforza LL. (1994). High-resolution of human evolutionary trees with polymorphic microsatellites. Nature 368: 455–457. [DOI] [PubMed] [Google Scholar]
  7. Campagne P, Smouse PE, Varouchas G, Silvain JF, Leru B. (2012). Comparing the van Oosterhout and Chybicki-Burczyk methods of estimating null allele frequencies for inbred populations. Mol Ecol Res 12: 975–982. [DOI] [PubMed] [Google Scholar]
  8. Cavalli-Sforza LL, Edwards AWF. (1967). Phylogenetic analysis: model and estimation procedures. Am J Hum Genet 19: 233–257. [PMC free article] [PubMed] [Google Scholar]
  9. Chapuis MP, Estoup A. (2007). Microsatellite null alleles and estimation of population differentiation. Mol Biol Evol 24: 621–631. [DOI] [PubMed] [Google Scholar]
  10. De Garine-Wichatitsky M, De Meeûs T, Chevillon C, Berthier D, Barre N, Thévenon S et al. (2009). Population genetic structure of wild and farmed rusa deer (Cervus timorensis russa in New-Caledonia inferred from polymorphic microsatellite loci. Genetica 137: 313–323. [DOI] [PubMed] [Google Scholar]
  11. De Meeûs T. (2014). Statistical decision from k test series with particular focus on population genetics tools: a DIY notice. Infect Genet Evol 22: 91–93. [DOI] [PubMed] [Google Scholar]
  12. De Meeûs T, Beati L, Delaye C, Aeschlimann A, Renaud F. (2002). Sex-biased genetic structure in the vector of Lyme disease, Ixodes ricinus. Evolution 56: 1802–1807. [DOI] [PubMed] [Google Scholar]
  13. De Meeûs T, Guégan JF, Teriokhin AT. (2009). MultiTest V.1.2, a program to binomially combine independent tests and performance comparison with other related methods on proportional data. BMC Bioinformatics 10: 443. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. De Meeûs T, Koffi BB, Barré N, de Garine-Wichatitsky M, Chevillon C. (2010). Swift sympatric adaptation of a species of cattle tick to a new deer host in New-Caledonia. Infect Genet Evol 10: 976–983. [DOI] [PubMed] [Google Scholar]
  15. De Meeûs T, McCoy KD, Prugnolle F, Chevillon C, Durand P, Hurtrez-Boussès S et al. (2007). Population genetics and molecular epidemiology or how to "débusquer la bête". Infect Genet Evol 7: 308–332. [DOI] [PubMed] [Google Scholar]
  16. Dieringer D, Schlötterer C. (2003). Microsatellite analyser (MSA): a platform independent analysis tool for large microsatellite data sets. Mol Ecol Notes 3: 167–169. [Google Scholar]
  17. Fox J. (2005). The R commander: a basic statistics graphical user interface to R. J Stat Softw 14: 1–42. [Google Scholar]
  18. Garnier-Géré P, Dillmann C. (1992). A computer program for testing pairwise linkage disequilibria in subdivided populations. J Hered 83: 239. [DOI] [PubMed] [Google Scholar]
  19. Goudet J, Raymond M, De Meeûs T, Rousset F. (1996). Testing differentiation in diploid populations. Genetics 144: 1933–1940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Guillot G, Leblois R, Coulon A, Frantz AC. (2009). Statistical methods in spatial genetics. Mol Ecol 18: 4734–4756. [DOI] [PubMed] [Google Scholar]
  21. Jost L. (2008). GST and its relatives do not measure differentiation. Mol Ecol 17: 4015–4026. [DOI] [PubMed] [Google Scholar]
  22. Kalinowski ST. (2002). Evolutionary and statistical properties of three genetic distances. Mol Ecol 11: 1263–1273. [DOI] [PubMed] [Google Scholar]
  23. Kempf F, McCoy KD, De Meeûs T. (2010). Wahlund effects and sex-biased dispersal in Ixodes ricinus, the European vector of Lyme borreliosis: new tools for old data. Infect Genet Evol 10: 989–997. [DOI] [PubMed] [Google Scholar]
  24. Kone N, Bouyer J, Ravel S, Vreysen MJB, Domagni KT, Causse S et al. (2011). Contrasting population structures of two vectors of African trypanosomoses in Burkina Faso: consequences for control. PLoS Negl Trop Dis 5: e1217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Leblois R, Estoup A, Rousset F. (2003). Influence of mutational and sampling factors on the estimation of demographic parameters in a "Continuous" population under isolation by distance. Mol Biol Evol 20: 491–502. [DOI] [PubMed] [Google Scholar]
  26. Meirmans PG, Hedrick PW. (2011). Assessing population structure: FST and related measures. Mol Ecol Res 11: 5–18. [DOI] [PubMed] [Google Scholar]
  27. Mélachio T, Tito, Tanekou, Simo G, Ravel S, De Meeûs T et al. (2011). Population genetics of Glossina palpalis palpalis from central African sleeping sickness foci. Parasit Vectors 4: 140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Nei M, Chesser RK. (1983). Estimation of fixation indices and gene diversities. Ann Hum Genet 47 (Pt 3): 253–259. [DOI] [PubMed] [Google Scholar]
  29. Peakall R, Smouse PE. (2012). GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research - an update. Bioinformatics 28: 2537–2539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Pinheiro JC, Bates DM. (2000) Mixed-Effects Models in S and S-PLUS. Springer-Verlag: New York, USA. [Google Scholar]
  31. Pinheiro JC, Bates DM, DebRoy S, Sarkar D, R Core Team. (2014). nlme: linear and nonlinear mixed effects models. R package version 31-117 ed 49.
  32. R Development Core Team. (2016). R Foundation for Statistical Computing: Vienna, Austria Available at: http://www.R-project.org.
  33. Raufaste N, Bonhomme F. (2000). Properties of bias and variance of two multiallelic estimators of FST. Theor Popul Biol 57: 285–296. [DOI] [PubMed] [Google Scholar]
  34. Rougeron V, Bañuls AL, Carme B, Simon S, Couppie P, Nacher M et al. (2011). Reproductive strategies and population structure in Leishmania: substantial amount of sex in Leishmania Viannia guyanensis. Mol Ecol 20: 3116–3127. [DOI] [PubMed] [Google Scholar]
  35. Rousset F. (1997). Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics 145: 1219–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rousset F. (2008). GENEPOP’007: a complete re-implementation of the GENEPOP software for Windows and Linux. Mol Ecol Res 8: 103–106. [DOI] [PubMed] [Google Scholar]
  37. Séré M, Kaboré J, Jamonneau V, Belem AMG, Ayala FJ, De Meeûs T. (2014). Null allele, allelic dropouts or rare sex detection in clonal organisms: simulations and application to real data sets of pathogenic microbes. Parasit Vectors 7: 331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Slatkin M. (1987). Gene flow and the geographic structure of natural populations. Science 236: 787–792. [DOI] [PubMed] [Google Scholar]
  39. Smouse PE. (2010). How many SNPs are enough? Mol Ecol 19: 1265–1266. [DOI] [PubMed] [Google Scholar]
  40. Takezaki N, Nei M. (1996). Genetic distances and reconstruction of phylogenetic trees from microsatellite DNA. Genetics 144: 389–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Watts PC, Rousset F, Saccheri IJ, Leblois R, Kemp SJ, Thompson DJ. (2007). Compatible genetic and ecological estimates of dispersal rates in insect (Coenagrion mercuriale: Odonata: Zygoptera) populations: analysis of ‘neighbourhood size’ using a more precise estimator. Mol Ecol 16: 737–751. [DOI] [PubMed] [Google Scholar]
  42. Weir BS, Cockerham CC. (1984). Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370. [DOI] [PubMed] [Google Scholar]
  43. Wright S. (1943). Isolation by distance. Genetics 28: 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wright S. (1965). The interpretation of population structure by F-statistics with special regard to system of mating. Evolution 19: 395–420. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1
Click here for additional data file. (19KB, docx)
Supplementary Table S2
Click here for additional data file. (18.8KB, docx)
Supplementary Table S3
Click here for additional data file. (19.3KB, docx)
Supplementary Table S4
Click here for additional data file. (19.4KB, docx)
Supplementary Table S5
Click here for additional data file. (18.8KB, docx)
Supplementary File
Click here for additional data file. (15KB, docx)
Supplementary File S1
Click here for additional data file. (453.4KB, xlsx)
Supplementary File S2
Click here for additional data file. (631.7KB, xlsx)
Supplementary File S3
Click here for additional data file. (11.4KB, xlsx)
Supplementary File S4
Click here for additional data file. (89.7KB, xlsx)
Supplementary File S5
Click here for additional data file. (102.3KB, xlsx)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES