Abstract
Genomic selection holds a great promise to accelerate plant breeding via early selection before phenotypes are measured, and it offers major advantages over marker-assisted selection for highly polygenic traits. In addition to genomic data, metabolome and transcriptome are increasingly receiving attention as new data sources for phenotype prediction. We used data available from maize as a model to compare the predictive abilities of three different omic data sources using eight representative methods for six traits. We found that the best linear unbiased prediction overall performs better than other methods across different traits and different omic data, and genomic prediction performs better than transcriptomic and metabolomic predictions. For the same maize data, we also conducted genome-wide association study, transcriptome-wide association studies and metabolome-wide association studies for the six agronomic traits using both the genome-wide efficient mixed model association (GEMMA) method and a modified least absolute shrinkage and selection operator (LASSO) method. The new LASSO method has the ability to perform statistical tests. Simulation studies show that the modified LASSO performs better than GEMMA in terms of high power and low Type 1 error.
Introduction
Genome-wide association studies (GWAS) and genomic selection (GS) are promising fields where genomic technologies are well integrated into plant breeding practices. GWAS have enabled to dissect genetic architecture of complex traits in more than a dozen plants (Zhu et al., 2008). However, GWAS are less suitable for quantitative traits influenced by a large number of genes with small effects, so its utility to breeding is limited. GS has paved the way to overcome the limitation by using all genomic information simultaneously to predict phenotypes, thus avoiding information loss and reducing biases in marker effect estimates (Desta and Ortiz, 2014). Moreover, GS can increase the efficiency of plant breeding due to early selection before phenotypes are measured. GS has been applied to breeding in many aspects such as inbred performance prediction, parental selection and hybrid prediction (Riedelsheimer et al., 2012a; Crossa et al., 2014; Xu et al., 2014; Wang et al., 2017).
Since Meuwissen et al. (2001) first proposed this concept of GS along with several models, numerous statistical methods, including parametric and nonparametric methods, have been used to predict quantitative traits. Parametric methods include best linear unbiased prediction (BLUP; Henderson, 1975), least absolute shrinkage and selection operator (LASSO; Tibshirani, 1996), partial least squares (PLS; Gelandi and Kowalski, 1986) and Bayesian methods such as BayesA, BayesB and Bayesian LASSO (Yi and Xu, 2008; González-Recio and Forni, 2011); nonparametric methods include random forest (Svetnik et al., 2003), support vector machine (SVM; Maenhout et al., 2007) and reproducing kernel Hilbert spaces regression (RKHS; de los Campos et al., 2010). Recently, many investigators have evaluated the performance of various statistical methods used in GS. de los Campos et al. (2013) gave an overview of the parametric methods and concluded that BLUP performs well for most traits and BayesB yields slightly higher predictive accuracy for traits with large-effect quantitative trait loci (QTL). Riedelsheimer et al. (2012b) compared the predictive performance of five different GS methods for traits measured in maize inbred lines, and found that these methods differ slightly in their predictive abilities. Heslot et al. (2012) used 10 GS methods to predict the performance of 18 traits measured in different species, and found that RKHS was the best performer overall across traits and species. Howard et al. (2014) compared the predictabilities of parametric methods with nonparametric models using simulation data, and observed that parametric methods performed slightly better than nonparametric methods for predicting traits with more additive genetic component in their genetic architectures. However, all of the above comparisons were based on genomic data. As metabolomic and expression profiling technologies develop, metabolomic and transcriptomic data provide new sources for phenotypic prediction in several species, such as Arabidopsis thaliana, maize and rice (Meyer et al., 2007; Gärtner et al., 2009; Riedelsheimer et al., 2012a). It is still unknown how these parametric and nonparametric methods perform when using metabolites and transcripts for prediction.
Although GWAS are not designed for detecting QTL for highly polygenic traits, they help us gain insights into the genetic architecture of several important traits in maize including leaf architecture and disease resistance (Kump et al., 2011; Poland et al., 2011; Tian et al., 2011). Numerous statistical approaches have been proposed to perform GWAS, among which the mixed linear model is one of the most popular methods, as it is able to correct for population structure and family relatedness (Yu et al., 2006). Under the framework of the mixed linear model, several methods have been developed to reduce the computational demand, such as the efficient mixed model association (EMMA; Kang et al., 2008) and the genome-wide efficient mixed model association (GEMMA; Zhou and Stephens, 2012). These methods are single-locus methods that test the association between a single locus and the trait of interest at a time. However, it is known that quantitative traits are influenced by a number of QTL, so that models considering association of single locus at a time result in model misspecification, thus likely giving biased results (Gupta et al., 2013). In addition, single-locus methods usually require multiple test corrections for the P-value threshold, such as Bonferroni correction, to control the Type 1 error rate. This criterion is too stringent and many true associations may be missed (Zhang et al., 2011). In contrast, multi-locus associations can overcome these problems because these methods simultaneously use all genetic information of multiple loci and there is no need for multiple testing corrections due to the multi-locus nature (Zhang et al., 2011). Multi-locus methods have shown to perform better than single-locus methods. In multi-locus association studies, the number of markers is often larger than the sample sizes. LASSO is a powerful approach to address the problem, but it does not have a default method to calculate the P-values for markers.
In this article, we used genomic, transcriptomic and metabolomic data to predict the performance of six agronomic traits measured from 339 diverse maize inbred lines using eight representative methods including BLUP, LASSO, PLS, BayesA and BayesB for the parametric methods and RKHS, support vector machine using the radial basis function kernel (SVM-RBF), support vector machine using the polynomial kernel function (SVM-POLY) for the nonparametric methods, and compared the predictive abilities of three omic data and eight different methods. We also provided a new method based on Bayesian theory to perform a significance test for LASSO estimated marker effects, and we compared the modified LASSO method with GEMMA in terms of their statistical power and Type 1 error through simulations. We also used the LASSO method to detect significant single-nucleotide polymorphisms (SNPs), metabolites and transcripts for the six agronomic traits. Finally, we performed BLUP analysis in conjunction with GWAS to see whether or not using markers selected according to the result of GWAS can improve the predictive abilities.
Materials and methods
Material collection
Three omic (genomic, transcriptomic and metabolomic) data collected from 339 maize inbred lines were used for prediction. All lines were genotyped using Illumina MaizeSNP50 BeadChip (Ganal et al., 2011). RNA sequencing (RNA-seq) was subsequently performed on the immature seeds of 15 days after pollination for these 339 lines using 90 base pair pair-end Illumina (Fu et al., 2013). A total of 100K SNPs and 28 769 gene expression traits (transcriptomic data) were obtained. Metabolic profiling was carried out on mature maize kernels and 748 metabolites were detected using high-throughput liquid chromatography-tandem mass spectrometry analysis (Wen et al., 2014). We analyzed six yield-related traits to evaluate the efficacy of prediction: (1) ear length (EL), (2) ear diameter (ED), (3) ear row number (RN), (4) kernel number per row (KN), (5) ear weight (EW) and (6) cob weight (CW). Each trait was measured from five replicated experiments (2009 from three locations, 2010 from another two locations), and in each replicate, five plants from each line were sampled and the average phenotypic value was used for phenotypic analysis (Yang et al., 2014).
Methods of prediction
We used eight representative methods including five parametric methods (BLUP, LASSO, PLS, BayesA and BayesB) and three nonparametric methods (RKHS, SVM-RBF and SVM-POLY). The predictabilities were evaluated using a tenfold cross-validation where samples were randomly partitioned into 10 parts, 9 parts being used to estimate parameters and the remaining part being predicted. Thus, all the parts were predicted once and used nine times to estimate parameters. The predictive ability was defined as the correlation coefficient between the observed and predicted phenotypic values.
BLUP method
Let y be an n × 1 vector of phenotypic values of a quantitative trait for n individuals. The phenotypic vector is described by the following linear mixed model,
where X is a n × q design matrix, β is a q × 1 vector of fixed effects, m is the number of markers, Zk={Zjk} is an n × 1 vector of genotype indicators with Zjk=1 for the homozygote of the major allele, Zjk=0 for the heterozygote and Zjk=−1 for the homozygote of the minor allele, γk is a random effect of marker k, ε is an n × 1 vector of residual errors. Assume that ε~N(0,Inσ2) and γk~N(0,ϕ2/m), where σ2 is the residual variance and ϕ2 is a polygenic variance shared by all makers. The expectation of y is E(y)=Xβ and the variance–covariance matrix is
where 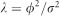 is the variance ratio and K is a marker-generated kinship matrix defined as
is the variance ratio and K is a marker-generated kinship matrix defined as
The restricted maximum likelihood was used to estimate parameters. When the sample size is large, it can be very costly to evaluate the likelihood function. The eigen-decomposition algorithm was used to estimate parameters, details of this algorithm can be found in Xu et al. (2014).
Let us partition the total number of individuals into a training sample and a test sample. Let Y1 be a vector of phenotypic values in the training sample and Y1 be a vector of phenotypic values in the test sample. Accordingly, X can be partitioned into X1 and X2. The kinship matrix and matrix V are partitioned correspondingly, as shown below,
The BLUP prediction of 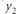 is also the conditional expectation of Y2 given Y1,
is also the conditional expectation of Y2 given Y1,
where all the parameters are substituted by the restricted maximum-likelihood estimates from the training sample. The predictability is defined as the Pearson correlation between y (observed values) and 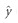 (the predicted values). The BLUP method was implemented in our own R program.
(the predicted values). The BLUP method was implemented in our own R program.
LASSO method
LASSO is a constrained form of ordinary least squares with the sum of the absolute values of the regression coefficients being smaller than a constant (Tibshirani, 1996). LASSO was first proposed as a tool in GS by Usai et al. (2009). In this study, LASSO was implemented in the R/glmnet package (Friedman et al., 2010).
PLS method
The PLS method incorporates the principal component analysis into the multilinear regression model. It transforms the original data into a new set of linearly uncorrelated components as predictors to predict the phenotype. However, it differs from principal component analysis in that components are constructed by maximizing the covariance between the response variable and the independent components. The PLS method was implemented in an R program called pls (Mevik and Wehrens, 2007).
BayesA and BayesB
They are two popular Bayesian approaches to genomic prediction. The only difference between these two methods lies in the prior distribution of parameters. BayesA assumes that the prior distribution of variances across markers follows a scaled inverse chi-square distribution, while BayesB assumes that the prior distribution is a two-component mixture with one component being a scaled inverse chi-square distribution and the other being a point mass at 0. All parameters in BayesA and BayesB were sampled using the Gibbs sampling algorithm and the Markov chain Monte Carlo algorithm (Meuwissen et al., 2001). BayesA and BayesB were implemented in an R package called BGLR (Perez and de los Campos, 2014).
SVM method
It is a kernel-based learning method for classification and regression. Maenhout et al. (2007) first applied this method to predict maize hybrid performance. SVM implicitly maps the input data into a high-dimensional feature space via a kernel function (for example, polynomial, Gaussian radial basis function, hyperbolic tangent kernel, the linear kernel). We chose the radial basis function (SVM-RBF) and the polynomial kernel functions (SVM-POLY; Karatzoglou et al., 2004), and implemented these two algorithms using an R package called kernlab.
RKHS method
The RKHS method has been proved to be an efficient machine learning tool, which has been used in many areas, such as spatial statistics and smoothing splines (de los Campos et al., 2010). Gianola et al. (2006) first applied the RKHS method to genomic prediction. The reproducing kernel is a key factor of model specification in RKHS. Both single-kernel models and multi-kernel models can be fitted in RKHS. Campos et al. Perez and de los Campos (2014) showed that the multi-kernel model is very useful for kernel selection. Here, we choose the multi-kernel approach and implemented the method in the R/BGLR package (Perez and de los Campos, 2014).
The websites for all the R software packages of the prediction methods used in this study are listed in Supplementary Table S1.
Integrating multiple omic data
For the BLUP method, the integration model is defined as
where Xβ represents some fixed effects; G, T and M are indicator variables of genome, transcriptome and metabolome, respectively; m, p and q are the number of SNPs, transcripts and metabolites, respectively; αk, δh and γi are effects of SNPs, transcripts and metabolites with 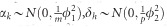 and
and 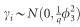 distributions, respectively;
distributions, respectively; 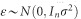 is a vector of residual errors. The expectation of y is E(y)=Xβ and the variance–covariance matrix is var(y)=V, where
is a vector of residual errors. The expectation of y is E(y)=Xβ and the variance–covariance matrix is var(y)=V, where
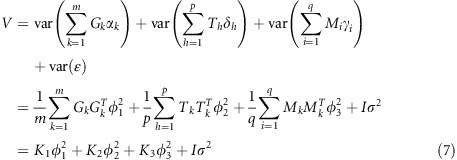 |
The variance components were estimated using the restricted maximum-likelihood method. The procedure of prediction is the same as the above BLUP method used for a single omic data set. For the other seven methods, we rescaled the predictors and combined three omic data together as the overall predictors for further prediction.
The LASSO method for GWAS
LASSO is a popular method in variable selection and we applied this method to detect significant markers. The LASSO method was implemented using an R package called R/glmnet. However, the software does not provide a standard error for an estimated effect. Here we adopted a Bayesian method of Xu (2013) to approximate the standard error for each selected marker effect. The LASSO model can be redefined as
where y is a n × 1 vector of the phenotypic values, Xkis a n × 1 design matrix for the kth selected markers, bk is the effect of this marker and ε is a n × 1 vector of residual errors. All markers are selected (with non-zero effect). Let 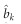 be the LASSO estimated effect for marker k and
be the LASSO estimated effect for marker k and 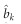 be the variance of
be the variance of 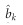 , which are interpreted as the Bayesian posterior mean and posterior variance, respectively. Let
, which are interpreted as the Bayesian posterior mean and posterior variance, respectively. Let
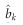 be the estimated marker effect from the data alone and its variance is defined as
be the estimated marker effect from the data alone and its variance is defined as
where 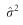 is the estimated residual error variance, which is defined as
is the estimated residual error variance, which is defined as
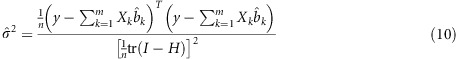 |
where
is the hat matrix. Here, X denotes the design matrix for all markers with non-zero effects after LASSO variable selection. The above residual error variance is the estimated residual variance from a generalized cross-validation analysis (Golub et al., 1979). This residual variance has corrected the overfitting caused by too many predictors in the model. Let 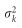 be the prior variance of bk. The prior variance can be defined as the expectation of
be the prior variance of bk. The prior variance can be defined as the expectation of 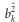 ,
,
The posterior variance can be obtained from the prior variance 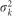 and the variance from the data, and described as
and the variance from the data, and described as
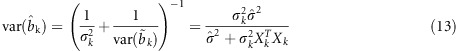 |
Substituting equation (13) into equation (12) yields
Solving for 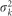 , we get
, we get
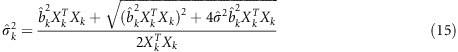 |
Substituting equation (15) into equation (13), we will have an estimated 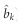 . Given the LASSO estimate
. Given the LASSO estimate 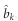 , we have a Wald test statistic for H0:bk=0,
, we have a Wald test statistic for H0:bk=0,
Assume that Wk follows a Chi-square distribution with one degree of freedom, the P-value is calculated from,
Simulation studies for GWAS
To test the power and Type 1 error of the proposed LASSO method for GWAS, we performed simulation experiments based on the genotypic data of 339 maize inbred lines. We assigned a total of 10 QTL distributed on the first eight chromosomes of the maize genome. The last two chromosomes contained no QTL and were used to evaluate the Type 1 error. The proportion of the phenotypic variance contributed by the 10 simulated QTL was 60%. Detailed information about the 10 simulated QTL is shown in Table 1. The polygenic and residual error variances were set at ϕ2=1 and σ2=1, respectively. We also simulated population structure effects using the first four principal components of the marker data. The population structure explained 10% of the total phenotypic variation. Phenotypes were simulated as the sum of the effects of the 10 QTL, the polygenic effect, the residual error and the population structure effect. We also compared the results of our method with GEMMA (Zhou and Stephens, 2012) in the simulation studies. A total of 100 replications were generated and analyzed by both the LASSO method and the GEMMA method. The statistical power of a QTL was calculated as the proportion of replicates where the P-value of the QTL was less than 0.05 for the LASSO method and 0.05/m or 1/m for the GEMMA method. The Type 1 error was defined as the average proportion of false positives for all markers in the last two chromosomes that contain no QTL.
Table 1. True effects and statistical powers of 10 simulated QTL and Type 1 error rates for the modified LASSO method and GEMMA drawn from 100 replicated simulation experiments.
| QTL | Chromosome | Position (bp) | Effect | R2a (%) |
Statistical power (%) |
||
|---|---|---|---|---|---|---|---|
| LASSO | GEMMA-Ab | GEMMA-Bc | |||||
| QTL-1 | 1 | 64 397 509 | 0.6137 | 2 | 36 | 2 | 0 |
| QTL-2 | 1 | 217 180 912 | 0.4196 | 2 | 49 | 10 | 1 |
| QTL-3 | 2 | 40 411 229 | 0.5500 | 4 | 68 | 5 | 0 |
| QTL-4 | 3 | 28 354 373 | 0.9151 | 4 | 72 | 58 | 27 |
| QTL-5 | 4 | 17 376 169 | 0.6681 | 6 | 95 | 89 | 58 |
| QTL-6 | 5 | 11 600 672 | 1.1541 | 6 | 98 | 88 | 65 |
| QTL-7 | 5 | 216 767 558 | 1.3985 | 8 | 99 | 98 | 91 |
| QTL-8 | 6 | 142 446 480 | 0.7337 | 8 | 98 | 99 | 87 |
| QTL-9 | 7 | 21 638 945 | 1.4079 | 10 | 99 | 100 | 100 |
| QTL-10 | 8 | 172 759 416 | 1.5636 | 10 | 99 | 100 | 98 |
| Type 1 error | 0.00139 | 0.00446 | 0.00056 | ||||
Abbreviations: GEMMA, genome-wide efficient mixed model association; LASSO, least absolute shrinkage and selection operator; QTL, quantitative trait loci.
R2: Proportion of the total phenotypic variation explained by the QTL.
GEMMA-A: Bonferroni correction with P-value less than 1/m, where m is the total number of markers.
GEMMA-B: Bonferroni correction with P-value less than 0.05/m, where m is the total number of markers.
Results
Comparison of predictive abilities
The predictive abilities of the six traits in maize obtained from all the eight methods (BLUP, LASSO, PLS, BayesA and BayesB, RKHS, SVM-RBF and SVM-POLY) are presented in Table 2. For genome, traits RN and ED have the highest predictive abilities across all methods, followed by traits EL and EW, with trait KN being the worst predictable trait. The largest differences in predictive ability among the eight methods range from 0.02 to 0.12 for the same trait. For transcriptome, the average predictive abilities of all traits are lower than those obtained from genome, and the predictive abilities are highest for RN (0.55) and lowest for CW (0.33). For CW and EL, the predictive abilities vary greatly across different methods with SVM-POLY being the best and LASSO being the worst, but for the other traits, the eight approaches have similar performances. For metabolome, the predictive abilities for the six traits are lower than those from genomic prediction, and metabolomic predictions for CW and EL are only around half of the genomic predictions. Large differences in predictive ability (>0.2) are observed between LASSO and BayesB for traits CW, ED and EW.
Table 2. Predictive abilities of six traits from three sources of omic data using eight statistical methods.
| Source of data | Trait | BLUP | LASSO | PLS | BayesA | BayesB | RKHS | SVM-RBF | SVM-POLY | Mean |
|---|---|---|---|---|---|---|---|---|---|---|
| Genome | CW | 0.4763 | 0.4517 | 0.4665 | 0.4692 | 0.4797 | 0.4707 | 0.4712 | 0.4774 | 0.4703 |
| ED | 0.5766 | 0.5515 | 0.5146 | 0.5781 | 0.5728 | 0.5962 | 0.5908 | 0.5677 | 0.5685 | |
| EL | 0.5262 | 0.4164 | 0.5195 | 0.5009 | 0.5162 | 0.5243 | 0.4985 | 0.5237 | 0.5032 | |
| EW | 0.5222 | 0.4696 | 0.4546 | 0.5133 | 0.5135 | 0.5264 | 0.5224 | 0.4926 | 0.5018 | |
| KN | 0.4667 | 0.3591 | 0.4402 | 0.4711 | 0.4609 | 0.4698 | 0.4537 | 0.4792 | 0.4501 | |
| RN | 0.5821 | 0.5256 | 0.5701 | 0.5834 | 0.5972 | 0.5756 | 0.5734 | 0.5845 | 0.5740 | |
| Transcriptome | CW | 0.3719 | 0.2050 | 0.3580 | 0.3534 | 0.3457 | 0.2976 | 0.3198 | 0.3819 | 0.3292 |
| ED | 0.5469 | 0.5248 | 0.5078 | 0.5477 | 0.5369 | 0.5257 | 0.5051 | 0.5402 | 0.5294 | |
| EL | 0.3412 | 0.2160 | 0.3903 | 0.3526 | 0.3504 | 0.2918 | 0.3251 | 0.3971 | 0.3331 | |
| EW | 0.4584 | 0.4565 | 0.4007 | 0.4593 | 0.4578 | 0.4285 | 0.4352 | 0.4363 | 0.4416 | |
| KN | 0.3937 | 0.4207 | 0.3440 | 0.3959 | 0.3941 | 0.3554 | 0.3600 | 0.3902 | 0.3817 | |
| RN | 0.5682 | 0.5077 | 0.5717 | 0.5686 | 0.5595 | 0.5403 | 0.5068 | 0.5791 | 0.5502 | |
| Metabolome | CW | 0.2840 | 0.3524 | 0.2461 | 0.2041 | 0.0725 | 0.3236 | 0.3313 | 0.2541 | 0.2585 |
| ED | 0.5633 | 0.5708 | 0.5382 | 0.5082 | 0.2040 | 0.5543 | 0.5204 | 0.4590 | 0.4898 | |
| EL | 0.2957 | 0.2603 | 0.2989 | 0.2767 | 0.1831 | 0.3122 | 0.3141 | 0.2885 | 0.2787 | |
| EW | 0.5149 | 0.5354 | 0.5024 | 0.4442 | 0.3221 | 0.5378 | 0.5267 | 0.4118 | 0.4744 | |
| KN | 0.3768 | 0.4079 | 0.3213 | 0.3543 | 0.2875 | 0.4118 | 0.4097 | 0.3021 | 0.3589 | |
| RN | 0.5088 | 0.4616 | 0.4732 | 0.4772 | 0.3121 | 0.5059 | 0.5045 | 0.3486 | 0.4490 |
Abbreviations: BLUP, best linear unbiased prediction; ED, ear diameter; EL, ear length; EW, ear weight; CW, cob weight; KN, kernel number per row; LASSO, least absolute shrinkage and selection operator; PLS, partial least square; RKHS, reproducing kernel Hilbert space; RN, ear row number; SVM-POLY, support vector machine using the polynomial kernel function; SVM-RBF, support vector machine using the radial basis function kernel.
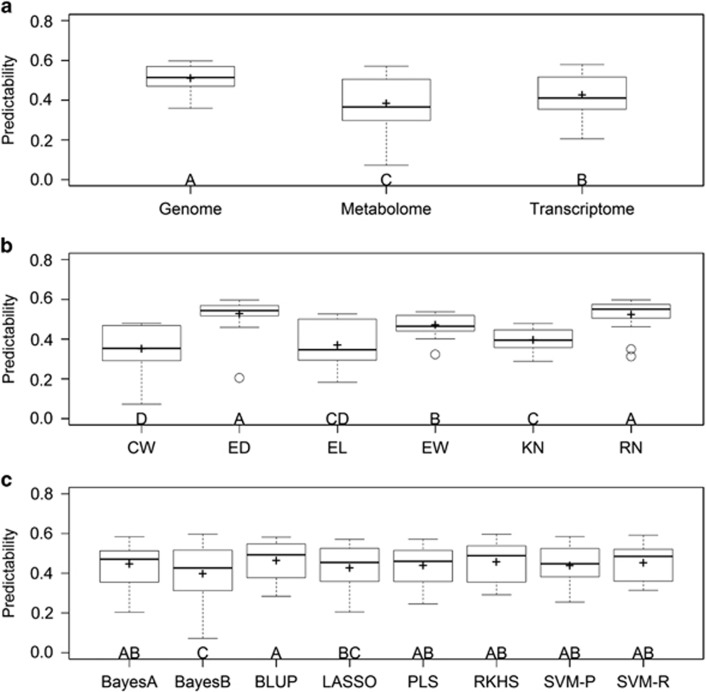
Using the predictive abilities of all 3 × 6 × 8=144 omic-trait-method combinations, we performed analyses of variances under a factorial design. All main effects and two-way interaction effects are significant except the interaction effect of method × trait (Table 3). Results of multiple comparisons for the main effects are illustrated in Figure 1. Predictabilities of the three omic data are significantly different, with genomic prediction being the best followed by transcriptomic and metabolomic predictions (Figure 1a). Among the six traits, RN and ED are the best predictable traits followed by EW and KN, and CW is the worst (Figure 1b). By comparing eight methods, BLUP performs the best and BayesB performs the worst, with other methods ranging between the two (Figure 1c). All two-way interaction effects are given in Supplementary Data S1, from which we find that RKHS is the best for genome prediction and metabolome prediction, whereas it is not efficient for transcriptome prediction. Although BLUP is not the best for each omic prediction, it consistently ranks near the top. BayesB works well in genomic prediction and transcriptomic prediction. However, it performs poorly for metabolomic prediction, which has an enormous negative impact on the overall performance of BayesB.
Table 3. Analyses of variances of predictability from a 3 × 8 × 6 factorial design with three sources of omic data, eight prediction methods and six traits.
| Source of variation | DF | Sum of squares | Mean squares | F-test | P-value |
|---|---|---|---|---|---|
| Ome | 2 | 0.3973 | 0.19863 | 221.152 | <0.0001 |
| Method | 7 | 0.0561 | 0.00802 | 8.929 | <0.0001 |
| Trait | 5 | 0.727 | 0.14541 | 161.895 | <0.0001 |
| Ome × method | 14 | 0.1987 | 0.01419 | 15.803 | <0.0001 |
| Ome × trait | 10 | 0.1543 | 0.01543 | 17.179 | <0.0001 |
| Method × trait | 35 | 0.0481 | 0.00138 | 1.531 | 0.0654 |
| Residual | 70 | 0.0629 | 0.0009 |
Figure 1.
Multiple comparisons illustrated by boxplots. In each panel, different capital letters above the group labels indicate significant differences between groups. In each box plot, the plus sign represents the mean predictability, the box defines the first and the third quantiles, the bold line in the box defines the second quantile (median), the open circles represent outliers. (a) Compares the predictabilities of the three omic data across six traits and eight methods. (b) Compares the predictabilities for the six traits over three omic data and eight methods. (c) Compares the predictabilities of the eight methods across three omic data and six traits.
Combined prediction
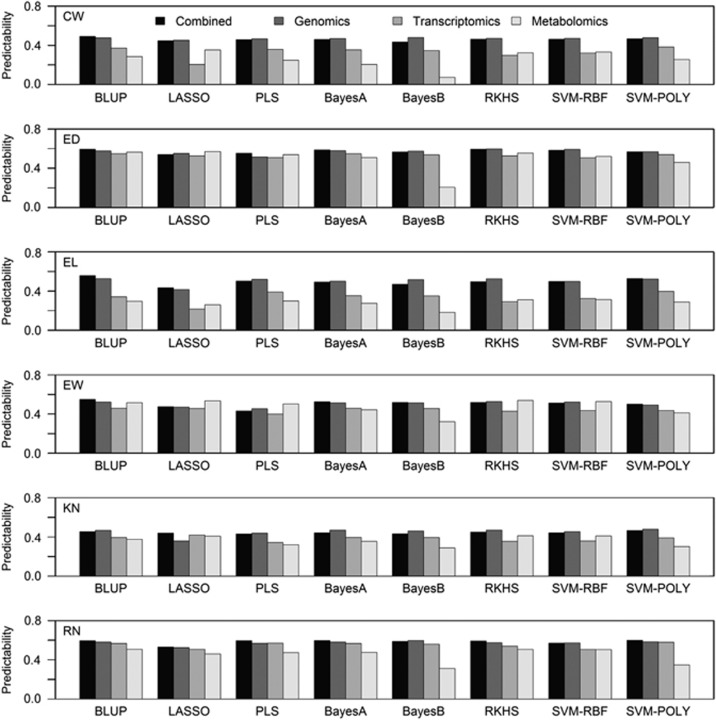
We also combined all three omic data into a single model to perform a combined prediction. Overall, the combined prediction has no obvious advantage over the best single omic prediction (Figure 2). For the BLUP method, combining data from different sources slightly improves the prediction for all traits except KN, whereas for other methods, the combined prediction rarely increases the predictive ability compared with the use of single source of data. For trait EW, metabolomic prediction is better than combined prediction when using LASSO, PLS, RKHS and SVM-RBF.
Figure 2.
Comparison of predictability for three sources of omic data and the combined analysis of the three omic data over six traits and eight methods. The three omic data are genomic, transcriptomic and metabolomic data. The six traits are labeled as CW, ED, EL, EW, KN and RN. The eight statistical methods are BLUP, LASSO, PLS, BayesA, BayesB, RKHS, SVM-RBF and SVM-POLY.
Simulation studies for GWAS
We used LASSO and other methods to predict six quantitative traits of maize. LASSO, however, can also be used for genome-wide association studies. We compared our LASSO method with GEMMA for GWAS under two criteria of Bonferroni correction (GEMMA-A and GEMMA-B). The statistical powers and Type 1 error obtained from 100 replicated simulations for the 10 QTL are given in Table 1. In general, both LASSO and GEMMA are powerful for QTL with large simulated effects that explain more than six percent of phenotypic variance. The LASSO method has substantially higher powers for the four small QTL than the GEMMA method, regardless of what P-value criteria are used. The Type 1 error are well controlled in all the cases, where GEMMA-B provides the best control of Type 1 error, followed by LASSO and GEMMA-B. Overall, the LASSO method performs better than GEMMA-A in statistical power and Type 1 error. Although GEMMA-B achieves better control of Type 1 error than the LASSO method, it has a much lower power in detection of small QTL.
GWAS for six traits of maize using LASSO and GEMMA
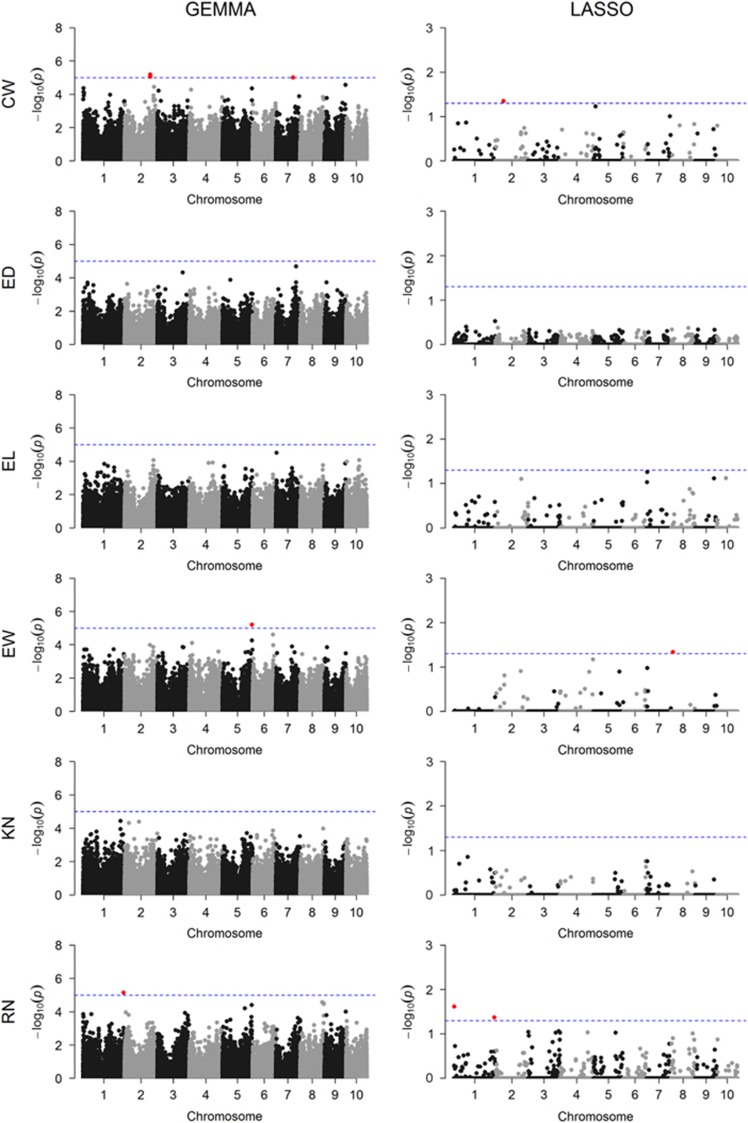
Manhattan plots of all six traits of maize using the GEMMA and LASSO methods are shown in Figure 3. When we set the Bonferrroni-corrected P-value threshold at 0.05/m=5.0E−7 for the GEMMA method, no SNPs were detected for any of the six traits. This criterion may be too stringent for GEMMA, so we set the threshold at 1/m=1.0E−5. The criterion for LASSO remains at 0.05 because it is a multiple marker model. A total of eight SNPs for three agronomic traits (CW, EW and RN) were identified from the two GWAS methods, of which four SNPs were detected by LASSO and the others were detected by GEMMA (Table 4). Neither method detected any significant SNP associated with the other three traits (ED, EL and KN). With GEMMA, two SNPs associated with CW were detected on chromosomes 2 and 7. Also, the LASSO method detected one SNP on chromosome 2. Two SNPs influencing EW located in chromosomes 5 and 8 were identified by GEMMA and LASSO, respectively. All three SNPs associated with RN are located on chromosome 1; the one detected by the LASSO method is located in 28 Kb upstream of a known gene ZmADF3 (GRMZM2G060702), a key regulator of actin dynamics in plant cells, which has an important role in kernel development (Qiao et al., 2016).
Figure 3.
Manhattan plots for six traits obtained from two GWAS methods (GEMMA and LASSO). The six traits are labeled as CW, ED, EL, EW, KN and RN. The dashed blue horizontal line in each Manhattan plot depicts the significance threshold and the red dot indicates significant SNPs. The significance thresholds are 1.002 × 10−5 (after Bonferroni correction) and 0.05 for GEMMA and LASSO, respectively. A full color version of this figure is available at the Heredity journal online.
Table 4. Significant SNPs identified for six traits using GEMMA and the modified LASSO method.
| Trait | Method | Chr | Position (kb) | Allele | Candidate gene | Annotation | P-value | R2(%) |
|---|---|---|---|---|---|---|---|---|
| CW | GEMMA | 2 | 185 583 | A/G | GRMZM2G414252 | Putative HLH DNA-binding domain superfamily protein | 6.23E−06 | 7.15 |
| GEMMA | 7 | 123 850 | T/C | GRMZM2G305406 | Unknown | 9.60E−06 | 7.50 | |
| LASSO | 2 | 59 011 | C/T | GRMZM2G412524 | Protein kinase G11A-like | 0.045 | 0.59 | |
| EW | GEMMA | 5 | 213 292 | G/A | GRMZM2G018573 | Unknown | 6.15E−06 | 6.35 |
| LASSO | 8 | 14 542 | G/T | GRMZM2G052869 | Metallothionein-like protein 2A | 0.046 | 0.51 | |
| RN | GEMMA | 1 | 294 137 | C/T | GRMZM2G055834 | Unknown | 7.12E−06 | 9.69 |
| LASSO | 1 | 1877 | C/G | GRMZM2G060265 | Scarecrow-like protein 6 | 0.024 | 0.76 | |
| LASSO | 1 | 293 269 | G/A | GRMZM2G060702 | Actin depolymerizing factor | 0.042 | 0.4 |
Abbreviations: Chr, chromosome; CW, cob weight; EW, ear weight; GEMMA, genome-wide efficient mixed model association; LASSO, least absolute shrinkage and selection operator; RN, ear row number; SNP, single-nucleotide polymorphism.
Metabolome-wide association studies using LASSO and GEMMA
We used the LASSO and GEMMA methods to detect significant metabolites associated with the six agronomic traits. Only two metabolites (n499 and n790) were detected for two traits (EN and KW) by GEMMA at the Bonferroni-corrected threshold (0.05/m=6.7E−05). The LASSO method identified a total of 15 significant metabolites for the six traits, which include the two metabolites detected by GEMMA (Supplementary Data S2). Some metabolites are significantly associated with more than one trait. For example, both metabolites n0710 and n0768 control CW and EW, and metabolite n0967 has a significant effect on three traits (EW, EL and KN). These metabolites may have an important role in maize ear development. Several metabolites have been detected in other species, such as n0710, n0075 and n0691. All the significant metabolites detected by LASSO explain a small fraction of phenotypic variation, and the strongest metabolite (n0499) only explains 3% of phenotypic variation for trait KN. However, this is not to say that the detected metabolites are not important. The small proportion of phenotypic variance explained may be due to the shrinkage nature of the LASSO method. It is worth noting that the number of metabolites is far less than the number of SNPs, whereas the number of significant metabolites is greater than the number of significant SNPs.
Transcriptome-wide association studies using LASSO and GEMMA
The LASSO and GEMMA methods were also used to detect significant transcripts associated with the six agronomic traits. No significant transcripts were identified for the six traits by GEMMA at Bonferroni-corrected P-value threshold (0.05/m =1.74E-6). Four significant transcripts for three agronomic traits (ED, KN and EW) were identified by LASSO (Supplementary Table S2). The two transcripts, GRMZM2G045243 and GRMZM2G126128, influencing EW were detected on chromosomes 2 and 4, respectively, both of which are protein-coding genes. Functions of the other two transcripts remain unknown. The strongest transcript (GRMZM2G001648) only explains 1.3% of phenotypic variation for trait ED. This may explain why GEMMA fails to detect any transcripts.
Genomic prediction using selected markers from GWAS
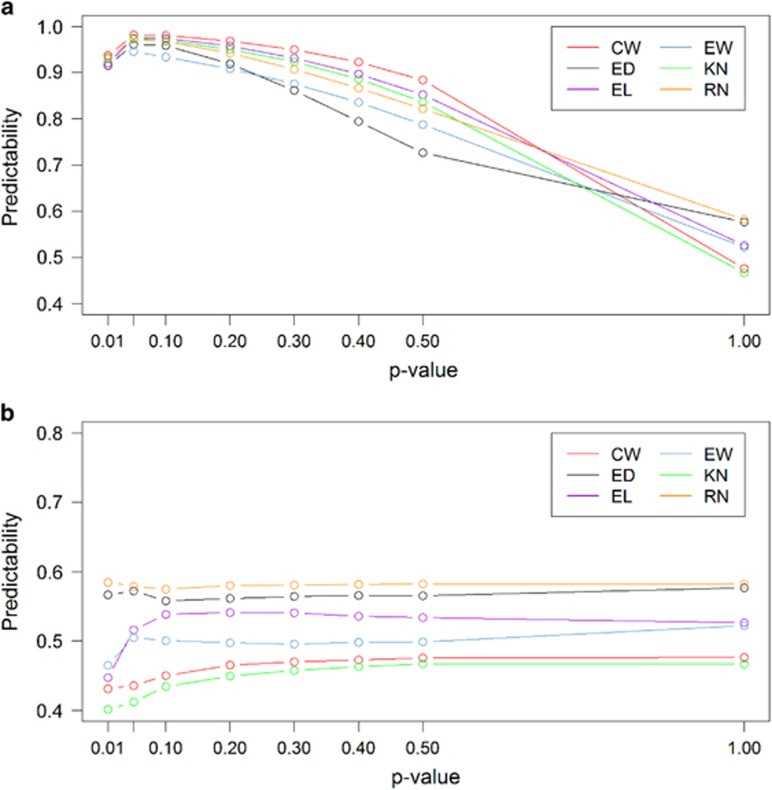
In a usual genomic prediction study, genome-wide markers are simultaneously included in a single model to predict the phenotypic values of a trait. However, most people outside the genomic selection community believe that markers with small or no effects on a trait may be detrimental to genomic selection if included in the model. They prefer using only selected markers that are associated with the trait of interest for prediction. In this study, we will answer the question whether using selected markers can improve genomic selection or not. We used selected markers from GWAS of the GEMMA method to predict phenotypes with the BLUP method under two different scenarios. Scenario A: markers were selected from the whole sample and only selected markers were used in the prediction, where predictabilities were drawn from 10-fold cross-validation. Scenario B: markers were selected within folds, where a GWAS was performed from each training sample and markers selected from the training sample were used to predict the trait values of the test sample. The markers were selected based on their P-values from the following sequences: 0.01, 0.05, 0.10, 0.2, 0.3, 0.4, 0.5 and 1.0, where P-value equal to 1.0 is equivalent to using all markers for prediction. The predictive abilities obtained from these two scenarios are illustrated in Figure 4. Figure 4a (the top panel) shows the result of scenario A, where markers were selected from the whole sample. When the P-value is small, the predictabilities are very high and they continue to increase until they reach a plateau when P≈0.05. After the plateau, the predictabilities start to decline and eventually reach the minimum values when P=1.0. This trend of the predictability change can mislead many investigators because the cross-validation using markers selected from the whole sample does not reflect the true prediction. The predictabilities are seriously biased upward. Using this result to report predictability is a kind of ‘cheating’, though unintentionally in many cases. Figure 4b (bottom panel) represents the actual predictabilities when markers were selected from training samples only. When the P-values are very small, the predictabilities are very low in four of the six traits. As the P-value increases, the predictability starts to increase and then quickly reaches a plateau. Further increase in P-value does not change the predictability very much. Overall, the integration of GWAS and prediction can significantly improve predictive ability in scenario A, but fail to increase predictive ability in scenario B. As scenario A cannot be achieved in actual genomic selection programs, we conclude that using selected markers for genomic selection does not help very much.
Figure 4.
Predictive abilities of BLUP for six traits using selected markers obtained via GWAS. Markers included in the prediction model are selected at seven different levels of P-value: 0.01, 0.05, 0.10, 0.2, 0.3, 0.4 and 0.5 (horizontal axis). (a) Markers are selected from the whole sample before cross-validation. (b) Markers are selected within folds of cross-validation.
Discussion
In this study, the average predictive ability was 0.38 from metabolomic data, 0.43 from transcriptomic data and 0.51 from genomic data across all traits and methods. Genome is still the most important predictor for maize. Riedelsheimer et al. (2012a) predicted seven heterotic traits in hybrid maize using 56 110 SNPs and 130 metabolites and found that the average predictive ability across seven traits was 0.73 from genome and 0.57 from metabolome. Gärtner et al. (2009) proposed to use 110 genetic markers and 181 metabolic markers to predict the heterosis of Arabidopsis thaliana and also found that predictive ability from metabolome was slightly lower than those from genome. Despite the fact that metabolites have proven to be useful in phenotypic prediction, they have the limitation that metabolites were measured at a specific moment, while some traits change dynamically at different developmental stages (Riedelsheimer et al., 2012a). In addition, we performed a combined prediction of three omic data and found no benefit from the combined analysis across traits and methods. However, Gärtner et al. (2009) proposed that combining data of both metabolites and SNPs leads to a substantial improvement of predictive ability. This may be due to the fact that they used a small number of genetic markers that were not able to capture information of the entire genome.
We also observed that the BLUP method slightly improved the combined prediction for most traits, while other methods slightly decreased the combined prediction for most traits. This may be because we assigned three different variances to three different sources of data in the mixed model analysis and these different variances were eventually used for BLUP prediction, whereas we simply combined the three types of predictors, albeit standardized, and placed them in a single model for other methods. Therefore, if we can give different sources of omic data a different set of weights, we may improve the combined prediction for other methods.
From the comparison of different prediction methods, we found that the BLUP method is the overall best performer, while BayesB is the worst one. Many studies have discovered that the genetic architecture has a strong impact on differences of predictive abilities among different prediction methods(Coster et al., 2010; Clark et al., 2011). The GWAS performed on this population did not detect any large-effect QTL, which suggests a polygenic genetic architecture for these agronomic traits. In the simulation study of Daetwyler, BLUP was not affected by the QTL number, whereas BayesB outperformed BLUP with lower numbers of QTL, but performed poorly compared with BLUP when the number of QTL was high (Daetwyler et al., 2010). Coster et al. (2010) also found that the predictive ability of selective shrinkage methods (LASSO and BayesB) decreased with an increased number of simulated QTL, whereas the PLS method was insensitive to the number of QTL. However, some analyses of real data showed that there were only small differences in predictive performance between different methods, regardless of the number and effects of QTL. Overall, shrinkage methods perform better for traits controlled by a few QTL with relatively large effects and BLUP is better suited for highly polygenic traits. In addition, we observed that predictive abilities obtained with the parametric and nonparametric methods were similar. It has been demonstrated that parametric methods had difficulty in capturing complex interactions such as epistatic effects, whereas nonparametric methods performed well for traits under epistatic genetic architectures (Gianola et al., 2006; Howard et al., 2014). Therefore, our similar predictive performance of parametric and nonparametric methods suggested that epistatic genetic effects may be negligible for these agronomic traits.
Currently, there is no method that fits all the data universally well. However, BLUP is often the best choice because its performance is good, in general, for all traits with omic data. In addition, BLUP is computationally more effective than other methods because we do not need to estimated marker effects. The fact that different methods perform differently across different traits and across different populations (Xu et al., 2014) leads to a new strategy of genomic selection. We should use all available methods to perform genomic selection and report the result from the ‘best’ method. Essentially, we are treating ‘method’ as a parameter and the best method is the maximum predictability estimate of the parameter method.
In this study, we provided an effective way to calculate the P-value of each marker for GWAS using the LASSO method. Although nonparametric methods, such as bootstrap, can also be used to calculate the standard error of an estimated marker effect and eventually provide a P-value, they are often costly in terms of computation. Simulation studies based on real genotype data of the maize population showed that the LASSO method performed well in terms of high power and low Type 1 error. One advantage of the multi-locus method over a genome-scanning approach is that no multiple test correction for P-value is needed. However, this method has its own limitation in that the number of markers cannot be too large, say >500k, because simultaneous estimation of that many effects in a single model is a real challenge without resort to a parallel computing scheme. In that case, we can perform multi-locus analysis on individual chromosomes. Recently, several two-step multi-locus methods have been developed to overcome that limitation (Li et al., 2011; Wang et al., 2016). The first step of these methods is to select a small fraction of makers using a less stringent criterion and then use the selected markers to conduct a multi-locus analysis in the second step. One issue with these methods is how to choose the appropriate critical value for marker selection in the first step.
We already demonstrated that using selected markers for genomic prediction does not improve the predictability. This does not mean that we cannot select markers for genomic selection. Figure 4b shows that when P=0.10 is used to select markers, the predictabilities of most traits already reach the plateaus. The number of markers that passed this criterion is about 9000 on average across traits. When a DNA chip is designed for genomic selection, a chip with 9K markers can be substantially cheaper than a chip with 90K markers. Therefore, selection of markers in genomic selection can be beneficial if genotyping more markers represents a proportional increase in cost.
Acknowledgments
The project was supported by the National Science Foundation Collaborative Research Grant 473 DBI-1458515 to SX, National Key Technology Research and Development Program of MOST (2016YFD0100303) and National Natural Science Foundation (91535103) of China to CX.
Footnotes
Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)
The authors declare no conflict of interest.
Supplementary Material
References
- Clark SA, Hickey JM, Van der Werf JH. (2011). Different models of genetic variation and their effect on genomic evaluation. Genet Sel Evol 43: 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coster A, Bastiaansen JW, Calus MP, van Arendonk JA, Bovenhuis H. (2010). Sensitivity of methods for estimating breeding values using genetic markers to the number of QTL and distribution of QTL variance. Genet Sel Evol 42: 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J, Pérez P, Hickey J, Burgueño J, Ornella L, Cerón-Rojas J et al. (2014). Genomic prediction in CIMMYT maize and wheat breeding programs. Heredity 112: 48–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daetwyler HD, Pong-Wong R, Villanueva B, Woolliams JA. (2010). The impact of genetic architecture on genome-wide evaluation methods. Genetics 185: 1021–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Gianola D, Rosa GJ, Weigel KA, Crossa J. (2010). Semi-parametric genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. Genet Res 92: 295–308. [DOI] [PubMed] [Google Scholar]
- de los Campos G, Hickey JM, Pong-Wong R, Daetwyler HD, Calus MP. (2013). Whole-genome regression and prediction methods applied to plant and animal breeding. Genetics 193: 327–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desta ZA, Ortiz R. (2014). Genomic selection: genome-wide prediction in plant improvement. Trends Plant Sci 19: 592–601. [DOI] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. (2010). Regularization paths for generalized linear models via coordinate descent. J Stat Softw 33: 1–22. [PMC free article] [PubMed] [Google Scholar]
- Fu J, Cheng Y, Linghu J, Yang X, Kang L, Zhang Z et al. (2013). RNA sequencing reveals the complex regulatory network in the maize kernel. Nat Commun 4: 2832. [DOI] [PubMed] [Google Scholar]
- Gärtner T, Steinfath M, Andorf S, Lisec J, Meyer RC, Altmann T et al. (2009). Improved heterosis prediction by combining information on DNA- and metabolic markers. PLoS One 4: e5220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganal MW, Durstewitz G, Polley A, Bérard A, Buckler ES, Charcosset A et al. (2011). A large maize (Zea mays L.) SNP genotyping array: development and germplasm genotyping, and genetic mapping to compare with the B73 reference genome. PLoS One 6: e28334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelandi P, Kowalski BR. (1986). Partial least-squares regression: a tutorial. Anal Chim Acta 185: 1–17. [Google Scholar]
- Gianola D, Fernando RL, Stella A. (2006). Genomic-assisted prediction of genetic value with semiparametric procedures. Genetics 173: 1761–1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub GH, Health M, Wahba G. (1979). Generalized cross-validation as a method for choosing a good raidge parameter. Technometrics 21: 215–223. [Google Scholar]
- González-Recio O, Forni S. (2011). Genome-wide prediction of discrete traits using Bayesian regressions and machine learning. Genet Sel Evol 43: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta PK, Kulwal PL, Jaiswal V. (2013). Association mapping in crop plants: opportunities and challenges. Adv Genet 85: 109–147. [DOI] [PubMed] [Google Scholar]
- Henderson CR. (1975). Best linear unbiased estimation and prediction under a selection model. Biometrics 31: 423–447. [PubMed] [Google Scholar]
- Heslot N, Yang H-P, Sorrells ME, Jannink J-L. (2012). Genomic selection in plant breeding: a comparison of models. Crop Sci 52: 146–160. [Google Scholar]
- Howard R, Carriquiry AL, Beavis WD. (2014). Parametric and nonparametric statistical methods for genomic selection of traits with additive and epistatic genetic architectures. G3 4: 1027–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Zaitlen NA, Wade CM, Kirby A, Heckerman D, Daly MJ et al. (2008). Efficient control of population structure in model organism association mapping. Genetics 178: 1709–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karatzoglou A, Smola A, Hornik K, Zeileis A. (2004). kernellab - An S4 Package for Kernel Methods in R. J Stat Softw 11: 1–20. [Google Scholar]
- Kump KL, Bradbury PJ, Wisser RJ, Buckler ES, Belcher AR, Oropeza-Rosas MA et al. (2011). Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat Genet 43: 163–168. [DOI] [PubMed] [Google Scholar]
- Li J, Das K, Fu G, Li R, Wu R. (2011). The Bayesian lasso for genome-wide association studies. Bioinformatics 27: 516–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maenhout S, De Baets B, Haesaert G, Van Bockstaele E. (2007). Support vector machine regression for the prediction of maize hybrid performance. Theor Appl Genet 115: 1003–1013. [DOI] [PubMed] [Google Scholar]
- Meuwissen THE, Hayes BJ, Goddard ME. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mevik B-H, Wehrens R. (2007). The pls Package: principal component and partial least squares regression in R. J Stat Softw 18: 1–24. [Google Scholar]
- Meyer RC, Steinfath M, Lisec J, Becher M, Witucka-Wall H, Törjék O et al. (2007). The metabolic signature related to high plant growth rate in Arabidopsis thaliana. Proc Natl Acad Sci USA 104: 4759–4764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez P, de los Campos G. (2014). Genome-wide regression and prediction with the BGLR statistical package. Genetics 198: 483–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poland JA, Bradbury PJ, Buckler ES, Nelson RJ. (2011). Genome-wide nested association mapping of quantitative resistance to northern leaf blight in maize. Proc Natl Acad Sci USA 108: 6893–6898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao D, Dong Y, Zhang L, Zhou Q, Hu C, Ren Y et al. (2016). Ectopic expression of the maize ZmADF3 gene in Arabidopsis revealing its functions in kernel development. Plant Cell Tissue Organ Cult 126: 239–253. [Google Scholar]
- Riedelsheimer C, Czedik-Eysenberg A, Grieder C, Lisec J, Technow F, Sulpice R et al. (2012. a). Genomic and metabolic prediction of complex heterotic traits in hybrid maize. Nat Genet 44: 217–220. [DOI] [PubMed] [Google Scholar]
- Riedelsheimer C, Technow F, Melchinger AE. (2012. b). Comparison of whole-genome prediction models for traits with contrasting genetic architecture in a diversity panel of maize inbred lines. BMC Genomics 13: 452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svetnik V, Liaw A, Tong C, Culberson JC, Sheridan RP, Feuston BP. (2003). Random forest: a classification and regression tool for compound classification and QSAR modeling. J Chem Inf Comput Sci 43: 1947–1958. [DOI] [PubMed] [Google Scholar]
- Tian F, Bradbury PJ, Brown PJ, Hung H, Sun Q, Flint-Garcia S et al. (2011). Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat Genet 43: 159–162. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. (1996). Regression shrinkage and selection via the Lasso. J R Stat Soc Series B Stat Methodol 58: 267–288. [Google Scholar]
- Usai MG, Goddard ME, Hayes BJ. (2009). LASSO with cross-validation for genomic selection. Genet Res 91: 427–436. [DOI] [PubMed] [Google Scholar]
- Wang S-B, Feng J-Y, Ren W-L, Huang B, Zhou L, Wen Y-J et al. (2016). Improving power and accuracy of genome-wide association studies via a multi-locus mixed linear model methodology. Sci Rep 6: 19444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Li L, Yang Z, Zheng X, Yu S, Xu C et al. (2017). Predicting rice hybrid performance using univariate and multivariate GBLUP models based on North Carolina mating design II. Heredity 118: 302–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen W, Li D, Li X, Gao Y, Li W, Li H et al. (2014). Metabolome-based genome-wide association study of maize kernel leads to novel biochemical insights. Nat Commun 5: 3438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S. (2013). Genetic mapping and genomic selection using recombination breakpoint data. Genetics 195: 1103–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S, Zhu D, Zhang Q. (2014). Predicting hybrid performance in rice using genomic best linear unbiased prediction. Proc Natl Acad Sci USA 111: 12456–12461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang N, Lu YL, Yang XH, Huang J, Zhou Y, Ali F et al. (2014). Genome wide association studies using a new nonparametric model reveal the genetic architecture of 17 agronomic traits in an enlarged maize association panel. PLoS Genet 10: e1004573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Xu S. (2008). Bayesian LASSO for quantitative trait loci mapping. Genetics 179: 1045–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Vroh BI, Yamasaki M, Doebley JF et al. (2006). A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet 38: 203–208. [DOI] [PubMed] [Google Scholar]
- Zhang F, Guo X, Deng H-W. (2011). Multilocus association testing of quantitative traits based on partial least-squares analysis. PLoS ONE 6: e16739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X, Stephens M. (2012). Genome-wide efficient mixed-model analysis for association studies. Nat Genet 44: 821–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu C, Gore M, Buckler ES, Yu J. (2008). Status and prospects of association mapping in plants. Plant Genome 1: 5–20. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.