Genetic heterogeneity underlying variation in a locally adaptive clinal trait in Pinus sylvestris revealed by a Bayesian multipopulation analysis

Abstract

Local adaptation is a common feature of plant and animal populations. Adaptive phenotypic traits are genetically differentiated along environmental gradients, but the genetic basis of such adaptation is still poorly known. Genetic association studies of local adaptation combine data over populations. Correcting for population structure in these studies can be problematic since both selection and neutral demographic events can create similar allele frequency differences between populations. Correcting for demography with traditional methods may lead to eliminating some true associations. We developed a new Bayesian approach for identifying the loci underlying an adaptive trait in a multipopulation situation in the presence of possible double confounding due to population stratification and adaptation. With this method we studied the genetic basis of timing of bud set, a surrogate trait for timing of yearly growth cessation that confers local adaptation to the populations of Scots pine (Pinus sylvestris). Population means of timing of bud set were highly correlated with latitude. Most effects at individual loci were small. Interestingly, we found genetic heterogeneity (that is, different sets of loci associated with the trait) between the northern and central European parts of the cline. We also found indications of stronger stabilizing selection toward the northern part of the range. The harsh northern conditions may impose greater selective pressure on timing of growth cessation, and the relative importance of different environmental cues used for tracking the seasons might differ depending on latitude of origin.

Introduction

Species that occur over wide ranges with abundant environmental variation are often locally adapted. Local adaptation is best documented with reciprocal transplant experiments by showing that each population has its highest relative fitness at its site of origin (Kawecki and Ebert, 2004). In such experiments, Hereford, 2009 found that 70% of studies showed local adaptation, while about half of the studies on plant populations have shown evidence of local adaptation (Leimu and Fischer, 2008). When reciprocal transplant experiments are not available, local adaptation can be inferred from correlations of phenotypic variation with environmental gradients, or with other population genetic methods (Savolainen et al., 2013).

Local adaptation implies that the populations are genetically differentiated for (often quantitative) traits conferring fitness effects that depend on the environment. Forest trees, for instance, show latitudinal clines in the timing of growth cessation or initiation (Savolainen et al., 2007; Alberto et al., 2013). Similarly, the timing of flowering is genetically differentiated between northern and southern populations in some herbs, such as purple loosestrife Lythrum salicaria (Olsson and Ågren, 2002) and Arabidopsis lyrata (Leinonen et al., 2011). Humans living in the high-altitude Tibetan plateau have many adaptations to the lower oxygen pressure, such as lower hemoglobin content compared with lowland inhabitants (Simonson et al., 2010).

The genetic basis of the traits conferring local adaptation is still poorly known, and contrasting results have been obtained between different species. Among plants, for instance, Arabidopsis thaliana has often been found to have large effect loci in many traits (for example, Atwell et al., 2010), whereas in maize flowering time and height are governed by large numbers of small effect loci (for example, Buckler et al., 2009). Furthermore, it is not clear how often trait variation is controlled by the same loci in different parts of a species range (parallel/convergent evolution) or how often an adaptive locus has significant fitness effects in only one part of the species range instead of showing trade-offs (conditional neutrality vs antagonistic pleiotropy). Improved understanding of the genetic architecture and the distribution of the effect sizes are important for defining quantitative genetics theory. Identifying the specific loci involved is useful for analyzing patterns of selection at the DNA level and for understanding the molecular nature and the networks underlying the trait variation. Likewise, breeding efforts and prediction of the responses to climate change can be aided by such knowledge. Resolving the genetics of any complex trait is, however, a challenging task.

Association studies are widely used for identifying the loci underlying complex traits. Many association analyses e.g. in humans have been conducted on single genetically homogeneous populations (The Welcome Trust Case Control Consortium, 2007) or with meta-analyses combining different data. The first association analyses on adaptation in natural plant populations were made on global samples of individual accessions of Arabidopsis thaliana (for example, Zhao et al., 2007) and on samples of multiple populations of forest trees (for example, Eckert et al., 2009).

A set of populations displaying clinal variation along an environmental gradient in a trait will likely also have allele frequency clines at some loci governing the trait. Such allele frequency clines result from interaction between spatially varying selection and gene flow (Slatkin, 1978). The work of Barton, 1999 suggests initially shallow and eventually steeper sequential clines consistent with the phenotypic change at some part of the trait governing loci. Some differentiation between populations is also predicted by Le Corre and Kremer, 2003 after the early stages of selection, as shown in their island model simulations. Small to moderate allele frequency changes have been observed in potentially adaptive loci after recent selection in e.g. humans (Turchin et al., 2012) and white spruce (Hornoy et al., 2015). However, loci underlying any other trait displaying correlated phenotypic variation may have similar clines. Furthermore, the colonization may have generated some transient or long-lasting patterns of spatial (clinal) variation of allele frequencies even at neutral loci (Excoffier and Ray, 2008; Frichot et al., 2015). Thus, genotype data may display some confounding population structure.

Many of the previous phenotypic association studies on plant adaptation along environmental gradients, (in trees, for example, González-Martínez et al., 2007; Ingvarsson et al., 2008; Eckert et al., 2009; Ma et al., 2010; Prunier et al., 2013) have used the single-locus based mixed-model method that corrects for the confounding due to different levels of relatedness between individuals in the sample by including an estimate of relatedness (and population structure) in the model (Yu et al., 2006; Kang et al., 2008). However, this method may fail to detect true causative single-nucloetide polymorphisms (SNPs) whose frequencies co-vary with environment as they can be mistaken as confounding variation and therefore end up being corrected for. Also, a single-locus approach can easily lead to inflation of test statistics (Yang et al., 2011).

Bud set timing in first year seedlings (a proxy for timing of yearly growth cessation) has moderate heritability (0.33–0.67) within individual populations of Scots pine (Savolainen et al., 2004) and in other conifers (Howe et al., 2003), and it is correlated with the length of growing season in older trees (Oleksyn et al., 1998). Timing of growth cessation is thought to be climatically adaptive with population-specific local optima and under local stabilizing selection (Savolainen et al., 2007). The selective pressure is toward synchronizing the period of yearly active growth with favorable environmental conditions. In most forest trees, the environmental signal of the approaching end of the favorable growth period likely comes from photoperiod (Oleksyn et al., 1998; see also Alberto et al., 2013) that again varies with latitude. The candidate genes for this trait are thus expected to be found mainly among the light perception and timekeeping genes, and genes interacting with these loci. The genes and networks of these functions have been extensively characterized especially in A. thaliana (reviewed by, for example, Andrés and Coupland, 2012), and to some extent also in coniferous trees (for example, Gyllenstrand et al., 2007; Avia et al., 2014). Genes involved in downstream cell responses to approaching winter, such as cold hardiness, are also good candidates (Wachowiak et al., 2009).

Here, we present a new Bayesian multilocus association analysis method for study designs where samples from multiple populations have been collected along an environmental gradient, and phenotypic traits likely related to local adaptation measured. We apply our model to Scots pine (Pinus sylvestris), which is known to have a cline in the timing of bud set in first year seedlings (for example, Mikola, 1982). We examine the associations with bud set timing in SNPs derived from genes related to signal perception (including genes with timekeeping or light perception functions), SNPs from genes related directly to stress (especially cold) tolerance, and SNPs from genes with functions presumably unrelated to functions relating to yearly growth cessation, or genes with unknown function. We aim to find a limited set of loci influencing the observed variation in bud set among the markers included, and examine their effect sizes. We also inspect genetic heterogeneity—are the same loci responsible for the variation in the north and in the central European populations as initially assumed?

New multilocus model for Bayesian analysis of multipopulation data

A multipopulation setup essential for local adaptation studies poses a challenge for association studies, especially when there is a continuum of relatedness among the sample populations and the trait of interest forms a cline along the same transect. Overcorrecting for population structure can lead to false negatives when the structure in the trait of interest resembles the structure in neutral genetic variation. Our new method aims at overcoming this problem by placing most emphasis on within-population variation, simultaneously over multiple populations. Our model also aims at simultaneous estimation of SNP effects of a small subset of loci associated with the trait in order to reduce the inflation of test statistics that often occurs with single-locus tests.

To achieve these goals, we use shrinkage based Bayesian variable selection in our regression model to identify phenotype-genotype associations across populations. Phenotypic variation—simultaneously within all study populations—is examined and SNPs that are associated with the biggest variation are considered significant. SNP effects are assumed to be additive within and across loci and to be independent of the effects of other SNPs. Furthermore, genetic SNP effects are assumed to be constant over populations but heterogeneous variances are assumed for residual terms of each population. Thus, heritability is allowed to vary from one population to the next, improving the fit of the model.

The following multilocus association model is used to explain phenotypes:

where Y_kj is the phenotype outcome of family j in population k, μ_k the overall effect of population k, β_m the additive effect of the marker m, X_kjm the genotype state of family j in population k at marker m (described in more detail below), and ε_kj ~N(0,σ²_k) the error terms distributed with population-specific variances σ²_k, respectively. Associations are studied in two complementary steps; the first step utilizes the within-populations variation, but importantly, simultaneously across all populations. The second, complementary step uses within-population permuted data within the same model framework. This step aims to find associations that lack power in the first step, and due to permutation, in effect reduces to study variation between populations. More details on the model are given in Materials and Methods.

Materials and methods

Plant material and common garden experiment

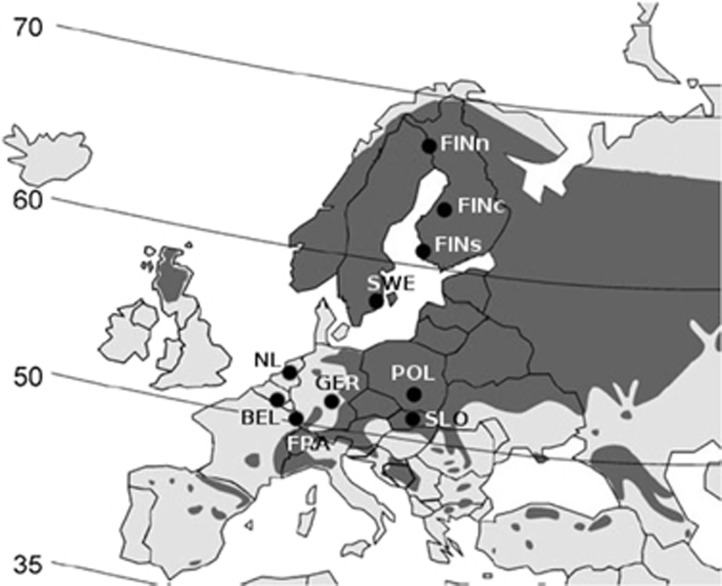
Ten P. sylvestris populations across Europe were sampled, spanning about 20° of latitude (Figure 1). Each population sample consisted of seeds from 18–30 mother trees, for a total of 274 families. 25 open-pollinated seeds from each mother tree were used, forming half-sib families. The samples represented natural populations with the exceptions of the Belgian, Dutch, German and Slovakian samples, which originated from seed orchards. These orchards are based on more than 25 genetically distinct genotypes from a limited area. The individual genotypes have been vegetatively propagated to produce large numbers of ramets. These ramets produce open-pollinated seeds, resulting in a seed population that is very similar to the nearby natural populations, at least at marker loci (Muona and Harju, 1989).

Figure 1.

The origins of P. sylvestris samples in this study. The darker area represents the western part of Scots pine distribution. Further details in Table 1.

The seeds were sown between 9 and 13 June 2003 in a common greenhouse experiment. The test site was situated at the research station of the Natural Resources Institute Finland (Luke) in southern Finland (latitude 60°37', longitude 24°26', altitude 120 m). The experiment was carried out in five completely randomized blocks. Within each block, five seeds from each half-sib family (experimental unit) were randomly assigned to a row plot of five consecutive single seedling pots. Pots were in trays of 40, with edge rows, filled with Kekkilä M6 peat. The temperature in the greenhouse was kept above 18 °C during the night and above 20 °C during the day. During the germination period average air humidity was 72% and during the growing period 62%. Plants grew in ambient day length. Monitoring started on 15 July and continued until 25 November. Each seedling’s bud set status was recorded once per week (Avia et al, 2014). Missing values were due to lack of germination and some seedlings not setting bud. A summary of the plant material is given in Table 1.

Table 1. Summary of plant material and phenotyping and genotyping success.

Population	Country	Latitude	Longitude	n (fam)a	n (obs)b	Missingc
FINn	Finland	67°11'	24°03'	26/22	388	48.3%
FINc	Finland	63°45'	24°05'	30/30	746	0.5%
FINs	Finland	60°52'	21°20'	30/30	743	0.9%
SWE	Sweden	56°28'	15°55'	30/30	744	0.8%
NL	The Netherlands	52°06'–52°30'	05°39′–06°27'	29/28	747	0.4%
BEL	Belgium	49°58'–50°20'	04°55'–05°38'	19/18	498	0.4%
POL	Poland	50°41'	20°05'	30/30	749	0.1%
GER	Germany	50°15'	10°30'	18/18	448	0.4%
SLO	Slovakia	47°44'–49°37'	16°50'–22°34'	30/30	748	0.3%
FRA	France	48°51'	07°52'	29/28	747	0.4%

All populations grow in low altitudes.

^aNumber of families in phenotype estimation/number of families successfully genotyped.

^bNumber of seedlings for phenotype observations.

^cMissing values due to lack of germination and some seedlings not setting bud.

Analysis of phenotypic data

As the phenotype was measured from individuals of half-sib families but only maternal genotype information was available, estimated breeding values based on best linear unbiased predictors were used as pseudo-observations for the maternal phenotypes. The use of estimated breeding values as pseudo-observations in association studies has been criticized by Ekine et al., 2014. However, due to large and constant family size, this treatment should not increase the number of false positives in our data. To estimate population-specific trait means as well as variance components, a linear mixed-model of the following form was applied to each population separately:

where Y_kjiq is the number of days from sowing to bud set recorded for the qth seedling belonging to family j planted in the ith block on plot ji in population k, m_k the overall fixed mean effect of population k, f_kj the random effect of the jth family (best linear unbiased predictor), b_i the fixed effect of the ith block, p_kji the random effect of plot ji in population k and e_kjiq the random error term. The best linear unbiased predictors for family means were predicted by

The variance components were estimated using the method of restricted maximum likelihood (Patterson and Thompson, 1971). For the Swedish and German populations, between-plot variances were estimated to be so close to zero such that these variance components contributed less than 5% to the total sum of variance components. In these cases, models were refitted omitting plot effects.

Linear regressions of the form population mean vs latitude of origin were used to quantify the steepness of the phenotypic cline. Genetic parameters were calculated as follows: the additive genetic variance 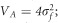; the total phenotypic variance 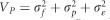(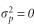=0 when plot effects were omitted); and narrow sense heritability h²=V_A/V_P. Evolvability was defined as the additive genetic coefficient of variation , where V_A is population-specific additive genetic variance and 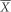is population-specific mean (Houle, 1992).

Genotype data

SNP discovery

We designed a SNP array of 768 SNPs for Illumina GoldenGate assay. 237 SNPs originated from 56 gene fragments sequenced in our laboratory in various population sets (see Pyhäjärvi et al., 2011; Kujala and Savolainen, 2012 and references therein). The number of SNPs extracted per gene fragment varied from one to 11. The selection of SNPs was based on the Illumina SNP score, and distance and linkage disequilibrium between SNPs. Illumina SNP score was determined with Illumina ADT (Assay Design Tool, Illumina, 2015) that uses information on the flanking sequences to identify SNPs with high likelihood of success.

Another 531 SNPs from 341 gene fragments were obtained from a conifer re-sequencing project CRSP (Comparative Re-Sequencing in Pinaceae, Wegrzyn et al., 2008). CRSP data for P. sylvestris were based on sequencing haploid megagametophytes of 12 trees across Europe. The initial SNP calling from these fragments was done by CRSP, with an automated pipeline PineSAP (Wegrzyn et al., 2009). These SNP calls were verified visually. Typically one or two SNPs (three in some cases) per fragment were selected. Selection was again based on the Illumina SNP score, and distance and linkage disequilibrium between SNPs.

Genotyping and defining the genotypes

DNA for genotyping was extracted from pooled megagametophytes of mother trees. On average, 19 megagametophytes were pooled for each sample. For extraction we used Nucleospin Plant II (Macherey-Nagel) with buffer PL1. Genotyping was conducted in CNG (Centre National de Génotypage, Evry, France). The genotyping method used here (Illumina GoldenGate assay) is usually applied to diploid tissue and an intensity score is reported for the presence of a certain nucleotide variant/SNP allele. Thresholds are then applied to distinguish between the three possible genotypes at a nucleotide site SNP. In diploid tissue, a SNP allele A₁ is present at either 100% intensity (for homozygote A₁A₁), 50% (heterozygote A₁A₂), or 0% (homozygote A₂A₂). In a pool of haploid megagametophytes, however, the proportion of allele A₁ in a heterozygote is not necessarily 50%, because the megagametophyte pool consists of a binomial random sample of A₁ and A₂ alleles. Therefore, we redefined the thresholds to distinguish between the three possible genotypes obtained from pooled haploid tissues.

From among the genotypes delivered by CNG, we discarded SNPs that gave no call, were either monomorphic or heterozygous in all or most of the genotyped samples, or had a significant portion of missing genotype calls. We also tested each SNP for Hardy–Weinberg equilibrium in each of the 10 populations by the exact test suggested by Wigginton et al., 2005 and excluded SNPs with P-values < 0.05 in at least two populations. This rather strict requirement was motivated by the fact that Scots pine shows high inbreeding depression in early life stages and therefore the genotypic ratios of adults follow Hardy–Weinberg expectations (Kärkkäinen et al., 1996). The strict requirement was therefore chosen to minimize the risk of low-quality genotypes. Furthermore, we excluded SNPs with minor allele frequencies <0.05. These filtering criteria left 351 SNPs for the association analysis. Missing genotypes (1.7%) were replaced by imputation using population-specific observed genotype frequencies.

In this study, mother trees were genotyped instead of the individual progeny. Even if we do not know the individual progeny genotypes, we can still predict the overall genotypic composition of the open-pollinated progeny based on known genotype of the mother tree and population-specific allele frequencies. At a biallelic locus, after random mating, a mother with genotype A₁A₁ will produce genotypes A₁A₁ and A₁A₂ in frequencies p_k and q_k in population k (most of the pollen is expected to arrive from at most a few hundred meters; reviewed in Savolainen et al., 2007). As the best linear unbiased predictor used as the response variable in the association analysis (see below) is in fact an estimate for the breeding value of the mother tree, which depends on population-specific allele frequencies under random mating in natural populations, the maternal genotype code was set to X_kjm = p_km, if the mother tree is a homozygote A₁A₁, to X_kjm = ½(p_km−q_km), if the mother is a heterozygote A₁A₂, and X_kjm = −q_km, if the mother tree is a homozygote A₂A₂, respectively. This genotype coding is based on the assumption that the SNPs act additively and that allele frequencies are in Hardy–Weinberg equilibrium. Technically this was done by weighting genotype state (−1, 0 or 1) in the model with corresponding probabilities.

Association analysis

Within-population analysis of association across multiple populations

Association analysis was done implementing the model described in Introduction (equation (1)). As all markers are simultaneously included in this multilocus model and the number of parameters is larger than the number of observations, shrinkage priors were assigned to the marker effects β_m to regularize the model and to draw effect sizes toward 0. The form of these priors resemble a spike and a slab with most probability mass on a short interval around 0 and little probability mass distributed on the rest of the support. Specifically, we assigned a prior in form of a mixture of three discrete uniform distributions to each additive effect β_m (Knürr et al., 2011 2013). The density of the distribution is:

This distribution is controlled by three hyperparameters: p_o is the prior probability of marker inclusion, l the maximal absolute effect size, and b the border value used to discriminate between influential and negligible effect sizes. The indicator functions (I) define the discrete supports of the three uniform distributions. This distribution allows a coherent framework for calculation of marker-specific Bayes factors. Following Knürr et al., 2011, we calculated the SNP-specific Bayes factors, BF_m for the hypotheses H₁: | β_m |> b and assessed the strength of evidence in favor of genetic association according to the common classification: evidence is considered very strong for 2ln(BF_m)>10, strong for 2ln(BF_m) ∈ (6, 10), positive for 2ln(BF_m) ∈ (2, 6), and not worth more than a bare mention for 2ln(BF_m) ∈ (0, 2).

In addition to the simultaneous analysis of all ten populations, subanalyses were employed for two subsets of the populations, one consisting of the four northern populations from Finland and Sweden, and the other including the six central populations from The Netherlands, Belgium, Poland, Germany, Slovakia and France. Power analysis of QTL detection is presented in Supplementary Information.

MCMC and prior specifications

We implemented a Gibbs sampler in the C programming language for the Bayesian model, which is an adaptation to the algorithm presented in Knürr et al., 2013. We simulated nine MCMC chains under varying prior specifications of p_{0 (}marker inclusion probability) and b (effect size border value) to approximate the respective posterior distributions. Inference of posterior results based on averages from different prior combinations allows assessment of the sensitivity and robustness of our analysis; the results should not depend on any specific prior value.

Specifically, we assigned each of the nine possible pairs in (p₀,b) ∈ {0.95, 0.99, 0.999} × {0.05, 0.1, 0.25} as the prior specification of individual MCMC chains. The maximal absolute effect size was kept constant at l = 10, because varying this parameter adds only minimal insight into the sensitivity and robustness of the analysis (Knürr et al., 2011). The prior distributions for the other model parameters were assigned as follows: for the overall population effects μ_k normal distributions with mean 0 and variance 10⁶; for the residuals ε_kj normal distributions with mean 0 and population-specific variance σ²_k, for these variances inverse-gamma distributions with shape parameter 0.01 and rate parameter 0.01.

Each MCMC chain had a length of 220 000 Gibbs iterations, of which we discarded the first 20 000 as a burn-in phase. We thinned the MCMC chains and saved only every 20th iteration to save disk space. Thus, our posterior results are based on nine MCMC samples each of size 10 000. The simulation took ~2 h on a 3 GHz desktop PC with 2 GB RAM memory.

Assessment of the false positive rate and the percentile for significant marker associations

To assess the global false positive rate (GFPR), we used a permutation approach that removes the association between the mother tree’s genotype and the estimated phenotype. This enables controlling GFPR, when a specific threshold for 2ln(BF) is used to discriminate between associated and non-associated markers. In addition, the comparison of the marker effects estimated from observed/non-permuted data against the corresponding null distribution arising from permuted data sets allows assessing the percentile for significant marker associations (referred as PSMA from this point forward; Churchill and Doerge, 1994). In the permutation analysis, phenotypic associations within populations were broken by assigning phenotypes Y_kj randomly to genotypes within populations. As earlier, nine pairs of marker inclusion probability and allele effect size in (p₀,b) ∈ {0.95, 0.99, 0.999} × {0.05, 0.1, 0.25} were used as prior combinations to maintain robustness. To generate approximately 100 permutations, each prior combination was used 11 times to reach satisfying number of MCMC chains (each corresponding to a single permutation), in which these nine prior combinations were equally represented (that is, 99 chains). Total of seven batches (replicates) of 99 chains were run and null distribution of each batch monitored to make sure that when all (9 × 11 × 7) MCMC samples were combined they represented a stable form of null distribution. Thus, the phenotypes were permuted 693 times to calculate a robust null distribution. The rest of the setup for the MCMC chains was identical with the one used for the nonpermuted data set. Permutations were done for each of the three sets of populations (all populations, northern, central).

Examination of between-population component of association

Our model requires that marker association is detectable within populations. If the allele frequencies at some markers are very extreme (or fixed) in some of the populations, or the size of the marker effect is small, the association might not be detected simply due to lack of power. We therefore complemented our analysis with another step which aimed at recovering these associations with the help of the extensive phenotypic variation between populations.

In this step, we used the same 693 MCMC chains as above for the permuted data sets. It is noteworthy that the population-specific allele frequencies and linkage disequilibrium structure in the set of genotypes remained unaltered in this approach, as phenotypes (and not genotypes) were permuted. Furthermore, permuting the phenotypes within populations had no effect upon the population-specific phenotype mean, nor on the phenotypic variation within populations. As mentioned above, we applied our multilocus association model to permuted data sets to create null distributions of SNP-specific 2ln(BF) for each SNP separately. We calculated the medians of the permuted null distributions of 2ln(BF) for each SNP separately, and visible outliers in box and whisker plot of these medians were then identified. Outliers in these plots are SNPs that persistently associate with the phenotype even when the within-population associations are missing. Another two box and-whisker plots of the distributions of 75% quantiles and 95% quantiles of 2ln(BF) were created to detect SNPs which not consistently, but fairly often showed association with the phenotype in the permuted data sets. Furthermore, regression coefficients of allele frequency vs population-specific phenotypic mean as well as the corresponding p-values were calculated for the outlier SNPs to investigate our expectation that the outlier detection step recovers associations of SNPs with extreme allele frequencies. Note that regression results only serve as additional information and were not used to identify the outlier SNPs.

In theory, the acquired associations in this permuted data can arise from (i) loci that are connected to timing of bud set, but not identified in the primary analysis due to lack of power, (ii) loci connected to another phenotype that covaries with timing of bud set across populations, or (iii) neutral loci where allele frequencies vary clinally resembling the cline in timing of bud set for demographic reasons. However, being identified as an outlier in this analysis essentially means that the allele frequency change in the marker locus has to be very similar to the change of the population mean in timing of bud set, and that the size of the corresponding genetic SNP effect has to agree with the amount of the observed additive within-population variation. Furthermore, multilocus methods intrinsically can correct for some population structure as the markers act as cofactors. The results of the outlier analysis should however be treated with caution until further validation.

Results

Characteristics of the phenotypic cline

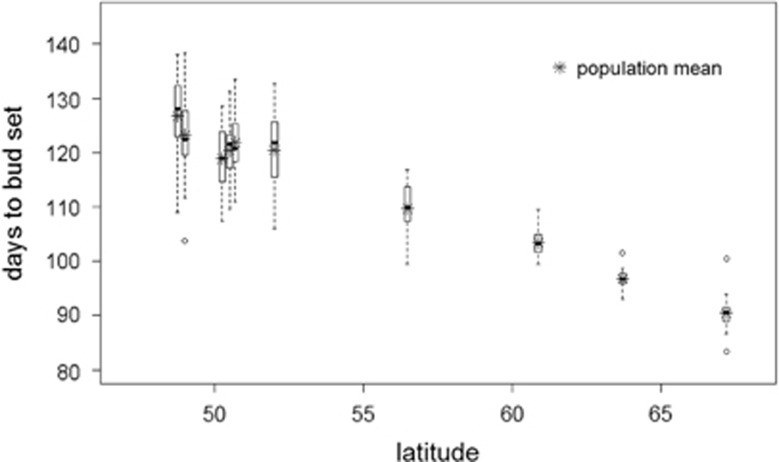
The population means of days from sowing to bud set ranged from 90.4 days for the Northern Finnish population to 126.8 days for the French population, a difference of five weeks (Table 2, Figure 2). Overall, the population means were highly correlated with latitude of origin (R²=0.98). Especially for the four northern populations, the correlation was tight (R²=0.99). Among the central populations, the correlation was lower (R²=0.40). Also, the cline was slightly steeper in the northern part of the range (slope coefficients −1.83 (northern populations) and −1.34 (central populations) bud set days/latitude degree). The phenotypic variances in the northern populations were smaller (less than 100 days²) than in the central ones (more than 300 days²). Heritabilities were intermediate to high (from 0.35 to 0.75) showing that there is a large genetic component between families within each population. Furthermore, both the additive genetic and environmental variances, and evolvability, varied between populations (Table 2).

Table 2. Results of the phenotype analysis on timing of bud set.

Population	Meana	VAb	VPc	h2d	s.e.(h2)e	CVAf
FINn	90.4	60.1	95.2	0.63	0.28	8.58
FINc	96.8	17.8	39.3	0.45	0.18	4.36
FINs	103.4	34.7	72.1	0.48	0.17	5.70
SWE	109.7	120.7	341.6	0.35	0.13	10.01
NL	120.5	249.5	408.4	0.61	0.21	13.11
BEL	120.4	178.2	396.1	0.45	0.21	11.09
POL	121.9	189.9	403.5	0.47	0.17	11.30
GER	118.9	200.8	520.3	0.39	0.18	11.92
SLO	123.2	247.4	345.6	0.72	0.23	12.77
FRA	126.8	295.1	391.8	0.75	0.24	13.55

^aPopulation average.

^bAdditive genetic variance (days²).

^cPhenotypic variance (days²).

^dHeritability (narrow sense).

^eStandard error of heritability.

^fAdditive genetic coefficient of variation (Houle, 1992).

Figure 2.

The distributions of family means of days to bud set. Each box and whisker plot represents one population.

SNP genotypes

After strict filtering for quality, for minor allele frequency (of at least 5%), and for deviation from Hardy–Weinberg equilibrium in at most one population, we were left with 351 SNPs with high quality genotypes. 104 of these SNPs were in genes sequenced in our laboratory and 247 originated from CRSP data. Together these represented total of 235 gene fragments of which 15, 34, and 186 originated from light perception and timekeeping genes, stress tolerance genes, or reference genes, with 40, 70 and 251 SNPs, respectively. The number of families successfully genotyped was 271. In these families, missing genotypes (1.7%) were imputed by using population-specific observed genotype frequencies.

Association analysis results

Within-population component of association

The phenotypic data were tested for association with the 351 high quality SNPs. The analysis yields 2ln(BF) values that are averages over nine possible prior combinations of marker inclusion probability and effect size. Therefore the reported values are thought to be robust, that is not sensitive to given prior values (cf. Knürr et al., 2013). In the simultaneous analysis of all ten populations, six SNPs showed values of 2ln(BF) larger than 2, that is, at least positive evidence in favor of association according to the common classification (Table 3). On the basis of permutation testing, using the threshold 2ln(BF) larger than 2 corresponded to a global false positive rate (GFPR) of 16.9%. To obtain a global false positive rate of 5%, the threshold had to be redefined to 2ln(BF) larger than 4.8. This value was exceeded by three of the reported SNPs (CL1414Contig1_01-182, 2_10306_01-354 and PRR1-991). Permutation testing yielded SNP-specific PSMAs (percentile for significant marker associations) with values larger than 0.95 for the same three SNPs. One of the SNPs reported (LP2-154) showed a value just below the 2ln(BF)-threshold and a SNP-specific PSMA of 0.94.

Table 3. SNPs with mean of 2lnBF larger than 2 in the within-population component of association.

SNP name	All				North				Central
	MaAFa	2lnBFb	βc	PSMA	MaAFa	2lnBFb	βc	PSMA	MaAFa	2lnBFb	βc	PSMA
CL1414Contig1_01-182	0.89	10.1	2.2	0.99	0.89	11.2	2.9	0.99	0.89
2_10306_01-354	0.60	7.3	0.8	0.99	0.57	5.4	0.5	0.98	0.62
PRR1-991	0.89	5.8	0.7	0.97	0.89	4.6	0.6	0.95	0.89
LP2-154	0.83	4.6	0.4	0.94	0.80	4.2	0.3	0.94	0.85
2_9291_02-618	0.88	4.0	0.6	0.90	0.90	2.8	0.3	0.83	0.87
CL1052Contig1_03-119	0.63	2.2	0.2	0.86	0.62				0.63
0_5204_01-315	0.62				0.61	2.1	0.1	0.87	0.63
CL1966Contig1_05-341	0.93				0.94				0.93	14.4	7.1	0.98
CL1487Contig1_04-135	0.85				0.84				0.87	6.3	1.8	0.90
CL4511Contig1_02-346	0.87				0.92				0.84	5.9	1.7	0.92
0_1439_01-147	0.89				0.92				0.87	5.3	1.1	0.89
Aco_f2-2100	0.89				0.87				0.90	4.0	0.6	0.76
Aco_f1-2961	0.93				0.93				0.94	2.5	0.2	0.49
6pgdB-810	0.77				0.78				0.77	2.1	0.2	0.65

Abbreviations: PSMA, percentile for significant marker association; SNP, single-nucleotide polymorphism.

2lnBF values corresponding to a global false positive rate less than 5% in bold.

2lnBF, β and PSMA are averages over nine MCMC chains with different prior combinations.

^aMajor allele frequency; average of population-specific frequencies.

^bPosterior mean of the 2log-transformed Bayes factor in favor of marker association.

^cMarker effect (days to bud set).

Very similar results were found in the subanalysis of the four northern populations (Table 3). Six SNPs exceeded the threshold value 2ln(BF) larger than 2. Five of them were identical to the ones associating with the full data (SNP 0_5204_01-315 was significant in this subanalysis but not in the full data). Permutation testing yielded a GFPR of 18.7% when setting the threshold at 2ln(BF) larger than 2. GFPR of 5% was obtained for a threshold of 2ln(BF) larger than 5.0. Only two SNPs (CL1414Contig1_01-182 and 2_10306_01-354) exceeded this threshold. PRR1-991 had a SNP-specific PSMA of 0.95 and again, LP2-154 showed a value of 2ln(BF) below the threshold and a SNP-specific PSMA of 0.94. The subanalysis of the six central populations identified seven SNPs with 2ln(BF) larger than 2 (Table 3), which corresponded to a GFPR of 46.2% according to permutation testing. None of these SNPs were found in the overall or northern analysis. Here, a GFPR of 5% was obtained for a threshold of 2ln(BF) larger than 7.2. This was exceeded by only one SNP (CL1966Contig1_05-341). Only this SNP showed a SNP-specific PSMA over 0.95.

The biggest effect size in our data was found in the central populations where SNP CL1966Contig1_05-341 had a marker effect of 7.1 days. The other six SNPs detected in the central populations had effect sizes less than 2 days. In the northern populations the largest effect was 2.9 days for SNP CL1414Contig1_01-182. The other five SNPs associated in the north had effect sizes less than one day. (Power analysis of QTL detection is presented in Supplementary Information).

Between-population component of association

In the complementary outlier detection step, several SNPs were identified (Table 4), most of which occurred in the overall analysis and in the northern subanalysis (four and six SNPs, respectively). Three of these (FTL2_f1-356, PhyN-2120 and CL1154Contig1_02-143) were shared between these two analyses. Only one SNP was identified in the southern subanalysis. The slope coefficients of the regression of population phenotypic mean vs population allele frequency were quite high for some of the SNPs found in this analysis step, although the corresponding P-values did not reach statistical significance at a level of 0.05. However, it should be noted that the low P-values also reflect low power in these regressions, where the number of data points were only ten (all populations), four (northern) and six (central), respectively. None of the SNPs detected as outliers showed a signal of association in the within-population analysis (above).

Table 4. Outlier SNPs identified in the between-population component of association.

SNP name	All				North				Central
	MaAFa	Outlierb	Regressionc		MaAFa	Outlierb	Regressionc		MaAFa	Outlierb	Regressionc
			P-value	Slope			P-value	Slope			P-value	Slope
FTL2_f1-356	0.95	95% (1)	0.14	−1.37	0.96	75% (3)	0.17	−1.07	0.94
						50% (1)
						95% (2)
UMN_2763_01-83	0.94	95% (2)	0.23	−1.76	0.95				0.94
PhyN-2120	0.94	95% (3)	0.06	−2.12	0.97	75% (2)	0.44	−1.70	0.92
CL1154Contig1_02-143	0.93	95% (4)	0.26	−0.52	0.98	75% (1)	0.22	−2.60	0.90
						95% (1)
CL1848Contig1_01-69	0.93				0.95	95% (3)	0.36	−1.75	0.92
0_1453_01-517	0.92				0.91	95% (4)	0.84	0.24	0.92
2_3720_01-180	0.92				0.97	95% (5)	0.33	−3.66	0.89
CHCS-189	0.90				0.87				0.92	95% (1)	0.18	0.32

The results are based on averages over nine MCMC chains with different prior combinations.

Note that regression results were not used to identify these outliers, but only serve as additional information to illustrate the correlation between population phenotypic means and allele frequencies.

^aMajor allele frequency; average of population-specific frequencies.

^bOutlier type: SNP was identified as an outlier in the box and whisker plots of medians (50%), 75% quantiles (75%) and 95% quantiles (95%); corresponding rank in brackets.

^cRegression: p-value and slope coefficient of the linear regression phenotypic population mean vs allele frequency in percentages. Thus the reported slope corresponds to the change of the phenotype in bud set days, when the allele frequency increases by 1%.

Discussion

Phenotypic cline

This European wide experiment of adaptive growth cessation trait in Scots pine showed a clear phenotypic cline; the mean bud set date was about two days earlier for each degree latitude in the latitudinal range between 52°N and 67°N. Between the central populations, the change per degree latitude was diminished to less than one day on average, and the correlation between latitude and mean bud set date was lower than in the north. This finding of a strong north-south cline is consistent with earlier work on Scots pine by, for example, Mikola (1982) who examined timing of bud set in several populations across Finland. Norway spruce, birch and poplar show similar clines in growth cessation traits within Scandinavia. In Sitka spruce a steep long cline is also seen along the Pacific coast of North America (see Alberto et al., 2013 and references therein).

The phenotypic variances were much larger in more southern populations than in the three Finnish populations. The high variances are not just environmental, as additive genetic variances and thus heritabilities were also high in the central populations. Evolvability also differed (defined as the additive genetic coefficient of variation, Houle, 1992); the Finnish populations showed lower CV_A values than more southern populations. The experiment was conducted in only one set of conditions in a greenhouse at latitude 61°, quite far from the origins of the Central European populations. We cannot completely rule out the possibility of the larger variances of the central populations being at least partly an experimental artifact. Earlier work by Mimura and Aitken, 2010 with Sitka spruce has, however, shown that the ranking of the bud set dates of populations is maintained in different experimental environments, and no marked change in variation was observed between these environments. It is possible that the large variances of the Central European populations in fact reflect weaker selection pressure compared with the harsh northern environments where the consequences of having a maladaptive genotype may be more severe. In line with this hypothesis, an analysis based on transfer trial series data of Eiche, 1966 showed that the change in survival and overall fitness of southern genotypes transferred northward is larger than the change in fitness of northern genotypes transferred southward for a similar latitudinal distance (Savolainen et al., 2007). The lower evolvability in the north can also reflect the past action of selection due to adaptation coupled with drift effects during colonization (see also Pujol and Pannell, 2008). In the perspective of possible future climate change, the central European populations seem to be more capable of adapting to new local optima in timing of bud set.

New method for multipopulation association

A new Bayesian analysis method was developed that enables combining data from multiple populations into one analysis without compromising discovery of trait controlling variants whose allele frequency patterns resemble the structure in neutral genetic markers. Basic single-locus methods for association with corrections for population structure (see Sillanpää, 2011 for review) can perform poorly especially when the structure resembles a ‘continuum of relatedness’ (Zhao et al., 2007) such as assumed for Scots pine along its main range. Single-locus mixed-models (Yu et al., 2006; Kang et al., 2008) have been widely used to correct for this kind of structure. Although mixed-models have been shown to perform well in many cases, a general drawback in mixed-model approaches is that they may lose power (by overcorrecting the structure) or may lead to false detections when candidate SNPs are included in calculation of genomic relationship matrix (see, for example, Würschum and Kraft, 2015).

The statistical model used in our method allows the full simultaneous Bayesian analysis of all genetic information available via a multilocus setup. Multilocus association models have been shown to perform well without including any mixed-model correction (polygenic term) to the model (for example, Pikkuhookana and Sillanpää, 2009; Kärkkäinen and Sillanpää, 2012; Würschum and Kraft, 2015). Association methods based on additive models are generally not very efficient in finding the smallest effect loci. Therefore, we focused our efforts on isolating the loci that have the biggest effects among the genotyped markers by using shrinkage of effect sizes. The main step in our method relies on the within-population associations to find a limited set of loci underlying the trait of interest. The associations that lack power within populations were further studied in the complementary step in our method, which omits the within-population information but rather utilizes the extensive phenotypic variation between populations. This step thus aims at recovering associations that go undetected within populations.

The two analysis steps yielded different SNPs, as expected. SNPs with very little variation inside populations (that is, extreme within-population frequencies) might show up in the between-population but not in the within-population analysis (due to lack of power). This in fact seems to be true in our case; SNPs detected as outliers in the between-population step showed more extreme frequencies than SNPs found with the first analysis step. The means of population-specific major allele frequencies were consistently higher than 0.9 in these markers, and some populations in the northern part were fixed for one allele at some of these SNPs. In the between-population step, an association signal could arise, in theory, from demographic factors creating clines in allele frequencies, or from another phenotype tightly covarying with bud set timing. An outlier status of a specific SNP is expected to be obtained only if its allele frequency change closely follows the change in population phenotypic mean. Also, the corresponding genetic SNP effect has to be consistent with the observed additive within-population variation (that is, not too large relative to the within-population additive genetic variance). Furthermore, multilocus models correct for population structure as the markers act as cofactors (Pikkuhookana and Sillanpää, 2009; Kärkkäinen and Sillanpää, 2012; Würschum and Kraft, 2015). Therefore, we suggest that the permutation approach holds promise to separate true associations from spurious. Nevertheless, the results need to be further validated as the possibility of spurious association, or association due to other covarying traits cannot be totally excluded here.

Cold tolerance and timing of bud set are correlated both between and (to lesser extent) within populations of Scots pine (Savolainen et al., 2004) and the evolution of these traits is obviously interlinked. If the correlation is high across populations, cold tolerance loci might also be detected as outliers. Interestingly, we found that a SNP from a stress related locus lp2 was associated with bud set timing in the main analysis. Thus, the additive genetic correlation in this case could result in finding a cold tolerance SNP associated to bud set within populations, too. Here, we have not evaluated the strength of the correlation of these two phenotypes. In future studies the interactions of these two traits should be further studied.

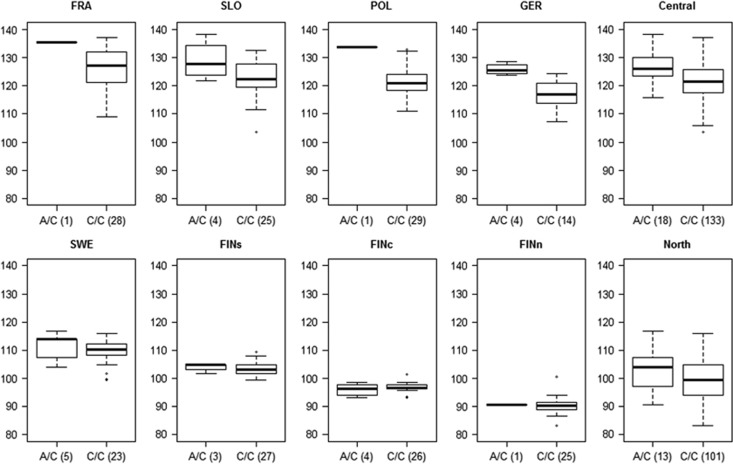
The need for careful control of population structure in our data is illustrated in Figure 3. The box and whisker plots represent the phenotypic variation in different genotype classes of SNP CL1966Contig1_05-341 that has a rather big effect in the central populations but not in the northern ones. Had we analyzed the northern data without requiring for the association to arise also within individual northern populations, we would have likely ended up with a spurious association in the northern analysis due to the allele ‘A’ being more frequent in more southern populations, where the time to bud set is longer. In the central populations, in contrast, the effect is seen within each population, too, and is likely a genuine association. Note that this SNP was not recovered in the north in the complementary outlier analysis. This gives further support to our conclusion that neutral clinal variation in allele frequencies alone does not easily make the SNP an outlier in the between population analysis.

Figure 3.

Distribution of family means of days to bud set in different genotype classes of SNP CL1966Contig1_05-341 (genotype counts in parentheses). On the left individual populations are shown, on the right the populations are combined (Central, North). Genotype A/A was omitted from this picture for clarity as it was observed in only a few populations. Only four out of six central populations are shown here.

22 SNPs found to associate with timing of bud set

Out of the 351 SNPs examined, a total of 22 SNPs showed evidence of being related to the timing of bud set at least in some part of the cline, and either in the within-population or between-population part of the analysis (see Supplementary Information for annotations and putative functions of the loci). Whether these are causative or linked polymorphisms remains to be studied. Previous candidate gene based association studies on timing of growth cessation have found similar or smaller numbers of associating loci; Ingvarsson et al., 2008 found 2 SNPs within and around a Populus tremula phytochrome gene, Ma et al., 2010 found six SNPs within P. tremula photoperiod genes, Holliday et al., 2010 reported 26 SNPs in Picea sitchensis, Olson et al., 2013 found 19 SNPs from eight genes out of 27 candidate genes studied in Populus balsamifera, and Prunier et al., 2013 identified 20 loci in Picea mariana. The percentage of variance explained by individual loci reported in these studies ranged from 1 to 15%.

The effect sizes in our data were mainly small; most were less than a day and a few between one and two days. Finding many small effect loci implies that despite the small sample size per population, our method has adequate power (power issues are further discussed in the Supplementary Material). The biggest effect was seen in the central populations where SNP CL1966Contig1_05-341 showed an effect of 7.1 days. In the northern populations the biggest effect (2.9 days) was seen in SNP CL1414Contig1_01-182. Especially interesting is the biggest marker effect in the central populations. Some of the genes (or gene families) associated here have been suggestive of locally adaptive functions in other tree species, too (for example, FTL2, and PRR- and phytochrome gene families in Norway spruce; Chen et al., 2012). Acknowledging the small genome coverage in our study, the level of molecular convergence relative to other tree species remains, however, to be studied further.

Indications of genetic heterogeneity

None of the 22 top associating SNPs were shared between the northern and central groups. This finding suggests that some parts of the underlying genetics differ between the northern and central European populations. Some of these variants may have no influence on creating variation in timing of bud set in one part of the range; some may have an effect in both parts, but of so much smaller size in one part that it was not detectable in this study. Obviously, with this modest number of SNPs, we do not capture all the variants affecting bud set in Scots pine, and most likely loci that have similar effects sizes in both north and central European populations do exist in the genome. In theory, the different outcomes could also be due to different allele frequencies in north vs central parts. Observed allele frequency differences were, however, small (Kujala and Savolainen, manuscript under preparation).

Another possibility for these results could be different linkage disequilibrium patterns across the studied range. A particular SNP could be in stronger linkage disequilibrium with the causative SNP in one part of the range than in another, which could falsely appear as genetic heterogeneity. Previous studies in Scots pine have nevertheless shown that haplotypes are mostly shared between different areas in the main range of this species. Haplotype based differentiation (H_ST; Hudson et al., 1992) between northern and central European regions is very small (on average 0.005 in haploid sequence data in Kujala and Savolainen, 2012). In four of the associated genes included in that data set, H_ST estimates are low (prr1: 0, 0128; lp2: 0, 0026; ftl2: 0, 0004; phyn: 0, 0045). The decay of linkage disequilibrium also did not differ much between northern and central populations in the data of Kujala and Savolainen, 2012. We therefore suggest that the differences in associating loci likely stem from different effects sizes of the SNPs, thus supporting our interpretation of genetic heterogeneity. Interestingly, the effect of variation in gigantea gene on timing of bud set in P. balsamifera was larger in a northern than in a southern common garden (for the same genetic material; Olson et al., 2013).

Genetic heterogeneity has been shown to be a very common feature in human disease (McClellan and King, 2010). Some adaptive traits have also been shown to be genetically heterogeneous, such as high altitude adaptation in humans (see, for example, Jeong and Di Rienzo, 2014) and highland adaptation in maize (Takuno et al., 2015). In these cases, however, the level of gene flow between the different sites of adaptation is lower than what is assumed between central and northern European populations of Scots pine. As stated above, the frequencies of associating SNPs are not differentiated between northern and central regions. It is possible that the same alleles in different environments have different phenotypic effects (for example, based on different temperatures or daylengths).

This is very intriguing finding in the light of the fact that the photoperiodic conditions—and the information content of the light/dark cycle—are very different in the northern versus central Europe. It has been suggested that Scots pine in the far north uses mainly light-dominant day timekeeping whereas Scots pine in more southern regions is dark-dominant. The two different timekeeping mechanisms might in fact both exist in individual plants, the light-dominant type being favored toward the north. The short (or unexisting) nights in the north during the summer months can render the dark timekeeping quite imprecise in the high latitudes, thus creating a need to use the information in the daylight spectra. The red, far red and blue light have been shown to affect the growth and growth cessation traits in Scots pine and among other trees (for example, Clapham et al., 2002).

The possibility of genetic heterogeneity must nevertheless be further studied and validated in forthcoming studies. Also it remains to be examined in more depth whether different standing variation from the various refugia could have resulted in different evolutionary solutions. At present, the colonization routes of Scots pine after the last glacial maximum are still not known in detail, especially the potential colonization from east (see, for example, Savolainen et al., 2011).

Conclusions

We developed a new Bayesian multilocus method for analysis of local adaptation in multipopulation data, which combines within-population analysis across populations, and also examines the between-population component of association. We found that both the genetic and environmental variances of timing of bud set were lower in the northern part of the Scots pine range. Furthermore, we found genetic heterogeneity between northern and central populations of Scots pine. Overall, these results support a view that the selection for an optimal timing of bud set is, for one, targeting different loci and/or pathways in northern versus central European Scots pine, and second, is stronger in the northern parts of the range. As the genomic resources of Scots pine and other conifers improve, we will soon not be limited to a set of candidate genes but will be able to study these issues with genome wide data. The results of this study also provide a starting point for using tools of genomic selection on these kinds of traits in forest tree populations.

Data archiving

Phenotype data, genotype scores, R scripts and other implementation files are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.dv413.