Incoherent Inputs Enhance the Robustness of Biological Oscillators

SUMMARY

Robust biological oscillators retain the critical ability to function in the presence of environmental perturbations. Although central architectures that support robust oscillations have been extensively studied, networks containing the same core vary drastically in their potential to oscillate, and it remains elusive what peripheral modifications to the core contribute to this functional variation. Here, we have generated a complete atlas of two- and three-node oscillators computationally, then systematically analyzed the association between network structure and robustness. We found that, while certain core topologies are essential for producing a robust oscillator, local structures can substantially modulate the robustness of oscillations. Notably, local nodes receiving incoherent or coherent inputs respectively promote or attenuate the overall network robustness in an additive manner. We validated these relationships in larger-scale networks reflective of real biological oscillators. Our findings provide an explanation for why auxiliary structures not required for oscillation are evolutionarily conserved and suggest simple ways to evolve or design robust oscillators.

INTRODUCTION

Biological oscillators drive essential physiological and developmental processes in all forms of life, from bacteria through vertebrates. These biological oscillators span a wide range of periods and molecular forms, including neural spikes (1 ms–10 s), cell cycles (10 min–24 hr), somitogenesis (25 min for zebrafish and 2 hr for mice), and circadian clock (24 hr), etc. Despite the complexity and diversity of these oscillators, their central network architectures are highly conserved (Bell-Pedersen et al., 2005; Cross et al., 2011), suggesting that network topology is a key factor in determining the properties of biological oscillations. Studies have focused on the core topologies of oscillators, to understand the systems-level characteristics such as periodicity and robustness (Castillo-Hair et al., 2015; Lomnitz and Savageau, 2014; Nguyen, 2012; Novak and Tyson, 2008; Woods et al., 2016).

In principle, a single negative feedback is required and sufficient to generate self-sustained oscillations (Friesen and Block, 1984; Ingolia and Murray, 2004; Lomnitz and Savageau, 2014; Novak and Tyson, 2008; Ferrell et al., 2011). However, known biological oscillators are organized into more complex network structures. Some of the additional structures, such as positive feedback loops, are not required for generating oscillations but are evolutionary conserved, which has raised a question of what functional role they may play. An appealing hypothesis is that they improve robustness, which is defined by likelihood of remaining self-sustained oscillations under a perturbation in the parameter space. It is an important characteristic for biological oscillators to function properly in a noisy environment. Studies on several biological oscillators such as cell cycles have supported this notion by showing that adding a self-positive feedback loop, in which a node can activate itself, to a core oscillatory circuit can increase the oscillator’s robustness, while adding a self-negative feedback loop to the same core cannot (Ananthasubramaniam and Herzel, 2014; Gerard et al., 2012; Tsai et al., 2008). However, whether positive feedback is necessary or sufficient to increase robustness has remained controversial. A recent study using synthetic circuits (Chen et al., 2015), has shown that adding a negative feedback to an oscillator could also increase its robustness. In addition, while both Wee1 and Cdc25 form positive feedbacks in embryonic cell cycles, only the one from Cdc25 is critical for the robustness of the oscillation period (Tsai et al., 2014). Moreover, a recent study on the p53 oscillation dynamics (Moore et al., 2015) demonstrated that only one out of the three microRNA-mediated positive feedbacks increases the robustness of the oscillator. These studies, each focusing on a specific set of biological oscillators, did not yield a converging conclusion. Importantly, it reveals the difficulty of identifying generalizable mechanisms through analyzing only a subset of oscillators. To obtain a complete picture beyond any chosen systems, a comprehensive mapping from the entire topology space to the function space is necessary.

Here we systematically analyzed the robustness of all oscillatory topologies with no more than three nodes, to search for structures that are most significantly associated with high oscillation robustness. In agreement with previous work (Castillo-Hair et al., 2015; Goldbeter, 2002; Novak and Tyson, 2008), we found that certain core network topologies are essential for robust oscillations. However, we also found that local modifications on a node of the network have a significant impact on the global network robustness. Specifically, we identified local motifs such that nodes receiving incoherent inputs (both positive and negative inputs) significantly increase the robustness of the network, while nodes with coherent inputs (only positive or negative inputs) decrease the robustness. The effect can be general as it is conserved in networks with higher node numbers and in various real biological oscillators whose models and parameters are experimentally supported. Nullcline analyses demonstrate that incoherent or coherent inputs differentially influence the robustness by extending or narrowing a node’s span of steady states. In addition, we found that incoherent inputs are enriched in almost all known natural and synthetic oscillators, suggesting that incoherent inputs may be a generalizable design principle that promotes oscillatory robustness.

RESULTS

Systematic Enumeration to Build a Complete Map of Oscillatory Networks

To map out the entire design space of enzymatic networks capable of robust oscillations, we enumerated and analyzed all 3,325 unique topologies containing no more than three nodes (Figure 1A, left; STAR Methods). This approach, while computationally plausible, has allowed for exhaustive analysis of all possible network configurations.

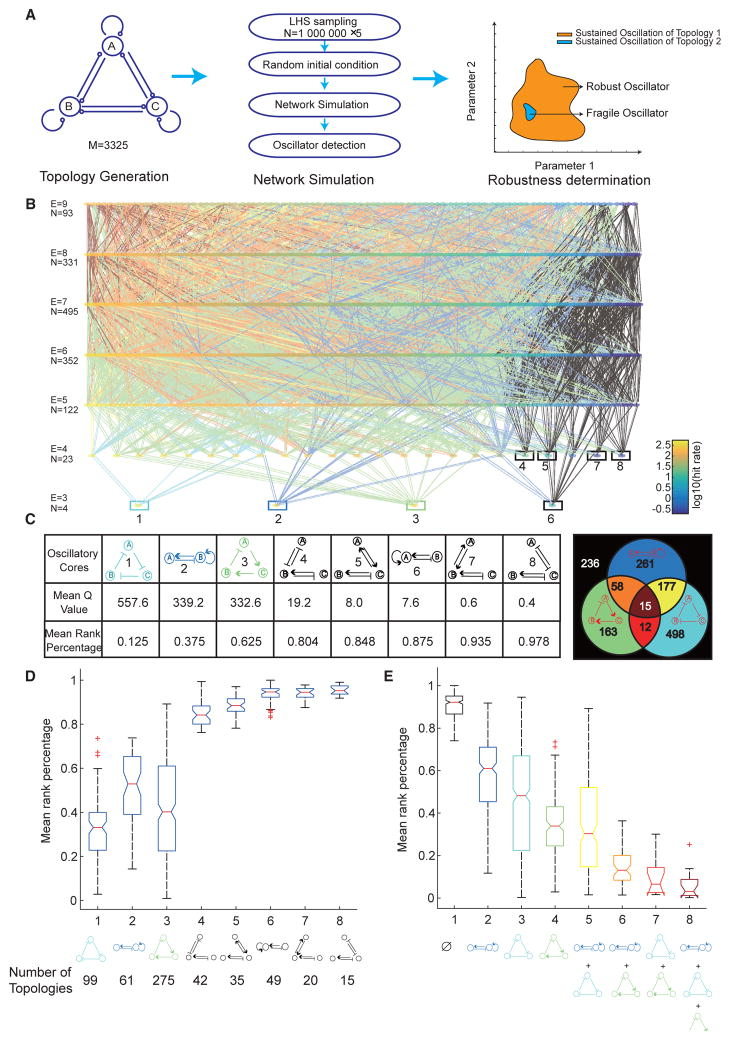
Figure 1. Enumeration Reveals a Complete Atlas of Two- and Three-Node Oscillators and Eight Oscillatory Cores.

(A) Schematic of a computational workflow for topology-to-function mapping of biological oscillators. Left panel: a complete enumeration of topologies with three nodes or fewer. Each node can generate outputs to (analogous to enzymes) or receive inputs from (analogous to substrates) other nodes, leading to 3,325 unique topologies. Middle panel: each topology is simulated (using the Runge-Kutta Dormand-Prince, or RKDP method) with 10⁶ parameter sets (×5 replicates) using Latin hypercube sampling (LHS) sampling in Log-space. The ranges of the parameter space are listed in Table S1. Each limit-cycle oscillator is detected numerically (STAR Methods). Right panel: robustness of each topology is calculated as the number of parameters that support oscillations (Q value) or as the rank percentage of the Q value.

(B) A complete map of 1,420 oscillatory topologies, whose robustness values span orders of magnitude. Each node is one topology. All topologies are laid out such that the topological complexity, represented by the number of edges (E), increases from bottom to top. Topologies with the same complexity are color sorted within the same row, according to their Q values in a logarithmic scale. Each row contains a total number of N topologies. Eight “oscillatory cores” at the bottom of the atlas are highlighted by bordered boxes, the color of each matching to the color of the corresponding core topology in the table in (C). Any two topologies with one-edge difference are connected. The color of the connection between the two topologies of each pair matches the color for a certain combination of cores that the upper-layer topology contains. All possible combinations of cores with corresponding colors are shown in the Venn diagram in (C).

(C) Eight oscillatory cores are listed in a table in decreasing (or increasing) order of mean Q value (or mean rank percentage of the Q value), each calculated from five replicates. The top three most robust cores are colored in cyan, blue, and green, and the rest cores are all colored in black. The Venn diagram on the right panel clusters all 1,420 topologies based on which combinations of the top three cores they consist of. The number on each region of the Venn diagram indicates the number of topologies in the set. The black region is for all topologies that contain none of the top three cores, i.e., topologies that contain only any one or more of the five non-robust cores.

(D) Boxplots of mean rank percentage of topologies containing only one of each of the eight cores that are listed in the x axis, showing that topologies with cores 1 to 3 are significantly more robust than those with all the other cores. The red + symbols represent outliers, whose values are higher than 75 percentile + 1.5 × (75 percentile – 25 percentile) or lower than 25 percentile − 1.5 × (75 percentile – 25 percentile). The number of topologies within each cluster is also listed at the bottom.

(E) Boxplots of mean rank percentage of topologies containing different combinations of robust cores (e.g., cores 1 to 3), regardless of the presence or absence of all other non-robust cores. The red + symbols represent outliers. The number of topologies within each cluster is listed in the Venn diagram in (C).

Using a well-established enzymatic model (Tsai et al., 2008) describing each node by an ordinary differential equation (see the model derivations in STAR Methods), and the Latin hypercube sampling method, each topology was simulated independently with a collection of 1,000,000 parameter sets randomly sampled within a pre-defined parameter space that is considered to be biologically relevant (Table S1; STAR Methods). Each random sampling experiment was repeated five times. Hence, we analyzed a total of approximately three billion dynamical systems (3,325 × 1,000,000 parameter sets), each having five replicates. Each individual dynamical system was further simulated with five random initial conditions to detect if it yields a unique limit cycle, featuring self-sustained oscillations (Figure 1A, middle; STAR Methods).

To measure the robustness of each topology and map it from the topology space to the function space, we computed the Q value, a well-established metric of robustness that quantifies the volume of parameter space supporting oscillation (Ma et al., 2009). We also compute the rank percentage of the Q value among the topologies with the same number of edges, which gives insights into the relative robustness without the effects due to various network complexity (Figure 1A, right; STAR Methods).

This analysis generated a comprehensive atlas of 1,420 oscillators, all “connected” such that one topology can transform to the other by adding or deleting one edge or one node (Figure 1B; STAR Methods). Such connectedness of all oscillators is an important prerequisite for the evolvability of robustness, suggesting that a robust solution can be found by changing one regulatory interaction at a time without losing the ability to generate oscillations. These oscillators all contain at least one negative feedback loop, confirming that the negative feedback is a general requirement for generating oscillations (Novak and Tyson, 2008). The atlas was laid out so that the topological complexity (scaled with number of edges) of the oscillators increased from bottom to top (Figure 1B). Oscillators of the same complexity were arranged within each row in decreasing order of Q values that spanned orders of magnitude, indicating a large variability of their ability to generate robust oscillations. The bottom-most eight topologies, which we define as “oscillatory cores,” serve as roots for all of the subsequent, more complicated, oscillators. They are minimized oscillatory networks that cannot be simplified further to another oscillatory network, and, thus, the simplest topologies that sustain oscillation.

Oscillatory Cores Set the Basic Levels of Robustness

The oscillatory cores exhibit a large discrepancy in robustness among themselves, with the top three performing significantly better than the rest (Figure 1C). Affirming the validity of our methods, they match the three most well-known central structures of biological oscillators, namely the repressilator (core 1), activator-repressor (core 2), and delayed negative feedback (core 3).

To determine whether these oscillatory cores were responsible for the large range of robustness we observed for all networks, we clustered topologies based on oscillatory core composition. We first compared clusters of topologies that contained only one of the eight cores, and found that topologies containing cores 1, 2, or 3 were on average significantly more robust than topologies containing any of the other cores (Figure 1D). These results suggested that the core structures play an essential role in determining a network’s robustness. These differences were compromised if we allowed topologies to contain more than one oscillatory core (Figure S1A). To quantify how combining cores can affect the network robustness, we also clustered topologies that only contained two oscillatory cores (Figure S1B). We found that robust cores (e.g., cores 1 to 3) combined each other resulting in a more robust network, while adding any one of the non-robust cores (e.g., cores 4 to 8) to any other core had little change on the robustness of the network. We therefore clustered all topologies that contained any combinations of cores 1, 2, and 3 regardless of the presence or absence of all other less-significant cores. We found that the average robustness of a cluster increased with the number of the robust cores they contained, suggesting that multiple robust cores could combine to promote the robustness of the networks in which they are embedded (Figure 1E).

Despite the high dependence of the average robustness on oscillatory cores, we also observed a large variation of robustness within each of the clusters that cannot be explained by their cores alone. In addition, it was unclear what mechanisms underlie the major differences in robustness among the cores themselves (Figure 1C). For example, cores 2 and 6 are both self-positive-plus-negative feedback loops except that core 2 has the self-positive feedback added onto the activator (node B), while core 6 is added onto the repressor (node A). This seemingly subtle difference resulted in a 45-fold change in robustness. Notably, core 2 is well conserved in natural and synthetic oscillators, while core 6 is rarely found in any biological oscillators. All these together, suggest that, in addition to the core architecture, certain auxiliary local structures may play a significant role in robust network performance.

Incoherent Inputs Enhance the Overall Robustness of an Oscillatory Network

We started by examining the influence of two auxiliary structures, namely a positive feedback and a negative feedback, both of which have been reported to improve the robustness of certain networks (Chen et al., 2015; Tsai et al., 2008). Our results, however, did not support a simple relationship between the addition of a positive or negative feedback and the increased robustness. Instead, the effect depended on the core structure and to which node of the core the feedback was added (Figure 2A). To systematically identify key structures that improve robustness independent of any specific oscillatory cores, we compared all neighboring topologies that differ by only one regulatory interaction but share the exact same oscillatory cores. Specifically, for each pair of these neighboring topologies, we decomposed them into small network structures (e.g., two-edge motifs as shown in Figure 2B), and calculated the difference in their network structure compositions and the resulting difference in their levels of robustness (measured as rank percentages of Q values). To identify which of the network structure components best predict the change in network robustness, we used a least-absolute shrinkage and selection operator, a statistical linear regression technique (STAR Methods). While none of the one-edge motifs significantly increased oscillator robustness (Figures S1C–S1G), we discovered several two-edge motifs (Figure 2C) that had a major impact on robustness. Notably, all incoherent input structures (one node that receives both activation and inhibition) tended to increase the robustness, while the coherent input structures (one node that receives either two activations or two inhibitions) tended to decrease the robustness. To confirm these results, we also calculated Spearman’s rank correlation coefficients (Figure S2A) and partial rank collection coefficients (Figure S2B), both of which resulted in the same conclusion. Remarkably, this simple “incoherent inputs rule” accurately predicted the differential influence of adding a positive or negative feedback loop to a core on its robustness (Figure 2A), and therefore unified the apparently conflicting results in the literature where either positive feedback or negative feedback was reported to promote robustness in different contexts (Chen et al., 2015; Gerard et al., 2012; Tsai et al., 2008). The rule also explained the divergent robustness levels we observed for the pairs of cores with similar designs (e.g., cores 2 and 6, cores 4 and 8, cores 5 and 7) in Figure 1C.

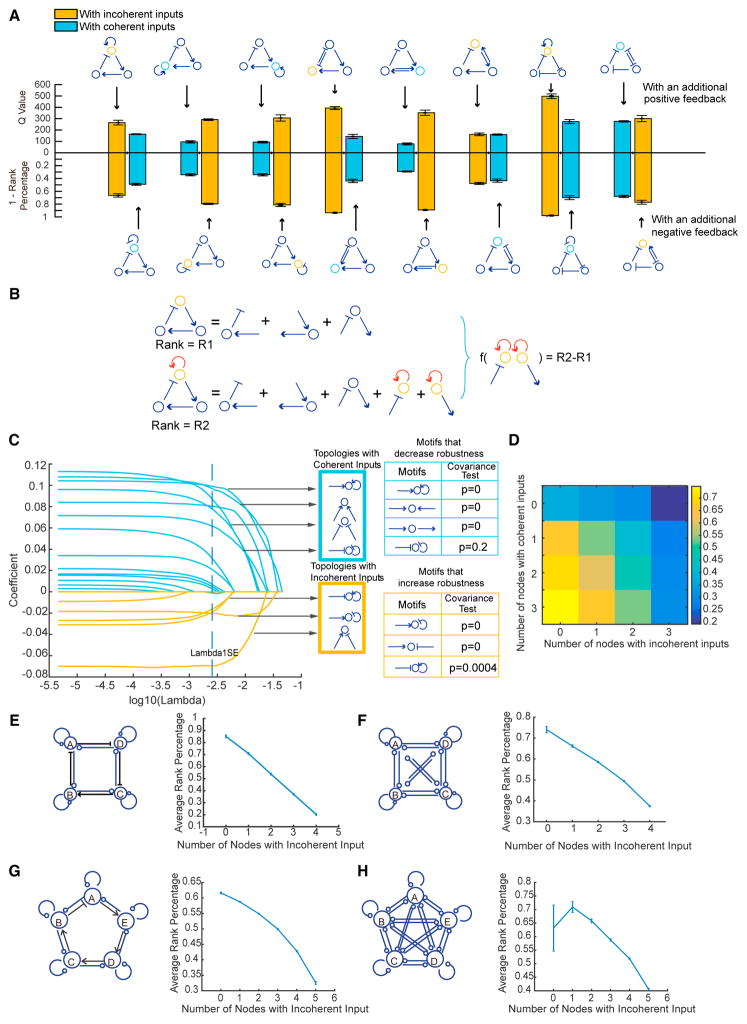
Figure 2. Incoherent Inputs Significantly Increase the Overall Robustness of an Oscillator.

(A) To test whether adding a positive or negative feedback to an oscillator increases its robustness, topologies of each of the eight pairs are compared regarding their robustness levels, measured as Q value (bar plots on top) or 1 – rank percentage (bar plots on the bottom). The left bar plot of each pair corresponds to the topology with an additional positive feedback (top row), and the right bar plot of each pair corresponds to the topology with an additional negative feedback (bottom row). The color of each bar plot indicates whether the topology contains a node with incoherent inputs (orange) or a node with coherent inputs (cyan). It shows that adding a positive feedback or a negative feedback does not always result in a higher level of robustness. Instead, of each pair, the topology with incoherent inputs is unanimously more robust than the one with coherent inputs, regardless of whether a positive or negative feedback is added, indicating that the “incoherent inputs” principle can be a fundamental rule that unifies otherwise divergent results.

(B) Schematic comparing a pair of neighboring topologies by calculating the difference in their network structure compositions and the resulting difference in their levels of robustness (measured as R2–R1).

(C) LASSO analysis on the dataset generated from (B) to estimate the coefficients (y axis) for all two-edge motifs at a certain λ value (x axis). Applying the 1 SE rule, any curve with coefficients above 0 at 1 SE is for a motif that decreases the robustness, and below 0 for a motif that increases the robustness. Interestingly, all motifs with incoherent inputs (highlighted in an orange-bordered box) significantly increase the robustness, while all motifs with coherent inputs (highlighted in a cyan-bordered box) significantly decrease the robustness. The p values using covariance test statistics (Lockhart et al., 2014) are shown in tables on the right.

(D) Heatmap of the mean rank percentages of the Q value for all topologies that are clustered based on the number of nodes with incoherent inputs (x axis) and the number of nodes with coherent inputs (y axis) they contain.

(E–H) Incoherent inputs promote the robustness of larger-scale networks. Left panels: (E) contains a total of 6,561 four-node topologies with a core four-node delayed negative feedback loop, and each topology is simulated with 10⁶ parameter sets; (F) contains 50,000 topologies that are randomly selected from all four-node configurations, each of which is sampled with 100 K parameter sets; (G) contains a total of 59,049 five-node topologies with a core five-node delayed negative feedback loop, each sampled with 100 K parameter sets; and (H) contains 50,000 topologies that are randomly selected from all five-node configurations, each sampled with 100 K parameter sets. Right panels: all topologies are clustered based on the number of nodes with incoherent inputs that they contain, and the mean rank percentage of the Q value is calculated for each cluster. Error bars: the SEM based on five replicates.

To examine whether these motifs contribute additively to the robustness of a network, we clustered all topologies based on the numbers of incoherent and coherent inputs embedded. The results show that the more incoherent inputs and the less coherent inputs that a network has, the more robustly it behaves (Figures 2D, S2C, and S2D). The same trends were also observed using different sampling methods, such as linear sampling (Figure S2E), an alternative model function based on Michaelis-Menten kinetics (Figure S2F), and different sampling ranges (Figures S3E and S3F).

To test these findings in larger-scale networks that consist of four or five nodes, we utilized two complementary strategies. First, we enumerated all topologies that contained a core of a four- or five-node “delayed negative feedback” (Figures 2E and 2G). Second, we relaxed this constraint to randomly sample 50,000 topologies out of all configurations (Figures 2F and 2H). Both approaches led to the same conclusion: the incoherent inputs and coherent inputs additively increased or decreased robustness in larger networks (Figures S2G–S2J).

To investigate which parameter is the most affected by adding incoherent input, we analyzed repressilator-derived networks in a generalized enzymatic model. We projected the parameter volume of each topology that supports oscillations onto one of its parameter axes, and then compared the projected distributions along all parameter axes for each pair of topologies. The results (Figures S3A–S3C) show that the distributions of thresholds, K, and Hill coefficients, n, changed significantly in response to incoherent inputs versus coherent inputs, and the most sensitive parameter is the K from the nodes with incoherent input. This result is confirmed by bifurcation analysis from the centroid of the parameter volume that support oscillations of a repressilator core (Figure S3D), which shows that the incoherent input increases the oscillatory range of K of the node.

To intuitively understand why incoherent inputs could improve robustness, we performed nullcline analysis on a node with a pair of incoherent or coherent inputs, or with a single input as a control. This analysis revealed that the range of steady states of a node varied with its input logics (Figures 3A and S4A–S4C). Specifically, the nullcline range of a node, compared with the control (i.e., a node receiving only a single input), increased when it received incoherent inputs and decreased when receiving coherent inputs. The nullcline range seemed to increase most dramatically from the control when the two input signals had opposite signs but a comparable strength. Since the oscillation trajectory needs to cross the nullcline, a larger nullcline range leads to a larger freedom of oscillatory variables, which allows for more flexible parameter selections regarding those variables. Therefore, the wider a nullcline spans, the greater is the potential of a system to generate sustained oscillations. This explains why certain patterns of local interactions on a node impose a significant impact on the overall performance of a network.

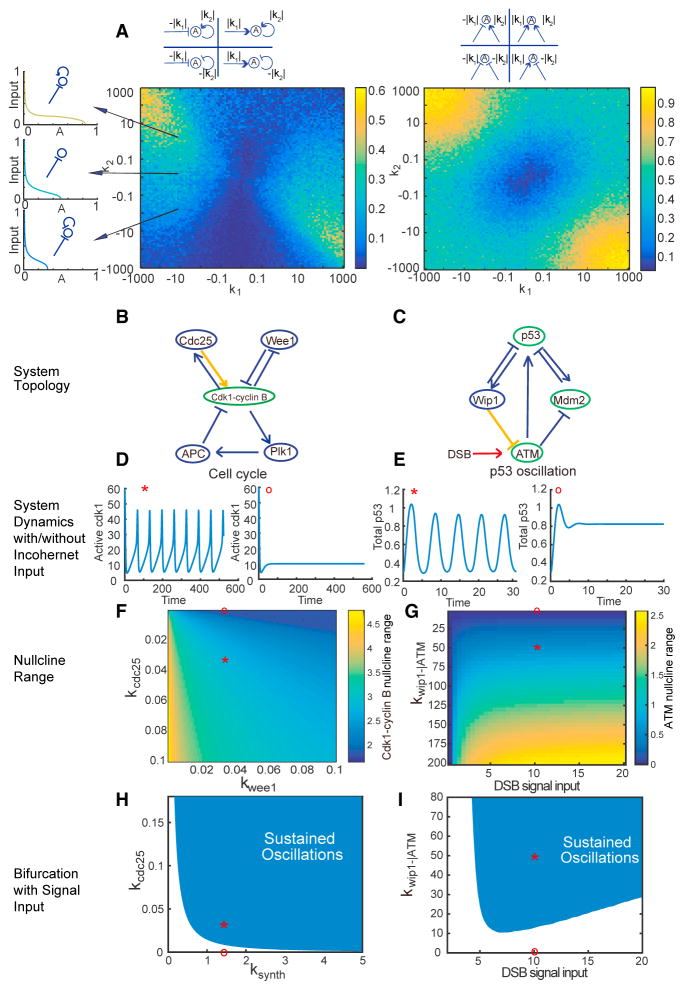
Figure 3. Incoherent Inputs Improve the Robustness of Biological Oscillators with Experimentally Estimated Parameters.

(A) Compared with a single input, incoherent or coherent inputs increase or decrease the nullcline range of a node, respectively. Left panel: heatmap of the nullcline ranges of node A that receives both an input of strength k₁ and a self-feedback of strength k₂. The value of k₁ (or k₂) can be positive or negative, representing activation or inhibition. The inset on the top shows the representative topologies for different combinations of k₁ and k₂ with positive or negative values. To eliminate any effect from parameters other than k₁ and k₂, the mean nullcline range is calculated from 100 simulations, with all parameters except for k₁ and k₂ randomly sampled within the parameter ranges listed in Table S1. The inset on the left shows three examples of nullcline for a node with the same negative input on one leg, but with an additional self-positive feedback, no additional input, or an additional self-negative feedback on the other leg (basal reaction rate = 0.1, self-regulation rate |k₂| = 1, input rate |k₁| = 10, EC₅₀ = 0.1, n = 2). Each nullcline is colored according to its nullcline range. Right panel: heat-map of the null-plane ranges of node A that receives both two inputs of strength |k₁| and of strength |k₂|. All notations are the same as in the left panel. Examples of nullplane are showing in Figures S4A–S4C.

(B and C) Topologies of the cell cycle (B) and p53 oscillator (C), where the nodes that receive incoherent inputs are labeled in green and the interactions of interest in yellow.

(D and E) Time courses of active Cdk1 levels (D) and total p53 levels (E), either with (labeled with *) or without (labeled with ○) the interactions labeled in yellow in (B and C). The results show that incoherent input is necessary for oscillation. The rest of parameter values are unchanged from the literature values (Batchelor et al., 2011; Tsai et al., 2014).

(F and G) Heatmaps of the nullcline ranges of Cdk1-cyclin B (F) and ATM (G), indicating that the strength of any of the incoherent inputs, such as Cdc25, Wip1–|ATM, or DSB, is positively correlated with the nullcline range, while the coherent input strength of Wee1 is negatively correlated with the nullcline range. The points labeled with * and ○ correspond to the same systems as in (D and E).

(H and I) Bifurcation analysis. The shaded regions denote the parameters compatible with sustained oscillations. The parameter ranges of the cyclin B synthesis rate constant k_synth (H) and DSB signal input strength (I), both as the essential clock inputs, become wider as the incoherent input strength k_Cdc25 (H) and k_Wip1–|ATM (I) increase. These results indicate that incoherent inputs increase the parameter choice for oscillation, and thus increase the robustness of the system. The points labeled with * and ○ correspond to the same systems as in (D and E).

Incoherent Inputs Increase Robustness in Real Biological Networks

To better understand the importance of incoherent inputs in “real-world” biological systems, we analyzed two well-known biological oscillators: embryonic cell cycles and the p53 system, both of which are highly conserved among organisms and have been extensively studied with well-established mathematical models and experimentally measured parameters (Batchelor et al., 2011; Tsai et al., 2014). The embryonic cell cycle (Figure 3B) centers on a core delayed negative feedback that is modified by a double-positive feedback loop through phosphatase Cdc25 and a double-negative feedback loop through kinase Wee1. Although both are self-reinforcing loops, Cdc25 forms an incoherent input to Cdk1-cyclin B1, while Wee1 forms a coherent input. Thus, this provides an ideal system to test our prediction. By adopting a published model with experimentally estimated parameters (Tsai et al., 2014), we found that removal of the incoherent input disrupted the ability of the system to oscillate, while removal of the coherent input did not (Figures 3D and S4D). By random parameter sampling centered on the experimentally measured parameter values (see parameter ranges in Table S2), we found that, the robustness of the oscillator, measured as the percentage of parameters that yielded sustained oscillations, increased with the strength of the Cdc25 loop until it reached a plateau (Figure S4D). An opposite trend was observed for the Wee1 loop (Figure S4D). These results held for different sampling methods and sampling parameter ranges (Figures S3G–S3L). These results suggested that Cdc25, as an incoherent input modification, is essential to maintain a robust cell cycle. The impact of Cdc25 on the cell-cycle robustness was further confirmed in both nullcline analysis and bifurcation analysis: as the strength of Cdc25 increased, so did the range of steady-state Cdk1-cyclin B1 activities (Figures 3F and S4G), and the ranges of several key bifurcation parameters (e.g., cyclin B1 synthesis rate in Figure 3H; Hill coefficients in Figures S4E and S4F), within which sustained oscillations occurred. In contrast, the strength of Wee1, as a coherent input modification to the core negative feedback architecture, played an opposite role (Figures 3F, S4E, and S4F).

In the second example, we studied the signaling network of the tumor suppressor p53, which cells utilize to respond to stresses such as DNA damage. Interestingly, the p53 network wires differently under different stimulations, leading to distinct dynamics and cell fates (Purvis et al., 2012). Explicitly, the p53 network oscillates in response to double-strand break (DSB), while it exhibits a single pulse under UV radiation. The key structure to sustain the oscillations is a negative interaction from Wip1 to ATM (Batchelor et al., 2011) (Figure 3C). This negative regulation from Wip1 (Shreeram et al., 2006), together with the positive regulation from the DSB-sensing complex (Mre11-Rad50-Nbs1) (Lee and Paull, 2005), form incoherent inputs to ATM. Removing either of the inputs terminated the oscillations (Figure 3E), while increasing the reaction rate constant of either input resulted in an extended nullcline range of ATM (Figures 3G and S4H). Similarly, through bifurcation analysis, the range of the DSB signaling input level that supports oscillations also widened with increasing rate constant of Wip1–|ATM (Figure 3I). Together, these results strongly demonstrated the significance of incoherent inputs in promoting robust biological oscillations.

DISCUSSION

So far, computational search for functional network motifs has mainly focused on the core topologies (Chau et al., 2012; Cotterell et al., 2015; Ma et al., 2009; Noman et al., 2015; Shah and Sarkar, 2011). Only a few studies (Chen et al., 2015; Gerard et al., 2012; Tsai et al., 2008) have highlighted the functional role of auxiliary structures. However, these studies have selectively examined the influence of one-edge structures, such as the self-positive and self-negative feedback loops, on a few pre-defined oscillatory cores, which may lack generality. In this present study, by analyzing all two- and three-node topologies through enumeration, we discovered key local motifs capable of improving the robustness of any oscillatory system. Notably, rather than the previously emphasized one-edge feedback loops, we found the most significant motifs are two-edge structures, namely the incoherent inputs, where a node is regulated by both positive and negative signals. This finding has implied the importance of how two signals interact, which in a way matters more than the absolute level of a signal itself. Its significance may be in line with that of an incoherent feedforward loop in signaling pathways, which can function as a robust fold-change detector (Ferrell, 2009).

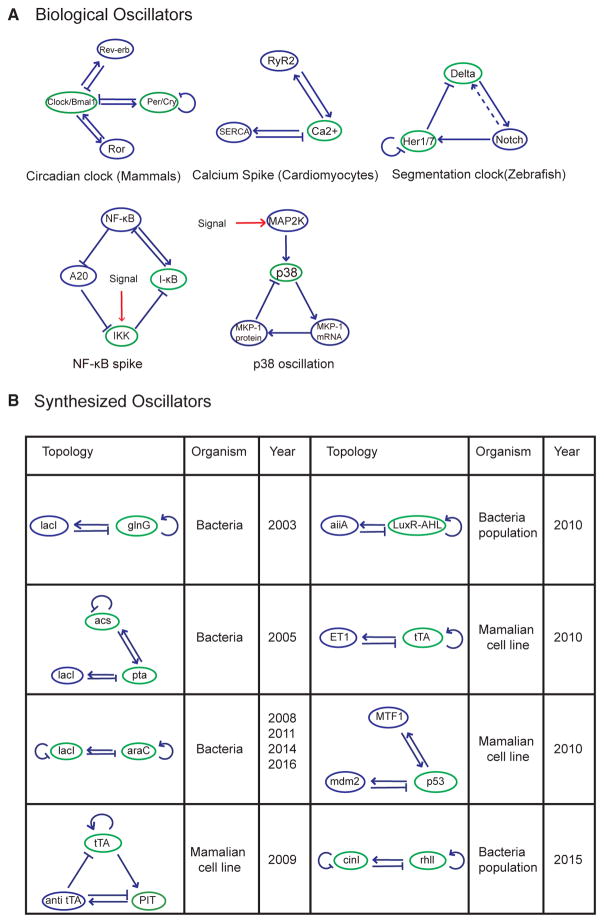
Indeed, incoherent inputs are highly enriched in all well-known biological oscillators, ranging from circadian clocks to signaling networks (Figure 4A), as well as many robust synthetic biological oscillators (Figure 4B). The only exception is the repressilator (Elowitz and Leibler, 2000), the first synthetic gene oscillator, which did not show great robustness until recent modifications (Potvin-Trottier et al., 2016). Given the simplicity of forming incoherent inputs, and that such minor modifications do not immediately change the oscillatory core structures, it provides a valuable guidance for designing robust synthetic oscillators as well as a feasible strategy to improve the robustness of an oscillator through gradual evolution.

Figure 4. Incoherent Inputs Are Enriched in Biological and Synthetic Oscillators.

(A) Examples of biological oscillators with incoherent inputs. Networks are shown for mammalian circadian clock (Bell-Pedersen et al., 2005), cardiomyocyte calcium spike (Liu and Priori, 2008; Periasamy et al., 2008), zebrafish segmentation clock (Mara and Holley, 2007), nuclear factor κB oscillation (Nelson et al., 2004; Zambrano et al., 2016), and p38 oscillation (Tomida et al., 2015). The nodes with incoherent inputs are labeled in green.

The signal inputs are labeled in red. The dotted line represents intercellular interaction.

(B) Example of synthetic oscillators with incoherent inputs (Atkinson et al., 2003; Butzin et al., 2016; Chen et al., 2015; Fung et al., 2005; Hussain et al., 2014; Stricker et al., 2008; Tigges et al., 2009, 2010; Toettcher et al., 2010).

In the analysis, we have generated a complete map of three-node oscillators where any pair of topologies that differ by only one regulatory interaction are connected. A similar connection map has been reported in a study on the evolution of robustness in circadian clocks by evolutionary search (Wagner, 2005). The high connectivity we observed in the oscillator design space suggests that a robust oscillator can be evolved by adding or deleting one regulatory interaction at each step without stopping oscillations. Furthermore, we have found the effects of multiple local motifs are additive. That is, the degree of robustness of an oscillator can increase or decrease with the numbers of nodes that receive incoherent or coherent inputs. This implies that natural evolution could repeatedly use the same strategy to develop a highly robust solution.

STAR★METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
Matlab R2016a	The MathWorks	https://www.mathworks.com
Boost C++ Libraries		http://www.boost.org
Algorithms for network motif simulation and sustained oscillator detection	This paper	https://github.com/zhengdali1990/netSearchPub

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Qiong Yang (qiongy@umich.edu)

METHOD DETAILS

Robustness Definition

Robustness was defined using a mathematical representation, $R_{a,P}^s=\int \psi (p)D_a^s(p)dp$, proposed by Hiroaki Kitano (Kitano, 2007), where the robustness (R) of a system (s) depends on function (a) under a set of perturbations (P). Here we assumed equal probability of perturbations of all parameters, which gives 1/N, where N is the total number of parameters. $D_a^s(p)$ is an evaluation function that determines to what degree the system still maintains function under a perturbation (p). $D_a^s(p)$ is 1 if the system maintains sustained oscillations, and otherwise 0. This definition is equivalent to Q value, defined as the number of sampled parameter sets that yield sustained oscillations (Ma et al., 2009; Tsai et al., 2008). A topology is more robust if there is a larger parameter volume to support oscillations. It also means that, under environmental perturbations on the parameters, such a system, having a higher Q value, is more likely to remain oscillatory.

The random sampling size is limited and the parameter-set range is finite, both of which may result in a Q value that is skewed by the dimension of a system (i.e. network complexity). For different purposes, studies have used different approaches, such as unscaled percentage of parameter sets (Ma et al., 2009; Tsai et al., 2008), or the probability distribution of the parameters based on Bayesian statistics (Woods et al., 2016), to restore the measure of robustness to some degree, so that it is less sensitive to dimension. In our study, to reconcile the dependence of robustness on network complexity (number of edges), we performed the normalization for the networks with the same complexity, and used the rank percentage of the Q value of each network as a robustness measurement. This way we avoided a direct comparison of the Q values among networks with different complexity.

Topology Enumeration

Here we enumerated all topologies with no more than three nodes. Many biological oscillators are centered on three-node negative feedback loops (Gene, mRNA, Protein) (Jenkins et al., 2015), and large networks can be decomposed into smaller networks (Han et al., 2004; Milo et al., 2002, 2004). The role of incoherent inputs we revealed from three-node networks was shown applicable in four-node and five-node networks and is likely generalizable to larger networks.

In our study, each topology can be represented by a 3×3 matrix. Each edge can be assigned to value 0 (no interaction), 1 (positive interaction) or −1 (negative interaction). This gives a total of 3⁹ =19683 networks. After removing all isometric equivalents by comparing networks in all possible permutations, the number becomes 3410. We then remove the network that has isolated nodes (only accepting input, giving output, or completely isolated), and the number of networks reduces to 3325. These include 2 one-node networks, 39 two-node networks and 3284 three-node networks.

Generalized Models for Enzymatic Networks

We mainly used a protein interaction model to describe the networks. Many biological oscillators, including the cell cycles and circadian clock of cyanobacteria, are protein systems (Golden and Canales, 2003). In our model, each variable corresponds to a node in the network, the value of which indicates the activity level of the protein that the node represents. Each node has both active and inactive forms, and these two forms can transform to each other at a basal rate. The interaction between any two nodes is enzymatic. We used a well-established model system (Equation 1) to describe the protein interactions (Tsai et al., 2008), which can be derived from mass action kinetics (Equations 3–9). To verify that the choice of specific function does not affect our result, we also tested our system by using Michaelis-Menten kinetics to model the interaction (Equation 2).

Let the activity of a protein on node i be A_i, the interaction type from node j to i be δ_ji and the interaction strength k_ji.

$${\delta }_{ji}=\{\begin{array}{cc}1& \mathrm{j}\text{activates}\mathrm{i}\\ 0& \text{No}\text{interaction}\\ -1& \mathrm{j}\text{inhibits}\mathrm{i}\end{array}$$

The ODE for node A can be represented as follows:

$$\frac{d{A}_i}{dt}=k_{\mathit{act}}(1-A_i)-k_{\mathit{inh}}{A}_i+\sum _j{k}_{ji}\frac{{\delta }_{ji}({\delta }_{ji}+1)}{2}{A}_i\frac{A_j^n}{K^n+A_j^n}-\sum _j{k}_{ji}\frac{{\delta }_{ji}({\delta }_{ji}-1)}{2}(1-A_i)\frac{A_j^n}{K^n+A_j^n}$$ (Equation 1)

To verify our result under different model conditions, we also applied a Michaelis-Menten kinetics model:

$$\frac{d{A}_i}{dt}=k_{\mathit{act}}(1-A_i)-k_{\mathit{inh}}{A}_i+\sum _j{k}_{ji}\frac{{\delta }_{ji}({\delta }_{ji}+1)}{2}{A}_j\frac{{(1-A_i)}^n}{K^n+{(1-A_i)}^n}-\sum _j{k}_{ji}\frac{{\delta }_{ji}({\delta }_{ji}-1)}{2}{A}_j\frac{A_i^n}{K^n+A_i^n}$$ (Equation 2)

Derivation of the Enzymatic Reaction Models

The model we used in the main text (i.e., Equation 1) can be derived from the simple mass action kinetics with a few assumptions, as follows. Consider a node A, and when there is no input from outside, the equations are as below:

$$\stackrel{k_{deg}}{\leftarrow }{A}_{\mathit{active}}\underset{k_{\mathit{act}}}{\overset{k_{in}}{\rightleftharpoons }}{A}_{\mathit{inactive}}\underset{k_{\mathit{synthesis}}}{\overset{k_{deg}}{\rightleftharpoons }}$$ (Equation 3)

$${\frac{d{A}_{\mathit{active}}}{dt}|}_{\mathit{basal}}=k_{\mathit{act}}{A}_{\mathit{inactive}}-\left(k_{deg}+k_{in}\right)A_{\mathit{active}}$$ (Equation 4)

If protein B activate A through binding, then

$$A_{\mathit{inactive}}+nB\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{A}_{\mathit{bind}}{B}_n\stackrel{k_2}{\to }{A}_{\mathit{active}}+nB$$ (Equation 5)

Assume that the binding and unbinding of proteins are fast, we have

$$\frac{\mathit{dAB}}{dt}=k_1[A_{\mathit{inactive}}]{[B]}^n-(k_{-1}+k_2)[A_{\mathit{bind}}{B}_n]=0$$ (Equation 6)

Assume that the binding between proteins are independent, we have

$$[A_{\mathit{bind}}{B}_n]=[A_{\mathit{total}}]-[A_{\mathit{active}}]-[A_{\mathit{inactive}}]$$ (Equation 7)

Then the interaction term can be represented by

$${\frac{d{A}_{\mathit{active}}}{dt}|}_{\text{interaction}}=k_2[A_{\mathit{bind}}{B}_n]=k_2([A_{\mathit{total}}]-[A_{\mathit{active}}])\frac{{[B]}^n}{K+{[B]}^n}$$ (Equation 8)

where $K=\frac{k_{-1}+k_2}{k_1}$ and the reaction rate of A is:

$$\frac{dA}{dt}=-k_{1,\mathit{basal}}A+k_{2,\mathit{basal}}(1-A)+k_2(1-A)\frac{{[B]}^n}{K+{[B]}^n}$$ (Equation 9)

Models for Real-World Biological Oscillators

The models we used to investigate the role of incoherent inputs in real-world biological oscillators are adopted from published work (Batchelor et al., 2011; Tsai et al., 2014).

Cell cycle model:

$$\begin{array}{l}\frac{d[\mathit{cdk}{1}_a]}{dt}=k_{\mathit{synth}}-k_{\mathit{dest}}[{\mathit{apc}}_a][\mathit{cdk}{1}_a]+\frac{1}{\sqrt{r}}{k}_{\mathit{cdk}1on}\left(1+p\frac{{[\mathit{cdk}{1}_a]}^{\mathit{ncdc}25}}{{[\mathit{cdk}{1}_a]}^{\mathit{ncdc}25}+ec{50}_{\mathit{cdc}25}^{\mathit{ncdc}25}}\right)[\mathit{cdk}{1}_i]\\ -\sqrt{r}{k}_{\mathit{cdk}1\mathit{off}}\left(1+p\frac{ec{50}_{\mathit{wee}1}^{\mathit{nwee}1}}{{[\mathit{cdk}{1}_a]}^{\mathit{nwee}1}+ec{50}_{\mathit{wee}1}^{\mathit{nwee}1}}\right)[\mathit{cdk}{1}_a]\\ \frac{d[\mathit{cdk}{1}_i]}{dt}=-k_{\mathit{dest}}[{\mathit{apc}}_a][\mathit{cdk}{1}_i]-\frac{1}{\sqrt{r}}{k}_{\mathit{cdk}1on}\left(1+p\frac{{[\mathit{cdk}{1}_a]}^{\mathit{ncdc}25}}{{[\mathit{cdk}{1}_a]}^{\mathit{ncdc}25}+ec{50}_{\mathit{cdc}25}^{\mathit{ncdc}25}}\right)[\mathit{cdk}{1}_i]\\ +\sqrt{r}{k}_{\mathit{cdk}1\mathit{off}}\left(1+p\frac{ec{50}_{\mathit{wee}1}^{\mathit{nwee}1}}{{[\mathit{cdk}{1}_a]}^{\mathit{nwee}1}+ec{50}_{\mathit{wee}1}^{\mathit{nwee}1}}\right)[\mathit{cdk}{1}_a]\\ \frac{d[{\mathit{plx}}_a]}{dt}=k_{\mathit{plxon}}\frac{{[\mathit{cdk}{1}_a]}^{\mathit{nplx}}}{{[\mathit{cdk}{1}_a]}^{\mathit{nplx}}+ec{50}_{\mathit{plx}}^{\mathit{nplx}}}({\mathit{plx}}_{\mathit{tot}}-[{\mathit{plx}}_a])-k_{\mathit{plxoff}}[{\mathit{plx}}_a]\\ \frac{d[{\mathit{apc}}_a]}{dt}=k_{\mathit{apcon}}\frac{{[{\mathit{plx}}_a]}^{\mathit{napc}}}{{[{\mathit{plx}}_a]}^{\mathit{napc}}+ec{50}_{\mathit{apc}}^{\mathit{napc}}}(1-[{\mathit{apc}}_a])-k_{\mathit{apcoff}}[{\mathit{apc}}_a]\end{array}$$

p53-ATR model:

$$\begin{array}{l}\frac{d[p{53}_{\mathit{inactive}}]}{dt}={\beta }_p-{\alpha }_{\mathit{mpi}}[\mathit{Mdm}2][p{53}_{\mathit{inactive}}]-{\beta }_{sp}[p{53}_{\mathit{inactive}}]\left(\frac{{[{\mathit{ATR}}_{\mathit{active}}]}^{n_s}}{{[{\mathit{ATR}}_{\mathit{active}}]}^{n_s}+T_s^{n_s}}\right)\\ +{\alpha }_{\mathit{wpa}}[\mathit{Wip}1][p{53}_{\mathit{active}}]-{\alpha }_{pi}[p{53}_{\mathit{inactive}}]\\ \frac{d[p{53}_{\mathit{active}}]}{dt}={\beta }_{sp}[p{53}_{\mathit{inactive}}]\left(\frac{{[{\mathit{ATR}}_{\mathit{active}}]}^{n_s}}{{[{\mathit{ATR}}_{\mathit{active}}]}^{n_s}+T_s^{n_s}}\right)-{\alpha }_{\mathit{wpa}}[\mathit{Wip}1][p{53}_{\mathit{active}}]-{\alpha }_{\mathit{mpa}}[\mathit{Mdm}2][p{53}_{\mathit{active}}]\\ \frac{d[\mathit{Mdm}2]}{dt}={\beta }_m[p{53}_{\mathit{active}}(t-{\tau }_m)]+{\beta }_{mi}-{\alpha }_{sm2}[{\mathit{ATR}}_{\mathit{active}}][\mathit{Mdm}2]-{\alpha }_m[\mathit{Mdm}2]\\ \frac{d[\mathit{Wip}1]}{dt}={\beta }_w[p{53}_{\mathit{active}}(t-{\tau }_w)]-{\alpha }_w[\mathit{Wip}1]\\ \frac{d[{\mathit{ATR}}_{\mathit{active}}]}{dt}={\beta }_{s2}[\theta (t)-\theta (t-t_{\tau })]-{\alpha }_s[{\mathit{ATR}}_{\mathit{active}}]\end{array}$$

p53-ATM model:

$$\begin{array}{l}\frac{d[p{53}_{\mathit{inactive}}]}{dt}={\beta }_p-{\alpha }_{\mathit{mpi}}[\mathit{Mdm}2][p{53}_{\mathit{inactive}}]-{\beta }_{sp}[p{53}_{\mathit{inactive}}]\left(\frac{{[\mathit{ATM}-P]}^{n_s}}{{[\mathit{ATM}-P]}^{n_s}+T_s^{n_s}}\right)\\ +{\alpha }_{\mathit{wpa}}[\mathit{Wip}1][p{53}_{\mathit{active}}]-{\alpha }_{pi}[p{53}_{\mathit{inactive}}]\\ \frac{d[p{53}_{\mathit{active}}]}{dt}={\beta }_{sp}[p{53}_{\mathit{inactive}}]\left(\frac{{[\mathit{ATM}-P]}^{n_s}}{{[\mathit{ATM}-P]}^{n_s}+T_s^{n_s}}\right)-{\alpha }_{\mathit{wpa}}[\mathit{Wip}1][p{53}_{\mathit{active}}]-{\alpha }_{mp}[\mathit{Mdm}2][p{53}_{\mathit{active}}]\\ \frac{d[\mathit{Mdm}2]}{dt}={\beta }_m[p{53}_{\mathit{active}}(t-{\tau }_m)]+{\beta }_{mi}-{\alpha }_{sm}[\mathit{ATM}-P][\mathit{Mdm}2]-{\alpha }_m[\mathit{Mdm}2]\\ \frac{d[\mathit{Wip}1]}{dt}={\beta }_w[p{53}_{\mathit{active}}(t-{\tau }_w)]-{\alpha }_w[\mathit{Wip}1]\\ \frac{d[\mathit{ATM}-P]}{dt}={\beta }_s[\theta (t)-\theta (t-t_{\tau })]-{\alpha }_s[\mathit{ATM}-P]-{\alpha }_{ws}[\mathit{ATM}-P]\frac{{[\mathit{Wip}1]}^{n_w}}{{[\mathit{Wip}1]}^{n_w}+T^{n_w}}\end{array}$$

Parameter Range Selections

In general networks, the parameter ranges are predefined, as shown in Table S1. These parameter selections are consistent with a study that used the same model (Tsai et al., 2008). We mainly used logarithmic sampling in our study, and most parameters have a range of 4 in log10-space. Linear sampling was also used to verify the results. The parameter ranges in the cell-cycle model are shown in Table S2. We also tested different parameter ranges (not shown), and the result is not altered. In the simulation of biological oscillators with fixed parameters, the parameters are kept unchanged from previous publications (Batchelor et al., 2011; Tsai et al., 2014).

Description of Topology Map

We compared every possible pair of topology. Any two topologies are connected as a pair if both topologies contain the same number of nodes, and if one topology can produce another topology by adding one edge. Two topologies with different number of nodes can be connected if one topology can produce another topology by adding at least two edges (Figure 1B).

Effects of One Edge Motifs on Oscillatory Robustness

The possible one edge motifs on a node are: self-positive, self-negative, node-to-node positive interaction (with another node), and node-to-node negative interaction (with another node). The relationship between the number of one edge motifs and the robustness are shown in Figures S1E and S1F, where the node-to-node negative interaction seems to have a positive correlation with the robustness. To find out whether this correlation may come from the oscillatory cores or the modification itself, we did pairwise comparison of all searched topologies and performed LASSO on these four modifications. The results showed that while positive interaction seems to decrease robustness, no modification can significantly increase the robustness (Figure S1G). To investigate the effect of combined one-edge motifs, we clustered topologies with positive interactions (both self-positive and node-to-node positive) and negative interactions (both self-negative and node-to-node negative) together. The results show that the numbers of positive interactions and negative interactions embedded in an oscillator do not have a simple correlation with the oscillator robustness (Figures S1C and S1D).

QUANTIFICATION AND STATISTICAL ANALYSIS

Simulation and Oscillator Detection

We used Dormand–Prince method in Boost library to simulate the equation (with relative error 10⁻⁶ and absolute error 10⁻⁸). Each system was simulated from t=0 to t=2000, which was long enough to detect most of the oscillations. During simulation, if a system reaches steady states, then it is not an oscillator. We monitored the recurrence of the states of nodes. The peak of a specific node is selected as reference. Let the time at peak i be t_i, and the values of all nodes are (x_i, y_i, z_i). If at least N consecutive (N=7 in our simulation) peaks that satisfy d((x_i,y_i,z_i),(x_i+1,y_i+1,z_i+1))<ε are found, and if the system satisfies: 1. Stable amplitude: $\frac{\mathit{std}(x_i)}{\mathit{mean}(x_i)}<\sigma$, σ=10⁻². 2. Stable period: $\frac{\text{std}({\mathrm{t}}_{i+1}-{\mathrm{t}}_i)}{\mathit{mean}({\mathrm{t}}_{i+1}-{\mathrm{t}}_i)}<\delta$, δ=10⁻² then the system is considered an oscillator.

Motif Selection

To identify local structures that lead to significant changes in network robustness, we compared all eligible topological neighbors on the atlas shown in Figure 1B, for their differences in network compositions (as a set of one-edge or two-edge motifs) and performances (computed as the rank difference of the two oscillators) (Figure 2B). All pairs selected must meet two criteria: (1) Their topologies only had one edge difference. (2) They shared the exact same oscillatory cores. Thus, we obtained a list of N = 1831 entries, each of which were calculated from one pair of topologies and consisted of p covariates and a single outcome, y_i. Then, we performed LASSO on this dataset to select the most significant motifs that are responsible for the changes of robustness, by solving:

$$\underset{{\beta }_0,\beta }{\mathit{min}}\left(\frac{1}{2N}\sum _{i=1}^N{(y_i-{\beta }_0-x_i^T\beta )}^2+\lambda \sum _{i=1}^N\mid {\beta }_j\mid \right)$$

Here, x_i:=(x₁,x₂,…,x_p)^T is the covariate vector for the i^th pair of oscillators, which contains p predictors, each as an integer. Each integer represents the difference between the pair with regards to their numbers of a certain motif (out of p=4 unique motifs for one-edge modifications and 21 for two-edge modifications). The outcome y_i is their robustness rank difference. λ is a nonnegative free parameter, to control for the amount of regularization of the fitting. The fitted coefficients β₀ and β are scalar and p-vector obtained at a certain λ value. We used ten-fold cross-validation and chose the largest λ such that generalization error (mean squared error) was within one standard error of its minimum value. The covariance test statistics was calculated, similar to a study (Lockhart et al., 2014), as a significance measurement for respective motifs.