Abstract
The amounts and types of available multimodal tumor data are rapidly increasing, and their integration is critical for fully understanding the underlying cancer biology and personalizing treatment. However, the development of methods for effectively integrating multimodal data in a principled manner is lagging behind our ability to generate the data. In this article, we introduce an extension to a multiview nonnegative matrix factorization algorithm (NNMF) for dimensionality reduction and integration of heterogeneous data types and compare the predictive modeling performance of the method on unimodal and multimodal data. We also present a comparative evaluation of our novel multiview approach and current data integration methods. Our work provides an efficient method to extend an existing dimensionality reduction method. We report rigorous evaluation of the method on large-scale quantitative protein and phosphoprotein tumor data from the Clinical Proteomic Tumor Analysis Consortium (CPTAC) acquired using state-of-the-art liquid chromatography mass spectrometry. Exome sequencing and RNA-Seq data were also available from The Cancer Genome Atlas for the same tumors. For unimodal data, in case of breast cancer, transcript levels were most predictive of estrogen and progesterone receptor status and copy number variation of human epidermal growth factor receptor 2 status. For ovarian and colon cancers, phosphoprotein and protein levels were most predictive of tumor grade and stage and residual tumor, respectively. When multiview NNMF was applied to multimodal data to predict outcomes, the improvement in performance is not overall statistically significant beyond unimodal data, suggesting that proteomics data may contain more predictive information regarding tumor phenotypes than transcript levels, probably due to the fact that proteins are the functional gene products and therefore a more direct measurement of the functional state of the tumor. Here, we have applied our proposed approach to multimodal molecular data for tumors, but it is generally applicable to dimensionality reduction and joint analysis of any type of multimodal data.
Keywords: Multimodal data, proteogenomics, phenotype prediction, nonnegative matrix factorization, dimensionality reduction
Background
Tumor genomics data are being produced at an unprecedented rate and scale due to the rapid development of next-generation sequencing technologies and provide us detailed information on tumors at a molecular level. In addition, advances in mass spectrometry (MS)-based proteomics technologies have improved the accuracy and depth of measurements1–4 and now allow for observation of a large set of proteins from tumor samples. The information obtained from proteomics is complementary to genomics and transcriptomics, and it is an open question how to integrate them to fully use the combined experimental data to gain insight into tumor biology and build clinically useful predictive models. Basic proteogenomics integration can be applied to improve protein identification,5–11 and mass spectral data can be used to improve genome annotation.6,7,12,13 Proteogenomic integration also promises to drive clinical diagnosis, drug discovery, and development. Molecular profiling of patient tissue can enable the generation of personalized, individual-specific treatment based on genetic and proteomic signatures.14
The increased availability of heterogeneous biomedical data requires computational frameworks that allow a principled joint processing of them. One of the major challenges in the analysis of such data sets is to preserve the statistical properties of individual modalities. Several methods have been proposed in recent years to combine multiple views of data from different data sets or their subsets. Xu et al15 identify 2 main driving principles in multiview learning: the consensus principle and the complementary principle. Uniform integration horizontally concatenates different modalities with different scales and statistical properties into a single view.15,16 Methods such as multiple kernel learning and subspace learning have been proposed to couple multiple data sources and model their latent interactions.16,17
Integrating classifiers from heterogeneous modalities pose multiple challenges. These classifiers should perform at least, as well as simple, unimodal classifiers; do model selection by taking into account multiple predictors; not overfit to the high-dimensional molecular data; work for both continuous and categorical variables; and take into account the cost of generating the data.18 In one approach, partial least-square approach was used for dimensionality reduction.18 Once the partial least-squares components were identified, random forests were used for outcome prediction.
Multiview learning is tightly coupled with other areas of machine learning such as ensemble learning and domain adaptation. Le Cao et al19 developed a mixture of experts model to integrate the continuous and categorical nature of transcript levels and clinical variables, respectively. Bovelstad et al20 applied dimensionality reduction only to the high-dimensional molecular data in their clinical-genomic models. Obulkasim et al21 combined clinical and molecular data in a stepwise manner. As molecular data may be expensive and difficult to obtain, the models were first built from clinical data. Neighborhoods of samples misclassified by the clinical data were identified, and subsequently, the more expensive molecular data were added. Multiview methods have been used to combine dimensionality reduction, clustering of individual modalities, and then late integration of these matrices followed by patient subtype identification.22 Further work has incorporated the known biological relationships between different types of molecular data (such as between promoters and genes) to enhance their integrated predictive performance.23 A recent approach for heterogeneous data integration have used nonparametric Bayesian methods to handle noisy, unstructured data with different modalities (transcript levels, digital pathology image data, and copy number data) in combination with prior information. When this method was applied in one breast cancer study, while transcript data gave the best predictive performance in most of the cases, the digital pathology data were much better at predicting death in estrogen (ER) receptor–positive cases.24
Machine learning has been applied to proteomics data for predictive modeling of candidate proteolytic peptides, cancer subtypes, clinical prognosis definition, and targeted therapy development.25–30 Methods for recursive feature selection from high-dimensional, noisy molecular data have been developed.31 Recent work using multimodal proteogenomics from The Cancer Genome Atlas (TCGA) data32 (now hosted at the Genomic Data Commons, https://portal.gdc.cancer.gov/), METABRIC data,33 and the Clinical Proteomic Tumor Analysis Consortium (CPTAC)34 has demonstrated that for these data sets combining multiple modalities does not improve the predictive performance over unimodal data.16,17,24 The Cancer Genome Atlas used reverse-phase protein array35,36 analysis of 172 proteins for measurement of protein levels. In contrast, MS-based proteomics can readily quantify thousands of proteins. A recent study from CPTAC has demonstrated that deep proteomics data can be more predictive of 10-year survival in breast cancer than the other data types.17 Analysis of proteogenomics data using machine learning techniques is a fairly new, unexplored territory and holds great promise of insights for cancer biology research.
The high dimensionality of unimodal and multimodal data, extending to tens of thousands of dimensions, requires dimensionality reduction techniques such as principal component analysis,37 independent component analysis,38 or nonnegative matrix factorization (NNMF).40,41 Dimensionality reduction techniques work by projecting the data to a new space of lower dimensions (fewer predictors) with each dimension being a combination of features The advantage of NNMF over other dimensionality reduction algorithms39,40 such as principal component analysis is that it is able to find meaningful, interpretable modules from the data where the number of dimensions is constrained by the number of samples. For example, in imaging data, NNMF is able to identify sparse, parts-based components corresponding to facial features. Nonnegative matrix factorization has also been used to integrate features from images and text from image tags for segmentation of images and label prediction from annotated multimedia data.41 Biological molecular data, such as transcript profiles, usually consist of nonnegative values, but methods such as principal component analysis may not guarantee nonnegativity after projection onto lower dimensional subspaces. In contrast, NNMF is able to capture the true nonnegative nature of such data and provides a parts-based, sparse representation of the data. Zhang et al42 have jointly analyzed predicted microRNA (miRNA)-gene interactions, miRNA and gene level profiles, and the gene-gene interaction network constructed based on protein-protein interaction and DNA-protein interaction networks in an NNMF framework. Their approach integrates miRNA and transcript profiles in a framework of multiple NNMFs and simultaneously integrates gene-gene interaction network data in a regularized manner where sparse penalties are applied to make the modules interpretable. In further work,43 Zhang et al developed a joint NNMF method where multiple types of genomic data such as DNA methylation, transcript levels, and miRNAs are projected onto a common coordinate system, in which heterogeneous variables weighted highly in the same projected direction form a multidimensional module. Other variations of NNMF include extensions to identify localized sets of genes across the data.44
Here, we present a novel approach for multiview molecular data integration that extends traditional NNMF to the joint factorization of different data matrices by extending an existing multiview approach to the joint treatment of different modalities of ‘omics data.41 We extend the formulation of an existing method to simultaneously do dimensionality reduction using the alternating least squares (ALS) method and phenotype prediction. We introduce heuristics to approximate the importance of each modality in a data-driven way before their joint factorization and consider these coupled, reduced matrices for outcome prediction. We then apply this to CPTAC proteogenomics data for phenotype prediction such as ER, progesterone (PR), and human epidermal growth factor receptor 2 (HER2) status in breast cancer; to tumor grade, tumor stage, and survival prediction in ovarian cancer; and to tumor stage, residual tumor, and survival prediction in colon cancer. In addition, we compare results from our method with results from the uniform integration of the same data. In going beyond techniques such as our previous work on TCGA data which used uniform integration, multiple kernel learning, and ensemble learning,16 this approach allows for dimensionality reduction and the joint estimation of latent components. Thereby, our approach captures the interactions between different data modalities.
Materials and Methods
In the following section, we describe the mathematical formulation for NNMF followed by our extension. We then describe the algorithm for prediction from multimodal data using this approach. Finally, we describe the heterogeneous CPTAC proteogenomics data used in the analysis.
Nonnegative matrix factorization
Formally, NNMF can be expressed as a least-squares optimization problem as shown in equation (1):
| (1) |
where is a data matrix with samples and features, is the reduced basis factors, and contains the coefficients of the linear combinations of the basis vectors to reconstruct the original data. In addition, k≤m and . An algorithm proposed by Lee and Seung39,45 for solving equation (1) uses multiplicative update as shown below:
Initialize and as random dense matrices.
- Repeat until convergence or maximum number of iterations:
where represents the elementwise Hadamard product (elementwise multiplication) and represents elementwise division of matrices and .
Adaptive multiview nonnegative matrix factorization
Akata et al41 extended the above formulation to multiview data. Their approach consisted of uncovering suitable matrices of basis vectors and for their multimodal imaging and text data implicitly coupled by the coefficient matrix to obtain 2 separate low-rank approximations X ≈ and Y ≈ . This was formalized as a convex combination of 2 separate constrained least-square problems as shown in equation (2):
| (2) |
such that and . is a user-specified constant that assigns weights for either modality. The authors adopt a fixed-point iterative multiplicative update solution to approximate , , and as shown in equations (3) to (5), respectively41:
| (3) |
| (4) |
| (5) |
A more generic formulation of equation (2) extending to an arbitrary number of modalities is as shown in equation (6):
| (6) |
such that , , and .
One disadvantage of multiplicative updates is that once an element in or becomes 0, it continues to remain 0, and the algorithm proceeds toward a fixed point45 and therefore multiplicative updates are more sensitive to initial choice of values. In contrast, ALS updates offer more consistency and flexibility and are easy to implement and can be faster than multiplicative updates or gradient descent-based solutions. The ALS updates to equation (2) are shown in equations (7) to (9):
| (7) |
| (8) |
| (9) |
The algorithm for solving equation (2) using the ALS methods45 is described as follows:
Initialize , , and as random dense matrices.
- Repeat until convergence or maximum number of iterations:
- Solve equation (7) for .
- Set all negative elements in to 0.
- Solve equation (8) for .
- Set all negative elements to to 0.
- Solve equation (9) for H.
- Set all negative elements in to 0.
After dimensionality reduction, we use these reduced matrices to train and test a support vector machine (SVM)46 binary classifier as described in the “Approach” section. We selected SVMs because of their robustness to overfitting and good performance in similar problems with high variable to sample ratios.46–48 We evaluated the predictive performance of the classifier using the area under receiver operating characteristic (ROC) curve (AUC).49 We first evaluated the performance of unimodal data. Dimensionality reduction in unimodal data was performed using NNMF, and the reduced matrix was used for classification. For our example of matrices and , let and represent the AUC performance of the reduced, unimodal matrices and . We scaled the AUC performance of the unimodal data to obtain a sense of the relative importance of each modality as shown in equation (10) for 2 data modalities and in equation (11) for an arbitrary number of modalities:
| (10) |
| (11) |
This is then used as the in our Adaptive Multiview NNMF method for multimodal data. Instead of an arbitrary choice of , our choice is now data driven. Unlike multiplicative updates which explicitly guaranteeing nonnegativity, ALS does a simple projection step to approximate nonnegativity and speeds up implementations, which is especially useful for high-dimensional biomedical data.
Approach
Our approach is summarized in the pseudocode below. Assume we have 2 nonnegative matrices and representing 2 heterogeneous modalities of ‘omics data.
| Algorithm: Adaptive Multiview Nonnegative Matrix Factorization |
|
Input: Nonnegative matrices and ( samples and features); Number of reduced basis factors k
Output: Predictive performance as measured by average area under ROC curve |
| Procedure: |
| 1: Repeat until maximum iterations |
| a. For each resampling iteration do: |
| i. Hold out specific test samples and . |
| ii. Initialize and to random positive values sampled from a Gaussian. |
| iii. Perform dimensionality reduction on unimodal matrices and using NNMF and prespecified number of dimensions, k, to obtain and . |
| iv. Train model on and using a support vector machine classifier. |
| v. Test model on and . To give the test samples a projection in the same space as the training data to get the reduced test data , we do the following transformation: and . |
| 2: Average cross-validation performances from and . |
| 3: Scale AUC performance, and , from unimodal matrices and to [0, 1] to obtain as shown in equation (10). |
| 4: Repeat until maximum iterations |
| a. For each resampling iteration do: |
| i. Hold out specific samples and . |
| ii. Perform dimensionality reduction on using multiview approach outlined in equations (7) to (9) iteratively until convergence to get , and . Use and from step 3. |
| iii. Train model on support vector machine classifier using concatenated, multimodal matrices and whereXtr ≈ and Ytr ≈ . |
| iv. To give the test samples a projection in the same space as the training data to get the reduced test data and , we do the following transformation for the test data: and
|
| v. Test model on uniformly integrated matrices and . |
| 5: Average cross-validation performance to obtain final AUC. |
Linear SVMs are supervised classification algorithms that classify samples into 2 classes, here, the presence or absence of a clinical phenotype, by calculating the maximal-margin hyperplane separating them. We have used a LIBSVM50 MATLAB interface with a linear SVM and a default cost parameter of 1. Missing values were imputed using the k-nearest neighbor rule in MATLAB.51
We used repeated nested 10-fold cross-validation52 and averaged results over the 10 repetitions from random subsampling of the original data. The cross-validation procedure divides the subsamples drawn into 10 nonoverlapping balanced subsets. The process is then repeated 10 times with 9 sets used for training and 1 for testing. Classifier performance was evaluated using the AUC, ie, the area under the curve obtained by plotting sensitivity against 1-specificity at different thresholds, where sensitivity is the number of true positives in the gold standard that are correctly classified and specificity is the number of correctly classified true negatives.49 Paired sample t tests were used to compare the performance between pairs of models. The adjustment for multiple comparisons in all statistical tests was performed using the Benjamini-Hochberg false discovery rate correction.53 The statistical significance was determined at .05 level using adjusted P values.
Data
The CPTAC analyzed the proteome and phosphoproteome of genome-annotated TCGA32,54–56 tumor specimens34,57–59 The analysis of the tumor specimens was done by high-resolution tandem MS. Prior to MS analysis, extensive peptide fractionation and phosphopeptide enrichment were performed to increase the depth of the analysis. The peptide mass spectra were identified using different database search algorithms that match the target spectra against known fragmented spectra of peptides contained in a protein sequence database.57–59 A label-free quantitation approach was used for the colon tumors, and an isobaric peptide labeling approach was used for breast and ovarian tumors.
The CPTAC breast cancer data set consists of a subsample of the 77 breast tumors selected from TCGA for MS-based proteomics and phosphoproteomics analyses.57 All PAM50-defined intrinsic subtypes were represented in the cohort: 25 basal-like, 29 luminal A, 33 luminal B, and 18 HER2 (ERBB2)-enriched tumors, and in addition 3 normal breast tissue samples. A total of 12 553 proteins (10 062 genes) and 33 239 phosphosites were quantified for the tumors. The phenotypes used for prediction from the breast cancer data set were ER status, PR status, and HER2 status (Table 1). The ER or PR status indicates whether the hormone ER or PR is supporting the spread and growth of the cancer cells.60,61 An abnormal activity of the HER2 can also play a role in cancer development.62 For our analysis, we retained the 5508 genes which were measured across all 4 modalities.
Table 1.
Characteristics of data sets/tasks used in this study.
| Breast cancer | N(0) | N(1) | Phosphoprotein | Protein level | Copy number | Transcript level |
|---|---|---|---|---|---|---|
| PR status (negative vs positive) | 34 | 43 | X | X | X | X |
| ER status (negative vs positive) | 23 | 54 | X | X | X | X |
| HER2 status (negative vs positive) | 58 | 19 | X | X | X | X |
| Ovarian cancer | ||||||
| Tumor stage (IC, IIA, IIB, IIC, IIIA and IIIB) vs IIIC | 19 | 50 | X | X | X | X |
| Tumor grade (G1, G2) vs G3 | 57 | 12 | X | X | X | X |
| Survival ≥ 1 y | 12 | 57 | X | X | X | X |
| Survival ≥ 2 y | 22 | 47 | X | X | X | X |
| Survival ≥ 3 y | 36 | 33 | X | X | X | X |
| Survival ≥ 4 y | 49 | 20 | X | X | X | X |
| Survival ≥ 5 y | 55 | 14 | X | X | X | X |
| Colon cancer | ||||||
| Tumor stage (I, IIA, IIB) vs (IIIA, IIIB, IV) | 52 | 38 | X | X | X | |
| Residual tumor R0 vs (RX, R1, and R2) | 68 | 12 | X | X | X | |
| Survival ≥ 1 y | 45 | 45 | X | X | X | |
| Survival ≥ 2 y | 70 | 20 | X | X | X | |
| Survival ≥ 3 y | 79 | 11 | X | X | X |
Abbreviations: ER, estrogen; HER2, human epidermal growth factor receptor 2; PR, progesterone.
N(0) and N(1) denote the number of subjects for classes 0 and 1, respectively. The encoding of classes is given in the first column.
The CPTAC ovarian cancer data set consists of a subsample of the MS-based proteomic characterization of 174 ovarian tumors previously analyzed by TCGA. In total, 169 of the 174 tumors were high-grade serous carcinomas.58 The CPTAC conducted an extensive MS-based proteomics and phosphoproteomic characterization of ovarian tumors. This resulted in quantitative measurements for a total of 9600 proteins from 174 tumors and 24 429 phosphosites from 6769 phosphoproteins in a subset of 69 tumors.58 In total, 69 samples had all the 4 modalities—copy number, transcript, protein, and phosphoprotein levels—measured. The phenotypes for prediction were tumor stage, tumor grade, and survival at greater than 1, 2, 3, 4, and 5 years of follow-up. For tumor stage prediction, stages IC, IIA, IIB, IIC, IIIA, IIIB, and very few samples from stage IV were considered to be in class 0, and samples from stage IIIC were considered to be in class 1 (Table 1). Ovarian cancer is difficult to diagnose in its early stages. Stages I and II represent cancer on one or both the ovaries, extensions to the uterus, fallopian tube, and other pelvic organs.63 Stages IIIA and IIIB are characterized by cancer in the upper abdomen less than 2 cm.63 Stage IIIC ovarian cancer represents visible cancer greater than 2 cm on one or both ovaries, fallopian tubes, and metastasis to nearby abdominal organs.63 In stage IV ovarian cancer, the cancer has metastasized to the fluid in the lungs.63 For tumor grade, G1 and G2 were considered in class 0 and G3 in class 1. Based on the International Federation of Gynecology and Obstetrics system, G1 and G2 represented well and moderately differentiated cells from normal cells that grow slowly. G3 represented highly differentiated cancer cells, which are widely different from normal cells, grow quickly, and are more likely to metastasize than G1 or G2 cells.64 In conjunction with predicting tumor grade and stage, we also built models to predict survival greater than 1, 2, 3, 4, and 5 years in ovarian cancer. Only a subset of 1441 genes was measured across all 4 modalities and retained for analysis of our proposed novel method.
The CPTAC colon cancer data set consists of a subsample of the 95 TCGA analyzed by liquid chromatography-tandem MS–based proteomics.59 A total of 3764 genes had both miRNA and protein measurements, and 90 samples had all the 3 modalities—copy number, transcript, and protein level—measured. The phenotypes for prediction were tumor stage, residual tumor, and survival at 1, 2, and 3 years of follow-up. For the purpose of binary classification, we considered samples in stages I, IIA, IIB to be in class 0 and samples in stages IIIA, IIIB, and IV to be in class 1. Class 0 represents different grades of tumor invasion—through the submucosa or the muscularis propria (stage I), through the muscularis propria into pericolorectal tissues (stage IIA), or penetration to the surface of the visceral peritoneum (stage IIB).65 In addition, for samples in class 0, no regional lymph node or distant metastasis is observed. For class 1, the tumor invades the submucosa or the muscularis propria or through the muscularis propria into the pericolorectal tissues (stage IIIA).65 In addition, for stage IIIB, the tumor can invade through the muscularis propria into the pericolorectal tissues or it can penetrate to the surface of the visceral peritoneum.65 In stages IIIA and IIIB, no distant metastases are observed. However, local metastases can happen in 1 to 3 lymph nodes and can deposit in regions such as the mesentery and subserosa. The different stages of residual tumor in colon cancer were R0, R1, R2, and RX. We considered samples with residual tumor as R0 to be class 0 and samples with residual tumor R1, R2, and RX to be in class 1 for binary classification (Table 1). R0 indicates the absence of residual tumor, whereas R1 denotes microscopic and R2 macroscopic tumors. R1 is reserved for tumors identified by histologic examination and R2 for tumors detected by clinical and pathologic examination.66 When the presence of tumor cannot be assessed even after extensive clinical and pathologic assessment, the category is denoted as RX. We also built models for predicting survival greater than 1, 2, and 3 years for this same cohort. There were very few samples in class 1 (Table 1) beyond year 3 for colon cancer. In total, 3756 genes were measured across all 3 modalities.
Details of the data sets and the clinical phenotypes considered are summarized in Table 1. The obtained data sets have been processed and normalized. We have performed rescaling of all data features to [0, 1] range to facilitate classifier learning. We included clinically relevant phenotypes for which there were at least 50 samples available and which were well defined in the data. Our initial cross-validation experiments indicated 50 to 60 components from NNMF to have comparable performance to using all the dimensions/features. Hence, for our experiments, we retained 50 to 60 components after dimensionality reduction.
Results
Combining multiple modalities of data did not improve predictive performance in the current experimental setting
Different data fusion strategies such as uniform integration and our proposed Adaptive Multiview NNMF algorithm did not overall improve the performance of multimodal data over unimodal data with any statistical significance in our present experimental settings (Figure 1). In the case of breast cancer clinical phenotypes, unimodal transcript levels were the most predictive of ER and PR status and copy number of HER2 status. In case of ovarian cancer, phosphoprotein levels were the most predictive of tumor stage and tumor grade, and protein levels were the most predictive of survival ≥1 year. In colon cancer data, protein levels were most predictive of tumor stage and residual tumor. In our previous work,16 we have demonstrated that the difference in the improvement in performance due to uniform integration compared with other state-of the-art data fusion strategies is statistically significant. We therefore compared the performance of our adaptive multiview NNMF with the performance of uniform integration (Figure 5). From Figure 5, we can observe that although overall multimodal data did not outperform unimodal data with any statistical significance, multiview learning with just 50 to 60 components did improve the performance of multimodal data integration as opposed to uniform integration. When multimodal data were fused using multiview NNMF, the proportion of cases in which multimodal models outperformed unimodal data increased to 14.6% of the cases from 4.6% of the cases in case of uniform integration. In addition, the percentage of cases where multimodal and unimodal data had comparable performances is greater in the case of the multiview methodology (20.8%) as compared with uniform integration (16.9%).
Figure 1.
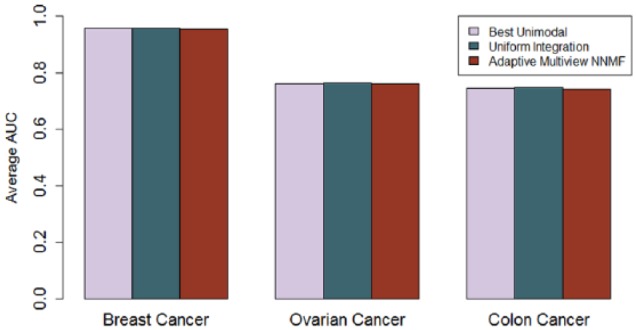
Comparison of the area under ROC curve performance for predictive models built with unimodal data and multimodal data integration using uniform integration and Adaptive Multiview NNMF averaged over all the phenotypes from each Clinical Proteomics Tumor Analysis Consortium data set. The average performance of the best unimodal data was overall comparable with the best models from uniform integration or Adaptive Multiview NNMF. AUC indicates area under ROC curve; NNMF, nonnegative matrix factorization algorithm; ROC, receiver operating characteristic.
Figure 5.
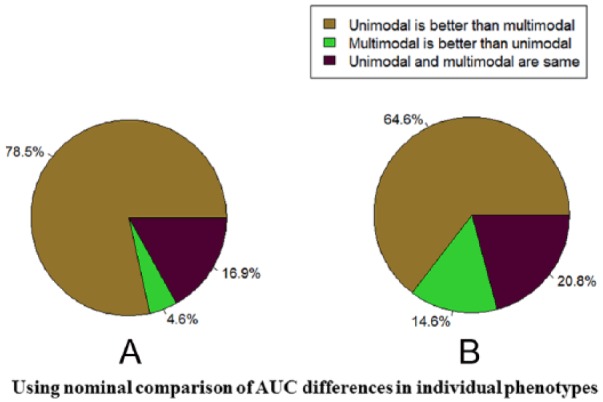
(A) Comparisons of unimodal best performing modality with both uniform integration and (B) Adaptive Multiview NNMF for the different tasks. Predictivity is measured by the area under receiver operating characteristic curve (AUC) performance. The results in (A) are obtained using nominal comparison of AUC differences in individual data sets/tasks using uniform integration, whereas the results in (B) are obtained using a nominal comparison of the AUC differences in individual data sets and tasks using Adaptive Multiview NNMF. NNMF indicates nonnegative matrix factorization algorithm.
Breast cancer: transcript levels outperformed other modalities in predicting ER and PR status and copy number outperformed other modalities in predicting the HER2 status
For the CPTAC breast cancer data, 77 had all 4 modalities—copy number, transcript, protein, and phosphoprotein levels. Our phenotypes of interest were PR and ER receptor status and HER2 status (Table 1). Our results from uniform integration are summarized in Supplemental Tables 1a and 1b. We built predictive models using both unimodal data and uniform integration of modalities. The best performing models for PR and ER status were based on transcript levels. For HER2 status, copy number outperformed all the other models. We performed additional analysis by excluding the main gene ERBB2 in case of HER2, PGR in the case of PR status, and ESR1 in the case of ER status. No statistically significant difference in performance was observed after excluding the main genes. Furthermore, we generated a consolidated gene list with 5508 genes measured across all the modalities. With the reduced gene set, the best performing models for PR and ER status were based on transcript levels. For HER2 status, copy number outperformed all the other models. We then applied NNMF to identify the top 50 to 60 components in case of both the original data and the consolidated gene set. From Figure 2, we can observe that the best performing modalities for PR status and ER status were the transcript levels (mean AUC ± standard error: 0.90 ± 0.02 and 0.98 ± 0.02, respectively). Other modalities such as protein levels and phosphoproteins had comparable performance with transcript levels in predicting PR and ER status but did not statistically outperform transcript levels. The best performing modality for HER2 receptor status was copy number (0.96 ± 0.01). Other modalities such as protein levels had statistically comparable performance (P > .05) but did not outperform copy number variation in predicting HER2 receptor status.
Figure 2.
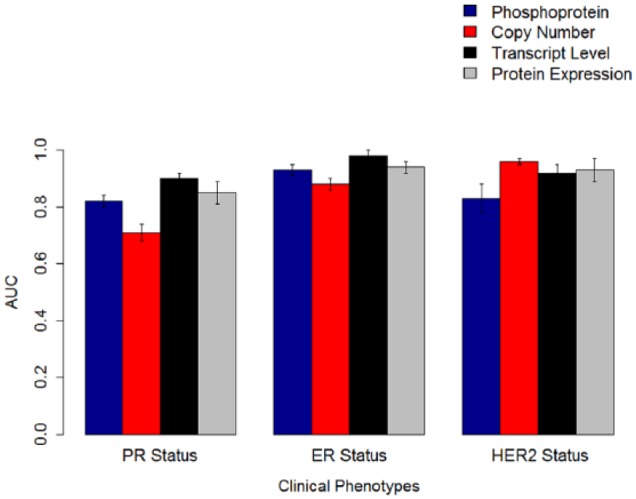
The AUCs for predictive models built with linear support vector machines on the Clinical Proteomic Tumor Analysis Consortium breast cancer data. Models built with transcript levels performed better than models built with other data modalities for PR status and ER status. For HER2 status, copy number was the most predictive modality. The error bars represent standard errors of the mean. AUC indicates area under receiver operating characteristic curve; ER, estrogen; HER2, human epidermal growth factor receptor 2; PR, progesterone.
We generated the for the Adaptive Multiview NNMF method using the AUC performance of the unimodal data from Table 2 using equation (11). The results of our multiview method (Table 2) in combining modalities for the CPTAC breast cancer data set, while comparable with individual modalities, did not overall statistically outperform individual modalities.
Table 2.
AUC performance for the CPTAC breast cancer data using NNMF for unimodal data and Adaptive Multiview NNMF method for multimodal data (top 50-60 components and 5508 genes).
| CPTAC breast cancer | PR status | ER status | HER2 status |
|---|---|---|---|
| Phosphoprotein (PP) level | 0.82 (0.02) | 0.93 (0.02) | 0.83 (0.05) |
| Copy number (CN) | 0.71 (0.03) | 0.88 (0.02) | 0.96 (0.01) |
| Transcript (T) level | 0.90 (0.02) | 0.98 (0.02) | 0.92 (0.03) |
| Protein (P) level | 0.85 (0.04) | 0.94 (0.02) | 0.93 (0.04) |
| PP, CN | 0.78 (0.03) | 0.91 (0.03) | 0.97 (0.03) |
| PP, GE | 0.86 (0.03) | 0.98 (0.02) | 0.87 (0.03) |
| PP, P | 0.85 (0.03) | 0.93 (0.03) | 0.91 (0.02) |
| CN, T | 0.82 (0.03) | 0.98 (0.03) | 0.97 (0.03) |
| CN, P | 0.75 (0.04) | 0.92 (0.04) | 0.97 (0.04) |
| T, P | 0.88 (0.03) | 0.99 (0.02) | 0.92 (0.04) |
| PP, CN, T | 0.84 (0.04) | 0.98 (0.02) | 0.86 (0.04) |
| PP, CN, P | 0.82 (0.02) | 0.94 (0.03) | 0.85 (0.03) |
| PP, T, P | 0.86 (0.03) | 0.98 (0.03) | 0.84 (0.02) |
| CN, T, P | 0.85 (0.03) | 0.97 (0.02) | 0.85 (0.04) |
| PP, CN, T, P | 0.87 (0.01) | 0.96 (0.01) | 0.88 (0.01) |
Abbreviations: AUC indicates area under receiver operating characteristic curve; CPTAC, Clinical Proteomic Tumor Analysis Consortium; ER, estrogen; HER2, human epidermal growth factor receptor 2; NNMF, nonnegative matrix factorization algorithm; PR, progesterone.
Bold values indicate the best unimodal performance. The numbers in parentheses indicate standard error.
Ovarian cancer: phosphoprotein levels outperformed other modalities in predicting tumor stage and tumor grade, and protein levels outperformed other modalities in predicting survival ≥1 year
We then analyzed the CPTAC ovarian cancer data. We only retained samples (69) that had all 4 modalities—copy number, transcript, protein, and phosphoprotein levels. Our phenotypes of interest and encoding are summarized in Table 1. Our results from uniform integration are summarized in Supplemental Tables 2a and 2b. We built predictive models using both unimodal data and uniform integration of modalities. The best performing models for predicting tumor stage and tumor grade were from the phosphoprotein data. For survival ≥1 year, protein levels were the most predictive modality. For survival ≥2 years and beyond, all the modalities had comparable performance. Our results are consistent with a similar analysis on the breast cancer data existing in literature using multiple kernel learning.17 Furthermore, we generated a consolidated gene list with 1441 genes measured across all the modalities. With the reduced gene set, the best performing models for tumor grade and tumor stage were phosphoprotein data. We then applied NNMF to identify the top 50 to 60 components in case of both the original data and the consolidated gene set. The best performing modalities for tumor stage and tumor grade were again from the phosphoprotein data. For survival, protein data had the best predictive performance for short-term (≥1 year) survival.
We generated for the Adaptive Multiview NNMF method using the AUC performance of the unimodal data (Table 3). Our results on both the unimodal data and the multimodal data are summarized in Table 3. The results of our multiview method in combining modalities while comparable with individual modalities did not statistically outperform individual modalities. The overall best performing modalities for tumor stage and tumor grade were phosphoprotein (0.73 ± 0.01 and 0.82 ± 0.01, respectively) and protein data for survival ≥1 year (0.81 ± 0.01) (Figure 3). Other modalities had statistically comparable but not superior performance with phosphoprotein and protein levels in predicting tumorigenesis and survival ≥1 year, respectively. All the modalities had comparable performance (Table 3) in predicting survival ≥2, 3, 4, and 5 years and were not statistically distinguishable.
Table 3.
AUC for the CPTAC ovarian cancer data using NNMF for unimodal data and Adaptive Multiview NNMF method for multimodal data (top 50-60 components and 1441 genes).
| CPTAC ovarian cancer | Tumor stage | Tumor grade | ≥1 y | ≥2 y | ≥3 y | ≥4 y | ≥5 y |
|---|---|---|---|---|---|---|---|
| Phosphoprotein (PP) level | 0.73 (0.02) | 0.82 (0.01) | 0.79 (0.02) | 0.71 (0.01) | 0.69 (0.01) | 0.69 (0.01) | 0.75 (0.01) |
| Copy number (CN) | 0.71 (0.01) | 0.80 (0.01) | 0.77 (0.02) | 0.70 (0.01) | 0.69 (0.01) | 0.70 (0.01) | 0.74 (0.01) |
| Transcript (T) level | 0.72 (0.01) | 0.76 (0.01) | 0.75 (0.02) | 0.71 (0.01) | 0.69 (0.01) | 0.69 (0.01) | 0.75 (0.02) |
| Protein (P) level | 0.72 (0.01) | 0.70 (0.02) | 0.84 (0.02) | 0.71 (0.02) | 0.68 (0.03) | 0.71 (0.02) | 0.74 (0.02) |
| PP, CN | 0.70 (0.02) | 0.82 (0.01) | 0.79 (0.01) | 0.71 (0.02) | 0.69 (0.01) | 0.70 (0.02) | 0.75 (0.02) |
| PP, GE | 0.71 (0.02) | 0.78 (0.01) | 0.76 (0.02) | 0.71 (0.02) | 0.68 (0.01) | 0.70 (0.02) | 0.72 (0.02) |
| PP, P | 0.71 (0.02) | 0.80 (0.02) | 0.84 (0.02) | 0.72 (0.02) | 0.67 (0.01) | 0.69 (0.02) | 0.75 (0.02) |
| CN, T | 0.74 (0.02) | 0.79 (0.02) | 0.75 (0.02) | 0.70 (0.02) | 0.70 (0.02) | 0.71 (0.02) | 0.74 (0.02) |
| CN, P | 0.69 (0.02) | 0.80 (0.02) | 0.79 (0.02) | 0.71 (0.02) | 0.68 (0.01) | 0.68 (0.02) | 0.76 (0.02) |
| T, P | 0.72 (0.02) | 0.73 (0.02) | 0.76 (0.02) | 0.71 (0.02) | 0.69 (0.02) | 0.71 (0.02) | 0.76 (0.02) |
| PP, CN, T | 0.72 (0.02) | 0.77 (0.02) | 0.77 (0.02) | 0.72 (0.01) | 0.70 (0.02) | 0.68 (0.02) | 0.74 (0.02) |
| PP, CN, P | 0.73 (0.02) | 0.81 (0.02) | 0.85 (0.02) | 0.71 (0.02) | 0.70 (0.02) | 0.70 (0.02) | 0.76 (0.02) |
| PP, T, P | 0.72 (0.02) | 0.76 (0.02) | 0.77 (0.02) | 0.74 (0.02) | 0.70 (0.02) | 0.71 (0.01) | 0.76 (0.2) |
| CN, T, P | 0.72 (0.02) | 0.76 (0.02) | 0.78 (0.01) | 0.71 (0.02) | 0.69 (0.02) | 0.69 (0.02) | 0.75 (0.02) |
| PP, CN, T, P | 0.73 (0.01) | 0.78 (0.01) | 0.77 (0.01) | 0.73 (0.01) | 0.70 (0.01) | 0.71 (0.01) | 0.76 (0.01) |
Abbreviations: AUC indicates area under receiver operating characteristic curve; CPTAC, Clinical Proteomic Tumor Analysis Consortium; NNMF, nonnegative matrix factorization algorithm.
Bold values indicate the best unimodal performance. The numbers in parentheses indicate standard error.
Figure 3.
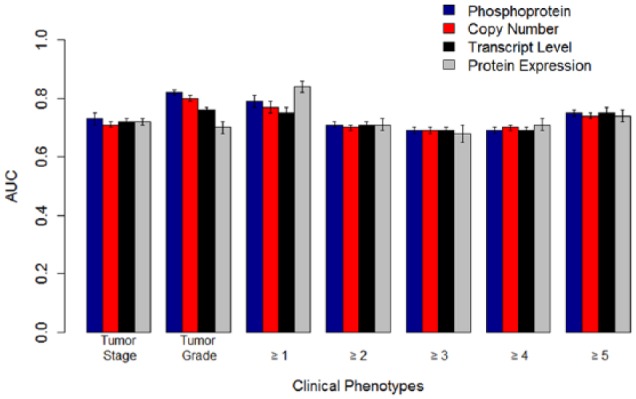
The AUCs for predictive models built with omics data and linear support vector machines on the Clinical Proteomic Tumor Analysis Consortium ovarian cancer data. The best performing models for tumor stage and tumor grade were based on phosphoprotein levels. For survival ≥2 years and beyond, all the modalities showed comparable performance. For survival ≥1 year, protein expression was the most predictive modality. The error bars represent standard errors of the mean. AUC indicates area under receiver operating characteristic curve.
Colon cancer: protein levels outperformed other modalities in predicting tumor stage and residual tumor
For the CPTAC colon cancer data, we retained samples (90) that had all 3 modalities—copy number, transcript, and protein levels. Our phenotypes of interest were tumor stage, residual tumor grade, and survival greater than 1, 2, and 3 years. Our results from uniform integration are summarized in Supplemental Tables 3a and 3b. We built predictive models using both unimodal data and uniform integration of modalities. The best performing models for tumor stage and residual tumor were protein data. Furthermore, we generated a consolidated gene list with 3764 genes measured across all the modalities. With the reduced gene set, the best performing models for tumor grade and residual tumor were the protein data. For survival status, all the modalities showed comparable performance. We then applied NNMF to identify the top 50 to 60 components in case of both the original data and the consolidated gene set. The best performing modalities for tumor stage and residual tumor grade were protein data.
We generated for the Adaptive Multiview NNMF method using the AUC performance of the unimodal data (Table 4). Our results are summarized in Table 4. The results of our multiview method in combining modalities while comparable with individual modalities did not statistically outperform individual modalities. The statistically significant best performing modalities for tumor stage and residual tumor for colon cancer were protein data (0.72 ± 0.02 and 0.82 ± 0.02, respectively, P < .05) (Figure 4). All the modalities had comparable performance (Table 4) in predicting survival.
Table 4.
AUC performance for the CPTAC colon cancer data using NNMF for unimodal data and Adaptive Multiview NNMF method for multimodal data (top 50-60 components and 3764 genes).
| CPTAC colon cancer | Tumor stage | Residual tumor | ≥1 y | ≥2 y | ≥3 y |
|---|---|---|---|---|---|
| Copy number (CN) | 0.67 (0.01) | 0.78 (0.02) | 0.67 (0.01) | 0.70 (0.03) | 0.79 (0.04) |
| Transcript (T) level | 0.67 (0.01) | 0.76 (0.03) | 0.68 (0.01) | 0.70 (0.03) | 0.78 (0.03) |
| Protein (P) level | 0.72 (0.02) * | 0.82 (0.02) * | 0.67 (0.02) | 0.70 (0.03) | 0.79 (0.03) |
| CN, T | 0.68 (0.02) | 0.66 (0.03) | 0.66 (0.01) | 0.69 (0.01) | 0.79 (0.02) |
| CN, P | 0.71 (0.02) | 0.72 (0.03) | 0.66 (0.01) | 0.69 (0.01) | 0.79(0.03) |
| GE, P | 0.71 (0.02) | 0.73 (0.03) | 0.67 (0.02) | 0.69 (0.02) | 0.79 (0.02) |
| CN, T, P | 0.71 (0.02) | 0.71 (0.03) | 0.66 (0.01) | 0.69 (0.02) | 0.76 (0.02) |
Abbreviations: AUC indicates area under receiver operating characteristic curve; CPTAC, Clinical Proteomic Tumor Analysis Consortium; NNMF, nonnegative matrix factorization algorithm.
Bold values indicate the best unimodal performance. The numbers in parentheses indicate standard error.
P < .05.
Figure 4.
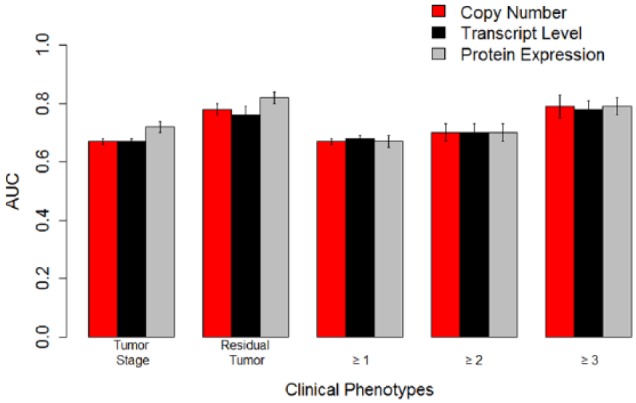
The AUCs for predictive models built with omics data with linear support vector machines on the Clinical Proteomic Tumor Analysis Consortium colon cancer data. The best performing models for tumor stage and residual tumor were based on protein levels. The error bars represent standard errors of the mean. AUC indicates area under receiver operating characteristic curve.
Detailed results for all CPTAC data sets from uniform integration can be found in an additional file (see Supplemental Tables 1a, 1b, 2a, 2b, 3a, and 3b). The P values from the statistical tests for comparing performance from Adaptive Multiview NNMF and adjusted P values after corrections due to multiple comparisons have been reported in Supplemental Table 4.
Discussion
Predictive modeling of proteogenomics data is a fairly new and unexplored research area driven by developing bioinformatics methods. In this work, we extended and simplified a model for multiview integration of modalities. The method extends NNMF to the joint analysis of different types of heterogeneous data. Multiview NNMF is cast as a convex combination of individual optimization problems and we solve it using the ALS method. Prior to uniform integration, the individual optimization problems in the formulation for unimodal matrices are coupled via a common coefficient matrix. Thereby, the approach avoids ad hoc combinations of different types of features and thus preserves their statistical properties.
An arbitrary choice of weight given to each modality can be suboptimal for the learning algorithm. Therefore, we propose to use the AUC of the unimodal data performance as the weight for each modality. Other possible heuristics to weight the importance of each modality include the inverse of the number of mislabeled samples or the number of uniquely mislabeled samples by each modality. The weights can also be generated from a completely different data set and considered to be prior information.
Our algorithm did not improve the performance of multimodal data beyond individual data with any statistical significance. The combination of data sets did not result in an improvement for the particular phenotypes such as tumor stage, tumor grade, and survival that we considered. In general, we found that the modality with a global coverage closest to molecular function contains the most predictive information. Our results are in agreement with existing literature on similar data sets.16,17,24 However, for predicting more complicated phenotypes such as chronic fatigue syndrome or body mass index where multiple genetic, lifestyle, and environmental factors are at play, combining data sets may result in an improvement of performance. The method also shows promise in improving the performance of multimodal data beyond uniform data integration in addition to dimensionality reduction (Figure 5). Results from the breast cancer data set are in agreement with earlier existing studies with transcript levels being the most predictive modality.16,24 Results for survival prediction from the ovarian cancer data and colon cancer data set are in agreement with an existing study on survival prediction for breast cancer showing that large-scale proteomics data being the most predictive modality for survival greater than 1 year.17 For tumor phenotypes from both ovarian and colon cancers, proteomics data had superior predictive performance compared with transcript levels and copy number variation data. This result is unsurprising as most cellular, regulatory processes in diseases such as cancer happen at the level of proteins.
One limitation of our experimental setting is we have used only 1 classifier, SVM, for comparison of uniform integration and our proposed algorithm for multimodal data integration. A thorough benchmarking classification and additional data fusion methods can be more effective in comparison. Furthermore, the study has limited sample sizes of 77, 69, and 90 patients for breast, ovarian, and colon cancers, respectively. Wider profiles and numbers of patients than have been captured in these studies and additional modalities such as imaging data,67 laboratory results, and social and environmental markers can augment these models.
Tumor grade and lesion stage can be important factors in predicting survival and individualizing treatment,68 and residual tumor after surgery can be the best predictor of survival for ovarian cancer.69 Earlier studies have shown that stage IIIA in colon cancer is associated with a statistically significant improved survival than stage IIB patients.70 In our study, we can further map predicted survival outcome to tumor stage or grade. A study such as ours, which focuses on biologically and clinically meaningful phenotypes such as individual stages and grades of tumors, can be useful in clinical decision support and can further advance diagnosis and personalized targeted therapies.
The superior performance of phosphoprotein and protein data in predicting tumor stage, tumor grade, and residual tumor in ovarian cancer and colon cancer data encourages the multi-omics profiling of wider tumor subtypes, grades, and stages to drive targeted therapies than have been captured in this study. As more and more complicated phenotypes and modalities of data than have been incorporated in this study are generated, we foresee that multiview dimensionality reduction methods such as the one proposed here become more useful and important.
Acknowledgments
The authors would like to thank Zhi Li for his help with clinical data preparation used in the experiments. The authors would also like to thank Drs Kelly Ruggles, Aristotelis Tsirigos, Itai Yanai, and Alexander Statnikov for useful discussions and feedback on this work.
Footnotes
Peer review:Five peer reviewers contributed to the peer review report. Reviewers’ reports totaled 2150 words, excluding any confidential comments to the academic editor.
Funding:The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research work is supported by the National Cancer Institute (NCI) CPTAC award U24 CA210972, a contract 13XS068 from Leidos Biomedical Research, Inc., and by a grant from the Shifrin-Myers Breast Cancer Discovery Fund.
Declaration of conflicting interests:The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Author Contributions: BR conceived and designed the experiments and code. BR, WL, and DF analyzed the data; contributed to the writing of the manuscript; agree with manuscript results and conclusions; jointly developed the structure and arguments for the paper; made critical revisions; and approved final version. All authors reviewed and approved the final manuscript.
References
- 1. Aebersold R, Mann M. Mass spectrometry-based proteomics. Nature. 2003;422:198–207. [DOI] [PubMed] [Google Scholar]
- 2. Hu Q, Noll RJ, Li H, Makarov A, Hardman M, Graham Cooks R. The Orbitrap: a new mass spectrometer. J Mass Spectrom. 2005;40:430–443. [DOI] [PubMed] [Google Scholar]
- 3. Wang H, Yang Y, Li Y, et al. Systematic optimization of long gradient chromatography mass spectrometry for deep analysis of brain proteome. J Proteome Res. 2015;14:829–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Yang F, Shen Y, Camp DG, 2nd, Smith RD. High-pH reversed-phase chromatography with fraction concatenation for 2D proteomic analysis. Expert Rev Proteomics. 2012;9:129–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Nesvizhskii AI. Proteogenomics: concepts, applications and computational strategies. Nat Methods. 2014;11:1114–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Menschaert G, Fenyo D. Proteogenomics from a bioinformatics angle: a growing field [published online ahead of print December 15, 2015]. Mass Spectrom Rev. doi: 10.1002/mas.21483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Ruggles KV, Krug K, Wang X, et al. Methods, tools and current perspectives in proteogenomics. Mol Cell Proteomics. 2017;16:959–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ruggles KV, Tang Z, Wang X, et al. An analysis of the sensitivity of proteogenomic mapping of somatic mutations and novel splicing events in cancer. Mol Cell Proteomics. 2016;15:1060–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Fridy PC, Li Y, Keegan S, et al. A robust pipeline for rapid production of versatile nanobody repertoires. Nat Methods. 2014;11:1253–1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Wang X, Li Y, Wu Z, Wang H, Tan H, Peng J. JUMP: a tag-based database search tool for peptide identification with high sensitivity and accuracy. Mol Cell Proteomics. 2014;13:3663–3673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Li Y, Wang X, Cho JH, et al. JUMPg: an integrative proteogenomics pipeline identifying unannotated proteins in human brain and cancer cells. J Proteome Res. 2016;15:2309–2320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Jaffe JD, Berg HC, Church GM. Proteogenomic mapping as a complementary method to perform genome annotation. Proteomics. 2004;4:59–77. [DOI] [PubMed] [Google Scholar]
- 13. Castellana N, Bafna V. Proteogenomics to discover the full coding content of genomes: a computational perspective. J Proteomics. 2010;73:2124–2135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Tenenbaum JD, Avillach P, Benham-Hutchins M, et al. An informatics research agenda to support precision medicine: seven key areas. J Am Med Inform Assoc. 2016;23:791–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Xu C, Tao D, Xu C. A survey on multi-view learning. arXiv preprint arXiv:1304.5634. https://arxiv.org/abs/1304.5634. Published 2013.
- 16. Ray B, Henaff M, Ma S, et al. Information content and analysis methods for multi-modal high-throughput biomedical data. Sci Rep. 2014;4:4411–4421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ma S, Ren J, Fenyö D. Breast cancer prognostics using multi-omics data. AMIA Jt Summits Transl Sci Proc. 2016;2016:52–59. [PMC free article] [PubMed] [Google Scholar]
- 18. Boulesteix AL, Porzelius C, Daumer M. Microarray-based classification and clinical predictors: on combined classifiers and additional predictive value. Bioinformatics. 2008;24:1698–1706. [DOI] [PubMed] [Google Scholar]
- 19. Le Cao KA, Meugnier E, McLachlan GJ. Integrative mixture of experts to combine clinical factors and gene markers. Bioinformatics. 2010;26:1192–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bovelstad HM, Nygard S, Borgan O. Survival prediction from clinico-genomic models—a comparative study. BMC Bioinformatics. 2009;10:413–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Obulkasim A, Meijer GA, van de, Wiel MA. Stepwise classification of cancer samples using clinical and molecular data. BMC Bioinformatics. 2011;12:422–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Serra A, Fratello M, Fortino V, Raiconi G, Tagliaferri R, Greco D. MVDA: a multi-view genomic data integration methodology. BMC Bioinformatics. 2015;16:261–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Switnicki MP, Juul M, Madsen T, Sorensen KD, Pedersen JS. PINCAGE: probabilistic integration of cancer genomics data for perturbed gene identification and sample classification. Bioinformatics. 2016;32:1353–1365. [DOI] [PubMed] [Google Scholar]
- 24. Savage RS, Yuan Y. Predicting chemoinsensitivity in breast cancer with ‘omics/digital pathology data fusion. Roy Soc Open Sci. 2016;3:140501–140514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Deeb SJ, Tyanova S, Hummel M, Schmidt-Supprian M, Cox J, Mann M. Machine learning-based classification of diffuse large B-cell lymphoma patients by their protein expression profiles. Mol Cell Proteomics. 2015;14:2947–2960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Tyanova S, Albrechtsen R, Kronqvist P, Cox J, Mann M, Geiger T. Proteomic maps of breast cancer subtypes. Nat Commun. 2016;7:10259–10270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Daemen A, Griffith OL, Heiser LM, et al. Modeling precision treatment of breast cancer. Genome Biol. 2013;14:R110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Daemen A, Griffith OL, Heiser LM, et al. Erratum to: modeling precision treatment of breast cancer. Genome Biol. 2015;16:95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Swan AL, Mobasheri A, Allaway D, Liddell S, Bacardit J. Application of machine learning to proteomics data: classification and biomarker identification in postgenomics biology. OMICS. 2013;17:595–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Lawless C, Hubbard SJ. Prediction of missed proteolytic cleavages for the selection of surrogate peptides for quantitative proteomics. OMICS. 2012;16:449–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Zhang X, Lu X, Shi Q, et al. Recursive SVM feature selection and sample classification for mass-spectrometry and microarray data. BMC Bioinformatics. 2006;7:197–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Cancer Genome Atlas Research Network, Weinstein JN, Collisson EA, et al. The Cancer Genome Atlas Pan-Cancer analysis project. Nat Genet. 2013;45:1113–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Curtis C, Shah SP, Chin SF, et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature. 2012;486:346–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Ellis MJ, Gillette M, Carr SA, et al. Connecting genomic alterations to cancer biology with proteomics: the NCI Clinical Proteomic Tumor Analysis Consortium. Cancer Discov. 2013;3:1108–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Tibes R, Qiu Y, Lu Y, et al. Reverse phase protein array: validation of a novel proteomic technology and utility for analysis of primary leukemia specimens and hematopoietic stem cells. Mol Cancer Ther. 2006;5:2512–2521. [DOI] [PubMed] [Google Scholar]
- 36. Nishizuka S, Charboneau L, Young L, et al. Proteomic profiling of the NCI-60 cancer cell lines using new high-density reverse-phase lysate microarrays. Proc Natl Acad Sci U S A. 2003;100:14229–14234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Jolliffe I. Principal Component Analysis. New York, NY: Wiley Online Library; 2002. [Google Scholar]
- 38. Hyvärinen A, Karhunen J, Oja E. Independent Component Analysis. Vol 46 Hoboken, NJ: John Wiley & Sons; 2004. [Google Scholar]
- 39. Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. [DOI] [PubMed] [Google Scholar]
- 40. Brunet J-P, Tamayo P, Golub TR, Mesirov JP. Metagenes and molecular pattern discovery using matrix factorization. Proc Natl Acad Sci U S A. 2004;101:4164–4169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Akata Z, Thurau C, Bauckhage C. Non-negative matrix factorization in multimodality data for segmentation and label prediction. Paper presented at: 16th Computer Vision Winter Workshop; February 2011; Mitterberg, Austria. [Google Scholar]
- 42. Zhang S, Li Q, Liu J, Zhou XJ. A novel computational framework for simultaneous integration of multiple types of genomic data to identify microRNA-gene regulatory modules. Bioinformatics. 2011;27:i401–i409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Zhang S, Liu CC, Li W, Shen H, Laird PW, Zhou XJ. Discovery of multi-dimensional modules by integrative analysis of cancer genomic data. Nucleic Acids Res. 2012;40:9379–9391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Carmona-Saez P, Pascual-Marqui RD, Tirado F, Carazo JM, Pascual-Montano A. Biclustering of gene expression data by non-smooth non-negative matrix factorization. BMC Bioinformatics. 2006;7:78–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Berry MW, Browne M, Langville AN, Pauca VP, Plemmons RJ. Algorithms and applications for approximate nonnegative matrix factorization. Comput Stat Data An. 2007;52:155–173. [Google Scholar]
- 46. Boser BE, Guyon IM, Vapnik VN. A training algorithm for optimal margin classifiers. Paper presented at: Proceedings of the Fifth Annual Workshop on Computational Learning Theory; July 27-29, 1992; Pittsburgh, PA. [Google Scholar]
- 47. Hastie T, Tibshirani R, Friedman JH. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd ed. New York, NY: Springer; 2009. [Google Scholar]
- 48. Vapnik VN. Statistical Learning Theory. New York, NY: Wiley; 1998. [Google Scholar]
- 49. Narendra V, Lytkin NI, Aliferis CF, Statnikov A. A comprehensive assessment of methods for de-novo reverse-engineering of genome-scale regulatory networks. Genomics. 2011;97:7–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol. 2011;2:27. [Google Scholar]
- 51. Troyanskaya O, Cantor M, Sherlock G, et al. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17:520–525. [DOI] [PubMed] [Google Scholar]
- 52. Hsu C-W, Chang C-C, Lin C-J. A practical guide to support vector classification. 2003:1–16. http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=A6BD7E0C169F25964A9136AFE5AA82BB?doi=10.1.1.224.4115&rep=rep1&type=pdf. [Google Scholar]
- 53. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Roy Stat Soc B. 1995;289–300. [Google Scholar]
- 54. Cancer Genome Atlas Network. Comprehensive molecular portraits of human breast tumours. Nature. 2012;490:61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Cancer Genome Atlas Research Network. Integrated genomic analyses of ovarian carcinoma. Nature. 2011;474:609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Cancer Genome Atlas Network. Comprehensive molecular characterization of human colon and rectal cancer. Nature. 2012;487:330–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Mertins P, Mani DR, Ruggles KV, et al. Proteogenomics connects somatic mutations to signalling in breast cancer. Nature. 2016;534:55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Zhang H, Liu T, Zhang Z, et al. Integrated proteogenomic characterization of human high-grade serous ovarian cancer. Cell. 2016;166:755–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Zhang B, Wang J, Wang X, et al. Proteogenomic characterization of human colon and rectal cancer. Nature. 2014;513:382–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Hammond MEH, Hayes DF, Dowsett M, et al. American Society of Clinical Oncology/College of American Pathologists guideline recommendations for immunohistochemical testing of estrogen and progesterone receptors in breast cancer (unabridged version). Arch Pathol Lab Med. 2010;134:e48–e72. [DOI] [PubMed] [Google Scholar]
- 61. Osborne CK, Yochmowitz MG, Knight WA, 3rd, McGuire WL. The value of estrogen and progesterone receptors in the treatment of breast cancer. Cancer. 1980;46:2884–2888. [DOI] [PubMed] [Google Scholar]
- 62. Slamon DJ, Leyland-Jones B, Shak S, et al. Use of chemotherapy plus a monoclonal antibody against HER2 for metastatic breast cancer that overexpresses HER2. New Engl J Med. 2001;344:783–792. [DOI] [PubMed] [Google Scholar]
- 63.Types & Stages of Ovarian Cancer. http://ovarian.org/about-ovarian-cancer/what-is-ovarian-cancer/types-a-stages. Accessed August 2, 2017.
- 64. Kosary CL. FIGO stage, histology, histologic grade, age and race as prognostic factors in determining survival for cancers of the female gynecological system: an analysis of 1973-87 SEER cases of cancers of the endometrium, cervix, ovary, vulva, and vagina. Semin Surg Oncol. 1994;10:31–46. [DOI] [PubMed] [Google Scholar]
- 65. American Joint Committee on Cancer. Missions and objectives. http://www.cancerstaging.org/. Accessed August 2, 2017.
- 66. Wittekind C, Compton CC, Greene FL, Sobin LH. TNM residual tumor classification revisited. Cancer. 2002;94:2511–2516. [DOI] [PubMed] [Google Scholar]
- 67. Kong J, Cooper LA, Wang F, et al. Integrative, multimodal analysis of glioblastoma using TCGA molecular data, pathology images, and clinical outcomes. IEEE Trans Biomed Eng. 2011;58:3469–3474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Yasuda M, Nakabayashi Y, Isonishi S, et al. [A study on factors influencing survival in stage I ovarian cancer]. Nihon Sanka Fujinka Gakkai. 1985;37:1191–1196. [PubMed] [Google Scholar]
- 69. Aletti GD, Dowdy SC, Gostout BS, et al. Aggressive surgical effort and improved survival in advanced-stage ovarian cancer. Obstet Gynecol. 2006;107:77–85. [DOI] [PubMed] [Google Scholar]
- 70. O’Connell JB, Maggard MA, Ko CY. Colon cancer survival rates with the new American Joint Committee on Cancer sixth edition staging. J Natl Cancer Inst. 2004;96:1420–1425. [DOI] [PubMed] [Google Scholar]


