The performance of inverse probability of treatment weighting and full matching on the propensity score in the presence of model misspecification when estimating the effect of treatment on survival outcomes

Abstract

There is increasing interest in estimating the causal effects of treatments using observational data. Propensity-score matching methods are frequently used to adjust for differences in observed characteristics between treated and control individuals in observational studies. Survival or time-to-event outcomes occur frequently in the medical literature, but the use of propensity score methods in survival analysis has not been thoroughly investigated. This paper compares two approaches for estimating the Average Treatment Effect (ATE) on survival outcomes: Inverse Probability of Treatment Weighting (IPTW) and full matching. The performance of these methods was compared in an extensive set of simulations that varied the extent of confounding and the amount of misspecification of the propensity score model. We found that both IPTW and full matching resulted in estimation of marginal hazard ratios with negligible bias when the ATE was the target estimand and the treatment-selection process was weak to moderate. However, when the treatment-selection process was strong, both methods resulted in biased estimation of the true marginal hazard ratio, even when the propensity score model was correctly specified. When the propensity score model was correctly specified, bias tended to be lower for full matching than for IPTW. The reasons for these biases and for the differences between the two methods appeared to be due to some extreme weights generated for each method. Both methods tended to produce more extreme weights as the magnitude of the effects of covariates on treatment selection increased. Furthermore, more extreme weights were observed for IPTW than for full matching. However, the poorer performance of both methods in the presence of a strong treatment-selection process was mitigated by the use of IPTW with restriction and full matching with a caliper restriction when the propensity score model was correctly specified.

1 Introduction

There is an increasing interest in estimating the causal effects of treatments using observational (non-randomized) data. In observational studies, there are two primary estimands of interest: the average treatment effect (ATE) and the average treatment effect in the treated (ATT).^1,2 The former denotes the average effect of treatment in an entire population or sample when that entire population or sample is moved from control to treated, while the latter denotes the average effect of treatment in those subjects who were ultimately treated. The estimand that will be of greater interest is dictated by the nature of the treatment, the research question, and the context of the study. The ATE may be of interest if one can imagine potentially imposing or applying the treatment to all eligible subjects. The ATT may be relevant in settings in which one would not impose the treatment on all eligible subjects. In many pharmacoepidemiological studies, the ATE will be of greater interest when comparing the effects of medications and drug therapies on patient outcomes, since the barriers to placing a patient on a given pharmaceutical treatment compared to a competing pharmaceutical therapy may be relatively low. In many of these settings, one could conceive of imposing or directing treatment to a specific agent, assuming that the patient had no contraindications to any of the study medications. However, when studying the effects of time-intensive rehabilitation programmes, the ATT may be of greater interest, since the barriers to patients initiating and completing treatment may be high. Another context when the ATT may be of interest is when the intervention is potentially harmful, and there is no thought that all individuals in the population would be exposed to it (e.g. drug abuse or unemployment).

In observational studies, subjects are not assigned randomly to different treatment groups. Instead, treatment assignment is often influenced by subject characteristics. Thus, there are frequently systematic differences in baseline characteristics between treatment groups. This can result in confounding, in which differences in outcomes between treatment groups are due, at least in part, to systematic differences in baseline covariates between the treatment groups. Applied investigators in medical and epidemiological research are increasingly using methods based on the propensity score to reduce or minimize the effects of confounding due to measured baseline covariates.³ The propensity score is the probability of treatment assignment conditional on observed baseline covariates.⁴ There are four broad ways in which the propensity score can be used to estimate the effect of treatment in observational studies: matching, inverse probability of treatment weighting (IPTW), stratification, and covariate adjustment.^4–6

When matching on the propensity score, the most common implementation is pair-matching, in which pairs of treated and control subjects are formed who share a similar value of the propensity score.^3,7,8 Alternative matching methods include many-to-one matching and variable ratio matching.^9–11 For a review of different matching methods, the reader is referred elsewhere.¹² A rarely used alternative matching method is full matching.^13,14 Full matching constructs strata consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. While full matching is described as a matching method, it falls at the intersection of matching, subclassification and weighting: it involves the formation of strata consisting of treated and control subjects and then incorporates weights that are derived from the stratification. An optimal full matching is one that minimizes the average within-stratum differences in the propensity score between treated and control subjects. For the remainder of the paper, we shall use the term ‘full matching’ to refer to an optimal full matching.

There are at least two attractive features of full matching compared to other matching approaches. First, it includes all subjects in the analytic sample. This is in contrast to conventional matching methods in which some subjects are excluded from the final matched sample. Because of this, it avoids bias due to incomplete matching, which can occur when some treated subjects are excluded from the matched sample.¹⁵ Second, it permits estimation of both the ATE and the ATT, whereas conventional pair-matching only allows for estimation of the ATT.

Survival or time-to-event outcomes occur frequently in the medical literature.¹⁶ Recent studies have compared the performance of different propensity score methods for estimating both conditional and marginal hazard ratios.^17–19 Propensity score methods were found to result in biased estimation of conditional hazard ratios. Furthermore, both stratification on the propensity score and covariate adjustment using the propensity score were shown to result in biased estimation of marginal hazard ratios. However, none of these previous studies included full matching as one of the analytic methods. A recent paper described how full matching could be used with survival outcomes when estimating the ATT.²⁰

While the use of full matching for estimating hazard ratios in the context of the ATT has been described recently, several issues remain to be explored. First, of the two main propensity score methods that permit estimation of the ATE for survival outcomes, what is the relative performance of full matching and IPTW using the propensity score? Second, of these two analytic methods, what is their relative sensitivity to misspecification of the propensity score model?

The objective of the current paper is two-fold. First, to compare the relative performance of full matching and IPTW for estimating marginal hazard ratios when the estimand of interest is the ATE. Second, to examine the effect of misspecification of the propensity score model when using full matching and IPTW to estimate marginal hazard ratios. We also consider the use of variations on these approaches that limit the influence of observations outside the range of common support (through a caliper in full matching and restriction with IPTW). The paper is structured as follows: in Section 2, we briefly describe propensity scores and statistical methods for estimating the effect of treatment when using full matching and IPTW. In Section 3, we describe a series of Monte Carlo simulations to compare the relative performance of full matching and IPTW for estimating marginal hazard ratios when the estimand of interest is the ATE and the propensity score model is correctly specified. In Section 4, we describe an extensive series of Monte Carlo simulations to examine the effect of misspecifying the propensity score model when using full matching and IPTW to estimate marginal hazard ratios. Finally, in Section 5, we summarize our findings and place them in the context of the existing literature.

2 Statistical methods

In an observational study of the effect of treatment on outcomes, the propensity score is the probability of receiving the treatment of interest conditional on measured baseline covariates: $e=Pr(Z=1|X)$, where X denotes the vector of measured baseline covariates.⁴ The propensity score is often estimated using a logistic regression model, with the propensity scores being the predicted probabilities generated by that model.

In constructing a full matching stratification, each subject is assigned to a matched set consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. Weights can be derived from the stratification imposed by the full matching. One set of weights permits estimation of the ATT, while a different set of weights permits estimation of the ATE. Weights that permit estimation of the ATT can be constructed as follows: treated subjects are assigned a weight of one, while each control subject has a weight proportional to the number of treated subjects in its matched set divided by the number of controls in the matched set.^21,22 The control group weights are scaled such that the sum of the control weights across all the matched sets is equal to the number of uniquely matched control subjects. Weights that permit estimation of the ATE can be constructed as follows: treated subjects are assigned a weight equal to the marginal probability of receiving the treatment in the overall sample multiplied by the number of subjects in the given subclass or stratum divided by the number of treated subjects in that subclass. Similarly, control subjects are assigned a weight equal to the marginal probability of receiving the control treatment in the overall sample multiplied by the number of subjects in the given subclass divided by the number of control subjects in that subclass.²³ Thus, if m and j denote the number of treated and control subjects in a given stratum, and q denotes the marginal probability of treatment in the overall sample, then the weights for treated and control subjects in the given stratum are $\frac{q(m+j)}{m}$ and $\frac{(1-q)(m+j)}{j}$, respectively.

When using IPTW to estimate the ATE, weights are computed that denote the probability of receiving the actual treatment that was received. If e denotes the estimated propensity score, then the original sample is weighted by the following weights: $\frac{Z}{e}+\frac{(1-Z)}{1-e}$ (i.e. treated subjects are assigned a weight equal to the reciprocal of the propensity score, while control subjects are assigned a weight equal to the reciprocal of one minus the propensity score).

Using either approach (full matching or IPTW) with survival outcomes, the hazard of the occurrence of the event of interest is regressed on an indicator variable denoting treatment status using a Cox proportional hazards model that incorporates the appropriate set of weights and that employs a robust variance estimator to account for the weights being estimated, rather than known with certainty.^19,24–26 Furthermore, when using full matching, the clustering of subjects within strata was taken into account when estimating standard errors.

3 The relative performance of full matching and IPTW for estimating marginal hazard ratios with a correctly specified propensity score model

We conducted a series of Monte Carlo simulations to examine the relative performance of full matching and IPTW when estimating the effect of treatment on survival outcomes when the target estimand is the ATE. In this section, we restrict our attention to scenarios in which the propensity score model has been correctly specified. We considered a range of scenarios in terms of the extent of confounding. The methods’ performances were assessed using the following criteria: (i) bias in estimating the true marginal log-hazard ratio; (ii) the mean squared error (MSE) of the estimated log-hazard ratio; and (iii) the empirical coverage rates of nominal 95% confidence intervals.

3.1 Monte Carlo simulations: methods

3.1.1 Data-generating process

For each subject, we simulated ten baseline covariates (X₁ to X₁₀) from independent standard normal distributions. The treatment-selection model was described by the following logistic model

$$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_8{X}_8+{\beta }_9{X}_9+{\beta }_{10}{X}_{10}$$

For each subject, we randomly generated a treatment status (Z = 1 denoting treated and Z = 0 denoting control) using this treatment-selection model. We then randomly generated a survival outcome for each subject using a process described by Bender et al.²⁷ For each subject, we defined the linear predictor (LP) as

$${\text{LP}}_i={\alpha }_{\text{treat}}{Z}_i+{\alpha }_1{X}_{1,i}+{\alpha }_2{X}_{2,i}+{\alpha }_3{X}_{3,i}+{\alpha }_4{X}_{4,i}+{\alpha }_5{X}_{5,i}+{\alpha }_6{X}_{6,i}+{\alpha }_7{X}_{7,i}+{\alpha }_8{X}_{8,i}+{\alpha }_9{X}_{9,i}+{\alpha }_{10}{X}_{10,i}.$$

For each subject, we generated a random number from a standard Uniform distribution: u ∼ U(0,1). A survival or event time was generated for each subject as follows: $(\frac{-\text{log}(u)}{\lambda e\text{LP}})1/\eta$. We set λ and η to be equal to 0.00002 and 2, respectively, as has been done in previous studies.^19,28,29 The use of this data-generating process results in a conditional treatment effect, with a conditional hazard ratio of exp(α_treat). However, we wanted to generate data in which there was a specified marginal hazard ratio. To do so, we modified a previously described data-generating process for generating data with a specified marginal odds ratio or risk difference.^30,31 We used an iterative process to determine the value of α_treat (the conditional log-hazard ratio) that induced the desired marginal hazard ratio. Such an approach has been used in previous studies.^17,19 We simulated data such that the true marginal hazard ratio for the effect of treatment on the hazard of the outcome was 0.8.

The regression coefficients in the treatment-selection model β₁ through β₁₀ were set equal to log(2), log(1.75), log(1.75), log(1.5), log(1.5), log(1.25), log(1.25), log(1.10), log(1.10), and log(1.05), respectively, while β₀ was set equal to zero. In the outcomes model, the regression coefficients α₁ through α₁₀ were set equal to log(1.1), log(1.1), log(1.25), log(1.25), log(1.5), log(1.5), log(2), log(2), log(1.75), and log(1.75), respectively. Thus, a one unit increase in the first covariate (X₁) doubled the odds of treatment (i.e. the odds ratio for exposure associated with the first covariate was 2), while a one unit increase in the same covariate resulted in a 50% increase in the hazard of the occurrence of the outcome (i.e. the hazard ratio for the effect of the covariate on the hazard of the outcome was 1.5). Since the variables were simulated to have unit variance, a one unit increase in a given variable is equivalent to a change in the covariate of one standard deviation. These values were selected to represent the magnitude of effect sizes typically encountered in many epidemiological and medical applications.

We used a factorial design to modify the scenario described earlier to allow for an amplification of the effect of each covariate on the treatment-selection process. The ith regression coefficient in the treatment selection model (labeled the “treatment-selection coefficients”) was changed from log(OR_i) to log(k × OR_i), thereby increasing the odds ratio for the effect of the ith covariate from OR_i to k × OR_i, for i = 1, … , 10. We allowed the value of k to take on the values from 1 to 10, in increments of one. Thus, a one-unit increase in the first covariate had an odds ratio for treatment that ranged from 2 (when k = 1) to 20 (when k = 10). For each of the 10 scenarios, we simulated 1000 datasets, each consisting of 1000 subjects.

3.1.2 Statistical analyses in simulated datasets

In each simulated dataset, we estimated the propensity score using a logistic regression model to regress treatment assignment on the 10 variables X₁ through X₁₀ (thus, the propensity score model was correctly specified). In each simulated dataset, an optimal full matching was created using the estimated propensity score. Methods identical to those described in Section 2 were used to estimate the effect of treatment on the hazard of the occurrence of the outcome using full matching and IPTW.

We also examined a modification of each of full matching and IPTW. These modifications attempt to address lack of overlap in the distribution of the propensity score between treated and control subjects. Conventional full matching does not place any constraints on the similarity of treated and control subjects placed in the same stratum. Thus, in the presence of strong confounding, it is possible that some strata will contain treated and control subjects whose propensity scores differ substantially. To address this limitation, we also examined the use of full matching with the imposition of a caliper restriction. To do so, we constructed a full matching in which subjects were matched on the logit of the propensity score with the restriction that treated and control subjects in the same stratum could not have logits of the propensity score that differed by more than 0.2 of the standard deviation of the logit of the propensity score. This caliper width was selected as it was found to result in superior performance across a range of scenarios when using pair-matching.³² Crump et al., in the context of weighted analyses, proposed a method for addressing limited overlap when estimating average treatment effects.³³ They proposed limiting the analytic sample to a proportion of the original sample. In a wide range of scenarios, they found that restricting the sample to those subjects whose propensity score lay in the interval [0.1, 0.9] resulted in a good approximation to the optimal subsample. Thus, in addition to using IPTW in the full sample, we also used IPTW in the subsample restricted to those subjects whose propensity score lay in the interval [0.1, 0.9].

Let θ denote the true treatment effect on the log-hazard ratio scale (=log(0.8)), and let θ_i denote the estimated treatment effect, also on the log-hazard ratio scale, in the ith simulated sample (i = 1, …, 1000). Then, the mean estimated log-hazard ratio was estimated as $\frac{1}{1,000}\sum _{i=1}^{1,000}{\theta }_i$ and the MSE was estimated as $\frac{1}{1,000}\sum _{i=1}^{1,000}({\theta }_i-\theta )2$. Ninety-five percent confidence intervals were constructed for each estimate of the treatment effect, and the proportion of confidence intervals that contained the true measure of effect was determined.

All analyses were conducted in the R statistical programming language (version 3.0.2). Full matching was implemented using the matchit function from the MatchIt package (version 2.4-21).^21,22 Full matching with a caliper restriction was implemented using the fullmatch function from the optmatch package (version 0.9-3).

3.2 Monte Carlo simulations: results

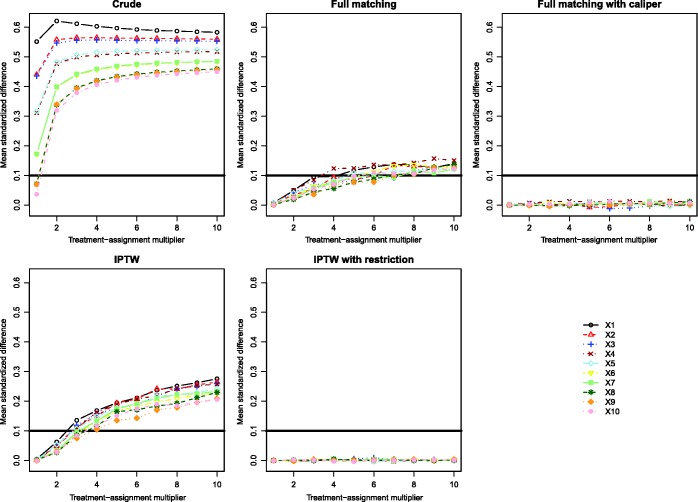
Standardized differences comparing the mean of each of the 10 baseline covariates between treated and control subjects are described in Figure 1. There is one panel for the standardized differences in the original (unweighted) sample, one for the standardized differences after full matching, one for the standardized differences after full matching with a caliper restriction, one for the sample that incorporates the IPT weights, and one for the restricted sample that incorporates the IPT weights. On each panel, we have superimposed horizontal lines denoting standardized differences of ±0.1, as some authors have suggested that standardized differences that exceed these thresholds may be indicative of meaningful imbalance.³⁴ When using the weights derived from either full matching or IPTW, the standardized differences are negligible when the treatment-selection process was weak to moderate. However, as the magnitude of the effect of the covariates on treatment-selection increased, the standardized differences increased. In general, better covariate balance was induced by the weights obtained from full matching than by the weights obtained from IPTW. It should be highlighted that in all of these scenarios, the propensity score model was correctly specified. Thus, even when the propensity score model has been correctly specified, if the effects of the covariates on treatment-selection are strong, then incorporating the weights derived from full matching or IPTW does not necessarily induce excellent balance in baseline covariates between the treatment groups. Meaningful residual differences can persist despite incorporating either set of weights. In contrast to this, the use of full matching with a caliper restriction or the use of IPTW in the restricted sample resulted in negligible imbalance in all baseline covariates between treated and control individuals, regardless of the strength of the treatment-selection process.

Figure 1.

Simulation 1: Mean standardized differences for the 10 baseline variables.

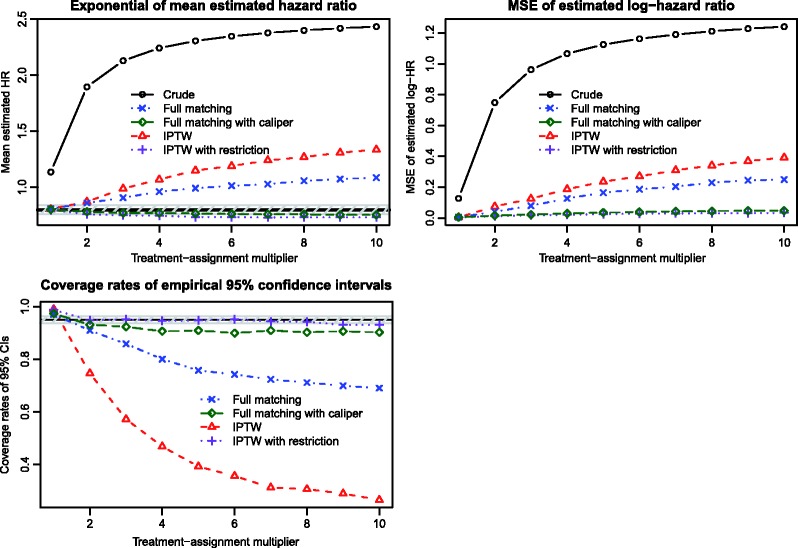
Results describing the estimation of the marginal hazard ratio are reported in Figure 2. There is one panel for each of the exponential of the mean estimated hazard ratio, the MSE of the estimated log-hazard ratio, and the empirical coverage rates of the estimated 95% confidence intervals. On the top-left panel (exponential of mean estimated hazard ratio), we have superimposed a solid horizontal line denoting the true effect of treatment (a hazard ratio of 0.8) and a shaded area denoting a relative bias of 5%. We have also presented estimates of the crude or unadjusted hazard ratio to facilitate an appreciation for the magnitude of the effect of confounding in the simulated datasets. When the magnitude of the effect of the covariates on treatment-selection is low to modest, then both full matching and IPTW resulted in estimation of the true marginal hazard ratio with negligible bias. However, as the magnitude of the effects of the covariates on treatment-selection increased, both methods tended to result in biased estimation. Full matching resulted in estimates with lower bias than did IPTW. Both full matching with a caliper restriction and the use of IPTW in the restricted sample resulted in estimates with negligible bias, regardless of the strength of the treatment-selection process. Full matching with a caliper restriction resulted in estimates with slightly less bias than did IPTW in the restricted sample.

Figure 2.

Simulation 1: Estimation of marginal hazard ratio.

Full matching resulted in estimates with lower MSE than did IPTW (top-right panel). However, both full matching with a caliper restriction and IPTW in the restricted sample resulted in estimates with substantially lower MSE than the estimates obtained using conventional full matching or IPTW.

When the treatment-selection process was weak, then both methods produced confidence intervals whose empirical coverage rates were approximately equal to the nominal level (lower-left panel). On this panel, we have superimposed a horizontal solid line denoting the empirical coverage rates of 0.95 (the advertised coverage rate). Based on our use of 1000 simulated datasets, an empirical coverage rate that is less than 0.9365 or greater than 0.9635 would be statistically significantly different from the advertised rate of 0.95 using a standard normal-theory test and a significance level of 0.05. The shaded area of the figure denotes empirical type I error rates that are not statistically significantly different from 0.95. As the magnitude of the effects of the covariates on treatment-selection increased, both methods resulted in confidence intervals with sub-optimal coverage rates. However, the empirical coverage rates for intervals obtained using full matching were closer to the nominal level than were the coverage rates for intervals obtained using IPTW. Both full matching with a caliper restriction and IPTW in the restricted sample resulted in confidence intervals whose empirical coverage rates were substantially closer to the advertised rate. In 7 of the 10 scenarios, the confidence intervals produced using IPTW in the restricted sample were not statistically significantly different from the advertised rate.

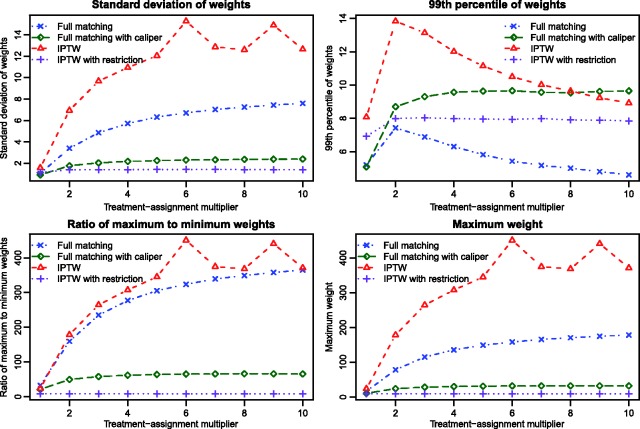
We conducted a set of secondary analyses to explore reasons for differences in the performance of full matching and IPTW. Within each simulated dataset, we computed the following quantities for each of the two methods: the standard deviation of the weights, the 99th percentile of the distribution of the weights, the ratio of the largest weight to the smallest weight, and the largest weight, and the maximum weight. We then determined the mean of each of these four quantities across the 1000 simulated datasets for each of the ten scenarios (Figure 3). When using full matching, three of the four quantities increased slowly as the magnitude of the effect of the covariates on treatment-selection increased. Each of these four quantities tended to be larger (sometimes substantially larger) when using IPTW than when using full matching. There were some scenarios in which extreme weights were observed for IPTW. For three of the four quantities, smaller estimates were obtained for both full matching with a caliper restriction and IPTW in the restricted sample than for conventional full matching and conventional IPTW.

Figure 3.

Simulation 1: Comparison of weights from full matching and IPTW.

4 Effect of misspecifying the propensity score model when using full matching and IPTW to estimate marginal hazard ratios

We conducted an extensive series of Monte Carlo simulations to examine the sensitivity of full matching and IPTW using the propensity score to misspecification of the propensity score model when estimating marginal hazard ratios and the target estimand is the ATE. We considered a range of scenarios in terms of the extent of confounding and the extent of model misspecification. The methods’ performances were assessed using the same criteria as above: (i) bias in estimating the true marginal log-hazard ratio; (ii) the mean squared error (MSE) of the estimated log-hazard ratio; and (iii) the empirical coverage rates of nominal 95% confidence intervals.

4.1 Monte Carlo simulations: methods

4.1.1 Data-generating process

Our simulations were based on a framework described by Setoguchi et al. that has subsequently been used by multiple groups of authors.^35–37 This framework incorporates different complexities for the formulation of the propensity score model, and allows researchers to examine the effect of misspecification of the propensity score model.

As in Setoguchi et al., we assumed that there were 10 baseline covariates (X₁ to X₁₀), of which four had standard normal distributions and six had Bernoulli distributions. Four of the 10 covariates affected both treatment selection and the outcome, three covariates affected treatment selection alone, while three covariates affected the outcome alone. Furthermore, there were three pair-wise correlations between select pairs of baseline covariates. Setoguchi et al. considered seven scenarios that differed in the nature of the true treatment-selection model:

1. Additivity and linearity (main effects only):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7$$
2. Mild non-linearity (one quadratic term):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_2{X}_2^2$$
3. Moderate non-linearity (three quadratic terms):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_2{X}_2^2+{\beta }_4{X}_4^2+{\beta }_7{X}_7^2$$
4. Mild non-additivity (four two-way interaction terms):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_1\times 0.5\times X_1{X}_3+{\beta }_2\times 0.7\times X_2{X}_4+{\beta }_4\times 0.5\times X_4{X}_5+{\beta }_5\times 0.5\times X_5{X}_6$$
5. Mild non-additivity and non-linearity (four two-way interaction terms and one quadratic term):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_2{X}_2^2+{\beta }_1\times 0.5\times X_1{X}_3+{\beta }_2\times 0.7\times X_2{X}_4+{\beta }_4\times 0.5\times X_4{X}_5+{\beta }_5\times 0.5\times X_5{X}_6$$
6. Moderate non-additivity (10 two-way interaction terms):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_1\times 0.5\times X_1{X}_3+{\beta }_2\times 0.7\times X_2{X}_4+{\beta }_3\times 0.5\times X_3{X}_5+{\beta }_4\times 0.7\times X_4{X}_6+{\beta }_5\times 0.5\times X_5{X}_7+{\beta }_1\times 0.5\times X_1{X}_6+{\beta }_2\times 0.7\times X_2{X}_3+{\beta }_3\times 0.5\times X_3{X}_4+{\beta }_4\times 0.5\times X_4{X}_5+{\beta }_5\times 0.5\times X_5{X}_6$$
7. Moderate non-additivity and non-linearity (10 two-way interaction terms and three quadratic terms):

   $$\text{logit}(Pr(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7++{\beta }_2{X}_2^2+{\beta }_4{X}_4^2+{\beta }_7{X}_7^2+{\beta }_1\times 0.5\times X_1{X}_3+{\beta }_2\times 0.7\times X_2{X}_4+{\beta }_3\times 0.5\times X_3{X}_5+{\beta }_4\times 0.7\times X_4{X}_6+{\beta }_5\times 0.5\times X_5{X}_7+{\beta }_1\times 0.5\times X_1{X}_6+{\beta }_2\times 0.7\times X_2{X}_3+{\beta }_3\times 0.5\times X_3{X}_4+{\beta }_4\times 0.5\times X_4{X}_5+{\beta }_5\times 0.5\times X_5{X}_6.$$

For greater details on the data-generating process, the reader is referred to the initial paper by Setoguchi et al.

For each subject, we randomly generated a treatment status (Z = 1 denoting treated and Z = 0 denoting control) using one of the seven treatment-selection models described earlier (A through G). We then randomly generated a survival outcome for each subject. In the original paper by Setuguchi et al., the authors simulated continuous outcomes. We modified their data-generating process to simulate survival or time-to-event outcomes using methods similar to those described in the previous section. For each subject, we defined the linear predictor (LP) as ${\text{LP}}_i={\alpha }_{\text{treat}}{Z}_i+{\alpha }_1{X}_{1,i}+{\alpha }_2{X}_{2,i}+{\alpha }_3{X}_{3,i}+{\alpha }_4{X}_{4,i}+{\alpha }_5{X}_{8,i}+{\alpha }_6{X}_{9,i}+{\alpha }_7{X}_{10,i}$. As in the first set of simulations, we simulated data such that the true marginal hazard ratio for the effect of treatment on the hazard of the outcome was 0.8.

The regression coefficients in the treatment-selection models were the same as those specified by Setoguchi et al.: β₁ through β₇ were set equal to 0.8, −0.25, 0.6, −0.4, −0.8, −0.5, and 0.7, respectively, while β₀ was set equal to zero. In the outcome model, the regression coefficients were also the same as those used by Setoguchi et al.: α₁ through α₇ were set equal to 0.3, −0.36, −0.73, −0.2, 0.71, −0.19, and 0.26, respectively. However, these latter regression coefficients are log-hazard ratios in our context, rather than linear regression coefficients.

We then used a factorial design to modify each of the seven scenarios described earlier to allow for an amplification of the effect of the covariates on treatment-selection or on the hazard of the outcome. The seven regression coefficients in the treatment selection model (labeled the “treatment-selection coefficients”): β₁, β₂, β₃, β₄, β₅, β₆, and β₇, were changed to k × β₁, k × β₂, k × β₃, k × β₄, k × β₅, k × β₆, and k × β₇, respectively. Similarly, the seven regression coefficients in the outcome model (labeled the “prognostic coefficients”): α₁, α₂, α₃, α₄, α₅, α₆, and α₇, were changed to m × α₁, m × α₂, m × α₃, m × α₄, m × α₅, m × α₆, and m × α₇, respectively. We allowed the value of k to take on the values from 1 to 10, while the values of m took on the values from 1 to 5, both in increments of 1. Thus, for each of the seven scenarios above (labeled A through G), we examined 50 sub-scenarios, in which the magnitude of covariate imbalance (the effect of covariates on treatment-selection) or the magnitude of the effect of covariates on the hazard of the outcome were allowed to vary. For each of the 350 scenarios (7 scenarios x 50 sub-scenarios), we simulated 1000 datasets, each consisting of 1000 subjects.

4.1.2 Statistical analyses in simulated datasets

In each simulated dataset, we estimated the propensity score using a logistic regression model to regress treatment assignment on the seven variables X₁ through X₇. The estimated propensity score model included only these seven main effects and excluded interactions and quadratic terms. Thus, in Scenario A, the propensity score model was correctly specified, while in the remaining scenarios, it was incorrectly specified. The remaining statistical analyses were identical to those described in Section 3. Note that Scenario A allows one to examine the relative performance of the two methods when the propensity score model is correctly specified. Thus, including Scenario A allowed us to examine the robustness of the observations in Section 3 under a different data-generating process.

4.2 Monte Carlo simulations: results

In examining the results of the simulations, note that Scenario A allows one to examine the relative performance of the two methods when the propensity score model is correctly specified. Scenarios B through G allow one to examine the effect of misspecifying the propensity score model on the performance of full matching and IPTW for estimating marginal hazard ratios when the target estimand is the ATE.

The mean standardized differences in the original sample for the seven covariates that had an effect on the outcome (X₁–X₄ and X₈–X₁₀) are reported in the different scenarios in Figure 4. There is one panel for each of the seven Setoguchi scenarios. On each panel, we have superimposed horizontal lines denoting standardized differences of ±0.1. Note that the scalar that modifies the effect of the covariates on the hazard of the outcome has no effect on standardized differences. Therefore, results are presented only for those scenarios in which this scalar was equal to one. Across the seven scenarios, one observes that there was moderate imbalance in prognostically important baseline covariates between treated and control subjects in the simulated datasets.

Figure 4.

Simulation 2: Mean standardized differences for the 7 prognostic variables.

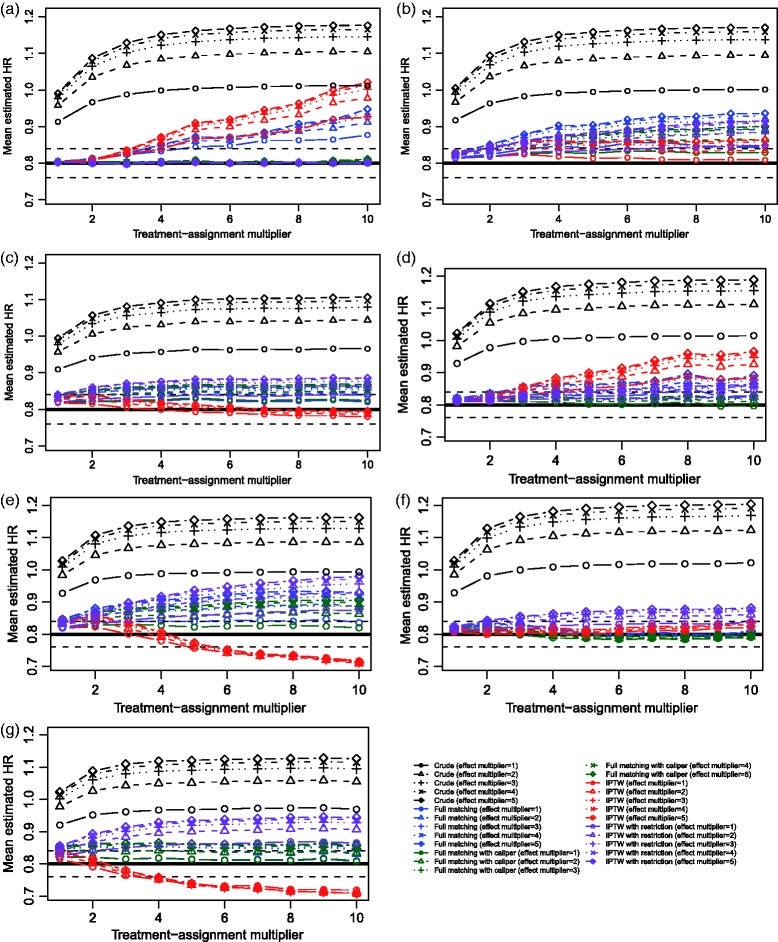
The exponential of the mean estimated log-hazard ratio across the 1000 simulated datasets for each scenario and each of the two estimation methods is reported in Figure 5. We have superimposed on each panel a solid horizontal line denoting the true effect of treatment (a hazard ratio of 0.8) and dashed vertical lines denoting a relative bias of 5%. We have also presented estimates of the crude or unadjusted hazard ratio, to facilitate an appreciation for the magnitude of the effect of confounding in the simulated datasets.

Figure 5.

Simulation 2: Exponential of mean estimated hazard ratio.

In examining the results for Scenario A, one notes that both propensity score methods resulted in negligible bias in estimating the treatment effect when the treatment-selection process was weak to moderate. However, as the strength of the treatment-selection process increased, the observed bias increased. Thus, even when the treatment-selection model was correctly specified, biased estimation of the marginal hazard ratio occurred for both methods. When the treatment-selection process was very strong, bias was modestly lower for full matching than for the IPTW approach. Both full matching with a caliper restriction and IPTW in the restricted sample resulted in estimates with negligible bias, regardless of the magnitude of the strength of the treatment-selection process. These observations confirm the findings described in Section 3.

In the remaining six scenarios, in which the propensity score model was misspecified, both propensity score methods tended to result in estimates with at most minor bias when the treatment-selection model was weak to modest. However, the magnitude of bias increased with the magnitude of the effect of the covariates on treatment selection. Results were inconsistent as to which of full matching and IPTW resulted in the least bias in these scenarios. Use of either full matching with a caliper restriction or IPTW in the restricted sample tended to result in estimates with appreciable bias. In Scenario G, the bias for the restricted IPTW estimates tended to exceed that of the unrestricted IPTW estimates.

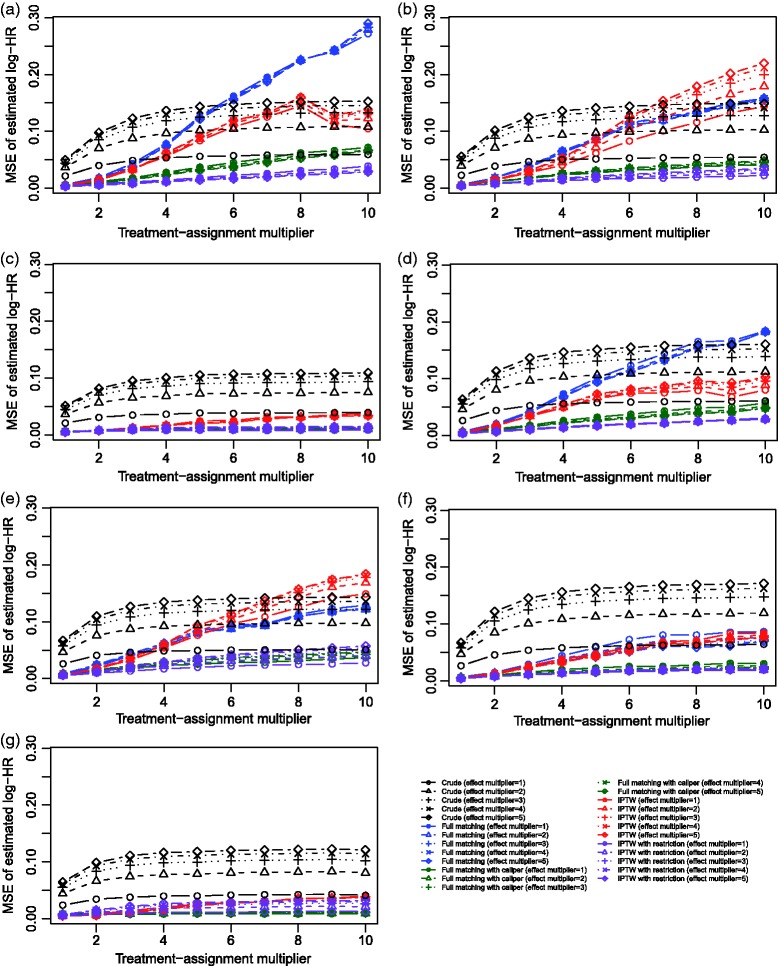
The MSE of the estimated log-hazard ratios are reported in Figure 6 for the seven different scenarios. In Scenario A, in which the propensity score model was correctly specified, one observes that IPTW resulted in estimates with lower MSE compared to those for full matching. Differences between the two methods were negligible when the magnitude of the effect of the covariates on treatment selection was weak, but differences in MSE between the two approaches increased as the magnitude of the effect of the covariates increased. These observations were inconsistent with those observed in Section 3. Furthermore, full matching with a caliper restriction and IPTW in the restricted sample resulted in estimates with lower MSE than the comparable unrestricted method. Across the remaining six scenarios in which the propensity score model was misspecified, results were inconsistent as to which method resulted in estimates with lower MSE. However, in general, full matching with a caliper restriction and IPTW in the restricted sample tended to result in estimates with lower MSE than the comparable unrestricted methods.

Figure 6.

Simulation 2: Mean squared error of estimated log–hazard ratio.

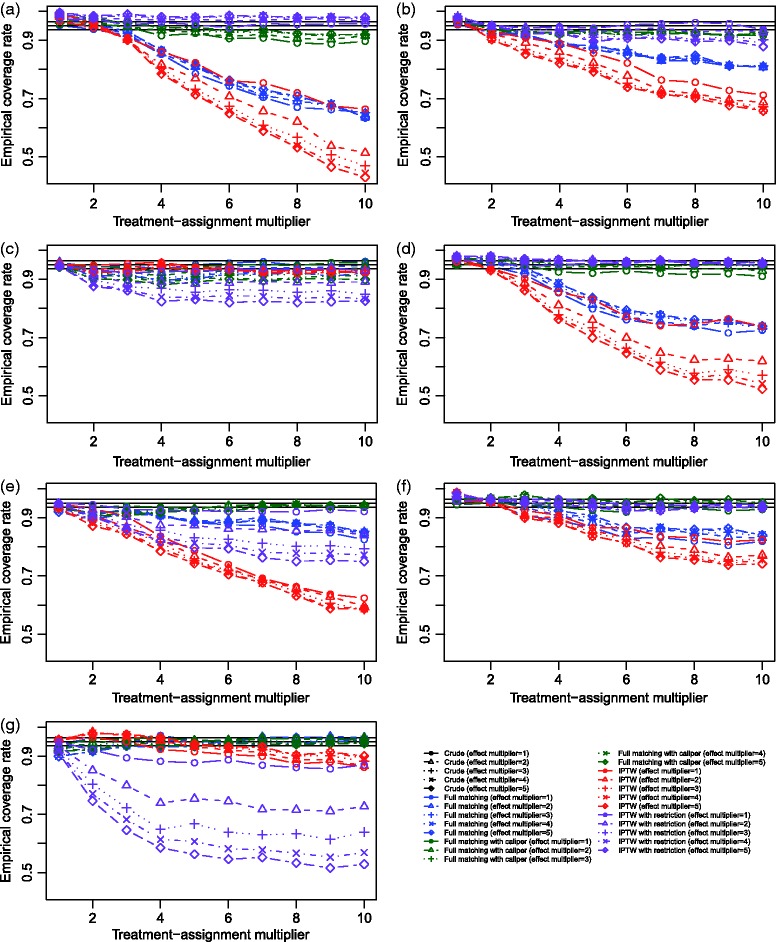
The empirical coverage rates of estimated 95% confidence intervals are reported in Figure 7 for the seven different scenarios. Coverage rates for the crude estimates are not displayed since they were below 50% across all scenarios. On each panel, we have superimposed three horizontal solid lines denoting empirical coverage rates of 0.95 (the advertised coverage rate) and 0.9365 and 0.9635. In examining the results for Scenario A, one observes that both methods produced confidence intervals that have approximately correct coverage rates when the treatment-selection process was weak, although those from full matching tended to be marginally closer to the nominal rate. However, even when the propensity score model is correctly specified, the empirical coverage rate is significantly lower than the nominal rate when the magnitude of the effect of the covariates on treatment selection is strong. These observations confirm those observed in Section 3. The empirical coverage rates in the remaining six scenarios in which the propensity score model is incorrectly specified are inconsistent. In most scenarios, when the effect of the covariates on treatment-selection is weak, then the empirical coverage rates are approximately correct. Each restricted estimation method tended to result in 95% confidence intervals whose empirical coverage rates were closer to the advertised rate compared to those of the corresponding unrestricted method.

Figure 7.

Simulation 2: Empirical coverage rates of 95% confidence intervals.

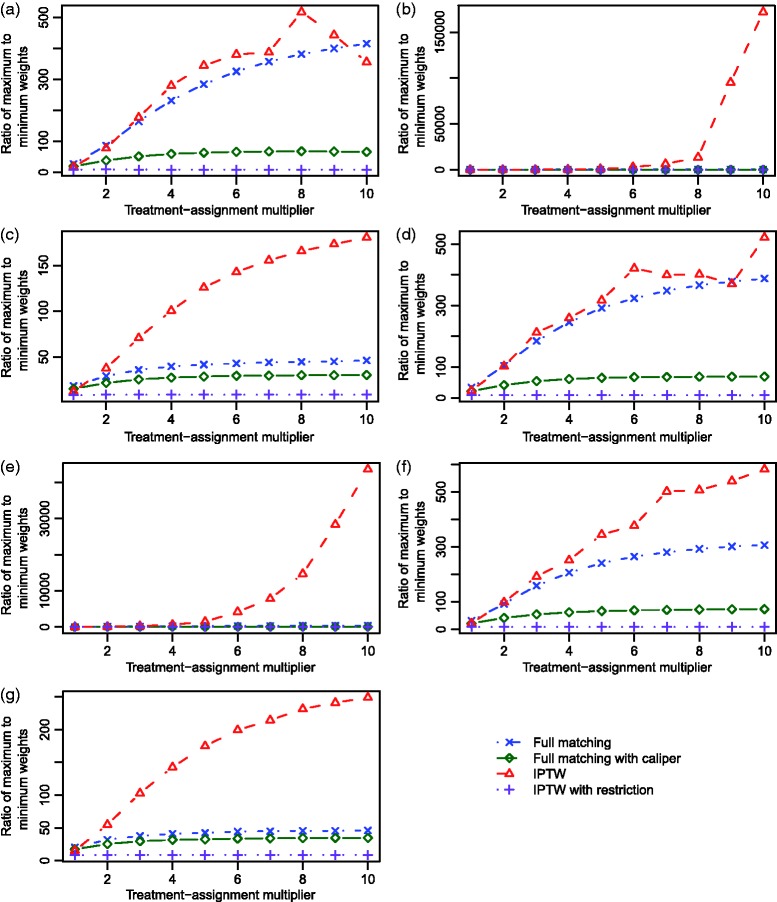
The ratios of the maximum weight to the minimum weight across the different scenarios are described in Figure 8. Two observations warrant mention. First, for the two unrestricted methods, this ratio increased as the magnitude of the effect of the covariates on treatment selection increased. Second, this ratio tended to be larger for IPTW than for full matching. Furthermore, these ratios tended to be lower for the two restricted approaches than for the two unrestricted approaches.

Figure 8.

Simulation 2: Ratio of maximum to minimum weights (ITPW and Full matching).

5 Discussion

Propensity score methods are frequently used in the medical and epidemiological literature for estimating the effects of treatments, exposures and interventions when using observational data. Of the commonly used propensity score methods, only IPTW allows for estimation of marginal hazard ratios with negligible bias when the estimand is the ATE.¹⁹ Conventional pair-matching allows for estimation of the ATT. Full matching is a rarely used matching method that was proposed by Rosenbaum.¹³ Amongst the advantages of full matching is that it permits estimation of both the ATE and the ATT, depending on how the strata are weighted. We conducted an extensive series of simulations to explore the relative performance of IPTW and full matching for estimating marginal hazard ratios when the target estimand is the ATE. We found that both full matching and IPTW resulted in estimation of the marginal hazard ratio with negligible bias when the treatment-selection model was weak and the propensity score model was correctly specified. Similarly, when the treatment-selection model was weak, both approaches resulted in minimal bias even if the propensity score model was incorrectly specified. However, if the treatment-selection model was strong, then biased estimation was observed to occur, even if the propensity-score model was correctly specified. We also examined two methods that imposed restrictions on each of full matching and IPTW: full matching with a caliper restriction and IPTW using a restricted sample. Both of these methods tended to result in estimates of treatment effect with negligible bias when the propensity score model was correctly specified, regardless of the strength of the treatment-selection process.

We used bias, MSE, and empirical coverage rates of estimated confidence intervals to evaluate the performance of the two different estimation methods. However, we would suggest that in the current context, greater attention should be paid to bias than to the other measures. Iacus et al. quote Rubin as stating “First, since it is generally not wise to obtain a very precise estimate of a drastically wrong quantity, the investigator should be more concerned about having an estimate with small bias than one with small variance. Second, since in many observational studies the sample sizes are sufficiently large that sampling variances of estimators will be small, the sensitivity of estimators to biases is the dominant source of uncertainty.”³⁸ (page 2). This suggests that one should be interested primarily in bias when estimating the effect of model misspecification on the performance of different propensity score methods. We provided information on MSE and coverage to complement the exploration of bias.

Both full matching and IPTW were observed to result in biased estimation of the true marginal hazard ratio when the treatment-selection model was strong. We speculate that the reasons for this phenomenon differed between the two approaches. IPTW can suffer when there are very high weights.³⁹ This can occur when treated subjects have a very low propensity score or when control subjects have a very high propensity score. It is possible that this can occur more frequently when there is a very strong treatment-selection model. Different approaches have been proposed to address the presence of extreme weights, including the use of standardized weights, trimmed weights or truncated weights,^25,40 or the use of a non-parametric estimation procedure, such as random forests or generalized boosted models, for estimating the propensity score model.^35,41 These strategies were not explored in the current study, but merit examination in subsequent research. Full matching entails forming matched sets consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. In the presence of a very strong treatment-selection process, it is likely that there will be some matched sets consisting of either one control subject and a very large number of treated subjects or one treated subject and a very large number of control subjects (in using full matching to examine the effect of coaching for the SAT on test scores, Hansen observed a similar phenomenon, with at least one strata consisting of one treated subject and 161 controls¹⁴). This can result in the singleton in the matched set being assigned a very large weight, which could introduce instability and bias into the estimated effect. In a series of exploratory analyses, we examined characteristics of the distribution of weights when the propensity score model was correctly specified. We observed that the maximum weight and the ratio of the maximum to minimum weight tended to increase as the magnitude of the effect of the covariates on treatment selection increased. Furthermore, more extreme weights were observed for IPTW than for full matching. We suggest that these observations may explain two of our findings. First, the presence of more extreme weights may explain why greater bias was observed for IPTW than for full matching when the propensity score model was correctly specified. Second, the increase in extreme weights as the strength of the treatment-selection process increased is a plausible explanation for the increased bias in estimation that was observed as the strength of the treatment-selection process increased.

In summary, we found that both IPTW and full matching resulted in estimation of marginal hazard ratios with negligible bias when the ATE was the target estimand and the treatment-selection process was weak to moderate. However, when the treatment-selection process was strong, then both methods resulted in biased estimation of the true marginal hazard ratio, even when the propensity score model was correctly specified. Full matching with a caliper restriction and IPTW in a restricted sample resulted in estimates with negligible bias when the propensity score model was correctly specified.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. Dr. Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation. This study was supported in part by an operating grant from the Canadian Institutes of Health Research (CIHR) (Funding number: MOP 86508). Dr. Stuart’s time was supported by the National Institute of Mental Health, R01MH099010.