Reflectance-mode interferometric near-infrared spectroscopy quantifies brain absorption, scattering, and blood flow index in vivo

Abstract

Interferometric near-infrared spectroscopy (iNIRS) is a new technique that measures time-of-flight- (TOF-) resolved autocorrelations in turbid media, enabling simultaneous estimation of optical and dynamical properties. Here, we demonstrate reflectance-mode iNIRS for noninvasive monitoring of a mouse brain in vivo. A method for more precise quantification with less static interference from superficial layers, based on separating static and dynamic components of the optical field autocorrelation, is presented. Absolute values of absorption, reduced scattering, and blood flow index (BFI) are measured, and changes in BFI and absorption are monitored during a hypercapnic challenge. Absorption changes from TOF-resolved iNIRS agree with absorption changes from continuous wave NIRS analysis, based on TOF-integrated light intensity changes, an effective path length, and the modified Beer–Lambert Law. Thus, iNIRS is a promising approach for quantitative and non-invasive monitoring of perfusion and optical properties in vivo.

Quantifying optical properties to infer chromophore concentrations [1] and quantifying scattered light dynamics to infer scatterer motion [2] are ongoing goals of near-infrared spectroscopy (NIRS) [3]. In biological tissue, the absorption coefficient, if measured at multiple wavelengths, yields oxy-hemoglobin concentration, de oxy-hemoglobin concentration, and oxygen saturation. Coherent intensity fluctuations of multiply scattered light, if analyzed with a model informed by optical properties, yield scatterer motion due to blood flow [4]. The combination of oxygen saturation, hemoglobin content, and blood flow provides tissue oxygen consumption.

Continuous wave (CW) NIRS measures reemitted light intensity and is the simplest and most widely used NIRS method [1,3]. However, accurate quantification of baseline optical properties using only light intensity requires additional assumptions about scattered path length, instrumentation loss, and extra cerebral confounds [3]. Hence, baseline oxygen saturation remains challenging to quantify robustly using CW NIRS. For baseline optical properties, time-domain (TD) and frequency-domain (FD) approaches [5,6] add an additional dimension to the measurement space to reduce the number of required assumptions.

To determine blood flow, diffuse correlation spectroscopy (DCS) quantifies temporal intensity fluctuations of coherent light scattered from dynamic tissue [2,4]. DCS critically depends on optical properties in two ways. First, since DCS is a CW approach, the relevant field autocorrelation is an average of field autocorrelations over all photon path lengths, weighted by the optical property-dependent photon time-of-flight (TOF) distribution [7,8]. Second, the total photon momentum transfer, which depends on the reduced scattering coefficient ( ${\mu }_s^{\prime }$) in the diffusion regime, is required to relate dynamics to an effective diffusion coefficient or blood flow index (BFI). In addition, conventional DCS requires ergodicity since it derives field autocorrelations from intensity fluctuations [9].

Recently, interferometric NIRS (iNIRS), based on the TOF-resolved measurement of coherent light reemitted from a turbid medium, was introduced [10]. This approach is based on interferometry using a tunable laser to achieve path length resolution [11,12]. A two-dimensional measurement of reemitted light provides TOF-resolved autocorrelations, from which optical and dynamical properties can be derived [10]. The iNIRS method recently was shown to also provide TOF-resolved field autocorrelations, more directly related to scatterer dynamics than TOF-integrated intensity autocorrelations provided by DCS [13]. In this Letter, we validate iNIRS in reflectance mode using calibrated phantoms, and in the brain of a nude mouse, showing that iNIRS can simultaneously and non invasively quantify optical properties and BFI in vivo.

Here, we make use of the two-dimensional field autocorrelation, $G_1^{(\text{iNIRS})}({\tau }_s,{\tau }_d)={\langle {\mathrm{\Gamma }}_{rs}^{\ast }({\tau }_s,t_d){\mathrm{\Gamma }}_{rs}({\tau }_s,t_d+{\tau }_d)\rangle }_{t_d}$, measured as a function of TOF (τ_s) and lag time (τ_d). Γ_rs(τ_s, t_d) is the TOF-resolved mutual coherence function of the reference and sample fields (U_r and U_s, respectively): ${\mathrm{\Gamma }}_{rs}({\tau }_s,t_d)={\langle U_r^{\ast }(t_s,t_d)U_s(t_s+{\tau }_s,t_d)\rangle }_{t_s}$.

A light path can be envisioned as a series of scattering events, either from stationary tissue (static) or from blood (dynamic), where each scattering event has an associated momentum transfer q and phase shift δr · q [14], where δr is scatterer displacement. Thus, the instantaneous TOF-resolved scattered optical field from the sample can be written as U_s(τ_s, t_d) = U_c(τ_s) + U_f(τ_s, t_d) where U_c is the static field contribution, arising from paths with static scattering events or dynamic scattering events with negligible phase shift, while U_f is the dynamic field contribution, arising from paths with dynamic scattering events with a phase shift. The static contribution is understood to be nonergodic over a certain time scale [9]. Hence, the autocorrelation measured in iNIRS becomes [13]

$$G_1^{(\text{iNIRS})}({\tau }_s,{\tau }_d)=[I_c({\tau }_s)+G_{1,f}({\tau }_s,{\tau }_d)]\ast I_0({\tau }_s),$$ (1)

where I_c(τ_s) = |U_c(τ_s)|² is the static distribution of time-of-flight (DTOF), $G_{1,f}({\tau }_s,{\tau }_d)={\langle U_f^{\ast }({\tau }_s,t_d)U_f({\tau }_s,t_d+{\tau }_d)\rangle }_{t_d}$ is the dynamic autocorrelation, I₀(τ_s)is the instrument response function (IRF), I_f(τ_s) = G_1,f(τ_s, 0)is the dynamic DTOF, and “*” denotes convolution with respect to τ_s.

The static (I_c, slowly decorrelating) and dynamic (G_1,f, rapidly decorrelating) components of the field autocorrelation function may be associated with different photon paths. The ratio of static to dynamic components should diminish for larger TOFs, as momentum transfer from dynamic scattering is more probable for long paths than short paths. By independently assessing these two components, these paths may be independently probed. This new approach of correlation gating is used here to improve the accuracy of iNIRS analysis. In our in vivo experiment, some photons may propagate through tissue without experiencing dynamic scattering events. Such static photons may not pass through blood, may not be diffuse, and thus should be excluded from an analysis that assumes diffuse photons and an ergodic, uniformly absorbing medium. By using correlation gating to exclude I_c and analyze I_f or G_1,f, it may be possible to better satisfy the assumptions of the MBLL and diffusion theory for an ergodic, uniformly absorbing medium. By evaluating Eq. (1) at τ_d = 0, we obtain that $I_s^{(\text{iNIRS})}({\tau }_s)=G_1^{(\text{iNIRS})}({\tau }_s,0)=I_s({\tau }_s)\ast I_0({\tau }_s)$, or the temporal point spread function (TPSF) is equal to the DTOF, I_s(τ_s) = I_c(τ_s)+I_f(τ_s), convolved with the IRF. Alternatively, $I_s^{(\text{iNIRS})}({\tau }_s)$ could have been obtained through conventional temporal speckle averaging. Since G_1,f(τ_s, τ_d) decorrelates with increasing τ_d, the static TPSF can be determined by $I_c^{(\text{iNIRS})}({\tau }_s)={lim}_{{\tau }_d\to \infty }{G}_1^{(\text{iNIRS})}({\tau }_s,{\tau }_d)=I_c({\tau }_s)\ast I_0({\tau }_s)$. Practically, the asymptotic limit is replaced by a time scale, τ_d = τ_d,c, that experimentally defines the boundary between static and dynamic components. The TOF-dependent decay rate ξ(τ_s) of G_1,f(τ_s,τ_d) relates to the effective diffusion coefficient of light scatterers. Last, by subtracting $I_c^{(\text{iNIRS})}({\tau }_s),G_{1,f}^{(\text{iNIRS})}({\tau }_s,{\tau }_d)=G_{1,f}({\tau }_s,{\tau }_d)\ast I_0({\tau }_s)$ yields the dynamic TPSF: $I_f^{(\text{iNIRS})}({\tau }_s)=G_{1,f}^{(\text{iNIRS})}({\tau }_s,0)=I_f({\tau }_s)\ast I_0({\tau }_s)$.

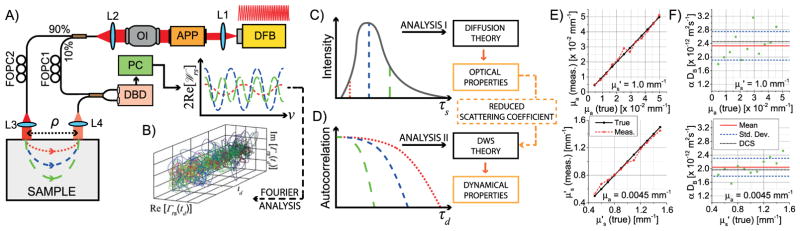
The spectral density, 2Re[𝒲_rs(ν, t_d)], related to Γ_rs(τ_s, t_d)by a Fourier transform [10], is measured over time t_d and ν (conjugate variable to τ_s) by a Mach^—Zehnder interferometer with a narrow linewidth, rapidly tunable distributed feedback (DFB) laser [Fig. 1]. Light is divided into reference and sample arms [Fig. 1(A)]. The collimated sample beam irradiates the turbid medium, and the diffusively reflected light is collected at a distance ρ away. The light paths are combined with a fiber coupler (780HP) and detected by a differential detector. The digitized electronic signal approximates 2Re[𝒲_rs]. Since the laser is swept in frequency, short photon paths produce smaller beat frequencies than long paths, provided that the reference arm TOF is shorter than the shortest sample arm TOF [Fig. 1(A)]. TOF is thus encoded as electronic frequency and can be decoded by re sampling and inverse Fourier transformation [10] to yield the complex Γ_rs time series [Fig. 1(B)].

Fig. 1.

Reflectance-mode iNIRS. (A) A Mach–Zehnder interferometer with a frequency tuned, temporally coherent light source measures a spectral interference signal (2Re[𝒲_rs(ν)]) produced by optical fields from the reference and sample arms. DFB, distributed feedback laser centered at λ₀ = 855 nm with a tuning range of ~60 pm and static coherence length of >100 m; APP, anamorphic prism pair; OI, optical isolator; FOPC, fiber optical polarization controller; DBD, dual balanced detector; L1–L4, lenses; PC, personal computer. (B) TOF-resolved fluctuations of Γ_rs, obtained by inverse Fourier transformation of 2Re[𝒲_rs], determine both TPSFs and autocorrelations. (C) In analysis I, TPSFs are used to obtain optical properties. (D) In analysis II, TOF-resolved field autocorrelations yield scatterer dynamics, using the reduced scattering coefficient and DWS theory. (E) Optical properties of fluid phantoms, in which varying amounts of India Ink and Intralipid 20% were mixed in water, were obtained using Eq. (2) with n = 1.33 and ρ = 7.5 mm and then compared to true values. (F) Phantom dynamics were extracted by fitting TOF-dependent autocorrelations with DWS theory and compared with DCS analysis of TOF-integrated autocorrelations (note that the probability of dynamic scattering, α, is unity for these samples).

In analysis I [Fig. 1(C)], the resulting TPSFs are fit to the expression for TOF-resolved diffuse reflectance from a semi infinite turbid medium [15], ℛ(ρ, τ_s), to extract optical properties (μ_a and ${\mu }_s^{\prime }$). For perpendicularly incident collimated light,

$$\mathcal{R}(\rho ,{\tau }_s)=\frac{exp[-{\mu }_{a}c{\tau }_s/n-{\rho }^2/2{\sigma }_t^2]}{4\pi {\sigma }_t^2{\tau }_s^{3/2}\sqrt{4\pi Dc/n}}\left\{z_{0}exp\left[-\frac{z_0^2}{\varkappa ({\tau }_s)}\right]+\left(z_0+2z_b\right)exp\left[-\frac{{\left(z_0+2z_b\right)}^2}{\varkappa \left({\tau }_s\right)}\right]\right\},$$ (2)

where c denotes the speed of light, $D=\frac{1}{3{\mu }_s^{\prime }}$ is the diffusion coefficient, z₀ = 3D denotes the depth of the positive image source, while z_b = 2D(1 + R)/(1 − R) is the extrapolated boundary corresponding to the negative image source located at z = −z₀ − 2z_b, and R = −1.4399n⁻² + 0.7099n⁻¹ + 0.6681 + 0.0636n denotes the reflection coefficient [16], which depends on the refractive index n, and ϰ(τ_s) = 4Dcτ_s/n, whereas ${\sigma }_t^2={\sigma }_s^2+{\sigma }_d^2+2Dc{\tau }_s/n$ incorporates the extended source and detector collimated modes, described by Gaussian intensity distributions with experimentally determined variances of ${\sigma }_s^2=0.09{\text{mm}}^2$ and ${\sigma }_d^2=0.04{\text{mm}}^2$, respectively [10].

To incorporate finite TOF resolution, ℛ(ρ, τ_s)is then convolved with the IRF. The shape of the IRF is determined from a free-space transmission measurement. To obtain the reflectance-mode IRF, the transmission-mode IRF is then shifted along the TOF axis, so its peak coincides with τ_s = 0. This reference point is obtained from the peak location of the TPSF acquired for ρ = 0 and corrected based on Monte Carlo simulations. The fitting window starts at τ_s = 35 ps to exclude some nondiffuse, early light and continues into the tails as long as the peak-normalized TPSF values are larger than 0.1. Fitting results (based on N = 40,000 iNIRS signals acquired with a laser sweep duration of ~10 μs at 50 kHz with ~25 mW incident power) in fluid phantoms [Fig. 1(E)] support the capability to quantify optical properties within the physiological range.

Given the optical properties, sample dynamics can be obtained from analysis II [Fig. 1(D)]. According to diffusing wave spectroscopy (DWS) theory, the TOF-resolved normalized field autocorrelation is [7] $g_1^{\left(\text{DWS}\right)}\left({\tau }_s,{\tau }_d\right)=exp[-\xi \left({\tau }_s\right){\tau }_d]$, where $\xi \left({\tau }_s\right)=2k^2\alpha D_B{\mu }_s^{\prime }c{\tau }_s/n$ is the TOF-resolved decay rate, where k is the medium wave number, αD_B is the BFI, the product of the probability of dynamic scattering, α, and the effective diffusion coefficient, D_B [4]. Thus, the field fluctuation rate increases with photon path length, l = cτ_s/n, and ${\mu }_s^{\prime }$. In iNIRS, both are known, so the sample dynamics, quantified αD_B, can be directly determined by fitting $g_{1,f}^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)=G_{1,f}^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)/G_{1,f}^{\left(\text{iNIRS}\right)}\left({\tau }_s,0\right)$ with DWS theory. This procedure neglects the possibility of multiple decay rates, weighted by the DTOF, within the IRF window (~45 ps FWHM). For fluid phantoms [Fig. 1(F)], we obtained αD_B = (2.33 ± 0.42) × 10⁻¹² m² s⁻¹ and αD_B = (2.04 ± 0.26) × 10⁻¹² m² s⁻¹ for samples with varying absorption and scattering, respectively, in agreement with prior results [10]. TOF-integrated autocorrelations were fit with correlation diffusion Equation solutions for reflectance as in DCS [4]. The average DCS αD_B value is shown in Fig. 1(F) as a dotted line.

Next, iNIRS was performed in a nude mouse (male, SKH-1E Charles River) brain during a hypercapnic challenge in vivo. Anesthesia was induced using a mixture of isoflurane, medical air, and oxygen. The mouse was placed on a heating pad and immobilized in a stereotactic frame. Isoflurane was maintained at 1.2% v/v during data acquisition to maintain vasoreactivity. After recording the TPSF for ρ = 0, the source and detector light beams were separated by a distance ρ = 7.5 mm between the parietal cortices of the right and left hemispheres. The CO₂ supply was changed from 0% (normocapnia) to 7.5% (hypercapnia) and then back to 0%. During each stage, measurements containing N = 40,000 iNIRS signals (0.8 s per measurement) were recorded at intervals of ~17 s. Last, the reference arm signal alone was acquired. All experimental procedures and protocols were reviewed and approved by the UC Davis Institutional Animal Care and Use Committee.

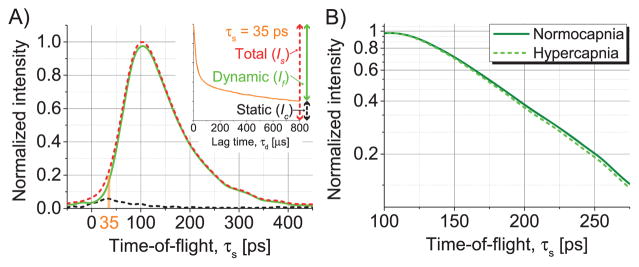
In vivo, $I_s^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$ and $I_f^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$ [Fig. 2(A)] were fit with ℛ(ρ, τ_s) *I₀(τ_s) The static component was estimated at τ_d,c = 0.8 ms. While this cutoff is reasonable for the mouse brain [17], more general fitting approaches are also possible to estimate the static component. To determine the baseline scattering properties, fitting was first performed on the data sets for FiCO₂ = 0% with n = 1.4 and both μ_a and ${\mu }_s^{\prime }$ as free parameters. Next, for consistency with the CW NIRS approach described below, scattering was fixed to the average baseline value of ${\mu }_s^{\prime }=0.831{\text{mm}}^{-1}$ for I_s and ${\mu }_s^{\prime }=0.854{\text{mm}}^{-1}$ for I_f Then, the fitting procedure was repeated for all time points to determine absorption coefficients. The average baseline absorption was μ_a = 2.62 × 10⁻² mm⁻¹ for I_s and μ_a = 2.67 × 10⁻² mm⁻¹ for I_f [Fig. 2(B)].

Fig. 2.

TPSFs from a mouse brain in vivo. (A) The normocapnic TPSF with resolved static and dynamic components, determined from the autocorrelation (example at τ_s = 35 ps in inset). The static component is significant for short TOFs only, suggesting more superficial paths. For brevity, the superscript (iNIRS) was omitted in the inset. (B) The asymptotic slope of the hypercapnic dynamic TPSF is larger than the normocapnic one due to increased absorption during hypercapnia (Fig. 3).

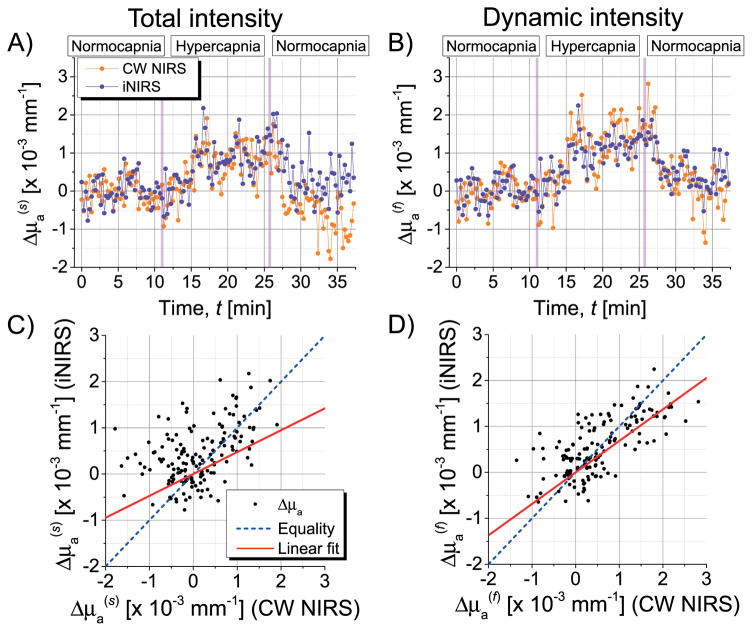
To compare conventional CW NIRS with iNIRS, unnormalized total (s) and dynamic (f) TPSFs were integrated over τ_s The resulting TOF-integrated intensities, ℐ_s(t) and ℐ_f(t) with t denoting the time at which each data set was recorded), yielded temporal optical density changes $\mathrm{\Delta }{\text{OD}}_{s,f}(t)=ln[{\mathcal{I}}_{s,f}^{(0)}]-ln[{\mathcal{I}}_{s,f}(t)]$. The baseline intensities ${\mathcal{I}}_{s,f}^{(0)}$ were computed by averaging ℐ_s(t) or ℐ_f(t) over the first ~10 minutes of the experiment. Given the optical density changes, absorption changes were determined from the modified Beer–Lambert law (MBLL): $\mathrm{\Delta }{\mu }_a^{(s,f)}(t)=\mathrm{\Delta }{\text{OD}}_{s,f}(t)/{\overline{l}}_{s,f}$, in which l̄_s,f is the average path length [18], determined as the centroid of the total (l̄_s = 31.03 mm) or dynamic (l̄_f = 31.24 mm) TPSFs. Absorption changes, Δμ_a, determined using either the MBLL (CW NIRS) or Eq. (2) (iNIRS), are compared in Fig. 3. Note that iNIRS analysis is based on the TPSF shape alone, while the MBLL uses the detected intensity. Both methods show an absorption increase linked to increases in blood oxygenation and blood volume. We hypothesize that the so-called “static” component may fluctuate slowly over minutes during the experiment, leading to changes in ℐ_s(t) which CW NIRS analysis incorrectly attributes to absorption changes [Figs. 3(A) and 3(C)]. Importantly, correlation gating isolates the dynamic intensity and improves agreement between methods [Figs. 3(B) and 3(D)].

Fig. 3.

Cross validation of absorption changes determined by iNIRS and CW NIRS in vivo. (A) The total TOF-integrated TPSF includes static signals and thus leads to some discrepancy between iNIRS and CW NIRS. This discrepancy is reduced when the static component is excluded. (B) Parametric plots of absorption changes based on (C) total and (D) dynamic intensity show that agreement is better for dynamic intensity (p < 0.001 for a paired t-test of distances from the line of equality).

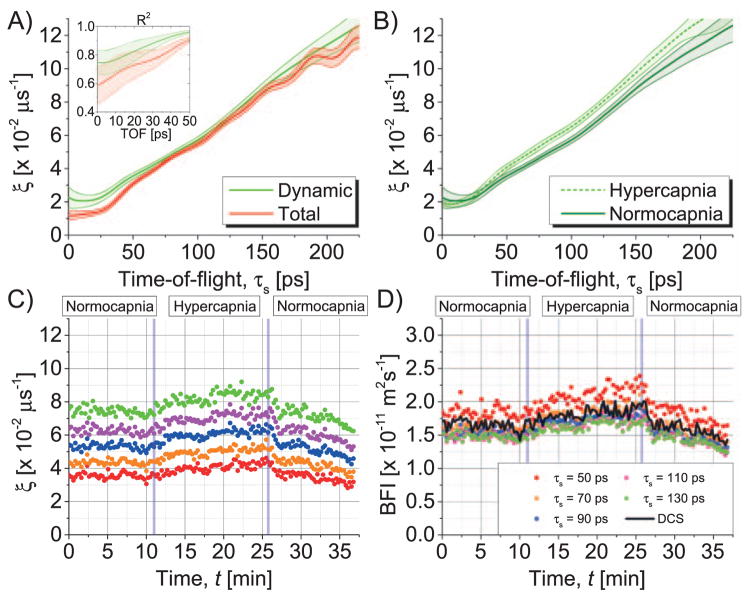
Field autocorrelation decay rates, ξ(τ_s), were used to determine BFI (αD_B) via DWS theory and then compared to DCS analysis. As shown in Fig. 4(A), averaged normocapnic decay rates (DRs) of total [ $G_1^{(\text{iNIRS})}$] and dynamic [ $G_{1,f}^{(\text{iNIRS})}$] autocorrelations increase with TOF. At short TOFs the static component reduces the DR of the total autocorrelation and worsens the R² value of the exponential fit (inset). Except for the short TOF range, where DTOF weighting within the IRF window [Eq. (1)] increases DRs, dynamic autocorrelation DRs are almost linear with TOF as predicted by DWS theory. Therefore, time courses of dynamic autocorrelation DRs [Fig. 4(C)] differ depending on TOF, but BFIs agree for sufficiently large TOF [Fig. 4(D)]. Figures 4(B) and 4(D) suggest that vasodilation during hypercapnia increases cerebral blood flow. Moreover, BFIs determined by TOF-resolved iNIRS analysis and DCS analysis agree.

Fig. 4.

BFI quantification by iNIRS in vivo. (A) Averaged normocapnic autocorrelation DRs increase with photon path length. For each TOF, R² values for exponential fits to field autocorrelations, both with and without correlation gating (“dynamic” and “total” in inset, respectively), were converted to z-scores by Fisher transformation. Paired t-tests on the z-scores revealed that correlation gating increased R² values for all TOFs (p < 0.001). (B)–(D) Averaged hypercapnic DRs are larger than their normocapnic counterparts due to the transient increase in BFI. Shaded regions in (A) and (B) denote standard deviations.

In summary, we demonstrated reflectance-mode iNIRS for continuous monitoring of a mouse brain in vivo during a hypercapnic challenge. Since iNIRS can measure the mean path length, iNIRS can quantify CW NIRS based on the MBLL. At the same time, iNIRS provides absorption and scattering coefficients based on fitting by diffusion theory and flow indices based on fitting by diffusing wave spectroscopy. Though iNIRS BFI values are in agreement with prior DCS measurements in mice [19], further cross validation is warranted. Ongoing work will optimize detection sensitivity and penetration depth for brains of larger species and compare iNIRS to conventional DCS. iNIRS integrates capabilities of NIRS and DCS into a single modality and may be a promising approach for a quantitative, noninvasive oxygenation and metabolism monitoring system in vivo.