Coil-to-coil physiological noise correlations and their impact on fMRI time-series SNR

Abstract

Purpose

Physiological nuisance fluctuations (“physiological noise”) are a major contribution to the time-series Signal to Noise Ratio (tSNR) of functional imaging. While thermal noise correlations between array coil elements have a well-characterized effect on the image Signal to Noise Ratio (SNR₀), the element-to-element covariance matrix of the time-series fluctuations has not yet been analyzed. We examine this effect with a goal of ultimately improving the combination of multichannel array data.

Theory and Methods

We extend the theoretical relationship between tSNR and SNR₀ to include a time-series noise covariance matrix Ψ_t, distinct from the thermal noise covariance matrix Ψ_0, and compare its structure to Ψ₀ and the signal coupling matrix SS^H formed from the signal intensity vectors S.

Results

Inclusion of the measured time-series noise covariance matrix into the model relating tSNR and SNR₀ improves the fit of experimental multichannel data and is shown to be distinct from Ψ₀ or SS^H.

Conclusion

Time-series noise covariances in array coils are found to differ from Ψ₀ and more surprisingly, from the signal coupling matrix SS^H. Correct characterization of the time-series noise has implications for the analysis of time-series data and for improving the coil element combination process.

Introduction

As the BOLD contrast increases with magnetic field strength, the sensitivity of functional MRI (fMRI) is increasingly restricted by signal fluctuations due to physiological processes, which modulate the measured brain signals. These fluctuations can include cardiac and respiratory pulsations, as well as spontaneous hemodynamic fluctuations in blood volume and oxygenation level. The variance of the physiological signal modulations has been seen to scale with the amplitude of the signal intensity in gradient echo, echo planar imaging (EPI) fMRI time-series (1), an effect which has been verified for various acquisition parameters and field strengths (2). These prior studies demonstrated that physiological noise fluctuations dominate and limit the time-series signal-to-noise ratio (tSNR) when the individual images have high image signal-to noise ratio (SNR₀). Thus, physiological noise is especially limiting at higher field strengths [7 Tesla (7T)] and at lower spatial resolutions. The tSNR improvements in BOLD imaging with field strength or with improved detection coils are dependent on the balance between physiological and thermal noise. This ratio is itself dependent on the image acquisition parameters, such as flip angle, echo time (TE), (1,2), spatial resolution (2), and parallel imaging acceleration factor (3) since these parameters determine signal levels and thus the physiological noise variance.

The measurement of the thermal noise sources present in MR images has been well characterized (4,5) and the noise correlations between thermal noise in the individual receiver channels of a multi-coil image are well characterized by the thermal noise covariance matrix, Ψ₀. The thermal noise covariance matrix represents the channel-to-channel coupling of thermal sample noise and is now commonly included in the final array coil reconstructions to optimize SNR₀ in the final channel-combined image. Conversely, ignoring thermal noise correlations in the array combination process can lead to reduced SNR₀.

Previous work (3) has also characterized the temporal fluctuations, caused by physiological processes, in a voxel or region of interest (ROI) in the array-element combined image or in images from a single-channel coil, but does not address the potential case where channel-to-channel covariances in the time-series fluctuations differ from those in the image noise.

In this work, therefore, we analyze the covariance of the time-series fluctuations between any two channels, to form the time-series noise covariance matrix, Ψ_t. In the case of phantom data with no physiological noise, this matrix is expected to be identical to the thermal noise covariance matrix, Ψ₀. But we note that no studies, that we know of, have compared the time-series and individual image covariance matrices (Ψ_t and Ψ₀). Therefore, in this work we additionally compare these two matrices and find them to differ. We then extend the Krueger-Glover model of physiological noise (1) to include these covariance matrices. We show that a non-zero matrix can be interpreted as a component of physiological noise that does not scale with signal strength but is unaccounted for, in the image noise. We also show that this type of noise source leads to a modification in the Krueger-Glover relationship between tSNR and SNR₀ (1) and thus has consequences for the interpretation of where a given acquisition stands in the trade-off between thermal and physiological noise sources. The presence of this additional physiological noise source also has implications for how array channels should be combined for fMRI. Finally, we test the proposed model with non-accelerated EPI time-series at 3T and 7T in Gray Matter (GM), White Matter (WM) and Cerebrospinal Fluid (CSF) for a range of imaging coil arrays, in-plane spatial resolutions, and echo times.

Theory

Because thermal noise and physiological noise sources are statistically independent, the total noise standard deviation (σ_t) for each voxel in the fMRI time-series is a combination of the Gaussian-distributed thermal image noise standard deviation (σ₀), which is MR signal independent, and the physiological noise standard deviation (σ_p) (i.e. σ_p includes hemodynamic induced fluctuations, cardiac, respiratory, and system instabilities). The above relationship is given by,

$${\sigma }_t^2={\sigma }_0^2+{\sigma }_p^2$$ [1]

Krueger and Glover have examined the relationship between the fMRI tSNR and SNR₀ in gradient-echo EPI acquisitions when a single-channel coil was used and introduced a model where the physiological noise standard deviation (σ_p) is proportional to the amplitude of the MR signal (S) σ_P = λS, where λ is the proportionality constant. In other words, as the signal level increases, the physiological noise becomes dominant. Time-series SNR and SNR₀ are defined for a voxel in the time-series as:

$${\mathit{SNR}}_0=\frac{\overline{S}}{{\sigma }_0},\text{and}$$ [2]

$$\mathit{tSNR}=\frac{\overline{S}}{\sqrt{{\sigma }_0^2+{\sigma }_p^2}}$$ [3]

where S̄ is the mean MR signal intensity across the time-series. This leads to the relationship between tSNR and SNR₀ :

$$\mathit{tSNR}=\frac{{\mathit{SNR}}_0}{\sqrt{1+{\lambda }^2·{\mathit{SNR}}_0^2}}$$ [4]

In this case, for large SNR₀, tSNR is asymptotically limited to 1/λ. In the current study, we will refer to Eq. 4 as the KG-model (Krueger-Glover model). The constant λ has an echo time (TE) dependence, as previously reported (1). Breaking σ_p into a BOLD and non-BOLD components, ${\sigma }_p^2={\sigma }_B^2+{\sigma }_{NB}^2$ and using the differing TE dependence of these two contrasts, ${\sigma }_B=c_1·TE·S·\mathrm{\Delta }{R}_2^{\ast }$ and σ_NB = c₂·S, then

$${\lambda }^2=c_1^2·\mathrm{\Delta }{R}_2^{\ast 2}·{TE}^2+c_2^2,$$ [5]

where c₁ and c₂ are constants determining the relative contributions of the two components.

The relationship in Eq. 4 assumes that the SNR₀ is measured in a way that renders it comparable to the tSNR, as described by Kellman & McVeigh (4,5). This calculation requires (a) access to the complex-valued, uncombined image data from the individual receivers before their combination to form the final image, (b) measurement of the thermal noise covariance matrix describing how the noise is coupled among the receivers and, of course, (c) knowledge of how the individual receivers’ data are combined to form the final image. Additionally, if the image SNR is low, the altered noise distribution of the magnitude-valued data comprising the final image must be accounted for. If this procedure is not followed, the relationship in Eq. 4 will be altered. The comparison between tSNR and SNR₀ for array coils has previously been performed following this procedure (3).

In an array coil, the correlations between the channels must be considered for each noise source (if they differ) as well as the complex-valued weights used to combine the multi-channel data. This is commonly done for the thermal noise component of the array coils (7), but the potentially different covariance matrix of the physiological noise has been previously overlooked. Here we extend the existing treatment of the channel-to-channel noise covariances to include the physiological sources as well as the thermal noise.

Thermal image noise in the array components is described by the thermal noise covariance matrix Ψ₀. It is typically measured by digitizing the thermal noise present when no radiofrequency (RF) excitation is given (S=0). The covariance matrix Ψ₀ is then used in the calculation of the complex-valued weights used to combine the coil data into a single image with maximum SNR₀ (7). Forming a vector, w, of these complex-valued weights for each pixel, the thermal SNR (SNR₀) in a pixel of the final image is given by (7, 8):

$${\mathit{SNR}}_0=\frac{\mid w^{H}S\mid }{\sqrt{w^H{\mathrm{\Psi }}_{0}w}}$$ [6]

where S is the vector of mean signals across all channels for that pixel. Both S and w are therefore vectors of length N_coils (number of coils) and S^H as its Hermitian transpose of S.

The tSNR of a particular voxel in the time-series, formed from the combined channels, is expected to take a similar form:

$$\mathit{tSNR}=\frac{\mid w^{H}S\mid }{\sqrt{w^H{\mathrm{\Psi }}_{t}w}}$$ [7]

where Ψ_t is the total channel noise covariance matrix for the time-series fluctuations from physiological and thermal sources. Thus each element (i, j) in the time-series noise covariance matrix Ψ_t corresponds to the covariance measured between coils i and j at a given pixel, and is estimated via the unbiased sample covariance estimate:

$${\mathrm{\Psi }}_t^{i,j}=\frac{1}{N_{tp}-1}\left(S_i^H{S}_j\right)=\frac{1}{N_{tp}-1}\left({\overline{S}}_i^{\ast }{\overline{S}}_j{N}_{tp}\right),$$ [8]

where S_i is a N_tp×1 vector of time samples for coil i of the measured resting-state fMRI signal, and $\overline{S_i}$ is the scalar-valued mean signal across time for coil i. N_tp represents the number of time-points acquired in the time-series data set.

In analogy with the Krueger-Glover model, which separates the total time-series variance ( ${\sigma }_t^2$) into two components (image noise variance, ${\sigma }_0^2$ and physiological noise variance, ${\sigma }_P^2$), we analyze Ψ_t as a sum of Ψ₀ (thermal noise covariance matrix) and a physiological noise covariance matrix, Ψ_p, across channels. Assuming that thermal noise and physiological noise are statistically independent, the total noise covariance matrix is given by,

$${\mathrm{\Psi }}_t={\mathrm{\Psi }}_0+{\mathrm{\Psi }}_p$$ [9]

The tSNR can be expressed in terms of the SNR₀, as

$$\mathit{tSNR}=\frac{\mid w^{H}S\mid }{\sqrt{w^H{\mathrm{\Psi }}_{0}w+w^H{\mathrm{\Psi }}_{p}w}}=\frac{{\mathit{SNR}}_0}{\sqrt{1+\frac{w^H{\mathrm{\Psi }}_{p}w}{w^H{\mathrm{\Psi }}_{0}w}}},$$ [10]

In the KG-model, the physiological noise standard deviation is proportional to the amplitude of the MR signal, σ_P = λS. This implies that, given the value of λ, the physiological noise variance can be predicted for a given tissue class from the signal level alone. In order for Eq. 10 to reduce to the KG-model for the multi-channel case, the Ψ_p must be proportional to an outer product of the mean signal vectors, as is shown in the following. Explicitly, it must be the case that Ψ_p = λ²SS^H. Each entry (i, j) in the N_coils × N_coils outer-product matrix SS^H at a particular voxel captures the product of the mean signal levels between coils i and j at that voxel, thus SS^H represents the signal coupling between the coil channels. If this relationship holds, then w^HΨ_pw = λ²w²SS^H and Eq. 10 becomes,

$$\mathit{tSNR}=\frac{{\mathit{SNR}}_0}{\sqrt{1+\frac{{\lambda }^2{\mid w^{H}S\mid }^2}{w^H{\mathrm{\Psi }}_{0}w}}}=\frac{{\mathit{SNR}}_0}{\sqrt{1+{\lambda }^2{\mathit{SNR}}_0^2}},$$ [11]

Eq. 11 corresponds to the KG-model of Eq. 4.

If Ψ_p = λ²SS^H then the standard KG-model applies to multi-channel data, otherwise the physiological noise covariance may be expressed as

$${\mathrm{\Psi }}_p={\lambda }^{2}S{S}^H+C_{\alpha }$$ [12]

where C_α is a symmetric matrix (because Ψ_p and SS^H are both symmetric by definition). Then Eq. 10 becomes:

$$\mathit{tSNR}=\frac{{\mathit{SNR}}_0}{\sqrt{1+{\lambda }^2{\mathit{SNR}}_0^2+\frac{w^H{C}_{\alpha }w}{w^H{\mathrm{\Psi }}_{0}w}}}=\frac{{\mathit{SNR}}_0}{\sqrt{1+\alpha +{\lambda }^2{\mathit{SNR}}_0^2}}$$ [13]

Here we define the new term as alpha, α:

$$\alpha =\sqrt{\frac{w^H{C}_{\alpha }w}{w^H{\mathrm{\Psi }}_{0}w}}$$ [14]

Based on the above theory, a more general model is introduced, denoted as Physiological Noise Covariance model (PNC-model), for acquisitions performed with multi-channel coils. Thus, Eq. 13 corresponds to the PNC-model.

Methods

Data Acquisition

Data acquisition was performed on a Siemens 7T whole-body scanner equipped with a head gradient insert (AC84, 80 mT/m maximum gradient strength and maximum slew rate of 400 T/m/s) and a Siemens 3T MAGNETOM Trio, a Tim System, (Siemens Healthcare, Erlangen, Germany). On the 7T system, data were acquired using a custom made 32-channel (32Ch) receive-only array coil (similar layout to the 3T product 32Ch array coil) (9). On the 3T system, data were acquired using three head coils (Siemens Healthcare, Erlangen, Germany); 1Ch birdcage volume coil, 12Ch array and 32Ch array coils with the system’s body coil for transmission. A home-built transmit-only birdcage coil was used at 7T.

Data from the same four healthy volunteers were acquired on the 3T and 7T scanners, across all RF coils and spatial resolutions. Two additional subjects were imaged on both systems using a multi-echo EPI sequence to examine the TE dependence of the model parameters. Written informed consent was obtained from all the subjects using an experimental protocol approved by institutional review board. To control subjects’ movement, foam pads were used for head immobilization. All subjects were asked to relax while in the scanner with their eyes closed. Automatic slice prescription, based on alignment of localizer scans to a multi-subject atlas, was used in the 3T acquisitions to achieve a consistent slice prescription across different RF coils at the 3T (10). Agar gel phantom data also acquired using the same protocols as the human data.

To evaluate the signal and noise characteristics of the single-echo EPI acquisitions using multi-channel coils, resting-state time-series were collected using a single-shot gradient echo EPI sequence. Prior to each scan, two “dummy” scans were acquired and discarded to allow longitudinal magnetization to reach equilibrium. Data from each coil and at each field strength were collected at six different in-plane resolutions: 1×1 mm², 1.5×1.5 mm², 2×2 mm², 3×3 mm², 4×4 mm² and 5×5 mm², using TR/flip = 5400 ms/90°, 60 time-points and 3 mm thick slices with orientation parallel to the anterior commissure-posterior commissure line. For the 7T data an additional high spatial resolution (1 mm isotropic) time-series was acquired to sample data at a resolution where thermal noise dominates. The TE was set to values commonly used to optimize BOLD contrast at each field strength: 30 ms and 20 ms at 3T and 7T, respectively. Acquisition protocols were optimized for each resolution and field strength (see Supporting Table S1 and Supporting Table S2). No parallel imaging acceleration was used (see Discussion).

Multi-echo EPI acquisitions were performed on both 3T and 7T at three different resolutions of 2 mm, 3 mm and 4 mm isotropic with TR=3 s, 10 slices. Multiple runs were acquired to obtain time-series with echo times in the range between 10 ms and 150 ms with increments of 5 ms. For all EPI acquisitions, images with no RF excitation were also acquired to determine the thermal image noise (σ₀ and Ψ₀).

Data Reconstruction

For all the above experiments, k-space data were saved for offline reconstructions, which was performed with custom software written in Matlab, (MathWorks Inc., Natick, MA, USA), to account for all image reconstruction steps that might affect the final image SNR, as described previously (3).

The data from the multiple receive coils were combined using standard procedures such as the root Sum-of-Squares (rSoS) method which uses weights derived from the measured intensity level itself (i.e. the N_chan×1 vector S̄ is used as the weights). Additional weight vector choices were assessed such as the ‘birdcage’ combination where the complex-valued weight vector, w, is the signal values averaged over a small ROI in the center of the FOV and is used as the weighting vector for all pixels. This combination causes phase cancelation between neighboring elements, which reduces SNR (especially for voxels at the periphery of the brain), but mimics the flat spatial profile achieved by a volume coil.

tSNR and SNR₀ Calculation

To ensure a stable EPI time-series, subject head movement and linear trends were removed from the data prior to data analysis. Time-course SNR (tSNR) maps were then generated from the mean pixel value across time-points divided by their temporal standard deviation. SNR₀ was calculated using the method of Kellman and McVeigh (4,5), which includes several correction factors to allow direct comparison between SNR₀ and tSNR when multi-channel arrays are used. Our implementation of this approach to quantifying SNR₀ was previously described in detail (3) and a summary is presented here for completeness. In particular, to generate the SNR₀ maps in absolute SNR units, this method utilizes four correction factors to account for the (a) effective noise bandwidth, (b) the number of samples contributing to each image pixel during the Fourier transform (accounting for any oversampling in the readout direction), (c) the signal-level-dependent magnitude bias correction provided by the non-central Chi distribution (which is the generalization of the Rician distribution (11) to multiple-channel array coil data combined via root-sum-of-squares (6)) and (d) the complex-valued thermal noise contribution to the measurement. The last correction arises from the fact that thermal noise is complex-valued; the sample noise covariance matrix must be normalized by $\sqrt{2}$ since the standard observation model assumes that the signal is real-valued while the noise is complex-valued with independent and identically distributed real and imaginary parts (i.e., drawn from a zero-mean Gaussian distribution with equal variances) (4,5).

The standard deviation of the thermal noise (σ₀) and the thermal noise covariance matrix (Ψ₀) estimated from a pure noise measurement with no RF excitation. Note that here this term is calculated from raw complex-valued noise data prior to any Fourier transformation.

Data Processing

Measurements of tSNR and SNR₀ were evaluated in ROIs of cortical GM, WM and ventricular CSF and values averaged across subjects. To accurately account for voxels only in the specific brain components, segmented masks of GM, WM and CSF, were generated using the FSL FAST segmentation tool (12) from the high-resolution anatomical data (1mm isotropic MPRAGE). Subsequently the spatial registration and transformations of these segmentations were computed and applied from the anatomical space to the EPI space for each subject and each spatial resolution. This registration and mapping was performed using the FSL FLIRT tool with a linear 12 parameter model (13). The probability masks for each tissue class were next manually edited by removing obviously misclassified voxels and thresholding out voxels with lower probabilities of belonging to a particular tissue class (t<0.3). These masks were next applied to the tSNR and SNR₀ maps to determine GM, WM and CSF averages for the subject. Measurements were performed on each slice, each subject and each resolution. The final SNR values were averaged over all subjects.

Data Analysis

The relationship between tSNR and SNR₀ for all brain classes was examined by fitting to the data the two different models (KG-model and PNC-model) using a Matlab built-in non-linear least squares algorithm.

By plotting tSNR as a function of SNR₀ for different resolutions (Figs. 1 and 2), the parameter α was estimated from the result of fitting the PNC-model to the data. The parameter λ was similarly estimated for the KG-model for comparison purposes. Both parameters were assumed to be constant for each tissue class (GM, WM, and CSF); therefore, a single value was estimated from data pooled across each tissue mask. The relative goodness-of-fit as measured by Akaike Information Criteria (AIC) (14). AIC is a goodness-of-fit measure for comparing the goodness-of-fit to the data of two or more statistical models with potentially different numbers of parameters. AIC consists of a two-term criterion: a goodness-of-fit term and a model complexity term that penalizes potential over-fitting.

Figure 1.

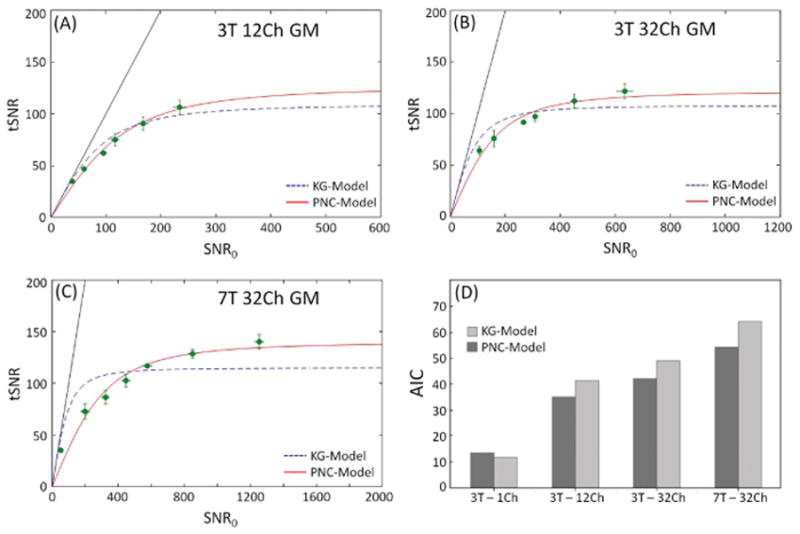
Time-series SNR (tSNR) as a function of SNR₀ for 3T 12Ch (A) and 32Ch (B) coils, (C) 7T 32Ch array using both models. The dotted line is the fit to the KG-model and solid line is the PNC-model. Each circle corresponds to one of the six spatial resolutions examined, from left to right 1×1, 1.5×1.5, 2×2, 3×3, 4×4, 5×5 mm² in-plane and a fixed slice thickness of 3 mm. Measurements derived from areas of cortical gray matter ROIs and averaged over all subjects. Six resolutions were used at 3T, while seven resolutions were used at 7T. In (D) the AIC of the fit to each model is shown. All data reconstructed using the rSoS combination method.

Figure 2.

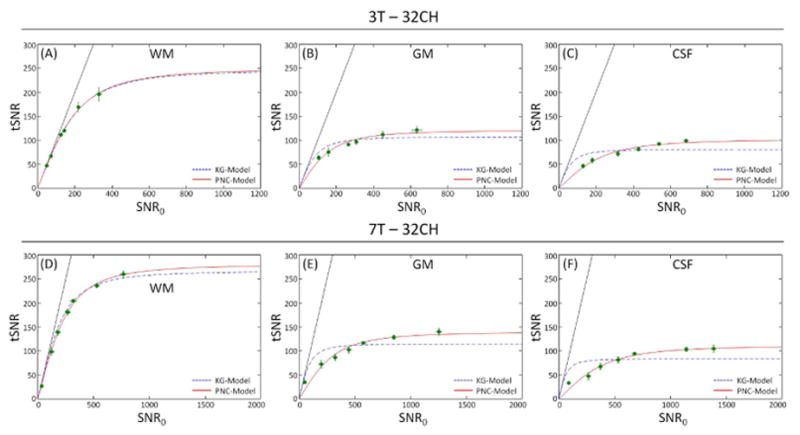
SNR in fMRI time-series (tSNR) as a function of image SNR (SNR₀) for different tissue classes (WM, GM and CSF) for the 3T (A, B, C) and 7T (D, E, F) 32Ch array data when image SNR was modulated with voxel size. Each point represents the average and SD error bars over all subjects, (because of their small size, some of the error bars are contained within the symbols). The dotted line is the fit to the KG-model (Eq. 4) and solid line corresponds to the PNC-model (Eq. 13). All data reconstructed using the rSoS combination method.

To assess the dependence of α on channel count, we performed an additional analysis on our 32Ch data. In this specific analysis we estimated α directly (using Eq. 14) using an estimate of C_α calculated from Ψ_P and S and using the relationship in Eq. 12 and the weight vectors w generated by either the root-sum-of-squares or birdcage-like combination method, but choosing distinct, random subsets of coils ranging from 2 to 30 coil elements. In this analysis, the weights of the unused coils are simply set to zero. We refer to the number of elements used in this analysis as N_used. We limited the analysis to 100 combinations of element choices for each N_used value tested. To distinguish the value of α obtained from the model fit from that computed directly from the covariance matrix, we refer to the value estimated directly from the measured covariance matrices as α̂. For each subset we computed α̂ using Eq. 14 on a pixel-wise basis, and then pooled across all subsets and all channel counts to calculate a two-dimensional histogram of the number of voxels found with a given α̂ value and as a function of the total number of channels in each subset.

Results

Figure 1 shows tSNR as a function of SNR₀ for the single-echo EPI data for the 3T 12Ch and 32Ch coil, 7T 32Ch array, as well as the AIC to estimate the goodness of fit of each model to the data. Each data point in the tSNR vs. SNR₀ plot represents one of the six spatial resolutions studied and corresponds to the SNR value averaged across the cortical gray matter ROI and over all subjects. The dotted line is the fit to the KG-model (Eq. 4) and solid line is the PNC-model (Eq. 14). The relative goodness-of-fit between the competing models was characterized using the AIC for each model and each coil configuration (Fig 1D). The 1Ch (i.e. volume coil) and 12Ch at 3T are adequately parameterized by the KG-model, although the 12Ch shows a higher deviation. For example, for the 1ch coil AIC was 11.8 and 13.6 for the KG- and PNC-models, respectively. For the 12Ch the KG-model and PNG-model gave 41.5 and 35.1, respectively, for 3T data. The 32Ch coils showed higher deviation from the KG-model and an improved fit to the PNC-model. The 32Ch coil AIC was 49.1 and 42.1 for KG- and PNC-model, respectively, at 3T and 64.3 and 54.3 at 7T.

Figure 2 shows the relationship between tSNR and SNR₀ for the different tissue classes (WM, GM and CSF) for the 32Ch array combined with rSoS for 3T and 7T. At each field strength, data from white matter ROIs is well parameterized by the KG-model, while the cortical gray matter and CSF exhibit a greater deviation from this model and better agreement with the proposed PNC-model. From the fit data, we also estimated the PNC-model parameter α, which also serves as a metric of the appropriateness of the KG-model (α=0 for the KG-model). The minimum value of α is observed for the 3T WM data (α=0.16) and the highest value of α is found in CSF at 7T (α =4.16) where we expect the largest physiological noise fluctuations. The α values observed for WM, GM and CSF were, respectively, 0.16 ± 0.10, 1.26 ± 0.54, 2.50 ± 0.68 at 3T and 0.52 ± 0.15, 2.39 ± 0.64, 4.16 ± 1.05 at 7T (Figure 3). This result suggests that the need for the extra model term is dependent on the tissue class, with tissues having strong physiological noise contributions requiring a larger modification to the KG-model.

Figure 3.

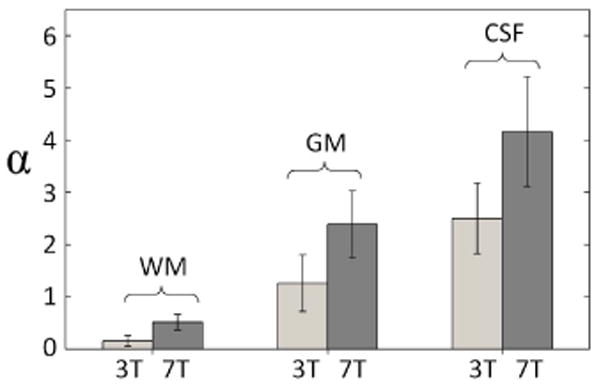
Bar graph of the estimated α values for each tissue class from the data of Figure 2, with gray and black bars corresponding to 3T and 7T respectively.

Figure 4 shows phantom data at 3T from 12Ch and 32Ch coils for different in-plane resolutions, reconstructed with the conventional rSoS method. Each point represents the average measures over large ROIs. Again the dotted and solid lines represent the KG- and PNC-models respectively. The phantom measurements suggest that the two models have almost identical fitting and the α values are very close to zero. To investigate the effect of the reconstruction method on the model fit, phantom data were also reconstructed using the ‘birdcage’ combination method for both the 32Ch and 12Ch coils (data not shown). The results were very similar to the conventional rSoS reconstruction method, with α values very close to zero.

Figure 4.

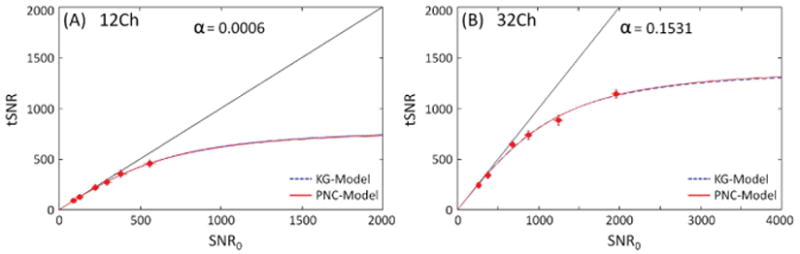
Relationship of tSNR as a function of SNR₀ for phantom data at 3T for 12Ch (A) and 32Ch (B) arrays. Phantom data reconstructed using the conventional rSoS method.

Figure 5 shows the different α obtained from GM regions for three different array channel combination methods of the 7T 32Ch array data. Figure 5A shows a single-channel from the 32Ch array (all weights in w equal to zero except one). Fig. 5B shows the ‘birdcage’ combination where a single set of weights is determined in the form of the complex-valued weight vector is the signal value taken in the center of the brain for each channel, and Fig. 5C shows the rSoS combination. Similarly to the other graphs, dotted and solid lines correspond to KG- and PNC-models, respectively. To illustrate the image appearance for the different coil combination methods, thumbnails with representative images are shown within each graph panel. Single-channel data show a good correspondence to the KG-model while this correspondence is not as good for the ‘birdcage’ combination and even worse for the 32Ch rSoS SNR combination data, where the PNC-model shows a substantially better fit to the data. Correspondingly, the parameter α increases as we move from single-channel data to the 32Ch with rSoS SNR combination weights. This result suggests that the additional parameter in the proposed model is dependent on the weights chosen to combine the data (as well as the number of channels used).

Figure 5.

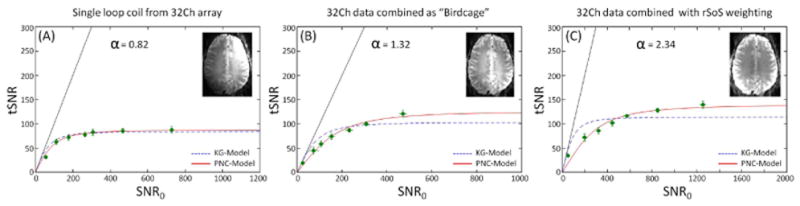
Three different array channel combination methods for 7T gray matter exhibiting the effect of the combination weights to the relationship of tSNR vs SNR₀. From left to right, (A) single loop data from the 32Ch array, (B) data were generated by combining the individual coil elements with a birdcage combination and (C) using the rSoS combination method. Estimated α values are given on each graph. Similarly to other figures, SNR₀ was modulated by varying the voxel size and the two models are shown in dotted (KG-model) and solid (PNC-model) lines. Thumbnails with representative images of each combination are shown on each graph.

In Figure 6, we compare 3T GM single-channel volume coil acquired data (Fig. 6A) to the ‘birdcage’ 32Ch combination method (Fig. 6B). Again dotted and solid lines correspond to KG- and PNC-models, respectively, and the image appearance for the different coils and their combination methods illustrated as thumbnails within each graph panel. Although both datasets correspond to the birdcage coil (one is an actual birdcage coil and the other is synthetically obtained), the α value is different. For the single-channel volume coil (Fig. 6A), α is almost zero (α = 0.26) and the KG-model fits better to the data as shown in the AIC test (Fig. 1D). However, for the synthetically obtained birdcage data (Fig. 6B) the PNC-model best characterizes the data and α = 0.69. The 32Ch coil data showed higher deviation from the KG-model and an improved fit to the PNC-model (α = 1.26). This shows that there is a physiological noise cancellation when data combined in the ‘birdcage’ mode compared to the 32Ch with rSoS SNR combination weights, but still the synthetic birdcage combination has a higher α value than the data acquired with the real birdcage volume coil, which has no channels to form a physiological noise correlation between.

Figure 6.

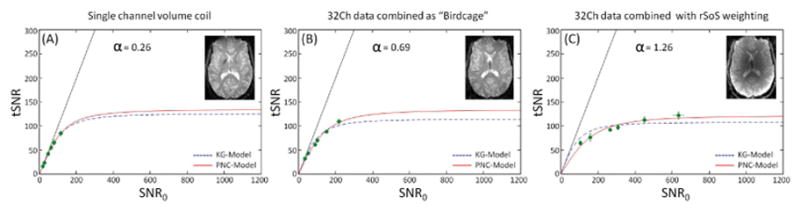
3T array channel combination methods compared to true volume coil acquisition. From left to right, (A) single channel birdcage coil, (B) data were generated by combining the individual coil elements with a birdcage combination and (C) using the rSoS combination method. Estimated α values are given on each graph. Similarly to other figures, the two models are shown in dotted (KG-model) and solid (PNC-model) lines and measurements performed in ROIs of gray matter. Thumbnails with representative images of each coil and coil combination are shown on each graph.

In Figure 7, the model parameters λ and α are shown as a function of TE at 3T in regions of gray matter. A clear dependence on the TE is shown for λ (as also demonstrated by Eq. 5). For higher TE, λ increases monotonically, however the value of α parameter remained constant as TE increased. This behavior suggests that the additional model parameter is not primarily driven by ‘BOLD-like’ physiological noise in the brain.

Figure 7.

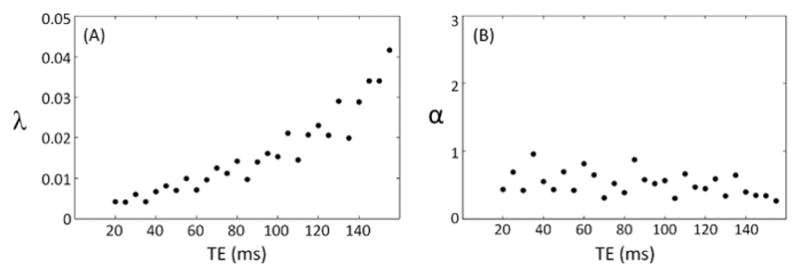
Dependence of the model parameters λ and α on TE at 3T 32Ch array in regions of gray matter.

Figure 8 shows the computed matrices SS^H, Ψ_p, and Ψ₀ for three different GM voxels acquired with the 3T 32Ch array. Firstly, the physiological noise covariance matrix, Ψ_p, is distinctly different in structure to the thermal noise covariance matrix, Ψ₀. While the SS^H and Ψ_p are similar in some ways for the second and third voxel, they are distinctly different for the first. A sampling of many voxels showed a range of similarity in the structure of the SS^H and Ψ_p matrix. Since α is zero (and thus the KG-model sufficient) only when SS^H and Ψ_p are identical to a scale factor, this suggests that α takes on a range of values for gray matter voxels.

Figure 8.

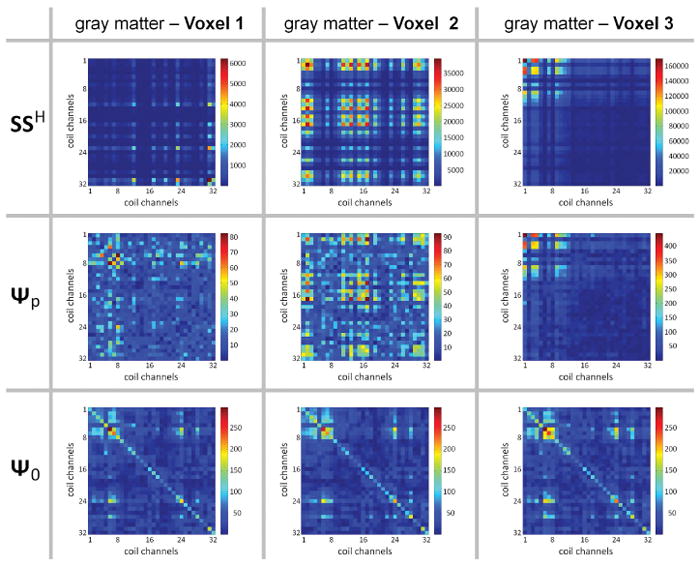
Varying levels of agreement between the signal and noise statistics. Statistical matrices are shown across coil channels taken from a single representative subject (1×1×3 mm³ images, 3T, 32Ch array coil). (Top row) Average (over the time-series) of the signal level matrix SS^H. (Middle row) Physiological noise covariance matrix Ψ_p. (Bottom row) Thermal noise covariance matrix Ψ₀. Each column shows the matrixes from a single voxel within the cortical gray matter mask. For Voxel 1, the structure of the SS^H matrix is substantially different from the Ψ_p matrix, whereas for Voxel 2 there is some common structure between these two matrices, while for Voxel 3 the two matrices appear to be identical up to a global scaling. Note that the Ψ₀ matrix is virtually identical across the voxel positions, and is distinct from both the SS^H and Ψ_p matrices.

Figure 9 shows the histogram of estimated α values (α̂) as a function of the number of coil channels included in the combined data. Gray matter pixels are analyzed from the 1×1×3 mm³ 3T images. Fig. 9A shows the birdcage-like array combination and Fig. 9B shows the root-sum-of-squares combination. The α̂ values generally monotonically increase with coil count, reaching an approximate asymptote after the number of included channels reaches approximately 25. The observed value of α̂ is about 0.6–1.2 for the birdcage combination and about 1–2 for the root-sum-of-squares combination, agreeing with the values of α calculated from the above tSNR vs. SNR₀ plots.

Figure 9.

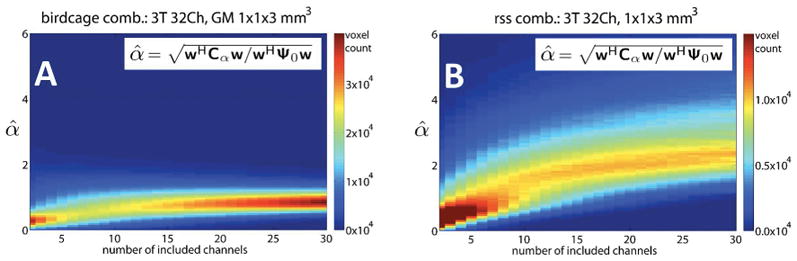
Dependence of α̂ on the total number of coil channels included in the combined pixel. Shown are 2D histograms depicting the value of α̂ as a function of the number of coil channels in the combined data from a single representative subject (1×1×3 mm³ images, 3T, 32Ch array coil). Combinations of channels were formed using both: (A) global weights from a birdcage-like combination or (B) weights for the rSoS of those channels. The color scale represents the number of EPI voxels falling within a particular bin. The bin is determined by the number of channels included in the array combination (horizontal axis) and the observed α̂ value (vertical axis). For both combination methods, the value of α̂ increases nonlinearly as the number of channels increases, converging to a value in the range of 2–3 for the rSoS SNR combination and 0.6–1.2 for the birdcage combination.

Discussion

Understanding the relationship between tSNR and SNR₀ is critical since tSNR is a principle determinant of the sensitivity of the fMRI experiments to BOLD contrast (in addition to TE and $\mathrm{\Delta }{R}_2^{\ast }/R_2^{\ast }$) and SNR₀ is the readily controlled metric (via resolution, flip angle, coil choice or field strength). Thus, the tSNR vs. SNR₀ relationship guides our decisions concerning the many trade-offs between acquisition parameters and BOLD sensitivity. In this work we investigate the need for a modified model describing the behavior of physiological noise in the fMRI time-series in multi-channel acquisitions and assess the new model’s dependence on acquisition parameters, tissue class, coil-combination methods and as a function of field strength and TE.

We provide evidence associating the new model parameter with the channel-to-channel noise correlations of the physiological fluctuations. We suggest that the time-series noise covariance matrix describing these correlations might be different from both the matrix describing the thermal noise covariance and the signal level matrix. We show that when the physiological noise covariance matrix is simply proportional to the signal level matrix, then the proposed model reduces to KG-model. But if the correlations of the physiological noise sources among the array elements are more general (not proportional to the signal level matrix) then the model is extended to include an additional model parameter (α, in this case), as shown with both experimental evidence and a mathematical derivation. This parameter corresponds to the influence of the type of physiological fluctuations not distributed among the array elements in the same way as the signal. The extended model (PNC-model) can be used to accurately characterize the tSNR vs. SNR₀ relationship.

The value of the new parameter (α) is solely determined by the deviation of the physiological noise covariance matrix from the signal level matrix (Eq. 14) and can be viewed as a physiological noise source, which is independent of signal strength, but is a “fictitious” noise source since it actually arises from any differences in structure between the physiological noise covariance matrix and the signal matrix, i.e., it embodies differences in signal coupling and noise coupling across the array channels.

However, the physical meaning of this noise component is not yet clear. Why is the covariance matrix between the channels formed from the time-series fluctuations different from the signal intensity matrix and the thermal noise covariance matrix; i.e. why does the non-thermal part of time-series noise covariance not simply follow the signal level relationship between the coils? There are a few mechanisms where the physiological fluctuations covariance matrix Ψ_p is not expected to act like the signal coupling matrix SS^H, and this can contribute to a physical explanation of the extended model.

Under the KG-model interpretation, the physiological noise is not a true noise source per se but rather it is a modulation of the signal intensity by uncontrolled forces (such as blood-volume fluctuations) which are not accounted for but are sufficiently complex to “look” like noise. The action of the modulation experienced by a voxel (usually dephasing) happens inside that voxel. Namely its signal is modulated by random or sufficiently complex biological fluctuations. Some examples are (a) fluctuations in deoxyhemoglobin that modulate signal in the voxel through the BOLD effect, or (b) fluctuations due to pulsatile flow (for a voxel with a partial volume of CSF). In these two examples, both the source of the fluctuations and their action (dephasing) is local to the voxel—the local signal is modulated by a local physiological effect. Additionally, the source of the modulation can be coherent across several voxels. The physiological mechanism could be a global physiological effect, such as blood CO₂ changes due to variations in breathing, or from the global susceptibility gradients produced by lung inflation. In these cases, the effect is not spatially localized (e.g., the susceptibility effect of the lungs dephases signal in the whole lower-half of the brain). However, the effect on the signal is still local: dephasing across the voxel due to the respiratory-dependent field gradient. In the case of global physiological effects, the only difference compared to the local physiological effects is that multiple voxels are affected in nearly the same way, but in both cases these physiological effects still cause a modulation of the signal as described by the KG-model. However, the signal level and the noise variance measured at a single voxel by two distinct coil elements are affected differently such that the noise is not described by KG-model.

One possible noise source that could not be described by the KG-model is when the signal intensity changes are generated from modulation upstream in the RF detection chain, rather than at the location of the voxel. Consider, for example, that a subject’s heart rate can be seen in an inductance measurement of a surface coil placed on the brain. This is most likely due to blood pressure/volume changes in the scalp changing over the cardiac cycle. Because blood is highly conductive, a cerebral blood volume (CBV) fluctuation is like moving a conductive plane toward and away from the coil during the cardiac cycle, an effect that raises or lowers the inductance of the coil. But, the coil’s inductance is also a determinant of its signal detection efficiency. Thus, this source of physiological signal modulation occurs not through dephasing of signal at the pixel level but by modulating the gain of the receive chain (at the coil/detection level). The coupling of the CBV fluctuation to the inductance of the coil element could cause noise modulations that affect the signal levels and noise variances measured at a single voxel by two distinct coils differently.

Another example of physiological fluctuations “happening” at the detector level is from head motion within the array. If the head moves between two image volumes, motion correction can bring the volumes into near perfect alignment (under ideal circumstances), but as the head moves through the spatial gradient of detector sensitivity profiles, it incurs an intensity modulation. The aligned image time-series will have increased temporal variance from this process. Unlike the KG-model, where a pixel’s physiological noise standard deviation is described solely by its tissue class and signal level, this is no longer the case for multi-channel arrays. Consider, for example, two gray matter pixels of the same intensity one at the vertex and one in the left temporal lobe. If the head moves left to right, the pixel in the left temporal lobe will experience a sizable intensity change as it moves in the direction of the coil sensitivity profile gradient. The voxel at the vertex, however, moves along an isocontour of the coil sensitivity profile and experiences little intensity change. The KG-model would have these two voxels experience the same physiological noise because they have the same tissue type and same intensity. But under this detector-level mechanism, they violate this central assertion of the KG-model. This mechanism breaks the relationship between the voxel’s signal level and its time-series variance.

This discrepancy between the physiological noise covariance matrix and the signal matrix also appears to vary across space even within the GM compartment (see Fig. 8) and this discrepancy may vary smoothly over the brain (15,16). Furthermore, we show experimental data supporting the view that the value of α depends on the coil combination method and number of channels used in the reconstructed image. The observed value for α ranged from near zero for the image time-series from a single channel of the 32Ch array to values that significantly alter the tSNR of an image time-series for rSoS combinations of the array channel data.

The new PNC-model was used further to characterize the tSNR dependence on SNR₀ for multi-channel array coil acquisitions across field strengths of 3T and 7T. Fitting the time-series data from different tissue components (e.g., GM, WM, and CSF) showed that the largest values of α were needed in the tissue with the highest levels of physiological fluctuations (GM and CSF), whereas the values of α were relatively small for WM. Additionally, the value of α is small for phantom data and for WM. This supports a physiological noise origin for α as opposed to an alternative proposal, which explains the need for α ≠0 as a mis-scaling of the SNR₀ measurement, perhaps due to incomplete accounting for the magnitude bias in array coil data. Although the need for the additional term appears to be related to the physiological noise correlations, the model parameter α does not appear to depend on TE in our 3T data (and is therefore not expected to vary with TE at 7T as well). This could perhaps reflect the fact that the degree of physiological noise coupling between channels is itself not a strong function of TE.

Future investigations into the discrepancy between the physiological noise covariance matrix and the signal matrix could quantify the relative contribution of various physiological noise sources, such as changes during to the respiratory or cardiac cycles or longer term modulations. Because the origins of this discrepancy are not likely to be “BOLD-like” due to the lack of a dependency of α on TE, a complete explanation of this effect would have to take into account the interaction between the elements of the array coil and the measured fMRI signal. The possible explanations provided above for how physiological noise covariance could vary across the array are likely hold for different array coil geometries and are expected to persist at higher field strengths, but we have demonstrated that the relative influence of physiological noise correlation appears to vary with both coil geometry (see Fig. 5) and field strength (see Fig. 3).

Comparison of the 3T birdcage volume coil acquisitions and the “birdcage-like” synthetic combination of the 32Ch array data reveals differences in the behavior of the model fits to these two data sets, even though they both correspond to a birdcage coil image. Within the cortical GM, qualitatively the volume coil data appears to be equally well characterized by both the KG-model and the PNC-model (Fig. 6A), but the value of α for this data is close to zero (0.26). This observation is confirmed quantitatively by the AIC test (Fig. 1D) showing that the KG-model is a better fit to the data than the PNC-model. However, the synthetic birdcage combination generated from the 32Ch array data is better characterized by the PNC-model, whose fit yielded an increased α value (0.69). This value of α is still lower than the value seen from fitting the 32Ch data combined with the conventional rSoS method (Fig. 6C). Therefore the synthetic ‘birdcage’ combination formed from the 32Ch data acts to lower the value of α relative to the conventional combination, making the behavior of the synthetic ‘birdcage-combined’ 32Ch data similar to but not identical to the data acquired with a true birdcage volume coil. This suggests that the global channel weights used in the synthetic ‘birdcage’ combination of the 32Ch data somehow cancel out the physiological noise coupling seen in the physiological noise covariance matrix, and thereby lower the value of α. This further suggests that the value of α is likely to vary with different coil array detector layouts and geometries.

In this work, no parallel imaging acceleration was used. We have previously demonstrated (3) accelerated parallel imaging causes a reduction of SNR but that the relationship between SNR₀ and tSNR is largely unaffected. Calculation of alpha is expected to be more computationally expensive because in accelerated parallel imaging reconstructions the transformation from k-space into the image domain is no longer a simple unitary operation and the result is that the thermal noise covariance varies spatially (17). Furthermore, because parallel imaging techniques such as Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA) (18) estimate missing data through linear combinations of acquired data across all coils, the spatial pattern of the discrepancy between the physiological noise covariance matrix and the signal matrix could be affected. Notwithstanding these technical challenges in quantifying α and the relationship between physiological noise covariance and the signal matrix, it is expected that physiological noise correlations will similarly affect the relationship between tSNR and SNR₀ in both accelerated and unaccelerated data.

A closer look at the proposed model reveals that the parameters α and λ control distinct aspects of the tSNR–SNR₀ curve and are, therefore, independent from each other. Specifically, α parameterizes the slope of the linear component at low SNR₀ values (i.e., the thermal noise-dominated regime) and λ parameterizes the level of the flat, asymptotic component of the curve found at high SNR₀ values (i.e., physiological noise-dominated regime). Because the parameters control different components of this curve, and are, therefore, largely independent from one another, the values of the two model parameters are expected to be unique for a particular data set, and, therefore, the fitting procedure is more likely to provide a solution that converges toward a global minimum.

In addition to analyzing the behavior of the new parameter, we are also able to use the time-series data to compute the physiological noise covariance matrix. We show that mathematically, when the physiological noise is proportional to SS^H, the SNR calculation is identical to the SNR relationship provided by the KG-model. Therefore, having the physiological noise covariance matrix, Ψ_p, be proportional to SS^H is the logical extension of the KG-model to coil arrays. Yet experimental evidence shows that while this is mostly the case, Ψ_p can be measured in a time series and shown to be different from SS^H, and at the same time the relationship between tSNR and SNR₀ can be shown to deviate from the KG-model. Unlike the thermal noise covariance matrix, which is expected to be invariant across the object, both the physiological noise covariance matrix and the signal level matrix SS^H differ significantly from location to location in the brain.

Hutton et al. pointed out that many sites do not retain the uncombined data or knowledge of the thermal noise covariance matrix and simply measure the standard deviation (SD) in an ROI in a signal-free area of the image (19). They pointed out that for high-SNR data this simplified SNR measurement (which they referred to as SNR₀′) differs from the rigorously measured image SNR0 only by a scale factor. Thus SNR₀′ = κ SNR₀. We note that this relationship is only expected to hold for high-SNR data due to the magnitude bias problem (4,5,6). However, it is often the case in practical fMRI data that SNR₀ is sufficiently high that the magnitude bias issue can be ignored.

In conclusion, we extend the Krueger-Glover model to include a physiologicial noise covariance matrix and show that when the relationship σ_P = λS is generalized to Ψ_P = λSS^H, then the general form of the tSNR vs. SNR₀ relationship is preserved. We show that a non-zero matrix C_α can be interpreted as a component of physiological noise that does not scale with signal strength but is unaccounted for in the image noise. We also show that this type of noise source leads to a modification in the Krueger-Glover relationship between tSNR and SNR₀ and thus has consequences for the interpretation of where a given acquisition stands in the trade-off between thermal and physiological noise sources. We propose some possible examples of “physiological” noise in arrays whose level is not dependent on the local signal intensity. We show that the deviation from C_α = 0 is relatively small for white matter and largest in cerebral gray matter and cerebrospinal fluid, the two largest contributors to physiological noise. Finally, the presence of this additional physiological noise source also has implications for how array channels should be combined for fMRI. Previously they were combined with knowledge of only Ψ₀ to maximize SNR₀ with the assumption that this would also maximize tSNR. But when C_α ≠ 0, optimizing SNR₀ is not sufficient, suggesting that the time-series noise covariance matrix (Ψ_p) should be measured and considered in the choice of coil combination weights to optimize tSNR.

Supplementary Material

Supp TableS1. Supporting Table S1.

Acquisition parameters for different resolutions at 3T

Supp TableS2. Supporting Table S2.

Acquisition parameters for different resolutions at 7T