Clear evidence for item limits in visual working memory

Abstract

There is a consensus that visual working memory (WM) resources are sharply limited, but debate persists regarding the simple question of whether there is a limit to the total number of items that can be stored concurrently. Zhang and Luck (2008) advanced this debate with an analytic procedure that provided strong evidence for random guessing responses, but their findings can also be described by models that deny guessing while asserting a high prevalence of low precision memories. Here, we used a whole report memory procedure in which subjects reported all items in each trial, and indicated whether they were guessing with each response. Critically, this procedure allowed us to measure memory performance for all items in each trial. When subjects were asked to remember 6 items, the response error distributions for about 3 out of the 6 items were best fit by a parameter-free guessing model (i.e. a uniform distribution). In addition, subjects’ self-reports of guessing precisely tracked the guessing rate estimated with a mixture model. Control experiments determined that guessing behavior was not due to output interference, and that there was still a high prevalence of guessing when subjects were instructed not to guess. Our novel approach yielded evidence that guesses, not low-precision representations, best explain limitations in working memory. These guesses also corroborate a capacity-limited working memory system – we found evidence that subjects are able to report non-zero information for only 3–4 items. Thus, WM capacity is constrained by an item limit that precludes the storage of more than 3–4 individuated feature values.

Introduction

Working memory (WM) is an online memory system where information is maintained in the service of ongoing cognitive tasks. Although there is a broad consensus that WM resources are sharply limited, there has been sustained debate about the precise nature of these limits. On the one hand, discrete-resource models argue that only a handful of items can be maintained at one time, such that some items fail to be stored when the number of memoranda exceeds the observer’s capacity (Awh, Barton, & Vogel, 2007; Cowan, 2001; Rouder et al., 2008; Zhang & Luck, 2008). On the other hand, continuous resource models argue that WM storage depends on a central pool of resources that can be divided across an unlimited number of items (Bays & Husain, 2008; van den Berg, Shin, Chou, George, & Ma, 2012; Wilken & Ma, 2004).

Of course, it has long been known that memory performance declines as the number of memoranda increases in a WM task. For example, Luck and Vogel (1997) varied the number of simple colors in a change detection task that required subjects to detect whether one of the memoranda had changed between two sequential presentations of a sample display. They found that while performance was near ceiling for set sizes up to three items, accuracy declined quickly as set size increased beyond that point. This empirical pattern is well described by a model in which subjects store 3–4 items in memory and then fail to store additional items. However, the same data can be accounted for by a continuous resource model that presumes storage of all items, but with declining precision as the number memoranda increases (Wilken & Ma, 2004). According to continuous resource accounts, increased errors with larger set sizes are caused by insufficient mnemonic precision rather than by storage failures (but for a critique of this account see Nosofsky & Donkin, 2016b). Thus, a crux issue in this literature has been to distinguish whether performance declines with displays containing more than a handful of items are due to storage failures or sharp reductions in mnemonic precision.

In this context, Zhang and Luck (2008) offered a major step forward with an analytic approach that provides separate estimates of the probability of storage and the quality of the stored representations. They employed a continuous recall WM task in which subjects were cued to recall the precise color of an item from a display with varying numbers of memoranda. Their key insight was that if subjects failed to store a subset of the items, there should be two qualitatively distinct types of responses within a single distribution of response errors. If subjects had stored the probed item in memory, responses should be centered on the correct color, with a declining frequency of responses as the distance from the correct answer increased. But if subjects had failed to store the probed item, then responses should be random with respect to the correct answer, producing a uniform distribution of answers across the entire space of possible colors. Indeed, their data revealed that the aggregate response error distribution was well described as a weighted average of target-related and guessing responses. Thus, Zhang and Luck (2008) provided some of the first positive evidence that working memory performance reflects a combination of target-related and guessing responses.

Subsequent work, however, has argued that the empirical pattern reported by Zhang and Luck (2008) can be explained by continuous resource models that presume storage of all items in every display (van den Berg, Awh, & Ma, 2014; van den Berg et al., 2012). A key feature of these models has been the assumption that precision in visual WM may vary substantially; thus, while some items may be represented precisely, other representations in memory may contain little information about the target item. Using this assumption, van den Berg et al. (2012) showed that they could account for the full distribution of errors – including apparent guessing – and that their model outperformed the one proposed by Zhang and Luck (2008). Indeed, converging evidence from numerous studies has left little doubt that precision varies across items in these tasks (e.g., Fougnie, Suchow, & Alvarez, 2012). That said, the question of whether precision is variable is logically separate from the question of whether observers ever fail to store items in these procedures. To examine the specific reasons why one model might achieve a superior fit over another, it is necessary to explore how distinct modeling decisions influence the outcome of the competition. Embracing this perspective, van den Berg, Awh and Ma (2014) carried out a factorial comparison of WM models in which the presence of items limits and the variability of precision were independently assessed. Although this analysis provided clear evidence that mnemonic precision varies across items and trials, the data were not decisive regarding the issue of whether working memory is subject to an item limit. There was a numerical advantage for models that endorsed item limits, but it was not large enough to draw strong conclusions. Thus, the critical question of whether item limits in visual working memory elicit guessing behavior remains unresolved.

Here, we report data that offer stronger traction regarding this fundamental question about the nature of limits in working memory. Much previous work has focused on explaining variance within aggregate response-error distributions (i.e. the shape of the response distribution and how it changes across set sizes). Here, we chose a different route. Rather than developing a new model that might explain a small amount of additional variance in “traditional” partial report datasets, we developed a new experimental paradigm in which subjects recalled—in any order that they wished—the precise color (Experiment 1a) or orientation (Experiment 1b) of every item in the display. This procedure has the key benefit of measuring the quality of all simultaneously remembered items, and it yields the clear prediction that if there are no item limits, then there should be measurable information across all responses. To anticipate the results, this whole report procedure provided rich information about the quality of all items within a given trial as well as subjects’ metaknowledge of variations in quality. Observers consistently reported the most precisely remembered items first, yielding monotonic declines in information about the recalled item with each successive response. Critically, for the plurality of subjects, the final three responses made were best modeled by the parameter-free uniform distribution that indicates guessing. In additional analyses and experiments, we showed that subjective guess ratings tracked mixture model guessing parameter (Experiments 1 & 2), that output interference could not explain our estimates of capacity (Experiment 2), and that making subjective guess ratings did not drive our evidence for guessing (Experiment 3). Finally, we used simulations to question a key claim of the variable precision model – that representations used by this model all contain measurable information. Previously, others have suggested that the variable precision model may mimic guess responses with ultra-low precision representations (Nosofsky & Donkin, 2016b; Sewell, Lilburn, & Smith, 2014). Here, we advanced these claims by showing that variable precision models that eschew guessing posit a high prevalence of memories that are indistinguishable from guesses. Moreover, the frequency of these putative representations precisely tracked the estimated rate of guessing in models that acknowledge item limits.

In sum, there has been a longstanding debate over whether there is any limit in the number of items that can be stored in working memory. Our findings provide compelling evidence that working memory is indeed subject to item limits, disconfirming a range of prior models that deny guessing entirely or posit an item limit that varies from trial to trial without any hard limit in the total number of items that can be stored (e.g. Sims, Jacobs, & Knill, 2012; van den Berg et al., 2014). Instead, our results point toward a model where each individual has a capacity ceiling (e.g. 3 items), but they frequently under-achieve their maximum capacity, likely due to fluctuations in attentional control (Adam, Mance, Fukuda, & Vogel, 2015).

2. Experiment 1

2.1. Materials and Methods

2.1.1. Experiment 1a: Color memoranda

2.1.1.1 Subjects

22 subjects from the University of Oregon completed Experiment 1a for payment ($8 per hour) or class credit. All participants had normal color vision and normal or corrected-to-normal visual acuity, and all gave informed consent according to procedures approved by the University of Oregon institutional review board.

2.1.1.2. Stimuli

Stimuli were generated in MATLAB (The MathWorks, Inc., Natick, MA, www.mathworks.com) using the Psychophysics Toolbox extension (Brainard, 1997; Pelli, 1997). Stimuli were presented on a 17-inch flat cathode ray tube computer screen (60 Hz refresh rate) on a Dell Optiplex GX520 computer running Windows XP and viewed from distance of approximately 57 cm. A chin rest was not used, so all visual angle calculations are approximate. A gray background (RGB = 128 128 128) and a white fixation square subtending .25 by .25 degrees of visual angle appeared in all displays. In Experiment 1a, subjects were asked to remember the precise color of squares in the memory array, each subtending 1.7 by 1.7 degrees. Colors for memory stimuli were chosen randomly from a set of 360 colors taken from a CIE L*a*b* color space centered at L = 54, a = 18 and b = −8. Note, colors were generated in CIE L*a*b* space, but they were likely rendered with additional variability; monitors were not calibrated to render true-equiluminant colors. Others have compared calibrated versus uncalibrated monitors and found consistent results (Bae, Olkkonen, Allred, & Flombaum, 2015; Bae, Olkkonen, Allred, Wilson, & Flombaum, 2014). Uncalibrated monitors may exaggerate the amount of variability in precision across different colors in the color wheel.

Spatial positions for colored stimuli were equidistant from each other on the circumference of circle with a radius of 3.75 degrees around the fixation point. At test, a placeholder array of dark gray squares (RGB = 120 120 120) and a color wheel (radius = 11.9 degrees of visual angle) appeared, and the mouse cursor was set to the fixation point. The color wheel rotated on each trial so that subjects could not use spatial locations of colors to plan responses. When a placeholder item was selected for response, its color changed to light gray (RGB = 145 145 145). During response selection, the selected square changed colors to match the color that matched the current position of the mouse cursor; after response selection the selected square returned to dark gray.

2.1.1.3. Procedures

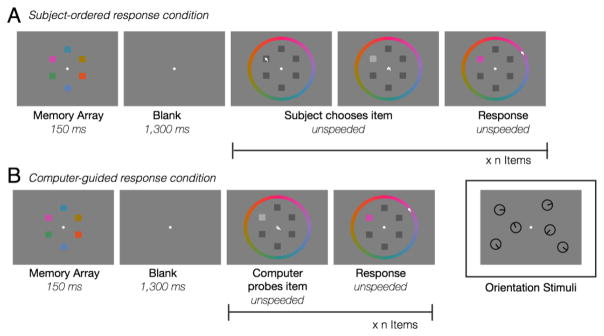
The session for Experiment 1a lasted approximately 1.5 hours and participants completed 5 blocks of 99 trials (99 trials per set size). On each trial, a memory array with one, two, three, four or six colored squares appeared briefly (150 ms) followed by a blank retention interval (1000, 1200, or 1300 ms). Retention interval length was jittered to add variability and were collapsed for analyses. There were not enough trials to separately fit model parameters to each retention interval duration. After the retention interval, the test display appeared, containing the color wheel and placeholder squares. The response order was determined freely by the subject. Subjects chose the first response item by clicking on one of the dark gray placeholders; the dark gray placeholder turned light gray, indicating that this square was chosen for response. The mouse cursor was set back to the fixation point to avoid any response bias based on spatial proximity of a chosen square to a section of the color wheel. Then, the subject selected a color on the color wheel that best matched their memory of the square. During each response, participants were instructed to indicate their confidence with a mouse click. Participants were instructed to use one mouse button to make their response if they felt they had “any information about the item in mind,” and to use the other mouse button to indicate when they felt they “had no information about the item in mind.” After responding to the first item, the mouse was set back to the fixation point. Subjects repeated the item selection and color selection procedure until they had responded to all of the items. After finishing all responses, the placeholder squares disappeared and the next trial began after a blank inter-trial interval (1300 ms).

2.1.2. Experiment 1b: Orientation memoranda

2.1.2.1. Subjects

23 subjects from the University of Chicago participated in Experiment 1b for payment ($10 per hour). Three subjects participated in the study but were not included in the final sample because they left the session early (2 subjects) or stayed for the full session but failed to complete all trials (1 subject); this left a total of 20 subjects for analysis. All participants had normal or corrected-to-normal visual acuity, and all gave informed consent according to procedures approved by the University of Chicago institutional review board.

2.1.2.2. Stimuli

Stimuli were presented on a 24-inch LCD computer screen (BenQ XL2430T; 120 Hz refresh rate) on a Dell Optiplex 9020 computer running Windows 7 and viewed from distance of approximately 70 cm. A chin rest was not used, so all visual angle calculations are approximate. In Experiment 1b, subjects were asked to remember the precise orientation of a line embedded in a circle (see inset of Fig. 1). The stimuli in each memory array had a radius of approximately .9 degrees of visual angle, and their orientations were randomly chosen from 360 degrees of orientation space. Stimuli were presented on a gray background (RGB = 85 85 85), and a white fixation circle appeared in all displays (diameter = .14 degrees). Dark gray placeholder circles (RGB = 45 45 45) were used during the test period. Spatial positions of the discs were randomly placed within a box 6.6 degrees of visual angle to the left and right of fixation and 6.1 degrees above and below fixation, with the stipulation that there must be a minimum distance of 1.25 items between items’ centers.

Figure 1. Task design.

Panel A depicts the order of events in Experiment 1. Panel B depicts the order of events in Experiment 2. Color stimuli were used in Experiment 1a and 2a, the orientation stimuli (inset) were used in Experiment 1b and 2b.

2.1.2.3. Procedures

Procedures in Experiment 1b (orientation) were similar to Experiment 1a. Each experimental session lasted approximately 2.5 hours and subjects completed 20 blocks of 50 trials (200 trials per set size). On each trial in Experiment 1b, a memory array with one, two, three, four or six black orientation stimuli appeared briefly (200 ms) followed by a blank retention interval (1000 ms). After the retention interval, the test display appeared, containing dark gray placeholder circles. The response order was determined freely by the subject. Subjects responded to each item by first clicking on the location of the item they wished to report. After selecting the item, the gray placeholder circle was replaced by a black test circle. Participants then used the mouse to click the edge of the circle at the location of the remembered orientation. During each response, participants were instructed to indicate their confidence with a mouse click. Participants were instructed to use one mouse button to make their response if they felt they had “any information about the item in mind,” and to use the other mouse button to indicate when they felt they “had no information about the item in mind.” After responding to all items, the next trial began with the blank inter-trial interval (1000 ms).

2.1.3. Fitting Response Error Distributions

2.1.3.1. Model-free circular statistics

To quantify change in mnemonic quality without committing to contentious model assumptions, we used a circular statistics measure to quantify mnemonic performance. Circular statistics were calculated using “CircStat”, a circular statistics toolbox for MATLAB (Berens, 2009); for more information on statistics in circular space, see Zar (2010). Response error distributions are centered around 0 degrees of error in a circular normal space (e.g. −180 degrees is the same as 180 degrees of error). The direction and variability of data-points in a given response error distribution can be described by the mean (“circ_mean.m”; Zar (2010) pp. 612) and the mean resultant vector length (MRVL; r, “circ_r.m”; Zar (2010) pp. 615) of the distribution. The circular mean indicates the average direction of data-points (e.g. the central tendency), whereas MRVL indicates the variability of data-points. MRVL varies from 0 (indicating a complete absence of information about the target) to 1 (indicating perfect information about the target).

2.1.3.2. Model fitting

In addition to using circular statistics, for some analyses we fit a mixture model to response error distributions (Zhang and Luck, 2008). Although there is debate regarding the mixture model’s assumption that subjects sometimes guess, this analytic approach allowed us to compare subjects’ self-reports of guessing to the frequency of guess responses postulated by these mixture models. Thus, response errors for each response at each set size were fit for each subject with a mixture model using a maximum likelihood estimation procedure in the MemToolbox package (Suchow, Brady, Fougnie, & Alvarez, 2013, www.memtoolbox.org). The mixture model fits response errors with a mixture of two distributions, a Von Mises distribution (circular normal) and a uniform distribution. The contribution of the uniform distribution to the response error distribution is described by the guessing parameter, g, and the dispersion of the Von Mises component is described by the precision parameter, sd.¹ The guessing parameter ranges from 0 to 1, and quantifies the “proportion of guesses” in the distribution, whereas the precision parameter is given in degrees (higher values indicate poorer precision). Using MemToolbox, we could also compare BIC values for the mixture model to an all-guessing model (uniform distribution).

2.2. Results and Discussion

In Experiment 1 we tested for the presence of guessing in response errors. A model of working memory that includes item limits and guessing predicts uniformly distributed responses for items that subjects cannot recall. That is, some responses are based on positive knowledge of the target, and some responses are completely random. To preview our results, we found that a uniform distribution (with zero free parameters) was the best-fitting distribution for a substantial portion of responses and that subjects consistently reported that these responses were guesses. Data from Experiment 1 and all following experiments are available on our Open Science Framework project page, https://osf.io/kjpnk/.

2.2.1. Change in quality across set sizes and responses

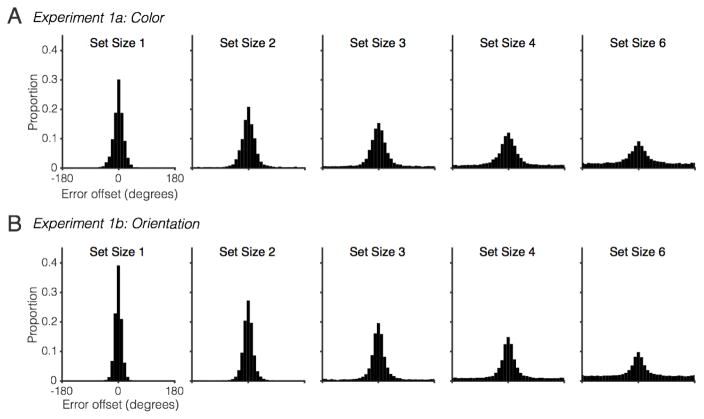
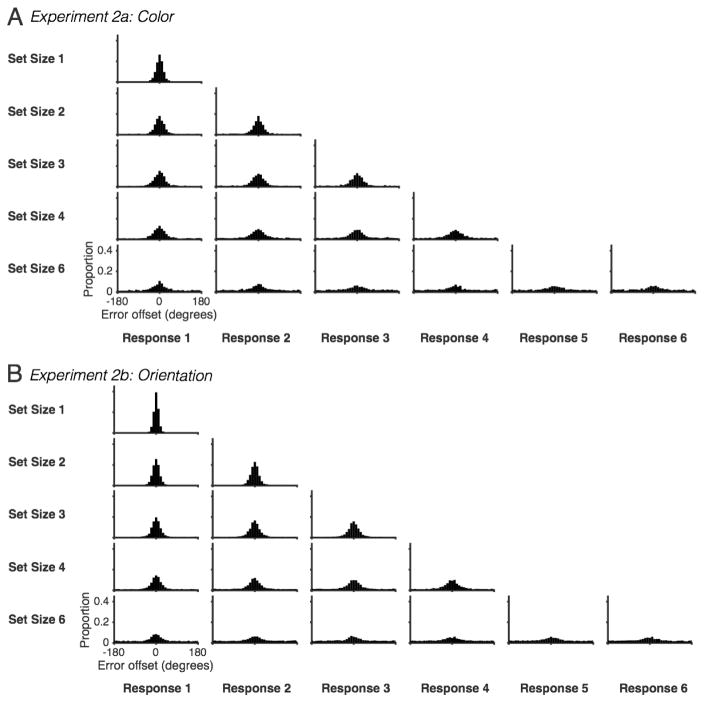
To examine the effects of set size, we collapsed across all responses to create the response error distribution for each set size. Consistent with the previous literature, we observed a systematic decline in MRVL across set sizes (Fig. 2) in Experiment 1a (Color), F(2.45,51.38) = 431.9, p < .001, η_p² = .95, and Experiment 1b (Orientation), F(1.45,27.62) = 675.58, p < .001, η_p² = .97². As the memory load increased, the distribution of response errors became increasingly diffuse, indicating that on average less information was stored about each memorandum. Importantly, overall MRVL values and the slope of their decline across set sizes was similar to that observed in past studies using single probe procedures.³ Below, a more detailed analysis of Experiment 2 findings will provide further evidence for this observation. Thus, requiring the report of all items did not induce qualitative changes in performance at the aggregate level. Nevertheless, as the following results will show, the whole report procedure provided some important new insights about the distribution of mnemonic performance across the items within a trial.

Figure 2. Aggregate data for Experiment 1.

Collapsing across all responses within a set size, we see a typical decline in precision with increasing memory load.

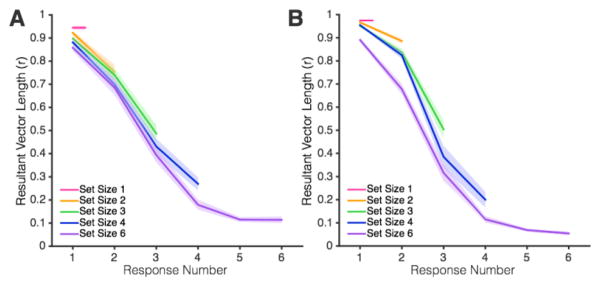
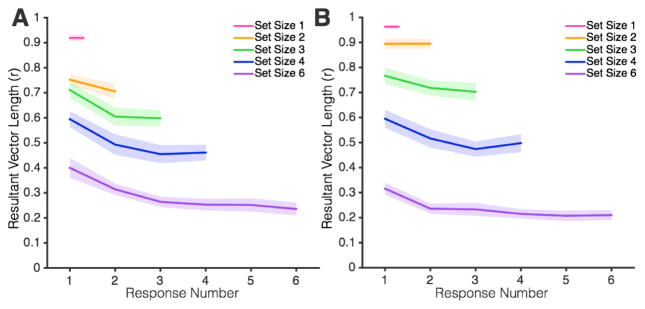
Next, we examined the effect of response order within each set size. Recall that subjects were free to recall each item in whatever order they chose. As Figures 3 and 4 show, there was a strong tendency for subjects to report the best remembered items first. There was a sharp drop in MRVL from early to late responses within a trial. A repeated-measures ANOVA for each set size with a within-subject factor for response order showed a clear main effect of response order for all set sizes in Experiment 1a (Table 1) and Experiment 1b (Table 2). Planned contrasts comparing each earlier response to the last response revealed that performance declined monotonically with response order, except for between the fifth and sixth responses in the set size six condition where MRVL values were hovering just above the floor of 0 (p = .96 for Experiment 1a, p = .13 for Experiment 1b). MRVL decreased by on average .18 per response in Experiment 1a and .19 per response in Experiment 1b. From the first to the last response in set size 6, estimates of mean resultant vector length decreased by .74 in Experiment 1a and .84 in Experiment 1b (maximum possible difference of 1.0), reaching minimum values of between 0.05 and 0.10. To summarize, when subjects were allowed to report all items in any order that they chose, we observed a consistent drop in target information with each additional response. This suggests that subjects reported the best remembered items first, and that they had strong meta-knowledge of which items were remembered the best. Below, we will show that subjects’ explicit reports of guessing were also quite accurate in tracking their mnemonic performance.

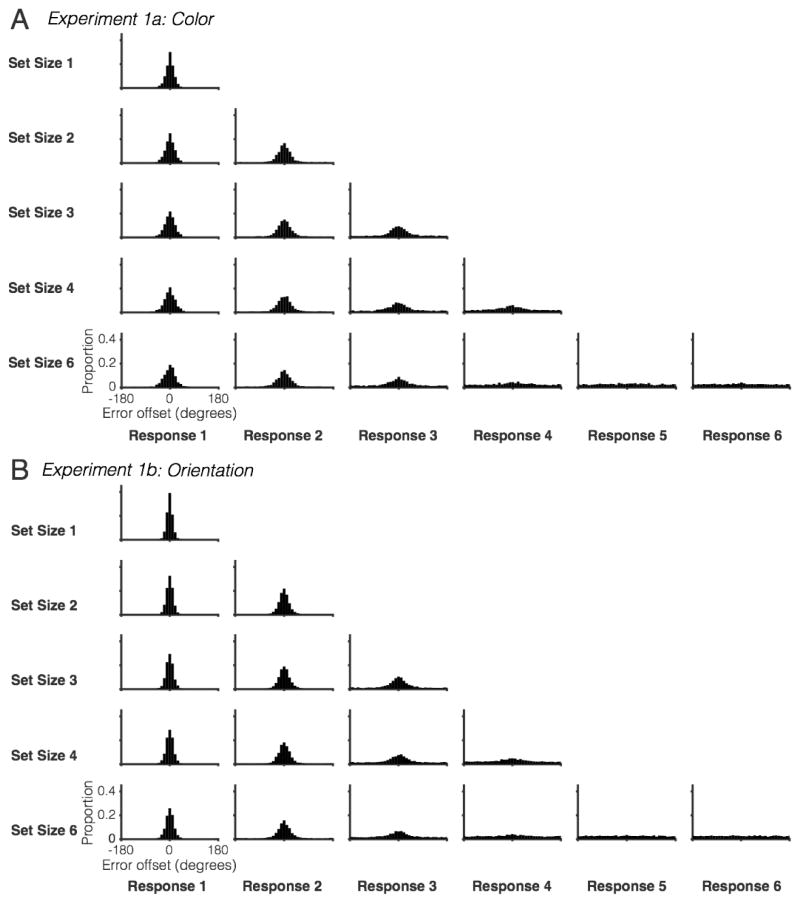
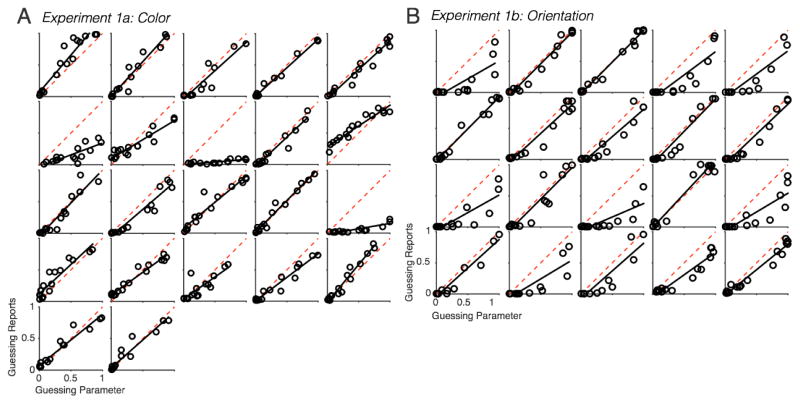
Figure 3. Subject-ordered responses reveal representations that covary with response order.

All set sizes and responses are shown for (A) Experiment 1a and (B) Experiment 1b.

Figure 4. Mean resultant vector length across responses in Experiment 1a (A) and Experiment 1b (B).

Shaded error bars represent 1 Standard Error.

Table 1.

Change in Mean Resultant Vector Length across responses in Experiment 1a.

Set Size	df1	df2	F	p	ηp2
2	1	21	42.4	<.001	.67
3	2	42	129.5	<.001	.86
4	2.2	45.4	223.8	<.001	.91
6	2.8	58.4	295.2	<.001	.93

Table 2.

Change in Mean Resultant Vector Length across responses in Experiment 1b.

Set Size	df1	df2	F	p	ηp2
2	1	19	66.1	<.001	.78
3	1.2	21.9	116.1	<.001	.86
4	1.5	28.3	217.3	<.001	.92
6	2.1	40.2	389.5	<.001	.95

2.2.2. Evidence for guessing in the set size 6 condition

Thus far, the findings from the whole report procedure have mirrored those found in past studies using single-item probes. The shape of the aggregate error distribution, as well as the decline in MRVL values with increasing set size, fell in line with past studies. Going beyond this, testing all items in each trial provided new insight into the full range of memory performance across each item in the sample array. Notably, there appeared to be uniform error distributions – the distribution predicted when subjects fail to store the relevant item – for the fifth and sixth items recalled in the set size 6 condition (see Fig. 3). This may be a critical observation. While past work has shown that it is difficult to adjudicate between models that endorse guessing and those that propose high prevalence of low fidelity memories, the whole report procedure appears to provide clear evidence of guessing behavior in the set size 6 condition.

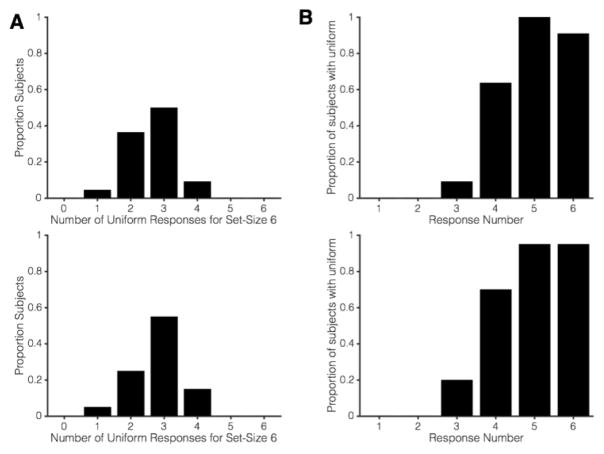
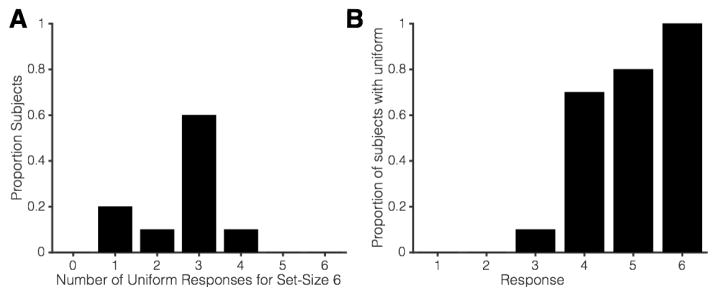
To objectively test the hypothesis that subjects guessed during later responses, we used a BIC approach to compare the fit of a uniform distribution with the fit of a mixture model⁴ (the simplest implementation of some guessing plus some information) using MemToolbox (Suchow et al., 2013). Any reliable central tendency in the error distribution should yield a lower BIC value for such a mixture model than for the uniform model. If, however, guessing alone is adequate to explain performance, then the BIC value should be lower for the uniform distribution. For each participant, we operationally defined a capacity limit by counting the number of empirically-defined uniform distributions during Set Size 6 trials. Our logic for this operational definition of capacity is as follows: participants tended to report items in order of decreasing quality, and we would expect that a participant who stored 3 items would first report these items before making any guess responses. Thus, they would have 3 non-uniform responses and 3 uniform responses. Participants who maximally stored different numbers of items would be expected to have different numbers of uniform distributions. Note, this analysis relies on the assumption that participants had robust metaknowledge that enabled them to report items in declining order of quality. Thus, if an individual had poor meta-awareness of stored items (i.e. they sometimes reported their best items toward the end of the trial), then this operational definition of capacity would over-estimate that individual’s capacity limit. This analysis revealed that all subjects had between one and four responses best described by a uniform distribution, and that these were the last items reported in the trial (Fig. 5, Tables S1 and S2). In Experiment 1a (Color), the average number of uniform responses was 2.64 (SD = .73), and in Experiment 1b (Orientation) the average number was 2.80 (SD = .77). Supplementary analyses revealed that the uniformity of later responses cannot be explained by a sudden increase in the tendency to report the value of the wrong item (Analysis S1, Table S3). However, some guess responses may be due to retrieval failures rather than to lack of storage (Harlow & Donaldson, 2013; Harlow & Yonelinas, 2016). We also found that circular statistics approaches to test for uniformity yield similar conclusions (Analysis S2). In sum, we obtained clear positive evidence that the final responses in the set size 6 condition were guesses.

Figure 5. Number of uniform responses for Set Size 6 in Experiments 1a and 1b.

(A) Histogram of subjects’ total number of Set Size 6 responses that were best fit by a uniform distribution. Top: Color Condition; Bottom: Orientation Condition. (B) Number of subjects’ responses best fit by uniform distributions as a function of response number. Top: Color Condition; Bottom: Orientation Condition.

Our estimates of individual differences in capacity closely tracked the range found in the literature. A majority of participants had an estimated capacity between 3 and 4 items, and there was some variability on either side of this (Fig. 5). Thus while every subject in this study showed evidence of an item limit, there was no evidence for a common storage limit across observers, in line with past work that has documented individual variations in neural markers of WM storage (e.g. Todd & Marois, 2004, 2005; Unsworth, Fukuda, Awh, & Vogel, 2015; Vogel & Machizawa, 2004) and behavioral measures of performance (e.g. Engle, Kane, & Tuholski, 1999; Vogel & Awh, 2008; Xu, Adam, Fang, & Vogel, in press). Likewise, previous modeling efforts have acknowledged the need to account for individual differences in performance; models allow parameters to vary across individual subjects (e.g. Bays, Catalao, & Husain, 2009; van den Berg et al., 2014; Zhang & Luck, 2008).

2.2.3. Strong correspondence between subjective reports of guessing and the guessing parameter in a mixture model

Previous work has demonstrated that subjective confidence strongly predicts mnemonic precision (Rademaker, Tredway, & Tong, 2012) and correlates strongly with fluctuations in trial-by-trial performance (Adam & Vogel, 2017; Cowan et al., 2016). Our finding that subjects consistently reported the best-remembered items first also suggests that subjects have strong meta-knowledge regarding the contents of working memory. To provide an objective test of this interpretation, we examined whether or not subjects’ self-reports of guessing fell in line with the probability of guessing estimated with a standard mixture model (Zhang and Luck, 2008). A tight correspondence between subjects’ claims of guessing and mixture model estimates of guessing would demonstrate that subjects have accurate meta-knowledge and bolster the face validity of the guessing parameter employed in mixture models.

To examine the correspondence between subjective and objective estimates of guess rates, we fit a separate mixture-model to response errors for each response within each set size (16 total model estimates per subject). We also calculated the percentage of subjects’ responses that were reported guesses (guess button used) for each of these 16 conditions. Then, we correlated the g parameter with the percentage of reported guessing. If there is perfect correspondence between the guessing parameter and subjective reports of guessing, a slope of 1.0 and intercept of 0.0 would be expected for the regression line. The resulting relationship between the model and behavioral guessing was strikingly similar to this idealized prediction (Fig. 6). The average within-subject correlation coefficient was r = .94 (SD = .05, all p-values < .001) in Experiment 1a and r = .93 (SD = .06, all p-values < .001) in Experiment 1b, indicating a tight relationship between the model’s estimates of guessing and subjects’ own reports of guessing. Participants were on average slightly over-confident (as indicated by a slope slightly less than one when the model’s guessing parameter was plotted on the x-axis). In Experiment 1a, participants had an average slope of .80 (SD = .29) and intercept of .03 (SD = .08). In Experiment 1b, participants had an average slope of .83 (SD = .19) and intercept of −.05 (SD = .02). In sum, the striking correspondence between mixture model estimates of guessing and subjective reports of guessing suggests that subjects had excellent metaknowledge. The frequency with which subjects endorsed guessing precisely predicted the height of the uniform distribution estimated with a standard mixture model.

Figure 6. The relationship between behavioral guessing and modeled guessing in Experiment 1b.

Each panel shows an individual’s correlation between reported guessing and the mixture model g parameter for each of 16 conditions (every response made for Set Sizes 1–4 and 6). The red dotted line represents perfect correspondence between behavioral guessing and modeled guessing (slope = 1, intercept = 0).

2.2.4. Output interference as a potential source of guessing behavior

The data from Experiment 1 provide compelling evidence that that a substantial portion of subjects’ responses were best characterized by a uniform distribution associated with guessing. Because subjects tended to respond first with the items that they remembered the best, these uniform distributions were observed in the last items that were reported within the whole report procedure. An important alternative explanation, however, is that the decline in memory performance across responses may have been due to output interference. Specifically, we considered whether merely reporting the initial items could have elicited the drop in performance that we saw for the last items reported within each trial. Indeed, output interference has been demonstrated in past studies of working memory (Cowan, Saults, Elliott, & Moreno, 2002). Thus, Experiment 2 was designed to measure the strength of output interference in our whole report procedure. Subjects in Experiment 2 had to respond to the items in a randomized order specified by the computer. If the uniform responses that we observed in Experiment 1 were due to output interference, then we should observe a similar drop in performance across responses in Experiment 2. Furthermore, a randomized response-order design allowed us to decouple confidence ratings from response order. In Experiment 1, confident responses never occurred at the end of the trial. By randomly selecting the order of report in Experiment 2, we had the opportunity to observe whether subjects also guessed when they were making the earliest responses in a trial.

3. Experiment 2

3.1. Materials & Methods

3.1.1. Experiment 2a: Color memoranda

3.1.1.1. Subjects

17 subjects from the University of Oregon completed Experiment 2a. All participants had normal color vision and normal or corrected-to-normal visual acuity, and they were compensated with payment ($8/hour) or course credit. All participants gave informed consent according to procedures approved by the University of Oregon institutional review board.

3.1.1.2. Procedures

Stimuli and procedures in Experiments 2a were identical to Experiment 1a except for the order in which responses were collected. On each trial, the response order was determined randomly by the computer on each trial, which will be referred to as a “random response” order. In Experiment 2a (color), one of the remembered items turned light gray, indicating that the participant should report the color at that location. The participant used the mouse to click on the color in the color wheel that best matched the memory for the probed square. The response process repeated until subjects had responded to all of the items in the display. Participants were again instructed to use the two mouse buttons to indicate their confidence in each response.

3.1.2. Experiment 2b: Orientation memoranda

3.1.2.1. Subjects

21 subjects from the University of Chicago completed Experiment 2b. One participant began participation, but left the session early. After analyzing the data, one additional participant was excluded for poor performance (> 30% guessing rate for set size 1). This left a total of 19 subjects for data analysis. All participants had normal color vision and normal or corrected-to-normal visual acuity. Participated were compensated with payment ($10/hour) and all gave informed consent according to procedures approved by the University of Chicago institutional review board.

3.1.2.2. Procedures

Trial events in Experiment 2b were identical to Experiment 1b except for the order in which responses were collected. At test, the cursor was set on top of one of the remembered items. The participant used the mouse to rotate the probed item to the remembered orientation, and clicked to set the response. After a response was collected, the test item was replaced by a gray placeholder circle, and a new untested item was probed. The response process repeated until subjects had responded to all of the items in the display. Participants were again instructed to use the two mouse buttons to indicate their confidence in each response.

3.2. Results & Discussion

3.2.1. Changes in response quality across set sizes and responses

The whole report procedure was meant to tap into the same cognitive limits that have been observed in past studies using single-item probes. Thus, an important goal was to determine whether this procedure produced the same kinds of error distributions that have been observed in studies employing single-item probes. In the random response-order condition, participants were probed on all of the items in a randomized fashion. Thus, the first probed response in this condition was similar to a typical partial-report procedure, where only one item is randomly probed and output interference cannot influence the results. We compared overall performance in the free-response order experiments (i.e. combining all responses into one set size level distribution) to performance for the first randomly probed item in the random response-order experiments. Then, we quantified the quality for each set size distribution using MRVL. For color stimuli (Experiments 1a and 2a), an ANOVA with within-subjects factor Set Size and between-subjects factor Experiment revealed that there was no main effect of Experiment on MRVL, F(1,37) = 0.12, p = . 72, η_p² = .003. Likewise, there was no main effect of Experiment for orientation stimuli (Experiments 1b and 2b), F(1,37) = 0.17, p = .68, η_p² = .005. These null results suggest that the free-response whole report procedure elicited similar aggregate error distributions as observed in past procedures that have probed only a single item.

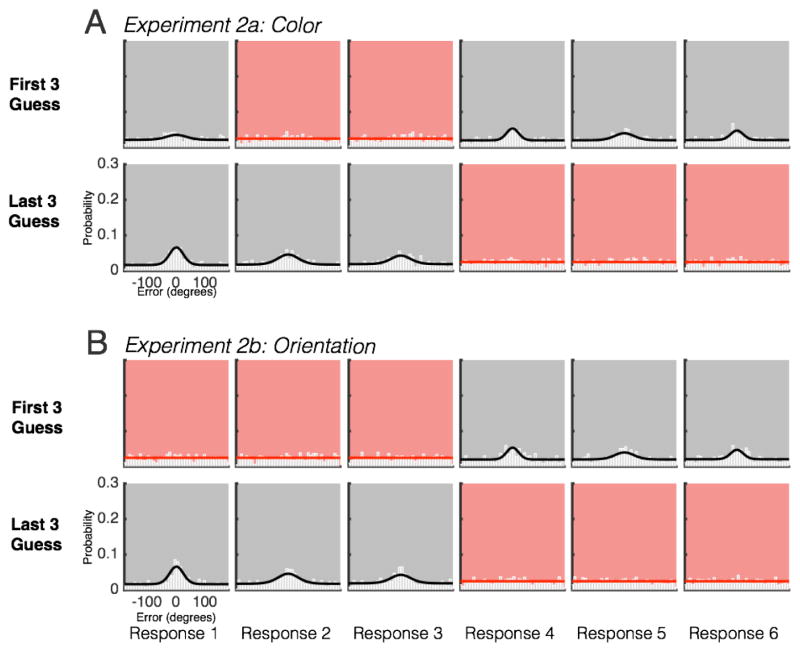
To more directly measure the effect of output interference within the random response-order experiments, we examined how response quality changed across responses made within each set size. A decline in MRVL values across responses in Experiment 2 would provide positive evidence for output interference. Indeed, the results revealed some decline in performance across responses. Critically, however, the slope of this decline was far shallower than when subjects chose their own response order in Experiment 1 (Fig. 7 and Fig. 8). To quantify the decline in mnemonic quality across responses, we again calculated MRVL values for each response within each set size, and we ran a repeated-measures ANOVA for each set size with the within-subjects factor Response. There was a significant main effect of response for all set sizes in Experiment 2a (Table 3). In Experiment 2b, there was no significant main effect of response for Set Size 2 (p = .96) but there was a significant difference for all other set sizes (Table 4). However, while these findings provide some evidence of output interference, there were striking differences from the pattern that was observed in Experiment 1. In Experiment 1, we observed a monotonic decline in memory quality across all responses, such that aggregate error distributions were completely uniform for the fifth and sixth responses. By contrast, in Experiment 2 only the first response was consistently better than the final response. Rather than an accumulation of output interference across each successive response, this empirical pattern suggests an advantage for the first response or two. In Experiment 2a, planned contrasts comparing each earlier response to the last response revealed that performance was better for only the first response for Set Sizes 3 and 4 and for the first and second responses for Set Size 6. In Experiment 2b, contrasts revealed that only the first response was significantly better than the final response for all set sizes.

Figure 7. Computer-ordered responses reveal representations that are relatively unaffected by response order.

All set sizes and responses are shown for (A) Experiment 2a and (B) Experiment 2b.

Figure 8. Mean resultant vector length for responses in Experiment 2a (A) and Experiment 2b (B).

Shaded error bars represent 1 Standard Error.

Table 3.

Change in Mean Resultant Vector Length across responses in Experiment 2a.

Set Size	df1	df2	F	p	ηp2
2	1	16	11.75	.003	.42
3	2	32	25.3	<.001	.61
4	3	48	18.4	<.001	.53
6	5	80	14.9	<.001	.48

Table 4.

Change in Mean Resultant Vector Length across responses in Experiment 2b.

Set Size	df1	df2	F	p	ηp2
2	1	18	.003	.96	<.001
3	2	36	16.1	<.001	.47
4	3	54	25.0	<.001	.58
6	5	90	13.3	<.001	.43

To summarize, although both Experiments 2a and 2b produced evidence for a modest amount of output interference, the slope of this decline in the computer-guided condition was more than six times shallower than when subjects chose the response order themselves in Experiment 1 (Fig. 8). While resultant vector length decreased by 0.18–.19 per response in the self-ordered experiments (Exp. 1a and 1b), it decreased by only .04 and .02 per response in Experiments 2a and 2b. That is, output interference could at most explain around 16% of the decline observed in Experiment 1. Thus, the effect of output interference alone cannot explain the dramatic decrease in performance during the self-ordered response procedure used in Experiment 1. Instead, we conclude that subjects in Experiment 1 used metaknowledge to report the best stored items first. Thus, the final responses in the subject-ordered conditions contained no detectable information about the target.

3.2.2. Subjective ratings of guessing again predict uniform-distributed responses

Experiment 2 replicated the finding that participants’ subjective ratings of guessing strongly corresponded with mixture-model estimates of a guessing parameter. We fit a mixture model to each response within each set size (i.e. Set Size 2 first response, Set Size 2 second response, etc.), and we quantified the percentage of responses that the subjects reported guessing with a mouse button click. In line with the earlier results, we found a tight relationship between participants’ subjective reports of guessing and the mixture model’s estimation of a guess state. One subject in Experiment 2a showed no relationship between confidence ratings and mixture model parameters, because they reported that every item was not a guess (they did not use both buttons). This subject was not included in metaknowledge analyses. On average, the strength of the within-subject correlation was r = .91 (SD = .03, all p-values < .001) in Experiment 2a and r = .94 (SD = .06, all p-values <.001) in Experiment 2b. Once again, subjects were slightly over-confident. When plotting the model’s guessing parameter on the x-axis, the average slope was 0.89 (SD = .16) for Experiment 2a and 0.70 (SD = .25) for Experiment 2b; the average intercept was −.01 (SD = .13) for Experiment 2a and −.06 (SD = .04) for Experiment 2b.

If the guessing we observed in Experiment 1 was due to output interference, then purely uniform error distributions should remain concentrated in the final responses of the trial even when the order of report was randomized in Experiment 2. By contrast, if the drop in performance across responses in Experiment 1 resulted from a bias to report the best remembered items first when subjects controlled response order, then guesses should be evenly distributed across responses in Experiment 2 when response order was randomized. This predicts that there should be some trials in which the best stored items happened to be probed last while items that could not be stored were probed first. Such a pattern of results could not be explained by an output interference account. Thus, we used subjects’ confidence ratings to identify two types of trials from Experiment 2: (1) Trials where the three items probed late in the trial were guess responses and (2) Trials where the three items probed early in the trial were guess responses. We took these trials across subjects and binned them together, then tested whether a uniform distribution best fit each response in the trial. Consistent with a mnemonic variability account of Experiment 1, we found that uniform error distributions occurred early -- but not late -- in the trial when participants reported guessing for the early responses (Fig. 9). Likewise, when participants indicated that they were guessing during the final three responses, purely uniform distributions were observed for the last three – but not the first three – responses. BIC values are listed in the supplementary materials, Tables S4 and S5. Thus, Experiment 2 showed that guessing prevalence was decoupled from response order, arguing against an output interference account of the observed uniform distributions. This analysis also gives insight into subjects’ metaknowledge accuracy; subjective confidence ratings nicely tracked the location of guess response (early versus late). However, these ratings were imperfect; “confident” responses still contained a sizeable uniform component, indicating that participants sometimes had less information in mind than they reported, converging with earlier evidence (Adam & Vogel, 2017).

Figure 9. Response distributions for set-size 6 trials in Experiment 2, split by when participants reported guessing.

Trials are binned by whether participants reported the first three responses as guesses (top row) or the final three response as guesses (bottom row) in (A) Experiment 2a and (B) Experiment 2b.

3.2.3. The role of instructions in guessing

Experiments 1 and 2 both provided compelling evidence that participants do not remember all items with a set size of 6 items, and that the observed guesses were not a result of output interference. Nevertheless, we also considered whether the specific instructions subjects received in our study may have influenced their tendency to guess. In both experiments, we asked participants to make a dichotomous “some” or “no” information confidence judgment. Gathering confidence ratings was extremely useful for validating the relationship between subjective guessing states and mixture model estimates of guess rates. However, we also wanted to assess whether instructions that emphasized the possibility of guessing may have artificially encouraged guessing behaviors. To test this possibility, we ran a similar whole report procedure in which we eliminated the meta-knowledge assessment and participants were instructed to never randomly guess.

4. Experiment 3

4.1. Materials & Methods

Ten participants from the University of Chicago community participated in Experiment 3 for payment ($10/hour). Stimuli and procedures were nearly identical to Experiment 1b; participants were asked to remember the orientation of 1, 2, 3, 4 or 6 items and to report all items in any order they chose. However, participants did not make confidence ratings using the two mouse buttons. During the instruction period, the experimenter instructed the participants that they should remember all of the items. Participants were instructed: “Even if you feel you have no information in mind, do your best when making your responses. Even the information that you have in mind is extremely imprecise, it will still lead you in the right direction.”

4.2. Results & Discussion

Even though participants were not instructed to dichotomously report guess states, we still observed responses that were best described by a uniform distribution (Fig. 10). Using a BIC approach to compare the fit of a uniform distribution with the fit of a mixture model, we found a mean of 2.6 uniform distributions (SD = .97, range from 1 to 4). Non-parametric tests of uniformity agreed with this number. To conclude, the key finding that some working memory responses are best fit by a uniform distribution was not a result of instructions that allowed for the possibility of guessing.

Figure 10. Number of uniform representations for Set Size 6 in Experiment 3.

(A) Histogram of subjects’ total number of Set Size 6 responses that were best fit by a uniform distribution. (B) Number of subjects’ responses best fit by uniform distributions as a function of response number.

5. Simulation results: Variable precision models mimic guessing behaviors by positing very low precision memories

Across several experiments, we have shown that guessing accounts for a large proportion of subjects’ responses when working memory load is high (e.g. ~50% of Set Size 6 responses). This result is apparently in conflict with past findings that a variable precision model that denies guessing (hereafter called “VP-no guessing”) is a strong competitor for models that presume a high prevalence of storage failures (van den Berg et al., 2014). How does the VP-no guessing model achieve close fits of these aggregate error distributions? We hypothesized that the VP-no guessing model may succeed by postulating memories that are so imprecise that they cannot be distinguished from random guesses. Indeed, others have noted that this is a potentially troubling feature of VP models (Nosofsky & Donkin, 2016b; Sewell et al., 2014). To test this hypothesis, we implemented a VP-no guessing model to fit the aggregate error distribution from Experiment 1a. This provided a clear view of the range of precision values used by this model to account for performance with six items. Next, we assessed what percentage of these memories could be distinguished from random guesses with varying amounts of noise-free data. To anticipate the findings, the VP-no guessing model posits memories that are undetectable within realistic experimental procedures, and it does so at a rate that tracks the guessing parameter within a standard mixture model.

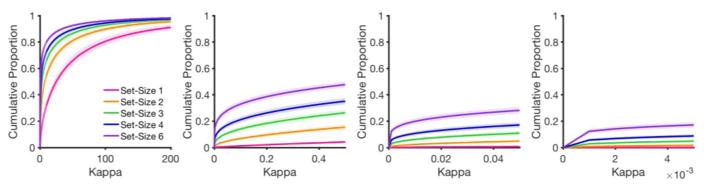
Using code made available from van den Berg et al. (2014, code accessed at http://www.ronaldvandenberg.org/code.html), we fit the VP-no guessing model to individuals’ aggregate data (i.e. combining all responses for a given set size) from Experiment 1a. The variable precision model proposes that precision for each item in the memory array is von Mises-distributed with concentration κ. The precision of the von Mises for each item in the memory array is randomly pulled from a range of possible precision values. The range of possible precision values is determined by a gamma-distributed higher-order distribution, and the shape of this gamma distribution changes with different numbers of target items. This particular implementation of the variable precision model fits parameters while simultaneously considering performance across all set sizes. For Set Size 1 memory arrays, the gamma distribution contains mostly high precision von Mises distributions; for larger memory arrays, the gamma distribution contains a larger proportion of low precision von Mises distributions (Fig. 11).

Figure 11. Cumulative distribution functions for the variable precision model across set sizes.

X-axis represents the concentration parameter of the von Mises distributions pulled from the higher order gamma distribution. Y-axis represents the cumulative proportion of trials in which a given concentration (κ) or less is pulled. From left to right, the scale of the x-axis is zoomed in to better illustrate the proportion of very low precision representations that make up each higher-order distribution. Shaded error bars represent 1 Standard Error.

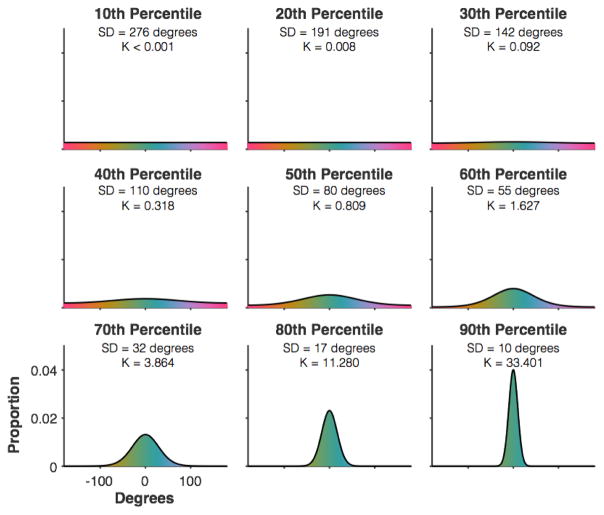
For this analysis, we focused on the higher-order distribution of precision values for the Set Size 6 condition. We found that the VP-no guessing model posits a high prevalence of representations with exceedingly low precision. To further visualize this point, we computed decile cut-offs for each participant, and then took the median value for each decile cut-off across participants. Figure 12 shows the probability density function for each decile of von Mises distributions posited by the VP-no guess model. As can be seen, the von Mises PDF appears, by eye, to be perfectly flat for a large proportion of Set Size 6 trials (20 –30%). Critically, this PDF visualization is hypothetical in that it assumes infinite numbers of samples from a von Mises PDF, and with infinite numbers of trials we can easily distinguish a diffuse von Mises distribution (e.g. 40^th Percentile, K = .318) from a uniform distribution. However, if we were to experimentally sample “trials” from the hypothetical PDF, our ability to distinguish this distribution from uniform would depend on the number of samples. Below, we show that variable precision models that deny guessing must postulate a very high prevalence of memory representations that cannot be detected with a feasible behavioral study.

Figure 12. Illustration of von Mises distributions used by the variable precision model to account for Set Size 6 performance.

Precision values of the von Mises distributions are given as both concentration (K) and standard deviation (SD) in degrees.

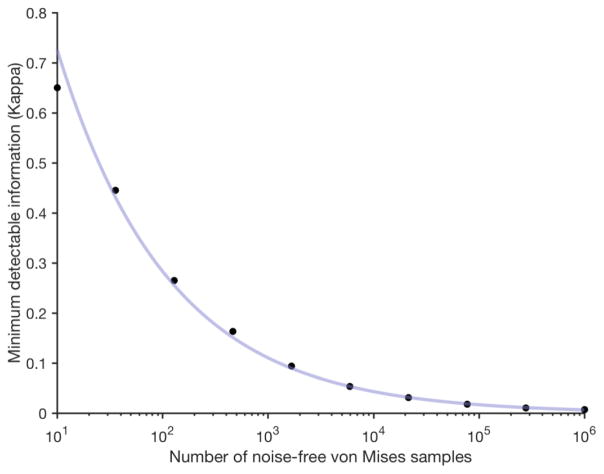
To illustrate how poor the VP-no guessing model’s hypothesized representations are, we ran simulations in which we used varying amounts to data to discriminate between a von Mises distribution of precision κ and a uniform distribution. We did so for a range of precision values and a range of trial numbers. We chose 10 log-spaced bins between 10 and 1,000,000 samples (“trials”), and we ran 200 iterations of randomly sampling trials from a von Mises distribution with various concentrations (κ). For each iteration, we compared the fit of the von Mises to the fit of a uniform distribution using BIC comparison in MemToolbox (Suchow et al., 2013), and we took the difference score in BIC fits for the uniform and the von Mises distributions. We defined our ability to discriminate from uniform as the precision value at which the 95% Confidence Intervals for a given number of trials remained in favor of the uniform. Discriminable precision values are shown as a function of the number of samples in Figure 13. With only 10 samples from a von Mises PDF, we could discriminate between uniform and a von Mises with κ = 0.65 (SD = 88 degrees). With 1,000,000 samples from a von Mises PDF, we could discriminate between uniform and a von Mises with κ = 0.007 (SD = 193 degrees). That is, a concentration of less than κ < .007 is so diffuse that the central tendency is undetectable with 1,000,000 samples of noise-free data sampled from a true von Mises distribution. Of course, because these simulations presume noise-free data, these simulations overestimate the true detectability of these putative representations in a real experiment.

Figure 13. The minimum detectable amount of information (Kappa) needed to distinguish a von Mises distribution from uniform as a function of the number of noise-free von Mises-distributed samples.

The fitted line is the linear fit of the log-transform of the sample number and the log-transform of the precision threshold.

Finally, we determined the prevalence of effectively undetectable memories for each subject (defined as those requiring at least one million trials to discriminate from uniform). On average, 22.0% (SD = 11.2%) of VP-no guessing distributions had a precision less than or equal to κ =.007, and this percentage ranged from 7.0% to 46.3% of a subjects’ higher-order distribution values. Further, the proportion of these representations was tightly coupled with mixture model estimates of the guess rate for Set Size 6 (r = .81, p <.001), underscoring the possibility that the VP-no guessing model is mimicking random guesses. Thus, although the VP-no guessing models can achieve close fits to aggregate error distributions, their success depends on the assumption that a substantial number of these memories would be literally undetectable with a feasible behavioral paradigm.

In cases of model mimicry, it is important to question which model is the mimic. Could it be that models endorsing guessing are mimicking low precision representations? We offer three arguments to the contrary. First and foremost, the whole report data from Experiments 1 and 2 revealed a high prevalence of error distributions that were best modeled by a uniform distribution with zero free parameters. Thus, while it has been difficult to adjudicate between models that endorse and deny guessing with the aggregate error distributions generated by partial-report studies, (van den Berg, Awh and Ma, 2014), whole report data provide clear positive evidence that the modal subject guesses about half of the time for Set Size 6. Second, participants report that they were guessing, and these subjective reports were excellent predictors of simple mixture-model estimates of guessing rates (Experiments 1 and 2). We contend that subjective judgments of whether an item has been stored are decidedly relevant for characterizing the contents of a memory system that is thought to hold information “in mind” (however, see general discussion for limitations to this claim). Finally, we think it’s reasonable to question the plausibility of “memories” that are as imprecise as those posited by variable precision models that deny guessing. For example, the VP-no guessing model requires that the worst memory out of six simultaneously-presented items would have a standard deviation of around 230 degrees. Based on our earlier simulation of trial numbers and precision values, this means that an ideal observer would require over 900 million trials to produce above-chance performance in detecting the largest possible difference in color or orientation (e.g., red vs. green, or horizontal versus vertical). At the least, there may be a consensus that such homeopathic amounts of information would be of little use for purposeful cognitive tasks.

6. General Discussion

Understanding the nature of capacity limits in working memory has been a longstanding goal in memory research. The capacity debate has been dominated by a theoretical dichotomy of “number” versus “precision.” Discrete resource models have argued that capacity is limited by the number of items that can be concurrently stored, and that subjects to resort to guessing when more than a handful of memoranda are presented (Fukuda, Awh, & Vogel, 2010; Zhang & Luck, 2008). By contrast, continuous resource models argue that mnemonic resources can be distributed amongst an unlimited number of items(Bays & Husain, 2008; van den Berg et al., 2012; Wilken & Ma, 2004). In addition, there is a growing consensus that mnemonic precision varies across items and across trials (e.g. Bae et al., 2014; Fougnie et al., 2012). In the present data, for example, item-by-item varations in precision were plainly demonstrated. However, variable mnemonic precision is compatible with both discrete resource models that propose an item limit and continuous resource models that allow for the storage of unlimited numbers of items. In sum, despite a proliferation of work a key aspect of the number/precision theoretical dichotomy has remained unresolved: Do participants guess? If so, do we need capacity limits to explain guessing behavior? Even some of the most sophisticated modeling efforts have reached a stalemate (van den Berg et al., 2014).

In this context, our findings provide compelling evidence that the modal subject guesses about half of the time with a memory load of six items. This confirmation of the guessing construct is critical for the broader idea that working memory performance differs both in terms of the number and the precision of the representations that are stored. Further, the variations in the number of items that individuals could store (2 – 5 items) aligned closely with past estimates of items limits in visual working memory (Cowan, 2001; Fukuda et al., 2010; Luck & Vogel, 1997; Zhang & Luck, 2008). Finally, Experiments 2a and 2b showed that output interference could not explain the powerful decline in mnemonic performance across responses that resulted in uniform distributions. While there was some evidence of output interference when all items were probed in a random order, it could not account for the dramatic declines in performance that were observed when subjects chose the order of their response. Thus, while past studies have shown that aggregate error distributions can be equally well fit by competing models that endorse and deny guessing behaviors, our whole report procedure provided unambiguous evidence for a high prevalence of guessing responses.

The finding that individual differences in capacity yielded similar findings to previous estimates rules out two key classes of models. First, this provides compelling evidence against “no guessing” models in which participants are able to store all items in the array. To account for individual differences in performance, “no guessing” models posit that participants with poor working memory performance have less precise memories, but store some information about all presented items. Our findings clearly rule out such a model; we did not find any participants for whom a “no guessing” model was best. Second, these results constrain models of trial-by-trial variability in performance. Some models have proposed that effective capacity (i.e. the number of stored items) varies from trial to trial, and it could do so in several ways. Models that include guessing while denying item limits propose that the number of stored items varies dynamically from trial to trial but is not limited by an upper bound. For instance, trial-by-trial performance may be Poisson- or uniform-distributed (van den Berg et al., 2014). On the other hand, item-limited models propose that performance varies from trial to trial, but only in one direction – below the capacity limit for each individual (Adam et al., 2015). Critically, the first class of models (dynamic but capacity-unlimited) also yield the prediction that the majority of subjects should show non-uniform distributions at all 6 response positions. Instead, we find support for the latter model (dynamic but capacity-limited); there is still some degree of guessing for early responses, indicating that subject frequently under-perform their maximum capacity. However, participants do not over-perform past a hypothetical “mean limit”, as shown by the pure uniform error distributions we observed for late response in the set size six condition.

Interestingly, objective estimates of guessing dovetailed with the subjects’ own reports of whether they had any information about the item in question. The frequency with which subjects endorsed guessing precisely tracked the guess rate as estimated by a standard mixture model (Zhang and Luck, 2008). Note, the alignment of the guessing parameter and subjective guess reports alone cannot distinguish between a guessing account and a variable precision account of working memory limits. For example the variable precision model might posit that participants will choose the “guess” label whenever mnemonic precision does not pass a certain threshold. However, the precise alignment of subjective ratings with the mixture model’s guess parameter greatly bolsters the face validity of the mixture model’s guessing parameter.

There is a growing consensus that working memory responses have variable precision. In particular, many recent papers have found that a large amount of variability in working memory precision may arise from stimulus-specific differences, such as color categories, orientation categories, or verbal labels (Bae et al., 2015, 2014; Donkin, Nosofsky, Gold, & Shiffrin, 2015; Hardman, Vergauwe, & Ricker, 2017; Pratte, Park, Rademaker, & Tong, 2017). However, there is growing doubt as to whether variability in precision is due to variations in the allocation of a mnemonic resource per se, as opposed to lower level differences in the quality of encoding or the imposition of categorical structure for different types of stimuli. For instance, recent work by Pratte and colleagues (2017) measured performance in a task that required the storage of orientations in working memory and replicated earlier work showing variability in precision across concurrently stored items in working memory. Rather than presuming that this variability reflects variation in the allocation of mnemonic resources per se (van den Berg et al., 2012), Pratte et al. showed that much of this variability was explained by higher precision for orientations near the horizontal and vertical meridians. This observation falls in line with the “oblique effect” that has been documented in past studies of visual perception (Appelle, 1972). Strikingly, when the oblique effect was incorporated into competing discrete and continuous resource models, discrete models that endorsed guessing were the clear winner of the model competition. In other words, once stimulus-driven sources of variable precision were acknowledged, the best account of the data posited a high prevalence of guessing responses.

Clear evidence for guessing in a working memory task has important implications for our taxonomy of the processes that determine memory performance. In past work, putative item limits in working memory have been argued to predict variations in fluid intelligence, scholastic achievement, and attentional control (e.g. Cowan et al., 2005; Engle et al., 1999; Fukuda, Vogel, Mayr, & Awh, 2010; Unsworth, Fukuda, Awh, & Vogel, 2014). A simple interpretation is that a common mental resource determines the number of items that can be stored in working memory and one’s ability to handle a variety of cognitive challenges. According to continuous resource models, however, it is not possible to measure individual differences in the number of items that can be stored in working memory, because all observers can store all items regardless of set size. By this account, the apparent variations in the number of items that can be maintained are an illusion created by limitations in memory quality. Thus, continuous resource models explicitly argue that individual differences in memory performance will be explained by a single factor that determines memory quality.

Evidence from Awh et al. (2007) challenged the idea that memory quality is the determining factor of working memory limits. They measured performance in a change detection task while manipulating the size of the changes that occurred in the test display. When changes were very large, they reasoned that subjects should be able to detect the change whenever the probed item had been stored, because precision should not be a limiting factor. When changes were relatively small, however, they reasoned that successful change detection would be limited more by memory quality, because more precise memories would be needed to detect a relatively small mismatch between the sample and test. By contrast, a continuous resource model asserts that precisely the same mnemonic resource determines performance with small and large changes, because there is no limit to the number of items that can be stored. Disconfirming this prediction, Awh et al. (2007) found that performance with big and small changes was completely uncorrelated, despite having positive evidence that both scores were reliable. This finding has since been extended by looking at the pattern of errors to big-change and small-change trials across multiple response probabilities (Nosofsky & Donkin, 2016a); participants frequently endorse that large changes are “the same” on big-change trials, even though they are capable of discriminating much smaller changes. Thus, number and precision may represent distinct facets of working memory ability.

Memory precision does not seem to be the limiting factor for detecting changes within displays, and there is also little evidence that precision predicts individual differences in working memory performance. Fukuda, Vogel, et al. (2010) carried out a latent variable analysis of a variety of change detection tasks that required the detection of either very large or small changes. This analysis revealed distinct factors for the detection of large and small changes, with no reliable cross loading between these factors. This result provides a robust confirmation of the earlier finding, suggesting that number and resolution may indeed be dissociable aspects of memory ability. Moreover, Fukuda, Vogel, et al. (2010) found that while the number factor was a robust predictor of fluid intelligence, there was zero evidence for such a link between precision and fluid intelligence. Likewise, capacity is reduced but precision is spared in people with schizophrenia (Gold et al., 2010). Thus, a two-factor model that distinguishes between the number of items stored and the precision of those mnemonic representations is needed to account for performance with large and small changes, and these two factors have unique relationships with fluid intelligence.

In conclusion, we present clear evidence for a high prevalence of guessing responses in a visual working memory task. When subjects were allowed to choose the order of report in a whole report memory task, we observed a monotonic decline in memory performance with each successive response, and the modal observer produced uniform error distributions – the hallmark of guessing – for three of the items in a six item display. Control experiments ruled out the hypothesis that output interference generated this monotonic decline in performance across responses; modest evidence of output interference was observed, but it accounted for only a modest proportion of the decline across responses. Instead, we conclude that subjects used accurate metaknowledge to report the best remembered items first. In turn, this yielded robust evidence of guessing behaviors when the last responses were examined, and supports the idea that working memory is subject to clear item limits.

Highlights.

• In a whole report task, participants report all items held in Working Memory (WM).

• We directly observed variable precision in working memory responses.

• For large arrays, many responses were best fit by a uniform guessing distribution.

• Robust evidence for guessing confirms the presence of item limits in WM storage.