Passive Acoustic Mapping with the Angular Spectrum Method

Abstract

In the present proof of principle study, we evaluated the homogenous angular spectrum method for passive acoustic mapping (AS-PAM) of microbubble oscillations using simulated and experimental data. In the simulated data we assessed the ability of AS-PAM to form 3D maps of a single and multiple point sources. Then, in the two dimensional limit, we compared the 2D maps from AS-PAM with alternative frequency and time domain passive acoustic mapping (FD- and TD-PAM) approaches. Finally, we assessed the ability of AS-PAM to visualize microbubble activity in vivo with data obtained during 8 different experiments of FUS-induced blood-brain barrier disruption in 3 nonhuman primates, using a clinical MR-guided FUS system. Our in silico results demonstrate AS-PAM can be used to perform 3D passive acoustic mapping. 2D AS-PAM as compared to FD- PAM and TD-PAM is 10 and 200 times faster respectively and has similar sensitivity, resolution, and localization accuracy, even when the noise was 10-fold higher than the signal. In-vivo, the AS-PAM reconstructions of emissions at frequency bands pertinent to the different types of microbubble oscillations were also found to be more sensitive than TD-PAM. AS-PAM of harmonic-only components predicted safe blood-brain barrier disruption, whereas AS-PAM of broadband emissions correctly identified MR-evident tissue damage. The disparity (3.2mm) in the location of the cavitation activity between the three methods was within their resolution limits. These data clearly demonstrate that AS-PAM is a sensitive and fast approach for PAM, thus providing a clinically relevant method to guide therapeutic ultrasound procedures.

I. Introduction

Focused ultrasound-induced microbubble oscillations (acoustic cavitation), either instigated by exceeding the pressure threshold for spontaneous cavitation activity in the targeted tissue [1], [2] or seeded by intravenously administered lipid-stabilized gas pockets [3], [4], superheated droplets [5] or other particles [6], offers the ability to noninvasively focus mechanical energy at cellular level. This localized energy deposition can be used to deliver drugs [7]–[9], fractionate tissue [2], lyse blood clots [10], amplify circulating biomarkers [11] and even remove amyloid plaque [12] and activate neuronal networks [13]. These applications, some of which are already entering Phase I clinical trials [14]–[16], suggest that the majority of mechanoreceptors found in living cells [17] may be responsive to forces exerted by microbubble oscillations. Thus, real-time methods to assess and visualize the inherently non-linear microbubble oscillations could both transform their use in the laboratory and warrant their safe and effective transition to the clinics.

During FUS exposure (sonication), microbubbles undergo stable or inertial volume oscillations (i.e. pulsations) that radiate strong, diverging spherical pressure waves (as much as ~ 10kPa) [18]. The information carried by these waves can be used to i) characterize the type of oscillations, as stable oscillations are accompanied with harmonic, ultra- and subharmonic emissions of the excitation frequency, and inertial oscillations are accompanied with broadband emissions [19], ii) localize the radiating bubbles, which act as point sources, and iii) potentially modulate the desired interaction noninvasively, as the strength of the emissions should also echo the strength of the oscillations, and by extension the deposited mechanical energy during the sonication. Passive acoustic imaging methods have the potential to combine this information, within a single image, and with very high sensitivity and specificity.

In passive acoustic imaging, the underlying idea is to exploit the (temporarily) coherent microbubble acoustic emissions recorded by receivers operated in passive mode (i.e. listening only) to form maps of microbubble activity, where the intensity is proportional to the strength of the emissions. The maps are formed on a point-by-point basis using a “delay and sum” operation, where the recorded RF-data from each element are delayed, then summed across different elements to produce a single trace that it is then squared and integrated to produce a single value per pixel. This time domain passive acoustic mapping (TD-PAM) algorithm has as input the entire bandwidth of the collected ultrasonic radiofrequency data (RF-data) [20]–[23]. The “delay and sum” operation has also been used for PAM in the frequency domain (FD-PAM), where the time delays are converted into a phase shift for each of the frequency components of the data (i.e., after taking the FFT of the RF data). With this approach specific frequency bands can be used to extract information about cavitation activity and location [24], [25]. An earlier method that is based on the Rayleigh-Sommerfeld integral can also be used for PAM in the frequency domain using a similar pixel-by-pixel operation [25].

For brain applications, skull-induced aberrations can be accounted for using anatomical information from CT scans [26], [27], while semi-quantitative methods that provide information about the relative strength of the emissions have already shown promising data [28], [29].

Despite the simplicity of the “delay and sum” operation, a major limitation of this approach comes from the fact that the algorithm runs on a time scale of the order of O(MxM), where M is the dimension of the image. Therefore, for large computational domains (i.e. image dimensions), which is always the case for the 2D and 3D clinical datasets, this method is inherently limited unless appropriate hardware is used to parallelize the computations [27]. Also, in order to provide frequency-selective passive acoustic maps, the unprocessed RF-data need to be filtered [30], which adds both complexity and processing time. While the frequency selectivity is solved with the FD-PAM, the time constraints of this algorithm remain [24]. To overcome these limitations new inherently fast and frequency selective methods are needed.

The angular spectrum (AS) method, a fast planar projection method, generally relates a field between two spatially separated planes by a projection operator in the frequency domain. Therefore, by knowing the field in one plane we can numerically estimate the field in other planes parallel to it. The AS method is a well-studied planar projection method for forward and back-propagation of acoustic fields [31]. It has been used for studying the acoustic field from ultrasound imaging probes and arrays in homogenous media [32], while several extensions for modeling spherical arrays [33] and propagation of sound in layered media have also been proposed and validated with experimental data [34]. A major advantage of planar projection methods, such as the AS method, is a substantial reduction in computation time compared to integral, such as the Rayleigh-Sommerfeld integral, or cross-correlation time domain approaches.

In the context of passive acoustic mapping, the AS method may offer several potential advantages. First, AS back-projection, due to the extensive use of the Fast Fourier Transform (FFT), runs in the order of O(M·log(M)), so the computational speed can be significantly higher than the time domain methods. This speed can be further augmented as the computations can be readily parallelized. Second, the AS method is a monochromatic back-projection method offering the possibility to perform reconstructions for frequency bands of interest (harmonic, ultra- and sub-harmonic) without the need for additional filtration. Third, through superposition, the AS approach can be extended to broadband emissions and, thus, be used for visualizing specific type of microbubble oscillations (stable or inertial) in the 3D space. While the latter two advantages are also present in the FD-PAM this method is still limited, by the time constraints of the delay and sum operation, albeit to a lesser extent by the TD-PAM. Superposition will increase total computation time for AS-PAM and FD-PAM with the number of frequency bins used.

In the present proof of principle study, the homogenous AS approach was evaluated for passive acoustic mapping using simulated and experimental data. In the simulated data, a point source with Gaussian envelope was propagated in homogenous media using a three-dimensional finite difference time domain numerical simulation. The propagated data were then collected by a virtual ultrasound imaging array, and the ability of the AS approach to form 3D maps of a single and multiple point sources was assessed in silico. Then, the AS approach for passive acoustic mapping (PAM) was assessed in the two dimensional limit and compared to the TD-PAM and FD-PAM first with simulations and then with experimental data. The experimental data were obtained during ultrasound-induced blood-brain barrier (BBB) disruption experiments in nonhuman primates using a clinical MRI-guided focused ultrasound (MRgFUS) system [22]. These comparisons aimed to validate the simulated data and demonstrate that the AS-PAM at frequency bands pertinent to different types of microbubble oscillations can predict different bioeffects.

From the above discussion it is evident that both ASPAM and FD-PAM are frequency domain methods, however for avoiding unnecessary confusion when comparing the two methods we will keep this terminology.

II. Material And Methods

A. Angular Spectrum Method

For time harmonic fields, the AS method, by substitution of the Helmholtz equation to the 2D Fourier integral, relates the acoustic field between two different planes with a transfer function (Fig. 1A). This operation is performed in the frequency domain using the angular spectrum of the recorded pressure at that plane and a transfer function [31], [32]. Therefore, by knowing the acoustic field in one plane (z₀) we can numerically estimate the field in other planes (z₁) parallel to it, as follows:

$$\mathrm{I}(\mathrm{x},\mathrm{y},{\mathrm{z}}_1,\omega )=\sum _{\forall \omega }{\left|{\text{FFT}}^{-1}\left\{{\mathrm{S}}_{{\mathrm{z}}_0}(\omega )·{\mathrm{e}}^{\mathrm{i}({\mathrm{z}}_1-{\mathrm{z}}_0)\sqrt{({\omega }^2/{\mathrm{c}}^2)-{\mathrm{k}}_{\mathrm{x}}^2-{\mathrm{k}}_{\mathrm{y}}^2}}\right\}\right|}^2,$$ (1)

where S_z0 (ω) is the frequency domain representation (i.e. 2D FFT) of the signal received by the array in the z₀ plane, ω is the angular frequency of a single radiating frequency component and the symbol ∀ω (“for all”) indicates summation (i.e. superposition) over all emitted frequencies (it can be replaced by a frequency band or performed for a single frequency), c, is the speed of sound, k, the wave number. The term FFT⁻¹ represents the 2D inverse FFT, and the exponential term $\left(exp\left(\mathrm{i}({\mathrm{z}}_1-{\mathrm{z}}_0)\sqrt{\left({\omega }^2/{\mathrm{c}}^2\right)-{\mathrm{k}}_{\mathrm{x}}^2-{\mathrm{k}}_{\mathrm{y}}^2}\right)\right)$ is the transfer function (or spectral propagator [35]). This formulation could also be used for 1D back-projections (y = 0,k_y = 0; 1Darray), while aliasing and wraparound errors associated with the FFT can be accounted for by sampling above the Nyquist limit and using zero padding [36].

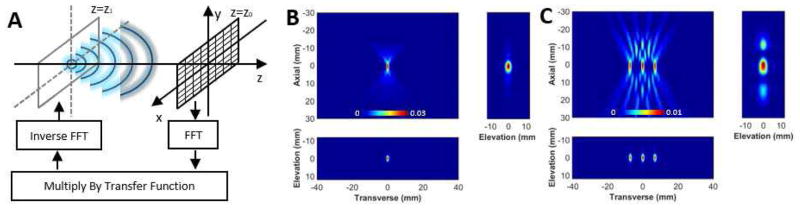
Fig. 1.

Insilico 3D passive acoustic mapping with the angular spectrum method. A) Graphic representation of the AS-PAM. The microbubble (point source) is at z=z₁, and the plane of the ultrasound imaging array is at z=z₀. First, the FFT of the recorded RF-data is determined. Then, it is multiplied with the transfer function. Finally, after an inverse FFT, the location of the microbubbles can be estimated. To form 2D and 3D images, these steps are repeated for different depths (z). B) 3D AS-PAM of a single point source. C) 3D AS-PAM with three point sources separated by 4 wavelengths. The image dimensions were x=200, y=650, t=1800; dt=23nsec; f-Nyquist=22 MHz. The back-propagation for a field of view of 25×80×70 mm, with 0.125 mm pixel size, in x and y direction and 0.55 mm, in z direction, was performed in 4.5s. All color maps are linear and expressed in a.u..

For passive acoustic mapping using the RF-data recorded by an ultrasound imaging array, several assumptions are needed. First, for 2D back-projections, the microbubbles oscillations occur in a plane parallel to the 2D array and, for 1D back-projections, in the imaging plane of the linear array. Next, multiple scattering is negligible (relatively weak emissions) and the wave travels in non-dissipative homogeneous media.

B. Time Domain Method

Using the time domain approach, the 2D image is also formed on a point-by-point basis using a “delay and sum” operation described here [20], [22]:

$$\mathrm{I}(\mathrm{x},\mathrm{z})=\sum _{\mathrm{t}=0}^{\mathrm{t}=\mathrm{T}}\left({\left|\sum _{\mathrm{i}=1}^{\mathrm{N}}\mid {\overrightarrow{\mathrm{r}}}_{\mathrm{n}}-\overrightarrow{\mathrm{r}}\mid ·\stackrel{\sim }{p}\left({\mathrm{r}}_{\mathrm{n}},\frac{\mid {\overrightarrow{\mathrm{r}}}_{\mathrm{n}}-\overrightarrow{\mathrm{r}}\mid }{{\mathrm{c}}_0}\right)\right|}^2-{\left|\mid {\overrightarrow{\mathrm{r}}}_{\mathrm{n}}-\overrightarrow{\mathrm{r}}\mid ·\stackrel{\sim }{p}\left({\mathrm{r}}_{\mathrm{n}},\frac{\mid {\overrightarrow{\mathrm{r}}}_{\mathrm{n}}-\overrightarrow{\mathrm{r}}\mid }{{\mathrm{c}}_0}\right)\right|}^2\right),$$ (2)

where r is the location of the point to be imaged, r_n is the location of the N array elements (transducers), p̃ are the passively recorded acoustic emissions by the n^th element in r_n location, N is the size of the array, $\mathrm{t}=\frac{\mid {\overrightarrow{\mathrm{r}}}_{\mathrm{n}}-\overrightarrow{\mathrm{r}}\mid }{{\mathrm{c}}_0}$, c₀ the speed of sound and T is the length of the recoded emissions. The multiplicative term |r − r_n| describes geometric wavefront loss. For a linear array (2D image), the three-dimensional vectors r are converted to image coordinates x (transverse) and z (axial) as follows $\mid \mathrm{r}-{\mathrm{r}}_{\mathrm{n}}\mid =\sqrt{{(\mathrm{x}-{\mathrm{x}}_{\mathrm{n}})}^2+{\mathrm{z}}^2}$; y = 0. In the current implementation, the AS-PAM does not account for the geometric wavefront loss. To compare the different algorithms this term, in the TD-PAM, was set to unity. The second term in Eq. 2 is used for subtracting incoherent background noise (i.e. the dc component) [37]. While, this formulation can be readily extended to account for skull-related aberrations [26], in the current implementation we used a constant speed of sound.

C. Frequency Domain Method

In FD-PAM an image is formed at each frequency using the “delay and sum” operation which is carried out in the frequency domain [24], [25]:

$$\mathrm{I}(\mathrm{x},\mathrm{z},\omega )=\sum _{}\left({\left|\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mathrm{S}}_{\mathrm{n}}(\omega )\mathrm{A}({\overrightarrow{\mathrm{r}}}_{\mathrm{n}},\overrightarrow{\mathrm{r}},{\mathrm{S}}_{\mathrm{n}})exp\left(\mathrm{i}\omega \frac{\mid {\overrightarrow{\mathrm{r}}}_{\mathrm{n}}-\overrightarrow{\mathrm{r}}\mid }{\mathrm{c}}\right)\right|}^2-\sum _{\mathrm{n}=1}^{\mathrm{N}}{\mid {\mathrm{S}}_{\mathrm{n}}(\omega )\mathrm{A}({\overrightarrow{\mathrm{r}}}_{\mathrm{n}},\overrightarrow{\mathrm{r}},{\mathrm{S}}_{\mathrm{n}})\mid }^2\right),$$ (3)

Here S_n (ω) is the frequency domain representation (i.e. 1D FFT) of the signal received on element n located at r_n as described above (Eq. 1), and A(r⃗_n,r⃗, S_n) is an optional apodization term. The time delays applied to the signal for each point in the image r⃗ are converted to phase shifts on the order of exp(iωt) in the frequency domain, where t = |r⃗_n − r⃗|/c gives the propagation time from each point in the image to the current element at a speed of sound c. Images may be formed at a single frequency of interest ω or summed over several frequencies after formation. Note that this version of the algorithm is very fast as the data are delayed in the frequency domain and summed over specific frequency bands, which eliminates the summation across the recorded RF-data of elements. The second summation term represents the DC component of the signal in a similar manner to the time domain method below. In the current implementation AS- and TDPAM do not include apodization terms, so A(r⃗_n,r⃗, S_n) was set to unity to allow comparison of the three methods.

It is important to clarify the AS-PAM is also a frequency domain method that uses a spectral propagator to form 2D images on line-by-line basis (or plane-by-plane in 3D) instead of a “delay and sum” operation that forms images on a point-by- point basis. From Eqs. 1 and 3 it is evident that the two methods should provide equivalent results.

D. Simulated Data and Procedures

A full three-dimensional finite difference time domain numerical simulation for linear acoustic propagation in heterogeneous, thermo-viscous media was used to numerically excite and propagate a synthetic point source towards a virtual 2D imaging array. The numerical simulation was developed and implemented in Matlab (The MathWorks, Natick, MA, USA), using previously-described methods [26]. The synthetic point source was generated using the “gauspuls” function in Matlab. In the current simulations, the propagation medium was uniform (tissue), the central frequency of the Gaussian point source was 0.88 MHz, and the virtual 2D imaging array was located near the end of the simulation grid. The simulations were performed using a single point source or multiple sources placed 35 mm away of the virtual array.

Using the data collected by the virtual array, we performed 2D planar projections with the AS-PAM algorithm (Eq. 1) for different depths. By stacking the planes one after the other we assessed its ability to visualize the location of the synthetic point source in 3D space. The reconstructed field of view was 25×80×70 mm, with a 0.125 mm pixel size in the x and y directions and 0.55 mm in the z direction. No binning was performed in the 3D maps. The sampling frequency in the simulated data was dictated by the numerical stability of the FDTD and was equal to 43 MHz.

Next, we tested AS-PAM in the 1D limit (y = 0, k_y = 0) using the data from the elements (1D array) that were in the same plane with the point source. To simulate the effects of spatial averaging across each of the 128 elements, these data were binned to 128 elements and used as inputs to the 1D AS-PAM reconstruction. For comparison, the same data were also used as inputs to the TD-PAM and FDPAM algorithms (Eqs. 2–3). Note that without the binning the TD-PAM is prohibitively computationally expensive due to excessive number of summations required to form the images. No other processing was performed. For all reconstructions we used a speed of sound of tissue of 1541m/s. The three back-projection methods were compared in terms of temporal and spatial resolution. Further, on a line by line basis, we added different levels of white Gaussian noise to the collected data, using the “awgn” function in Matlab, and assessed the ability of the three different PAM methods to localize the point sources at very high noise levels.

E. Experimental Methods and Procedures

The experimental data were collected as described in a previous study that investigated passive acoustic mapping during ultrasound-induced blood brain barrier disruption in rhesus macaques [22]. Briefly, a clinical MRI-guided focused ultrasound (MRgFUS) system (ExAblate 4000 low frequency, InSightec, Haifa, Israel), which was integrated with a clinical 3T MRI unit (GE Healthcare), was modified to provide the low-power sonications required for this application. This system, which uses a 1024-element phased array transducer, operates at a central frequency of 220 kHz and was driven in burst mode. This system is currently in Phase I clinical trials to deliver liposomal chemotherapy to gliomas using similar methods and procedures used here [16]. Briefly, a series of 10 ms bursts (100 bursts in total) were applied at a pulse repetition frequency of 1 Hz and acoustic power level of 1–2 W, which yielded an estimated peak negative pressure amplitude in the brain of 200–400 kPa [29]. Each sonication was combined with the microbubble ultrasound imaging contrast agent Definity (Lantheus Medical Imaging, North Billerica, MA, USA) at a dose of 40 μl/kg, as described before [38].

A research ultrasound imaging system (Verasonics, Redmond WA, USA) was programmed in Matlab to operate in passive mode to acquire the RF-data for the acoustic mapping. The ultrasound imaging probe (L382, Acuson, WA, USA) used in this study was a 128-element (82 mm) linear array with a 3.21 MHz central frequency and a bandwidth of approximately 75%. The array was incorporated into the therapeutic MRg-FUS phased array with an acoustic mirror (Fig. 3A). Only 64 elements could be used synchronously in receive. The ultrasound imaging array was approximately 120 mm away from the targeted regions (point source), similar to what is to be expected under clinical conditions. The two systems were synchronized using an external trigger and the first 180 μs of ultrasonic RF-data were recorded for each burst (50 overall) [22]. The sampling frequency in the experimental data was dictated by the imaging system (4x the central frequency of the US probe: 12.84MHz).

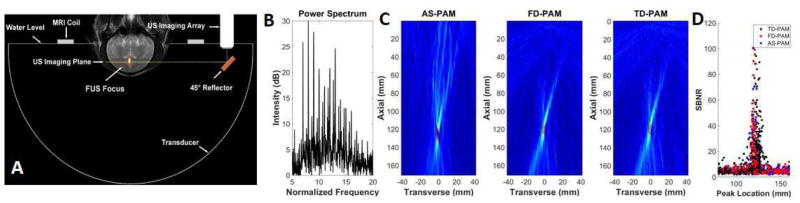
Fig. 3.

Invivo 2D passive acoustic mapping. A) The experimental setup used to test AS-PAM in vivo. A coronal T2-weighted MR image has been annotated to show the location of the FUS transducer and its focal region, the ultrasound imaging array that was connected to the research imaging engine, and the MRI surface coil. The annotations were drawn to scale with the location of the head in a typical position. B) The power spectra of the microbubble acoustic emissions used to perform passive acoustic mapping. C) AS-PAM (left) with all frequency components, FD-PAM (middle) with all frequency components and TD-PAM (right). In AS-PAM we superimposed the maps from all the available frequencies (1.2 MHz- 4.2 MH). D) The location of the peak value in the axial direction for all the maps as a function of the signal-to-noise ratio (SBNR).

The recorded RF-data were high-pass filtered (880 kHz cutoff frequency) to remove the 220 kHz MRgFUS frequency and electronic noise that happened to reside in the 500–800 kHz frequency band. No comb filtering or rejection of any specific spectral band was used in the emissions. Therefore, in the presence of broadband emissions, all possible types of oscillation, including inertial cavitation, will likely to be present in the maps. While the AS and FD approaches do not require filtered data, for comparison with TD-PAM, in all maps presented we used the filtered RF-data.

Earlier studies with this system demonstrated that imaging via the temporal bone in macaques resulted in minimal aberrations and good localization accuracy of microbubble activity at the focus of the MRgFUS system can be attained with TDPAM using the average speed of sound of the propagation media [22], [28]. The same average speed of sound (1537 m/s) was used in all reconstructions (Eqs. 1–3). It was estimated by the linear combination of the thicknesses and sound speeds in the water, brain tissue, and bone that were measured from MR and CT data [22].

For the AS- and FD-PAM reconstructions with the experimental data, we used two different approaches. In the first, we performed a frequency sweep with all the available frequencies (1.5 MHz– 4.2 MHz) and superimposed all the maps (480 frequency bins or 480 back-projections). In the second, the maps containing harmonic, ultra-harmonic and broadband frequencies were formed separately. For the harmonic and ultra-harmonic maps, we superimposed the maps from the 6^th – 19^th harmonic or ultra-harmonic of the MRgFUS frequency. For each case, to account for spectral leakage we used ±1 frequency bin (±6.3 kHz), which resulted in 42 frequency-selective reconstructions. The broadband or inharmonic emissions were defined as the emissions between the harmonic and ultra-harmonic frequency bands. For comparison, we used the same number of frequency bins (#42) across the spectrum (1.32–4.2 MHz). The frequency bands for one harmonic, ultra-harmonic and an equivalent broadband emissions are shown in Suppl. Fig. 1A. Therefore, in the second approach, for each data set (180 μs RF-data) we performed 126 back-projections in total and formed 3 maps composed of only harmonic, ultra-harmonic and broadband emissions.

In all maps, the axial × transverse field of view was set to 170×80 mm, which included the entire monkey head in the image. The distance between the targeted tissues and the imaging array was 120 mm. For all reconstruction approaches, the background data collected before the administration of the microbubbles were subtracted by the maps acquired with microbubbles.

In the current implementation, the maximum spatial frequencies that could be resolved were according to Nyquist limit: f_max = 1/(2 · dx) = 0.78mm⁻¹ as this this spatial frequency was above the diffraction limit. The cavitation maps appeared elongated along the axial direction of the array, which was perpendicular to the MRgFUS beam axial direction, due to the diffraction pattern of the array and not the pixel spacing in this direction. Nonlinear terms were not observed in any of these baseline maps. Zero padding with 512 elements was found to correct wraparound errors associated with the FFT in the AS-PAM. All the computations were performed using the computer used to control the Verasonics research platform, which had 12 GB memory and two 2.67 GHz CPUs (Mac Pro, Apple Inc., CA, USA)

F. MR Imaging

MRI was performed before the animal experiments for treatment planning. We used a 3D fast spoiled gradient echo sequence with inversion recovery preparation (TR/TE/TI: 5.3/2.0/600 ms, FA: 10°, FOV: 12 cm, matrix: 128×128, slice thickness: 2 mm) or a multi-slice T2-weighted Fast Spin Echo (FSE) sequence (TR/TE: 4500/85.8 ms; echo train length, ETL: 8; field of view, FOV: 12 cm; matrix: 256×256, slice thickness: 3 mm) for this planning [38].

At the end of each session (a few minutes after the last sonication), we acquired T1-weighted FSE images (TR/TE: 500/14 ms; ETL: 4; FOV: 12 cm; matrix: 256×256, slice thickness: 3 mm). These images were repeated after the administration of the MRI contrast agent Gd-DTPA (Magnevist, Berlex Laboratories, Inc., Wayne NJ) at a concentration of 0.1 mmol/kg of body weight as a bolus injection through the leg vein. This contrast agent normally does not extravasate into the brain, and signal enhancement after Gd-DTPA injection was used to identify regions of BBB disruption. A 3D T2*-weighted spoiled gradient echo sequence (TR/TE: 33/19 ms; FA: 15°; FOV: 12 cm; matrix: 256×256; slice thickness: 1 mm) was used to detect vascular damage. This sequence shows hypointense regions induced by tiny red blood cell extravasations (petechiae) that occur presumably due to inertial cavitation [38].

G. Statistical Analysis and Image Metrics

Overall, we used data from 780 bursts at 8 different experiments in 3 nonhuman primates. For comparing the ability of the passive acoustic maps to visualize the point sources we defined the Signal, described by the peak intensity in each map, to Background Noise Ratio (SBNR), which describes the noise level in a uniform part of the image. The image noise was calculated by the standard deviation of a 15 mm long line profile (18×1 pixel) adjacent to the peak intensity. The location of the line, which started more than 5 mm laterally of the peak value (5 times the transverse FWHM) is shown in Suppl. Fig. 1B. This approach excludes reconstruction related artifacts from the estimation of the noise that tend to appear before and after the point source location (axial direction). The peaks that were more than 20mm away of the expected cavitation activity were excluded by our accept criteria for successful PAM and SBNR determination. After thorough inspection of the maps SBNR equal to 10 was selected as threshold for confident cavitation activity localization. A paired t-test was used to compare the performance characteristics (SBNR) of the different back-projection methods.

III. Results

A. In Silico 2D and 3D AS-PAM

First, we evaluated the ability of the angular spectrum approach to perform passive acoustic mapping using simulated data. In silico volumetric reconstructions with the ASPAM algorithm (Eq. 1) were possible and provided accurate localization of the point source in 3D space with a virtual 25×80mm (200×650 element) imaging array (Fig. 1B). The field of view was relevant to clinical conditions (25×80×70mm) and, for a single frequency the volumetric map was performed in 4.5s. Using the numerical simulations with three point sources that were separated by 4 wavelengths we obtained similar results (Fig. 1C).

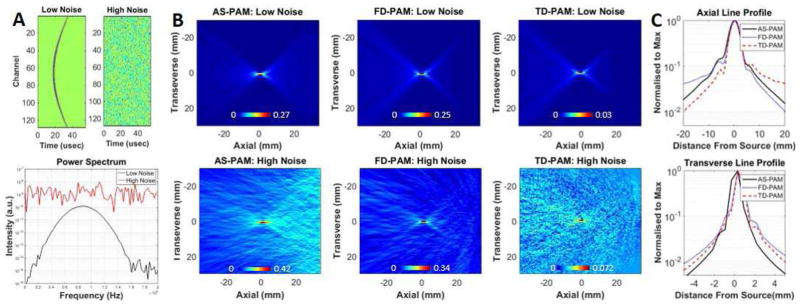
Then we compared the AS-PAM, FD-PAM and TD-PAM in 2D using a virtual linear array composed of 128 elements (Fig. 2). To obtain the same frequency bandwidth, 50 single-frequency maps covering the entire bandwidth of the Gaussian point source (Fig. 2A) were superimposed in the AS and FD-PAM. Comparable resolution and localization accuracy were evident (Fig. 2C and Table I) among the three different methods. All back-projection methods were able to accurately localize the point source even when the noise power was an order of magnitude higher than the signal (Fig. 2A). Interestingly, the SBNR with AS-PAM was more sensitive than the FD- and TD-PAM when the RF-data had low noise (740 vs 317 and 474). In the presence of high white noise the SBNR in the two frequency selective methods was similar and better than the TD-PAM suggesting that they can be more sensitive in the presence of noise (Fig. 2B). Furthermore, the AS-PAM reconstruction time was 10 and 200 times faster than FD- and TD-PAM respectively. Importantly for a single frequency bin, the maps with the AS-PAM could be reconstructed in 30ms, a twofold and 1300-fold improvement as compared to the FD- and TD-PAM respectively, while attaining slightly better SBNR (Table I).

Fig. 2.

Insilico 2D passive acoustic mapping. A) Above: Simulated RF-data with different levels of white Gaussian noise added (left low noise, right high noise). Below: Power spectra generated from RF-data of the middle element of the virtual array for the low and high noise level cases. B) AS-PAM (left), FD-PAM (middle) and TD-PAM (right) with low (top) and high (bottom) white Gaussian noise. For AS-PAM and FD-PAM, 50 single-frequency maps at 0.25–1.5 MHz were superimposed. C) Axial and transverse line profiles from the maps with the low noise for the three back-propagation methods. The reconstruction time for a field of view of 70×80 mm with 0.54×0.54 mm pixels was 0.5±0.01 s with AS-PAM; 5.9±0.5 s with FD-PAM and 38.8±0.9 s with TD-PAM (pixel size: 0.54 mm2) it was 58 s. The 2D maps are rotated by 90 degrees with respect to the 3D maps in Fig. 1. The images were set to zero by means of minimum signal subtraction. All color maps are linear and expressed in a.u..

TABLE I.

Comparison between AS-PAM, FD-PAM and TD-PAM

Simulated data1
Back-propagation method	Bandwidth (# Frequency bins)	Runtime (Sec)	FWHM (Axial)	FWHM (Transverse)	SBNR (Low noise)	SBNR (High noise)
TD-PAM	21.7×l03kHz	40.2±0.2	4.1	0.92	474	13±1
FD-PAM	24.3 kHz (#1)	0.06±0.002	4.0	0.87	229	16±7
FD-PAM	1215 kHz (#50)	2.2±0.09	4.2	0.93	317	37±7
AS-PAM	24.3 kHz (#1)	0.03±0.001	4.2	1.09	546	18±2
AS-PAM	1215 kHz (#50)	0.20±0.01	4.3	1.11	740	42±13
Experimental data2
Back-propagation method	Bandwidth(# Frequency bins)	Runtime (Sec)	FWHM (Axial)	FWHM (Transverse)	Peak location	SBNR>10 (# images)
TD-PAM	6.42 MHz	44.5±0.6	18.8±5.9 (med: 17.4)	1.9±0.4 (med: 1.8)	120.5±2. (med: 120.5)7	26±16.8 (#106/780)
FD-PAM	3 MHz (#480)	10.8±0.4	21.1±8.4 (med: 18.5)	1.9±0.5 (med: 1.8)	120.5±2.6 (med: 120.8)	28±19 (# 112/780)
AS-PAM	3 MHz (#480)	1.77±0.03	24.2±6.2 (med: 22.1)	2.5±1.2 (med: 2.1)	123.7±4.9 (med: 124.8)	29.5±20 (#118/780)

¹# of data points: 1790; image dimensions: 128×128 (TD-PAM & FD-PAM), 512×128 (AS-PAM); distance from Array: 34 mm.

²# of data points: 2048; image dimensions: 64×128 (TD-PAM & FD-PAM), 512×128 (AS-PAM); distance from Array: 120 mm.

FWHM and Peak location are expressed in mm. The FWHM was estimated by data-fit of the line profiles.

B. In Vivo 2D AS-PAM

To validate our in silico findings, we incorporated a linear array into a clinical MR guided Focused Ultrasound (MRgFUS) system (Fig. 3A) and collected acoustic emissions during experiments, where we combined FUS sonications with intravenously administered microbubbles to induce blood-brain barrier (BBB) disruption in non-human primates [22]. We compared the two approaches on 780 sets of RF data that were recorded during these sonications. To obtain the same frequency bandwidth, we created multi-frequency AS-PAM by summing all 480 of the individual frequency maps across the recorded spectra (Fig. 3B, See Supplemental Video 1). Figure 3C shows that the multi-frequency AS-PAM approach was able to form maps of microbubble activity in vivo with comparable resolution and localization accuracy as the FD- and TD-PAM approaches (See also Table I).

With these data, first, we estimated full width half maxima (FWHM) of the peak intensity for the three PAM methods. For the AS-, FD- and TD-PAM, in the axial direction, it was 24.2±6.2mm, 21.1±8.4mm, and 18.8±5.9mm respectively, whereas in the transverse direction it was 1.9±0.4mm for the FD- and TD-PAM and 2.5±1.2mm for AS-PAM. The mean axial position of the maximum microbubble activity was 120.5±2.6 for the FD- and TD-PAM and 123.7±4.9mm, for AS-PAM (Fig. 3D and Table I). While AS-PAM estimated the peak intensity further from the US array, the difference in the axial position (3.2 mm) between the three methods was well below their measured FWHM.

Next, we plotted the location of the peak value along the axial direction as a function of SBNR for the two reconstruction methods for all 780 datasets (Fig. 3D). We found that with multi-frequency AS-PAM, 118/780 maps had activity with SBNR greater than 10, whereas with FD- and TD-PAM 112 and 106 maps respectively fulfilled these criteria (average SBNR: 29.5±20, 28±19 and 26±17 for AS, FD- and TDPAM respectively). The images with low SBNR (SBNR<10) are from data collected either before the arrival of the bubbles in the target or had very weak microbubble acoustic emissions to provide meaningful information. The larger number of maps of AS and FD-PAM with SBNR>10 supports our in silico data that suggest that frequency selective reconstructions can be more sensitive than TD-PAM in the presence of noise.

The reconstruction times for a field of view of 80×170mm and a pixel size of 1.3 mm for the multi-frequency AS-, FD-, and TD-PAM were 1.77±0.03, 10.8±0.4s, and 44,5±0.6s respectively (AS-PAM is 6- and 25-fold faster than FD- and TD-PAM). For a single frequency, the AS-PAM reconstruction required only 20ms to produce an image – 3.5 and more than 2000 times faster than the FD- and TD-PAM reconstructions respectively.

Next, we evaluated the ability of the AS approach to reconstruct maps showing activity at frequency bands that correspond to only harmonics, ultra- harmonics and broadband (or inharmonic) emissions. The set of three frequency-selective maps, which each were the superposition of maps of 42 frequency bins, were all reconstructed in 0.48s, approximately 6 and 100 times faster than what was needed for the FD- and TD-PAM reconstructions respectively. The reconstruction times, the SBNR, and the FWHM for the different reconstructions with SBNR>10 are summarized in Table II.

TABLE II.

Comparison between Frequency selective AS-PAM and FD-PAM

Experimental Data
Back-propagation method	Bandwidth (#bins)	Runtime (Sec)	FWHM (Axial)			SBNR>10 (# images)
			Harmonics	Ultra-harmonics	Broad-band	Harmonics	Ultra-harmonics	Broad-band
FD-PAM	#42 #126	0.97±0.01 2.85±0.02	17.3±4.8 (med: 6.2)	14.3±3.0 (med: 13.4)	14.4±4.0 (med: 11.8)	29.6±21.1 (#214/780)	24.8±17.7 (#21/780)	18.8±6.6 (#9/780)
AS-PAM	#42 #126	0.18±0.002 0.48±0.001	22.1±6.0 (med: 0.6)	20.6±5.7 (med: 19.6)	23.4±6.2 (med:20.3)	28.2±17.7 (#204/780)	23.1±15.0 (#23/780)	19.2±11.7 (#9/780)
TD-PAM	6.42 MHz	44.5±0.6	All frequencies 18.8±5.9mm(med: 17.4)			All frequencies 26±16.8 (#106/780)

FWHM is expressed in mm. The FWHM was estimated by data-fit of the line profiles.

The frequency-selective AS-PAM reconstructions were investigated for characterizing the type of microbubble oscillations that occurred at different targets (Fig. 4A–D). Harmonic-only AS-PAM had comparable SBNR to TD-PAM and FDPAM (28.2±17.7 vs. 26.0±16.8/29.6±21.1). The number of images with a SBNR>10 was greater with the harmonic-only AS-PAM and FD-PAM reconstructions compared to TD-PAM (204/214 vs. 106), suggesting that the sensitivity of the ASPAM and FD-PAM methods is due to their ability to include only the frequency bands that contain useful information and thereby exclude background artifacts or noise.

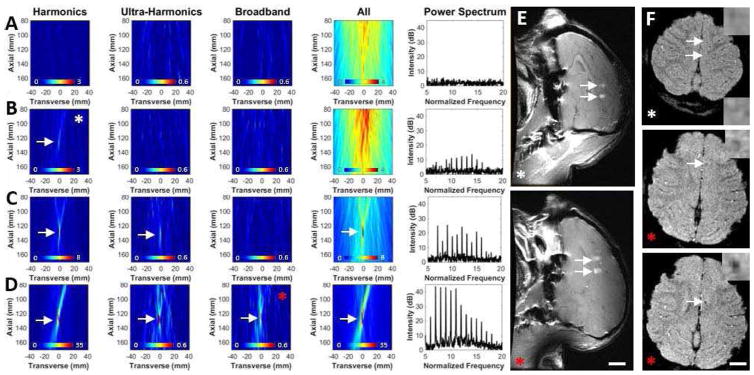
Fig. 4.

Invivo 2D frequency-selective AS-PAM for emissions with different frequency content and MRI assessment of the effects produced by the sonications in nonhuman primates. A) without microbubble acoustic emissions (control); B) with harmonic-only microbubble acoustic emissions; C) with harmonic and ultra-harmonic microbubble acoustic emissions without broadband emissions; D) with broadband microbubble acoustic emissions. The reconstruction time for all of the images needed to make these three frequency-selective maps was 0.48±0.001s. The reconstruction time for all frequencies-PAM was 1.77±0.03s. For clarity only part of the original 80×170 mm field of view is shown. Arrows indicate maps with SBNR>10. The images are perpendicular to the therapeutic beam path as shown in Figure 3A. All color maps are linear and expressed in a.u. E) BBB assessment with T1-weighted fast spin echo imaging after intravenous administration of MRI contrast agent. F) T2*-weighted spoiled gradient echo images that are sensitive to the presence of petechiae that can occur when inertial cavitation is produced. Inset is a magnification of the targeted region. The images are from two different experiments. The two targets sonicated in the top images in A and B had AS-PAM with harmonics only signal. The maps in B shows representative examples from this experiment (white asterisk). The AS-PAM acquired during sonication at the targets in the low image in E) and in the middle and lower images in F) had harmonic, ultra-harmonic and broadband signal. D shows representative maps from that experiment. BBB disruption and small hypointense spots (middle/bottom in F), indicative of petechiae, were observed in this case (red asterisk).

Frequency-selective reconstructions showing localized activity with ultra-harmonic and broadband frequency components appeared at some targets (Fig. 4C, D). The latter suggests that inertial cavitation occurred during sonication, which can result in vascular damage and extravasation of blood cells along with the BBB disruption. Such damage was evident in post-sonication MRI (Fig. 4F; red asterisk) only in the targets (2/8) where AS-PAM reconstructions showed broadband activity with SBNR>10 (Fig. 4D; red asterisk). In the other targets (6/8), a strong signal (SBNR>10) was observed only in the harmonics-only reconstructions (Fig. 4B, white asterisk), and BBB disruption was observed (Fig. 4E; white arrows and white asterisk) without MR-evident tissue damage (Fig. 4F; white asterisk). These results demonstrate that AS-PAM can be used to perform safe and effective FUS-BBB disruption.

IV. Discussion

Microbubbles in a time-varying pressure field undergo volume or shape changes and oscillations that lead to the emission of diverging pressure waves. These waves reveal useful information about the type of oscillation that is occurring. The presence or absence of broadband emissions, for example, can be used to identify stable and inertial cavitation activity, which lead to different bioeffects. By mapping this activity, it becomes possible to ensure that it is accurately localized and that only the desired oscillations are occurring. It may be possible to use this information to modulate the ultrasound exposures to achieve the desired effect, as the strength of the emissions should be echoed in the strength of the recorded emissions. To do so we need methods for fast, high resolution, frequency-selective, quantitative acoustic mapping.

The AS-PAM planar back-projection method presented here was able to localize microbubble oscillations at a high temporal resolution without compromising sensitivity and with very modest reduction in spatial resolution. AS-PAM was tested in silico and in vivo using a clinical MRgFUS system. In silico, when compared to the established TD-PAM approach, its reconstruction time was more than 1000-fold faster. All back-projection methods had similar localization accuracy, even when the noise power was an order of magnitude higher than the signal. In the presence of high noise (10-fold higher than the single element signal), this improvement in the SBNR is expected, as the signals from the point source (i.e. cavitation origin) are coherent and thus grow as N (where N is the number of elements in the array), whereas the noise grows as $\sqrt{\mathrm{N}}$ (assuming it is white noise), thus for N = 128 the gain in the SBNR is $128/\sqrt{128}=11.3$ in the TD-PAM. In the frequency selective reconstructions (AS- PAM and FDPAM), the results for both in-silico simulation and in-vivo experiments demonstrate an improvement in the SBNR over TD-PAM. This improvement is possibly due to the exclusion of frequency bins that do not incorporate information (or incorporate only noise). The higher amplitude areas in the axial direction of AS-PAM (Fig 2B) do not impose significant detection limitations (See also Figs. 3 and 4 and Table I and II). These data demonstrate that PAM is more sensitive than single element passive cavitation detection methods and should be the preferred method for guiding FUS procedures when safety is a major concern.

Considering that the images presented here are expressed in a.u., it is relatively challenging to directly compare the image intensities among the different methods, however one might assume that the DC offset might have significant impact on the delay and sum reconstruction algorithms. For providing quantitative images this disparity needs to be elucidated.

Excluding the apodization and geometric terms from FD- and TD-PAM shows that the “delay and sum” operations in the frequency and time domains respectively are equivalent, when comparable bandwidth is used. However, in terms of computational speed the FD-PAM is more advantageous, as it depends only on the [N × 1] values of the FFT at the current frequency of interest, while those in TD-PAM depend on the whole [N × T] RF data samples. The later will hold true as long as the frequencies of interest are less than T.

Both simulated and experimentally determined axial and transverse line profiles show that the AS-PAM has slightly higher FWHM. This might be related to the sparse sampling of the array (every other element), which reduced the frequencies that could be resolved with this method. The very small difference in the localization accuracy between the FD-PAM and TD-PAM both in the simulated and experimental data suggests that the differences in the bandwidth do not play a critical role in resolution. It is important to note that the frequency domains methods cover the entire bandwidth but at small frequency steps. However, closer inspection of the experimental data suggests that there is a small negative trend in the localization accuracy between the time domain and frequency domain methods, which is more pronounced in the AS-PAMs. More work to study and understand these small differences is required.

It is important to note, that application of the geometric correction to the “delay and sum” based methods broadens its FWHM and may make it similar to the AS-PAM [28]. However, methods to overcome this artifact and improve image resolution have recently been proposed [39].

Interestingly, both AS-PAM and FD-PAM formed with harmonic-only emissions from the experimental data were more sensitive than the TD-PAM (2 times more images with SBNR>10). In addition, AS-PAM and FD-PAM were able to create frequency-selective reconstructions at frequency bands pertinent to the different types of microbubble oscillations, thus, providing the ability to characterize the microbubble oscillations in vivo. The ability to use frequency bins that incorporate information and at the same time exclude bins with (electronic) noise has profound effect on the SBNR of the maps. This is more evident when the noise is very high (Figs. 2–4 and Table I, II). As a result, maps with AS-PAM with harmonics-only was shown to be predictive of safe and effective blood brain barrier disruption, whereas strong signal (SBNR>10) in maps of broadband emissions was predictive of MR-evident tissue damage. While more experiments are necessary in order to develop effective methods to control the sonications, particularly in the presence of a thicker human skull, these data clearly demonstrate the clinical utility of this method.

The incorporation of the ultrasound array to the clinical MRgFUS system suggests that this approach and back-projection algorithm can be readily applied to current clinical trials. These results also suggest that if a 2D imaging array is used, reconstruction of volumetric and frequency-selective AS-PAM could be achieved at computational speeds that are pertinent to real-time guidance of ultrasound therapies (e.g. 1–10 Hz for FUS-BBB disruption). AS-PAM can also be readily parallelized, as each frequency and image depth (z) can be reconstructed separately using a different processors and then summed to form the individual images (Figs. 1 and 4). In addition, for volumetric mapping the AS-PAM, as a planar projection method, can be extremely efficient computationally (Fig. 1). As we demonstrated 3D maps from 2D arrays composed of thousand elements can be performed in few seconds (~4s) with a desktop computer. Therefore, our results suggest that AS-PAM might be more appropriate for applications that the combination of computational speed with frequency selectivity and high SBNR is essential.

For utilizing the potential of PAM with 1D arrays, careful assessment of the frequency content of the emissions, the sensitivity of the different back-propagation methods and the maps is required in order to assess the impact of out-of-plane emissions. In the work presented, the length of the array elements (~8 mm) resulted to plane thickness that is comparable to the axial FUS focal region (8 mm). Therefore, considering that the FUS targets were placed, via electronic beam-steering, in the US imaging plane no out of plane emissions are expected. Also, we anticipate that the short duration, low power pulses and low F-number FUS used limited (i.e. below detection threshold) the propagation of the cavitation activity out of the FUS focus. If, however, such emissions were present we anticipate that they would lead to erroneous estimation in both the cavitation activity location and image intensity, irrespective of the reconstruction method used. More work in this direction is warranted.

The resolution in AS-PAM is related to the frequency content of the recorded acoustic emissions, the number and location of the transducer elements, and the number of the array elements used in the back-projection process [24]. With the linear array used in this work, the axial resolution was relatively poor. Using a 2D array with larger aperture this resolution can be improved and extended to 3D. Further, the compatibility of the AS-PAM with super-resolution imaging [40], offers the possibility for imaging beyond the diffraction limit [41], [42]. Therefore, the AS approach can potentially be used to perform very sensitive fast, high resolution, and frequency-selective passive acoustic imaging without the need of dedicated hardware.

In addition, the proposed back-projection algorithm can be extended to compensate for absorption, reflection and aberration of the emitted pressure wave, making it possible to extract, for example, quantitative information about the microbubble distribution even behind highly aberrating media such as the skull. These abilities will be particularly useful to the numerous FUS applications that harness acoustic cavitation, as the proposed approach and back-projection algorithm can be directly employed to laboratory investigations [7]–[13] as well as incorporated to current clinical trials [14]–[16].

Our long-term goal is to be able to accurately estimate the cellular or microvascular perturbations induced by oscillating microbubbles in order to develop translational tools for therapeutic and diagnostic applications that harness acoustic cavitation. We anticipate that if the acoustic propagation is correctly taken into account, this method will ultimately allow to relate the intensity in passive acoustic maps to the energy deposited to the cells, vessels and tissues in the targeted region. We envision that this ability will result in more precise, more controlled and more effective therapies in the brain and elsewhere.

V. Conclusion

AS-PAM was developed and tested in silico and in vivo using a clinical MRgFUS system. This approach enabled fast passive acoustic mapping that was as much as three orders of magnitude faster than the established time domain method. It was capable of producing frequency-selective maps that could discriminate between stable and inertial cavitation activity with a SBNR and spatial resolution comparable to frequency and time domain approaches that rely on the “delay-and-sum” operation for image formation. Overall, we anticipate that such methods will improve our ability to monitor and control cavitation-based therapies and thus accelerate their transition to the clinics.