Testing inhomogeneous solvation theory in structure-based ligand discovery

Significance

Water molecules play a crucial role in protein–ligand binding. Calculating the energetic consequences of displacing water upon ligand binding has challenged the field for many years. Inhomogeneous solvation theory (IST) is one of the most popular methods for distinguishing favorable from unfavorable water molecules, but little controlled, prospective testing at atomic resolution has been done to evaluate the method. Here we compare molecular docking screens with and without an IST term to gauge its impact on ligand discovery. We test prospective ligand-binding predictions that include an IST term, using crystallography and direct binding.

Abstract

Binding-site water is often displaced upon ligand recognition, but is commonly neglected in structure-based ligand discovery. Inhomogeneous solvation theory (IST) has become popular for treating this effect, but it has not been tested in controlled experiments at atomic resolution. To do so, we turned to a grid-based version of this method, GIST, readily implemented in molecular docking. Whereas the term only improves docking modestly in retrospective ligand enrichment, it could be added without disrupting performance. We thus turned to prospective docking of large libraries to investigate GIST’s impact on ligand discovery, geometry, and water structure in a model cavity site well-suited to exploring these terms. Although top-ranked docked molecules with and without the GIST term often overlapped, many ligands were meaningfully prioritized or deprioritized; some of these were selected for testing. Experimentally, 13/14 molecules prioritized by GIST did bind, whereas none of the molecules that it deprioritized were observed to bind. Nine crystal complexes were determined. In six, the ligand geometry corresponded to that predicted by GIST, for one of these the pose without the GIST term was wrong, and three crystallographic poses differed from both predictions. Notably, in one structure, an ordered water molecule with a high GIST displacement penalty was observed to stay in place. Inclusion of this water-displacement term can substantially improve the hit rates and ligand geometries from docking screens, although the magnitude of its effects can be small and its impact in drug binding sites merits further controlled studies.

The treatment of receptor-bound water molecules, which are crucial for ligand recognition, is a widely recognized challenge in structure-based discovery (1–4). The more tightly bound a water in a site, the greater the penalty for its displacement upon ligand binding, ultimately leading to its retention and the adoption of ligand geometries that do not displace it. More problematic still is when a new bridging water mediates interactions between the ligand and the receptor. Because the energetics of bound water molecules have been challenging to calculate and bridging waters hard to anticipate, large-scale docking of chemical libraries has typically been conducted against artificially desolvated sites or has kept a handful of ordered water molecules that are treated as part of the site, based on structural precedence (5–8).

Recently, several relatively fast approaches, pragmatic for early discovery, have been advanced to account for the differential displacement energies of bound water molecules (9–20), complementing more rigorous but computationally expensive approaches (18–22). Among the most popular of these has been inhomogeneous solvation theory (IST) (23–25). IST uses populations from molecular dynamics (MD) simulations on protein (solute) surfaces to calculate the cost of displacing individual water molecules (solvent) on that surface. IST has been used to calculate ligand structure–activity relationships (26–29), map protein binding sites for solvent energetics (28, 30, 31), quantify the energetic contribution of structural waters (25, 32), and understand water networks and how they rearrange in the presence of ligands (33). There have been several implementations of IST, including WaterMap (26, 27, 31) and STOW (32), and the approach has been integrated into library docking programs such as Glide (34, 35), DOCK3.5.54 (36), and AutoDock (37).

Notwithstanding its popularity, IST has rarely been tested in prospective library screens for its ability to prospectively predict ligands, their bound geometries, and the water molecules that they either do or do not displace (4). Here, we do so in a model cavity in cytochrome c peroxidase (CcP-gateless; CcP-ga), a highly defined, mostly buried site that is partially open to bulk solvent, and that binds small heterocyclic monocations. We and others have used this and related cavities as model systems for docking, owing to their small size, the dominance of one or two interaction terms in ligand binding, and the existence of thousands of plausible ligands among commercially available, dockable small molecules (38–41).

The CcP-ga cavity is particularly well suited to exploring the impact of ordered waters on the prospective discovery of novel ligands (Fig. 1). On binding, ligands displace between three and eight waters observed in apo structures (38, 39), whereas new waters can be recruited to bridge between the cavity and the ligands. The limited number of these waters and the tight definition of the site make exploration of the problem tractable. Also, the affinities of newly predicted ligands may be determined quantitatively and their structures may be determined to high resolution, making atomic-resolution testing plausible.

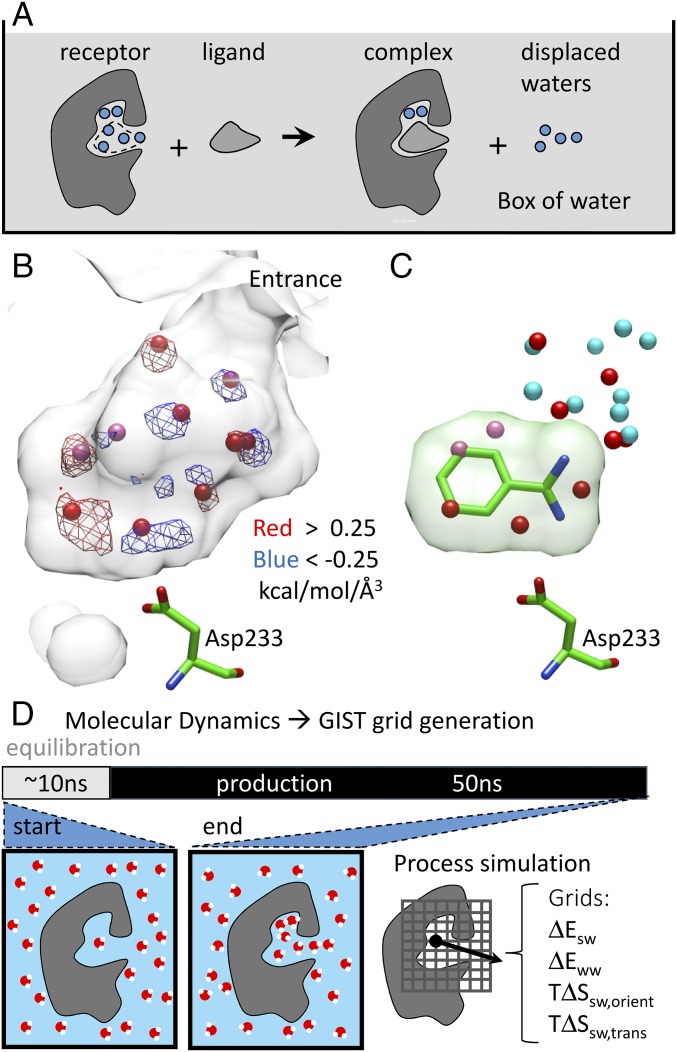
Fig. 1.

Receptor desolvation in the CcP-gateless cavity using grid-based inhomogeneous solvation theory. (A) Upon ligand binding, ordered water can be displaced, remain unaffected, or bridge between ligand and protein. (B) The CcP-gateless apo cavity (transparent surface) is filled with nine crystallographic water molecules (red spheres; pink spheres indicate half-occupancy) (PDB ID code 4NVA) and compared with GIST enthalpy grid maps representing unfavorable water positions (red mesh; >0.25 kcal⋅mol⁻¹⋅Å⁻³) and favorable water positions (blue mesh; <−0.25 kcal⋅mol⁻¹⋅Å⁻³). (C) Ligand benzamidine (PDB ID code 4NVC) displaces four apo-cavity waters (red spheres) and reorders several of the remaining waters (cyan spheres) about the ligand. (D) The GIST grids are calculated by postprocessing a molecular dynamics simulation of a restrained apo protein in a box of water.

We integrated GIST, the grid implementation of IST (30), into DOCK3.7. In GIST, MD simulations of the hydrated receptor are analyzed to yield spatially resolved information about water density and thermodynamics over the voxels (cubic grid cells) of a 3D grid covering the protein binding site (Fig. 1). The grid basis of GIST lends itself to docking because water-displacement energies can be precalculated and stored on a lattice of points, supporting the rapid scoring necessary for large library screens. These water energies can then be combined with the other terms of the DOCK3.7 physics-based scoring function.

We first tested including GIST in retrospective controls against 25 targets drawn from the DUD-E benchmark (42), composed of about 6,600 annotated ligands and 400,000 property-matched decoys (42) (SI Appendix, section S1). These enrichment calculations investigate the weighting of the GIST term (E_rec,desol) with other DOCK3.7 terms (43): van der Waals (E_vdW), electrostatic (E_es), ligand desolvation (E_lig,desol), and protein conformational energies (E_rec,conf) (Eq. 1).

$$E_{\text{score}}=E_{\text{rec},\text{desol}}+E_{\text{vdW}}+E_{\text{es}}+E_{\text{lig},\text{desol}}+E_{\text{rec},\text{conf}}$$ [1]

These retrospective calculations helped calibrate the term, assess its computational cost, and establish that it could be used without disrupting the balance of the other scoring terms.

More illuminating are prospective tests that we prosecuted against the model cavity. In screens of between 0.2 and 1.8 million compounds, we prioritized molecules by three criteria: (i) they are previously untested, (ii) they rank substantially better or worse with the GIST term than without it, or (iii) they bind differently due to the displacement of GIST-defined water molecules. A total of 17 molecules were purchased and tested experimentally for binding, and 9 ligand–CcP-ga crystal structures were determined. From these studies, several advantages of IST for ligand discovery emerged: The method meaningfully improved the selection of ligands, and was often right for the right reasons, correctly capturing the role of displaceable or implicitly bridging water. Still, and notwithstanding the great advantages of IST seen in other studies (26–29, 34), in controlled prospective discovery, at atomic resolution, its liabilities also emerge.

Results

Inhomogeneous solvation theory methods use a molecular mechanics potential energy function and water occupancies to calculate thermodynamic properties of water in the context of the receptor. In GIST, the energies of solute–water enthalpy (E_s,w), water–water enthalpy (E_w,w), translational entropy (TS_trans), and orientational entropy (TS_orient) are represented spatially in grid voxels. The receptor desolvation cost is calculated by summing the voxels displaced by a docked ligand (SI Appendix, sections S2 and S3) and added to the DOCK3.7 scoring function (cf. Eq. 1). To investigate how the GIST energies are best-weighted, and which GIST terms are most useful—as there are questions on this point in the literature (28, 37)—we began with retrospective calculations against the CcP-ga cavity, docking 46 known ligands against 3,338 property-matched decoys. We explored four different combinations of the GIST grids: (i) unscaled free energy (E_GIST = E_s,w + E_w,w + TS_trans + TS_orient), (ii) unscaled enthalpy (E_GIST = E_s,w + E_w,w), (iii) scaled free energy (E_GIST = E_s,w + 2 × E_w,w + TS_trans + TS_orient), and (iv) scaled enthalpy (E_GIST = E_s,w + 2 × E_w,w), both with the water–water term scaled by 2 (SI Appendix, sections S2 and S4, Fig. S2, and Table S1). Here, enthalpy was not normalized by occupancy (SI Appendix, section S2), in contrast to previous studies (28, 37), but still referenced to bulk water energy, as this produced the best enrichments. Following convention, negative GIST energies reflect favorable, costly-to-displace waters. We used adjusted logAUC to measure docking enrichment (39, 42–45); this metric weights each factor of 10 in docking rank order equally, beginning from the top 0.1%, prioritizing the performance of the very top ranking ligands or decoys in the docking screen (44). Scaled enthalpy performed the best (adjusted logAUC of 57.46 ± 1.84), closely followed by unscaled free energy (56.08 ± 1.42). Enthalpy alone performed the worst (49.50 ± 1.34). Setting E_GIST = E_s,w + 2 × E_w,w sets aside several GIST terms, but has precedence in earlier studies (28, 30).

We next explored the receptor desolvation term and the best scaling factor (α; Eq. S8) to bring the GIST value into balance with the other terms in Eq. 1 (SI Appendix, section S5, Fig. S3, and Table S2). Staying with the CcP-ga system, we considered eight scaling factors ranging from −8.0 to +8.0 for the weighting of E_GIST. Reassuringly, we found that the scaling factors of −1.0 (logAUC = 57.46 ± 1.84) and −0.5 (logAUC = 56.54 ± 2.10) behave better than overweighting the term by a factor of −8.0 (logAUC = 36.91 ± 1.52) or +8.0 (logAUC = 46.94 ± 2.07). Here, as in all calculations in this study, we based the GIST energies on MD simulations of 50 ns. These appeared to be sufficiently converged for docking, based on the small variance in performance using GIST grids from each of ten 5-ns subtrajectories (SI Appendix, section S6, Fig. S4, and Table S3).

Applying the same GIST terms used in the cavity (Eq. 1), we examined the impact of scaling factors on 25 DUD-E systems for which solvation likely plays a role. These 25 targets bind a diverse range of cationic (CXCR4, ACES, and TRY1), anionic (PUR2, AMPC, and PTN1), and neutral ligands (ITAL, KITH, and HS90a), and make water-mediated interactions (AMPC and EGFR). In these systems, we noticed that there were very few voxels in the GIST grids—on average 58 out of 210,000 total voxels—with extremely high magnitude absolute energies, ranging from 14.6 to 119.7 kcal⋅mol⁻¹⋅Å⁻³, between 101 and 391 σ (SDs) away from the mean voxel energies. These extrema seem to reflect the restrained MD simulations used for the GIST calculations, because when we allowed even side chains to move in the MD simulations they were much attenuated or entirely eliminated. Accordingly, we truncated the maximum absolute magnitude of the GIST grids at 3 kcal⋅mol⁻¹⋅Å⁻³ in these retrospective calculations (a value still on average 12σ away from the mean voxel energies); we also scaled the GIST energy by −0.5 when combining it with the other terms in the DOCK3.7 scoring function, which we found to perform slightly better than a simple weighting of –1.0 (SI Appendix, section S7 and Table S4 further describe the origins of the energy extrema and the retrospective docking performance under different weighting of the GIST term). In the retrospective docking screens, 13 of the 25 DUD-E systems had better enrichment versus docking without the GIST term, 6 had worse enrichment, and 6 were within ±0.5 logAUC difference (unchanged). The average logAUC difference over all systems is 0.53 better than no GIST (SI Appendix, section S7, Fig. S5, and Table S4). To get a sense of the impact of the GIST energies, the absolute value of the GIST term was about 6 kcal/mol for the top 100-ranked docked molecules in the 25 DUD-E targets, about 12% of the total docking score for these molecules. For the CcP-ga cavity, to which we will turn for prospective screens, the absolute GIST energy was about 8% of the total docking score for the top 100 docked molecules. The overall impact of GIST on the DUD-E benchmarks is modest, and perhaps the most important result to emerge from these retrospective controls is that the GIST term may be added without disrupting the docking scoring function, retaining physically sensible results.

We next turned to prospective docking screens against the CcP-ga cavity, with and without an unweighted (−1.0) GIST term, looking to predict cavity ligands and their geometries. The GIST grids identified four favorable water sites in the pocket, including one close to Asp233, and three unfavorable water sites, including two regions close to the heme and one near Gly178, a residue that can hydrogen bond with ligands through its backbone (SI Appendix, section S8, Fig. S6, and Table S5). We docked two purchasable fragment libraries, one straight from ZINC (zinc15.docking.org) of ∼200,000 molecules prepared at pH 6.4 [virtual screen (VS)1], and 1.8 million molecules built at a pH of 4.0 (VS2), which favors positively charged molecules typically recognized by the cavity Asp233. We sampled, in VS1, 462.5 million orientations of the library molecules and ∼15 billion scored conformations; 95,000 of the 200,000 molecules could be fit in the site. From the larger VS2 screen, 5.9 billion orientations and about 319 billion scored conformations were sampled; 1.09 million molecules could be fit in the site. To isolate the effect of the GIST term on our screening performance, we ran each screen twice, with and without the GIST term.

Most of the top-ranking 1,000 molecules are shared between the GIST and non-GIST screens: 667 are shared in VS1, whereas 532 are shared in the larger VS2 (Fig. 2), reflecting the comparatively small magnitude of the GIST energies relative to the overall docking score (below). We focused on those molecules that experienced rank changes of a half-log (3.16-fold) or better. For instance, a molecule that changed rank from 30th to 100th, or from 400th to 1,300th, on including the GIST term would be prioritized. From the smaller screen (VS1), 217 docking hits improved ranks by at least half a log order with the GIST term, whereas 282 had ranks that were better by at least this amount without the GIST term. For the larger VS2 screen, 2,421 had half-log–improved ranks with GIST whereas 2,869 had ranks that improved by at least half a log order without it. There were also several molecules for which the inclusion of the GIST term greatly changed the docked geometry; these we also considered for testing.

Fig. 2.

Comparison of GIST and non-GIST screens. (A) Results from VS1 of 200,000 molecules. (B) Results from VS2 of 1.8 million molecules. (Top Right) Venn diagrams of the top 1,000-ranked molecules from the GIST screen in red and non-GIST in blue. (Bottom Left) Overlapping regions.

Based on these criteria, 17 molecules were acquired for experimental testing. Compounds 3 to 14 were selected because their ranks improved with GIST (pro-GIST), whereas compounds 15 to 17 were selected because of better ranks without the GIST term (anti-GIST) (Table 1). We also looked for molecules where a substantial pose change occurred between the two scoring functions (e.g., compounds 1 and 2; Table 1 and SI Appendix, Table S6). Finally, we considered implicit water-mediated interactions to be favorable regions in the GIST grid within hydrogen-bonding distance to ligand and protein, although no explicit water molecules were used. This occurred with compounds 3 to 6 (Table 1). In selecting these compounds, we were sometimes led to compounds that we expected, based on past experience with this cavity, to be GIST failures. For instance, compounds 3 through 6 adopted an unusual geometry in the site, giving up a direct ion pair with Asp233 to hydrogen bond with backbone carbonyls, owing to a large implicit desolvation cost for docked orientations where the ion pair was formed. These poses were relatively favored by the GIST term, but we expected them either not to bind or to bind to form the ion pair. Conversely, we expected the molecules deprioritized by GIST to bind, in contrast with the GIST term, also based on precedence of other molecules. For both classes of molecules it was the GIST prediction that was confirmed, to our surprise.

Table 1.

Candidate CcP ligands, prioritized with and without GIST energies for ranking and geometry, experimentally tested for both

^*Positive GIST values are penalties.

^†Molecule not in assayable form. NB, nonbinder; <5 mM. n.d., not determinable; compound interferes with absorbance peaks. ∼, assay interference of compound 10 before saturation was reached.

^‡RMSDs are calculated with the Hungarian algorithm (lower bound). G, GIST pose; NG, non-GIST pose; –, no crystal structure available. Single values for the same G vs. NG pose.

Pro-GIST.

We tested the binding of 14 GIST-favored molecules, determining X-ray crystal structures for 9 of them. All crystallographic datasets were collected to at least 1.6-Å resolution and refined to R_free values under 20%, indicating good global model quality. Locally, electron density maps for the ligands in the cavity were unambiguous as early as unrefined initial F_o − F_c maps. Final 2mF_o − DF_c composite omit maps (46) show unbiased electron density for the binding-site ligand and water molecules (Fig. 3). This allowed ready placement of the ligands and ordered water molecules in the final stages of refinement. Automatic refinement of ligand and water occupancies showed that ligands are unequivocally present in the binding site (between 88 and 93% occupancy); the complex with compound 14 refined to 73% occupancy in the presence of 26% MES from the crystallization buffer (SI Appendix, Fig. S7 and Table S7). We modeled all ligands in a single conformation, with only compound 2 showing difference density for an alternative ligand conformation. Electron densities of binding-site waters are generally well defined (Fig. 3), indicating extensive water networks that interact with both ligand and protein.

Fig. 3.

Comparison of experimental and predicted binding poses. Superposition of crystallographic (green) and predicted ligand poses (GIST docking poses in purple; differential non-GIST docking poses for compounds 1 and 2 in orange). 2mF_o − DF_c omit electron density maps (blue mesh) are shown at 1σ for binding-site ligand and water molecules (red spheres), with hydrogen bonds shown as red dashed lines. Nine compounds are shown (with PDB ID codes): (A) compound 1, 5U60; (B) compound 2, 5U5W; (C) compound 3, 5U5Z; (D) compound 8, 5U61; (E) compound 9, 5U5Y; (F) compound 10, 5UG2; (G) compound 11, 5U5X; (H) compound 12, 5U5U; and (I) compound 14, 5U5V. For clarity, cocrystallized MES for compound 14 is omitted (cf. SI Appendix, Fig. S7).

Of the 14 docked molecules favored by the GIST term, 13 (93%) could be shown to bind, typically by a UV-vis Soret band perturbation assay (Fig. 4 and SI Appendix, Fig. S8) (47). Affinities for 11 ligands were determined at least in duplicate and fit to a one-site binding model with R² values of at least 95%. Two molecules were only observed bound in their cocomplexed crystal structures, owing to assay interference (Table 1). The K_d values of the GIST-prioritized molecules ranged from 1.3 μM to 3.5 mM, with eight better than 1 mM. For these fragments the ligand efficiencies ranged from 1.0 to 0.28 kcal/mol per atom (SI Appendix, Table S6).

Fig. 4.

Three representative ligand-binding curves. The Soret band shift is shown as a function of ligand concentration (µM). The plots for compounds 3 and 9 are on a linear scale whereas, for clarity, the x axis of the plot for compound 11 is on the log scale. The dotted lines indicate the K_d. Circles and bars are the mean and estimated error of two observations, respectively.

Compound 11, ranking 358th with GIST but 1,212th without GIST, had a K_d value of 1.3 μM. Compound 11 has a slightly unfavorable GIST energy of 0.28 kcal/mol, owing to its calculated displacement of a bound water. Nevertheless, its rank improved relative to the non-GIST docking screen, reflecting even larger penalties for other, formerly higher-ranking molecules. On determination of its structure to 1.54-Å resolution, the crystallographic geometry corresponded closely to that predicted by docking, with an RMS deviation of 0.44 Å (Fig. 3 and Table 1). Similar effects were seen for compounds 8, 10, 12, and 14, whose energy scores were only modestly affected by GIST, and for which docking well-predicted the subsequently determined crystallographic geometry.

Unexpectedly, compounds 3 through 6 were predicted by the GIST docking to interact indirectly with the critical Asp233 via an implicitly ordered water molecule (i.e., an area with a high water-displacement penalty). Such a geometry, although not unprecedented for CcP cavity ligands, is rare, as cationic ligands typically ion pair with this aspartate. In the apo cavity this aspartate is solvated by one bound water (39, 40) whose displacement by cationic moieties, although typical, undoubtedly has an energy cost. Indeed, according to GIST, such a penalty is incurred by molecules such as 7, which dock to maximally displace these waters and ion pair with the aspartate. Conversely, compounds 3 through 6 dock so as to retain these waters, and compound 3, instead of ion pairing with Asp233, flips its imidazole to hydrogen bond with the carbonyl oxygen of Leu177 and only interacts, via the other side of the imidazole, with Asp233 through a water network. This surprising prediction was confirmed crystallographically: The imidazole interacts with the Leu177, and an ordered water molecule is unambiguously present in the electron density (Fig. 3). Indeed, even the placement of this bridging water substantially agrees with the GIST calculation, differing only by 0.7 Å. The relatively poor ranks of molecules such as 3 when the GIST term is left out is explained by their more distant electrostatic interaction with Asp233 versus molecules that ion pair with it, uncompensated by the advantage of leaving the ordered water molecules undisplaced—a term only modeled by including the GIST penalty. That said, inclusion of the GIST term did not always get this balance correct. Compounds 1 and 9, although predicted to interact directly with the aspartate, also flip to interact with the Leu177 carbonyl crystallographically (Fig. 3); that is, even with the GIST term, the correct balance between ion pairing and water displacement was not achieved. We also note that compounds that do ion pair with Asp233 typically bind 10-fold tighter than those that bind via water-mediated interactions (SI Appendix, Table S8).

Compounds 1 and 2 were chosen because inclusion of the GIST term changed their docked geometries. Compound 2 docks to hydrogen bond with Asp233 while only partly impinging on what are, according to GIST, hard-to-displace water molecules (still incurring a GIST penalty of 2 kcal/mol). In the non-GIST docking, conversely, 2 flips and shifts such that its quinolone nitrogen hydrogen bonds with the backbone oxygen of Gly178 while its amine hydrogen bonds with Asp233 and its methyl occupies an unfavorable water site near the heme. The two poses differ by an RMSD of 3.2 Å. In the subsequently determined CcP-ga–2 crystal structure, 2 adopts a geometry that closely agrees with the GIST pose (RMSD of 0.3 Å) but differs by 3.2 Å from the non-GIST docking pose (Fig. 3 and Table 1). For three compounds, 1, 9, and 10, however, we consider the crystallographic complexes to be different from either the GIST or non-GIST docking pose, although none exceed the commonly used cutoff of 2-Å RMSD (Fig. 3 and Table 1).

Anti-GIST.

Compounds 15 to 17 ranked much better without the GIST term than with it, and their GIST-based ranks, between 6,000 and 15,000, would have put them outside the range normally considered as viable for screens of this size; all three sterically complemented the binding site well. Whereas we could determine neither an affinity nor a crystal structure under high soaking concentrations for compound 17, compounds 15 and 16 either bound very weakly, worse than 5 mM, or undetectably. This is consistent with their GIST-based deprioritization, owing to their displacement of well-bound water molecules from the cavity. It is interesting to note that the benzimidazole of 15 and the imidazole of 16 are both common among CcP-ga ligands [Table 1 and previous studies (38, 39, 41)]. Hence, this antiprediction is not simply a matter of trivial functional group bias or ionization—indeed, we ourselves expected these molecules to bind—but seems to reflect detailed assessment of fit and presumably water displacement.

Discussion

Inhomogeneous solvation theory has been enthusiastically greeted as a way to model the role of bound water molecules in ligand discovery (25, 27, 28, 31), and has been widely incorporated into discovery methods (34–37). Despite its successes (4, 26, 27, 29), the method has not been tested in prospective, controlled discovery screens at atomic resolution. Three key observations emerge from this study. First, the inclusion of a water-displacement energy noticeably improved the prospective docking screens. Of the molecules prioritized by the water-displacement term, 13 of 14 bound when tested, and one of these, compound 11, was the most potent ligand yet found for the CcP-ga cavity, with a K_d of 1.3 μM (ligand efficiency of 1.0 kcal/mol per atom). Correspondingly, of the three molecules ranked higher by the non-GIST versus the GIST docking, none could be shown to bind. Second, the predicted molecules were often right for the right reasons. The docking poses that were based on the water-displacement term corresponded closely to the crystallographic results in six of nine structures. Compellingly, in the CcP-ga–3 complex, the ligand adopts an unusual pose that does not interact directly with the crucial Asp233 but rather docks to conserve a hard-to-displace, bridging water, as predicted by the GIST energetics. Third, and notwithstanding these favorable results, the water-displacement term, at least in this implementation, had a modest effect in overall ranking, and can introduce its own errors. The term had little effect on retrospective enrichment against the DUD-E benchmark, and there remained remarkable overlap between the top 1,000 docking-ranked ligands with and without the term in the CcP-ga screens (Fig. 2, Venn diagrams). Also, in three of the nine crystal structures, there were important differences between the GIST-based docking poses and the experimental results. Whereas several of the predicted molecules were potent both by the standards of the site and by ligand efficiency, several others were of modest affinity compared with other ligands previously discovered for this cavity.

The ability to prioritize likely molecules and deprioritize unlikely ones is among the strongest results to emerge from this study. Compellingly, 13/14 molecules selected using GIST bind, whereas none of the GIST-deprioritized molecules did so. Including the GIST term accounts for penalties of displacing water upon ligand binding, which can change both rank and pose. These changes can reveal molecules that would otherwise not have been prioritized for testing. Such molecules include those that replace the hallmark hydrogen bond with Asp233 with an alternative pose that exploits a costly-to-displace water to mediate this ionic interaction, as for compounds 3, 9, and 10. Just as important, including the GIST term deprioritizes decoys we would otherwise have ranked highly, such as molecules 15 to 17.

Often, the GIST-predicted molecules were right for the right reasons; six of nine crystal structures corresponded closely to the docking predictions. This is most striking in those structures in which the GIST term correctly predicted an ordered water molecule that would be costly to displace, favoring a ligand geometry where such a water would be included in the complex with the ligand. Two notable examples are compound 2, where the GIST-predicted pose differed substantially from that without the GIST term, and was confirmed by subsequent crystallography, and compound 3, whose crystal structure confirms a water-mediated interaction with Asp233 and an unusual interaction with the carbonyl oxygen of Leu177 (Fig. 3). The water site that 3 retains is one of the most favorable in the cavity; summing up the voxels that contribute to it leads to 4.3 kcal/mol in the GIST calculation (SI Appendix, section S8). Similarly, compounds 8, 11, and 12 interact with a water network toward the pocket entrance that is implicitly predicted by the GIST grids (SI Appendix, Fig. S6, regions s5 to s7); in the CcP-ga–8 complex, three crystallographic waters correspond to regions s5 to s7 from those predicted by GIST.

Notwithstanding these successes, inclusion of the water-displacement term only improves docking so far. The GIST term failed to correctly predict the poses of compounds 9 and 10, and several compounds prioritized by GIST, such as 3, 5, 6, and 8, had K_d values >1 mM, which is weak for cavity ligands, if still decent by ligand efficiency (Table 1 and SI Appendix, Table S6). Retrospectively, at best a modest improvement in enrichment was observed in the benchmarking screens on 25 DUD-E (42) targets (SI Appendix, Fig. S5), and there was substantial overlap among the top-scoring ligands in GIST and non-GIST docking screens (Fig. 2). Partly, these effects reflect the small magnitude of the net GIST energies: for the top 100 docked molecules from a library screen the term averaged 12% of the overall DOCK3.7 (43) energy score in these systems (6 kcal/mol at a –0.5 GIST weighting). This is small enough that the term could be overwhelmed by the errors in other docking terms (48), reducing its impact. Intriguingly, its beneficial effects were greatest in those benchmarking sets that had a mixture of favorable and unfavorable water sites. Mechanically, at least as implemented here, the GIST term is costly, increasing the time of a docking screen by on average sixfold (SI Appendix, section S10 and Table S9), although there may be ways to avoid this cost.

These caveats should not distract from the main observations of this study—the ability of GIST to meaningfully improve large library docking screens. The inclusion of a water-displacement term successfully prioritized molecules that did bind on testing and deprioritized those that were found not to, in the teeth of high rankings from the identical scoring function that did not include the GIST term, and even our own expectations. Overall, docking with the GIST term led to a 93% hit rate, with six of nine crystallographic structures in agreement with the docking predictions. The contrast between successful prospective and mediocre retrospective prediction partly reflects the biases toward good performance already baked into the benchmarking sets, however unintentionally. It also reflects our reluctance to optimize the weighting of the scoring function terms for optimal retrospective performance, aware of the oft-described tradeoffs between retrospective optimization and prospective prediction (49). Finally, it is worth noting that in implementing GIST, we only considered the energetic consequences of displacing ordered waters, and did not model the specific interactions between ligands and such waters, which play a role in most protein–ligand complexes (6, 7, 38, 50, 51). Here, such interacting waters, which can appear with a ligand to bridge between it and the protein surface, were only implicitly modeled as high-energy, hard-to-displace regions. Including bridging waters explicitly would add new favorable interactions to ligand recognition, adding to the currently small-magnitude water term. Even without such bridging waters, this study does support the pragmatism of including a displaceable water energy term such as IST, which can materially improve the success of docking ligand prediction and geometry.

Methods

Experimental Affinities and Structures.

The protein was purified and crystallized as described (39) (SI Appendix, section S11). The crystallographic protein–ligand complexes were deposited in the Protein Data Bank (PDB) as 5U60 (1), 5U5W (2), 5U5Z (3), 5U61 (8), 5U5Y (9), 5UG2 (10), 5U5X (11), 5U5U (12), and 5U5V (14) (SI Appendix, Table S10). Affinities were measured at least in duplicate, by monitoring the shift of the heme Soret band.

Molecular Dynamics.

MD were conducted and analyzed with AMBER 14 (52). AMBER's tleap program was used to prepare all proteins for the simulations: The protein systems were placed in a box of TIP3P water such that all atoms were at least 10 Å from the boundary of the box. For CcP-ga, 10 crystallographically observed waters were included in or near the binding site. The heme was parameterized as previously (53) (SI Appendix, section S11 and Table S11).

The module PMEMD.cuda (54) was used to carry out simulations on graphics processing units (GeForce; GTX 980). The equilibration run consisted of two minimizations of up to 6,000 steps followed by six 20-ps runs at constant volume where the temperature of the simulation was raised from 0 to 298.15 K (Fig. 1D). Langevin dynamics (55) were used to maintain the temperature of the simulation with a collision frequency of 2.0 ps⁻¹. Next, a constant-pressure (NPT) run allowed the volume of the box to adjust for 5 ns to maintain 1 bar of pressure. Finally, constant-volume (NVT) simulations were performed for 5 ns, under the same conditions as the subsequent production simulations. Production NVT simulations were performed for 50 ns. All protein heavy atoms were restrained with a 5 kcal⋅mol⁻¹⋅Å⁻² force constant. TheShake algorithm (56) was used with a 2-fs time step. Periodic boundary conditions were applied, and the particle mesh Ewald (57) method was used to calculate long-range electrostatics.

GIST Grids.

GIST grids were generated using the CPPTRAJ (58, 59) trajectory analysis program from AmberTools 14 (52) by processing the 50-ns trajectories with a grid spacing of 0.5 Å. The grids were combined using Python scripts (SI Appendix, section S2) that are available at docking.org/∼tbalius/Code.html and will be made available with the next DOCK release.

Docking.

Scripts and programs in the DOCK3.7 distribution (43) were used to prepare the receptors and ligand databases for docking and to carry out the library screens. Blastermaster.py was used to prepare the protein (SI Appendix, section S11). For GIST, proteins were aligned using Chimera (60) into the simulation’s frame of reference before DOCK preparation. RMSDs were calculated with the Hungarian algorithm in DOCK6.6 (61).