Intraflagellar transport velocity is governed by the number of active KIF17 and KIF3AB motors and their motility properties under load

Significance

Intraflagellar transport (IFT)—cargo transport inside cilia—is mediated by two different kinesin-2 motors: the slower KIF3AB and the faster KIF17. It was not understood how ciliary cargos, called IFT trains, could attain velocities that exceed the unloaded rate of KIF3AB. We find that high IFT velocities cannot be explained by KIF3AB motors speeding up in response to being pulled forward by their KIF17 partners. Instead, IFT velocity is governed by an equilibrium between a slower state, where at least one KIF3AB motor on the train is actively participating in transport, and a faster state, where KIF3AB motors disengage, and only KIF17 motors ferry the train. The more often IFT trains access the faster state, the higher their overall velocity.

Abstract

Homodimeric KIF17 and heterotrimeric KIF3AB are processive, kinesin-2 family motors that act jointly to carry out anterograde intraflagellar transport (IFT), ferrying cargo along microtubules (MTs) toward the tips of cilia. How IFT trains attain speeds that exceed the unloaded rate of the slower, KIF3AB motor remains unknown. By characterizing the motility properties of kinesin-2 motors as a function of load we find that the increase in KIF3AB velocity, elicited by forward loads from KIF17 motors, cannot alone account for the speed of IFT trains in vivo. Instead, higher IFT velocities arise from an increased likelihood that KIF3AB motors dissociate from the MT, resulting in transport by KIF17 motors alone, unencumbered by opposition from KIF3AB. The rate of transport is therefore set by an equilibrium between a faster state, where only KIF17 motors move the train, and a slower state, where at least one KIF3AB motor on the train remains active in transport. The more frequently the faster state is accessed, the higher the overall velocity of the IFT train. We conclude that IFT velocity is governed by (i) the absolute numbers of each motor type on a given train, (ii) how prone KIF3AB is to dissociation from MTs relative to KIF17, and (iii) how prone both motors are to dissociation relative to binding MTs.

Intracellular transport is carried out by microtubule (MT)-based motor proteins of the kinesin and dynein superfamilies (1–4). Cargo, in the form of vesicles, organelles, and nucleoprotein complexes, is generally transported by teams of motors acting in concert. A good deal of previous experimental and theoretical effort has been devoted to determining how cargo transport might be explained quantitatively in terms of the underlying nanomechanical properties of individual motors (5). However, developing such a framework presents challenges: it requires both a detailed characterization of behavior of single motors under both assisting and hindering loads, and also context-dependent measurements in vivo, including determinations of the numbers and types of motors active in transporting cargo. For many important transport processes, including anterograde intraflagellar transport (IFT) (6–10), such data remain unavailable or incomplete. As a consequence, to model the behavior of multiple motors, a variety of ad hoc and experimentally unverified assumptions have been made about motor properties under load. Here, we show how teams of kinesin-2 motors—namely, both homodimeric and heterotrimeric forms of kinesin-2 (1–4, 11–17)—cooperate during anterograde IFT by (i) characterizing the motility properties of both motors using single-molecule optical trapping techniques in vitro and (ii) contextualizing our findings with the aid of recent data obtained in vivo (10).

Homodimeric kinesin-2 is formed from a dimer of identical polypeptide chains, each carrying a conserved N-terminal motor domain, a coiled-coil-forming stalk (the dimerization domain), and a C-terminal tail that can bind cargo (12, 13, 16–20) (Fig. 1A). The dimer is processive, translocating 1–2 µm, on average, toward the plus-end of MTs at speeds of 0.8–1.5 µm/s (6, 7, 20, 21). This motor plays a major role in dendritic transport (2, 17–19, 22–27) and IFT (8, 17, 19, 28–30), facilitating the generation and maintenance of cilia (8, 9, 17, 19, 28, 29, 31–35). Heterotrimeric kinesin-2, in contrast, is composed of two nonidentical polypeptide chains carrying distinct motor domains, along with a nonmotor accessory protein, KAP (11, 13–15, 17). Its two N-terminal motor domains dimerize via a coiled-coil stalk, with KAP binding near the C-terminal tail region (17, 36–38). This motor is also processive, moving ∼0.5 µm toward the plus-end of MTs at speeds of 0.3–0.5 µm/s (7, 39–41). In addition to its role in axonal and cytoplasmic transport (17, 42–45), heterotrimeric kinesin-2 contributes to ciliary maintenance via IFT (8, 9, 17, 28–32, 35, 46–49).

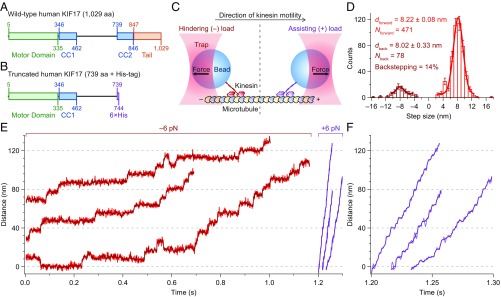
Fig. 1.

KIF17 maintains processivity under assisting and hindering loads. (A and B) Schematic representation of (A) wild-type KIF17 and (B) the truncated KIF17 construct used in this study. Shown are the motor domain (green), coiled-coil regions (CC1 and CC2; blue), C-terminal tail (orange), and His-tag (violet). (C) Graphical representation of the single-molecule optical trapping assay. Both hindering- (−; Left) and assisting-load (+; Right) experimental geometries are depicted (not to scale). (D) Step-size histogram of 549 KIF17 steps obtained under a 6-pN hindering load at saturating ATP conditions (2 mM). Distributions of forward (red; $N_{\text{forward}}=471$) and backward (burgundy; $N_{\text{back}}=78$) steps are shown, along with Gaussian fits (solid lines) and fit parameters (legend; mean ± SE). (E) Representative records of KIF17 runs under 6-pN hindering (red) and 6-pN assisting (purple) loads under saturating ATP conditions. Unfiltered records (light) are overlain by median-filtered data (dark; seven-point sliding window). (F) Expanded timescale for the assisting-load records shown in E.

Kinesin-2 class motors are given different names in various species (17). In Caenorhabditis elegans—in which much of the IFT research has been performed—homodimeric kinesin-2 is called OSM-3, and heterotrimeric kinesin-2 is called kinesin-II, or KLP20/11 (17). Vertebrate homodimeric kinesin-2 is called KIF17 (17). Two vertebrate forms of heterotrimeric kinesin exist, KIF3AB and KIF3AC, formed by the dimerization of the KIF3A polypeptide with either KIF3B or KIF3C (17, 50–52). For simplicity, we refer below to homodimeric kinesin-2 from all organisms as “KIF17” and the IFT-relevant form of heterotrimeric kinesin-2 as “KIF3AB.”

Significant progress has been made in understanding how KIF17 and KIF3AB cooperate during anterograde IFT (6–10). Investigations of C. elegans cilia have revealed that once an IFT train enters the cilium, both KIF17 and KIF3AB motors transport the train along doublet MTs that comprise the axonemal middle segment (MS) (6–8, 10, 53). After reaching the singlet MTs in the axonemal distal segment (DS) (53), KIF17 motors transport the train alone for the remainder of the trip to the ciliary tip (6–8). Based on the work of Prevo et al. (10), KIF3AB motors are responsible for conveying IFT trains into the cilium, after which they are gradually replaced by KIF17 motors, in a so-called handover zone that spans the MS.

Despite these advances, how the different types of kinesin-2 motors cooperate during IFT remains unclear. When motors attached to a common cargo attempt to move at different rates, the cargo velocity is limited by the speed of the slowest MT-bound motor. During IFT, however, trains typically travel at rates that are intermediate between the unloaded velocities of the slower KIF3AB motors and the faster KIF17 motors (6–8, 10). How, then, do IFT trains achieve velocities in excess of 1 µm/s (10) when the unloaded velocity of KIF3AB is only a fraction of that value (7, 39–41)?

Because their comparatively slower velocities would cause them to trail KIF17 motors when transporting a common cargo, KIF3AB motors functioning in teams must be regularly subjected to assisting loads, acting along the direction of translocation. One straightforward possibility is that these assisting loads pull KIF3AB motors forward, thereby eliciting an increase in their velocity. In that case, the degree of velocity increase would depend on the ratio of KIF17 to KIF3AB motors attached to the IFT train. Implicit in this scenario is that at least one of the KIF3AB motors must remain bound to the MT at all times.

A different mechanism that can explain IFT velocities entails alternation between a fast IFT state, where none of the KIF3AB motors on the train are MT-bound, and transport is therefore by KIF17 alone, and a slow IFT state, where one or more KIF3AB motors remain active. In this scenario, the accessibility of the fast state is determined by the probability that all KIF3AB motors in the train simultaneously detach from the MT. IFT velocity would then depend on the number of MT-bound KIF3AB motors, rather than on the ratio of kinesin-2 types on a given train. Having fewer MT-bound KIF3AB motors—to facilitate occupancy of the fast state—would be favored by (i) a lower number of KIF3AB motors on the train; (ii) a higher rate of force-dependent dissociation from MTs, $k_{\text{off}}$, for KIF3AB motors subjected to assisting loads, exceeding the corresponding release rate for KIF17 under hindering loads; (iii) the load-independent MT-binding rate, $k_{\text{on}}$, of KIF3AB being lower than the corresponding rate for KIF17; and (iv) the MT-dissociation rate, $k_{\text{off}}$, for KIF3AB exceeding its MT-binding rate, $k_{\text{on}}$. Although dozens of kinesin-2 motors are known to be attached to each train throughout the handover zone (10), the fraction of these that might be bound to the MT remains unknown.

Disambiguating the candidate mechanisms explaining IFT velocities necessitates investigating the behavior of individual molecules of KIF17 and KIF3AB under both assisting and hindering loads. Toward that end, we performed single-molecule optical trapping assays to characterize the properties of truncated human KIF17 under constant loads and extended our previous investigation of a mouse KIF3AB construct (40) to include assisting loads.

Results

KIF17 Is Processive Under Load.

We produced and expressed a recombinant construct consisting of the first 738 amino acids (aa) of human KIF17 carrying a C-terminal His-tag (Fig. 1 A and B). Using an optical force clamp to apply constant, piconewton-scale loads, we found that KIF17—like other kinesin proteins (40, 54–56)—takes ∼8.2-nm steps, maintains processive motility under load, and takes occasional backsteps under hindering load (Fig. 1 C‒F).

Assisting Loads Induce Only Modest Velocity Increases for KIF3AB Compared with KIF17.

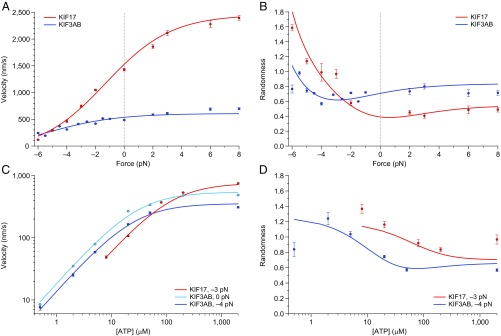
We characterized KIF17 motility under a series of applied loads and ATP concentrations, and extended our KIF3AB dataset (40) to cover assisting loads (Fig. 2 and Fig. S1). Consistent with previous reports (6, 7, 20, 21), the unloaded velocity of KIF17 under saturating ATP conditions exceeded that of KIF3AB by a factor of ∼3. KIF17 was also faster than KIF3AB across a wide range of applied forces: the two motors exhibited comparable velocities only under hindering loads of ∼5 pN or more (Fig. 2A). The velocities of both motors increased under assisting loads, but the effect was modest for KIF3AB, whereas it was pronounced for KIF17 (Fig. 2A). Differences in motor randomness [a metric for the irregularity of the step timing, whose inverse supplies a lower bound on the number of rate-limiting transitions in the mechanochemical cycle (57)] were also observed under load (Fig. 2B).

Fig. 2.

Comparison of KIF17 and KIF3AB behavior under load. (A and B) Single-molecule (A) velocity and (B) randomness (solid circles; mean ± SE; $N=49–530$) measurements as a function of applied load for KIF17 (red) and KIF3AB (blue). Data were obtained in the presence of 2 mM ATP. (C and D) Single-molecule (C) velocity and (D) randomness (solid circles; mean ± SE; $N=22–319$) measurements as a function of ATP concentration for KIF17 (red) and KIF3AB (blue) under a constant load (legend). In all panels, solid lines represent global fits to the minimal four-state model (Fig. 3). Hindering-load and unloaded data for KIF3AB are reproduced from ref. 40.

Fig. S1.

ATP dependence of KIF17 motility under load. (A and B) Single-molecule KIF17 (A) velocity and (B) randomness measurements as a function of applied load (solid circles; mean ± SE; $N=49–552$) in the presence of 2 mM (red) or 0.02 mM (orange) ATP. Solid lines, global fits to the four-state model (Fig. 3). Data for 2 mM ATP are reproduced from Fig. 2 A and B for comparison.

A Minimal Four-State Model Captures the Mechanochemistry of KIF17 and KIF3AB.

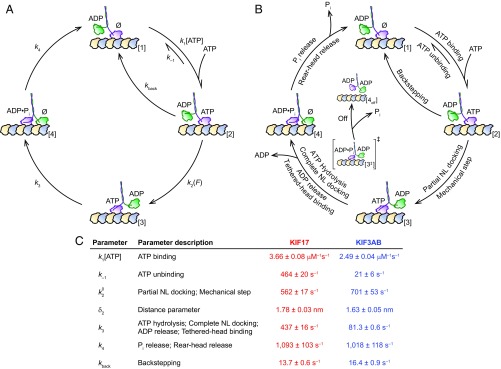
To establish which aspects of the mechanochemical cycles of the two motors account for the motility differences, we modeled the experimental data (Fig. 2 and Fig. S1) by a minimal, four-state representation of the kinesin cycle (Fig. 3 A and B). Beginning from the one-head-bound (1-HB), ATP-waiting state (56, 58, 59), the first transition, [1] → [2], involves reversible ATP binding to the MT-bound head (60), and is represented by an ATP-dependent forward rate, $k_1$, and an ATP-independent reverse rate, $k_{-1}$. The next transition, [2] → [3], entails a partial docking (61) of the kinesin neck linker [NL; a ∼17-aa-long element linking the head to the stalk (62, 63)] to the bound head (64), shifting the tethered head forward. This transition incorporates the mechanical step of the cycle and is modeled by a force-dependent rate, $k_2\left(F\right)=k_2^0\exp \left[F{\delta }_2/k_{\text{B}}T\right]$, where $k_2^0$ is the unloaded rate constant, $F$ is the applied load, ${\delta }_2$ is a characteristic distance parameter, and $k_{\text{B}}T$ is Boltzmann’s constant times the absolute temperature. Partial docking might involve either (i) docking of a segment of the NL, with the remainder remaining undocked, or (ii) a shift in equilibrium between two states of the NL, where the NL is fully docked or undocked (61). ATP hydrolysis triggers the completion of NL docking (61) in the bound head, allowing the tethered head to release ADP and bind the MT. These events are unified within a single transition, [3] → [4], and represented by a force-independent rate constant, $k_3$. The release of inorganic phosphate (P_i) and rear-head detachment (65), modeled by a force-independent rate constant, $k_4$, revert the motor to its ATP-waiting state, [4] → [1], having moved one step forward. Randomness values exceeding unity (57) (Fig. 2 B and D) are accommodated by a rearward stepping transition at rate $k_{\text{back}}$.

Fig. 3.

KIF17 and KIF3AB mechanochemical cycles captured by a four-state model. (A) A minimal four-state representation of the kinesin cycle, shown alongside (B) the partial-docking model (61), where the states and transitions in the four-state model are given specific interpretations. The first transition of the cycle, [1] → [2], which entails reversible ATP binding to the MT-bound, apo (Ø) head in the 1-HB ATP-waiting configuration, is modeled by an ATP-dependent forward rate, $k_1$, and an ATP-independent reverse rate, $k_{-1}$. Once ATP binds, the NL domain partially docks to the bound head, shifting the tethered head forward, [2] → [3]: this transition is modeled by a force-dependent rate, $k_2\left(F\right)$ and corresponds to the mechanical step. Subsequent ATP hydrolysis leads to completion of NL docking, release of ADP by the tethered head, and MT binding, [3] → [4]. In the minimal model, these events are captured by a single, force-independent rate constant, $k_3$. This transition entails passage through an implied 1-HB, posthydrolysis transition state [3^‡], from which either (i) the tethered head binds the MT, successfully completing the step, [3^‡] → [4], or (ii) the bound head prematurely hydrolyses ATP, resulting in motor dissociation from the MT, [3^‡] → [4_off]. Finally, the cycle is completed by P_i release and rear-head dissociation, which are jointly modeled a force-independent rate, $k_4$. A load-independent back-stepping transition, $k_{\text{back}}$, has also been incorporated. (C) Parameters (mean ± SE) obtained from global fits of KIF17 (red) and KIF3AB (blue) velocity and randomness data in Fig. 2 and Fig. S1 to the model in A.

Analytical expressions for the velocity and randomness for this model (Materials and Methods) were fit globally to the KIF17 and KIF3AB data (Fig. 2 and Fig. S1); parameter values are supplied in Fig. 3C. We find that the ATP binding rate ($k_1$) of KIF17 is ∼50% greater than that of KIF3AB, whereas both the ATP unbinding ($k_{-1}$) and ATP hydrolysis ($k_3$) rates are an order of magnitude greater for KIF17 than for KIF3AB. All other physical parameters are comparable.

ATP Hydrolysis Precedes Completion of the KIF17 Step.

Although not explicitly incorporated in the minimal four-state model, having ATP hydrolysis precede entry into the two-heads-bound (2-HB) state, [3] → [4], implies the existence of a posthydrolysis, 1-HB transition state [3^‡] with a fully docked NL (Fig. 3). This state is based on the partial-docking model (61), where only after the MT-bound head has hydrolyzed ATP and fully docked its NL [3^‡] is the partner head able to advance to the next MT binding site. The run length (RL)—the distance translocated before motor dissociation—is determined by a competition between tethered-head binding ([3^‡] → [4]) and premature dissociation ([3^‡] → [4_off]) (61). Positing that the tethered head is unable to bind the MT until after ATP hydrolysis implies that the branch-point governing the RL occurs posthydrolysis. The partial-docking model therefore predicts that RL will remain unchanged in response to a reduced ATP concentration, or to a reduced ATP hydrolysis rate, whereas it will increase in response to a stabilization of the posthydrolysis, bound ADP·P_i state [3^‡] via a reduction in the P_i release rate (61).

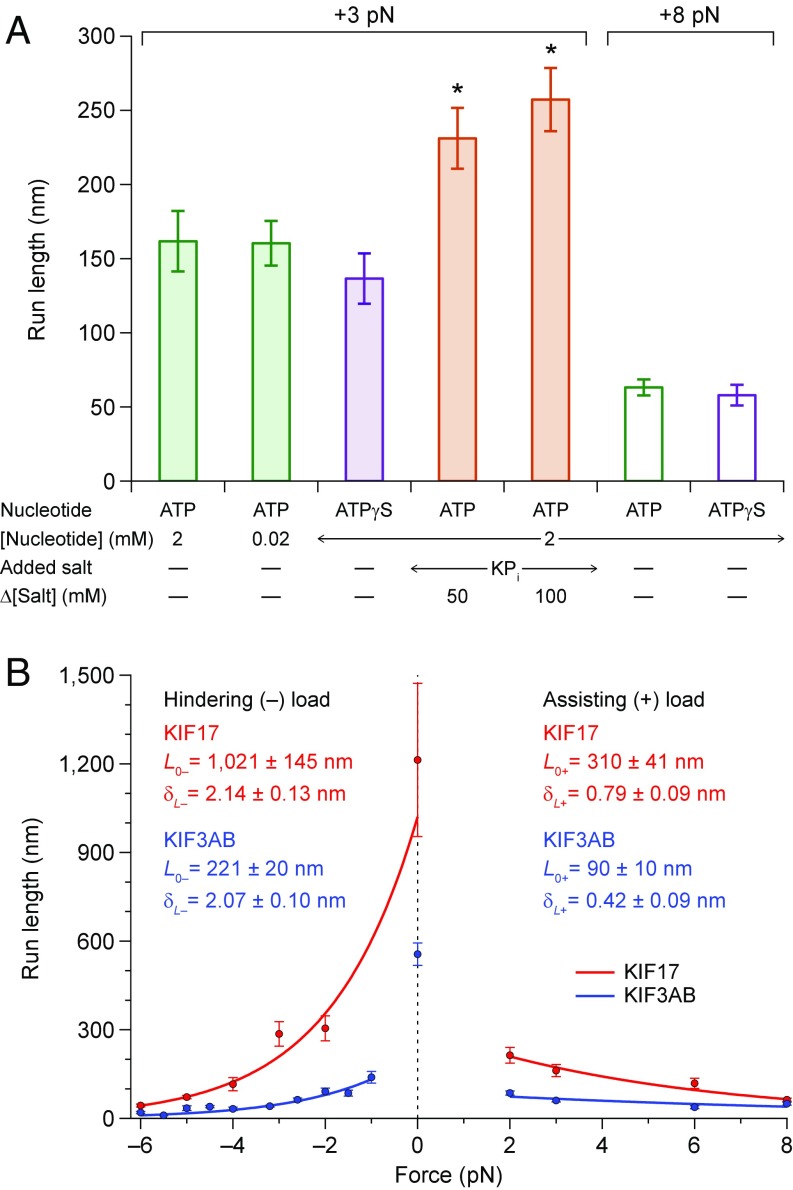
To test these predictions for kinesin-2, we examined how KIF17 RL responded to modified assay conditions under moderate assisting loads (Fig. 4). Consistent with the partial-docking model, decreasing the ATP concentration or reducing the hydrolysis rate by replacing ATP with ATPγS (a slowly-hydrolyzable ATP analog) produced no change in RL. However, reducing the P_i release rate through the addition of potassium phosphate (KP_i) led to a statistically significant RL increase.

Fig. 4.

Processivity: KIF17 and KIF3AB RLs under load. (A) KIF17 RL data (mean ± SE; $N=118–322$) under assisting loads of 3 pN (solid bars) and 8 pN (open bars). Measurements were made in the presence of either ATP (green) or ATPγS (purple), and in the presence or absence of added KP_i (orange). Buffer conditions are indicated beneath the corresponding bars. The addition of phosphate (orange) induced a statistically significant RL increase (*$P\le 0.05$; t test) relative to the absence of added phosphate (green) under otherwise comparable conditions. No such increase was detected under varying nucleotide conditions in the absence of added phosphate. (B) RL measurements (solid circles; mean ± SE; $N=49–530$) as a function of applied load for KIF17 (red) and KIF3AB (blue). Data were obtained in the presence of 2 mM ATP. Assisting- and hindering-load RL measurements were fit separately to $L\left(F\right)=L_0\exp \left[-\left|F\right|{\text{δ}}_L/k_{\text{B}}T\right]$, where $L_0$ is the unloaded RL and ${\delta }_L$ is the characteristic distance parameter. Exponential fits (lines) and corresponding $L_0$ and ${\delta }_L$ parameters (legend; mean ± SE) are shown. Hindering-load and unloaded data for KIF3AB are reproduced from ref. 40.

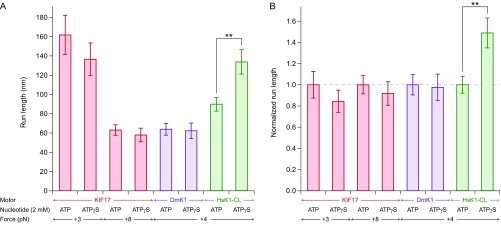
In contrast, a recent investigation of NL kinetics (66) in a Cys-light (CL) human kinesin-1 [HsK1-CL, which carries six cysteine mutations in each motor domain (64)] showed that its NL fully docks upon ATP binding. In this case, the tethered head should be capable of binding the MT after ATP binding by the bound partner head, which implies that reducing the ATP hydrolysis rate should lead to an increase in processivity. Consistent with that prediction, we observed a nearly 50% increase in RL in the presence of saturating levels of ATPγS, compared with ATP (Fig. S2).

Fig. S2.

Processivity of human CL kinesin-1 is enhanced by reducing its ATP hydrolysis rate. (A) RL measurements (mean ± SE; $N=118–322$) under assisting loads for KIF17 (red), DmK1 (purple), and HsK-CL (green). Data were collected in the presence of either ATP or ATPγS (2 mM); buffer and force conditions are specified beneath the corresponding bars. For HsK1-CL, replacing ATP with ATPγS produced a statistically significant increase in RL (**$P\le 0.01$; t test). No corresponding increase was observed for KIF17 or DmK1. KIF17 measurements are the same as those in Fig. 4A; DmK1 data are reproduced from ref. 61. (B) RL measurements from A normalized to baseline RLs in the presence of ATP for each construct and force condition.

RLs and Dissociation Rates of KIF17 and KIF3AB Are Asymmetric with Respect to Load.

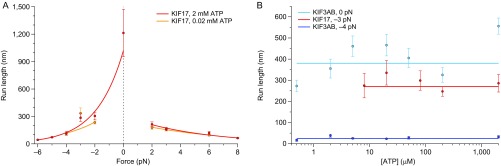
Further investigation of kinesin-2 RL under load (Fig. 4B) revealed that KIF17 is significantly more processive than KIF3AB under equivalent load. The RLs of the two motors also exhibited dramatic asymmetry with respect to the direction of load. Their force dependence was nearly identical under hindering loads (${\delta }_{L-}$), but not under assisting loads (${\delta }_{L+}$), and was independent of the ATP concentration (Fig. S3). Dissociation rates ($k_{\text{off}}$)—equivalent to the quotient of velocity and RL—for KIF17 ($k_{17,\text{off}}$) and KIF3AB ($k_{3\text{AB},\text{off}}$) also exhibited asymmetry with the load direction (Fig. 5A).

Fig. S3.

ATP dependence of KIF17 and KIF3AB RLs under load. (A) KIF17 RL measurements as a function of applied load (solid circles; mean ± SE; $N=49–552$) in the presence of 2 mM (red) or 0.02 mM (orange) ATP. Solid lines represent exponential fits to assisting- and hindering-load RL measurements. The 2 mM ATP data are reproduced from Fig. 4B for ease of comparison. (B) RL measurements as a function of ATP concentration (solid circles; mean ± SE; $N=22–319$) for KIF17 (red) and KIF3AB (blue) under a constant load (see legend). Linear fits (solid lines) to RL data are shown. The KIF3AB data are reproduced from ref. 40.

Fig. 5.

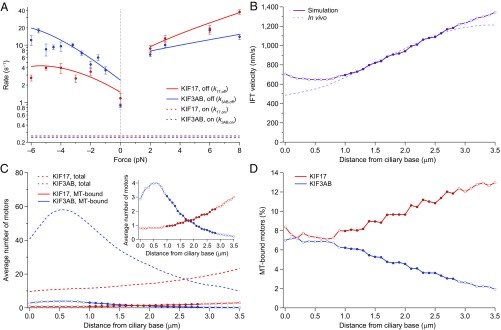
IFT velocities are recapitulated by simulations based on experimental parameters. (A) Dissociation rate measurements ($k_{\text{off}}$; solid circles; mean ± SE; $N=49–530$) for KIF17 (red) and KIF3AB (blue) as a function of load. Fits to dissociation rates (solid lines) were obtained by dividing fits to KIF17 and KIF3AB velocities (Fig. 2A) by the corresponding hindering- and assisting-load RL fits (Fig. 4B). Load-independent MT-binding rates ($k_{\text{on}}$; dashed lines) that generated IFT velocities that best agreed with in vivo findings (10) are shown (Fig. S4). (B) Simulated IFT velocities (circles; solid line) versus distance from the ciliary base compared with in vivo data (dashed line) from Prevo et al. (10). IFT velocities tend to be overestimated (empty circles) in the TZ (<1 µm from the base) and in the distal portions of the MS (beyond ∼2.8 µm; see text). (C) The total numbers of each type of motor on an IFT train as a function of distance from the base (dashed lines), measured by Prevo et al. (10) in vivo, graphed together with the numbers of MT-bound motors (circles; solid lines) based on the simulations (Materials and Methods). (Inset) The MT-bound motor data are rescaled to show greater detail. (D) Estimated percentage of total motors that are MT-bound as a function of distance, from the data in C. In C and D, solid circles are plotted in the region between 1.0 µm and 2.8 µm from the base; the TZ and distal MS are plotted using open circles. Velocities (B) and numbers of MT-bound motors (C and D) are mean values obtained from 40 Monte Carlo simulations (20,000 transitions each) sampled at 0.1-µm spacing (Materials and Methods) with $k_{17,\text{on}}=0.258\hspace{0.17em}{\mathrm{s}}^{-1}$ and $k_{3\text{AB},\text{on}}=0.244\hspace{0.17em}{\mathrm{s}}^{-1}$ (Fig. S4).

When teams of kinesin-2 motors ferry the same cargo, KIF3AB motors are subjected to assisting loads as they get pulled forward by faster KIF17 motors; conversely, KIF17 motors experience hindering loads from their trailing KIF3AB counterparts. Comparing the dissociation rates for the two motors under opposite loading directions is therefore germane to IFT. We observed that $k_{3\text{AB},\text{off}}$ under assisting loads exceeded $k_{17,\text{off}}$ for hindering loads across the entire range of loads.

Simulations Based on Single-Molecule Results Recapitulate IFT Motility.

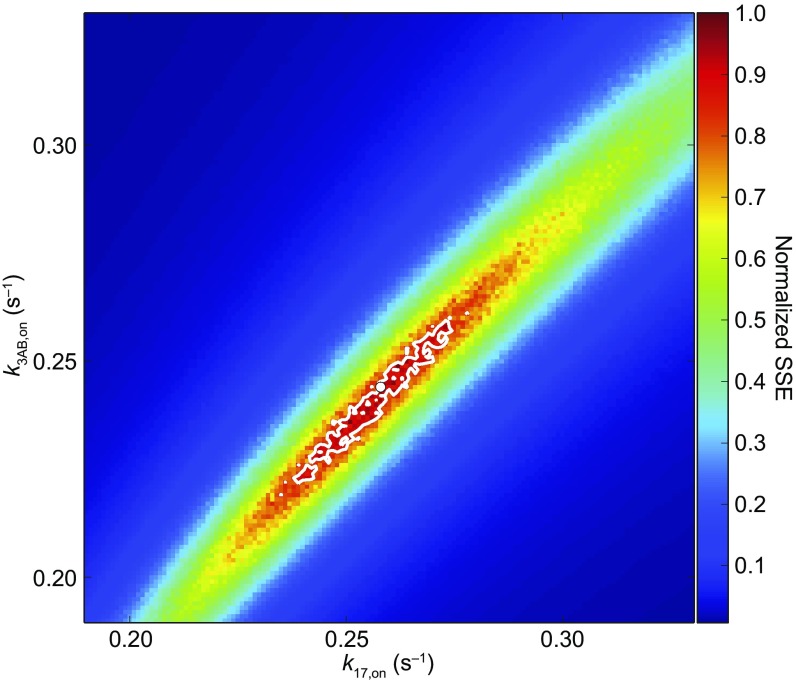
Modeling how motors coordinate during IFT depends not only on a knowledge of the load-dependent velocities and off-rates for KIF17 and KIF3AB but also knowledge of their load-independent MT-binding rates ($k_{\text{on}}$). We carried out Monte Carlo simulations of IFT transport as a function of distance from the ciliary base, based on (i) single-molecule velocity (Fig. 2A) and $k_{\text{off}}$ (Fig. 5A) data, (ii) previously published determinations of the numbers of each type of kinesin-2 motor attached to IFT trains at various distances (10), and (iii) a pair of $k_{\text{on}}$ values assumed for KIF17 ($k_{17,\text{on}}$) and KIF3AB ($k_{3\text{AB},\text{on}}$) motors (Materials and Methods). By minimizing the sum-square error (SSE) (67) between the simulated IFT velocities and the corresponding in vivo data (10) at a series of points along the cilium, we found the best agreement when $k_{17,\text{on}}=0.26\mathrm{\pm }0.02\hspace{0.17em}{\mathrm{s}}^{-1}$ and $k_{3\text{AB},\text{on}}=0.24\mathrm{\pm }0.03\hspace{0.17em}{\mathrm{s}}^{-1}$ (Fig. 5B and Fig. S4). The values for the two motors are the same within error and lower by an order of magnitude than the corresponding $k_{\text{off}}$ values, across all loads (Fig. 5A).

Fig. S4.

Simulations using experimental parameters allow estimation of MT-binding rates for kinesin-2. Contour plot displaying the normalized SSE (67) between simulated IFT velocities and those measured in vivo (10) over the region spanning 1.0 µm to 2.8 µm from the ciliary base (Fig. 5B) for a series of KIF17 ($k_{17,\text{on}}$) and KIF3AB ($k_{3\text{AB},\text{on}}$) MT-binding rates (Materials and Methods). For each pair of MT-binding rates, ranging from 0.19 s⁻¹ to 0.33 s⁻¹, sampled at 0.001-s⁻¹ intervals, SSE values were obtained from 40 Monte Carlo simulations (20,000 transitions each), sampled at 0.1-µm intervals. The minimum SSE (white dot), corresponding to a normalized SSE of 1.0, occurred for $k_{17,\text{on}}=0.258\hspace{0.17em}{\mathrm{s}}^{-1}$, $k_{3\text{AB},\text{on}}=0.244\hspace{0.17em}{\mathrm{s}}^{-1}$. Uncertainties in the estimated binding rates were computed from the confidence contour at 15% above the minimum (67).

We note that the simulation tends to overestimate the IFT velocity (Fig. 5B) in the transition zone (TZ), which spans the first ∼1 µm of the cilium, and in the most distal portions of the MS, beyond ∼2.8 µm from the base. This is understandable, because within the TZ abundant Y-link proteins and transition fibers (29, 34) likely hinder IFT trains and reduce IFT velocity by causing an increase in $k_{\text{off}}$ (by blocking the progress of motors) or a reduction in $k_{\text{on}}$ (by reducing motor access to the MT). In a similar vein, a “traffic jam” of IFT trains at the juncture formed by the overlap of DSs of the two cilia that comprise the phasmid chemosensory apparatus (10) likely accounts for reduced velocities in the distal region of the MS. This interpretation is bolstered by the observation of an increased train density at this juncture, followed by an abrupt increase in IFT velocity once the juncture is passed (10). In formulating estimates for $k_{17,\text{on}}$ and $k_{3\text{AB},\text{on}}$ we therefore disregarded the TZ and the distal portion of the MS (Fig. 5B). Our simulation predicts that only a small fraction of the motors attached to IFT trains are bound to the MT at any given time, and therefore that IFT occurs in the single-molecule, or near-single-molecule, regime (Fig. 5 C and D).

Discussion

Although KIF17 and KIF3AB display different motility properties (Fig. 2 and Fig. 4B), we conclude that their differences arise chiefly from variations in the rates of only a few transitions within the mechanochemical cycle (Fig. 3), namely, in their respective ATP affinities and hydrolysis rates. Whereas ATP hydrolysis ($k_3$) is the slowest transition for both KIF17 and KIF3AB under unloaded but saturating-ATP conditions, it is rate-limiting only for KIF3AB. Because the unloaded rate ($k_2^0$) of the mechanical step ($k_2\left(F\right)$) for KIF17 is only ∼30% faster than $k_3$, modulating $k_2\left(F\right)$ by the application of an external load markedly affects the catalytic cycle. Because the overall cycle rate sets the velocity, the similarity of $k_2^0$ to $k_3$ explains the steep load-dependence of KIF17 velocity: even a few piconewtons are sufficient to speed up or slow down KIF17 relative to its unloaded speed (Fig. 2A). In the case of KIF3AB, by contrast, $k_2^0$ is an order of magnitude greater than $k_3$, thereby leading to a cycle that is rate-limited by $k_3$, and considerably less sensitive to load.

Our interpretation of the transition rates (Fig. 3) is based on the partial-docking model (56, 61) and is supported by the assisting-load KIF17 measurements of RL (Fig. 4A). The model garners additional support from recent observations of gold-nanoparticle-labeled kinesin-1 heads during stepping, which showed that decreasing the hydrolysis rate prolongs the residence time in a 1-HB state (68). Furthermore, investigations of the NL kinetics of Eg5—a kinesin-5 motor (1, 3, 4)—have shown that ATP hydrolysis stabilizes the docked state (66). We are therefore inclined to speculate that the partial-docking mechanism may hold across multiple kinesin families. We note that although the partial-docking model does allow for the possibility of small mechanical substeps in the kinesin cycle, no such substeps were apparent in records of KIF17 (Fig. 1 E and F) or KIF3AB (40) translocation at our level of resolution.

Recent work probing the extent of NL docking in human CL kinesin-1, however, has led to the suggestion that ATP binding alone may be sufficient to induce full NL docking in that construct (66). Although the increase in RL elicited by ATPγS in HsK1-CL, which decreases the hydrolysis rate of the motor (Fig. S2), is fully consistent with recent results (66), no such increase was found for a non-CL kinesin-1 (56, 61). The failure of CL human kinesin-1 to behave similarly to its wild-type counterpart may be attributable to its six cysteine mutations, which also lead to an unusual force–velocity relationship (56).

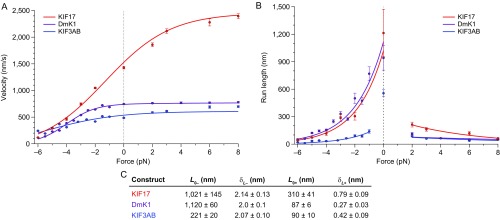
Differences in the load-dependent velocities, processivities, and mechanochemical cycles among various kinesin family motors have previously been attributed to structurally conserved features, notably to the length of the NL (69). To our surprise, we found that aspects of the motility properties of KIF17 and KIF3AB—which are both kinesin-2 motors with identical-length NLs of 17 aa—are more similar to those of kinesin-1 than to each other, despite kinesin-1 having a NL of 14 aa (Fig. S5). In other words, whereas the motility properties of KIF17 and KIF3AB under load differ significantly from each other (Figs. 2A and 4B), the velocities and RLs of each of these two kinesin-2 motors bear similarities to those of kinesin-1 over restricted force ranges (Fig. S5). For example, KIF17 and kinesin-1 RLs are identical under hindering loads, whereas the KIF3AB RL is lower than that of KIF17 across the entire range of hindering loads. Similarly, the KIF3AB RL under assisting loads is indistinguishable from that of kinesin-1 but lower than the KIF17 RL under the same force regime. The velocity of KIF3AB approaches that of kinesin-1 as increasing forward loads are applied, whereas the velocity of KIF17 exceeds that of both KIF3AB and kinesin-1 across all assisting loads. These findings suggest that differences between motors may derive from subtle structural variations, and that the motility properties of well-characterized motors cannot be assumed to extend to as-yet uncharacterized motors, even within the same kinesin family. Detailed characterization of each kinesin motor may be necessary to explain its functional role.

Fig. S5.

Kinesin-2 motility properties bear similarities to kinesin-1. (A) Velocity measurements as a function of applied load (solid circles; mean ± SE; $N=49–818$) for KIF17 (red), KIF3AB (blue), and DmK1 (purple). All data were taken at 2 mM ATP. Global fits to velocity data (solid lines) are based on the four-state model. (B) RL measurements as a function of applied load (solid circles; mean ± SE; $N=49–818$) for KIF17 (red), KIF3AB (blue), and DmK1 (purple), under the same buffer conditions. Fits to assisting- and hindering-load RL measurements (solid lines) to the function $L\left(F\right)=L_0\exp \left[-\left|F\right|{\mathrm{\delta }}_L/k_{\text{B}}T\right]$ (definitions of variables are given in the main text). (C) Tabulated $L_0$ and ${\delta }_L$ parameters for both hindering- and assisting-load regimes (mean ± SE). DmK1 data and fits (56), and hindering-load and unloaded KIF3AB measurements (40), are reproduced from previous work. Velocity and RL data, as well as associated fits, are taken from Figs. 2A and 4B.

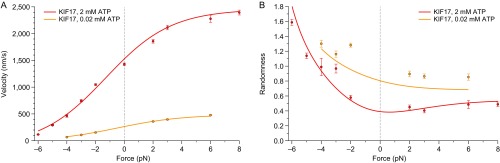
This investigation of KIF17 and KIF3AB load-dependent mechanochemistry supplies a mechanistic explanation for kinesin-2 cooperation during IFT. Because the velocity of KIF3AB is limited to ∼700 nm/s by its hydrolysis rate (Figs. 2A and 3C), IFT train velocities exceeding 1 µm/s (10) cannot be attributed to an increase in velocity induced by assisting loads from other types of motors. Instead, we find that the IFT velocity is governed by the equilibrium between a KIF3AB-limited, “slow” IFT state and a “fast” IFT state, where all KIF3AB motors on the train must be simultaneously dissociated from the MT. Although dozens of kinesin-2 motors are known to be present on IFT trains throughout the handover zone (10), we expect only a fraction of them to be bound to the MT at any given time (Fig. 5 C and D). This prediction is directly derivable from our data: (i) KIF3AB is more prone to dissociation under assisting loads than KIF17 is under hindering loads of the same magnitude ($k_{3\text{AB},\text{off},+}>k_{17,\text{off},-}$) and (ii) both motors have an order-of-magnitude faster rate of MT dissociation than binding ($k_{\text{off}}>>k_{\text{on}}$) (Fig. 5A). Aided by the progressively decreasing number of KIF3AB motors on trains as they progress toward the tip of a cilium (10), the number of MT-bound KIF3AB motors is correspondingly reduced (Fig. 5 C and D), which, in turn, gradually enhances IFT velocities up to ∼1.2 µm/s by the end of the handover zone (Fig. 5B).

A quantitative understanding of both the load-dependent velocity and load-dependent processivity of motor proteins, along with some knowledge of their relative numbers and rates of association, is required to model the nanomechanical behavior when multiple motors are attached to a common cargo. In conclusion, we find that IFT motion cannot be simply described as a form of “tug of war,” with subsets of motors competing directly at different forces, but neither can it be simply described as a “relay race,” where one subset of motors is systematically replaced by another as transport progresses. Instead, IFT offers aspects of both: a slower state that represents a competition between kinesin-2 motors governing transport in regions where the cargo velocity is limited by slower, but comparatively more numerous, KIF3AB motors, and a faster state that dominates in more distal regions of the cilium, where IFT trains are ferried by faster KIF17 motors alone, due to both reduced numbers and to the limited processivity of KIF3AB. We anticipate that measurements of IFT transport at improved spatiotemporal resolution (10) may reveal discrete alternations between velocities, indicative of slow and fast states that average out to the intermediate velocities observed for IFT trains (Fig. 5B).

The IFT mechanism described here hints at a means by which cargo transport toward ciliary tips might be tuned in response to cellular needs. Because the anterograde velocity of an IFT train is determined by the likelihood that at least one KIF3AB motor is MT-bound, we speculate that IFT velocity might be tuned by (i) regulating the attachment of KIF3AB motors to IFT trains in the handover zone, or by (ii) modulating the rate of KIF3AB binding to MTs, via obstacles on the MT or factors in the intracellular environment.

Materials and Methods

Protein Expression and Purification.

A truncated human KIF17 gene consisting of the first 738 aa of the full-length motor (National Center for Biotechnology Information accession no. NP_065867) fused to a C-terminal His-tag was commercially synthesized (Integrated DNA Technologies). The use of a truncated construct avoided known autoinhibitory effects associated with the CC2 (coiled-coil 2) and tail domains (20). The truncated KIF17 gene was transferred to a pBiEx-1 plasmid (Novagen) and subsequently expressed in Sf9 cells. Cell growth and lysate preparations were performed as described (70). The clarified lysate was mixed 1:1 with binding buffer and added to 100 μL of Ni-NTA agarose resin (Invitrogen) that was preequilibrated with binding buffer (discussed below). Following incubation for 1 h on a rotator, the resin was washed three times in binding buffer with a 10-min mixing step between each wash. Finally, KIF17 was eluted in several steps, using 200 μL of elution buffer each time, before flash freezing in liquid nitrogen and storage at −80 °C. Both binding and elution buffers were pH 7.9 and composed of 20 mM Tris, 500 mM NaCl, 5 mM MgCl₂, 10% (wt/wt) sucrose, 1 mM DTT, and 75 μM ATP. The two buffers differed in imidazole content: the binding buffer contained 40 mM imidazole, whereas the elution buffer contained 500 mM imidazole. Note that DTT and ATP were added to each buffer immediately before purification.

Separately, a full-length heterodimeric mouse KIF3AB construct with a C-terminal His-tag was expressed in Sf9 cells and purified as described, a gift from W. Hancock, Pennsylvania State University, State College, PA (40, 71). A truncated CL human kinesin-1 construct (HsK1-CL) (60, 64, 72) consisting of the first 560 N-terminal amino acids of the motor and carrying a series of cysteine mutations (C7S, C65A, C168A, C174S, C294A, C330S, and C421A) was expressed in BL21 Escherichia coli cells and purified as before, a gift from S. Rosenfeld, Mayo Clinic, Rochester, MN (60, 73). Both the KIF3AB and HsK1-CL constructs used in this study were from the same stock used in our previous work (40, 56).

Single-Molecule Optical Trapping Assay.

The motility assay has been described in detail previously (56, 60, 61). Briefly, experiments were performed in PEM80 motility buffer (80 mM Pipes, 1 mM EGTA, and 4 mM MgCl₂) at pH 6.9, 2 mM DTT, 10 µM Taxol, and 3 mg⋅mL⁻¹ BSA. Before introduction into flow cells, an oxygen-scavenging system, composed of 50 µg⋅mL⁻¹ glucose oxidase, 12 µg⋅mL⁻¹ catalase, and 3 mg⋅mL⁻¹ glucose (final concentrations) was added to the motility buffer. Procedures for preparing flow cells, kinesin incubations, and 440-nm polystyrene beads are the same as in prior work (60). Unloaded (0 pN) velocity and RL measurements were obtained by video tracking (60); an optical force clamp was used to study kinesin motility under controlled hindering or assisting loads (60, 61, 74).

Data Analysis.

As previously described (56, 61), mean RLs under load were determined by first categorizing individual RL measurements, $x$, into those that fell within the interval $x_1<x<x_2$ and those that exceeded the upper bound of the interval, namely $x>x_2$. For all loads, the lower limit was set to $x_1=30$ nm and the upper limit to $x_2=$ 150 nm. Based on the number of runs in each interval ($N_{\mathrm{1,2}}$), mean RLs ($L$) were calculated from the expression $L=\left(x_2–x_1\right)/\ln \left(N_1/N_2+1\right)$, with the SE (${\sigma }_L$) estimated by ${\sigma }_L=L\sqrt{N_1/\left(N_2\left(N_1+N_2\right)\right)}/\ln \left(N_1/N_2+1\right)$. These expressions assume that RLs are exponentially distributed. Mean RLs in the absence of load (0 pN) were determined based on exponential fits to histograms of individual runs. Fitting excluded the first bin of each histogram, as well as all bins with fewer than six counts. Mean velocity and randomness measurements were obtained and analyzed as previously described (60, 61). All mean dissociation rates ($k_{\text{off}}$) were obtained by dividing the velocity by the RL at the corresponding load condition.

Modeling.

We developed analytical expressions for the velocity ($v$) and randomness ($r$) as functions of the applied load (F) and ATP concentration ([ATP]) for the minimal four-state kinetic scheme shown in Fig. 3A using an established formalism (56, 60, 75) and Mathematica (Version 10; Wolfram Research). These expressions are supplied in the Supporting Information. The seven free parameters for KIF3AB and KIF17 (Fig. 3C) were constrained using Igor Pro 6 (Wavemetrics) by global fits to their respective velocity and randomness datasets (Fig. 2 and Fig. S1).

Simulation.

To simulate the velocity of an IFT train ferried by a given number, N, of KIF3AB ($N_{3\text{AB}}$) and KIF17 ($N_{17}$) motors, we calculated the properties of each state in a $\left(N_{3\text{AB}}+1\right)\times \left(N_{17}+1\right)$ space. Here, a state with coordinates ($i_{3\text{AB}},i_{17}$) gives the IFT velocity for the corresponding number of MT-bound KIF3AB ($i_{3\text{AB}}$) and KIF17 ($i_{17}$) motors, where $0\le i_{3\text{AB}}\le N_{3\text{AB}}$ and $0\le i_{17}\le N_{17}$. The velocity ($v_{i_{3\text{AB}},i_{17}}$) for a ($i_{3\text{AB}},i_{17}$) state is given by

$$v_{i_{3\text{AB}},i_{17}}=\{\begin{array}{cc}0& \hspace{1em}if\hspace{0.17em}{\text{i}}_{3\text{AB}},i_{17}=0\\ v_{3\text{AB}}^0& \hspace{1em}if\hspace{0.17em}{i}_{17}=0\\ v_{17}^0& \hspace{1em}if\hspace{0.17em}{i}_{3\text{AB}}=0\\ v_{\text{eq}}\left(F_{\text{eq}},i_{3\text{AB}},i_{17}\right)& \hspace{1em}if\hspace{0.17em}{i}_{3\text{AB}},i_{17}\ne 0\end{array}.$$

Here, $v_{3\text{AB}}^0$ and $v_{17}^0$ are the unloaded velocities (0 pN) for each of the motors (Fig. 2A), and $v_{\text{eq}}\left(F_{\text{eq}},i_{3\text{AB}},i_{17}\right)$ represents the equilibrium train velocity in states where at least one motor of each type is bound to the MT ($i_{3\text{AB}},i_{17}\ne 0$). At equilibrium, the assisting load produced by KIF17 acting on KIF3AB is equivalent in magnitude to the hindering load experienced by the KIF17 motors. Because this equilibrium load $\left(F_{\text{eq}}\right)$ is distributed over $i_{3\text{AB}}$ KIF3AB and $i_{17}$ KIF17 motors, the load per motor is given by $F_{\text{eq}}/i_{3\text{AB}}$ for KIF3AB and $-F_{\text{eq}}/i_{17}$ for KIF17. As such, $v_{\text{eq}}\left(F_{\text{eq}},i_{3\text{AB}},i_{17}\right)$ and the corresponding $F_{\text{eq}}$ value were determined by solving the relation $v_{3\text{AB}}\left(F_{\text{eq}}/i_{3\text{AB}}\right)=v_{17}\left(-F_{\text{eq}}/i_{17}\right)$, where $v_{3\text{AB}}\left(F_{\text{eq}}/i_{3\text{AB}}\right)$ and $v_{17}\left(-F_{\text{eq}}/i_{17}\right)$ are velocity functions for the four-state model (Modeling), with parameters set to the values obtained from the global fits (Fig. 3C).

In our simulations, only those transitions representing the binding or dissociation of a single motor are allowed. The transition rate ($k_{\text{transition}}$) out of a state consisting of $i_{3\text{AB}}$ and $i_{17}$ MT-bound motors ($i_{3\text{AB}},i_{17}$) is given by

$$k_{\text{transition}}=\{\begin{array}{cc}\left(N_{3\text{AB}}-i_{3\text{AB}}\right)k_{3\text{AB},\text{on}}& for\left(i_{3\text{AB}},i_{17}\right)\to \left(i_{3\text{AB}}+1,i_{17}\right)\\ i_{3\text{AB}}{k}_{3\text{AB},\text{off}}\left(\frac{F_{\text{eq}}}{i_{3\text{AB}}}\right)& for\left(i_{3\text{AB}},i_{17}\right)\to \left(i_{3\text{AB}}-1,i_{17}\right)\\ \left(N_{17}-i_{17}\right)k_{17,\text{on}}& for\left(i_{3\text{AB}},i_{17}\right)\to \left(i_{3\text{AB}},i_{17}+1\right)\\ i_{17}{k}_{17,\text{off}}\left(\frac{-F_{\text{eq}}}{i_{17}}\right)& for\left(i_{3\text{AB}},i_{17}\right)\to \left(i_{3\text{AB}},i_{17}-1\right)\end{array}.$$

Here, $k_{3\text{AB},\text{on}}$ and $k_{17,\text{on}}$ are the load-independent MT-binding rates for the motors, and $k_{3\text{AB},\text{off}}$ and $k_{17,\text{off}}$ are the load-dependent dissociation rates (Fig. 5A), determined (as previously) from the ratio of velocity (Fig. 2A) to RL (Fig. 4B) from fits to the data. The dissociation rate of an individual KIF17 or KIF3AB motor transporting an IFT train is a function of the load each motor experiences, which depends on the number of MT-bound motors ($i_{3\text{AB}}$ and $i_{17}$) and the common load they bear $\left(F_{\text{eq}}\right)$.

Beginning from the state corresponding to an IFT train with a single bound motor—namely ($\mathrm{1,0}$) or ($\mathrm{0,1}$)—a random number generator determined which state was accessed next, weighted by the relative transition rate to each of the available, adjacent states. Each simulation consisted of 20,000 transitions. Because each state represents the velocity of an IFT train ferried by $i_{3\text{AB}}$ KIF3AB and $i_{17}$ KIF17 motors, both the average train velocity and the average numbers of MT-bound motors could be determined directly from the distribution of states accessed in the simulations.

To simulate IFT velocity as a function of distance from the ciliary base (Fig. 5B), the simulation procedure described above was iterated for pairs of $N_{3\text{AB}}$, $N_{17}$ values that were previously published (Fig. 5C, dashed lines) over a series of positions in the first 3.5 µm of the cilium, spaced by 0.1-µm intervals. At each position, the IFT velocity was determined by averaging the velocities from 40 simulations, comprising 20,000 transitions each. Likewise, the average number of MT-bound KIF17 and KIF3AB motors was determined by averaging $i_{3\text{AB}}$ and $i_{17}$ values from 40 simulations (Fig. 5C).

Finally, we estimated values for $k_{3\text{AB},\text{on}}$ and $k_{17,\text{on}}$ that best recapitulated IFT velocities observed in vivo (10). For an array of $k_{3\text{AB},\text{on}}$ and $k_{17,\text{on}}$ values, we computed the SSE between (i) IFT velocities at 1.0 µm to 2.8 µm from the base of the cilium, sampled at 0.1-µm intervals (Results) and (ii) the corresponding velocities measured in vivo (Fig. S4). The $k_{3\text{AB},\text{on}}$ and $k_{17,\text{on}}$ values explored ranged from 0.19 s⁻¹ to 0.33 s⁻¹, sampled at 0.001-s⁻¹ intervals. SSE values were normalized (${\text{SSE}}_{\text{norm}}$) to the minimum SSE (${\text{SSE}}_{\min }$) (67) between simulated and in vivo velocities according to ${\text{SSE}}_{\min }/{\text{SSE}}_{k_{3\text{AB},\text{on}},k_{17,\text{on}}}$, where ${\text{SSE}}_{k_{3\text{AB},\text{on}},k_{17,\text{on}}}$ is the SSE for a pair of $k_{3\text{AB},\text{on}}$ and $k_{17,\text{on}}$ values. Values corresponding to ${\text{SSE}}_{\text{norm}}=1.0$ were $k_{3\text{AB},\text{on}}=0.244\hspace{0.17em}{\mathrm{s}}^{-1}$, $k_{17,\text{on}}=0.258\hspace{0.17em}{\mathrm{s}}^{-1}$. Uncertainties for these MT-binding rates were computed from a 15% threshold of the contour plot of ${\text{SSE}}_{\text{norm}}$ values (Fig. S4), yielding estimated rates of $k_{3\text{AB},\text{on}}=0.24\mathrm{\pm }0.03\hspace{0.17em}{\mathrm{s}}^{-1}$ and $k_{17,\text{on}}=0.26\mathrm{\pm }0.02\hspace{0.17em}{\mathrm{s}}^{-1}$. The simulation code was written in Python and is available upon request.

SI Materials and Methods

Based on the minimal four-state kinetic scheme of Fig. 3A, the analytical expression for the velocity, $v$, as a function of external load and ATP concentration is

$$v\left(F,\left[\text{ATP}\right]\right)=\frac{d_{\text{step}}{k}_1\left[\text{ATP}\right]k_3{k}_4\left(k_2^0{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}-k_{\text{back}}\right)}{k_1\left[\text{ATP}\right]k_2^0{k}_3{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}+k_2^0{k}_4{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}\left(k_1\left[\text{ATP}\right]+k_3\right)+k_3{k}_4\left(k_1\left[\text{ATP}\right]+k_{-1}+k_{\text{back}}\right)}$$

and the randomness function, $r$, is

$$\begin{array}{l}r\left(F,\left[\text{ATP}\right]\right)=1-\frac{2k_{\text{back}}}{k_{\text{back}}-k_2^0{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}}\\ +\frac{2k_1\left[\text{ATP}\right]\left(k_{\text{back}}-k_2^0{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}\right)k_3{k}_4\left(k_3{k}_4+k_{-1}\left(k_3+k_4\right)+k_{\text{back}}\left(k_3+k_4\right)+k_1\left[\text{ATP}\right]k_3+k_1\left[\text{ATP}\right]k_4+k_2^0{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}\left(k_1\left[\text{ATP}\right]+k_3+k_4\right)\right)}{{\left(k_3{k}_4\left(k_1\left[\text{ATP}\right]+k_{-1}+k_{\text{back}}\right)+k_2^0{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}\left(k_3{k}_4+k_1\left[\text{ATP}\right]\left(k_3+k_4\right)\right)\right)}^2}\\ -\frac{2k_1\left[\text{ATP}\right]k_{\text{back}}\left(k_3+k_4\right)}{k_3{k}_4\left(k_1\left[\text{ATP}\right]+k_{-1}+k_{\text{back}}\right)+k_2^0{\text{e}}^{\frac{F{\mathrm{\delta }}_2}{k_{\text{B}}T}}\left(k_3{k}_4+k_1\left[\text{ATP}\right]\left(k_3+k_4\right)\right)}.\end{array}$$

In these equations, $d_{\text{step}}$ is the kinesin step size (taken to be 8.2 nm), $k_{\text{n}}$ are the load-independent rates of the minimal model (Fig. 3A), $k_2^0$ is the unloaded rate constant of the solitary load-dependent transition, ${\delta }_2$ is a characteristic distance parameter, and $k_{\text{B}}T$ is Boltzmann’s constant times the absolute temperature (Materials and Methods).