Abstract.
Accurate automatic segmentation of the prostate in magnetic resonance images (MRI) is a challenging task due to the high variability of prostate anatomic structure. Artifacts such as noise and similar signal intensity of tissues around the prostate boundary inhibit traditional segmentation methods from achieving high accuracy. We investigate both patch-based and holistic (image-to-image) deep-learning methods for segmentation of the prostate. First, we introduce a patch-based convolutional network that aims to refine the prostate contour which provides an initialization. Second, we propose a method for end-to-end prostate segmentation by integrating holistically nested edge detection with fully convolutional networks. Holistically nested networks (HNN) automatically learn a hierarchical representation that can improve prostate boundary detection. Quantitative evaluation is performed on the MRI scans of 250 patients in fivefold cross-validation. The proposed enhanced HNN model achieves a mean ± standard deviation. A Dice similarity coefficient (DSC) of and a mean Jaccard similarity coefficient (IoU) of are used to calculate without trimming any end slices. The proposed holistic model significantly () outperforms a patch-based AlexNet model by 9% in DSC and 13% in IoU. Overall, the method achieves state-of-the-art performance as compared with other MRI prostate segmentation methods in the literature.
Keywords: deep learning, holistically nested edge detection, holistically nested networks, magnetic resonance images, prostate, segmentation
1. Introduction
Segmentation of T2-weighted (T2W) prostate magnetic resonance images (MRIs) is important for accurate therapy planning and aiding automated prostate cancer diagnosis algorithms. It plays a crucial role in many existing and developing clinical applications. For example, radiotherapy planning for prostate cancer treatment requires accurate delineation of the prostate in imaging data (mostly MR and CT). In current practice, this is typically achieved by manual contouring of prostate in a slice-by-slice manner using either the axial, sagittal, coronal view, or a combination of different views. This manual contouring is labor intensive and prone to inter and intraobserver variance. Accurate and automatic prostate segmentations based on three-dimensional MRI would seemingly offer many benefits, such as efficiency, reproducibility, and elimination of inconsistencies or biases between operators performing manual segmentation. However, automated segmentation is challenging due to the heterogeneous intensity distribution of the prostate MRI and the complex anatomical structures within and surrounding the prostate.
Recent literature on automatic prostate segmentation of MRIs focuses on atlas, shape, and machine-learning models. Klein et al.1 proposed an automatic segmentation method based on atlas matching. The atlas consists of a set of prostate MRIs and corresponding prelabeled binary images. Nonrigid registration is used to register the patient’s image with the atlas images. The best matching atlas images are selected and the segmentation is an average of the resulting deformed label images and thresholding value by a majority voting rule. Shape-based models are widely used by MRIs prostate segmentation. Yin et al.2 proposed an automated segmentation model based on normalized gradient field cross-correlation for initialization and a graph-search-based framework for refinement. Ghose et al.3 proposed the use of texture features from approximation coefficients of the Haar wavelet transform for propagation of a shape and active appearance model (AAM) to segment the prostate. Toth and Madabhushi4 extended the traditional AAM model to include intensity and gradient information, and used level-set to capture the shape of statistical model information with a multifeature landmark-free framework.
Many successful approaches were proposed to use feature-based machine learning. Maan et al.5 proposed a method to train multispectral MRI, such as T1, T2, and proton density weighted images, and used parametric and nonparametric classifiers, Baysian-quadratic, and k-nearest neighbor, respectively, to segment the prostate. Habes et al.6 proposed an support vector machine (SVM)-based algorithm that allows automated detection of the prostate on MRIs. The developed method utilizes SVM binary classification on 3-D MRI volumes. Automatically generated 3-D features, such as median, gradient, anisotropy, and eigenvalues of the structure tensor, are used to generate the classification binary masks for segmentation.
Applying the deep-learning architecture to automatic segmentation from prostate MRIs is an active new research field with only a few studies addressing this area of research. Liao et al.7 proposed a deep-learning framework using independent subspace analysis to learn the most effective features in an unsupervised manner for automatic segmentation of the prostate from MRIs. Guo et al.8 proposed a deformable automatic segmentation method by unifying deep feature learning with the sparse patch matching. Milletari et al.9 presented a 3-D volumetric deep convolutional neural networks (CNNs) to model axial images and optimize the training with a Dice coefficient objective function. It utilized a V-net or U-net model and a 3-D-based convolutional and deconvolutional architectures to learn the 3-D hierarchal features. Yu et al.10 extended the 3-D V-net or U-net model by incorporating symmetric residual-net layer blocks into the 3-D convolutional and deconvolutional architecture. Yu’s team won first place in the Medical Image Computing and Computer Assisted Interventions Conferences, “Prostate MR Images Segmentation”-challenge 2012 prostate segmentation challenge.11
Building on those exciting and successful approaches, we proposed an enhanced holistically nested networks (HNN) model, which is a fully automatic prostate segmentation algorithm that can cope with the significant variability of prostate T2 MRIs. The major contribution of this paper is a simple and effective automatic prostate segmentation algorithm that holistically learns the rich hierarchical features of prostate MRIs utilizing saliency edge maps. The enhanced HNN model is trained with mixed coherence enhanced diffusion (CED) images and T2 MRIs, and fuses the predicted probability maps from CED and T2 MRIs during testing. The enhanced model is robust to prostate MRI segmentation and provides promising segmentation results.
2. Methods
2.1. Patch-Based Convolutional Neural Network Classification: AlexNet Architecture
In previous work,12 we investigated the AlexNet deep CNN (DCNN) model13 to refine the prostate boundary. The atlas-based AAM serves as the first tier of the segmentation pipeline, initializing the deep-learning model by providing a rough boundary estimate for the prostate. The refinement process is then applied to the rough boundary generated from the atlas-based AAM model in the second tier. This is a 2-D patch-based pixel classification approach, which predicts the center pixel from local patches.
The DCNN refinement model generates the patches along the normal line of prostate boundary.12 We generate a normal line (blue line) from each boundary point as shown in Fig. 1(a). Each square patch is centered on the tracing point with square sides parallel to the and axes. The red square patch centered on the boundary point represents the positive (red box) class. The normal line of each boundary point is used as the tracing path for the negative and undefined patches. We walk along the normal line 20 pixels in both inward and outward directions, collecting patches within the specified distance constraint. The green square patches on the two end points of the normal line are classified as negative patches. The pink square patches in between are classified as undefined patches. Figure 1(a) shows the patches generated from a single normal line.
Fig. 1.
AlexNet patches generation and VOIs contours prediction. (a) Patches along normal line, (b) probability map, and (c) final contour from probability map.
After the first-tier segmentation model initializes the rough prostate boundary, the DCNN classifier is applied to classify the unlabeled patches around the boundary in testing. Test image patches are generated from the normal lines of the contour [Fig. 1(a)]. Each image patch is centered on a point along a normal line with the patch square oriented parallel to the and axes. During testing, all the patches are classified by the trained DCNN model to generate energy probability maps. Figure 1(b) shows the pixel-based probability map along the normal line. The red color band shows the high-probability candidate points of the prostate boundary. The blue and yellow bands represent the low-energy candidate points. The final contour [Fig. 1(c)] is extracted from the probability map with the highest likelihood. A simple tracing algorithm searches for the highest likelihood point from the probability map on each normal line and fits a B-spline to these points to produce the final boundary.
The overall architecture of the DCNN is depicted in Fig. 2. Several layers of convolutional filters can be cascaded to compute image features in a patch-to-patch fashion from the imaging data. The whole network is executed as one primary network stream. The architecture contains convolutional layers with interleaved max-pooling layers, drop-out layers, fully connected layers, and softmax layers. This last fully connected layer is fed to a two-way softmax which produces a distribution over two class labels corresponding to probabilities for “boundary” or “nonboundary” image patches. The AlexNet is a first generation deep-learning model with the training and testing constrained to fixed size patches, such as patches. The whole architecture can be considered as a single path of multiple forward and backward propagations. To roughly estimate the number of patches being used in the training phase, with the given 250 images: (1) each training fold (fivefold cross-validation) contains 200 images, (2) each image has around 15 volume of interest (VOI) contours to present the prostate, (3) each contour has 128 points, and (4) patches are traced with 40 pixels along each normal line. This simple patches collection mechanism readily creates over 15 million patches (positive, negative, and nonlabel) to train one AlexNet deep-learning model. With those 15 million patches, the last three fully connected layers in AlexNet (Fig. 2) generate a huge amount of parameter space during training, which makes the training step infeasible on a general purpose graphics card, such as the Titan Z card. Overfitting can also easily occur. To train the model with a feasible parameter space, we discard the patches in between the center and ending points [Fig 1(a), pink boxes, nonlabel] of the normal line to combat overfitting and reduce the training patches size to around 1 million. We directly trained the 1 million patches with AlexNet architecture. None of the data augmentation (i.e., rotation and flip) is conducted in the training process. GPU acceleration, based on the open-source implementation by Krizhevsky et al.,13 allows efficient training and fast execution of the CNN in testing.
Fig. 2.
AlexNet DCNN architecture.
2.2. Holistic Classification: Holistically Nested Networks Architecture
In our second method, we use the HNN architecture to learn the prostate interior image-labeling map for segmentation. The HNN model represents the second generation of the deep-learning model. This type of CNNs architecture was first proposed by Xie and Tu14 under the name of holistically nested edge detection (HED), which combines deep supervision with fully CNNs to effectively learn edges and object boundaries, and to resolve the challenging ambiguity problem in object detection. The original proposed work was primarily used to detect edge and object boundaries in natural images. We would argue that HNN architecture could learn the deep hierarchical representation from general raw pixel-in and label-out mapping functions to tackle semantic image segmentation in the medical imaging domain. Due to recent successful work in applying HNN to pancreas segmentation15 and lymph node16 detection in computed tomography (CT) images, we investigated the feasibility of applying the HNN deep-learning model to MR prostate segmentation. HNN is designed to address two important issues: (1) training and prediction on the whole image end-to-end, i.e., holistically, using a per-pixel labeling cost and (2) incorporating multiscale and multilevel learning of deep image features using an auxiliary cost function at each convolution layer. HNN computes the image-to-image or pixel-to-pixel prediction maps from any input raw image to its annotated labeling map, building fully CNNs and deeply supervised nets.15 The per-pixel labeling cost function makes it feasible that HNN can be effectively trained using only several thousand annotated image pairs. This enables the automatic learning of rich hierarchical feature representations and contexts that are critical to resolve spatial ambiguity in the segmentation of organs.
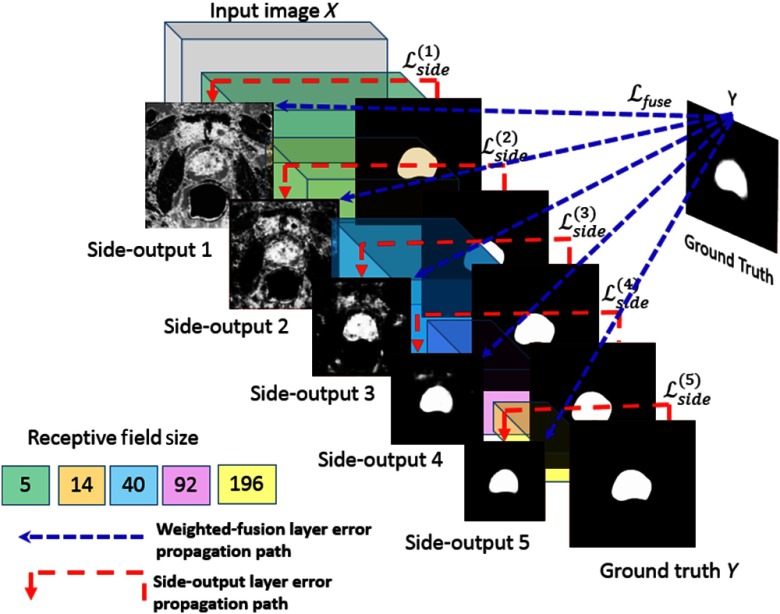
In contrast to the AlexNet DCNN model, HNN emphasizes an end-to-end edge detection system, a system inspired by fully CNNs with additional deep supervision on top of the VGGNet 16.17 The network structure is initialized based on an ImageNet pretrained VGGNet model. From literature, it has been shown that fine-tuning CNNs pretrained on general image classification tasks is helpful for image edge detection.14 Previous work18 also shown that pretrained on ImageNet is also very effective in dealing with histopathology images. We utilized the same HNN architecture and hyperparameter settings that were used for the Berkeley segmentation dataset and benchmark (BSDS 500).14 Our network structures for training are maintained the same as for BSDS. The prostate HNN segmentation model was fine-tuned from BSDS 500 using the prostate training images. We used the Visual Geometry Group (VGG) weights (ImageNet VGG model)14 for fine-tuning the prostate masks which was performed when the HNN was trained on BSDS 500 parameters. The HNN networks comprise a single stream deep network with multiple side-outputs (Fig. 3), which are inserted after each convolutional layer. The architecture consists of five stages with strides of 1, 2, 4, 8, and 16. The side-output layer is a convolutional layer of one-channel output with sigmoid activation. The outputs of HNN are multiscale and multilevel with the side-outputs plane size becoming smaller and receptive field size becoming larger. Each side-output produces a corresponding edge map at a different scale level, and one weighted-fusion layer is added to automatically learn how to combine outputs from multiscale, as shown in Fig. 3. The added fusion layer computes the weighted average of side-outputs to generate the final output probability map. Due to the different scale levels of side-output, all the side-outputs probability maps are up-sampled to the size of the original input image size by bilinear interpolation before fusion. The entire network is trained with multiple error propagation paths (dashed lines). With cross multiple scales, especially at the top level of the network, the trained network is heavily biased toward learning very large structure edges and missing low-signal edges. Ground truth is used with each of the side-output layers to compensate the weak edge lost and play a role as deep supervision. We highlight the error in back-propagation paths (red dashed lines in Fig. 3) to illustrate the deep supervision performed at each side-output layer after the corresponding convolutional layer. The fused layer also back-propagates the fused errors (blue dashed lines in Fig. 3) to each convolutional layer.
Fig. 3.
Schematic view of HNN architecture (adapted from Ref. 14 with permission).
To formulate the HNN networks for prostate segmentation in the training phase, we denote our training data set as , where refers to the ’th input raw image, indicates the corresponding ground truth label for the ’th input image, and denotes the binary ground truth mask of the prostate interior map for corresponding . The network is able to learn features from those image pairs along from which interior prediction maps can be produced. In addition to standard CNN layers, an HNN network has side-output layers as shown in Fig. 3, where each side-output layer functions as a classifier with corresponding weights . All standard network layer parameters are denoted as W. The object function of the side-output layers is
| (1) |
where denotes an image-level loss function for side-outputs, computed over all pixels in a training image pair and . Due to the heavy bias toward nonlabeled pixels in the ground truth data, a per-pixel class-balancing weight is introduced14 to automatically balance the loss between positive and negative classes. A class-balanced cross-entropy loss function can be used in Eq. (1) with iterating over the spatial dimensions of the image
| (2) |
where is simply , , and and denote the ground truth set of negatives and positives, respectively. In contrast to Ref. 14, where is computed for each training image independently, we use a constant balancing weight computed on the entire training set. This is because some training slices might not have positive classes at all, i.e., slices at the prostate at the apex and base, and otherwise would be ignored in the loss function. The class probability is computed on the activation value at each pixel using the sigmoid function . The prostate interior map prediction can be obtained at each side-output layer, where is the activation of the side-output layer . Finally, a weighted-fusion layer is added to the network that can be simultaneously learned during training. The loss function at the fusion layer is
| (3) |
where with being the fusion weight. is the distance measured between the fused predictions and the ground truth label map. The cross-entropy loss is used as the overall HNN loss function, which is minimized using standard stochastic gradient descent and back propagation
| (4) |
During testing phase, with new image , the prostate binary mask prediction maps and are generated from both side-output layers and the weighted-fusion layer. HNN denotes the edge maps produced by the networks.
| (5) |
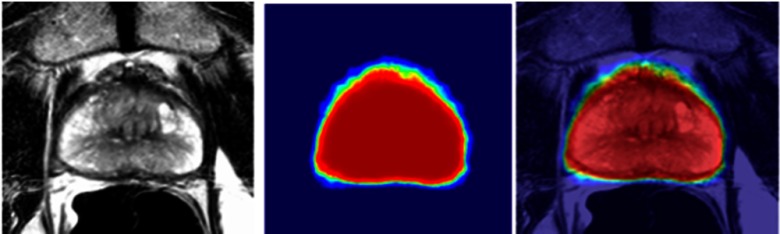
After HED prediction, the layer generated probability map is used to search the final contour. One straightforward approach is to apply the HNN model to prostate segmentation directly as shown in Fig. 3. Basically, we extract two-dimensional (2-D) slices from 3-D MRIs. Corresponding 2-D image slice and binary mask (generated from ground truth) pairs compose the training set. During the testing phase, 2-D slices are extracted from 3-D MRIs and run against the trained HNN model to generate the prediction probability map. A morphology operation of identifying the object runs against the probability map to remove small noise regions and searches for the largest region to represent the prostate. The morphology filter generates the prostate shaped binary mask from the probability map and converts the mask to the final VOI contour. The tested image fused with the probability map is shown in Fig. 4.
Fig. 4.
Fused images with prediction probability map.
2.3. Enhanced Holistically Nested Networks Model
Applying the HNN model directly to the 2-D prostate image is a simple and an effective approach. It can holistically learn the image features for prostate interior and exterior anatomical structures. However, a few issues impose new concerns with the simple approach: (1) A 2-D image contains rich anatomical information, especially the structure outside the prostate region. Will semantic learning of the large prostate exterior region be necessary? (2) Will the heterogeneous intensity distribution of the prostate MRI affect the HNN model segmentation performance? How is the prostate boundary enhanced in case of the intensity variation? (3) Is training the 2-D MRIs alone with one single HNN model sufficient? With those concerns in mind, we further investigate the feasibility to improve the prostate segmentation performance.
The proposed enhanced HNN model is composed of a few major building blocks to address the above mentioned issues. Figure 5 shows the schematic pipeline diagram of the enhanced HNN model in the training phase: (1) Crop the MRIs from an original size of to a smaller region with focus on the prostate whole gland, 25% of pixels removed from the top, bottom, left, and right of the original image. (2) Apply the median and interquartile range (IQR) to scale the cropped image intensity range between 0 and 1000, then rescale between [0, 255]. The IQR is the difference between the upper and lower quartiles. It can be considered a more robust measure of spread, whereas the median can be considered a more robust measure of center tendency. In this preprocessing step, the median and IQR scaling are calculated as
| (6) |
where is the intensity set of the whole-cropped 3-D image after sorting and is the voxel intensity. The median and IQR scaling play an alternative role to histogram equalization to work around the prostate intensity variation issue. (3) For the MRI alone, the noise and low-contrast regions contribute to the major artifacts. As a consequence, some edge boundaries might be missing or blended with the surrounding tissues. We apply a CED filter based on Weickert19 to obtain the boundary-enhanced feature image. The CED filters are relatively thin linear structures to enhance the gray-level edge boundaries, which can efficiently help the HNN model learn the semantic features. (4) The cropped CED and MRIs were mixed with corresponding binary masks to train one single HNN model, which enables the DCNN architecture to build up the internal correlation between CED and MRIs in the neural networks. The overall image preprocessing steps are shown in Fig. 6.
Fig. 5.
Enhanced HNN model training pipeline.
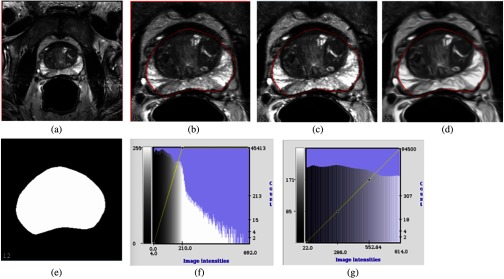
Fig. 6.
An example of MR prostate image preprocessing steps: (a) The original 3-D MRI slice, dimension . (b) The cropped image after 25% region reduction from top, bottom, left, and right. (c) Applying median + IQR scaling to generate the MRI slices before HNN training. (d) CED applies to image after median + IQR scaling. (e) Corresponding prostate binary masks for both MR and CED images. (f) The histogram of the original MRI after cropping. (g) The histogram after applying median + IQR with intensity scaling range from 0 to 1000, lastly rescaled to [0, 255] to fit to the PNG image format for training. After the preprocessing steps, the median + IQR scaling generated MRI slice and the CED image slice with binary mask pairs are mixed together to train one single HNN model.
The proposed enhanced HNN architecture is shown in Fig. 7. The input of the HNN model is the mixed MRI and CED image slices with corresponding binary masks after preprocessing. Each MRI and CED slice shares one corresponding binary mask and formulates two image slices and binary mask pairs. Each pair is a stand-alone. At each training fold (fivefold cross-validation, 200 images), several thousand independent MRI and CED pairs mix together (pair-wise) to constitute the training set. The HNN architecture still functions as a stand-alone model with the extended capability to handle multifeature (multimodality) image pairs. The HNN architecture can semantically learn the deep representation from both MRI and CED images, and build the internal CNNs between the two image features and corresponding ground truth maps. The HNN produces per-pixel prostate probability map pairs (MRI and CED) from each side-output layer simultaneously with ground truth binary mask pairs acting as the deep supervision. This is the first attempt to train the different image features with a single stand-alone HNN model. In previous works, we already applied the HNN model to pancreas segmentation15 and lymph node16 detection in CT images. Both methods independently trained interior binary masks and edge boundary binary masks with the HNN model. During testing phase, the two HNN models generated interior and edge boundary probability maps, which are aggregated with a random forest model to refine the final segmentation. As compared with our previous works, the proposed enhanced HNN model takes advantage of different image features (or modalities) to train one single HNN model, which can potentially improve the reliability of the semantic image segmentation task, i.e., MRI prostate segmentation. The proposed model lets the HNN architecture naturally learn appropriate weights and biases across different features in the training phase. When the trained network converges, we experimentally find that the fifth side-output layer is very close to the prostate shape, which makes the fusion layer output trivial. However, the fusion layer outputs can still be used to generate the probability map. During the testing phase, we can simply merge the probability maps produced from the fifth layer of the MRI and CED side-outputs and directly generate the final prostate boundary. Thus, the morphology postprocessing step of training the 2-D MRIs alone with one single HNN model can eventually be eliminated.
Fig. 7.

Schematic view of enhanced HNN model (adapted from Ref. 14 with permission).
Figure 8 shows a fully automated prostate segmentation pipeline in the testing phase. First, the test image is cropped to a smaller image with 25% pixel reduction from the image boundaries. Second, the median + IQR scaling and CED-enhanced filter generate the corresponding MRI and CED 2-D image slices. Third, the MRI and CED slices run against the trained HNN model to simultaneously produce the probability maps from the HNN’s fifth layer of side-outputs. Fourth, the generated maps are translated into the original image space. Finally, merge and threshold the two probability maps into a binary mask, and create the final VOI contours from the binary mask.
Fig. 8.
Enhanced HNN model testing pipeline.
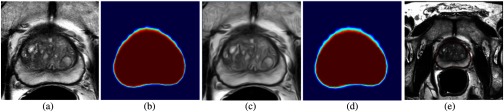
The testing phase: Figs. 9(a) and 9(c) show the cropped MRI and CED slices after median + IQR scaling and rescaled in range between [0, 255]. Figures 9(b) and 9(d) are the probability maps predicted from the trained HNN model fifth layer. Figure 9(e) is the final prostate VOI contour generated by combining the two probability maps, then simply thresholding the largest component into a binary mask and converting it into the final boundary.
Fig. 9.
Probability maps predicted from the enhanced HNN model. (a) MRI slice, (b) MRI probability map, (c) CED slice, (d) CED probability map, and (e) final VOI contour.
The proposed enhanced HNN model can effectively capture the complex MRI prostate shape variation in the testing phase. The cropping image step discards nonprostate regions and allows the HNN architecture to learn finer details from the ground truth map. The prostate interior binary masks are the major midlevel cue for delineating the prostate boundary. Combining CED and MRI slices with the interior ground truth map and training with one single HNN model could be beneficial for semantic image segmentation tasks. During the training phase, the HNN model can naturally build up the internal correlation CNNs networks across different image features (or modalities). The enhanced HNN model can elevate the overall performance of MRI prostate segmentation.
3. Experimental Results
3.1. Data
The proposed enhanced HNN model is evaluated with 250 MRI data sets, which are provided by National Cancer Institute, Molecular Imaging Branch. The MRIs are obtained from a 3.0 T whole-body MRI system (Achieva, Philips Healthcare). T2W MRIs of the entire prostate were obtained in axial plane at a scan resolution of , field of view 140 mm, and image slice dimension . The center of the prostate is the focal point for the MRI scan. All the images are acquired using an endorectal coil, which is routinely used for imaging the prostate. The prostate shapes and appearances impose large variations across different patients. There is a wide variation in prostate shape in patients with and without cancer that incorporates variability relating to prostate hypertrophy and extracapsular extension (ECE) (capsular penetration). However, in our cases, there were a few examples of ECE that caused marked prostatic boundary distortion. The impact of capsular involvement is a minor factor on our segmentation algorithm accuracy. Among all the 250 cases, almost all prostates have abnormal findings, mainly due to benign prostatic hyperplasia, which causes all prostates to look different. Although most cases include cancer in our population, it is uncommon for the capsule of the prostate to be affected by cancer, thus the segmentation. Each image is related to one patient with corresponding prostate VOI contours. The gold standard contour VOIs are obtained from the expert manual segmentation, which is created and verified by a radiologist. These VOIs are considered as the ground truth of the evaluation. The axial T2W MRI was manually segmented in a planimetric approach (slice-wise contouring of the prostate in axial view) by an experienced genitourinary radiologist (B. T., with cumulative experience of 10 years reading and segmenting 700 prostate MRIs/year) using a research-based segmentation software (pseg, iCAD Inc., Nashua, New Hampshire). Those segmentations were all performed during clinical read out of the prostate MRIs to document the prostate volume in clinical reports.
3.2. Experiments
With the given 250 images, our experiments are conducted on splits of 200 images for training and the other 50 images for testing in fivefold cross-validation. Each fold is trained with one deep-learning model independently of the others. Three experiments are conducted for each fold to evaluate the final segmented VOI contours with the ground truth VOI contours in binary mask-based comparison. We briefly describe the training process of each experiment: (1) AlexNet model: 2-D patches (positive and negative) are collected along the normal line as described in Sec. 2.1 from the 200 images. The generated 1 million patches oriented parallel to and axes are used to train one AlexNet deep-learning model. (2) HNN_mri model: around 5000 2-D MRI slices and corresponding VOI binary mask pairs are used to train one HNN model. Those image pairs are fine-tuned with the BSDS 500 architecture and hyperparameter setting14 to generate the prostate specific HNN model. (3) HNN_mri_ced model: after the preprocessing step, around 10,000 2-D MRI slices and binary mask pairs and 2-D CED and binary mask pairs are mixed (pair-wise) together to train one stand-alone HNN model. During the testing phase, the remaining 50 images (in each fold) run against each trained model to generate the probability maps. For each proposed method, we use a different strategy to extract the VOI contours from the probability map: (1) AlexNet approach: we identify the highest probability point along the normal line and use B-spline to smooth the final VOI contours. (2) HNN_mri stand-alone model: we utilize the morphology with identity object operation to filter out the largest region from the probability map and convert it to the final VOIs. (3) HNN_mri_ced multifeature stand-alone model: we directly threshold the probability map from the fifth side-output layer to generate the final VOI contours. The performance evaluation is done by converting final VOI contours to binary masks and comparing the binary masks.
3.3. Evaluation
The segmentation performance (Table 1) was evaluated with (1) Dice similarity coefficient (DSC), (2) Jaccard (IoU), (3) Hausdorff distance (HDRFDST, mm), and (4) average minimum surface-to-surface distance (AVGDIST, mm). All the metrics are calculated without trimming any ending contours or cropping data to the (5% and 95%) probability interval to avoid outliers for a distance-based measure. The mask-based performance measure uses the EvaluateSegmentation tool20 to compare the ground truth and segmented masks. Statistical significance of differences in performance between the proposed deep-learning models is determined using the Wilcoxon signed rank test to compute the value, DSC, IoU, and HDRFDST. The HNN model with MRI alone elevates the mean DSC from 81.03% to 86.86% () and the mean IoU from 68.57% to 77.48% (), which is a significant improvement over the AlexNet deep-learning model used for contour refinement. The enhanced HNN model (MRI + CED) further boosts the segmentation performance by 3% () from the HNN MRI stand-alone model in both DSC and IoU. Those results demonstrate that to train one single HNN model across different image features (or modalities) can essentially improve the reliability of semantic image segmentation. In the case of MRI prostate segmentation, the enhanced HNN model can capture the complex prostate shape variation in the testing phase. The enhanced model also achieves HDRFDST of (), which indicates that HNN MRI + CED is more robust than HNN MRI alone and AAM AlexNet models in the worst case scenario.
Table 1.
Testing phase fivefold cross-validation: the quantitative MRI prostate segmentation performance results of comparing AAM + AlexNet (Alex), HNN MRI alone (HNN_mri), HNN MRI + CED (HNN_ced) methods in four metrics of DSC (%), Jaccard index (IoU) (%), HDRFDST (mm), and AVGDIST (mm). Best performance methods are shown in bold.
| DSC (%) | Jaccard (IoU) (%) | HDRFDIST (mm) | AVGDIST (mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alex | HNN_mri | HNN_ced | Alex | HNN_mri | HNN_ced | Alex | HNN_mri | HNN_ced | Alex | HNNMRI | HNN_ced | |
| Mean | 81.03 | 86.86 | 89.77 | 68.58 | 77.48 | 81.59 | 15.25 | 17.41 | 13.52 | 0.37 | 0.34 | 0.16 |
| Std | 6.34 | 7.60 | 3.29 | 8.72 | 10.50 | 5.18 | 9.27 | 11.72 | 7.87 | 0.22 | 0.54 | 0.08 |
| Median | 82.34 | 89.30 | 90.33 | 69.98 | 80.66 | 82.37 | 12.54 | 13.20 | 11.33 | 0.32 | 0.16 | 0.13 |
| Min | 56.45 | 52.07 | 71.13 | 39.32 | 35.20 | 55.20 | 4.12 | 4.24 | 4.24 | 0.08 | 0.06 | 0.06 |
| Max | 94.39 | 94.65 | 94.62 | 89.39 | 89.84 | 89.79 | 55.52 | 93.10 | 63.54 | 1.68 | 4.04 | 0.69 |
A few examples of patient cases are shown in Fig. 10. The green color represents the ground truth and the red color represents the segmentation results of the enhanced HNN model. Figure 10 also shows the 3-D surfaces overlapping between proposed model-generated surface and the ground truth surface for each patient. Perceptually, the proposed method shows promising segmentation results from the best, normal, and worst cases. Noticeable volume difference and high Hausdorff distance are primarily contributed from the erroneous contours at apex and base. Overall, the proposed enhanced HNN model could be highly generalizable to other medical-imaging segmentation tasks.
Fig. 10.
Examples of enhanced HNN model segmentation results. Ground truth (green) and segmentation (red). (a) With best performance case, (b, c) two cases with DSC score close to mean, and (d) the worst case.
3.4. Implementation
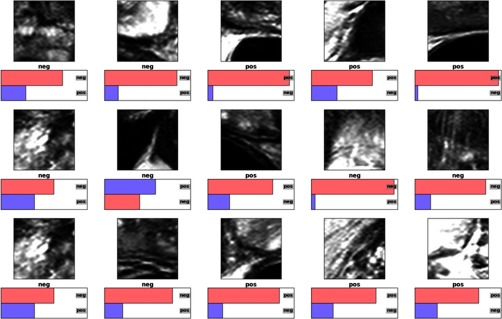
The first AAM + AlexNet method was composed of two major building blocks. The first building block was implemented by the Stegmann et al.21 AAM model in medical image processing analysis and visualization (MIPAV)22 with Java, which was already open-sourced with MIPAV release. The traditional AAM stand-alone model required many images and VOIs to capture shape variations. Training a single AAM model with large numbers of image textures and VOIs always generates an irregular shape and unstable segmentation in practice. With a little engineering hack, we implemented the atlas-based AAM training with subgroups to ensure that relatively similar images and VOIs shapes can be trained with a higher number of eigenvalues in the principle component analysis model. An exhaustive searching algorithm with the atlas generates many groups to capture the shape and texture variations. This atlas-based AAM strategy can reduce the segmentation errors. Detailed implementation can be found in Ref. 12. After the AAM model generates the initial VOI contours, we apply the patches-based AlexNet deep-learning model to refine the boundary. We used the open-source implementation (C++ and Python) by Krizhevsky et al.13,23 as the AlexNet architecture. Rectified linear units are used as the neuron model instead of the standard neuron model and as in Ref. 13. For each training fold, we applied the random sampling to the training set, which divides the training set into a random training subset and a testing subset. However, we did not apply random initialization to the 1 million patches before training. To qualitatively access how well the CNN had learned the prostate boundary, Fig. 11 demonstrates typical classification probabilities on a random subset of “positive” and “negative” image patches for one test case. The probability for each patch of being centered on the prostate boundary (“positive”) and for being off the boundary (“negative”) are shown. The correct ground truth label is written under each image patch. The category with the highest CNN probability is shown as the top bar and is displayed in pink if correctly classified, and in violet if incorrectly classified (using the implementation by Ref. 23). With data augmentation, we rotate each patch to 90, 180, and 270 deg, and flip each patch in and axes. This approach downgrades the training and testing time, and yields no improvements in both Dice score and Hausdorff distance. We end up using the generated patches to train the AlexNet deep-learning model directly without any data augmentation.
Fig. 11.
Test case prediction with AlexNet CNN.
For the second HNN_mri stand-alone method, we utilized the HED implementation (C++ and Python) from Refs. 14 and 24 as the base HNN architecture. The method was implemented using the latest Caffe library and built on top of the fully convolutional networks25 and deeply supervised nets.26 We utilized the same HNN architecture and hyperparameter settings of BSDS 500.14 We also used the VGG weights14 for fine-tuning the prostate masks when the HNN is trained on BSDS 500. The hyperparameters (choosing values) include: batch size (1), learning rate (), momentum (0.9), weight decay (0.0002), number of training iterations (30,000; divide learning rate by 10 after 10,000 iterations). We also implemented MIPAV Java routines to handle image processing and VOI extraction from the probability maps after HNN prediction. The fusion layer side-output generates a [0, 1] probability map, which is scaled to [0,255] and thresholded between [240,255]. Then, a morphology operation of identifying objects (MIPAV) with flood value 1 is applied to flood filling all possible regions and filtering out the largest region to represent the prostate. Finally, the 2-D region mask is converted to VOI contours.
For the third Alex_mri_ ced single stand-alone HNN method, we simply used the stand-alone HNN model in the second method without any modification, and implemented a Java wrapper in MIPAV to handle the preprocessing step, multifeatures (multimodality) image I/O, and dual probability maps interpolation after the HNN prediction. When we trained the model, multifeature image pairs (MRI and CED 2-D slices with binary masks) were fed into the single stand-alone HNN architecture and we let the networks naturally build the deep representation among multifeature images. The CED filter was implemented in MIPAV with the following parameters: derivative scale (0.5), Gaussian scale (2.0), number of iterations (50), 25D (true). After the HNN prediction generating the MRI and CED probability maps from the fifth side-output layer, we fused the two maps into one, and simply applied the threshold filter [240, 255] to build the largest region mask and convert it to final VOI contours.
3.5. Running Time
Using the AAM + AlexNet method, the approximate elapse time to train one AAM model is around 2 h for 200 images in each fold. To train the patches-based AlexNet deep-learning model, it takes about 5 days to train just one model on a single Titan Z GPU. Once trained, the average running time for each test image is as follows: the AAM model takes 3 min to generate the initial VOIs contours. The patches generation from the initial contours, predicting the probability map from AlexNet model, and converting the map to final VOIs contours combine together take around 5 min. Thus, the complete processing time for each test image is around 8 min.
Training on the HNN_mri stand-alone model takes about 2 days on a single NVIDIA Titan Z GPU. For a typical test image (), it takes the HNN model less than 2 s to generate the probability and 1 s for the Java routine to convert the probability map into the final VOIs. The total segmentation time for each test image is 3 s, which is significantly faster than the AAM + AlexNet method.
The HNN_mri_ced method spends extra time to handle the preprocessing and postprocessing steps. The CED filter is a time-consuming step, which takes about 30 s for each image to generate the CED image. Training the HNN model based on the MRI and CED pairs from each fold takes 2.5 days on a single Titan Z card. The whole processing time for each test image to generate the final VOIs contours is around 2 min.
4. Discussion and Conclusion
To the best of our knowledge, the proposed enhanced performance of the HNN model is close to the state of the art for MRI prostate segmentation with reported mean DSC () in the fivefold cross-validation. To compare directly with other methods in the literature is difficult due to different data sets, scanning protocols, manual intervention versus fully automatic, and number of images utilized in the experiments. Table 2 shows the rough comparison of our method with other notable results from literature. The qualitative data show that our method produces relatively reliable MRI prostate segmentation without trimming any erroneous contours at apex and base, i.e., trimming end contours at 5% or .
Table 2.
Quantitative comparisons between proposed method and other notable methods from the literature.
| Methods | DSC + Std. dev (%) | HDRFDIST (mm) | AVGDIST (mm) | Images | Evaluation | Trim () |
|---|---|---|---|---|---|---|
| Klein et al.1 | 50 | Leave-one-out | Yes | |||
| Toth and Madabhushi4 | 108 | Fivefold validation | Yes | |||
| Liao et al.7 | 30 | Leave-one-out | Yes | |||
| Guo et al.8 | 66 | Twofold validation | Yes | |||
| Milletari et al.9 | Promise 12(80) | Train:50, test:30 | Yes | |||
| Yu et al.10 | 89.43 | 5.54 | 1.95 | Promise 12(80) | Train:50, test:30 | Yes |
| Korsager et al.27 | 67 | Leave-one-out | Yes | |||
| Chilali et al.28 | Promise 12(80) | Train:50, test:30 | Yes | |||
| HNNmri+ced | 250 | Fivefold validation | No |
The measured running time revealed that the two HNN-based methods outperform the patch-based AlexNet method in both training and testing phases. This is primarily due to the huge parameter space created during convolution by AlexNet architecture. The multiscale and multilevel HNN architectures converge faster than the AlexNet counterpart because of the removal of the fully connected layers from VGGNet 16 and replacement with the side-output layers. Although the enhanced HNN_mri_ced model spends extra time to perform image pre and postprocessing steps, the multifeatures training and prediction mechanism improve the segmentation performance by 3% from the HNN_mri stand-alone model. Thus, the proposed enhanced HNN model is a better choice than the AlexNet model in both processing time and segmentation performance.
The AlexNet is the first generation deep-learning model with the training and testing constrained to fixed size patches, such as patches. The AlexNet DCNN model focuses on automatic feature learning, multiscale convolution, and enforcement of different levels of visual perception. However, the multiscale responses produced at the hidden layers are less meaningful, since feedback must be back-propagated through the intermediate layers. The patch-to-pixel and patch-to-patch strategies significantly downgrade the training and prediction efficiency. The major drawbacks of AlexNet are: (1) a huge parameter space is created from the last three fully connected layers, which downgrades the training performance and limits the number of patches being trained on a single graphics card, i.e., Nvidia Titan Z card; (2) with unbalanced patch labeling, the AlexNet model easily runs into overfitting; and (3) each patch () is convolved to maintain a hierarchical relation inside the patch itself. There is no contextual or correlation information between patches during the training phase.
The HNN_mri model represents the second generation of the deep-learning model. In contrast to the AlexNet DCNN model, HNN emphasizes an end-to-end detection system, a system inspired by fully CNNs with deep supervision on top of VGGNet 16. Advantages over the first generation of the AlexNet model are: (1) training and prediction on the whole image end-to-end using per-pixel labeling cost, (2) incorporating multiscale and multilevel learning through multipropagation loss, (3) computing the image-to-image or pixel-to-pixel prediction maps from any input raw image to its annotated labeling map, (4) integrated learning of hierarchical features, and (5) much faster performance than AlexNet model due to the fact that HNN produces the segmentation for each slice in one single steam line path, and speeds up the processing time without running the segmentation for each of many patches.
The enhanced HNN_mri_ced model compresses multifeatures (multimodality) into the single stand-alone HNN model. To address the three concerns from the single stand-alone HNN_mri model, the enhanced model (1) utilizes cropping to remove large nonprostate regions and makes the HNN training more accurate and efficient, (2) median + IQR filter normalizes the MRI to curb the large intensity distribution variation issue, and (3) CED and MRI slices are fed into the single stand-alone HNN architecture to let the HNN model naturally learn and build the deep representation from multifeatures and multiscale, to enhance the HNN prediction reliability.
In conclusion, we present a holistic DCNN approach for automatic MRI prostate segmentation, exploiting multifeatures (MRI + CED or modalities) training with one single HNN model, generating robust segmentation results by fusing MRI- and CED-predicted probability maps. The previous AlexNet deep-learning approach typically used a patch-based system, which can be inefficient in both training and testing, and has limited segmentation accuracy. The proposed enhanced HNN model can incorporate multiscale and multilevel feature learning across multiple image features (or modalities), and immediately produces and fuses multiscale outputs in an image-to-image fashion. The enhanced HNN model elevates the segmentation performance from the AlexNet deep-learning model by 9% in mean DSC and 13% in mean IoU, which significantly ( ) improves the segmentation accuracy. In addition, the proposed model achieves close to state-of-the-art performance as compared with other literature approaches. The enhanced HNN model with multifeatures (or modalities) approach is generalizable to other medical imaging segmentation tasks, such as organs or tumors in future research.
Acknowledgments
This work was supported by the Intramural Research Program of the National Institutes of Health, Center of Information Technology, Clinical Center, and National Cancer Institute. We thank NVIDIA for the K40, Titan X GPU donations to our groups.
Biography
Biographies for the authors are not available.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Klein S., et al. , “Automatic segmentation of the prostate in 3D MR images by atlas matching using localized mutual information,” Med. Phys. 35(4), 1407–1417 (2008). 10.1118/1.2842076 [DOI] [PubMed] [Google Scholar]
- 2.Yin Y., et al. , “Fully automated prostate segmentation in 3D MR based on normalized gradient fields cross-correlation initialization and LOGISMOS refinement,” Proc. SPIE 8314, 831406 (2012). 10.1117/12.911758 [DOI] [Google Scholar]
- 3.Ghose S., et al. , “Texture guided active appearance model propagation for prostate segmentation,” Lect. Notes Comput. Sci. 6367, 111–120 (2010). 10.1007/978-3-642-15989-3 [DOI] [Google Scholar]
- 4.Toth R., Madabhushi A., “Multifeature landmark-free active appearance models: application to prostate MRI segmentation,” IEEE Trans. Med. Imaging 31(8), 1638–1650 (2012). 10.1109/TMI.2012.2201498 [DOI] [PubMed] [Google Scholar]
- 5.Maan B., van der Heijden F., Futterer J. J., “A new prostate segmentation approach using multispectral magnetic resonance imaging and a statistical pattern classifier,” Proc. SPIE 8314, 83142Q (2012). 10.1117/12.911194 [DOI] [Google Scholar]
- 6.Habes M., et al. , “Automated prostate segmentation in whole-body MRI scans for epidemiological studies,” Phys. Med. Biol. 58(17), 5899–5915 (2013). 10.1088/0031-9155/58/17/5899 [DOI] [PubMed] [Google Scholar]
- 7.Liao S., et al. , “Representation learning: a unified deep learning framework for automatic prostate MR segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2013), Vol. 16, No. 2, pp. 254–261 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Guo Y., Gao Y., Shen D., “Deformable MR prostate segmentation via deep feature learning and sparse patch matching,” IEEE Trans. Med. Imaging 35(4), 1077–1089 (2016). 10.1109/TMI.2015.2508280 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Milletari F., Navab N., Ahmadi S., “V-Net: fully convolutional neural networks for volumetric medical image segmentation,” in IEEE, Fourth Int. Conf. on 3D Vision (3DV), pp. 565–571 (2016). [Google Scholar]
- 10.Yu L., et al. , “Volumetric ConvNets with mixed residual connections for automated prostate segmentation from 3D MR images,” in Thirty-First AAAI Conf. on Artificial Intelligence, pp. 66–72 (2017). [Google Scholar]
- 11.Litjens G., et al. , “Evaluation of prostate segmentation algorithms for MRI: the promise 12 challenge,” Med. Image Anal. 18(2), 359–373 (2014). 10.1016/j.media.2013.12.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cheng R., et al. , “Active appearance model and deep learning for more accurate prostate segmentation on MRI,” Proc. SPIE 9784, 97842I (2016). 10.1117/12.2216286 [DOI] [Google Scholar]
- 13.Krizhevsky A., Sutskever I., Hinton G., “ImageNet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, pp. 1097–1105 (2012). [Google Scholar]
- 14.Xie S., Tu Z., “Holistically-nested edge detection,” in Proc. of the IEEE Int. Conf. on Computer Vision (ICCV 2015), pp. 1395–1403 (2015). [Google Scholar]
- 15.Roth H. R., et al. , “Spatial aggregation of holistically-nested networks for automated pancreas segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2016), pp. 451–459 (2016). [Google Scholar]
- 16.Nogues I., et al. , “Automatic lymph node cluster segmentation using holistically-nested neural networks and structured optimization in CT images,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2016), pp. 388–397 (2016). [Google Scholar]
- 17.Simonyan K., Zisserman A., “Very deep convolutional networks for large-scale image recognition,” in Int. Conf. on Learning Representations (ICLR 2015) (2015). [Google Scholar]
- 18.Xu Y., et al. , “Deep convolutional activation features for large scale brain tumor histopathology image classification and segmentation,” in IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, pp. 947–951 (2015). 10.1109/ICASSP.2015.7178109 [DOI] [Google Scholar]
- 19.Weickert J., “Coherence-enhancing diffusion filtering,” Int. J. Comput. Vision 31(2), 111–127 (1999). 10.1023/A:1008009714131 [DOI] [Google Scholar]
- 20.Taha A. A., Hanbury A., “Metrics for evaluating 3D medical image segmentation: analysis, selection, and tool,” BMC Med. Imaging 15(1), 1–29 (2015). 10.1186/s12880-015-0068-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stegmann M. B., Ersboll B. K., Larsen R., “FAME-a flexible appearance modeling environment,” IEEE Trans. Med. Imaging 22(10), 1319–1331 (2003). 10.1109/TMI.2003.817780 [DOI] [PubMed] [Google Scholar]
- 22.McAuliffe M. J., et al. , “Medical image processing, analysis, and visualization in clinical research,” in Proc. 14th IEEE Symp. on Computer-Based Medical Systems (CBMS 2001), pp. 381–386 (2001). [Google Scholar]
- 23.Krizhevsky A., Sutskever I., Hinton G. E., “ImageNet classification with deep convolutional neural network,” in Neural Information Processing Systems (NIPS), pp. 1097–1105 (2012). [Google Scholar]
- 24.Xie S., Tu Z., “Holistically-nested edge detection,” in Proc. IEEE Int. Conf. on Computer Vision (ICCV), pp. 1395–1403 (2015). [Google Scholar]
- 25.Shelhamer E., Long J., Darrell T., “Fully convolutional networks for semantic segmentation,” IEEE Trans. Pattern Anal. Mach. Intell. 39(4), 640–651 (2017). 10.1109/TPAMI.2016.2572683 [DOI] [PubMed] [Google Scholar]
- 26.Lee C. Y., et al. , “Deeply supervised nets,” in Artificial Intelligence and Statistics (AISTATS), JMLR Proc., Vol. 38, pp. 562–570 (2015). [Google Scholar]
- 27.Korsager A. S., et al. , “The use of atlas registration and graph cuts for prostate segmentation in magnetic resonance images,” Med. Phys. 42(4), 1614–1624 (2015). 10.1118/1.4914379 [DOI] [PubMed] [Google Scholar]
- 28.Chilali O., et al. , “Gland and zonal segmentation of prostate on T2W MR images,” J. Digital Imaging 29(6), 730–736 (2016). 10.1007/s10278-016-9890-0 [DOI] [PMC free article] [PubMed] [Google Scholar]