Evaluation of dose calculations accuracy of a commercial treatment planning system for the head and neck region in radiotherapy

Abstract

Aim

The objective was to quantify dose calculation accuracy of TiGRT TPS for head and neck region in radiotherapy.

Background

In radiotherapy of head and neck cancers, treatment planning is difficult, due to the complex shape of target volumes and also to spare critical and normal structures. These organs are often very near to the target volumes and have low tolerance to radiation. In this regard, dose calculation accuracy of treatment planning system (TPS) must be high enough.

Materials and methods

Thermoluminescent dosimeter-100 (TLD-100) chips were used within RANDO phantom for dose measurement. TiGRT TPS was also applied for dose calculation. Finally, difference between measured doses (D_meas) and calculated doses (D_calc) was obtained to quantify the dose calculation accuracy of the TPS at head and neck region.

Results

For in-field regions, in some points, the TiGRT TPS overestimated the dose compared to the measurements and for other points underestimated the dose. For outside field regions, the TiGRT TPS underestimated the dose compared to the measurements. For most points, the difference values between D_calc and D_meas for the in-field and outside field regions were less than 5% and 40%, respectively.

Conclusions

Due to the sensitive structures to radiation in the head and neck region, the dose calculation accuracy of TPSs should be sufficient. According to the results of this study, it is concluded that the accuracy of dose calculation of TiGRT TPS is enough for in-field and out of field regions.

1. Background

Head and neck cancers (HNCs) consist of the oral cavity, nasopharynx, oropharynx, larynx, hypopharynx, nasal cavity, salivary glands, par nasal sinuses and thyroid cancers.¹ These cancers arise from digestive tracts, mucous lining of respiratory, lymph nodes, and salivary glands.² Radiotherapy is applied as a HNC treatment modality either alone or in combination with chemotherapy or surgery.1, 3 One of the techniques in radiation therapy of head and neck cancer is the wedged field technique.⁴ Wedge filters are commonly applied to modify the dose distribution and make it uniform within the target volume.5, 6, 7, 8

Treatment planning for head and neck cancers is difficult, due to the complex shape of target volumes and also to spare critical organs such as the parotid glands, mandible, spinal cord, brainstem, and normal structures. These organs often are near to the target volumes and have low tolerance to radiation.⁴ Hence, special attention needs to deliver dose to the tumor, while to keep the dose of the organs at risk as low as possible. To achieve this goal, treatment planning systems (TPSs) should calculate the dose exactly.

There are several studies relevant to dose calculation accuracy of different algorithms and TPSs in radiotherapy; however, most of them were carried out in a water phantom and/or in regions other than the head and neck.9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19

2. Aim

To the best of our knowledge, there is no investigation on the accuracy of dose calculations of TiGRT TPS in head and neck region. Therefore, the aim of this study was to assess the accuracy of dose calculations in this region for TiGRT TPS in the presence of wedged fields.

3. Methods and materials

3.1. Treatment planning and irradiation of the phantom

A computed tomography scan of the head and neck region of a RANDO phantom (Phantom Laboratory, NY, USA) was taken to produce a treatment plan. The Rando phantom is made of bone-equivalent, soft tissue-equivalent or lung-equivalent tissues. Each slice of the phantom has holes which are plugged with bone-equivalent, soft-tissue-equivalent or lung-equivalent pins which can be replaced by TLD holder pins.²⁰ The images of the Rando phantom were transported to TiGRT TPS version 1.2 (LinaTech, Sunnyvale, CA, USA). According to user's manual of TiGRT TPS, the TPS uses a three dimensional photon dose calculation algorithm based on full scatter convolution (FSC), developed to facilitate accurate and fast calculations. According to the manual, this algorithm separates the absorbed dose (D) in a given point into the primary dose (D_p) and the scatter dose (D_s):

$$D=D_{\text{p}}+D_{\text{s}}$$ (1)

The primary dose D_p ($\overrightarrow{r}$) is obtained based on the convolution algorithm, using the following formula:

$$D_{\text{p}}(\overrightarrow{r})=\iiint {\varphi }_p(\overrightarrow{r^{\prime }})k_{\text{p}}(\overrightarrow{r}-\overrightarrow{r^{\prime }})d{V}^{\prime }$$ (2)

where ${\varphi }_{\text{p}}(\overrightarrow{r^{\prime }})$ is photon fluence at the surface of a ray passing through the surface to point $\overrightarrow{r^{\prime }}$ and $k_{\text{p}}(\overrightarrow{r}-\overrightarrow{r^{\prime }})$ denotes the electron transport kernel, explaining the dose distribution around the primary interaction site of the photon. This demonstrates that the electron transport modeling by this algorithm has been taken into account, and the electron dose deposition kernel can be scaled for heterogeneities such as lung, bone and air cavities. Finally, V′ states the differential calculation volume at point $\overrightarrow{r^{\prime }}$. The scatter dose $D_{\text{s}}(\overrightarrow{r^{\prime }})$ is derived from the following convolution equation:

$$D_{\text{s}}(\overrightarrow{r})=\iiint {\varphi }_{\text{p}}(\overrightarrow{r^{\prime }})k_{\text{s}}(\overrightarrow{r}-\overrightarrow{r^{\prime }})d{V}^{\prime }$$ (3)

In FSC algorithm, multiple scattering of photons is discarded and $k_{\text{s}}(\overrightarrow{r}-\overrightarrow{r^{\prime }})$ is the first scatter fluence kernel. This kernel can be derived from the electron transport kernel.

In this study, two lateral parallel opposed fields were planned, in which one of them was wedge field and another was open field. A source axis distance technique was applied to deliver 200 cGy dose to the selected point (the center slice No. 5 of the RANDO phantom). The treatment fields covered the slices of No. 2–7 of the RANDO phantom. The irradiated area on the RANDO phantom is shown in Fig. 1. Before irradiation, the thermoluminescent detector-100 (TLD-100) chips were placed in special points of the RANDO phantom. The RANDO phantom was irradiated based on the treatment plan with 6 MV X-rays emitted from a Siemens Primus accelerator (Siemens AG, Erlangen, Germany). Doses received by the TLD-100 chips were measured and compared with doses calculated by TPS.

Fig. 1.

Irradiated area on the RANDO phantom.

It is notable that the dose calculation in the indicated points of the phantom (D_calc) was as one point. The points of dose calculation by the TPS were considered centers of TLDs.

3.2. Calibration of applied dosimeters and dosimetric method

Readout and analysis of TLD-100 was carried out in the medical physics research center (Mashhad, Iran), which has a specific protocol for TLD analysis. TLD-100 produced by Harshaw Company that made of LiF, Mg, and Ti with the size of 3 mm × 3 mm and thickness of 0.9 mm were used in this study. TLD-100 chips have a reproducibility of approximately ±1.5% (1 SD). TLD-100 chips were calibrated as mentioned in previous works.21, 22, 23 Briefly, 15 TLD-100 chips were placed in a Perspex holder. This holder was located on a 30 cm × 30 cm × 20 cm water equivalent phantom to create a full scatter conditions. A 15 mm water equivalent slab was placed on the holder to make a build-up region. First, they were irradiated to determine their individual efficiency correction coefficient (ECC). Then, they were irradiated with 50 cGy and readout by Harshaw reader to determine reader calibration factor. Finally, all of the TLD-100 chips were irradiated with 50 cGy and their individual ECC were determined. 47 dosimeters were placed in the different regions of slices of No. 4, 5, 8 and 9 of the RANDO phantom. 3 dosimeters were used to measure the background radiation.

It is noteworthy that the effective point of measurement for the TLD-100 chips was considered at the middle of its height. Also, to have the high accuracy of dosimetry results, measurements were repeated 3 times.

3.3. Analysis of results

For analysis of the results, TRS 430²⁴ and TECDOC 1540²⁵ protocols were applied. These protocols provide information on quality assurance (QA) of TPSs. According to these protocols, the difference between the calculated and the measured dose is defined based on Eq. (4):

$$\delta [\%]=100\times \frac{(D_{\text{cal}}-D_{\text{meas}})}{D_{\text{meas}}}$$ (4)

where D_meas and D_calc are the measured dose by TLD-100 chips and the calculated dose by TPS, respectively. Finally, the difference values were obtained for in-field and outside field regions and were compared to the tolerance limit suggested in TRS 430 and TECDOC 1540 protocols.

4. Results

Slices of No. 4, 5, 8 and 9 of RANDO phantom were selected to assess the accuracy of dose calculations in head and neck region; as slices of No. 4 and 5 were used to assess the in-field regions and slices of No. 8, 9 and some points in slices of No. 4 and 5 were applied to evaluate the outside field regions.

In these slices, doses measured by TLD-100 chips were compared with corresponding values calculated by TiGRT TPS. These results are illustrated in the following tables. Table 1, Table 2 list the D_meas, the D_calc, and the difference between D_meas and D_calc in the selected points of slices of No. 4 and 5 of RANDO phantom, respectively. It is noteworthy that the bolded digits in Table 1, Table 2 are the measured/calculated doses obtained for the outside field regions.

Table 1.

The measured dose (D_meas), the calculated dose (D_calc) and the differences between the D_meas, the D_calc in the selected points for slice No. 4 of RANDO phantom.

No. TLD	Location of TLD	Dmeas (cGy)	Dcalc (cGy)	Difference between Dcalc and Dmeas (δ)
1	Out of field	16.81	12.73	−24.25
2	Out of field	17.27	13.88	−19.58
3	Out of field	16.69	14.08	−15.72
4	In field	208.27	197.81	−5.02
5	In field	189.08	193.35	2.26
6	In field	194.65	194.85	0.10
7	In field	187.92	195.46	4.01
8	In field	201.15	197.00	−2.06
9	In field	199.54	196.04	−1.75
10	In field	195.96	193.35	−1.33
11	In field	208.42	200.65	−3.73
12	In field	207.42	209.27	0.89
13	In field	196.62	205.96	4.75
14	In field	200.23	201.54	0.65
15	In field	198.19	204.04	2.95
16	Penumbra	40.19	24.77	−38.37
17	Penumbra	53.23	31.69	−40.46
18	Penumbra	90.77	60.88	−32.92
19	Penumbra	129.88	115.85	−10.81

Table 2.

The measured dose (D_meas), the calculated dose (D_calc) and the differences between the D_meas, the D_calc in the selected points for slice No. 5 of RANDO phantom.

No. TLD	Location of TLD	Dmeas (cGy)	Dcalc (cGy)	Difference between Dcalc and Dmeas (δ)
20	Out of field	16.35	14.27	−12.76
21	Out of field	14.96	14.23	−4.93
22	In field	192.92	191.38	−0.80
23	In field	185.85	192.27	3.46
24	In field	199.19	193.54	−2.84
25	In field	179.12	190.85	6.55
26	In field	190.08	193.54	1.82
27	In field	191.15	195.46	2.25
28	In field	194.77	195.85	0.55
29	In field	183.12	187.54	2.42
30	In field	199.77	210.46	5.35
31	In field	192.69	203.42	5.57
32	In field	196.88	202.88	3.05
33	In field	195.50	200.12	2.36
34	In field	32.35	34.42	6.36
35	In field	56.42	54.04	−4.22
36	In field	96.19	98.81	2.72
37	In field	132.46	129.92	−1.92
38	Out of field	10.38	9.54	−8.11
39	Out of field	11.35	10.23	−9.94

Fig. 2, Fig. 3 show the location of TLDs in slices No. 4 and 5 of RANDO phantom (a) and image of these slices of RANDO phantom and the location of points corresponding to the measured points in TiGRT TPS (b), respectively.

Fig. 2.

The location of TLDs in slice No. 4 of RANDO phantom (a) and image of slice No. 4 of RANDO phantom and the location of points corresponding to the measured points in TiGRT TPS (b).

Fig. 3.

The location of TLDs in slice No. 5 of RANDO phantom (a) and image of slice No. 5 of RANDO phantom and the location of points corresponding to the measured points in TiGRT TPS (b).

Fig. 4 illustrates the dose differences (%) between the measured doses by TLD-100 and the calculated doses using TiGRT TPS for in-field regions.

Fig. 4.

The dose differences (%) between the measured doses by TLD-100 and the calculated doses using TiGRT TPS for in-field regions.

Table 3, Table 4 list the D_meas, the D_calc, and the difference between D_meas and D_calc in the selected points of slices of No. 8 and 9 of RANDO phantom for out of field regions, respectively.

Table 3.

The measured dose (D_meas), the calculated dose (D_calc) and the differences between the D_meas, the D_calc in the selected points for slice No. 8 of RANDO phantom for out of field regions.

No. TLD	Dmeas (cGy)	Dcalc (cGy)	Difference between Dcalc and Dmeas (δ)
40	28.62	19.69	−31.15
41	27.19	22.69	−16.60
42	36.73	21.73	−40.86
43	34.15	24.88	−27.15

Table 4.

The measured dose (D_meas), the calculated dose (D_calc) and the differences between the D_meas, the D_calc in the selected points for slice No. 9 of RANDO phantom for out of field regions.

No. TLD	Dmeas (cGy)	Dcalc (cGy)	Difference between Dcalc and Dmeas (δ)
44	7.96	5.81	−26.97
45	8.19	6.46	−21.15
46	7.50	7.12	−4.97
47	7.65	7.00	−8.62

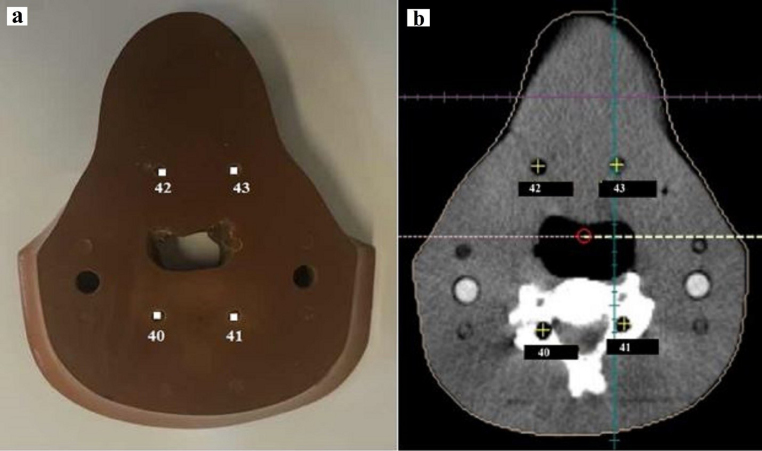
Fig. 5, Fig. 6 show the location of TLDs in slices of No. 8 and 9 of RANDO phantom (a) and image of these slices of RANDO phantom and the location of points corresponding to the measured points in TiGRT TPS (b), respectively.

Fig. 5.

The location of TLDs in slice No. 8 of RANDO phantom (a) and image of slice No. 8 of RANDO phantom and the location of points corresponding to the measured points in TiGRT TPS (b).

Fig. 6.

The location of TLDs in slice No. 9 of RANDO phantom (a) and image of slice No. 9 of RANDO phantom and the location of points corresponding to the measured points in TiGRT TPS (b).

Fig. 7 illustrates the dose differences (%) between the measured doses by TLD-100 and the calculated doses using TiGRT TPS for outside field regions.

Fig. 7.

The dose differences (%) between the measured doses by TLD-100 and the calculated doses using TiGRT TPS for outside field regions.

5. Discussion

In this research, the accuracy of dose calculation in the head and neck region for TiGRT TPS (version 1.2) using TLD-100 was quantified; as both of the in-field and outside field regions were evaluated.

The results show that for in-field regions, in some points, the TiGRT TPS overestimated the dose compared to the measured doses by TLD-100, and for other points underestimated the dose. For outside field regions, the TiGRT TPS underestimated the dose compared to the measured doses by TLD-100. Our results related to out of field regions were consistent to several studies26, 27, 28; as results of these studies showed that TiGRT TPS underestimated the dose of out-of-field regions for most points.

According to protocols of TECDOC 1540 and TRS 430 that provide information on QA of TPSs, tolerance limit for more complex geometry (i.e. inhomogeneous phantom with wedge field) and in-field regions (i.e. high dose-small dose gradient regions) is 4% and in outside field regions (i.e. low dose-small dose gradient regions) is 50%. The results of this study showed that for most points, the difference values between D_calc and D_meas (%) for the in-field regions were within the tolerance limit. Farhood et al.²⁸ assessed accuracy of dose calculation of TiGRT TPS for physical wedge fields. They concluded that the accuracy of dose calculation of mentioned TPS for physical wedged fields in the central axis, off-axis, and build-up regions is adequate. Mahmoudi et al.²⁷ evaluated the accuracy of photon dose calculation in radiotherapy of malignant pleural mesothelioma. Their results showed that accuracy of dose calculation of TiGRT TPS in the presence of heterogeneity, shield, and interfaces is inadequate in compared to Monte Carlo simulation data. The results of our study were consistent with results of the above-mentioned studies. Also, the findings demonstrated that for most points, the difference values between D_calc and D_meas (%) for the out of field regions were within the tolerance limit. In a study on the accuracy of dose calculation of TiGRT TPS for physical wedged fields in water phantom, the results showed that accuracy of dose calculation of this TPS is insufficient for out-of-field regions.²⁸ The results of our study were inconsistent with their results that this can be due to complexity geometry of our study compared to their study (i.e. assessment in RANDO phantom vs. water phantom). In another study, Bahreyni Toossi et al.²⁶ evaluated accuracy of dose calculations for outside field in breast region. They showed that TiGRT TPS compared to TLD-measured dose generally underestimate the dose of outside points; as the mean underestimation of doses of outside field was 39%. Their results were consistent with results of our study.

Since in the head and neck region, there are several sensitive structures to radiation with low dose tolerances, considerable attention must be paid to treatment planning of this area. Hence, QA of TPSs for treatment planning of tumors in head and neck region is very important.

It is noteworthy that application of TLD is accepted as a tool for QA in radiation therapy. TLDs have a number of advantages such as high sensitivity, small physical size, and tissue equivalence.²⁹ Some studies have applied TLDs for QA of TPSs.26, 30, 31, 32

There are several limitations in the present study. This research was investigated only for 6 MV photons and for a special geometry (i.e., head and neck region with wedge field).

For future research, evaluation of the dose calculation accuracy of the other TPS for head and neck or other body regions will be interesting.

6. Conclusions

Due to the sensitive structures to radiation in the head and neck region, the dose calculation accuracy of TPSs should be sufficient. In this study, the accuracy of dose calculations of TiGRT TPS in this region was investigated. The findings demonstrated that for the most points, the accuracy of dose calculation of TiGRT TPS is within tolerance limit for in-field and out of field regions.

Conflict of interest

None declared.

Financial disclosure

This work was financially supported by the office of vice president for research of Mashhad University of Medical Sciences.