Model Simulation and Experimental Validation of Intratumoral Chemotherapy Using Multiple Polymer Implants

Abstract

Radiofrequency ablation has emerged as a minimally invasive option for liver cancer treatment, but local tumor recurrence is common. To eliminate residual tumor cells in the ablated tumor, biodegradable polymer millirods have been designed for local drug (e.g., doxorubicin) delivery. A limitation of this method has been the extent of drug penetration into the tumor (< 5 mm), especially in the peripheral tumor rim where thermal ablation is less effective. To provide drug concentration above the therapeutic level as needed throughout a large tumor, implant strategies with multiple millirods were devised using a computational model. This dynamic, 3-D mass balance model of drug distribution in tissue was used to simulate the consequences of various numbers of implants in different locations. Experimental testing of model predictions was performed in a rabbit VX2 carcinoma model. This study demonstrates the value of multiple implants to provide therapeutic drug levels in large ablated tumors.

INTRODUCTION

Radiofrequency (RF) ablation has emerged as a viable alternative to surgery for the treatment of hepatocellular carcinoma (HCC) and colorectal metastases to the liver (CRM) [1, 25]. While its ease of use and minimally invasive nature have allowed this treatment modality to reach the forefront of ablative cancer treatments, tumor recurrence has been significant, particularly when RF ablation is applied percutaneously [2, 4, 10]. To address this limitation, biodegradable polymer implants were designed to release chemotherapeutic drugs into tumors after RF ablation. These polymer implants in the form of millirods have been tested in normal liver tissue [20, 23] as well as in experimental liver tumors in rabbits [28, 29]. Despite promising in vivo results, the clinical use of millirods may be limited by the inability to deliver a drug to distal regions of the remnant tumor. While ablation increases the extent of drug penetration into the tumor, therapeutic concentrations of drug are only found within 5 mm of the implant surface [29]. Unfortunately, this distance may be inadequate to treat HCC or CRM, which are often greater than 2 cm in diameter [6, 26]. Therefore, a polymer millirod treatment strategy should be developed that can deliver drugs to targeted regions and thus be applicable to clinically encountered tumors.

Multiple polymer millirods can be implanted within a tumor to increase the volume in which the drug concentration is above the therapeutic level. This approach has a number of potential advantages. First, multiple implants can increase the total amount of drug delivered to the tumor without a large increase in systemic drug exposure. Second, multiple implants in a single tumor can decrease the average distance between implants and the target tissue at the ablated periphery, where the risk for recurrence is highest.

Previous work suggests that using multiple polymer millirods in a single tumor is a feasible treatment strategy. In an attempt to more thoroughly eradicate the tumor, most hepatic lesions are treated by “overlapping” zones of ablation applied via minimally invasive, laparoscopic or open procedures [1, 24]. In each of these cases, an implant could be inserted after each RF application to achieve a favorable geometric distribution of implants. Other cancer treatments have also adopted the multiple implant approach. For example, prostate cancer treatment with brachytherapy has embraced geometric distribution of implants, using the placement of multiple radioactive seeds to deliver ionizing radiation to tumors [8]. In this treatment, seed placement is planned by an experienced medical physicist, but considerable effort has been directed towards designing software to predict radiation coverage and speed treatment design [14]. Intratumoral treatment designs have also used multiple drug containing implants to optimize the spread of drug within the treated region. For treating gliomas, up to 8 BCNU-impregnated polyanhydride implants (Gliadel^® wafers) are placed into the resection cavity after surgery [9]. Clinical trials have used up to 5 stereotactic injections per patient of 5-fluorouracil (5-FU)-containing microspheres into brain tumors [15, 16]. One recent report on the placement of multiple doxorubicin implants into dog prostates indicated that multiple implants could be highly effective in locally delivering chemotherapy to potential tumors [17]. These precedents suggest that placing multiple polymer millirods in a single tumor is a feasible and potentially effective strategy.

Although a multiple implant scheme is likely to improve drug distribution throughout a tumor, the ideal treatment approach and degree of benefit provided are not known. Simulation of drug distribution in tumors using a mathematical model of drug transport can be effective in the assessment of multiple implants. Results from model simulations can be used to predict drug exposure throughout the tumor, analogous to using computational tools to plan tumor radiation doses during prostate brachytherapy [12, 31]. A major advantage of using model simulation is that drug exposures can be rapidly evaluated and can minimize costly animal experiments. Based on predicted drug concentrations, simulated implant configurations can be compared based on predicted treatment efficacy. Additionally, model simulations can be used to evaluate drug exposures in different regions of the ablated tumor, especially near the tumor periphery where the thermal dose may not be sufficient to cause cell death [7].

In this study, we report the development of a multiple implant strategy for treating RF ablated tumors. A three-dimensional (3-D) model of drug transport in tissue was developed to simulate local drug concentrations in ablated liver tissue and liver tumors. Comparisons were made between millirod treatments using center, peripheral, and combined arrangements of 1–6 doxorubicin containing polymer implants. Experiments with a liver tumor model in rabbits were used to determine the extent to which simulation results were valid. To our knowledge, this paper describes the first use of RF ablation combined with multiple chemotherapy implants to treat experimental tumors. Additionally, the use of the drug transport model provides new insight into predicting drug distribution after a multimodal treatment that can be used to design future treatments.

METHODS

Drug transport model

The dynamic distribution of drug concentrations was simulated for two tissue conditions: (A) normal liver tissue with an ablated central core (Figure 1a) and (B) normal tissue surrounding a tumor with an ablated central core (Figure 1b). For these tissue conditions, one or more polymer millirods were placed in various arrangements. From each polymer millirod, doxorubicin (DOX) diffused into tissue according to a dynamic, 3-D transport model. In tumor tissue, DOX can be bound, i.e., coupled to molecules in the cell which prevent its diffusion, and unbound, i.e., free to move by convection or diffusion. Measurement of DOX concentrations in murine tumors has demonstrated DOX bound to intracellular molecules such as DNA can account for as much as 95% of total DOX [13]. Modeling free and bound DOX transport requires two transport equations. However, when the binding rate is in rapid, the local free and bound DOX are nearly in equilibrium so that only one equation of total DOX concentration is sufficient to describe the drug distribution dynamics in tissue [5]. Furthermore, DOX transport in ablated livers can be adequately modeled without including a convection term [19]. Under these conditions, the governing equation for total DOX concentration C is:

$$\frac{\partial C}{\partial t}=D{\nabla }^{2}C-\gamma C$$ (1)

where D is the apparent diffusion rate coefficient (m²s⁻¹) and γ is the apparent rate coefficient of elimination (s⁻¹) by perfusion and metabolism. Initially, no drug is in the tissue:

$$t=0:C=0$$ (2)

At the implant (im) surface, the drug concentration was assumed to vary with time and was linearly interpolated from experimental measurements from single implants placed in tumors and ablated tumors [29]:

$$r=R_{\mathit{\text{im}}}:C_{\mathit{\text{im}}}=f(t)$$ (3)

This boundary condition, f(t), is a constant plateau for the first four days, after which the concentration slowly decreases between day 4 and day 8. This boundary condition is similar to previously published experimental measurements from rat livers [19]. Far enough into the non-ablated normal liver (nl), the drug concentration was assumed negligible because of the elimination process:

$$r=R_{\mathit{\text{nl}}}:C_{\mathit{\text{nl}}}=0$$ (4)

For condition (A) with normal tissue, the drug concentration and flux were assumed continuous at the boundary between the ablated normal liver (al) and non-ablated liver (nl):

$$r=R_{\mathit{\text{al}}}:C_{\mathit{\text{al}}}=C_{\mathit{\text{nl}}},D\nabla C_{\mathit{\text{al}}}=D\nabla C_{\mathit{\text{nl}}}$$ (5)

For condition (B) with a tumor surrounded by normal tissue, the drug concentration and flux were assumed continuous at the boundary between the ablated tumor core (at) and non-ablated tumor (nt):

$$r=R_{\mathit{\text{at}}}:C_{\mathit{\text{at}}}=C_{\mathit{\text{nt}}},D\nabla C_{\mathit{\text{at}}}=D\nabla C_{\mathit{\text{nt}}}$$ (6)

and at the boundary between the non-ablated tumor (nt) and surrounding normal liver (nl):

$$r=R_{\mathit{\text{nt}}}:C_{\mathit{\text{nt}}}=C_{\mathit{\text{nl}}},D\nabla C_{\mathit{\text{nt}}}=D\nabla C_{\mathit{\text{nl}}}$$ (7)

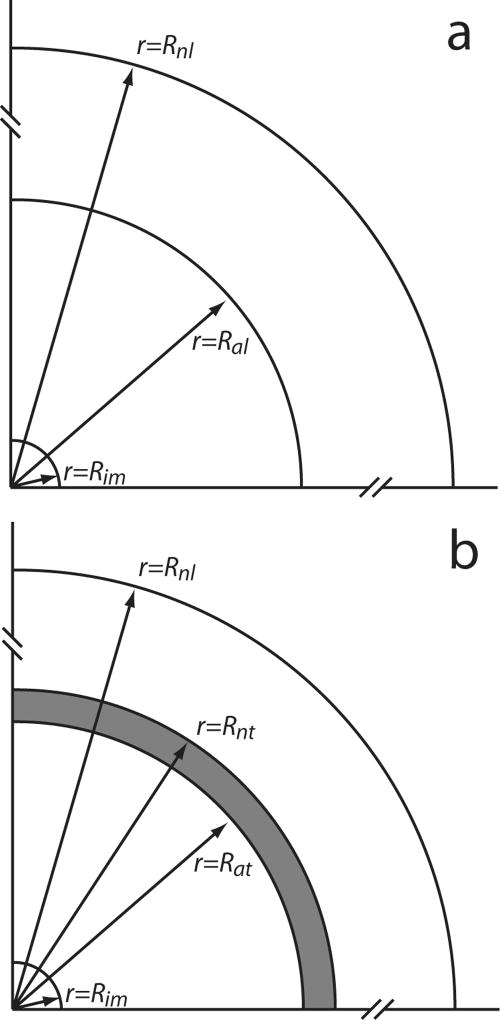
Figure 1.

Schematic representation of regions around the polymer implant assumed in simulating drug distribution in tissue: (a) normal liver with an ablated core; and (b) liver with a partially ablated tumor. The radii of the implant (im), ablated liver tissue (al), non-ablated liver (nl), ablated tumor (at), and non-ablated tumor (nt) are indicated by the arrows. The dark region at the periphery of ablated tumor is considered to have greater risk of tumor recurrence because of lower heat exposure. Distances not to scale.

Simulation strategy

This model was used to simulate the dynamics of doxorubicin concentration distributions in tissue from implanted polymer millirods over 8 days based on finite-element code COMSOL 3.3 (Burlington, MA) with Cartesian coordinates. All geometries were meshed using the fine adaptive mesh setting within COMSOL, which provided a spatial resolution of < 0.1 cm within regions of geometric complexity. Further decreases in mesh size had a negligible effect on the simulation outcomes.

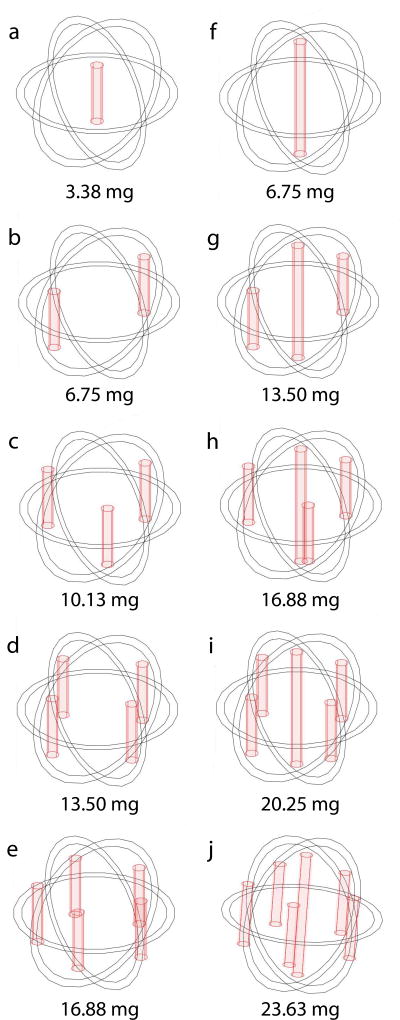
For tissue condition (A) without a tumor, we assumed a spherical ablated region, R_im ≤ r ≤ R_al = 0.9cm, surrounded by normal liver tissue, R_al < r ≤ R_nl = 4cm. Under this condition, simulations were performed to emulate placement of implants in an ablated rabbit liver for model validation. For condition (B), we assumed a spherical tumor with an ablated tumor core, R_im ≤ r ≤ R_at = 0.9cm; a non-ablated tumor rim, R_at ≤ r ≤ R_nt = 1.0cm, and surrounding region of normal liver tissue, R_nt < r ≤ R_nl = 4cm. This condition, which corresponded to an incompletely ablated tumor with a peripheral rim of viable tumor, was used to predict drug concentration distributions in scenarios with various, multiple implant tumor placements (Figure 2). Two scenarios used either a short (8 mm) or long (16 mm) millirod implanted centrally; four scenarios used only short millirods peripherally implanted; four scenarios used short millirods peripherally implanted and a long millirod centrally implanted. All peripheral implants were placed 7 mm from the center of the ablated region. Short and long implants contained 3.4 and 6.8 mg of doxorubicin, respectively, which resulted in total doxorubicin doses in these scenarios ranging from 3.4 to 23.6 mg. This compared well to the recommended intravenously administered therapeutic dose of doxorubicin, which was 7.9–14.8 mg for rabbits [27]. All simulated doses were well below the estimated lethal dose (LD50) of 63.3 mg [3].

Figure 2.

Multiple implant configurations for simulating drug distribution in tissue with a 2.0 cm diameter tumor (denoted by the outer sphere) with a 1.8 cm diameter ablated tumor core (denoted by the inner sphere). Single central implant with different lengths: (a) 8 mm; (f) 16 mm. Two to five peripheral 8-mm long implants (b–e). Peripheral 8-mm long implants and a central 16-mm long implant (g–j). Total doxorubicin doses are shown below each design.

Diffusion and elimination parameter values

Model parameters were chosen based on previous estimates made from experimental doxorubicin distributions in ablated rat liver and ablated rabbit tumors [19, 30]. Parameter values are listed in Table 1. The doxorubicin diffusion and elimination rate coefficients could be considered constant under certain conditions and as functions of position and time under other conditions. In non-ablated and ablated normal liver tissue as well as non-ablated tumor, these coefficients have constant values. In ablated tumor regions, diffusion and elimination rate coefficients had to be considered as functions of position or time in order to simulate available data. Previous studies suggested that the DOX diffusion rate coefficient D in ablated tumors depends on position: higher in the central ablation region and lower in the outer region as indicated by histology [30]. For this study, the diffusion rate coefficient in ablated tumor (R_im ≤ r ≤ R_at) was expressed as a function of position (r):

$$R_{\mathit{\text{im}}}\le r\le \alpha R_{\mathit{\text{at}}}:D=D_{\mathit{\text{at}}};\alpha R_{\mathit{\text{at}}}<r\le R_{\mathit{\text{at}}}:D=D_{\mathit{\text{at}}}-\left[\frac{r-\alpha R_{\mathit{\text{at}}}}{R_{\mathit{\text{at}}}-\alpha R_{\mathit{\text{at}}}}\right][D_{\mathit{\text{at}}}-D_{\mathit{\text{nt}}}]$$ (8)

where α = 0.47 was chosen so that the diffusion rate coefficient was constant within a central region of the ablated tumor (D_at) and decreased linearly to the value in non-ablated tumor (D_nt). Previous estimates of doxorubicin diffusion in ablated tumors required coeffcients that varied as a function of position and were greater near the centrally placed ablation probe, where temperature distributions are likely higher. This theory has been substantiated by histological findings in the ablated tissues [30]. In the ablated tumor, the elimination rate coefficient was expressed as a function of time γ = γ_at(t):

$$0\le t\le t_1:{\gamma }_{\mathit{\text{at}}}(t)=0;t_1\le t\le t_2:{\gamma }_{\mathit{\text{at}}}(t)=\left[\frac{t-t_1}{t_1}\right]{\gamma }_{\mathit{\text{at}}}(t_2)$$ (9)

For comparison to experimental results, t₁= 4 days and t₂=8 days. The elimination rate coefficient is expected to be negligible for the first 4 days after an ablation that destroys tumor and vascular cells, abolishing both metabolism and perfusion. Between days 4 and 8, tissue and vascular cells develop as inflammation is resolved in the ablated region [30].

Table 1.

Simulation parameter values

Parameter	Abbreviation	Value
Diffusion, non-ablated livera	Dnl	6.7 × 10−11 m2s−1
Diffusion, ablated livera	Dal	1.1 × 10−11 m2s−1
Diffusion, non-ablated tumorb	Dnt	5.0 × 10−11 m2s−1
Diffusion, ablated tumor centerb	Dat	8.8 × 10−11 m2s−1
Elimination, non-ablated livera	γnl	9.6 × 10−4 s−1
Elimination, non-ablated tumora	γnt	0.6 × 10−4 s−1
Elimination, ablated tumor (day 0)b	γat(day 0)	0 s−1
Elimination, ablated tumor (day 8)b	γat(day 8)	0.6 × 10−4 s−1

^aQian, et al.[19].

^bWeinberg, et al. [30].

Evaluation of simulated drug treatments

The presumed efficacy of treatments was related to drug (doxorubicin) concentration [DOX] distribution. Several measures were computed for comparison. For these calculations, the tumor was divided into two regions: an inner core (75% of tumor volume) and an outer risk volume (25% of tumor volume). Average drug concentrations were calculated for the whole tumor volume or risk volume over time (t₂=8 days). Treatments were further compared by calculating the fractions of whole tumor and risk volume for which drug concentrations were greater than a therapeutic target concentration, [DOX*]=12.8 µg/g, or 2 times the therapeutic value of doxorubicin in VX2 tumor [21, 22]. Two times the therapeutic concentration was chosen to provide a safety margin above which most cells could be assumed to be killed by the drug.

Manufacture of polymer implants

Doxorubicin-containing millirods were fabricated by combining 65% poly(D,L-lactide-co-glycolide) (PLGA) microspheres, 13.5% doxorubicin, and 21.5% NaCl (w/w) using a previously published compression-heat molding procedure [18]. The mixture was blended with a mortar and pestle, packed into a Teflon tube (1.6 mm outside diameter), and compressed with steel plungers (1.6 mm inside diameter) at 90°C for 2 hours. Final implants were cylindrical with an approximate diameter of 1.6 mm and length of 8.0 mm.

Animal model and treatment

All animal experiments were approved by the Institutional Animal Care and Use Committee at Case Western Reserve University and followed all applicable guidelines. One multiple implant scenario selected from the simulated scenarios was tested both in ablated liver tissue and ablated liver tumors. To test in ablated liver, the abdomens of New Zealand White rabbits (n = 2) were opened just below the sternum. The liver was gently exposed and lifted, and a 17-gauge, 1 cm exposed tip ablation probe (Radionics, Burlington, MA) was inserted into the middle lobe of the liver. Tissue in contact with the tip was heated to a temperature of 90°C, as measured by a thermocouple sensor in the ablation probe, for 9 minutes. After ablation, polymer millirods were inserted into the ablated region in the pattern selected. If necessary, implants were secured in place by covering the puncture with resorbable gelatin foam and suturing it in place with a 6-0 monocryl suture. The abdomen was then closed.

A combined treatment of rabbit liver tumors with RF ablation and doxorubicin millirods was performed based on a modification of a previous technique [29]. VX2 carcinomas (n = 2) were implanted in the liver and were allowed to grow for 28 days until they reached an approximate diameter of 2.0 cm. After 28 days, the abdomen was reopened, and a 17-gauge ablation probe with a 2-cm exposed tip (Radionics) was placed into the center of the tumor. The tissue was heated and maintained at a temperature of 90°C for 9 minutes to ablate a sphere with a diameter of approximately 1.8 cm in the center of the tumor. After ablation, DOX-containing millirods were placed into the ablated tumor. In each of the groups, one of the rabbits was euthanized at each time point, 4 and 8 days after ablation.

Tumor evaluation

Tumors were removed from the surrounding liver tissue and sliced in half parallel to the front surface of the liver. One half of the tumor was fixed in formalin solution and the other half of the tumor was frozen at −20°C. Frozen liver sections 100 µm thick were sliced from each section using a cryostat microtome (Leica CM3050S) and then scanned with a fluorescent imager (Molecular Dynamics Fluorimager SI). The fluorescence value of ablated tissue background was subtracted using a background subtraction algorithm. The net fluorescence intensity (NFI) was empirically related to [DOX] (µg/g), NFI = 194·[DOX]^0.67 [28]. The fixed tissue was embedded in paraffin, sliced, and stained with hematoxylin and eosin (H&E) or Masson’s trichrome (MTC). Histology slides were subsequently used to identify the location of each tissue region in the DOX concentration maps.

RESULTS

Simulated drug distributions using multiple implants

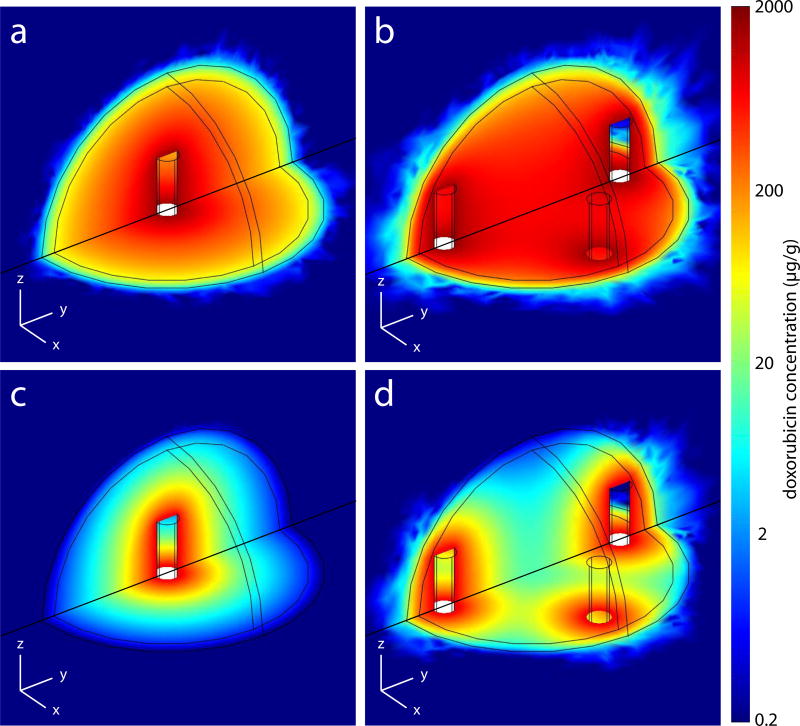
To quantify the advantage of multiple implants over a single implant in treating incompletely ablated tumors, a comparison was made between using 1 central implant and 4 peripheral implants. These scenarios correspond to the configurations shown in figure 2a and figure 2d, respectively. Doxorubicin (DOX) concentration distributions determined from model simulations for the two scenarios at 4 and 8 days after implantation are shown in Figure 3. On day 4, DOX concentrations in the ablated tissue were high in both scenarios (Figures 3a and 3b). However, the doxorubicin concentration ([DOX]) of the non-ablated tumor rim, or risk volume, was higher in the multiple implant case. This pattern continued to day 8, when it was more evident because of decreasing [DOX] in the single implant case (Figures 3c and 3d). Over the 8 day period, the average [DOX] in the whole tumor was 119 µg/g using 1 implant and 290 µg/g using 4 peripheral implants. In the risk volume, average [DOX] over 8 days was 16.9 and 99.3 µg/g, respectively, for the two scenarios. Much of this advantage was expected, as the total DOX dose had been increased by a multiple of 4. However, the risk volume exposure increased roughly 6 fold, indicating that repositioning the implants offered more than a dose dependent increase in drug delivery to the periphery. On day 4, the [DOX] was above the therapeutic threshold concentration ([DOX*]) in 100% of the risk volume with 4 implants, but only in 78% of the risk volume with a single implant.

Figure 3.

Simulated drug concentration distributions in tissue with 2.0 cm diameter tumor and 1.8 cm ablated tumor core on day 4 (a, b) and day 8 (c, d). Single implant in the center (a, c). Four implants spaced around the periphery (b, d).

Comparison of multiple implant configurations

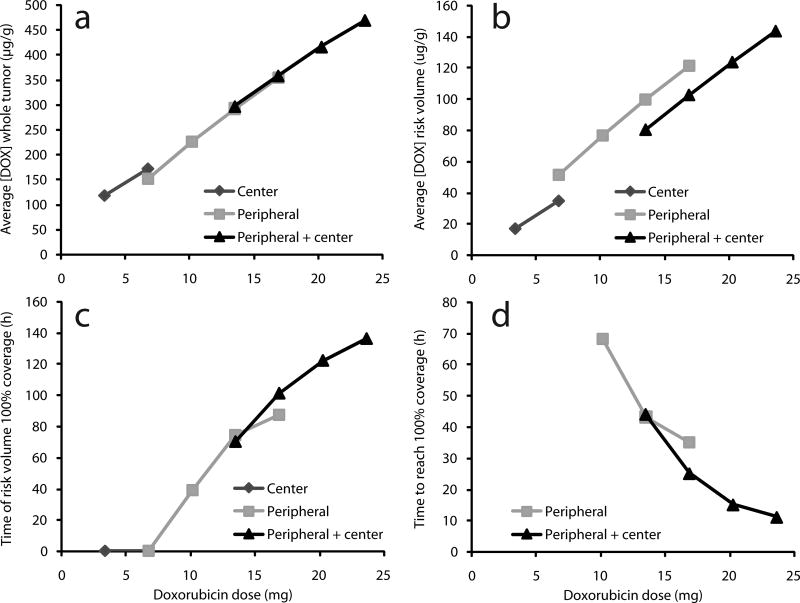
Multiple implant strategies were quantitatively compared using measures of average [DOX] in the whole tumor and the risk volume (Figures 4a and 4b). The average [DOX] increased almost linearly with total DOX dose, which depended primarily on the number of implants rather than implant configuration. In the risk volume, however, average [DOX] depended on the implant distribution in the tumor. For the same DOX dose, the average [DOX] in the risk volume from peripheral configurations was approximately 20 µg/g above the average [DOX] from peripheral + center configurations with equivalent dosage.

Figure 4.

Characteristics of simulated drug distribution with central implant, peripheral implants, or peripheral+central implants as a function of total DOX dose. Average doxorubicin concentration [DOX] over 8 days in (a) the entire tumor or (b) outer tumor rim (risk volume). (c) Simulated duration for which [DOX] ≥ 12.8 µg/g in entire risk volume. (d) Time after implantation at which [DOX] ≥ 12.8 µg/g in entire risk volume.

Implant configurations were also compared based on the duration for which 100% of the risk volume had [DOX] above [DOX*] (Figures 4c and 4d). Center only configurations never reached the [DOX*] for 100% of the risk volume, nor did the peripheral configuration with only 2 millirods. All other configurations with total DOX dose ≥ 10 mg achieved [DOX*] for 100% of the risk volume and the duration of [DOX] ≥ [DOX*] in 100% of the risk volume increased with DOX dose. No significant difference was seen between peripheral and peripheral + center treatment strategies. Configurations were also compared based on the time required for [DOX] to reach [DOX*] in 100% of the risk volume. Shorter times are more desirable because the cells around the periphery have had less time to recover from the heat exposure and may have a decreased tolerance to DOX. More implants decreased the time required for [DOX] ≥ [DOX*] in 100% of the risk volume. At high doses of DOX, the peripheral + center strategy offered an advantage, primarily because it increased the time at which drug was delivered to the poles of the tumor. Otherwise, all treatments for which [DOX] ≥ [DOX*] in 100% of the risk volume did so in 11–68 hours. Configurations with equivalent total DOX doses did have some qualitative treatment differences. As expected, the peripheral implants provided [DOX] ≥ [DOX*] over much of the tumor equator, but relatively less at the poles of the tumor. The advantage of the peripheral + center strategy was [DOX] ≥ [DOX*] around much of the poles of the tumor rather than at lateral regions of the tumor surface.

Multiple implant treatment of ablated liver

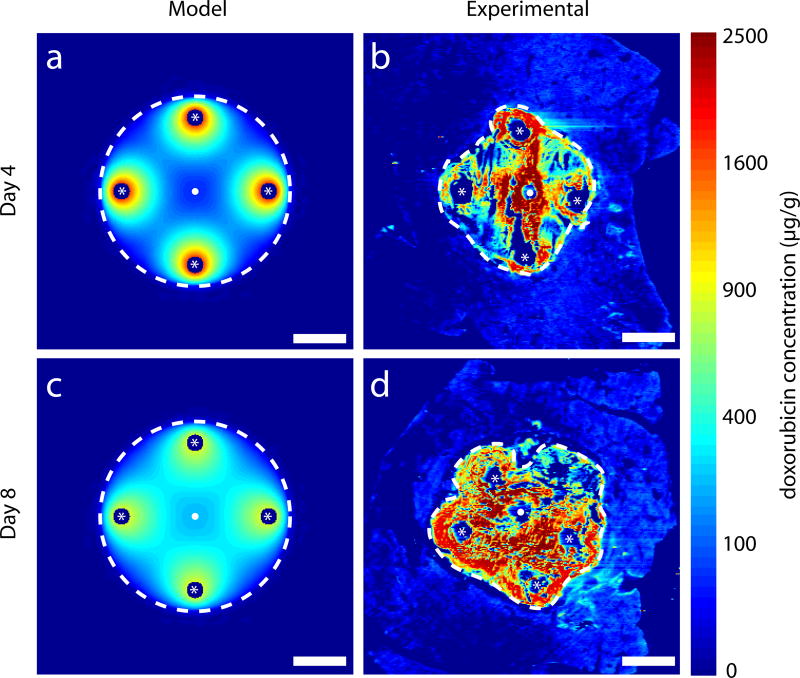
In an in vivo experiment, normal rabbit livers were implanted after thermal ablation with 4 peripheral polymer millirods with DOX (Figure 2d). A comparison of [DOX] predicted from the model simulation and measured from experimental data is shown in Figure 5. From model simulation, [DOX] was high in the tissue surrounding the implants on day 4. The distribution of DOX continued throughout the ablated region, particularly toward the center of the ablated region by day 8. A similar trend was observed in the experimental data, but the observed [DOX] was markedly higher than predicted. Median [DOX] in the ablated region was almost three times higher from experimental data as compared to simulated data. However, the model accurately predicted that [DOX] ≥ [DOX*] in more than 98% of the ablated tissue at days 4 and 8. From experimental data, the drug penetration distance, i.e. the distance from the ablation center at which [DOX]<[DOX*], was 8.5 mm on day 4 and 9.5 mm on day 8. A summary of [DOX] information is compiled in Table 2.

Figure 5.

Simulated drug distribution in ablated normal tissue compared to DOX distribution in images of ablated normal liver from in vivo rabbit experiments with four peripheral implants (located at white asterisks). Ablated regions are within white dashed lines. Thermal ablation source located at white dots. Model simulated DOX distributions on day 4 (a) and day 8 (c). DOX distributions from experimental images on day 4 (b) and day 8 (d). Fixation or preservation artifact in experimental images arose from fracture of brittle ablated tissue during slicing. Scale bars are 5 mm.

Table 2.

Doxorubicin coverage of simulated and experimental tissues.

	Model		Experimental
	Day 4	Day 8	Day 4	Day 8
Ablated liver model (Condition A)
Area of ablated liver (mm3)	254	254	155	186
Ablated liver over [DOX*] (%)	98.3%	98.8%	98.0%	98.3%
[DOX] in ablated liver (µg/g)a	205 [117–430]	295 [192–398]	590 [166–1311]	1008 [361–1796]
Ablated tumor model (Condition B)
Area of ablated tumor (mm3)	254	254	343	418
Area of non-ablated tumor (mm3)	60	60	195	90
Non-ablated tumor over [DOX*] (%)	100%	61%	87%	65%
[DOX] in non-ablated tumor (µg/g)a	140 [78–232]	20 [8–56]	79 [30–173]	26 [7–87]

^aValues shown are the median concentration. Brackets contain the 25^th and 75^th percentiles.

Multiple implant treatment of liver with ablated tumor

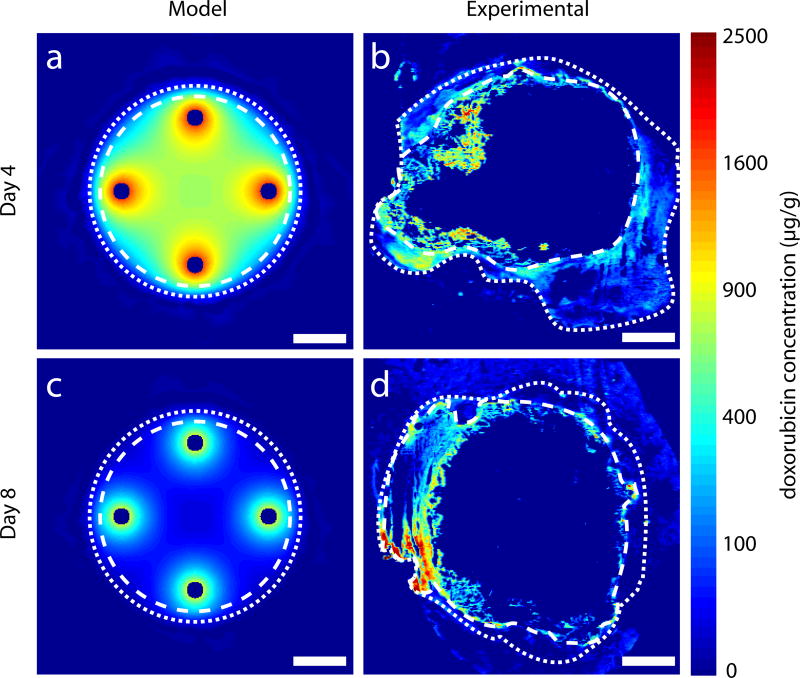
In an in vivo experiment, VX2 liver tumors in rabbits were thermally ablated and implanted with 4 peripheral polymer millirods with DOX (Figure 2d). Although the model simulation tumor size was 2 cm in diameter, tumors were approximately 2.5 cm and had a cystic core when treated. Distribution of [DOX] from model simulations and experimental slices are shown in Figure 6. Measured [DOX] distributions (Figures 6b and 6d) were more irregular in experimental tumors than in the simulated spheres, reflecting the underlying asymmetry and inhomogeneity of the liver tumors. [DOX] could not be measured in the center of the tumor because of the cystic core of the tumor, but at the periphery of the ablated tumor [DOX] distributions appeared similar in simulation and experimental data. A quantitative summary of [DOX] in the tumors is given in Table 2. With respect to [DOX] ≥ [DOX*] in the non-ablated tumor rim, the experimental data were similar to model predictions. On day 4, however, [DOX*] was attained in 87% of this region instead of the predicted 100%. Median [DOX] was also similar between model predictions and experimental measurements. For the non-ablated tumor rim on day 4, the median model predicted [DOX]=140 µg/g was higher than the experimentally measured median [DOX]=79 µg/g. However, there was considerable overlap between the middle 50% of the points. On day 8, the model predicted median concentration [DOX]=20 µg/g, which corresponded to the experimentally measured median [DOX]=26 µg/g. Overall, the experimental values for [DOX] in the non-ablated tumor rim were close to the model-predicted values. Both experimental and model simulated regions in which [DOX] ≥ [DOX*] exhibited the same trend: peaking on day 4 and decreasing slightly by day 8.

Figure 6.

Simulated drug distribution in ablated tumor tissue compared to DOX distribution in images of ablated tumor liver from in vivo rabbit experiments with four peripheral implants. The outer extent of the ablated regions is within white dashed lines and the outer extent of the non-ablated tumor is within white dotted lines. Model simulated DOX distributions on day 4 (a) and day 8 (c). DOX distributions from experimental images on day 4 (b) and day 8 (d). Central portion of ablated tumor is not visible in experimental images because of extensive necrosis. Scale bars are 5 mm.

DISCUSSION

Computational model

From drug-containing polymer millirods implanted in tissue after thermal ablation, drug enters surrounding tissue and produces concentration distribution patterns that depend on the location of the implants. Especially with several implanted millirods, prediction of spatial distribution dynamics of the drug concentration requires a mathematical model and computer simulation. Simulations were obtained using a commercial code (COMSOL 3.3) that implements a finite-element method (FEM). This code was used to deal with the complexity of asymmetric placements of multiple implants and a wide range of inputs, boundary conditions, and tissue properties. Furthermore, this code was able to deal with diffusion and elimination rate coefficients that vary with time and location in tissue. This computational model could be used in the future to simulate complex treatment scenarios based on imaging data.

The boundary conditions in this study are based on the assumptions that the rate of drug release measured experimentally from a single implant would be uniform on all surfaces of the implant and that they would be the same for each of the multiple implants placed asymmetrically within a tumor. As a practical matter, the variation of these boundary conditions from implant to implant is probably of second-order importance relative to the spatial variability of tissue properties.

Simulation of drug distributions in ablated tissue

Model simulation of drug distributions using multiple implants provided a basis for quantifying the expected effects on tumor recurrence. In the peripheral rim of the ablated tumor (i.e., risk volume), the risk of tumor recurrence is higher because it may be exposed to sublethal heating during ablation [11]. As shown in Figure 3, peripheral implants can significantly increase the drug concentration in the risk volume. However, different central and peripheral implant configurations can result in different levels of therapeutic drug levels in the entire tumor and in the risk volume and the time at which these levels are reached (Figure 4). In general, the therapeutic level was reached more quickly and over a greater tumor volume with more implants that have a greater total dose. Within the ablated tumor, where the rate of drug diffusion is relatively quick and the rate of elimination is relatively low, different configurations are less important than the total drug dose in determining drug levels over the entire tumor volume. Peripheral implants, however, can lead to higher drug concentration in the risk volume, but this requires multiple implants in appropriate locations.

Central and peripheral implant configurations

Using peripheral implants either with or without a central implant allowed the drug concentration to reach therapeutic levels throughout the entire tumor, a finding which was not seen with a single central implant (Figure 4). With a central implant, much of the drug dose was delivered to the core of the ablated region tumor instead of the risk volume. Increasing the total drug dose to achieve therapeutic drug levels can potentially have systemic side effects. Appropriate placement of peripheral implants can reach therapeutic levels more quickly and in more of the risk volume without a central implant even with the same total drug dose (Figures 4b and 4d). The accuracy of model simulations must be tested by comparison to data from in vivo experiments.

Comparison of simulated and in vivo drug distributions

Of the simulated configuration of multiple implants, four peripheral implants produced therapeutic drug levels in the entire tumor over a relatively short time period. Comparable in vivo experimental studies were performed with four implants in ablated rabbit livers, either normal or with tumors. In normal ablated liver, [DOX] from experimental images was much higher than simulated drug concentrations in the central ablated region (Figure 5). One reason for the lower simulated drug concentration is that model parameter values were taken from studies with ablated rat liver [19], which may differ from ablated rabbit liver because different tissue types have different vascularity and density. Additionally, the assumed drug concentration at the implant boundary was taken from a single implant placed in a small ablated tumor [29], which may inadequately represent boundary drug concentrations with multiple implants in close proximity. Nevertheless, model simulation of the overall trend in average drug concentration corresponds to that observed experimentally. Moreover, the model predicted that 98% of the ablated region would reach therapeutic target concentrations in accord with estimates from experimental [DOX] images.

Model predictions of [DOX] distribution in ablated liver tumors were compared to experimental [DOX] measurements from ablated VX2 liver tumors in rabbits (Figure 6). Experimental tumors were larger than anticipated and had a necrotic center from which no [DOX] data was available (Figures 6b and 6d). Furthermore, since the location of the thermal ablation source could not be located from the experimental images, the relative locations of the experimental implant could only be estimated. However, at the periphery of the ablated tumors, particularly in the non-ablated rim, [DOX] was well above the therapeutic [DOX*]. Average [DOX] and the fraction of the area where [DOX] was above the therapeutic [DOX*] from model predictions were in agreement with corresponding measures from experimental images. Whereas simulated [DOX] values exceeded [DOX*] over the entire tumor on day 4, experimental [DOX] measurements exceeded [DOX*] in 87% of the tumor rim. Factors that could explain this disparity include the heterogeneity of the experimental tumor tissue or variability in the size and shape of the tumor and the ablated regions. Despite the difference, the average drug concentration values in the non-ablated tumor overlapped considerably between simulated and experimental data (Table 2). On day 8, coverage of the non-ablated tumor correlated much more closely between the model and experimental data, which have values of 61% and 65%, respectively. Overall, for tumor areas > 5 cm² in the central cross section, [DOX] surpassed [DOX*] in a large fraction of the tumor rim on both days. The success of achieving this therapeutic drug level with polymer millirods in such a large tumor is a major step toward the use of these implants in practical clinical situations.

Conclusion

Simulation of drug concentration distribution in ablated tissue from multiple implants can be successful in predicting optimal implant strategies that can be tested experimentally. The combination of model simulations with a small set of animal experiments is much more efficient in determining an optimal implant strategy for treating large tumors than a much larger set of animal experiments alone.