Abstract.
Interactive segmentation is a promising approach to solving the pervasive shortage of reference annotations for automated medical image processing. We focus on the challenging task of glioblastoma segmentation in magnetic resonance imaging using a random forest pixel classifier trained iteratively on scribble annotations. Our experiments use data from the MICCAI Multimodal Brain Tumor Segmentation Challenge 2013 and simulate expert interactions using different approaches: corrective annotations, class-balanced corrections, annotations where classifier uncertainty is high, and corrections where classifier uncertainty is high/low. We find that it is better to correct the classifier than to provide annotations where the classifier is uncertain, resulting in significantly better Dice scores in the edema (0.662 to 0.686) and necrosis (0.550 to 0.676) regions after 20 interactions. It is also advantageous to balance inputs among classes, with significantly better Dice in the necrotic (0.501 to 0.676) and nonenhancing (0.151 to 0.235) regions compared to fully random corrections. Corrective annotations in regions of high classifier uncertainty provide no additional benefit, low uncertainty corrections perform worst. Preliminary experiments with real users indicate that those with intermediate proficiency make a considerable number of annotation errors. The performance of corrective approaches suffers most strongly from this, leading to a less profound difference to uncertainty-based annotations.
Keywords: glioblastoma, segmentation, interactive, online
1. Introduction
Semantic segmentation is a key component of machine image understanding. It is the separation of logically coherent structures that allows computers to deduce meaningful information and relate it to the image’s individual components. Automated machine learning methods such as convolutional neural networks have recently become extremely successful in a variety of image segmentation problems, including those in the medical domain,1 but they rely on large bodies of annotated data for training, a resource that is typically scarce when it comes to medical images. Interactive segmentation methods can be used to create such training data from scratch, i.e., using only live inputs from a user, but the process is often a time-consuming one. Most medical images can only be annotated by a small number of trained experts, so it is crucial to have efficient techniques that require as little time and effort as possible. Because their output is guided by an expert user, such techniques also lend themselves to applications that require both speed and reliability, for example, radiologists performing fast tumor volumetry to accurately monitor tumor progression. This further leverages the high diagnostic potential of modalities such as computed tomography, positron emission tomography, ultrasound or magnetic resonance imaging (MRI).
The purpose of this work is to establish methods that enable expert users to generate high-quality segmentations of medical image data with only a small number of input annotations. The interactive segmentation technique we base our work on trains a classifier on a small number of labeled pixels and predicts labels for all remaining pixels. The user can see intermediate results and the underlying data to perform additional interactions in order to improve the resulting segmentation in an iterative fashion. The question of what would be the optimal next annotation pertains to the domain of active learning,2 where the premise is that the algorithm can query an oracle (the user in this case) for the correct label of some data point to improve its prediction, but only at great cost, hence the need to keep the number of queries minimal. Semantic segmentation is nontrivial in this context, because the instances are strongly correlated and users will rarely perceive them as separate entities. On top of that, the large number of instances, especially when working in three-dimensional (3-D), makes many computations infeasible. The use of superpixels can reduce the complexity of the problem, but previous studies focus more on generic computer vision tasks,3,4 where the difficulty is not so much the correct delineation of an object—most have pretty clear boundaries—but instead assigning the correct label out of a large number of possible categories. The challenge in medical images is often not the large number of classes but instead to correctly identify entities that exhibit no clear boundary and an appearance similar to their surroundings. Work on a pixel-level basis using scribble annotations and Gaussian processes was performed by Triebel et al.,5 but they only work with two-dimensional images of everyday objects.
Notable work in the medical domain was put forward by Top et al.,6,7 who rely on an active contour for segmentation and construct a measure of uncertainty that is then used to identify a plane (which can be oblique) of maximal uncertainty, in which the user is asked to provide additional inputs. Their work was implemented in the software TurtleSeg. While their measure of uncertainty should generalize to various segmentation techniques, the authors use a contour-based approach, which is suboptimal for problems like ours, where there are no clear boundaries. Additionally, radiologists are trained to assess images in the predefined orientations, so that oblique planes might be more confusing than helpful. We choose to restrict ourselves only to axial, sagittal, and coronal planes for annotation.
Konyushkova et al.8 worked with superpixels and specifically incorporated correlations with neighboring superpixels into a measure of geometric uncertainty that is then used to identify a plane for optimal annotation, which will again be generally oblique. Interestingly, the authors evaluate their approach on MRI data of glioblastoma patients, the same task we will work on. We will compare our results with theirs in Sec. 4. Note, however, that their mode of interaction is binary, meaning the user must only decide on a boundary between the inside and outside of a target object. Our segmentation approach naturally incorporates multiclass segmentation.
Maiora et al.9 and Chyzhyk et al.10 both combined a random forest classifier with active learning to segment abdominal aortic aneurysm and stroke lesions, respectively. Both also employ pixel-level annotations and an interactive workflow but require users to annotate with single pixel accuracy. The segmentation problems they tackle are binary and their query measure is the standard deviation of the class labels, which, if at all, makes sense only for binary categorization (using 0 and 1 as numerical values).
We focus on glioblastoma segmentation as a task that has been quite extensively studied in the context of the brain tumor segmentation (BraTS) challenge11 and that poses a challenging multiclass segmentation problem in medical image analysis. We base our interactive segmentation process on a random forest classifier, which has proven to be the best overall choice of classifier on a wide range of tasks12 and has achieved very good results for the specific task of glioblastoma segmentation.13–16 An implementation of such a segmentation scheme using random forests is offered by the open source ilastik framework.17 The classifier predicts labels for all pixels in an image based on a few manually annotated pixels. In an iterative process, the user is asked to provide additional annotations to improve the segmentation. Normally, the choice of where to annotate next in the process is left entirely to the user. Our contribution is the proposal of five interaction methods to ensure optimal usage of user inputs that use the classifier uncertainty, an expert user’s knowledge of the correct segmentation and also a combination of both. To the best of our knowledge, we are the first to evaluate how useful uncertainty information is compared to correctness information in this setting.
2. Materials and Methods
We compare five different methods of placing annotations in an online interactive segmentation task. In an iterative process, a user annotates a small part of an image (i.e., a small number of pixels) and a classifier is trained on these inputs to predict labels for all image pixels. The result is displayed back to the user so they can input additional annotations to refine the result until satisfied. In this setting, we compare interaction modes (i.e, certain rules users adhere to in the annotation process) based on the classifier uncertainty as well as the user’s knowledge of the correct segmentation. The specific task we investigate is the segmentation of MRI brain scans of glioblastoma (high-grade glioma) patients into multiple tissue categories.
All data and the experiment script can be found online.18–20
2.1. Data
We conduct our experiments using data from the 2013 BraTS challenge11 comprising MRI scans of glioblastoma patients. The entire dataset consists of both real (acquired at field strengths of 1.5 T or 3 T) and synthetic MRI data for both low-grade and high-grade glioma patients. In our experiment, we intentionally leave out the synthetic data, because they “are less variable in intensity and less artifact-loaded than the real images,”11 as well as the low-grade glioma data, because we find the high-grade ones to be more challenging.
The remaining data comprise 20 individual subjects, for each of which there are four 3-D image volumes of different MR contrasts available: native T1-weighted (T1), contrast-enhanced (Gadolinium) T1 (T1ce), native T2 (T2), and native T2-weighted fluid attenuation inversion recovery (FLAIR). An example of what these contrasts look like is given in Fig. 1.
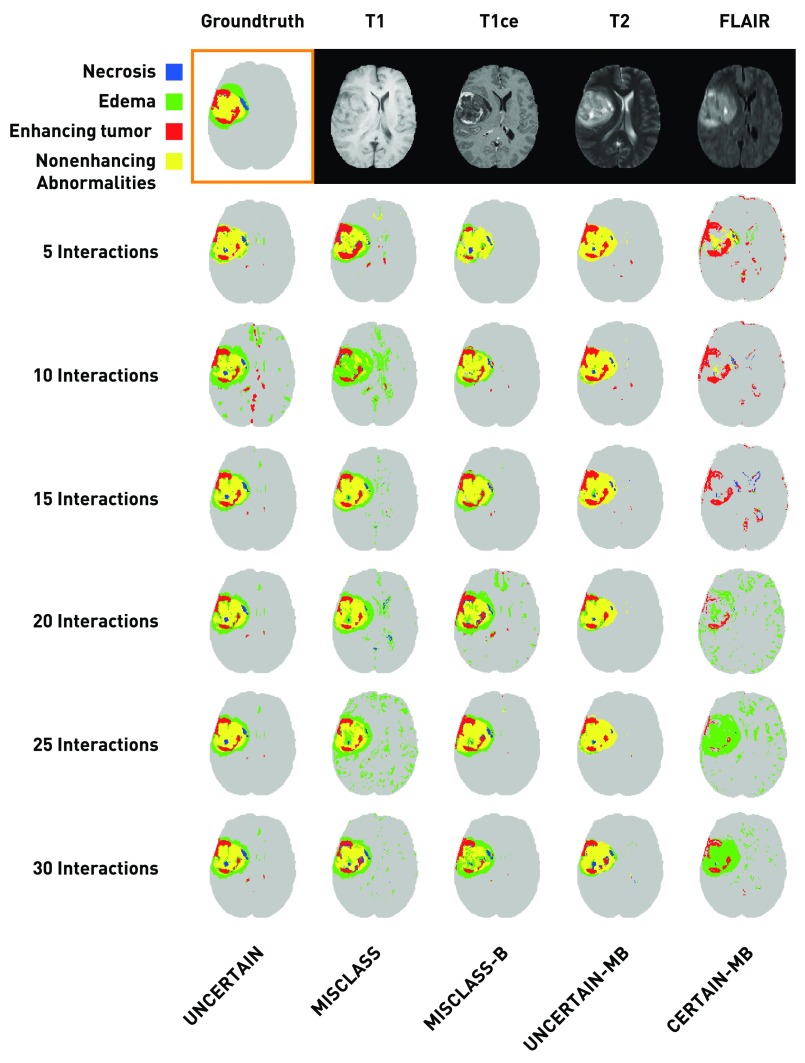
Fig. 1.
Exemplary segmentation results after 5 to 30 interactions for each annotation mode (patient HG0004, axial slice 101, third run) along with the corresponding groundtruth segmentation and the four base channels. The results are not representative of the overall segmentation quality for a given method, but show that in general the algorithm needs little data to roughly approximate the solution and that most annotations only refine the result. In almost all cases, there remain very small falsely classified regions throughout the healthy brain, indicating that our results would benefit from postprocessing. We neglect postprocessing in this work, as it is more appropriate at the end of the interactive routine, not in every step.
The available data for each patient are already coregistered, resampled to 1-mm isotropic resolution, and skull-stripped by the challenge authors, we further apply the following preprocessing:
-
•
Compute the T1ce to T1 difference map as a fifth channel as proposed in Ref. 21.
-
•
Perform N3 bias-field correction for T1, T1ce, T2, but not FLAIR, because edema signatures can look similar to field inhomogeneities in this contrast.
-
•
Apply histogram-matching (3-D-slicer’s22 HistogramMatching routine), excluding voxels below mean intensity.
-
•
Normalize intensities by mean cerebral spinal fluid value (which is obtained by automatic segmentation).
For a more detailed description of the effect of these processing steps, see Ref. 15. We then compute the following feature maps:
-
•
Gaussian smoothing ();
-
•
Gaussian gradient magnitude ();
-
•
Laplacian of Gaussian ();
-
•
Hessian of Gaussian eigenvalues (three feature maps, );
-
•
Structure tensor eigenvalues (three feature maps, ).
This results in a feature vector length of 95. Most image volumes have a size of (some patients differ slightly), so that a patient is described by a matrix.
Our choice of features is motivated by their success in earlier15,23 work. We do not perform any feature selection on the above set of features, which might show some redundancy among the maps and would allow us to select an equally performant subset, but in this work, we are not interested in the most computationally efficient implementation of the interaction process and simply accept that there is room for optimization in this regard. Similarly, we are aware that there could be features that would potentially improve our results, for example, features that better capture long-range correlations24 or learned features from neural networks. The latter approach can yield very rich and descriptive features, but for amounts of data as small as ours, there is a chance that the learned features are more discriminative (i.e., telling one image from another) than descriptive (i.e., describing the semantic contents of an image). Instead, we opt for easy to compute and reliable features.
For each of the 20 patients, there is a groundtruth segmentation available that was obtained by manually merging segmentations from four different raters. The segmentations describe five different tissue categories:
-
0.
healthy tissue/background;
-
1.
necrosis;
-
2.
edema;
-
3.
nonenhancing abnormalities;
-
4.
enhancing tumor.
We additionally define the whole tumor region as the union of all four nonbackground classes. Figure 1 shows an example of a groundtruth segmentation and the corresponding MR contrasts. The enhancing tumor is best identified from hyperintensities in the T1ce image within the gross tumor region. The necrosis and the nonenhancing tumor regions typically exhibit very similar signatures and are often hard to distinguish. They are hypointense in T1-weighted images and hyperintense in T2-weighted images with heterogeneous texture. In the given example, the necrotic region looks smoother with more pronounced intensity anomaly compared to the nonenhancing tumor, but both are often more similar. Note that this patient is unusual, because in the majority of cases, the central part of the tumor is dominated by necrosis with less pronounced nonenhancing regions. The edema can be identified from hyperintense signatures in T2-weighted images, especially FLAIR, that do not belong to the other tumor regions.
2.2. Classifier
The classifier we employ is a random forest,25 an ensemble classifier that builds multiple decision trees from randomly bootstrapped samples of the training data. Random forests have proven to be the best generic choice of classifier12 and were also used very successfully for glioblastoma segmentation.13–16 Our decision for random forests is further supported by the availability of toolkits for interactive segmentation that also employ random forests and scribble annotations.17,26
The classifier works on a per-pixel basis, meaning that each pixel, represented by a 95-dimensional feature vector (see previous section), is treated as a separate instance, and all MRI channels and precomputed features are used simultaneously. The decision trees are built from the annotated pixels, which constitute the training set in each case. A single decision tree is formed from a number of training instances by repeatedly looking at one or more feature dimensions (note that each instance is usually a point in a high-dimensional space, in our case 95 dimensions). The set is then split into two subsets at the point that maximizes or minimizes a desired criterion (e.g., resulting in versus ), creating two nodes. The process is repeated at each node with the remaining training instances until the tree has reached a predefined depth or nodes contain only a single instance and cannot be split further. A single tree makes a class prediction by simple lookup, i.e., it checks for each split, in which of the two subsets the new instance belongs and follows those splits until it arrives at a leaf node, i.e., one that is not split further and assigns the new instance whatever label the majority of training instances at the final node have.
A random forest is simply a collection of decision trees that were built on a randomly drawn subset of the training data (with replacement, so training instances can contribute to more than one tree), making it a bagging classifier. A prediction by the forest is made (for all unannotated pixels in each step) by letting each decision tree vote for a class. The relative number of votes a label/class receives is treated as its probability and the label with the highest number of votes is assigned to the tested instance. A good overview of random forests and related classifiers can be found in Ref. 27.
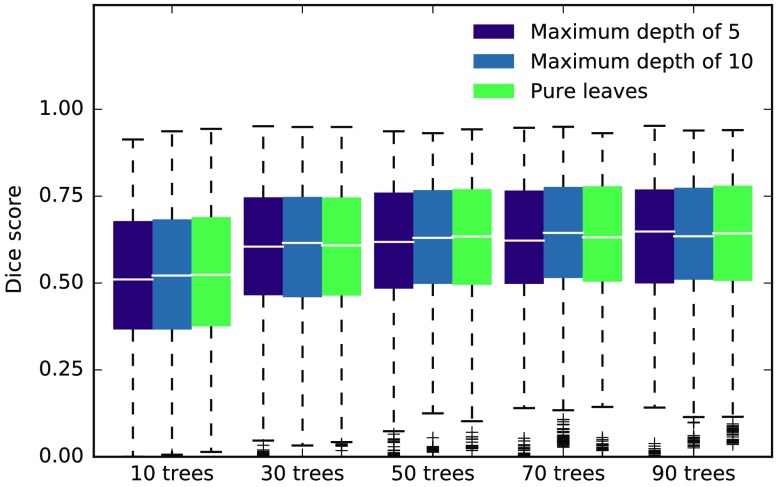
To see the influence of the random forest parameters on our experiments, we performed a coarse grid search with the two parameters we expect to be most relevant, the number of trees in the forest and the maximum depth of the trees. Deeper trees generally mean that the forest fits more closely to the training data and in turn loses generalization ability. Because our experiments always treat one subject at a time, this is desired behavior. Figure 2 shows the median Dice scores along with lower and upper quartile ranges for the best performing method in the interval between 10 and 30 interactions, using data for the necrotic, edema, and enhancing region (we left out the nonenhancing region because of very low scores and the whole tumor region to not effectively count the edema twice). The depth of the trees seems to have virtually no influence on the results in the tested range. Performance increases with the number of trees, especially for smaller , but the differences are not statistically significant. While a smaller number of trees speed up the training and prediction, we choose to work with 50 trees and a maximum depth of 10. We utilize the prediction probabilities, which are simply determined by counting votes in the forest, so that a small number of trees essentially round those probabilities to less accurate values. We further use the Gini impurity as a split criterion and look at features in each split.
Fig. 2.
Results of the parameter grid search. We repeated our experiments with different combinations of the number of trees and the maximum depth of the forest. The results here show the median Dice score with boxes extending from lower to upper quartile values for the best performing method MISCLASS-B over the interval from 10 to 30 interactions, taking into consideration data from necrotic, edema, and enhancing regions. The depth of the forest (increasing from left to right in each group) has little influence on the results, while they seem to improve with the number of trees, especially from 10 to 30. However, the differences are not statistically significant.
Note that in our experiments we build an entirely new forest after each new input. There are approaches that do not require rebuilding the forest entirely, making the process much faster. However, these online forests28,29 always try to approximate the results of completely rebuilding the forest, so we chose to not include them as an additional possible source of error.
2.3. User Interactions
Our goal is to simulate experts in an interactive annotation and segmentation process. We want to establish how the expert should interact with the algorithm and whether uncertainty information from the algorithm can be used to guide the user in the process. Because we assume the user to be an expert radiologist, we also assume they are able to see and interact with all three orientations (axial, coronal, and sagittal) as well as all four MRI channels simultaneously. This depends on the implementation; typical medical image viewers use a layout with four views, so one possible configuration—the one we chose—is that the orientations occupy three views (leaving the fourth for arbitrary information) and the users can use hotkeys to cycle through the MRI channels. Alternatively, the user could select a single orientation and view all four channels in parallel. Most importantly, we assume that the experts possess knowledge of the correct segmentation that they wish to transfer onto the image. The basic concept of the iterative segmentation process is that in each step the user sees the current output of the algorithm, ideally as an overlay, to compare it with the underlying data, and then interacts with the algorithm by providing additional training instances.
The interaction process is based on scribble annotations. That means that the user can impaint pixels in the image to label them as belonging to a certain class (note that we use the terms class and label interchangeably), similar to a paintbrush tool found in almost any image editing application. Theoretically, this would allow the user to paint in any way they desire (single disconnected pixels, large round blobs, etc.), but the most common and intuitive way to annotate in such a scenario is by painting lines, or scribbles. The classifier is trained on the labeled pixels and the resulting segmentation is presented to the user so they can add a new input to improve the output.
We deliberately choose to oversample the interaction process by allowing only very short scribbles of 10 connected pixels and by updating the prediction after each scribble annotation. Experienced users usually make multiple annotation scribbles before updating the prediction, especially in the beginning, where the algorithm requires at least some data from all classes for a somewhat reasonable prediction. In our simulation, we skip this initial step by initializing the algorithm with 50 randomly drawn pixels, weighted by class occurrence so that each class receives at least one training instance. (For each class, we count the relative number of pixels belonging to the class and multiply it by 50. The rounded result is the number of pixels we draw randomly from within the class. Should the number be zero, we draw one pixel from the class and in turn draw one fewer from the largest class, which is always the background. The classifier is trained once with these 50 instances after which the simulated interactions start.) We found 50 to be the lowest number of initial training points to achieve a reasonable initialization. The purpose of this step is to skip those interactions in which the classifier does not have knowledge of all classes. All methods use the same set of initial points, of course. We discuss this further in Sec. 3.
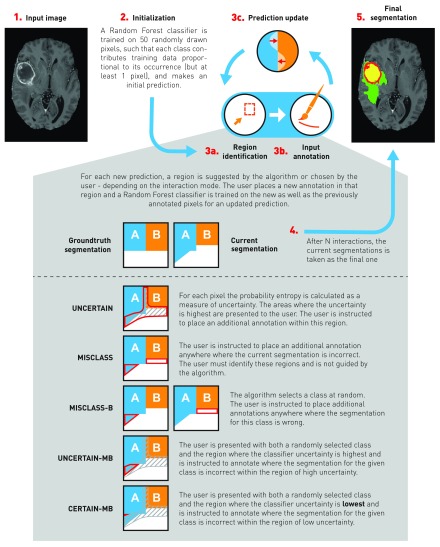
Now that we have established how the users place their annotations, i.e., by painting a small number of connected pixels with the correct label, we come back to the question of where user inputs should be given to create a high-quality segmentation with the least amount of interactions. To this end, we define five interaction modes, each characterized by a region in which the user will place their annotation randomly in each step, based on classifier uncertainty (information the algorithm possesses) or on correctness (information the user possesses). These regions will of course change in each step. Abstract examples for all methods are given in Fig. 3. While the simulated users will generally annotate randomly within a specified region, we place some further constraints on the inputs to make them more realistic. The scribbles, which we fix at a length of 10 pixels, must be connected. They must further be in one of three main planes (axial, sagittal, and coronal). They must lie entirely within the specified region and finally they must not cross classes.
Fig. 3.
Visualization of the interactive annotation process. Starting with the input data (1.), the process is first initialized (2., see Sec. 2.3 for details) to get an initial prediction. Then, the interactive annotation loop begins. Depending on the annotation mode either the algorithm or the user selects a region for annotation (3a.) and annotates randomly within that region (3b.). From there, a new classifier is trained on all annotated pixels for an updated prediction. The process is repeated times, after which the current segmentation (4.) is taken as the final segmentation (5.). For each annotation mode, an exemplary region is shown, in which the simulated user will annotate, based on an abstract groundtruth and corresponding example segmentation. Note that for demonstration purposes there is only low and high uncertainty, and no intermediate region, hence the regions for UNCERTAIN-MB and CERTAIN-MB share a border.
-
1.
UNCERTAIN: Place annotations randomly in regions of high classifier uncertainty. To simulate this, we first divide the uncertainty into five quantiles and keep only the regions belonging the highest quantile. We then find the largest connected region of those and randomly annotate within this region. The dividing into five quantiles might seem somewhat arbitrary, but we empirically found that using the top 20% of the uncertainty still resulted in large enough regions that one could comfortably annotate, while smaller numbers would often yield very small and thin regions that require pixel accuracy annotations. There is certainly room for optimization, perhaps by using an adaptive uncertainty threshold, but we leave this problem for future research.
-
2.
MISCLASS: The user identifies falsely classified regions in the segmentation overlay from the previous step and then randomly annotates anywhere in the entire error region. This implicitly weights classes by occurrence. This method depends on our assumption that the user has knowledge of the correct segmentation and is able to falsely identify classified regions in the segmentation overlay. It does not use uncertainty information.
-
3.
MISCLASS-B: The algorithm chooses a class at random and the user identifies and annotates in falsely classified regions (both false positive and false negative) for that particular class in the segmentation overlay. This weights classes equally. The method also depends on the assumption that the user has knowledge of the correct segmentation and is able to identify falsely classified regions. It does not use uncertainty information.
-
4.
UNCERTAIN-MB: A combination of UNCERTAIN and MISCLASS-B; annotations are placed where the region identified by UNCERTAIN and the error region for a randomly chosen class intersect. Should there be no intersection, ignore uncertainty region, i.e., fall back to MISCLASS-B. This method utilizes both uncertainty and correctness information.
-
5.
CERTAIN-MB: Essentially the same as UNCERTAIN-MB, but now we identify the region where the classifier is most certain, meaning the lowest of five quantiles of the uncertainty. This might seem counterintuitive, but we hypothesize that if the classifier is very certain about an error, the corrective annotation should have a much stronger effect. Again, if there is no intersection, fall back to MISCLASS-B.
To get an idea of how users would annotate intuitively, we let four users (1 to 4 years experience working with glioblastomas) annotate a subset of randomly selected patients. In total, we recorded four separate assessments for each of four different patients, where each rater performed two assessments on a given patient, first with no instructions and then following the UNCERTAIN approach as a comparative baseline. The result for the whole tumor region is shown in Fig. 6 and we will discuss it in Sec. 4. The measure of uncertainty we use is the probability entropy
| (1) |
where is the probability that pixel belongs to class . We also tried confidence and probability margin2 as uncertainty measures, but the results were not meaningfully different. The work presented here uses the probability entropy.
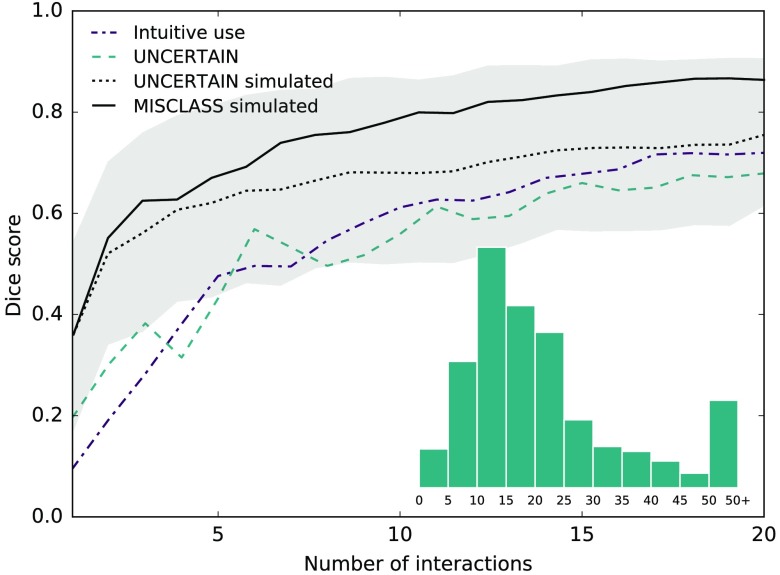
Fig. 6.
Interactions by real human users with between 1 and 4 years experience working with glioblastomas for whole tumor region. Users were first asked to annotate without instructions, then used the UNCERTAIN method in separate runs. For comparison, the simulated UNCERTAIN (along with standard deviation) as well as MISCLASS annotations are given. The latter is methodically most similar to the users’ intuitive approach. Intuitive annotations perform better than annotations in uncertain regions, likely because the majority of annotations users provide are corrective. Overall scores are lower than what was achieved in the simulations, likely because users do not fully satisfy our assumption that they possess knowledge of the correct segmentation. Because the number of data collected from real users was small in number, the comparison to simulated interactions should be understood qualitatively. Inlay: the distribution of scribble lengths.
2.4. Evaluation
We wish to evaluate the quality of the segmentation over time, i.e., as a function of the number of interactions. The de facto standard for segmentation assessment in the medical domain is the Sørensen–Dice coefficient, for two binary segmentations , defined as
| (2) |
It is a binary measure, and in each case, we compute the scores for all classes separately. We also evaluated Jaccard index, precision, and recall but could not find anything that would meaningfully add to our findings, so we elect not to show those results.
For each patient and for each interaction method, we evaluate the Dice scores over the course of 50 interactions. After each interaction step, the classifier is trained on all pixels that were annotated in the current and the previous interactions. We use no training data from other patients or from earlier assessments of the same patient. A prediction is always made on the entire 3-D image volume for the current patient that is then compared with the corresponding groundtruth segmentation. We repeat the process five times for each patient and average the results to suppress random variations, treating the 5-run average as a single measurement. For our first analysis, we then also average the scores for all patients and compare the different interaction methods by means of the Dice score as a function of the number of interactions.
For our second analysis, we do not average scores across patients. We perform a statistical comparison of the methods after 20 interactions. The findings are not very dependent on the evaluation point and after roughly 20 interactions the benefit of additional annotations becomes rather small. For each pair of methods and each region, we use a Wilcoxon signed-rank test30 to find the likelihood that the two sets of measurements (a set of measurements meaning the scores for the 20 different patients of a given method) originate from the same distribution (not all our measurements are normally distributed). We choose a base significance threshold of and apply Bonferroni correction for 50 individual tests (5 regions times 10 comparisons), resulting in an adjusted threshold of . Note that the results are not independent, so the correction is likely stronger than necessary.
3. Results
Figure 1 shows exemplary segmentation results for a single patient (HG0004, axial slice 101) and a randomly chosen run for 30 interactions in steps of 5. For comparison, the groundtruth segmentation and the four base channels (features) are displayed. These results of course are only a single sample from a stochastic process and are not necessarily representative of the overall performance of the approaches. However, a few things can be seen that were similar in the majority of cases. In general, very little training is necessary to get a rough estimate of the desired result (with the exception of CERTAIN-MB in this case). Most later inputs introduce rather small changes and only refine the segmentation. The segmentation does not necessarily improve in each step; in most cases, this is due to considerable changes in the edema region. Finally, there are almost always a number of very small false positive regions dispersed throughout the healthy part of the brain. We will discuss these findings in detail in Sec. 4.
To obtain quantitative results, we simulate the interactive segmentation process 5 times for 20 different patients. Note that the classifier uses only live input annotations for the current subject and does not incorporate knowledge from other patients or earlier assessments. In each step, the training set consists of all pixels annotated by the simulated user and the test set is the remainder of unannotated pixels. The results from the 5 runs are averaged and treated as single measurements.
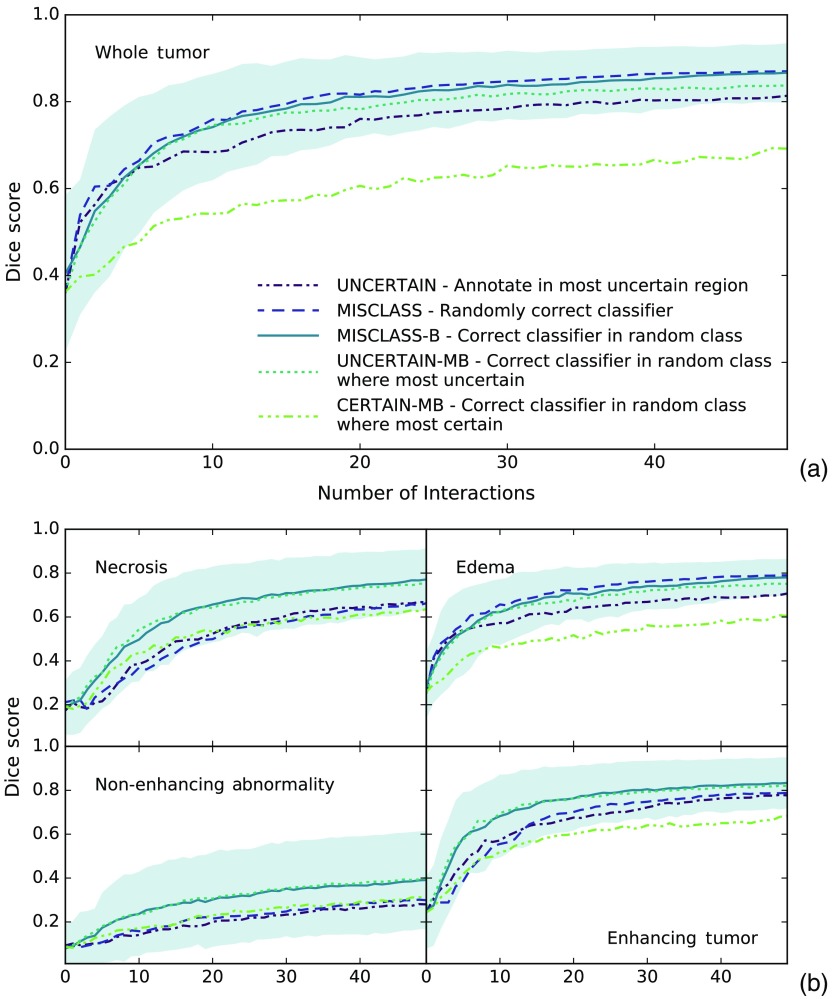
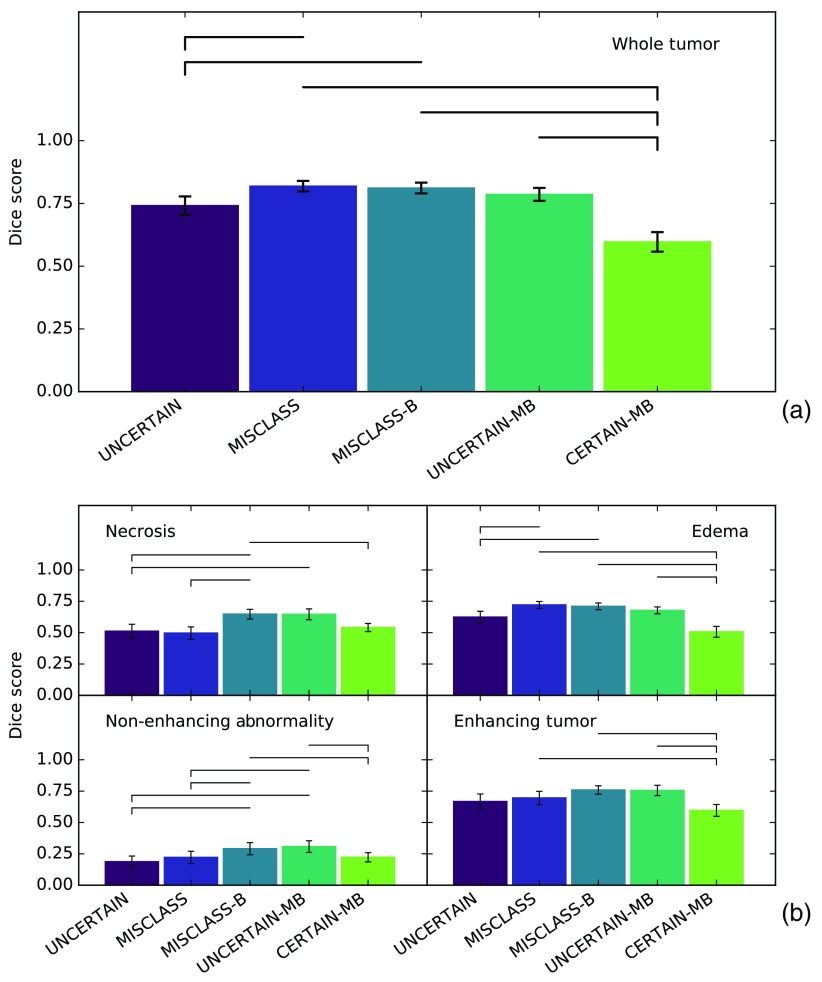
Figure 4 shows the Dice score over time for all methods and tumor classes including the standard deviation of the 5-run patient means for the overall best performing method MISCLASS-B to illustrate how scores vary across different patients. Other methods’ standard deviations are comparable. Figure 5 represents a cross section of Fig. 4 and shows mean Dice scores after 20 interaction cycles for all methods and classes. Highlighted are all pairs of methods with a significant () performance difference. For a full overview of test scores (-values, test statistics, and difference of medians), see Table 1. The section is split into (1) a comparison of annotations in uncertain regions (UNCERTAIN) and corrective annotations (MISCLASS and MISCLASS-B) and (2) a comparison of the best of those methods (MISCLASS-B) with corrective annotations in very uncertain (UNCERTAIN-MB) and very certain (CERTAIN-MB) regions.
Fig. 4.
Dice score as a function of the number of interactions for (a) whole tumor and (b) other tumor regions. Filled area shows standard deviation of patient means for MISCLASS-B to give an estimate of the spread of scores across patients. Standard deviations for other methods are comparable. MISCLASS-B and UNCERTAIN-MB show the overall best performance in all regions. In the larger regions edema and whole tumor, MISCLASS performs similarly, in smaller regions (necrotic core, enhancing, and nonenhancing tumor) MISCLASS and UNCERTAIN perform comparably. CERTAIN-MB is always among the poorest performing methods.
Fig. 5.
Dice score after 20 interaction cycles for (a) whole tumor and (b) other tumor regions. Errors show standard error of the mean. Horizontal bars indicate that for the Wilcoxon signed-rank test of the two methods, with a dash indicating the method with poorer performance. This is essentially a cross section of Fig. 3 after 20 interactions. Again, in the larger regions (edema and whole tumor) MISCLASS, MISCLASS-B, and UNCERTAIN-MB perform comparably while in the other region MISCLASS-B and UNCERTAIN-MB dominate and UNCERTAIN and MISCLASS perform similarly. CERTAIN-MB performs poorly in all regions.
Table 1.
Pairwise comparison of all methods for each tumor region after 20 iterations, using a Wilcoxon signed-rank test and 5-run averages for each patient. Displayed are test statistic and -value results as well as the difference of the medians for each comparison. Highlighted in bold are comparisons where . This threshold is the result of a base significance level of , Bonferroni corrected by 50 individual comparisons.
| Methods | Whole tumor |
Necrosis |
Edema |
Nonenhancing abnormalities |
Enhancing tumor |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| Statistic |
|
Statistic |
|
Statistic |
|
Statistic |
|
Statistic |
|
|
| UNCERTAIN versus MISCLASS | 11 | 101 | 0.881 | 13 | 88 | 0.526 | 81 | 0.370 | ||
| 0.049 | ||||||||||
| UNCERTAIN versus MISCLASS-B | 12 | 12 | 13 | 10 | 45 | 0.025 | ||||
| UNCERTAIN versus UNCERTAIN-MB | 45 | 0.025 | 4 | 58 | 0.079 | 4 | 32 | 0.006 | ||
| UNCERTAIN versus CERTAIN-MB | 19 | 0.001 | 99 | 0.823 | 33 | 0.007 | 45 | 0.025 | 57 | 0.073 |
| 0.150 | 0.100 | 0.114 | ||||||||
| MISCLASS versus MISCLASS-B | 65 | 0.135 | 15 | 62 | 0.108 | 15 | 40 | 0.015 | ||
| 0.031 | 0.015 | |||||||||
| MISCLASS versus UNCERTAIN-MB | 32 | 0.006 | 19 | 0.001 | 36 | 0.010 | 11 | 38 | 0.012 | |
| 0.047 | 0.040 | |||||||||
| MISCLASS versus CERTAIN-MB | 0 | 78 | 0.313 | 0 | 96 | 0.737 | 12 | |||
| 0.222 | 0.138 | 0.129 | ||||||||
| MISCLASS-B versus UNCERTAIN-MB | 30 | 0.005 | 100 | 0.852 | 32 | 0.006 | 84 | 0.433 | 100 | 0.852 |
| 0.016 | 0.025 | |||||||||
| MISCLASS-B versus CERTAIN-MB | 0 | 7 | 0 | 12 | 0 | |||||
| 0.191 | 0.124 | 0.123 | 0.052 | 0.173 | ||||||
| UNCERTAIN-MB versus CERTAIN-MB | 2 | 18 | 0.001 | 1 | 12 | 0 | ||||
| 0.176 | 0.154 | 0.098 | 0.114 | 0.175 | ||||||
3.1. Annotating Uncertain Regions Versus Classifier Correction
In both Figs. 4 and 5, it can be seen that annotations in uncertain regions (UNCERTAIN) perform worse than class-balanced classifier corrections (MISCLASS-B) across all categories and over time, and the difference after 20 interactions is significant in all regions but the enhancing tumor with .
Annotations in uncertain regions (UNCERTAIN) also perform worse than random corrective annotations (MISCLASS) in the whole tumor region and the edema. The difference after 20 interactions is significant for both the whole tumor () and the edema (). Performances are roughly on par in the smaller necrosis, enhancing and nonenhancing regions.
Random classifier corrections (MISCLASS) perform significantly worse than class-balanced corrections (MISCLASS-B) in the necrotic core regions () and the nonenhancing regions (). They also perform worse in the enhancing tumor region but without a significant difference after 20 interactions. In the larger whole tumor and edema regions, both are roughly on par.
3.2. Combination of Uncertainty-Based Annotations and Classifier Correction
As outlined above, MISCLASS-B is among the top performing approaches in all tumor regions. We now compare it with UNCERTAIN-MB and CERTAIN-MB; both methods are designed to work like MISCLASS-B and to additionally incorporate uncertainty information to improve segmentation results. We intentionally leave out the comparison of UNCERTAIN-MB and CERTAIN-MB with MISCLASS and UNCERTAIN.
Figures 4 and 5 show that CERTAIN-MB, the class-balanced corrective annotations in the most certain regions, is always among the poorest performing approaches and performs significantly worse than balanced corrections (MISCLASS-B) as well as balanced corrections in uncertain regions (UNCERTAIN-MB) after 20 interactions across all classes except for the necrotic core, where (but not ) for the comparison between CERTAIN-MB and UNCERTAIN-MB.
Balanced classifier corrections (MISCLASS-B) and the combination of that approach with annotations in uncertain regions (UNCERTAIN-MB) perform similarly well across class with a slight advantage for the former over the latter in the whole tumor and edema regions. However, the difference after 20 interactions is not significant in any of the tissue classes.
We mentioned in Sec. 2.3 that we initialize the algorithm with 50 random training instances, distributed among the classes by their relative occurrence. The purpose of this is to skip the initial steps where the classifier has too little information about a given class and essentially stays constant at 0 or a very low score. This can be seen in Fig. 4 in the necrotic region. The score appears to be at a constant low before increasing quite sharply. Without initialization, this effect would be much more pronounced and visible in all classes. The best final Dice scores out of all methods after 50 interactions for each class are 0.870 for the whole tumor, 0.771 for necrosis, 0.789 for the edema, 0.400 for the nonenhancing abnormalities, and 0.833 for the enhancing tumor.
4. Discussion
In this work, we propose five different methods of providing annotations in the context of online interactive segmentation based on a pixel classifier that receives inputs in the form of annotation scribbles. We compare them with respect to their ability to evoke inputs that let the classifier make faithful predictions with minimal interactive effort. Our analysis is based on a random forest classifier and the challenging task of segmenting multiple glioblastoma tissue classes in magnetic resonance images.
The methods we propose use uncertainty information from the classifier and correctness information from the user. Interactive segmentation based on scribbles is not a new concept and neither is the usage of uncertainty information in interactive segmentation.5,9,10 But to the best of our knowledge, we are the first to compare in this context the merits of inputs in regions of high uncertainty and inputs that correct the classifier. Consequently, we know of no prior work that attempts to combine both in this context.
We recognize that our approach is quite specific in the sense that we tested methods that could be applied to almost any choice of classifier only on a single one, namely a random forest; however, this was motivated by this classifier’s remarkable performance across a multitude of challenges (see Sec. 2.2). Indeed, the final Dice scores we obtain after 50 interactions compare favorably to previously reported results on the same dataset.11,31 It should also be noted that our methodology is such that it does not translate easily to larger datasets, because it requires the user to have knowledge of the full dataset at a given time, so we can only treat a single image volume at once. We further make the assumption that the user knows the correct segmentation and is able to identify falsely classified regions, which is not a trivial assumption for complicated tasks like tumor segmentation. Finally, it should be noted that what we define as uncertainty, i.e., the probability entropy, is not an uncertainty in the Bayesian sense but only a measure of how confident the classifier is in its prediction. In other words, this type of uncertainty tells us how certain the prediction is, given our model, but not how certain we can be that our model is correct. A potential bias of our model would mostly stem from the features we employ, and there is no reasonable way to test if a given combination of model and features is ideal because of the sheer number of possible combinations. There is of course the possibility to perform feature selection on a given set of features to make the representation more efficient, but that was not our goal. We rely on what has worked well in the past and recognize that there might be even better approaches.
We observe that in general the algorithm needs relatively little training data to get a rough estimate of the correct segmentation (especially the whole tumor region) and that most later inputs only refine the segmentation. Interestingly, while the results on average improve over time, this is not necessarily the case for any single experiment. Especially decisions with unclear boundaries, for example the transition from the edema to healthy tissue, can change quite drastically with small changes in the training set. This behavior can be seen in the exemplary results in Fig. 1 for MISCLASS between steps 20 and 25. Note that the classifier finds edema regions throughout the brain. That is because we do not enforce contiguity. Indeed, almost all segmentations have at least some small false positive regions that are not connected to the main tumor. Clearly, our segmentations would benefit from postprocessing to ensure connectedness and to create smoother boundaries, but such a step would be appropriate only after a workflow like the one we present and is hardly feasible in an interactive setting, which is why we intentionally exclude it from our experiments.
Another interesting observation one can make in the examples we present is that the algorithm picks up a patch of necrosis in the center of the tumor, whereas the groundtruth segmentation classifies it as nonenhancing tumor. The two classes have very similar imaging signatures, and judging from the MRI channels, it would be an entirely reasonable decision to classify the patch as necrosis. Evidently, the interactive segmentation workflow can serve to give the user feedback on their perceived correct segmentation. In a comparable setting, this was shown to reduce inter- and intrarater variability.23
We compare the following annotation methods: annotations where the classifier uncertainty is highest (UNCERTAIN), annotations that randomly correct the classifier (MISCLASS), annotations that correct the classifier, but with equal distribution of inputs among classes (MISCLASS-B) as well as balanced corrections in regions of high uncertainty (UNCERTAIN-MB) as well as regions of low uncertainty (CERTAIN-MB). Note that we first compare UNCERTAIN, MISCLASS, and MISCLASS-B, where MISCLASS-B emerges as the best performing approach, and then compare only MISCLASS-B with UNCERTAIN-MB and CERTAIN-MB, neglecting the remaining comparisons.
4.1. Annotating Uncertain Regions Versus Classifier Correction
Comparison of annotations in regions of high classifier uncertainty (UNCERTAIN), random corrective annotations (MISCLASS), and class-balanced corrective annotations (MISCLASS-B) indicates that it is generally preferable to let users annotate falsely classified regions, assuming the user has complete knowledge of the correct segmentation, because MISCLASS-B performs better than UNCERTAIN in all regions and significantly so in all but the enhancing tumor region, whereas MISCLASS performs significantly better than UNCERTAIN in the whole tumor and edema regions. The difference between MISCLASS and MISCLASS-B can be attributed to the fact that the problem is one with a large class imbalance. The edema and whole tumor regions are generally large or not much smaller than the background, and hence are automatically balanced with respect to the background, in which case there is no functional difference between MISCLASS and MISCLASS-B. This is reflected in the results where both exhibit very similar performance in those two classes. In the smaller regions on the other hand, MISCLASS-B performs better (significantly so in the necrotic and the nonenhancing region), because purely random annotations are more likely to miss those regions, resulting in fewer training data from which the classifier can learn to discern them. This will likely hold true for most scenarios with a strong class-imbalance. Note that our findings also suggest that classifier uncertainty and classification error are generally not congruent.
4.2. Combination of Uncertainty-Based Annotations and Classifier Correction
Because MISCLASS-B, the class-balanced corrective annotations, proved to be such a successful approach, we were curious if it could be combined with knowledge about the classifier uncertainty. We had two opposing hypotheses in this regard: either that performing the corrective annotations in the most uncertain regions could boost the performance or, to the contrary, that doing so in the most certain regions could improve the performance, because the corrective effect should be stronger in the latter case. The second idea is clearly refuted by our results as CERTAIN-MB was among the poorest performing approaches for all tissue classes and performed significantly worse than MISCLASS-B and UNCERTAIN-MB across all classes. UNCERTAIN-MB on the other hand performed about as well as MISCLASS-B, but did not improve upon the performance of MISCLASS-B, so that both of our hypotheses can be dismissed. Because of the additional computational cost of computing the uncertainty, it is beneficial to prefer MISCLASS-B over UNCERTAIN-MB.
Out of the publications mentioned in Sec. 1, Konyushkova et al.8 are the only ones who report the Dice score as a function of the number of interactions for a comparable task and we will compare our results with theirs in some detail. Konyushkova et al. apply their geometric uncertainty sampling to the 2012 BraTS challenge data while we use data from the following year. It is not immediately clear what their segmentation objective is, as the 2012 BraTS challenge specifies two tumor categories. We assume the authors just segmented both tumor classes as a union, like the whole tumor category we evaluate. In visual comparison, the curves Konyushkova et al. obtain exhibit the same characteristics as ours, with a steep incline in the beginning that gradually becomes smaller. Interestingly, the methods they compare perform virtually the same for the first 10 interactions up to a Dice score of 0.4, which is exactly the range of scores we skip by providing initial training samples. The authors compare four different query methods, one of which is very similar to UNCERTAIN, as it always selects the most uncertain superpixel for annotation. Not including the first 10 interactions, their method achieves scores of (0.4, 0.5, 0.6, and 0.65) in the first steps of 10 interactions while ours achieves (0.4, 0.65, 0.7, and 0.75) in the same interval (rounded to 0.05 accuracy). Their method seems to asymptotically approach a score of 0.75, ours tends toward 0.8. Their best performing method stays just below 0.8, whereas ours is again at an advantage of about 0.05 points. Note that this comparison is based on a visual assessment of the results of Konyushkova et al. Interestingly, they also report that random sampling results in an almost constant Dice score. We could confirm this, but chose to omit the result, as it is in no way representative of a realistic user.
To get an estimate of how a real user would approach the problem, we let four different users with varying experience (1 to 4 years in the relevant domain) annotate four randomly selected patients, first without instructions (see Fig. 6). Our hypothesis was that users would intuitively tend to a corrective annotation style, but because the individuals cannot all be considered experts, we let them annotate using the UNCERTAIN method as a baseline, as it does not rely on correctness information. Users did indeed annotate in a corrective manner but less pronounced than expected. In total, 79/197 annotations were fully corrective (compared to 54/212 for UNCERTAIN) and 146/197 majority corrective (compared to 116/212 for UNCERTAIN), but of course we cannot assess whether noncorrective annotations were intended to be that way. The strokes users placed were mostly between 10 and 25 pixels in length, so that our simulations are in fact quite realistic in this regard, but this could be due to demonstration bias.
It would be interesting to know how the mistakes our users made correlate with the uncertainty the experts exhibited in the creation of the groundtruth segmentations. Unfortunately, the challenge organizers did not make any predictions available that would allow us to compute actual uncertainties, so we can only get a qualitative estimate of this by creating a consensus map from the four raters’ final segmentations. We assigned every pixel the number of raters that agreed on its label, from 1 (complete disagreement) to 4 (complete agreement) and found that of the errors our raters made intuitively, 30.7% (36.2% for UNCERTAIN) were in regions with full expert agreement, 53.7% (49.8% for UNCERTAIN) where three experts agreed, 15.1% (12.8% for UNCERTAIN) where two experts agreed, and 0.5% (1.2% for UNCERTAIN) where experts disagreed completely. Considering that the groundtruth experts showed full agreement in 98.9% of the images (due to large and unambiguous background classes), it is clear that many of our raters’ mistakes can be explained by an inherent uncertainty in the groundtruth data. This is not surprising as it highlights one of the major challenges in medical image computing: the virtually complete absence of true groundtruth data. We could argue that because using the UNCERTAIN method our raters made fewer mistakes in ambiguous regions, our algorithm’s guidance mitigates this effect to an extent, essentially leading to segmentations that are more consistent with the underlying data, but the data are too few to make a statistically relevant statement about this.
As seen in Fig. 6, intuitive annotations by our raters only showed a slight margin over uncertainty-guided annotations; however, the data we collected are again too few in number to support this finding in a statistically significant manner, which is why we excluded them from Sec. 3. The scores obtained for the UNCERTAIN approach were lower than in our simulation, which is not surprising, as not all our users can be considered experts. Except for the first few interactions, the simulated UNCERTAIN interactions lie well within the standard deviation of the simulated ones; however, we wish to emphasize that this does not imply any statistical meaning. The number of data we collected for real user interactions disallow a rigorous analysis and the comparison is to be understood qualitatively. The same holds for the comparison of the users’ intuitive approach with simulated MISCLASS interactions, which were methodically the most similar to the users’ largely corrective annotations. Here, the difference between simulated and real interactions is even larger than for UNCERTAIN, most likely because users did not exclusively employ corrective annotations. This is, in part, due to the fact that not all users can be considered full experts in the domain and suggests what we would expect to find in a more rigorous real user study: methods that rely solely on correctness information and hence on the user will suffer more strongly if our assumption of perfect expert knowledge is violated. Consequently, we would expect to see a strong decrease in the performance of MISCLASS and MISCLASS-B while UNCERTAIN-MB should be less and UNCERTAIN least affected. That could also mean that for nonexpert users, UNCERTAIN-MB could in fact be the best approach, unlike in our experiments, as we discuss below.
Overall, our simulations showed that correcting the classifier is significantly more efficient than providing inputs where it is uncertain. This is not too surprising; it is easy to imagine that corrections will on average effect stronger change in the model than assertive ones. More surprising was the fact that a combination of both yielded no additional benefit. We assume that corrections will on average happen automatically at points where the classifier is uncertain about its output, which would result in MISCLASS-B and UNCERTAIN-MB performing similarly, which is what we observed. At the same time, we found a significant difference between UNCERTAIN and MISCLASS-B. This would then imply that on average the error regions are a subset of the high uncertainty regions. In the cases we inspected visually, we found most of the error regions to overlap with the uncertainty regions to a large extent but not entirely.
Our findings could give the impression that uncertainty information is virtually useless to query inputs from a user, which would let them stand in contrast to existing literature in the active learning domain. But that is not the case, because we strongly rely on the assumption that the user possesses knowledge of the correct segmentation. If we were to omit this constraint and compare our UNCERTAIN method with completely random annotations, it would fare much better. We tested this, and completely random annotations performed even worse than CERTAIN-MB (in line with the findings by Konyushkova et al.8), obviously because small regions will almost never be annotated. However, it is in no way reasonable to assume that a real user would just place random annotations, which is why we did not include these results.
We chose the probability entropy as a measure of uncertainty mainly because it is very easy to compute. The question remains whether there are other, maybe more complex, measures of uncertainty or ways to query inputs from the user at certain points that would achieve even better results. This is of course the key objective in active learning, where numerous methods to tackle this problem have been proposed (Settles2 gave a good introduction to the different groups of approaches). The ones that formulate most precisely what we want to achieve, like expected model change and expect error reduction, are unfortunately also among the most computationally expensive. We see potential in methods that exploit committees such as the random forest classifier we are using. It might be worth exploring ways to intelligently reweight individual trees based on how well they agree with new inputs and criteria to reject existing and to build new trees. As an additional benefit, this could also speed up the training and prediction steps.
To summarize, we found that interactive semantic segmentation of glioblastoma MRI based on a pixel-wise random forest classifier should be performed such that the user annotations correct the classifier with a roughly equal number of inputs for all tissue classes. This finding will be relevant for any similar problem with a large class imbalance. For problems with a balanced class distribution, it will still be advantageous to prefer corrective annotations over ones where the classifier exhibits high uncertainty. Applications that benefit from these findings are those that seek to create segmentations quickly but with reliability that renders automatic methods inapplicable. The creation of high-quality training data for the latter is one such example. In a clinical setting, interactive segmentation could be used for accurate tumor volumetry and, consequently, for accurate tumor progression monitoring.
It is quite evident that future work with extensive real user studies is necessary to confirm our preliminary findings with real human users as well as the results we obtained in user simulations. It should also be possible to further improve user simulations, for example, by letting the simulated users make erroneous annotations in a frequency similar to real users. This would also allow the exploration of our methods with users of varying skill level, not just experts. Our work should constitute a solid starting point for such investigations.
Biographies
Jens Petersen is a PhD candidate at the Department of Neuroradiology, Heidelberg University Hospital, as well as the Medical Image Computing Junior Group, German Cancer Research Center (DKFZ), Heidelberg, Germany. Having studied physics in Heidelberg, Madrid, and London, his research now focuses on the application of machine learning methods for medical image understanding, especially brain tumor segmentation.
Martin Bendszus is a professor of neuroradiology and medical director and chairman of the Department of Neuroradiology at Heidelberg University Hospital. He has received numerous national and international awards for his work on innovative imaging techniques, especially in MRI and MR neurography.
Jürgen Debus is the director of the National Center for Tumor Diseases, Heidelberg, Germany, the managing director of the Department of Radiation Oncology at Heidelberg University Hospital, the director of the Heidelberg Ion-Beam Therapy Center, and the director of the Heidelberg Institute of Radiation Oncology. He further leads the Clinical Cooperation Unit Radiation Oncology, DKFZ, Heidelberg, Germany, and is internationally renowned for his research in radiation oncology and radiation therapy.
Sabine Heiland is a professor at the Department of Neuroradiology and leader of the department’s section for experimental radiology at Heidelberg University Hospital. Her research interests include the development of techniques for functional and quantitative MRI, diffusion and perfusion MRI, and contrast agents for MRI and CT.
Klaus H. Maier-Hein leads the Medical Image Computing Junior Group, DKFZ, Heidelberg, Germany. He is an expert in radiologic data science and his research addresses today’s vast unexploited potential of medical imaging data, focusing on algorithmic and infrastructural advances in automated image processing including semantic segmentation, abnormality detection, and image-based quantitative phenotyping (i.e., “radiomics”).
Disclosures
The authors have no conflicts of interest to declare.
References
- 1.Litjens G., et al. , “A survey on deep learning in medical image analysis,” Med. Image Anal. 42, 60–88 (2017). 10.1016/j.media.2017.07.005 [DOI] [PubMed] [Google Scholar]
- 2.Settles B., “Active learning literature survey,” Technical Report 1648, University of Wisconsin, Madison: (2010). [Google Scholar]
- 3.Vijayanarasimhan S., Grauman K., “What’s it going to cost you?: predicting effort vs. informativeness for multi-label image annotations,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR ’09), pp. 2262–2269 (2009). 10.1109/CVPR.2009.5206705 [DOI] [Google Scholar]
- 4.Vezhnevets A., Buhmann J. M., Ferrari V., “Active learning for semantic segmentation with expected change,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR ’12), pp. 3162–3169 (2012). 10.1109/CVPR.2012.6248050 [DOI] [Google Scholar]
- 5.Triebel R., et al. , “Active online learning for interactive segmentation using sparse Gaussian processes,” in German Conf. on Pattern Recognition, pp. 641–652 (2014). [Google Scholar]
- 6.Top A., Hamarneh G., Abugharbieh R., “Spotlight: automated confidence-based user guidance for increasing efficiency in interactive 3D image segmentation,” in MCV: Int. MICCAI Workshop on Medical Computer Vision, pp. 204–213 (2010). [Google Scholar]
- 7.Top A., Hamarneh G., Abugharbieh R., “Active learning for interactive 3D image segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 603–610 (2011). [DOI] [PubMed] [Google Scholar]
- 8.Konyushkova K., Sznitman R., Fua P., “Introducing geometry in active learning for image segmentation,” in Proc. IEEE Int. Conf. on Computer Vision, pp. 2974–2982 (2015). [Google Scholar]
- 9.Maiora J., Ayerdi B., Graa M., “Random forest active learning for AAA thrombus segmentation in computed tomography angiography images,” Neurocomputing 126, 71–77 (2014). 10.1016/j.neucom.2013.01.051 [DOI] [Google Scholar]
- 10.Chyzhyk D., et al. , “An active learning approach for stroke lesion segmentation on multimodal MRI data,” Neurocomputing 150, 26–36 (2015). 10.1016/j.neucom.2014.01.077 [DOI] [Google Scholar]
- 11.Menze B. H., et al. , “The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE Trans. Med. Imaging 34(10), 1993–2024 (2015). 10.1109/TMI.2014.2377694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fernandez-Delgado M., et al. , “Do we need hundreds of classifiers to solve real world classification problems?” J. Mach. Learn. Res. 15(1), 3133–3181 (2014). [Google Scholar]
- 13.Zikic D., et al. , “Decision forests for tissue-specific segmentation of high-grade gliomas in multi-channel MR,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 369–376 (2012). [DOI] [PubMed] [Google Scholar]
- 14.Bauer S., et al. , “A survey of MRI-based medical image analysis for brain tumor studies,” Phys. Med. Biol. 58(13), R97–R129 (2013). 10.1088/0031-9155/58/13/R97 [DOI] [PubMed] [Google Scholar]
- 15.Kleesiek J., et al. , “Ilastik for multi-modal brain tumor segmentation,” in Proc. MICCAI-BRATS, pp. 12–17 (2014). [Google Scholar]
- 16.Goetz M., et al. , “DALSA: domain adaptation for supervised learning from sparsely annotated MR images,” IEEE Trans. Med. Imaging 35(1), 184–196 (2016). 10.1109/TMI.2015.2463078 [DOI] [PubMed] [Google Scholar]
- 17.Sommer C., et al. , “ilastik: interactive learning and segmentation toolkit,” in IEEE Int. Symp. on Biomedical Imaging: From Nano to Macro, pp. 230–233 (2011). 10.1109/ISBI.2011.5872394 [DOI] [Google Scholar]
- 18.Petersen J., “Processed BraTS 2013 HG data,” Data set, Zenodo (2017). 10.5281/zenodo.239084 [DOI]
- 19.Petersen J., “BraTS 2013 HG groundtruth,” Data set, Zenodo (2017). 10.5281/zenodo.274914 [DOI]
- 20.Petersen J., “jenspetersen/2017_JMI-v1.1,” Repository, Github (2017). 10.5281/zenodo.595810 [DOI]
- 21.Ellingson B. M., et al. , “Recurrent glioblastoma treated with bevacizumab: contrast-enhanced t1-weighted subtraction maps improve tumor delineation and aid prediction of survival in a multicenter clinical trial,” Radiology 271(1), 200–210 (2014). 10.1148/radiol.13131305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fedorov A., et al. , “3D slicer as an image computing platform for the quantitative imaging network,” Magn. Reson. Imaging 30(9), 1323–1341 (2012). 10.1016/j.mri.2012.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kleesiek J., et al. , “Virtual raters for reproducible and objective assessments in radiology,” Sci. Rep. 6, 25007 (2016). 10.1038/srep25007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kontschieder P., et al. , “GeoF: geodesic forests for learning coupled predictors,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), pp. 65–72 (2013). [Google Scholar]
- 25.Breiman L., “Random forests,” Mach. Learn. 45(1), 5–32 (2001). 10.1023/A:1010933404324 [DOI] [Google Scholar]
- 26.Petersen J., et al. , “A software application for interactive medical image segmentation with active user guidance,” in Proc. MICCAI-IMIC, pp. 70–77 (2016). [Google Scholar]
- 27.Hastie T., Tibshirani R., Friedman J., The Elements of Statistical Learning, Springer Series in Statistics, Springer, New York: (2009). [Google Scholar]
- 28.Wang G., et al. , “Dynamically balanced online random forests for interactive scribble-based segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, pp. 352–360 (2016). [Google Scholar]
- 29.Saffari A., et al. , “On-line random forests,” in IEEE 12th Int. Conf. on Computer Vision Workshops (ICCV Workshops), pp. 1393–1400 (2009). 10.1109/ICCVW.2009.5457447 [DOI] [Google Scholar]
- 30.Wilcoxon F., “Individual comparisons by ranking methods,” Biom. Bull. 1(6), 80–83 (1945). 10.2307/3001968 [DOI] [Google Scholar]
- 31.Pereira S., et al. , “Brain tumor segmentation using convolutional neural networks in MRI images,” IEEE Trans. Med. Imaging 35(5), 1240–1251 (2016). 10.1109/TMI.2016.2538465 [DOI] [PubMed] [Google Scholar]