Mechanics of Fluid-Filled Interstitial Gaps. I. Modeling Gaps in a Compact Tissue

Abstract

Fluid-filled interstitial gaps are a common feature of compact tissues held together by cell-cell adhesion. Although such gaps can in principle be the result of weak, incomplete cell attachment, adhesion is usually too strong for this to occur. Using a mechanical model of tissue cohesion, we show that, instead, a combination of local prevention of cell adhesion at three-cell junctions by fluidlike extracellular material and a reduction of cortical tension at the gap surface are sufficient to generate stable gaps. The size and shape of these interstitial gaps depends on the mechanical tensions between cells and at gap surfaces, and on the difference between intracellular and interstitial pressures that is related to the volume of the interstitial fluid. As a consequence of the dependence on tension/tension ratios, the presence of gaps does not depend on the absolute strength of cell adhesion, and similar gaps are predicted to occur in tissues of widely differing cohesion. Tissue mechanical parameters can also vary within and between cells of a given tissue, generating asymmetrical gaps. Within limits, these can be approximated by symmetrical gaps.

Introduction

The extracellular compartment is a significant determinant of tissue architecture. In sparsely populated mesenchymal tissues such as tendon, cartilage, or bone, cells are individually suspended in a self-supporting extracellular matrix (ECM) scaffold (1). By contrast, in many compact tissues such as multilayered epithelia, carcinoid tumors, or vertebrate embryonic primordia, cohesion is based on cell-cell adhesion (2, 3, 4, 5). In these tissues, interstitial space can nevertheless be present between cells, to support fluid balance, fluid transport, and diffusional transport of extracellular factors such as signaling molecules (6). Interstitial gaps vary in size, shape, and content, but often a liquid phase dominates, e.g., in the form of capillary exudate or a hyaluronan-rich fluid (6, 7, 8, 9).

In this article, we examine the tissue mechanical conditions for the formation of fluid-based interstitial gaps. We apply a concept of cell-cell adhesion that is based on the notion that the modulation of cell cortex contractile tension is an essential feature of adhesion, and that tissue surface tension is a measure of adhesion strength (10, 11, 12, 13, 14, 15, 16). This concept is well suited to model compact tissues and to predict basic features of interstitial gaps. To gain an initial understanding of gap mechanics, we first establish relationships among cortical tensions, intracellular pressure, interstitial pressure, gap size, and gap shape by analyzing uniform conditions and regular cell geometries where tensions and pressures at gaps are at equilibrium. We then explore the possible effects of tension and pressure variability on gap geometry, as cell-level fluctuations of tensions are essential for the liquidlike behavior of tissues (12, 17). In an accompanying article, we apply the theoretical model to characterize interstitial gaps in the Xenopus gastrula ectoderm. Together, our studies introduce an approach to analyze the maintenance of interstitial space in the context of basic mechanical properties of a tissue.

Methods

3D construction of the gap network

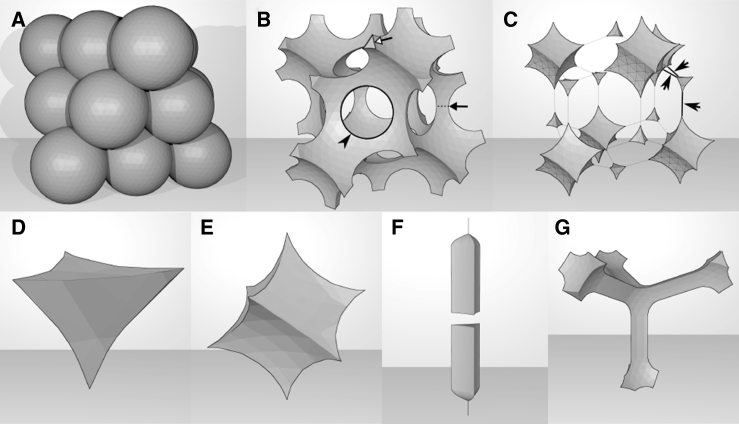
To visualize the gap network, icospheres were created and arranged in face-centered cubic (fcc) packing and then a convex hull polyhedron of the arranged icospheres was created. The Boolean difference between this polyhedron and the arranged icospheres was taken, resulting in a continuous network of gaps. A channel network (Fig. 2 G) was produced by connecting the vertices of the necks of tetrahedral lacunae such as those found in Fig. 2 B (open arrow) with channel segments. The surface curvatures of the models in Fig. 2, F and G, are approximations of gap shapes, not mathematically precise models based on a set of parameters. All modeling was done using the open-source 3D modeling software Blender (Blender Foundation, Amsterdam, Netherlands). The icospheres were four times subdivided and consisted of 1280 faces.

Figure 2.

Geometry of the interstitial space. We refer to the space between cells of a tissue as interstitium, and to its various elements as gaps, whether in 3D form or as their 2D representations, as seen in histological sections. In cell aggregates, gaps can in principle be due to the incomplete attachment of cells. An example is derived from the fcc packing of spherical cells (A), which leaves a continuous network of gaps (B) if attachments remain restricted to small circular contact areas (arrowhead). Two types of larger gap regions, the lacunae, are formed—tetrahedral lacunae (D) and cuboidal lacunae (E). These are connected in alternating fashion. We refer to the narrowest cross section of the connections as the neck (B, arrow). All necks are triangular with cusp-shaped corners (B, open arrow) and of identical size. When attachment is increased, contact areas eventually fuse, and lacunae can become isolated (C). However, insertion of fluid at cell edges generates channel segments (F) that eventually, given sufficient fluid volume, connect to form a channel network (C, arrows; G). Channels run along edges at three-cell junctions, are straight, have identical cross sections along their length, and connect lacunae (ECM fluid in a tissue of high relative adhesiveness).

Computation of asymmetrical gap sizes

Simulations of asymmetric, and symmetric gaps were created by determining the intersection of three circles, using the software Python (https://www.python.org/). Each circle consisted of 360 points and initially touched the other two at a point. Circles were then shifted to variably overlap, and the angles between each intersecting pair of circles as well as the arc lengths of the circle segments corresponding to gap sides were determined. One circle of a triplet was assigned a radius of 1.0 whereas the other two radii ranged in nine steps from 0.8 to 1.2. The distance between the origins of each circle was permitted to range from the sum of the respective radii (circles touching at a point) to the radius of the larger circle plus half the radius of the smaller circle. This range was also divided into nine equal steps to generate a set of distances between circles. Each individual configuration of circles generated was checked to remove any incorrect gaps that might have been produced due to the discrete nature and limited resolution of the circle creation step. A total of 55,095 configurations remained (93.3%) after removal of incorrect circle configurations.

Results and Discussion

Modeling a cell-cell adhesion-based tissue

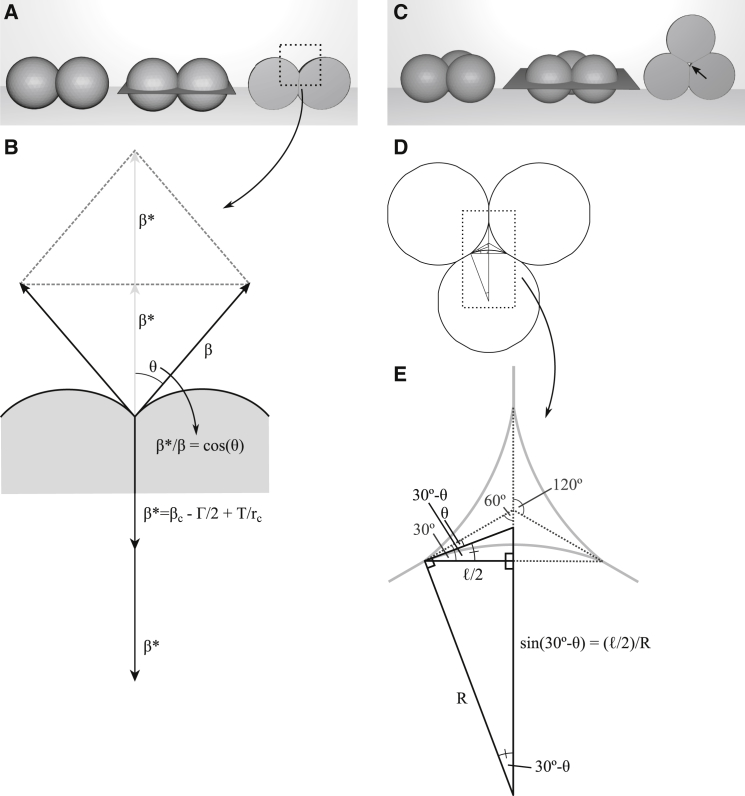
To model tissues whose cohesion depends on cell-cell adhesion, we build on the recent insight that the modulation of cell cortex contractile tension is an essential feature of adhesion (10, 11, 12, 13, 14, 15, 16). When isolated, cells of a tissue are spherical due to cortical tension β. Upon contact (Fig. 1 A), the cortical tension β of each cell is reduced to a residual tension β^∗ per cell in the contact area. At equilibrium, the contact angle θ between cells is related to the tensions as β^∗/β = cosθ (Fig. 1 B). The reduction of tension at cell contacts is in part due to the release of binding energy as cell surface adhesion molecules interact. This generates an adhesion tension Γ that counters cortex contraction (Fig. 1 B). However, it turned out that Γ is by far too small to account for the degree of cell-cell attachment seen in tissues (reviewed in (10, 16)), and cortical tension itself has to be reduced, from β at the free surface to β_c in the contact area (Fig. 1 B). The normal component of a positive line tension T at the periphery of the contact area may increase β^∗ by T/r_c, where r_c is the radius of the contact area (Fig. 1 B; see Appendix A: Symbols and Their Definitions for a list of symbols).

Figure 1.

Mechanics of cell-cell adhesion. (A) Two adherent cells modeled as intersecting spheres (left) are cleaved through their centers (middle) and shown with the cleaved aspect en-face (right). (B) A closeup of the boxed region in (A) shows tensions at equilibrium. The contact angle θ and tensions at the free surface, β, and at cell contacts, β^∗, are related as β^∗/β = cos(θ). Cortical tension at contacts β_c, adhesion tension Γ/2 and line tension T contribute to β^∗. (C) Between three adherent cells, a gap will be present when attachment is incomplete. When cells are cleaved through their centers, the gap (arrow) is at its narrowest. (D) Shown here is a schematic of this neck region from (C). (E) A closeup of the boxed region in (D) shows the relation between gap side length ℓ, radius of curvature R, and contact angle θ. Three right-angled triangles can be construed (bold lines), the largest one being composed of a smaller and a larger triangle. From the latter, the relation (ℓ/2)/R = sin(30°−θ) can be read off, which relates gap size to contact angle and to the radius of curvature of the gap surface.

Compact tissues are composed of cells adhering mutually in this manner (Fig. 2). Intuitively, the presence of gaps in such a tissue is expected to depend on the strength of adhesion between its cells, and tissue surface tension σ is an appropriate measure of adhesion strength (16, 18). It denotes the surface free energy per unit area of liquid-like tissues, and it is linked to the tensions, or surface free energies, at the cellular level by σ ≈ β–β^∗. In other words, adhesion strength is determined by the tension at the free surfaces of cells and by the degree of its reduction at cell-cell contacts (11, 15, 16). Measured tissue surface tensions and hence adhesion strength levels span an enormous, 1000-fold range (12, 16). Because often only the ratios of tensions are relevant, it is convenient to define a relative adhesiveness α as the tension reduction at contacts relative to the free surface cortical tension: α = (β–β^∗)/β (12). This allows us to write tissue surface tension as σ = αβ, with 0 ≤ α ≤ 1. Because α = 1 – (β^∗/β) = 1 – cos(θ), the relative adhesiveness α is given with the contact angle θ, i.e., the dimensionless number α confers both a physical and a geometrical meaning.

A continuous network of interstitial gaps at low relative adhesiveness α

Intuitively, interstitial gaps remain between aggregating cells when adhesion is weak and cell-cell attachment is incomplete, i.e., when α is sufficiently low (Fig. 2). Fragments of cell-cell adhesion-based tissues typically develop smooth surfaces with large contact angles θ. For such tissues, α-values of 0.6–0.8 were calculated from contact angle measurements, while interstitial gaps were regularly present (12). To see whether this empirically determined range of α-values is compatible with gaps due to incomplete attachment, or whether different mechanisms of gap maintenance must be assumed, we estimated critical values of α above which gaps begin to disappear. We first asked at what value of α the continuous network of interstitial channels begins to fragment into isolated lacunae (Fig. 2 B and C).

To examine the relationship between adhesion strength and the presence of interstitial gaps, we consider three identical, spherical, close-packed cells (Fig. 1 C). For β^∗ = β, the relative adhesiveness α = 0, i.e., adhesion is lacking and the three cells touch at points. If adhesion tension Γ alone were to mediate attachment, contacts would remain practically pointlike due to the low values of Γ. However, if cortical tension is also decreased in the contact area, β^∗ can be reduced noticeably (see above), and therefore the contact area between each pair of cells as well as α increases. As a result, the gap between the three cells shrinks until it is eventually occluded.

The gap is narrowest in the plane through the cell centers. In cross section, this neck region (Fig. 2 B) is cusp-shaped (Fig. 1 D), and the distance between two corners, the side length ℓ, is a measure of gap size (Fig. 1 E). Surfaces outside cell-cell contacts exhibit spherical curvatures due to a uniform pressure in all cells, and the curvature is identical on all free surfaces in the three-cell aggregate. Because cells are slightly deformed by mutual attachment, we replace the radius r of isolated cells by the radius of curvature R when calculating ℓ. All contact angles are also identical at equilibrium, and the cross section of the configuration corresponds to intersecting circles with threefold rotational symmetry around the central axis of the gap (Fig. 1 D). In the center of a gap, the virtual extensions of the cell-cell boundaries meet at 120°, and a right-angled triangle (smaller black triangle in Fig. 1 E) can be construed with angles of 90°, 30° − θ, and 60° + θ (Fig. 1 E). It is geometrically similar to the larger black triangle, for which (ℓ/2)/R = sin(30°−θ) or

$$\ell /R=\text{cos}\left(\theta \right)-{\left(3\right)}^{1/2}\text{sin}\left(\theta \right).$$ (1a)

Using $\text{cos}\left(\theta \right)=1-\alpha$ to relate this geometrical result to the relative adhesion strength,

$$\ell /R=1-\alpha -{\left(3\right)}^{1/2}{\left(2\alpha -{\alpha }^2\right)}^{1/2}.$$ (1b)

Neck size is maximal in the absence of adhesion at α = 0, when R = r and ℓ = r, i.e., ℓ equals the radius r of an isolated cell. Gaps then form a network of channels and lacunae continuous with the outside even when multiple three-cell units are arranged most densely in an fcc packing arrangement (Fig. 2). With increasing α, R increases slightly as cells of constant volume are deformed, and gap size decreases, until the areas of contact between cells touch and ℓ vanishes at the threshold α_t = 0.134, equivalent to a contact angle θ_t = 30°. At this threshold, gaps become occluded at necks, but are present above and below. Below this threshold, small tetrahedral and large cuboidal lacunae are all connected by channels passing through three-cell configurations (Fig. 2), but with their occlusion at α_t, the network breaks up into isolated lacunae. In random close packings, close three-cell configurations occur and their occlusion will disrupt the channel network. Fragmentation will be less regular, however, as four-sided necks are also present at channels passing between four cells arranged in a plane; these necks will require a higher α for occlusion.

Disappearance of isolated gap fragments with increasing relative adhesiveness α

The value α_t is much smaller than the observed relative adhesiveness of tissues, but although gaps start to disappear at this threshold, isolated fragments are still present even at fcc packing. To see how these remaining fragments disappear with further increases of α, we express the size of the contact area between adjacent cells as a function of relative adhesiveness. Given an uninterrupted network of interstitial channels that is continuous with the outside, the interstitial pressure p_i must not differ from the reference pressure p_o = 0 outside the tissue. However, when lacunae become isolated with increasing adhesiveness, their interstitial pressure can differ. To explore the general effects of further increases in adhesiveness, we discuss here the simple case where p_i = 0 and where the cell surfaces at lacunae continue to behave like free cell surfaces.

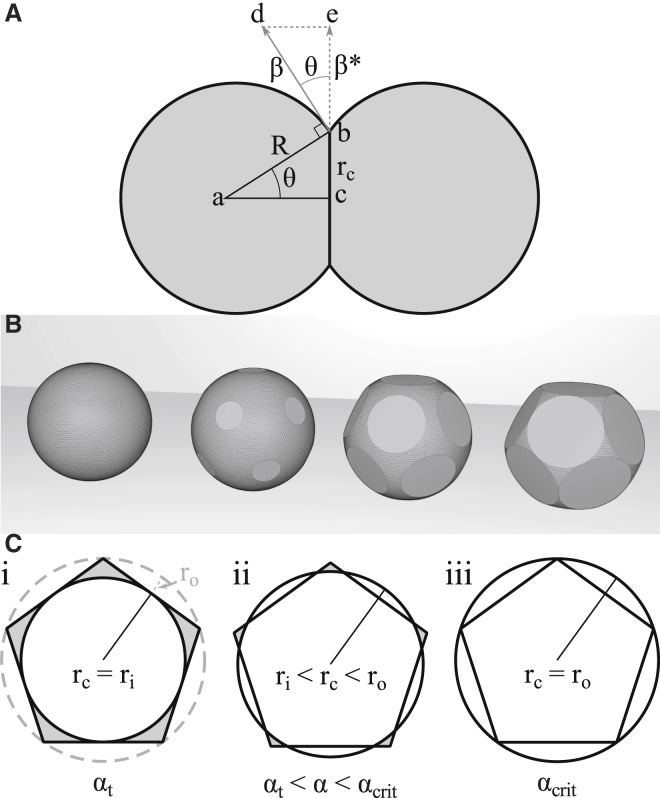
To obtain the contact area A of cells with radius r and radius of curvature R ≈ r during its initial increase, we replace the contact area radius r_c in A = πr_c² with r_c ≈ r sin(θ) by using the fact that θ occurs in two similar triangles in Fig. 3 A. With (sin)²θ = 1 – cos²(θ) and α = 1 – cos(θ), we obtain r_c² = r²(2 α – α²) and eventually,

$$A=\pi r^2\left(2\alpha -{\alpha }^2\right).$$ (2)

Figure 3.

Cell-cell and cell-interstitium surfaces at different degrees of low relative adhesiveness. (A) Contact area A = πr_c² of a pair of cells can be determined from the contact angle θ. The radius of the contact area can be calculated from the right-angled triangle abc, which is geometrically similar to the triangle bde formed by the contact angle and associated tensions. (B) Given here is a 3D visualization of the surface geometry of a cell in a low relative adhesiveness tissue with 12 evenly spaced neighbors, as relative adhesiveness progresses from α = 0 to α = α_t. At α = 0, cells are spherical (left). At relative adhesiveness 0 < α < α_t, contact areas remain circular and separate from one another (middle). At α = α_t, contact areas touch at points, thereby isolating the interstitial lacunae from each other (right). (C) As the radius of the contact surface (r_c) progresses from the in-radius r_i of a pentagon to the circumradius r_o of that pentagon, the surface exposed to the interstitial space (gray) shrinks, gradually transforming the contact surface from a circle into a pentagon at the critical relative adhesiveness α_crit.

Several such circular contact areas are present on each cell of an aggregate, and at small α, contact areas are isolated from each other (Fig. 3 B). As area size increases, contact areas eventually fuse completely to form the sides of a polyhedron. The critical relative adhesiveness α_crit at which this occurs depends on the type of cell packing. For an fcc packing of cells, the number of contacts per cell is 12. To estimate the magnitude of α_crit using a simpler geometry, we approximated the eventual contact areas at full attachment by 12 regular equally sized pentagons (Fig. 3 C), which together form a dodecahedron.

With increasing α, the circular contact area within a putative pentagon increases until it touches the sides of the pentagon at θ_t = 30° (α_t ≈ 0.134) and the radius r_c of the contact equals the in-radius r_i of the pentagon (Fig. 3 C i). Areas within the pentagon, but outside the circular contact area, correspond to surfaces delineating persisting gaps. A further increase of α expands the contact area into these free surfaces (Fig. 3 C ii). Eventually, gaps will have disappeared when the virtual contact area encircles the pentagon with a circumradius r_o (Fig. 3 C iii). In-radius and circumradius are related as r_o/r_i = 1.236 and hence areas A_o/A_i = 1.529. Using Eq. 2 with α_t = 0.134, we obtain A_i = πr²/4, and from A_o = 1.529 (πr²/4) = πr²(2α_crit – α_crit²) we calculate the critical adhesiveness α_crit = 0.214, which corresponds to θ_crit = 38°.

A condition p_i ≈ 0, as assumed here, could be generated by fluctuations in gap size over time (see accompanying article) that intermittently connect the interstitium to the outside and thus tend to equalize pressures. Increased pressure in well-isolated lacunae would increase their size, raising the threshold for their disappearance. Moreover, regular dodecahedra with 12 pentagonal faces are not space-filling, and tissue geometries are in fact more irregular. For example, they may be modeled as random foams, where the average number of contacts per cell is 13.4 (19). Here, pentagons constitute ∼70% of faces, but rectangles (10%) and hexagons (20%) are also present (20), and the above derivation of α_crit is sensitive to contact area shape. When we replaced a pentagon by a square of the same side length, we obtained α_crit = 0.293. Hexagons deviate less from a circle than pentagons, and the corresponding α_crit is lower. As another confounding factor, polygons will be irregular, and for the same polygon area, r_c will be larger in an irregular polygon, increasing α_crit. Overall, in random foamlike tissues, gaps will start to become fragmented at α_t = 0.134; a large fraction of the residual gap fragments should have completely disappeared above α_crit ≈ 0.214, and probably most above α_crit ≈ 0.293. In tissue sections, this should become apparent as an absence of gaps at most three-cell junctions. Because the relative adhesiveness α in tissues is two- to threefold higher than 0.293 (12), the presence of abundant gaps in such high-α tissues needs to be explained by a different mechanism, as detailed in the following sections.

It should be stressed that the presence and size of gaps due to incomplete attachment of cells depends on the relative adhesiveness α of cells in a tissue, not on the absolute strength of adhesion as expressed by tissue surface tension σ. If the cortical tension of cells is relatively weakly reduced upon contact, gaps should remain regardless of the initial magnitude of this tension and the final absolute adhesion strength attained. Whether low-α tissues actually exist in organisms or can be generated only experimentally remains to be seen. At any rate, controlling absolute adhesion strength and relative adhesiveness independently should be useful when engineering artificial tissues of desired mechanical strengths and interstitial permeabilities.

ECM fluid in a tissue of high relative adhesiveness

In the previous sections, we assumed that the surface of gaps behaved like the free, noncontacting surface of cells as encountered in cell pairs or on the surface of aggregates, i.e., that cortical tension at gap cell surfaces was β whereas the residual tension at contacts was β^∗ per cell. To explain the existence of stable gaps in high-adhesiveness tissues, we consider now the possibility that the free cell surface at gaps within a tissue assumes a value β_i that differs from β. This notion is motivated by empirical observations described in the accompanying article.

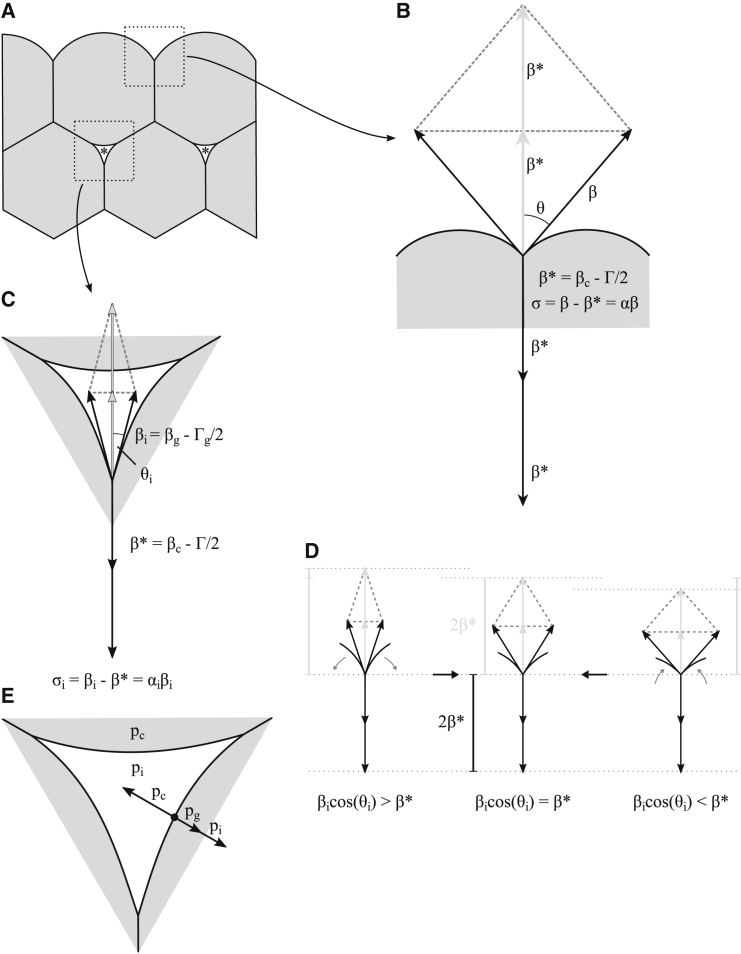
To understand how interstitial gaps can be generated in this way, we considered the possible effects of a small volume of liquidlike ECM inserted at a three-cell junction between cells. The presence of this fluid would locally separate the membranes of adjacent cells, allowing the newly formed free cell surfaces to assume a new tension β_i. Here we are not concerned with the work required for the initial separation, but with the new force equilibrium attained. At equilibrium, the contact angle and the curvature of the gap surface determine the cross-sectional size of such a gap, with the curvature being such that it balances the pressure difference between the gap and the cell interior (Fig. 4). Importantly, although the interstitial pressure p_i influences the shape and size of the gap (see the following section), we do not propose that an increased p_i is necessary to generate gaps. Even at p_i = 0 (i.e., when the interstitial pressure equals the pressure outside the tissue), locally isolating the three cells to allow them to assume tension β_i at their free surfaces is sufficient to generate an equilibrium state consistent with the presence of a gap (Fig. 4).

Figure 4.

Mechanics of fluid-filled interstitial gaps in cell-cell adhesion-based tissues. (A) Cross section of a basic model of a tissue is given. Interstitial spaces appear as three-sided gaps (asterisks). (B) Mechanics of cell-cell adhesion at the tissue surface is shown. The contact angle θ characterizes tension ratios at equilibrium. The cortical tension at the free cell surface (β) balances the tensile forces at the contact surface (β^∗). The difference between these tensions corresponds to the tissue surface tension σ. (C) Mechanical equilibrium at interstitial gaps is analogous to that at the tissue surface. The reduced tension β^∗ is equal to the tensile forces at the contact surface β_c minus the adhesion tension Γ/2. Analogously, the cortical tension at the gap surface β_g may be reduced by adhesive tension Γ_g/2 due to the adsorption of ECM molecules, resulting in a tension at the interstitial surface β_i. At equilibrium, an internal contact angle θ_i is defined. (D) Stability of gaps is shown. Tensions are drawn as in (C). When two free cell membranes at a gap at equilibrium (middle) zipper up (right), the contact angle increases and the resultant tension from the remaining free cell surfaces decreases (compare upper dashed lines). It no longer balances the reduced tension at cell-cell contacts, and the net tension shrinks the cell-cell contact to restore equilibrium. If the two membranes are peeled apart (left), a net tension (compare dashed lines) acts in the opposite direction. (E) Shown here is the role of hydrostatic pressures in determining the shape of the interstitial gaps. The hydrostatic pressure of a cell (p_c) exerts a force pointing into the interstitial space, which is counteracted by a force due to the interstitial pressure (p_i) as well as a force due to pressure generated by the contraction of the cortical cytoskeleton underneath the gap surface (p_g). Together, these pressures determine the radius of curvature at the gap surface at equilibrium.

In this way, a sufficiently large volume of ECM fluid can generate a channel segment whose cross-sectional shape and size is fixed along its length, as the same equilibrium conditions apply at all levels. Adding fluid volume increases the length of the segment, but not its cross-sectional size (Fig. 2 F). Thus, channel segments no longer fan out from narrow necks. The shape of cell edges in ectodermal tissue, examined in the accompanying article, is consistent with this conclusion (21). With increasing overall volume of ECM fluid in the tissue, individual channel segments will eventually fuse into a continuous interstitial network (Fig. 2 G). Channel cross sections are representatives of the interstitial space that will be met most frequently in histological sections, and in the following, we study regular gaps with threefold rotational symmetry, i.e., channel cross sections whose three contact angles and three radii of curvature are all identical (Fig. 4, A, C, and E). We do not model the shape and size of the lacunae at four-cell vertices, but we assume that Laplace’s law ensures that a constant mean curvature is maintained.

To derive the conditions for stable gaps, we consider that at gaps, the tension per cell at cell-cell contacts, β^∗, is replaced by tension β_i at the cell-gap interface such that at the tissue surface σ = β–β^∗ and within the tissue the adhesion strength at gaps σ_i = β_i – β^∗ = α_iβ_i. Further, at the tissue surface β^∗ = β_c – Γ/2 (Fig. 4, B and C). Note that for the contribution of the line tension T, the contact area radius of cell pairs r_c has to be replaced by approximately the radius of curvature of the tissue surface. Because this radius will typically be much larger than r_c, we neglect line tension effects normal to tissue surfaces. Moreover, as the edges of gap segments are straight, the contribution of any line tension to the force equilibrium for gap cross sections also vanishes. At gaps, cell-cell adhesion molecules disengage and the adhesion tension Γ/2 disappears. In the general case, Γ/2 is replaced by a similar tension Γ_g/2, for example, if ECM material is adsorbed to the cell surface (i.e., if the cell adheres to it at the gap). Likewise, cortical tension β_c may generally change to β_g at gaps, and thus β^∗ = β_c – Γ/2 is replaced by β_i = β_g – Γ_g/2 (Fig. 4 C). With cos(θ_i) = β^∗/β_i, the contact angle between cells at the gap θ_i is then

$$\text{cos}\left({\theta }_i\right)=\left({\beta }_c-\Gamma /2\right)/\left({\beta }_g-{\Gamma }_g/2\right).$$ (3a)

In the simplest case, cortical tension at gaps would not change at all and the ECM would not affect tension at the free cell surface, turning Eq. 3 a into cos(θ_i) = 1 – (Γ/2)/β_c, or equivalently,

$$\Gamma /2={\alpha }_i{\beta }_c={\sigma }_i,|{\beta }_g={\beta }_c,{\Gamma }_g/2=0.$$ (3b)

In this special case, the contact angle at gaps is solely determined by the adhesion tension and the cortical tension at gaps and in adjacent cell-cell contacts. Tension at gaps β_i is then much smaller than β (of the same order as β^∗), and hence for p_i ≈ 0 the cell surface curvature has to be higher at gaps than at the tissue surface to balance intracellular pressure. This allows for small gaps to form, i.e., for channels that are narrow relative to their length (which is of the order of the cell radius) and which are equally wide over their lengths until they merge at lacunae (Fig. 2 G).

These gaps are stable against small deformations. For example, if adjacent cells zippered up at the corner of a gap, their contact angle would increase, and β_i would no longer balance β^∗ (Fig. 4 D). The more the cells zipper up, the greater the imbalance will be, and the restoring tension, i.e., the excess component of β^∗, could be modeled as an elasticity. If cells detached instead of zippering up, an analogous elasticity would again restore the equilibrium state (Fig. 4 D).

Gap size in tissues of high relative adhesiveness

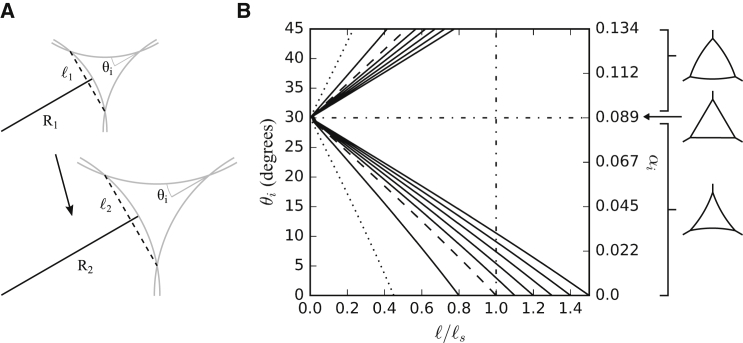
Next, we described the size ℓ of channel cross sections as a function of tensions and pressure differences at gaps. Generally, gap side length ℓ is proportional to the radius of curvature R for constant contact angle θ_i. This is because the overlapping circles that define a gap remain geometrically similar upon uniform scaling (Fig. 5 A). Note that these circles represent cell curvatures at gaps, not cells. In fact, as mentioned above, we have to distinguish now between R_s at the tissue surface and R_i at gaps, and rewrite (1a), (1b) for gaps,

$$\ell /R_i=\text{cos}\left({\theta }_i\right)-{\left(3\right)}^{1/2}\text{sin}\left({\theta }_i\right).$$ (4)

Equation 4 describes gaps by the geometrical variables ℓ, θ_i, and R_i (Fig. 5 A). Any two of these parameters determine the third one, and completely describe a regular gap. The relationship between contact angle and side length is almost linear, as it is for the neck size of gaps based on low relative adhesiveness (Fig. 5 B).

Figure 5.

Gap sizes and shapes in tissues of high relative adhesiveness. (A) Uniform scaling of gaps is shown. When all angles are constant, an increase in the radius of curvature from R₁ to R₂ produces a proportional increase in the gap side length from ℓ₁ to ℓ₂ without affecting interstitial contact angle θ_i. (B) Shown here is the relationship between contact angle θ_i and relative gap size ℓ/ℓ_s for various radii of curvature R_i. Gaps show an almost linear size increase with decreasing angles, and curves intersect the length axis at their respective R_i value. The value ℓ_s corresponds to ℓ at R_i = R_s = r, i.e., when cells touch at points (dashed line), and it is used here to normalize gap sizes. Gaps with an interstitial pressure p_i = 0 (dotted line) have a smaller normalized side length ℓ/ℓ_s, and side length increases with increasing p_i if other factors remain constant. Above θ_i = 30° (horizontal dash-dotted line), the curvature of the gaps becomes negative, and gap surfaces convex. The value ℓ_s sets an upper boundary for the gap side lengths (vertical dash-dotted line). Any gap side length exceeding it implies a dissociation of the tissue.

If we choose θ_i and R_i to characterize gaps, we can use tension and pressure equilibria, respectively, to link gap geometry to mechanical variables. Thus, cos(θ_i) = β^∗/β_i links the contact angle at gaps to the tension between cells and at the gap surface (Fig. 4 C). Furthermore, according to Laplace’s law, the pressure generated by the tension at the cylindrical gap surface is equal to β_i/R_i. At equilibrium, this pressure must balance the difference between a cell’s hydrostatic pressure p_c and the interstitial pressure p_i in the gap, (p_c–p_i) (Fig. 4 E). Hence R_i is linked to the cortical tension at gaps and to the pressures in cells and in gaps by

$$R_i={\beta }_i/\left(p_c-p_i\right).$$ (5)

Overall, by substituting θ_i and R_i with the tensions β^∗ and β_i and pressures p_c and p_i, gap size ℓ remains as the only geometrical variable and becomes

$$\ell =\left[\text{longer balance}\beta \ast -{\left(3\right)}^{1/2}{\left({\beta }_i^2-\beta {\ast }^2\right)}^{1/2}\right]/\left[p_c-p_i\right].$$ (6)

Because the cell-free surfaces of each cell at the tissue surface are approximated as spherical surfaces, Laplace’s law dictates that the intracellular pressure is related to the cortical tension of cells by p_c = 2β/R_s. For interstitial pressure p_i = 0, Eq. 5 gives R_i/R_s = β_i/2β. Because β_i < β, the curvature at gaps 1/R_i has to be increased to compensate for the lower cortical tension there. In contrast to gaps caused by incomplete attachment at low relative adhesiveness, where gap size approaches the cell radius as adhesiveness diminishes, gap size ℓ is limited here to a fraction of R_s even if the contact angle θ_i vanishes (Fig. 5 B).

The interstitial pressure p_i increases if the ECM fluid volume level is raised, up to a limit where a tissue disintegrates. At equilibrium, for any given contact angle θ_i, the gap cross-sectional area and hence the channel volume increases as the curvature of the gap surface decreases to accommodate the new pressure balance. For any given pressure difference (p_c–p_i), gap size and contact angle are almost linearly, inversely related, increasing from zero when θ_i = 30° to intersect the abscissa at ℓ = R_i (Fig. 5 B). With decreasing pressure difference (p_c–p_i), the radius of curvature R_i and hence gap size ℓ increase proportionally for any given contact angle. Gaps could now become even larger than the cell radius, but this would imply the separation of formerly attached cells. The potentially complex interstitial space of tissues under this condition will require a separate analysis.

Convex gaps, where cells bulge into the gaps, can only form under a positive pressure difference (p_c–p_i) if 0° ≤ θ_i < 30° and hence β^∗ ≤ β_i ≤ 1.155β^∗, or 1 ≤ (β_g – Γ_g/2)/(β_c – Γ/2) < 1.155. Compared to the severalfold reduction of tension from β to β^∗ in high-α tissues, the equivalent tension differences at gaps are confined to a narrow range, i.e., β_i is maximally 15.5% higher than β^∗. When (p_c–p_i) vanishes, R_i = ∞, i.e., gap channels are straight-sided in cross sections, and gap size is not determined. For p_i > p_c, R_i becomes negative (Eq. 5), and the respective gaps have concave sides as they are sustained by the higher hydrostatic pressure in the interstitium relative to the cell interior. This gap shape requires that 90° > θ_i > 30°, and with the right side of Eq. 4 being thus also negative, this yields a positive gap size for high pressures and high contact angles combined. For p_i < 0, i.e., for negative interstitial pressure due to the withdrawal of interstitial fluid from the tissue, R_i approaches zero as p_i decreases further and further.

Gap size, as expressed, e.g., in Eq. 6, depends indirectly on cell size through p_c = 2β/R_s. If p_i = 0, then ℓ ∼ R_s, i.e., with everything else being the same, gap size is proportional to cell size. For p_i > 0, gap size increases disproportionately faster with cell size, as ℓ ∼ R_s/(2β − R_s p_i). The complex relationship between cell radius r and cell shape at the surface of aggregates, i.e., the radius of curvature at the tissue surface, R_s, is analyzed in (15).

In summary, a given combination of θ_i and R_i corresponds to a gap of a unique size and shape for ℓ < r. However, it can be obtained by multiple combinations of mechanical parameters. Thus, θ_i is determined by the ratio of two tensions, β^∗/β_i, and R_i by the ratio of a tension and a pressure, β_i/(p_c–p_i), and θ_i and R_i remain constant when the respective ratios remain the same. This consideration implies that a given gap geometry can occur in tissues of very different adhesion strengths. Adhesion strength expressed as tissue surface tension σ = β–β^∗ varies by three orders of magnitude between tissues (12). If β^∗ and β_i change proportionally, contact angles θ_i and thus α_i remain constant according to cos(θ_i) = β^∗/β_i. If, furthermore, (p_c–p_i) is altered in the same proportion, R_i is also constant, and thus gap size and shape would remain the same regardless of the magnitude of tissue cohesion. Such a proportional variation of pressure differences is not unlikely: because σ = αβ and p_c = 2β/R_s, p_c will change proportionally at constant relative adhesiveness α, and for p_i = 0, gap size and shape will remain identical. For p_i > 0, this is the case only if p_i also changes proportionally, but when p_i is small relative to the cell hydrostatic pressure, any deviation from proportionality will be small, and gaps of similar size and shape should be found over large ranges of tissue cohesiveness.

Heterogeneity of gap sizes and shapes in a tissue: asymmetrical gaps

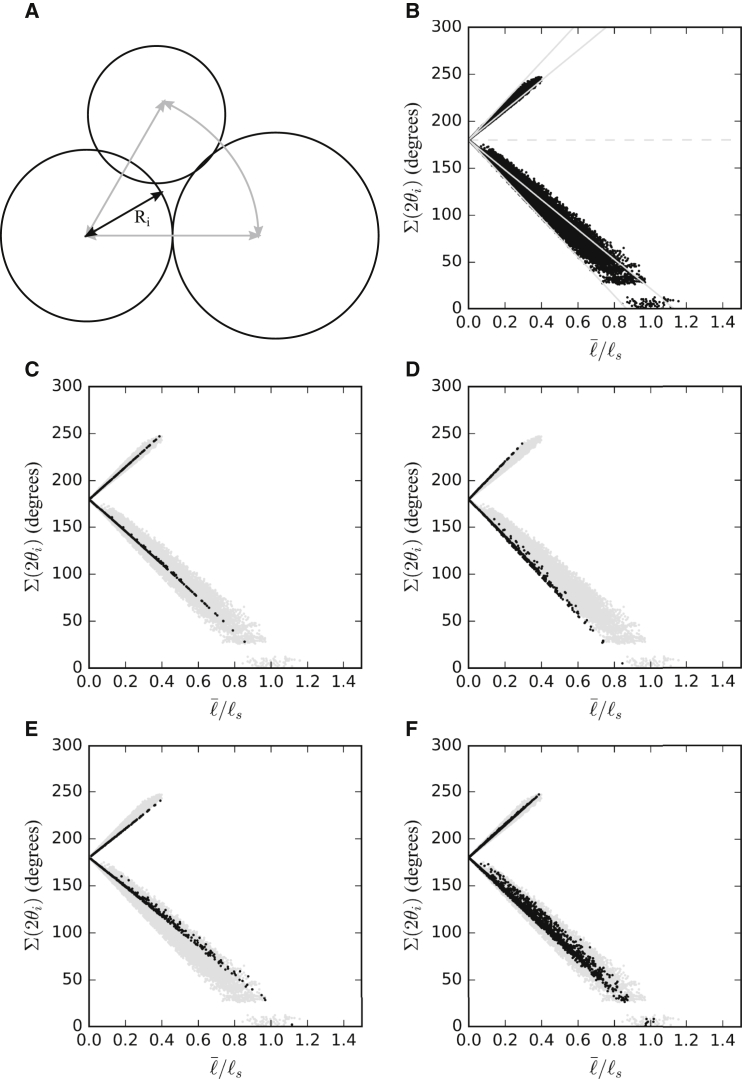
In a perfectly homogeneous tissue, gaps would be uniform in size and shape. However, cortical tensions and adhesion strength can vary from cell to cell (12, 22). Moreover, metabolically driven temporal fluctuations of tensions at cell-cell boundaries are a general and essential feature of tissues (17). Cortex contractility can vary independently between cells surrounding a gap and in different regions of each cell, and cell hydrostatic pressure can be different in different cells (22). As a result, contact angles at the three corners of an individual gap and the curvatures of a gap’s three edges can each have different values. Gaps generated in this way are represented by the space left between three partially overlapping circles as described above. However, the radii and center-to-center distances of the three circles can now vary, and be chosen such that predetermined sets of contact angles and gap edge curvatures are produced for a gap (Fig. 6 A).

Figure 6.

Simulation of asymmetrical gaps. (A) Schematic of gap generation is shown. The area between circles represents gaps. Distances between centers of circles (gray arrows) and radii of circles (gray arrows) can be changed to effect changes in radii of curvature R_i and contact angles θ_i. (B) Distribution of gap sizes obtained from the simulation is shown. A wedge-shaped distribution is observed when the sum of the contact angles (Σ(2θ_i)) is plotted against the average gap side length $\overline{\ell }$ normalized for ℓ_s. Dashed horizontal line indicates Σ(2θ_i) = 180°, i.e., the sum of the angles of a straight-sided triangle. Above that line, the curvature of the gaps becomes negative (three circles overlap), and gap surfaces convex (see Fig. 5B). As Σ(2θ_i) approaches zero, angles change drastically with small parameter changes in the simulation. This is reflected in the blank region between ∼13° and ∼25°. Leftmost gray line indicates the smallest possible average curvature in the simulation (0.867; radii 1, 0.8, and 0.8 combined), the rightmost line the largest average curvature (1.133; 1, 1.2, and 1.2 combined). Gap sizes can lie beyond this maximum, but not below the minimum. (C) Gaps with a radius of curvature of 1 on all three sides (black dots) lie close to the line of this respective curvature, within the gap domain (gray dots). (D) Gaps with an average radius of curvature of 0.8667 (black dots) comprise the leftmost region of the gap domain (gray dots), lying at or above the line of average curvature. (E) Gaps of an average curvature of 1.113 (black dots) likewise lie at or above the line of average curvature, but do not comprise the most extreme right region of the gap domain (gray dots). (F) When curvatures are allowed to vary under the requirement that their average curvature remains 1, gap sizes are more dispersed and cannot be approximated by a line representing gaps of constant curvature.

We asked to what degree asymmetrical gaps could be approximated by suitable symmetrical gaps. For symmetrical gaps, the relationship among contact angle, curvature, and size is given by Eq. 4. For asymmetrical gaps, each of these variables is represented by a respective triplet relating to the three corners and three sides of a gap. To understand to what extent these triplets can be replaced by their respective averages, we calculated the average side length $\overline{\ell }$ for symmetric and asymmetric gaps generated according to Fig. 6 A, where radii of curvature R_i at individual gaps arbitrarily varied between 0.8 and 1.2 (Fig. 6 B).

Symmetrical gaps should occupy a wedge-shaped domain in a ℓ−θ_i plot (Fig. 5 B), between the chosen minimum and maximum R_i (gray lines in Fig. 6 B). For the distribution of asymmetrical gaps, a wedge-shaped gap domain was indeed recovered when the average angle ${\overline{\theta }}_i$ was plotted against the average gap side length $\overline{\ell }$ (Fig. 6 B). Moreover, the lower boundary of the gap domain coincided with the line of minimum average $\overline{R_i}$, i.e., at this boundary asymmetrical gaps can be replaced with symmetrical ones whose R_i = $\overline{R_i}$. However, average gap sizes of asymmetrical gaps exceed the boundary for the maximal $\overline{R_i}$, i.e., these gaps are larger than symmetrical ones despite R_i = $\overline{R_i}$ (Fig. 6 B).

To trace the origin of this effect, we first simulated gaps where curvature was uniform at R_i = 1 on all sides of a gap, but where θ_i varied between corners. The calculated gap samples remained very close to the line of constant R_i = 1 (Fig. 6 C), indicating that angles varying between corners of individual gaps have little effect on the average gap side length as long as curvatures do not vary. In such a case, asymmetric and symmetrical gaps show practically the same relationship between contact angle (θ_i or ${\overline{\theta }}_i$) and size (ℓ or $\overline{\ell }$), and the average contact angle ${\overline{\theta }}_i$ determines the average size $\overline{\ell }$ regardless of whether the individual angles of a gap are identical or different.

The situation is different when both curvatures and angles vary within gaps. For example, for the minimum average radius of curvature possible in the simulation, a gap domain was recovered that spread from the line of this minimal $\overline{R_i}$ to larger gap sizes for the same average ${\overline{\theta }}_i$ (Fig. 6, B and D). Similarly, gap sizes spread from the line of maximal $\overline{R_i}$ to larger sizes (Fig. 6 E). In both cases, two sides shared the same curvature whereas the third side differed. If all three radii are varied such that their average per gap is nevertheless the same, e.g., $\overline{R_i}$ = 1, gap sizes deviate from the average to both sides by up to ∼10% when angles are allowed to vary within gaps (Fig. 6 F). Together, these effects explain the deviation of the overall simulated gap distribution from that of symmetrical gaps (Fig. 6 B).

In summary, the average gap side length $\overline{\ell }$ is not uniquely determined by the average contact angle ${\overline{\theta }}_i$ and the average radius of curvature $\overline{R_i}$ for asymmetrical gap shapes. If both angles and radii vary for a given gap, its average side length usually differs from that of a symmetrical one whose angles and radii are equal to these averages. However, for moderate variations of contact angles and radii, the length difference is small, and ℓ−θ_i plots of symmetrical and asymmetrical gaps are similar.

Conclusions

We found that generally, the presence of fluid-filled interstitial gaps in tissues does not depend on the absolute strength of tissue cohesion, but on the relative adhesiveness α, i.e., the ratio of tensions at free and at contacting cell surfaces. Gaps due to incomplete cell-cell adhesion are expected only for loose, flaky cell aggregates where α is very low. In compact tissues where α is high, stable gaps can be generated by the prevention of cell adhesion at three-cell junctions by fluidlike ECM and the establishment of low cortical tension at the gap surface. Two of the three variables–gap side length, contact angle at gap corners and gap surface curvature– completely describe a regular gap where all sides and angles are equal. These geometrical parameters depend on the cortical tensions at gaps and between cells, and on the hydrostatic pressures in cells and in gaps. Because the stability of gaps in high-α tissues depends not on absolute tension values, but on the ratio of tensions, gaps of the same size and shape can occur in tissues of widely differing cohesion. But tissue mechanical parameters vary not only between tissues, but usually also between and within cells of the same tissue. This variability gives rise to asymmetrical gaps where the three angles, curvatures, and side lengths of a gap differ. The average side length of such an asymmetrical gap is not uniquely determined by the averages of its contact angles and curvatures; in fact, it is often larger than predicted from the average angles and curvatures under the assumption that they were symmetrical.

Author Contributions

R.W. and D.B. conceived the research. R.W. and S.E.P. developed the theoretical analysis, and S.E.P. designed and performed the simulations. All authors wrote and revised the manuscript.

Editor: Jochen Guck.

Appendix A: Symbols and their definitions

Cell surface tensions

β, cortical tension at aggregate/tissue surface; β^∗, resultant reduced tension at cell-cell contacts per cell; β_c, cortical tension at cell-cell contacts per cell; β_i, cell surface tension at gap; β_g, cortical tension at gap; Γ, adhesion tension at cell-cell contacts; Γ_g, adhesion tension at gaps; T, line tension around cell contact areas.

Adhesion strengths

σ, tissue surface tension: absolute adhesion strength; σ_i, internal surface tension, adhesion strength at gaps; α, relative adhesiveness; α_t, threshold relative adhesiveness for gap fragmentation; α_crit, critical relative adhesiveness for gap closure; α_i, internal relative adhesiveness at gaps.

Pressures

p_c, cell hydrostatic pressure; p_i, interstitial pressure.

Geometry

r, radius of unattached, spherical cell; r_c, radius of cell-cell contact area; A, cell-cell contact area; R, radius of curvature; R_s, radius of cell surface curvature at tissue surface; R_i, radius of cell surface curvature at gaps; ℓ, gap size; ℓ_s, gap size between cells touching pairwise at a point; θ, contact angle at tissue surface; θ_i, contact angle at gap; θ_t, threshold contact angle for gap fragmentation; θ_crit, critical contact angle for gap closure.

Averages are denoted by overlining.