Mechanics of Fluid-Filled Interstitial Gaps. II. Gap Characteristics in Xenopus Embryonic Ectoderm

Abstract

The ectoderm of the Xenopus embryo is permeated by a network of channels that appear in histological sections as interstitial gaps. We characterized this interstitial space by measuring gap sizes, angles formed between adjacent cells, and curvatures of cell surfaces at gaps. From these parameters, and from surface-tension values measured previously, we estimated the values of critical mechanical variables that determine gap sizes and shapes in the ectoderm, using a general model of interstitial gap mechanics. We concluded that gaps of 1–4 μm side length can be formed by the insertion of extracellular matrix fluid at three-cell junctions such that cell adhesion is locally disrupted and a tension difference between cell-cell contacts and the free cell surface at gaps of 0.003 mJ/m² is generated. Furthermore, a cell hydrostatic pressure of 16.8 ± 1.7 Pa and an interstitial pressure of 3.9 ± 3.6 Pa, relative to the central blastocoel cavity of the embryo, was found to be consistent with the observed gap size and shape distribution. Reduction of cell adhesion by the knockdown of C-cadherin increased gap volume while leaving intracellular and interstitial pressures essentially unchanged. In both normal and adhesion-reduced ectoderm, cortical tension of the free cell surfaces at gaps does not return to the high values characteristic of the free surface of the whole tissue.

Introduction

Many tissues are held together not by an extracellular matrix (ECM) scaffold, but by direct cell-to-cell adhesion. Such compact, three-dimensional tissues pose the problem of how the degree of adhesion required for their integrity can be combined with the presence of interstitial gaps, as seen in vertebrate embryonic tissues (1, 2, 3) or tumors (4, 5). Interstitial gaps control the transport of extracellular fluid through tissues and between compartments of the body (6, 7), and in solid tumors, pressure gradients in the interstitium and consequent flows of interstitial fluid pose a main problem for drug delivery (8, 9). In embryonic tissues, the capacity for diffusive transport (10) and the resistance to tissue deformation in the course of morphogenesis (1) depend on the size and frequency of interstitial gaps.

Intuitively, a low degree of adhesion would allow for gaps to persist between cells that attach incompletely to one another. However, adhesion strength in tissues is often above the predicted threshold level for this effect, and other mechanisms must be considered (11). Thus, interstitial gaps could be filled with a solid-like ECM that determines their size and shape. However, gaps are often based on a fluid-like content, such as a hyaluronic acid (HA)-rich liquid ECM, or capillary exudate. For these cases, it can be shown in theory that the prevention of cell adhesion at three-cell junctions by the insertion of the fluid-like extracellular material, and a reduction of cortical tension at the free cell surfaces thus generated, is sufficient to maintain stable gaps (11).

In this article, we apply this theoretical result to Xenopus gastrula tissue. In the gastrula, cell adhesion is sufficiently strong to allow in principle for a tight, gap-less attachment of cells to each other (1, 11). Nevertheless, gaps are present at three-cell junctions between otherwise tightly packed cells. They can be visualized in histological sections and also in live embryos by x-ray diffraction imaging (12) and by confocal microscopy in live explants (13). Like similar gaps in other tissues (14, 15), they are filled with an HA-rich ECM fluid (16). With GFP-tagged protein as tracer, the gap content can be seen in the confocal microscope to flow readily when squeezed between actively moving cells, and fluorescence correlation spectroscopy revealed diffusion constants consistent with an almost water-like viscosity of the interstitial material (13). Thus, Xenopus gastrula tissues can serve as models for ECM fluid-induced interstitial gaps.

We focus here on the Xenopus ectoderm, and as in the accompanying article (11), we link the geometrical parameters that describe gaps—contact angle, gap side length, and radius of curvature—to tissue mechanical variables: cortical tension at gaps and between cells, and hydrostatic pressures in cells and in the interstitium. We quantitatively describe the ranges of sizes and shapes of interstitial gaps, and we use known and predicted mechanical properties of the ectoderm tissue to explain the stability of the interstitial space. We further show that our model can explain changes in gap shape and size caused by experimentally reduced cell-cell adhesion. Altogether, the results demonstrate the suitability of our model for the analysis of gap mechanics, and they refine previous notions about the overall tissue mechanical design of the early embryo.

Materials and Methods

Preparation of samples for transmission electron microscopy

Xenopus laevis eggs were fertilized in vitro. Stage 11 gastrulae were fixed overnight in 3% paraformaldehyde and 2.5% glutaraldehyde in 0.05 M cacodylate buffer (CB (pH 7.0)). The vitelline membrane was removed, and gastrulae were cut in half sagittally. After rinsing in 0.1 M CB ((pH 7.0) 3 × 10 min/wash), the embryo halves were submerged in a 0.1 M CB solution containing 1% osmium tetroxide (OsO₄). For visualization of the extracellular matrix, 1% lanthanum nitrate (Sigma-Aldrich, Oakville, Canada) was added to both fixatives according to Johnson (17). After rinsing with 0.1 M CB, samples were dehydrated through a graded series of ethanol solutions, embedded in 100% Spurr’s resin and cured at 65°C for 24 h. Ultrathin (90–100 nm) sections were obtained using a Leica (Wetzlar, Germany) EM UC6 microtome, and stained with 3% uranyl acetate in methanol for 1 h and Reynold’s lead citrate for 10 min.

Gap size, contact angle, and curvature measurements

Lengths and angles were measured using the AxioVision v4.8 image analysis software. Gap side length was measured as the distance between two corners of a gap at a tri-cellular junction, for all three sides of a gap, to calculate the average side length. Contact angles between adjacent cells were measured at all three corners of a gap. Cell surfaces at gaps were assumed to be circular arcs in sections, each spanning between two corners of a gap. The width W of an arc was measured as the distance between the respective corners, the height H perpendicularly starting from the center of the width line and ending at the surface of the cell. The radius of an arc, R, was then estimated according to the intersecting chord theorem using the formula $\mathit{r}=\left(\mathit{H}\text{/}2\right)+\left({\mathit{W}}^2\text{/}8\mathit{H}\right)$.

F-actin staining and fluorescence intensity measurements

Stage 11 embryos were fixed in 3.4% paraformaldehyde in modified Barth’s solution (MBS) (1) for 24 h before addition of 0.1% Triton X-100. After 15 min, the samples were washed twice in a 1% bovine serum albumin (BSA)/MBS solution (BSA/MBS; 5 min/wash). Samples were then stained for F-actin for 1 h in a solution of 0.01% Alexa-Fluor 488 phalloidin in BSA/MBS, and again in BSA/MBS (three times, 5 min/wash) before mounting in a glass-bottomed dish in MBS. Fluorescence imaging was performed using a TCS SP8 confocal microscope (Leica) with 20×/NA 0.75 oil immersion and 63×/NA 1.4 oil immersion lenses and fluorescence intensity was measured using ImageJ software version 1.51 n.

C-cadherin knockdown

X. laevis embryos were microinjected in 4% Ficoll solution with previously characterized translation-blocking C-cadherin morpholino antisense oligonucleotides (GeneTools) at the two-cell stage at 20 ng/blastomere, and incubated at 15°C in 1:10 MBS until stage 11, as described in (1, 18).

Results

Morphology of interstitial gaps in Xenopus gastrula ectoderm

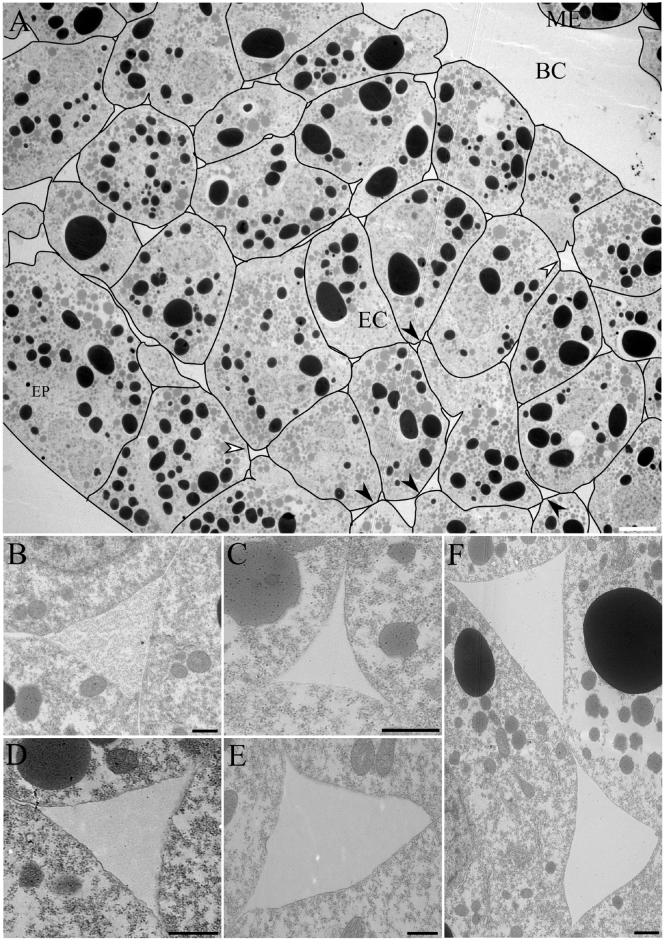
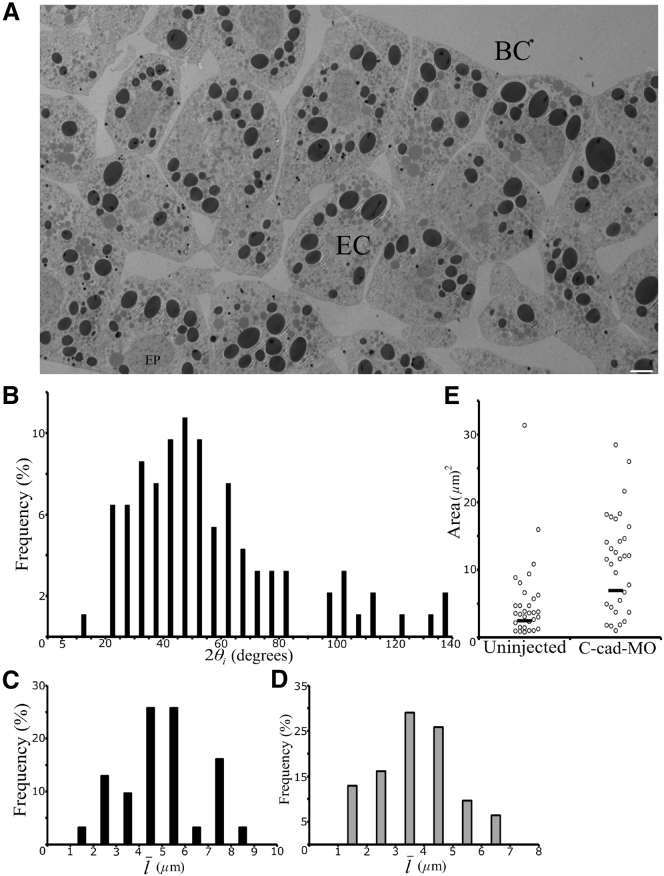
In the early gastrula, the ectoderm consists of closely packed deep cells between an epithelial layer at the embryo surface and a fluid-filled blastocoel cavity (Fig. 1 A). In sections, cell boundaries typically meet at three-cell junctions, which in three dimensions correspond to the aligned edges of the mutually attached polygonal cells. ECM-filled gaps occupy these junctions (Fig. 1, B–F). Although deep cells adhere to the epithelial layer as well as to each other, they do not interdigitate with epithelial cells but form a relatively smooth interface (Fig. 1 A). In the following, we focus on the gaps between deep cells. The triangular gaps show a range of shapes, generated by the combination of convex, straight, and concave gap borders, and varying contact angles at the corners (Fig. 1, B–F). Most commonly, gaps are cusp-shaped with three convex sides (36.7%), or with convex and straight sides combined (49.9%) (Fig. 1, B–D). Occasionally, adjacent gaps are close to each other, generating bow-tie shapes (Fig. 1, A and F). Four-sided gaps are also present (Fig. 1 A). No gapless three- or four-cell junctions were observed, indicating that the ectoderm is completely permeated by a continuous meshwork of channels running along cell edges. Gaps of similar size and shape were observed in the confocal microscope after formaldehyde fixation and phalloidin staining of the actin cytoskeleton (see Fig. 5). Moreover, the much larger gaps in the gastrula endoderm are sufficiently resolved by x-ray diffraction imaging of live embryos (12), and their size corresponds to that seen in the transmission electron microscope (J. Wen and R.W., unpublished data). Together, these observations suggest that the size and shape of interstitial gaps are sufficiently well preserved in the histological procedures employed.

Figure 1.

Transmission electron micrographs of ectoderm. (A) Overview of ectoderm, midsagittal section through a stage 11 Xenopus laevis gastrula with cell outlines indicated. Pixel dimensions are 3296 × 2568, with 53 nm/pixel. (B–F) Interstitial gaps of various shapes within the ectoderm. A tri-cellular gap stained for ECM using lanthanum nitrate is shown in (B). Black and white arrowheads in (A) denote bow-tie-shaped gaps and four-cell junctions, respectively. The white scale bar represents 10 μm and the black scale bars 1 μm. EC, ectoderm; EP, epithelium; BC, blastocoel; ME, mesoderm.

Figure 5.

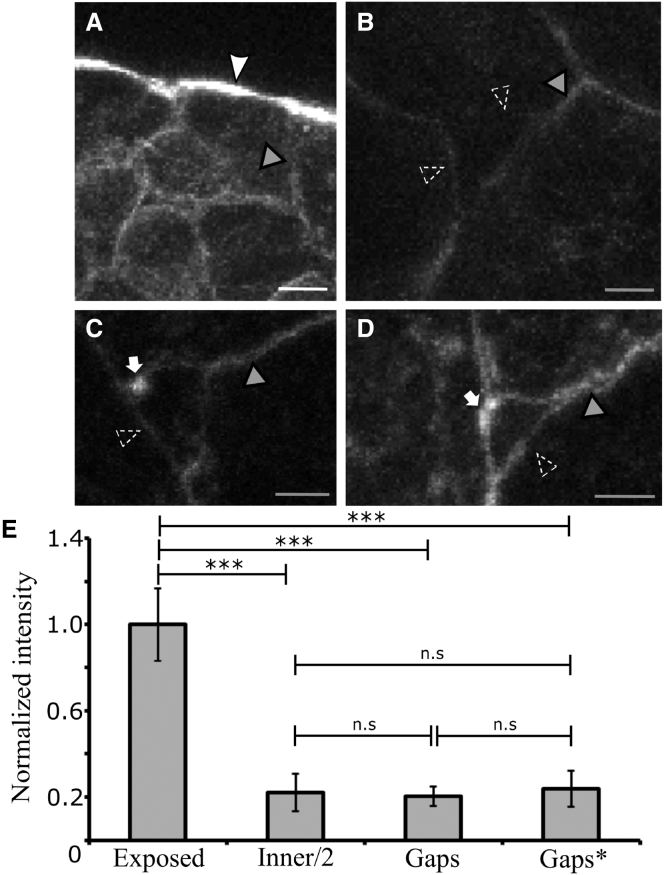
Distribution of F-actin in the ectoderm. (A–D) Phalloidin 488 staining reveals increased F-actin density on the exposed, blastocoelic surface of the ectoderm (white arrowhead in A) in comparison to cell-cell interfaces (gray arrowheads) and gaps (dashed arrowheads). Occasionally, F-actin puncta can be seen on one corner of a gap (white arrows in C and D). (E) Fluorescence intensities for all conditions were normalized to exposed surface values (^∗∗∗p < 0.001, n.s., not significant). Error bars represent standard deviations from the mean intensity values for exposed (n = 12 cells), inner cell-cell interfaces (n = 24), and gaps without (n = 21) and with actin puncta (Gaps^∗). The white scale bar represents 10 μm and the gray scale bars 3 μm.

The mechanics of fluid-filled interstitial gaps

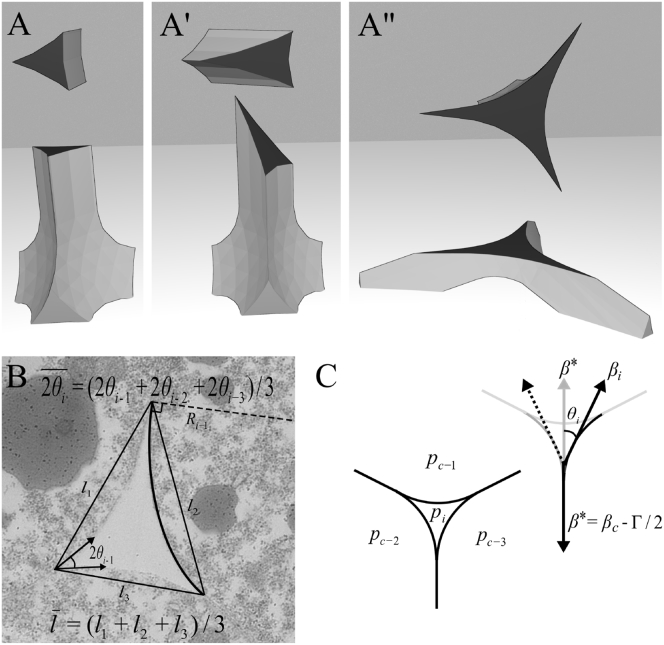
We summarize here theoretical results on the mechanics of fluid-filled interstitial gaps that were detailed in the accompanying article (11). We found that in tissues of high relative adhesiveness, such as the Xenopus ectoderm, channels along cell edges are expected to resemble elongate prism segments that each connect at cell vertices to three adjoining channels (11) (Fig. 2 A). In cross section, the geometry of such a gap appears as the intersection of three circles representing the surfaces of respective cells. If all cells are identical, the gap shows threefold rotational symmetry and can be described by any two of the three variables, gap length l, contact angle θ_i, and radius of curvature R_i (Fig. 2 B), which are related by

$$\ell \text{/}{\mathit{R}}_{\mathit{i}}=\text{cos}\left({\theta }_{\mathit{i}}\right)-{\left(3\right)}^{1/2}\text{sin}\left({\theta }_{\mathit{i}}\right).$$ (1)

Figure 2.

Gap structure and parameters. (A–A″) Three-dimensional illustration of an interstitial channel sectioned straight, obliquely, or at the branching zone to generate gaps that appear different in size and shape. (B) Geometric parameters of a gap. The mean side length of a gap was calculated from the three distances between adjacent corners of a gap and the mean angle from the three angles at each corner of a gap. (C) Mechanical parameters determining size and shape of a gap, including interstitial pressure, p_i, intercellular pressure, p_c, cortical tension, β_i at the free surface, and residual tension per cell, β^∗. Contributions are shown for the right cell only.

To link these geometrical variables to mechanical variables, we considered tension and pressure balances at gaps at equilibrium (Fig. 2 C). In this context, cell cortex tension and cell-cell adhesion are inseparable concepts (19, 20). Upon the engagement of cell adhesion molecules of contacting cells, binding energy is released that generates an adhesion tension and favors cell-cell attachment. However, the amount of energy thus released is not sufficient to overcome the cell rounding effect of the contractile cortical cytoskeleton of the cells. Therefore, cortical tension β has to be reduced in the contact area to attain a residual tension per cell, β^∗, to allow for substantial cell attachment (19, 20). Importantly, at the free cell surfaces at gaps, tension is not the same as at the free tissue surface, β, but as β_i it takes on values closer to β^∗. This consideration translates into a force balance (Fig. 2 C) β^∗/β_i = $\text{cos}\left({\theta }_{\mathrm{i}}\right)=\left({\beta }_{\mathrm{c}}-\Gamma \text{/}2\right)\text{/}\left({\beta }_{\mathrm{g}}-{\Gamma }_{\mathrm{g}}\text{/}2\right)$, where β_c is the cortical tension of a cell in the contact area, β_g the cortical tension at the gap surface, Γ/2 the adhesion tension per cell due to the release of binding energy, and Γ_g/2 the adhesion tension due to the adsorption of ECM material to the cell surface at gaps (11). As we will see, for normal ectoderm, the special case may apply that β_i = β_c = β_g and Γ_g/2 = 0, i.e., the only difference between tensions at contacts and at free gap surfaces could be the absence of an adhesion tension at the latter. In this case,

$$\text{cos}\left({\theta }_i\right)=1–\left(\Gamma /2\right)/{\beta }_{\text{c}}.$$ (2)

As detailed in the accompanying article (11), no pressure increase in the interstitium is required to generate gaps; the isolation of cell membranes at three-cell junctions by ECM fluid and the establishment of tension β_i at these separated membranes is sufficient if the conditions for the force balance at gaps given above are met. However, the interstitial pressure affects the curvature of the gap surface and the size of gaps. The pressure generated by the tension β_i = β_g – Γ_g/2 (β_i = β_c in the special case) at the cylindrically curved gap surface according to Laplace’s law is β_i/R_i and it balances the pressure difference between the cell interior, p_c, and the interstitium, p_i (Fig. 2 C), and hence, at equilibrium,

$${\mathit{R}}_i={\beta }_i\text{/}\left({\mathit{p}}_c-{\mathit{p}}_i\right).$$ (3)

A measure of the strength of cell-cell adhesion is tissue surface tension, σ, which approximately corresponds to the difference between the cortical tension at the free surface of the tissue, β, and the reduced tension, β^∗, at the contacts between cells: σ = β – β^∗ (11, 20, 21, 22). Mostly, tension ratios are relevant in our analysis, and the dimensionless relative adhesiveness, α, is the critical parameter in our context. It expresses the ratio of mechanical tensions at free and contacting cell surfaces, and ranges from 0 to 1. It allows us to write σ = αβ and also α = 1 – cosθ, i.e., α conveys both a geometrical and a mechanical meaning (1, 11). Gaps should be absent above an α_crit ∼ 0.3 irrespective of the absolute adhesion strength, σ (11), but α in gastrula tissues ranges from 0.66 to 0.75 (1), i.e., it is more than twice the threshold level. Formally, σ_i and α_i can be defined analogously for gaps, and

$${\mathit{\alpha }}_{\text{i}}=1-\text{cos}\left({\theta }_{\text{i}}\right)$$ (4)

and Eq. 2 becomes

$${\mathit{\sigma }}_{\text{i}}=\mathrm{\Gamma }/2={\mathit{\alpha }}_{\text{i}}{\beta }_{\text{c}}.$$ (5)

In real tissues, the mechanical variables that determine gap size and shape will vary between cells, and gaps will be more or less asymmetric. We observed that when this variation is small, the averages of the respective parameters may be used to describe gaps (11). Symbols are summarized in Table 1.

Table 1.

Symbols

Cell Surface Tensions
β	cortical tension at aggregate/tissue surfacea
β∗	residual tension at cell-cell contacts, per cella
βc	cortical tension at cell-cell contacts per cell
βi	cell surface tension at gap
βg	cortical tension at gap
Γ	adhesion tension at cell-cell contacts
Γg	adhesion tension at gaps
Adhesion Strengths
σ	tissue surface tension: absolute adhesion strengtha
σi	internal surface tension, adhesion strength at gaps
α	relative adhesiveness
αcrit	critical relative adhesiveness for gap closure
αi	internal relative adhesiveness at gaps
Pressures
pc	cell hydrostatic pressure
pi	interstitial pressure
Geometry
r	radius of circle circumscribing the gap
rc	radius of cell-cell contact area
R	radius of curvature
Rs	radius of cell surface curvature at tissue surface
Ri	radius of cell surface curvature at gap
l	gap size
θ	contact angle at tissue surface
θi	contact angle at gap

^aRefers to values from previous work (1).

Size of the interstitial channel network

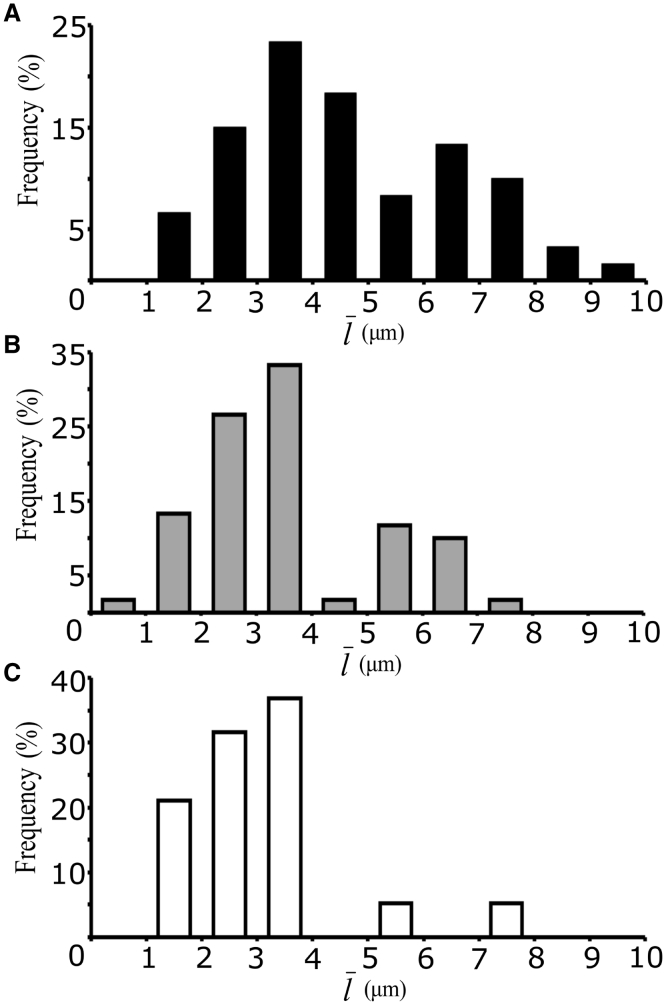
To analyze the spatial dimensions of the interstitial channel network, we characterized the size of a gap by the average length $\left(\overline{\mathit{l}}\right)$ of its three side lengths, l₁, l₂, and l₃, measured as the distances between its corners (Fig. 2 B). Two populations of gap sizes were observed (Fig. 3 A): a major size class at 1.5–5.5 μm, with an average of 3.5 μm, and a minor class between 5.5 and 9 μm. As to the origin of the two populations, we considered that cell edges, and hence channel lengths, are of the order of the cell radius of 12 μm (1). Thus, for the main peak of the distribution, gap sizes are small relative to edge lengths, consistent with sections cutting through the unbranched, straight part of channels (Fig. 2, A and A′). Sections through the branching regions will show larger gap sizes, generating the second peak of the size distribution (Fig. 2 A″).

Figure 3.

Gap size distribution. (A–C) Frequency of gap sizes based on their average side length. (A) Measured gaps (n = 120). (B) The same gaps as in (A) Steiner-ellipse corrected (n = 120). (C) Selection of gaps in (A) that appear equilateral in sections (n = 30).

The analysis of gap sizes is complicated by the fact that sections are randomly tilted with respect to channel axes. Tilting elongates the sides of gaps, and $\overline{\mathit{l}}$ will be overestimated (Fig. 2 A’). This effect can be corrected when gaps are equilateral. Then the true side lengths can be calculated for tilting-distorted gaps from a Steiner ellipse constructed around the observed gaps (Appendix A). If truly elongate gaps are present in the tissue, two types of error can occur. First, such gaps will wrongly be reduced to a smaller, equilateral size by the procedure. Second, elongate gaps that have come closer to equilateral in appearance by tilting, and hence larger, will not be corrected fully, and gap size will be overestimated. The two types of error tend to balance each other, but the exact range of gap sizes may yet be difficult to determine.

When we applied the Steiner ellipse procedure to our data (Fig. 3 B), overall gap size was reduced by up to twofold. Small gaps ranged from 0.75 to 4 μm, with an average of 2.7 μm, and large gaps from 5 to 8 μm. Notably, peaks became more distinct as gaps in the 4–5 μm range disappeared through the correction procedure, suggesting that this part of the size spectrum contained few equilateral gaps. When we counted the number of equilateral and nearly equilateral gaps by inspection of the original data, we found that the 4–5 μm size range was indeed devoid of such gap shapes (Fig. 3 C). However, equilateral gaps were frequent in the 1–4 μm size range, and distributed similarly to the corrected sizes in that range. As tilting of equilateral gaps inevitably increases gap size and generates nonequilateral shapes, these observations are consistent with the notion that gaps in the 4–5 μm size range were all generated by tilting from smaller gaps in the 1–4 μm range.

Both the corrected and the equilateral distributions of small gaps were strongly asymmetric, with a maximum at 3–4 μm. This is suggestive of a distinct gap size limit at 4 μm in this population. At the lower end of the corrected distribution, elongate gaps may have been mistakenly corrected to yield the smallest gaps there. However, when exclusively counting the nearly equilateral gaps, gap size can only be over-estimated, showing that small gaps down to 1 μm side length do indeed exist. In summary, the average gap side length, $\overline{\mathit{l}}$, in this population of small gaps varies between 1 and 4 μm, with a maximum between 3 and 4 μm and an average of ∼3 μm (Table 2).

Table 2.

Values

	Control	CAD-MO
β	0.23 ± 0.03 mJ/m2	0.24 ± 0.08 mJ/m2
β∗	0.060 ± 0.005 mJ/m2	0.15 ± 0.07 mJ/m2
βi	0.063 ± 0.005 mJ/m2	0.166 ± 0.004 mJ/m2
σi	0.003 ± 0.002 mJ/m2	0.016 ± 0.0105 mJ/m2
α	0.68	ND
αi	0.048 ± 0.033	0.094 ± 0.061
pc	16.8 ± 1.7 Pa	14.3 ± 0.7 Pa
pi	3.9 ± 3.6 Pa	1.7 ± 1.4 Pa
1/Rs	0.037 ± 0.029 μm−1	0.031 ± 0.023 μm−1
1/Ri	0.209 ± 0.379 μm−1	0.076 ± 0.174 μm−1
$\overline{\mathit{l}}$	2.7 μm	3.2 μm
2θ	143°	ND
$\overline{2{\theta }_i}$	36°	50°

Averages are denoted by overlining of symbols. values for β. β^∗ from previous work (1). ND, not determined.

The second population consisting of large gaps comprises ∼1/4 of the total number of gaps, and their sizes are about twice those of the smaller ones. This is consistent with gaps representing sections through the wide branching regions of the channel network (Fig. 2 A″). The height of a branching region should be of the order of the gap side length, i.e., ∼3 μm. With an edge length of 12 μm, the branching region takes up ∼1/4 and the unbranched part 3/4 of the edge length. This corresponds to the ratio of small- and large-gap-size classes (Fig. 3, A and B).

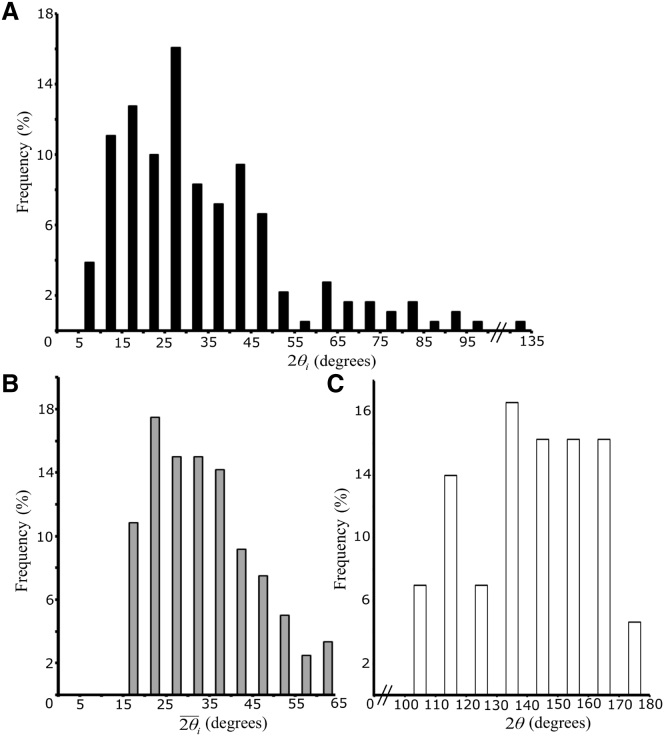
Contact angles and adhesiveness at gaps

To quantitate adhesiveness at three-cell junctions, we measured the angles between cells at the corners of gaps (Fig. 4 A). These are twice the contact angles, θ_i, and are related to the relative adhesiveness by α_i = 1 – cosθ_i. Angles ranged from 5 to 100°, with their frequency distribution being highly skewed toward small angles. Removing angles belonging to the class of large gaps identified above did not change the distribution (data not shown). The small angles $2{\theta }_i$ within the tissue contrast with those at its surface, which reflect the relative adhesiveness of the ectoderm as a whole (1, 11). Here, the average angle 2θ between cells, 143° (Fig. 4 C), corresponds to an α of 0.68. This value is close to that of ectoderm explants (1), suggesting that relative adhesiveness is very similar in vivo and in vitro.

Figure 4.

Frequencies of contact angles. (A) Angles measured at each point of contact between adjacent cells at 120 tri-cellular junctions (n = 360). (B) mean angles per gap of the same gaps as in (A) (n = 120). (C) Angles between adjacent cells at the blastocoel surface of the ectoderm (n = 43).

Two factors can in principle contribute to the large variation of $2{\theta }_i$ values: real differences in angle sizes and the dispersion of apparent sizes due to the random tilting of the plane of sectioning. If all of the observed variation were due to tilting, this should become obvious from the distribution of the averages of angle sizes per gap, $\overline{2{\theta }_i}$ (Fig. 4 B). In the case of straight-sided triangles, $\overline{2{\theta }_i}$ is 60° regardless of the degree and orientation of tilting. With curved sides, the sum of angles per gap can be larger or smaller than 180°, and $\overline{2{\theta }_i}$ larger or smaller than 60°. During tilting, the increase in some angle(s) of a gap will still be compensated for to some extent, though not exactly, by the decrease in others. The averages of angle sizes per gap, $\overline{2{\theta }_i}$, ranged from 15 to 65° (Fig. 4 B), indicating that true gap angles vary, at the least, between these values.

Furthermore, tilting contributed to gap side length variation by a factor of 2, and we expect a roughly proportional contribution to the angle size range, i.e., tilting can reduce the smallest actual angle by up to half of its true value and increase the largest one by up to twofold. Applied to the distribution of individual angles 2θ_i, this would suggest that angles truly vary between 15 and 65°, which is indeed the range of $\overline{2{\theta }_i}$ values measured. The very small number of $\overline{2{\theta }_i}$ values above 60° is consistent with the vast majority of gaps being of a convex shape, which requires that the sum of angles per gap is <180°.

We know from previous work that for the cohesion of the ectoderm, cell cortical tension, β, is reduced from an average of 0.23 mJ/m² at the free surface to an average residual tension (β_c – Γ/2) of 0.06 mJ/m² between cells (1) (Table 2). Generally, adhesion tension, Γ/2, is low; e.g., the contribution of cadherins is below 0.01 mJ/m² even for the highest cadherin densities (1), and at its low end, the range overlaps with the tension of nonspecific cell-cell adhesion of ∼0.001 mJ/m² (23). This low adhesion tension is negligible for the overall strength of ectoderm adhesion, and the main driver of adhesion is the reduction of cortical tension from β at the tissue surface to β_c within.

By contrast, adhesion strength at gaps within the ectoderm is in the range of adhesion tensions. Adhesion strength is given here by the internal surface tension, σ_i, i.e., the difference between the tension at the free surfaces of gaps (β_g – Γ_g/2) and the residual tension at cell contacts (β_c – Γ/2). For our average α_i of 0.048 ± 0.033 at gaps and with a previously measured β^∗ = (β_c – Γ/2) of 0.060 ± 0.005 mJ/m² (1), we obtained σ_i = 0.003 ± 0.002 mJ/m² (Table 2), which is at the lower end of probable adhesion tension values. It could be generated without any change in cortical tension, β_c, between gap surface and cell contact areas, simply by adhesion tension Γ/2 = 0.003 mJ/m² acting at cell contacts but not on free cell surfaces at gaps, according to σ_i = Γ/2 (Eq. 5). Even for a maximal angle at gaps of 65°, σ_i = 0.011 mJ/m², i.e., it is within the range of probable adhesion tensions, and no increase in cortical tension, β_c, at free gap surfaces would be required.

Consistent with this notion, staining with fluorescent phalloidin did not show an increase of cortical F-actin at gaps (Fig. 5). As expected, F-actin density is high at the ectoderm blastocoelic surface, and lower at cell-cell boundaries (Fig. 5 A). Considering that cell-cell interfaces represent the two cortices of two adjacent cells, F-actin staining is reduced to ∼1/5 of the free surface (Fig. 5 E). If staining intensity were directly proportional to cortical tension, as found previously for ectoderm cells (1), this would correspond to a relative adhesiveness, α, of 0.8. Importantly, cortex staining intensity at gaps does not increase to the tissue surface level (Fig. 5, B–D). In fact, the measured cortex density at gaps does not differ significantly from half the value at cell-cell boundaries (Fig. 5 E), suggesting that cortex tension per cell may also remain the same. This notion holds whether or not the occasional puncta of F-actin near corners of gaps (Fig. 5, C and D), of unknown origin or function, are included.

Cell-surface curvatures and intracellular and interstitial pressures

The third characteristic geometrical parameter besides side length and contact angle is the radius of curvature, R_i, of the cell surface at gaps. Curvature 1/R_i varies around an average of 0.209 ± 0.379 μm⁻¹. As expected, the higher cortical tension at the tissue surface is associated with a larger radius of curvature, and 1/R_s is 0.037 ± 0.029 μm⁻¹. Applying Laplace’s law, we calculated from this value and from a cortical tension at the tissue surface of β = 0.23 ± 0.03 mJ/m² (1) the average intracellular hydrostatic pressure, p_c = 2β/R_s, as 16.8 ± 1.7 Pa. To estimate the interstitial pressure, we calculated the pressure generated by the cortical tension, β_c, at gaps, p_g = β_c/R_i, using β_c = 0.060 ± 0.005 mJ/m² (1) and 1/R_i as above, and applied Laplace’s law to a cylindrical surface to obtain p_g = 12.9 ± 1.9 Pa. At pressure balance, the interstitial pressure, p_i = p_c – p_g, is slightly positive at 3.9 ± 3.6 Pa (Table 2). All values are relative to the pressure in the blastocoel cavity of the embryo.

Distribution of gap sizes and shapes

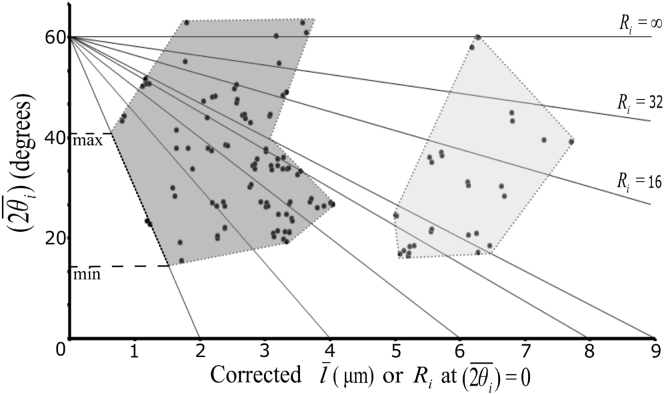
In homogeneous tissues where the relevant mechanical variables are uniform, all gaps should be symmetrical and of uniform size. However, ectoderm interstitial gaps differ in size and shape, and in a $\overline{2{\theta }_i}$-$\overline{\mathit{l}}$ plot, these gaps cover a characteristic region defined by the range of underlying mechanical variables (Fig. 6). Moreover, gaps are asymmetrical, as R_i and θ_i vary within individual gaps. We were able to analytically derive relationships between geometrical and mechanical parameters for symmetrical gaps and showed that the size of asymmetrical gaps is moderately increased when compared to symmetrical gaps, i.e., when we replaced the R_i and θ_i of symmetrical gaps with the respective averages per gap, $\overline{{\mathit{R}}_i}$ and $\overline{{\theta }_i}$, of the asymmetrical ones. Overall, however, the size distributions of regular and asymmetrical gaps are similar (11), and we apply our analysis of symmetrical gaps here to approximately describe our empirical data where gaps are characterized by the average side length, $\overline{\mathit{l}}$, per gap, corrected by the Steiner ellipse procedure, and the average $\overline{2{\theta }_i}$ of the three angles of a gap.

Figure 6.

The gap domain of the gastrula ectoderm. Shown is the relationship between mean angles per gap $\left(\overline{2{\theta }_i}\right)$, corrected average side length per gap, $\overline{\mathit{l}}$, and radii of curvature, R_i. Each dot represents an observed gap with the measured mean of angles and side length, respectively. Lines of constant radius, R_i, are approximated by straight lines that intersect the abscissa at l = R_i. Two groups of gaps can be distinguished, as outlined (shaded areas). For the dark gray group of smaller gaps, the gap domain and the maximal and minimal contact angle sums were read off for each R_i value shown at the intersections of the respective R_i lines with the outline of the gap domain (e.g., dashed horizontal lines for R_i = 2 μm).

In the $\overline{2{\theta }_i}$-$\overline{\mathit{l}}$ plot (Fig. 6), gaps form two groups, corresponding to the two peaks of the size frequency distribution (Fig. 3 B). The second peak in the size distribution and the right group of large gaps in Fig. 6 presumably correspond to sections through the branching zones of interstitial channels, as discussed above. The first peak of the frequency distribution and the left group of gaps in Fig. 6 corresponds to cross sections of interstitial channels, and its distribution was analyzed further.

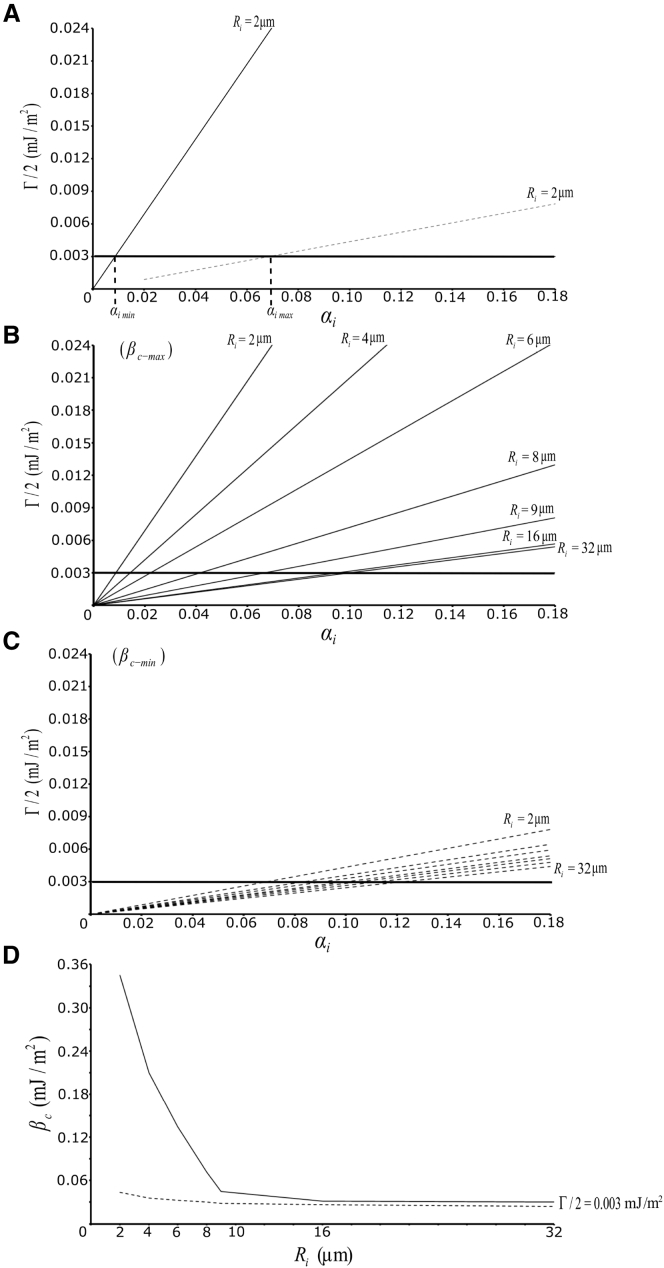
We asked how variations in cortical tension, β_c, adhesion tension, Γ/2, and the pressure difference between cell and interstitial gap, p_c – p_i, determine the range of possible gap shapes and sizes in the $\overline{2{\theta }_i}$-$\overline{\mathit{l}}$ plot. We noted that for each line of constant R_i that intersects the abscissa at R_i, maximal and minimal angles, θ_i-max and θ_i-min can be read off as the line crosses the gap domain (Fig. 6). Starting with the assumption that Γ/2 is constant at 0.003 mJ/m², as estimated above, we used Γ/2 = α_iβ_c (Eq. 5) to calculate the range of β_c values corresponding to the range of angles for each of a set of R_i values (Fig. 7, A–C). Thus, for a given R_i, β_c-max = (Γ/2)/(1 – cosθ_i-min), and β_c-min = (Γ/2)/(1 – cosθ_i-max). This is graphically illustrated in Fig. 7 A, where Γ/2 = α_iβ_c is seen to intersect Γ/2 = 0.003 mJ/m² at respective maximal and minimal α_i and, hence, θ_i values.

Figure 7.

Deduction of cortical tension and adhesion tension variations from the maximal and minimal contact angles. (A–C) Adhesion tension, Γ/2, as a function of relative adhesiveness, α_i, at gaps. The slope of the linear function equals cortical tension, β_c, and its intersection with the horizontal line of constant Γ/2 of 0.003 mJ/m² defines respective α_i values and hence contact angles. (A) Example R_i = 2 μm, maximal β_c line (solid), and minimal β_c line (dashed) were chosen to match minimal and maximal α_i values, respectively, and hence contact angles, as derived from Fig. 4. (B and C) Maximal and minimal lines as in (A) are shown separately for clarity for several R_i values. (D) Maximal and minimal β_c values corresponding to the slopes in (B) and (C) plotted as a function of R_i.

β_c decreased rapidly with increasing R_i for minimal angles, and it diminished much more slowly for the maximal angles, until both curves converged toward a common baseline (Fig. 7 D). This implies that β_c varies strongly at low R_i but maintains a minimal level of ∼0.03 mJ/m² when R_i > 9 μm. Minimal angles increase sharply for still higher R_i values, as seen from the $\overline{2{\theta }_i}$-$\overline{\mathit{l}}$ plot (Fig. 6). It is this increase in minimal angle levels that actually limits gap size to <4 μm, i.e., to less than one-third of the cell radius. To explore a possible variability of Γ/2, we assumed adhesion tension to vary around the measured average of 0.003 mJ/m² in our model calculations. However, this did not return meaningful maximal and minimal angles, as the curves for maximal and minimal β_c as a function of R_i intersected instead of converging (data not shown). This reinforced our initial assumption of a fixed Γ/2.

As to the possible variation in pressure differences, we considered that R_i = β_c/(p_c – p_i) (Eq. 3). Thus, with varying β_c, the pressure difference between cells and interstitium has to vary proportionally to maintain a constant R_i. At the minimal R_i = 2 μm, a variation of β_c between 0.35 and 0.044 mJ/m² would require the pressure difference to vary between 173 and 23 Pa according to Eq. 3. This range rapidly shrinks to between 4.5 and 1.5 Pa at the critical R_i = 9 μm. At higher R_i levels, cortical tension remains nearly constant and according to Eq. 3, the pressure difference (p_c – p_i) has to decrease to further increase R_i, to eventually remain at ∼1.5 Pa. These values are consistent with the average cell hydrostatic and interstitial pressures calculated above, and with the magnitude of the tissue mechanical parameters invoked.

Gaps in C-cadherin depleted ectoderm

C-cadherin is the main cell-cell adhesion receptor in the Xenopus gastrula. Its knockdown in the ectoderm by morpholino antisense oligonucleotide (C-cad-MO) reduces adhesion strength as expressed by tissue surface tension, σ, but residual C-cadherin and putative other adhesion factors (18) prevent complete tissue dissociation. C-cad-MO treatment leaves cortical tension β at the tissue surface unaffected but attenuates the cadherin-dependent downregulation of tension at contacts, β^∗ (Table 2) (1). Gap size and shape are affected by this experimental reduction of cell-cell adhesion, and as expected, cells appear more loosely attached (Fig. 8 A).

Figure 8.

Distribution of gap shapes in C-cad-MO-injected ectoderm. (A) Transmission electron micrograph of C-cad-MO ectoderm. Pixel dimensions are 2660 × 1662, with 53 nm/pixel. The scale bar represents 5 μm. EC, ectoderm; BC, blastocoel; EP, epithelium. (B) Angles in C-cad-MO ectoderm, measured at each point of contact between adjacent cells at 32 tri-cellular junctions (n = 96). (C and D) The frequency of gap sizes in C-cad-MO ectoderm, based on their average side length as measured (C) (n = 32) and Steiner ellipse corrected (D) (n = 32). (E) Interstitial areas within gaps at tri-cellular junctions in normal (uninjected) (n = 32) and C-cad-MO-injected ectoderm (n = 32).

We anticipated that with a change in tension ratios, contact angles may be altered by C-cadherin knockdown. In fact, the distribution of angles 2θ_i at the corners of gaps was shifted to larger values compared to uninjected ectoderm (Fig. 8 B). Assuming that as in normal ectoderm, the main peak approximates the true angle distribution, we estimated that, unexpectedly, the relative adhesiveness at gaps, α_i, increased twofold to 0.094 ± 0.061 mJ/m² upon C-cadherin knockdown. In C-cad-MO ectoderm, β^∗ is 0.15 ± 0.07 mJ/m² (1), and using σ_i = α_iβ_i = β_i – β^∗ we calculated a β_i of 0.166 ± 0.004 mJ/m² and a σ_i of 0.016 ± 0.011 mJ/m² (Table 2). The cell biological mechanism underlying this significant increase in σ_i remains to be examined.

Pressure differences are not significantly affected by the reduction of cadherin expression. Cortical tension at the tissue surface is 0.23 ± 0.03 mJ/m² (1), and we measured a curvature 1/R_s of 0.031 ± 0.023 μm⁻¹. Applying Laplace’s law, we calculated from these values the intracellular pressure, p_c = 2β/R_s, as 14.3 ± 0.7 Pa, which is only slightly lower than that of un-injected ectoderm. To estimate the pressure generated by the cortical tension at gaps, β_c/R_i, we used β_i as determined above for cadherin-depleted ectoderm and measured 1/R_i as 0.076 ± 0.174 μm⁻¹. This gave 12.6 ± 0.7 Pa, i.e., about the same pressure as in uninjected ectoderm. To balance pressures, the interstitial pressure, p_i, must be 1.7 ± 1.4 Pa, again similar to that of un-injected ectoderm (Table 2).

Gap side length, l, is only weakly increased in C-cad-MO ectoderm (Fig. 8 C). A minor peak of large gaps is observed, as in normal ectoderm, whereas the peak of smaller gaps is split in two upon C-cadherin depletion. Distinctions between peaks are obscured when size is corrected for section tilting (Fig. 8 D). For the population of smaller gaps, the average l increases by 20%, from 2.7 μm in uninjected ectoderm to 3.2 μm in C-cad-MO-injected tissue (Table 2). From Eq. 1, and with an average contact angle for the main angle peak of 23.7° and average curvature of 0.076 μm⁻¹, the average gap size in C-cad-MO embryos is predicted to be 2.9 μm, close to the 3.2 μm actually observed. The small discrepancy may be due to inaccuracies in angle measurement, as the calculation is very sensitive to this parameter. Although the gap side length is only weakly increased by C-cadherin knockdown, the curvature at the gap surface decreases strongly to compensate for the increased tension at gap surfaces, as pressure differences are unchanged. This leads to a twofold overall increase in average gap area from 5.2 to 11.2 μm² (Fig. 8 E), implying that gap volume is increased by ∼2-fold.

Discussion

In Xenopus gastrula ectoderm, ECM-filled channels at cell edges permeate the tissue, forming an uninterrupted network. Since cell adhesion in the ectoderm is too strong for gaps to be remnants of extracellular space left over after incomplete cell attachment, the ECM-enriched interstitial fluid must create conditions that can sustain these gaps. In an accompanying article, we derived a framework linking gap geometry to tissue mechanical variables, which we applied here to the analysis of the ectodermal interstitium. We measured gap side lengths, contact angles, and radii of curvature, and in conjunction with previously determined values for tensions at cell surfaces, we estimated cortical and adhesion tensions at gaps and cell hydrostatic and interstitial pressures to derive a tissue mechanical description of the gaps in normal and adhesion-attenuated ectoderm.

Tensions at gaps

In the ectoderm, the cortical tension at the tissue surface is reduced to one-fourth of its value as cells form contacts within the tissue (1), and cell cortex density is similarly reduced to one-fifth of its value. Surprisingly, cortical tension at the free surface of gaps does not return to that of the free outer surface of the tissue. In fact, the presence or absence of adhesion tension alone could quantitatively explain tension differences at cell contacts and at gaps: cortical tension at gaps remains the same as that between cells, as does the F-actin cortex density, and the slight excess of tension in gaps is solely due to the fact that adhesion tension reduces tension between cells but is absent in gaps. This assumption is suggested by our contact angle and F-actin staining data. It implies that the adhesion strength, σ_i, at gaps equals the adhesion tension, Γ/2. The molecular mechanisms of the downregulation of cortical tension upon cell contact are under active study (20), but it remains to be examined how a reduced cortex tension is maintained at free cell surfaces within a tissue but not at the tissue surface.

Gap contact angles, radii of curvature, and side lengths varied widely in the ectoderm, and we assumed that this is due to a corresponding variation of cortical and adhesion tensions. Surprisingly, to explain the minimal and maximal contact angles that we observed for the different gap surface curvatures, we had to assume that the small adhesion tension, Γ/2 = 0.003 mJ/m², varies little if at all. Cadherin densities differ considerably between individual ectodermal cells (1), but our preliminary data suggest that at gaps, cells are held together by noncadherin contacts whose molecular nature has yet to be identified (24). To obtain the observed variation of contact angles at constant adhesion tension, cortical tension between cells and at gaps, β_c, had to vary appropriately. In our model calculation, it ranged from 0.35 to 0.027 mJ/m², bracketing the average of 0.06 mJ/m² that had been determined independently (1). The depletion of C-cadherin in ectoderm increased cortical tension at contacts, but apparently also disproportionally at gap surfaces. If anything, one would expect a decrease, not an increase in adhesion tension Γ/2 upon cadherin knockdown, and thus the higher β_i/β_c ratio should be due to a slightly higher cortical tension at gap surfaces. However, tension here is still much lower than at the tissue surface. In future work, the CellFIT tool (25) could be applied to examine the regulation of tensions at gaps in more detail.

Intracellular and interstitial pressure

From our estimates of the variability of β_c we concluded that the pressure difference (p_c – p_i) had to vary between 1.5 and 173 Pa. Most of this variability is likely due to differences in intracellular pressure. Curved cell-cell boundaries (25) and differences in surface curvature between cells surrounding the same gap supported this notion. Average cell hydrostatic pressures deduced for normal and cadherin-reduced ectoderm represent pressure differences between cell interior and the blastocoel cavity, but they are comparable to those of other cell types (26, 27, 28). The pressure difference (p_c – p_i) is also affected by the interstitial pressure, p_i. For normal and adhesion-reduced Xenopus gastrula ectoderm, it is small compared to the intracellular pressure. In other interstitial gaps, for example, in tumors, a main factor is HA, whose swelling by hydration generates a fluid pressure (15). HA is also a main glycosaminoglycan in the Xenopus gastrula (29), and HA synthases Xhas1 and Xhas2 are expressed in the gastrula ectoderm (30, 31). Labeling with radioactive precursors indicated that glycosaminoglycan synthesis continues throughout gastrulation in Xenopus (32), providing a constant supply of ECM material to maintain an uninterrupted network of interstitial channels. HA degradation may contribute to the overall ECM balance, as the hyaluronidase Hyal2 is also expressed in the ectoderm (29).

The ectoderm is sealed off by a tight epithelial layer from the outside of the embryo, which should be impermeable to the ECM fluid. At the blastocoel surface, cells are connected through contacts of about 100 nm separation distance (D.B., unpublished data). HA synthesized by Xhas2 in the ectoderm is >1000 kDa in size (29), and its radius of gyration is thus >100 nm (33), probably too large for unhindered passage into the blastocoel. However, ECM material including HA is present in the blastocoel cavity (16, 32), and occasional gaps opening into that compartment are seen at the ectoderm surface. Possibly, the accumulation of ECM material in the interstitium is balanced in part by the punctuated release of material into the blastocoel, where it is preferentially degraded. To generate a pressure difference between interstitium and blastocoel of 4 Pa, a small steady-state HA concentration difference of 0.2 mg/mL would be sufficient (34). The sudden release of ECM fluid should lead to pressure fluctuations, whereas a net positive equilibrium pressure is maintained in the long term. Such a model is also consistent with interstitial pressure being conserved in the larger gaps of cadherin-depleted ectoderm. Apparently, the net production of ECM fluid is not limiting and is unaffected by cadherin depletion. The fluid balance could then be controlled by the interstitial pressure if a discharge of excess ECM fluid occurred whenever a threshold pressure is surpassed.

Temporal fluctuations of gap parameters

Tissue mechanical variables that determine gap sizes and shapes show temporal fluctuations. The magnitude of cortical tension fluctuations can be estimated from measurements of spontaneous cell-cell boundary length fluctuations in the ectoderm (1). Their average duration is 5.5 min and the average rate of length change is 2 μm/min. If all three cell-cell boundaries radiating from a gap contracted or expanded simultaneously, gap side length would widen or shrink maximally by ∼1.4 μm during 5 min. This total size difference of ∼3 μm matches the observed range of gap sizes, i.e., cell boundary fluctuations are at an order of magnitude that is consistent with a contribution to gap size variation.

During gap size changes, interstitial fluid flow must occur: a contraction-induced active reduction in gap size in a segment of a channel will cause a local pressure increase, and an active size increase will lower the interstitial pressure. To see whether gaps can remain close to tension and pressure equilibria during such processes, we estimated the pressure fluctuation for expected rates of gap volume changes (Appendix B). We found that pressure peaks should be <0.15 Pa, which is small compared to the baseline interstitial pressure of 4 Pa. It suggests that gap size changes driven by cortex tension fluctuations do not substantially contribute to variations in interstitial pressure, and that gaps are mostly near their shape and size equilibria during this process. However, cross-linking of HA by HA-binding proteins could increase ECM fluid viscosity and thus require larger pressure differentials, causing more significant fluctuations in interstitial pressure. Overall, interstitial flow is expected to be limited due to the shallow pressure gradients and the randomness of driving forces that cause frequent alternations of flow directions. Limited convection in the interstitial space suits the possible transport of morphogens, e.g., by diffusion that leads to the establishment of stable morphogen gradients (22).

Limitations and predictions

We were able to sketch the basic outlines of the mechanics of fluid-based interstitial gaps. Two main limitations of our analysis arise from the use of fixed and sectioned tissue to visualize interstitial gaps. First, although this approach has the advantage of being applicable to histological data, directly visualizing the exact three-dimensional shape of interstitial channels in living tissue by, e.g., confocal microscopy would refine our conclusions and also uncover possible fixation artifacts with regard to shape parameters. Second, cell-cell boundary fluctuations are an essential feature of compact tissues (35) and have been observed in gastrula ectoderm (1). However, data on the dynamics of interstitial gaps are lacking. We observed green-fluorescent-protein-filled gaps by confocal microscopy, but only in tissue explants where the frequency of gaps is reduced, and only close to the explant surface (13). We studied gastrula ectoderm because essential tissue mechanical data for normal and cadherin-depleted tissue were available, but to visualize gap shapes and dynamics, the poor optical properties of the yolk-rich ectoderm are problematic, and other systems, e.g., transparent embryos, will be advantageous. Also, direct measurement of tensions and pressures would test the model more rigorously. Conceptually, a better understanding of the mechanics of asymmetrical gaps is desirable, as their approximation by symmetrical gaps is limited.

Our model predicts how changes in variables such as adhesion tension, cortical tension, cell size, or adhesion strength, should affect gap geometry, i.e., their size and shape. The inverse procedure, to infer mechanical properties of a tissue from gap geometry, is more limited. Multiple combinations of mechanical parameters can yield the same gap shape and size as adhesion strength varies by three orders of magnitude, and gaps are expected to be fairly similar in different tissues (11). For example, when we measured gap sizes in fusing chicken palate using a published micrograph (2), it was on average 5 μm, similar to gap sizes in Xenopus ectoderm. However, when basic parameters such as tissue surface tension are known in addition, other variables can be reasonably estimated from the gap geometry, e.g., absolute pressure differences from gap boundary curvatures. However, relative measures can also provide valuable information, e.g., when contact angles at gaps, translated into relative adhesiveness, limit possible mechanisms of adhesion. As another example, the existence of concave gaps in a tissue not only implies that the interstitial pressure exceeds the intracellular pressure, but it also indicates a relative adhesiveness that ensures that contact angles exceed 30°. Given the multitude of different tissue types, our model provides a starting point for the classification of tissues and interstitial gaps according to mechanical criteria.

Conclusions

Interstitial channels that permeate the ectoderm of the Xenopus gastrula can be maintained by the insertion of a fluid-like ECM into the highly cohesive tissue, which allows the free cell surfaces created at gaps to assume cortical tensions consistent with gap stability. In sections, these channels appear as gaps, and their geometry depends on tissue mechanical variables such as cortical tension and hydrostatic pressure within and outside cells. The natural variation in cortex tensions and intracellular and interstitial pressures generates a spectrum of gap shapes and sizes. Tension differences between gap cell surfaces and cell-cell interfaces at gaps are small, on the order of magnitude of adhesion tensions. This can be explained by an adhesion tension being absent from the nonadhesive free cell surface at gaps while cortical tension is the same at cell contacts and at gap surfaces. Upon C-cadherin knockdown, cell adhesion is reduced and gap volume is increased, but intracellular and interstitial pressures remain essentially unchanged.

Author Contributions

R.W. and D.B. conceived the research. D.B. designed and performed the experiments. S.E.P. contributed the Steiner ellipse correction. All authors analyzed data and wrote and revised the manuscript.

Editor: Jochen Guck.

Appendix A: Correction for oblique sectioning

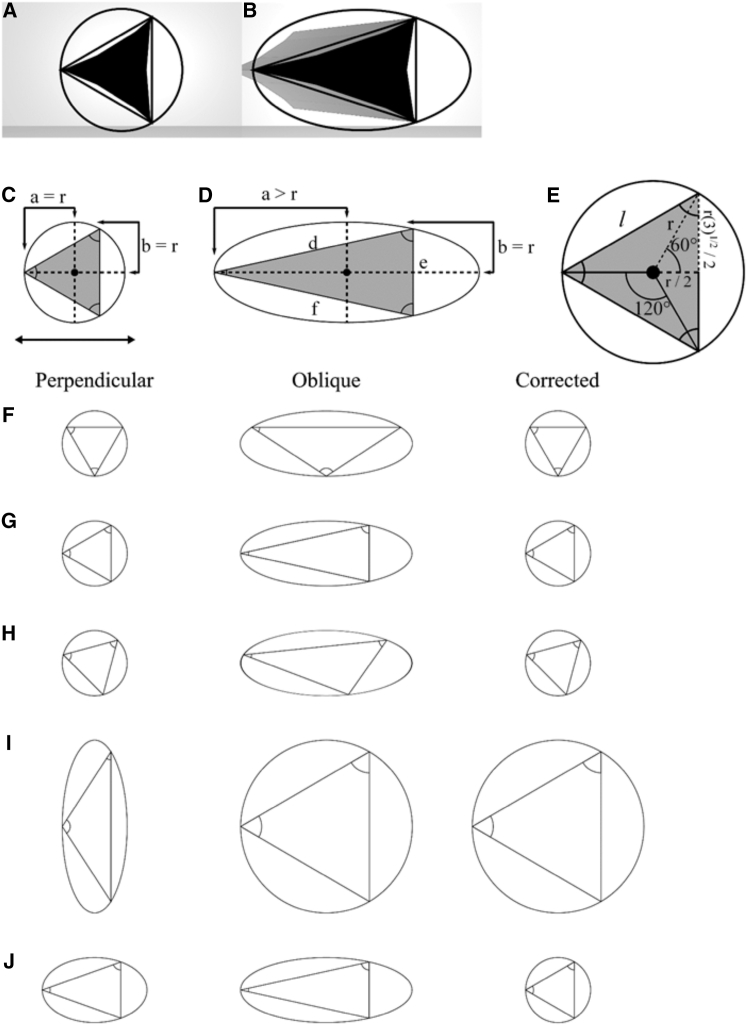
We consider channel-like interstitial gaps as defined by Parent et al. (11). When sectioned perpendicular to the long axis of the channel, an equilateral triangle can be constructed from the vertices of the symmetric gap obtained (Fig. 9 A). Rotating this triangle about its center generates a circle whose perimeter describes the possible locations of the vertices. This is equivalent to observing the gap in different orientations. If the gap is circumscribed by a circle all the way down the channel, a prism contained in a cylinder is formed. Taking a cross section of the cylinder at an angle results in an ellipse and a “stretched” triangle (Fig. 9 B). To correct for this deformation, we developed a procedure based on the properties of a Steiner ellipse. The Steiner ellipse correction allows one to transform any triangle into an equilateral triangle, thus correcting the distorting effects of oblique sectioning on gap shapes. The ellipse describes all possible positions of the vertices of this “stretched” triangle, it is the ellipse of least area that circumscribes the “stretched” triangle, and its center corresponds to the centroid of the stretched triangle. It is known as a Steiner ellipse (36). The Steiner ellipse correction rests on the assumption that sectioned tri-cellular gaps are in fact symmetrical, and that any observed asymmetry is due to oblique sectioning (Fig. 9, C and D). Though the semi-major axis, a, of the circumscribing circle may increase in an oblique section, the semi-minor axis, b, will remain the same (Fig. 9, C and D). Furthermore, it is clear from the diagrams in (Fig. 9 C) and (Fig. 9 D) that for both the circumscribing circle and the Steiner ellipse, the semi-minor axis is equal to the radius of the circumscribing circle:

$$\mathit{b}=\mathit{r}\mathit{.}$$ (A1)

Figure 9.

Steiner ellipse correction for oblique sectioning. (A and C) A section perpendicular to the long axis of an interstitial gap channel results in an equilateral triangle circumscribed by a circle with a semi-major axis, a, equivalent to a semi-minor axis, b. (B and D) An oblique section of a gap channel results in a stretched triangle circumscribed by an ellipse with a semi-major axis longer than the semi-minor axis. (D and E) The Steiner ellipse correction can be used to determine the side length, l, of the equilateral triangle using the three side lengths d–f of the stretched triangle. This transforms all gaps with various configurations of unequal side lengths to symmetric gaps with equal side lengths (F–J).

This property can be used to determine the side length, l, of the equilateral triangle using the three side lengths of the stretched triangle, d, e, and f (see Fig. 9 D), as follows.

The semi-minor axis of an ellipse can be determined from its side lengths by (37)

$$\mathit{b}=\frac{1}{3}\left(\sqrt{{\mathit{d}}^2+{\mathit{e}}^2+{\mathit{f}}^2-2\mathit{Z}}\right)$$ (A2)

$$\mathit{Z}=\sqrt{{\mathit{d}}^4+{\mathit{e}}^4+{\mathit{f}}^4-{\mathit{d}}^2{\mathit{e}}^2-{\mathit{e}}^2{\mathit{f}}^2-{\mathit{f}}^2{\mathit{d}}^2}.$$ (A3)

The side length, l, of the equilateral triangle is related to the radius, r, of the circumscribing circle by

$$\mathit{r}=\mathrm{l}/\left(3^{1/2}\right)$$ (A4)

(see Fig. 9 E).

By substituting Eqs. A2 and A3 into the left side of Eq. A1 and Eq. A4 into the right side, the relation

$$\mathit{l}=\left({\left(3\right)}^{1/2}/3\right){\left({\mathit{d}}^2+{\mathit{e}}^2+{\mathit{f}}^2-2{\left({\mathit{d}}^4+{\mathit{e}}^4+{\mathit{f}}^4-{\mathit{d}}^2{\mathit{e}}^2-{\mathit{e}}^2{f}^2-{\mathit{f}}^2{\mathit{d}}^2\right)}^{1/2}\right)}^{1/2}$$ (A5)

is produced.

The Steiner ellipse correction transforms all gaps whose three sides are not of equal length (i.e., asymmetric gaps) to symmetric gaps that have equal side lengths. This results in a change in contact angles, which may or may not all be equal. Some examples and their effects on shape are shown in Fig. 9, F–H. The closer the angle of an obliquely cut gap is to being bisected by the semi-major axis, the smaller it becomes relative to the perpendicularly sectioned gap. The closer the angle is to being bisected by the semi-minor axis, the larger it becomes. Unfortunately, it is not possible to distinguish obliquely sectioned gaps from truly asymmetric ones without imaging an entire channel as well as the two lacunae connected by it in Fig. 3 D. The effects of asymmetric gaps on the final data set, however, are expected to average out, as certain asymmetric shapes will lead to an overestimation of true gap size (Fig. 9 I), whereas others will lead to an underestimation (Fig. 9 J).

Appendix B

During cell boundary fluctuations, the volume, V, of a channel segment of gap side length l and length Δh changes approximately as dV/dt = 2lΔhdl/dt. This volume-change rate is equal to the difference between flow rates at the ends of the segment. Approximating the flow using the Hagen-Poiseuille equation and the channel cross-section area as A = l²/2, we obtain dV/dt = 2lΔhdl/dt = dV_i/dt – dV_o/dt = [l⁴/32πη] [dp/dh(h_i) – dp/dh(h_o)], where dp/dh(h_i) is the pressure gradient at one end of the segment and dp/dh(h_o) that at the other end. We considered a channel of length Δh = 4l where constriction induced a pressure peak, p_ip, halfway along its length, and assumed that the induced pressure, p_i, decreased exponentially to vanish at both ends where the channel branches and suddenly increases in diameter. At the symmetrical pressure peak, the flow rate is zero. Thus, dp/dh = (p_ip/l)e^−h/l, and with l = 3 μm, the rate of boundary constriction dl/dt = 2 μm/min (15), and the viscosity of a concentrated, physiological HA solution η = 0.1 Pa.s (38, 39), the peak pressure, p_ip, is 0.15 Pa. This value is an overestimate based on maximal gap constriction.