Pairwise Classifier Ensemble with Adaptive Sub-Classifiers for fMRI Pattern Analysis

Abstract

The multi-voxel pattern analysis technique is applied to fMRI data for classification of high-level brain functions using pattern information distributed over multiple voxels. In this paper, we propose a classifier ensemble for multiclass classification in fMRI analysis, exploiting the fact that specific neighboring voxels can contain spatial pattern information. The proposed method converts the multiclass classification to a pairwise classifier ensemble, and each pairwise classifier consists of multiple sub-classifiers using an adaptive feature set for each class-pair. Simulated and real fMRI data were used to verify the proposed method. Intra- and inter-subject analyses were performed to compare the proposed method with several well-known classifiers, including single and ensemble classifiers. The comparison results showed that the proposed method can be generally applied to multiclass classification in both simulations and real fMRI analyses.

Electronic supplementary material

The online version of this article (doi:10.1007/s12264-016-0077-y) contains supplementary material, which is available to authorized users.

Introduction

There are many analysis methods for exploring the mechanisms underlying the vast functions of the brain. They use not only the location of activated voxels but also other information like spatial dependency [1–3] or temporal correlation [4–8] of fMRI signals. Multi-voxel pattern analysis (MVPA) has been widely used to analyze the spatial pattern information for fMRI classification [9–12]. There are a large number of voxels in fMRI data, and only a small portion has decisive information for classification [13]. Therefore, a feature-selection strategy is crucial for the performance of a classification. Informative voxels are selected as features by well-known feature-selection methods such as analysis of variance (ANOVA) [13–17], support vector machine (SVM) [13, 18–20], and recursive feature elimination (RFE) [18].

General-purpose ensemble classifiers, including random forest [21] and random subspace ensemble [13], have been used in recent studies on spatial pattern analysis. The ensemble classifiers randomly select voxels for the feature set mainly because it is difficult to find the optimal subset of feature space in general applications for classification. For the detection of specific functional regions in the brain, the searchlight approach has been applied to fMRI classification [29–32]; this merges neighboring voxels into a feature vector and evaluates it. Since multiple brain regions can be involved in performing a mental function, multiple feature vectors are useful for fMRI classification, and the informative feature vectors can be distributed in various locations and sizes. However, no studies of fMRI-optimized classifiers have used multiple feature vectors to improve the classification performance.

This paper presents a binary classifier ensemble for fMRI analysis, where each binary classifier includes multiple sub-classifiers. The location and size of informative feature vectors for each sub-classifier are adaptively determined by customized searchlight analysis. Because the number of useful sub-classifiers also depends on the classification problem, the proposed method adaptively determines the number of sub-classifiers for each binary classifier. The proposed method combines the classification outputs from all sub-classifiers.

The proposed method applies ensemble learning to the multiple sub-classifiers to improve the fMRI classification. In contrast to the previous methods, the proposed method is optimized for fMRI analysis—it uses a searchlight approach to construct the sub-classifiers, exploiting prior knowledge that specific neighboring voxels can contain spatial pattern information specialized for specific functions.

The proposed method provides a multiclass classification framework, and can be applied to both binary and multiclass classifications. The multiclass classification problem can be solved by an ensemble of binary classifications [22]. Since binary classification is usually much easier to solve than multiclass classification, many studies have used a pairwise approach that turns a multiclass problem with N classes into N(N−1)/2 pairwise classifications, in which each pairwise classifier can be considered as an independent binary classification problem, and the output class is obtained by combining the results of all pairwise classifications. In particular, pairwise classification has gained a great deal of popularity for its exceptional performance [23]. Wu et al. [24] suggested a pairwise coupling method for multiclass classification, and Li et al. [25] used a pairwise classifier for tissue classification based on gene expression. Feature selection for pairwise classification has been studied to use the feature subspace with a high discriminative potential for each class-pair. Silva et al. and Ji et al. emphasized the importance of pairwise feature selection [26, 27], and Chen et al. [28] took advantage of the pairwise feature selection in gene selection. In multiclass fMRI classification, the informative regions can be distinctively distributed for each class-pair since different regions of the brain are associated with different functions, as shown in previous MVPA studies [9–12]. Therefore, each pairwise classifier can have its own optimum feature set for classification. The proposed method is the first approach that takes the pairwise-optimized feature set into account in fMRI multiclass classification.

In this study, simulation and fMRI experiments were performed to verify the proposed method, including intra- and inter-subject analyses using the well-known fMRI experiment of Haxby [9] with open-source data.

Materials and Methods

Methods

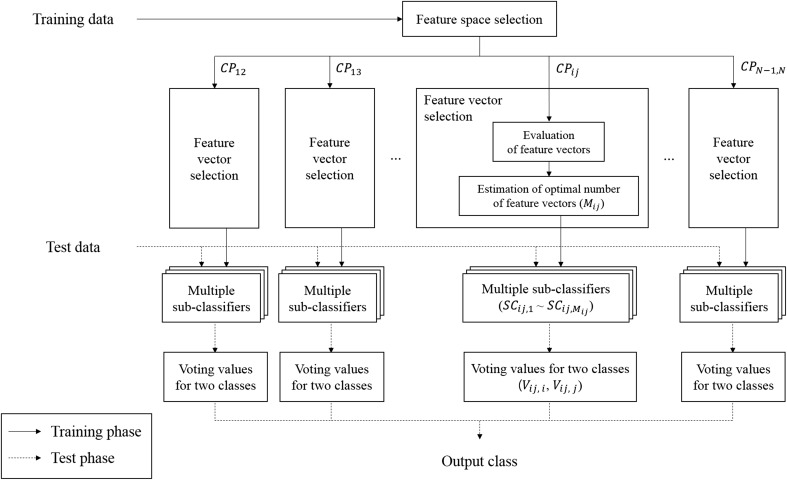
The proposed method consisted of an ensemble of sub-classifiers with an optimized feature set, and the classification output was made by voting from all the sub-classifiers. The method included a training phase and a test phase. The training phase had three stages: feature space selection, selection of feature vectors, and construction of the sub-classifiers. The test phase included classification and voting of the sub-classifiers (Fig. 1). Pseudocodes of the proposed method are described in the supplementary materials.

Fig. 1.

Flowchart of the proposed method. The straight lines refer to the training phase while the dashed lines refer to the test phase.

Training Phase

Feature Space Selection

First, the brain region was segmented according to the image intensity. Then the feature space for multiclass classification was determined by the conventional feature selection method before pairwise classification. The feature selection process was performed using brain regions of the training data. Five feature selection methods were used to select the informative feature spaces: whole brain, ANOVA, SVM-based feature selection, recursive feature elimination (RFE), and a ventral temporal cortex (VTC) mask. The detailed procedures of each feature selection method are described in the supplementary materials. All of the feature selection methods were used for the proposed and the previous classification methods for comparison.

Selection of Feature Vectors

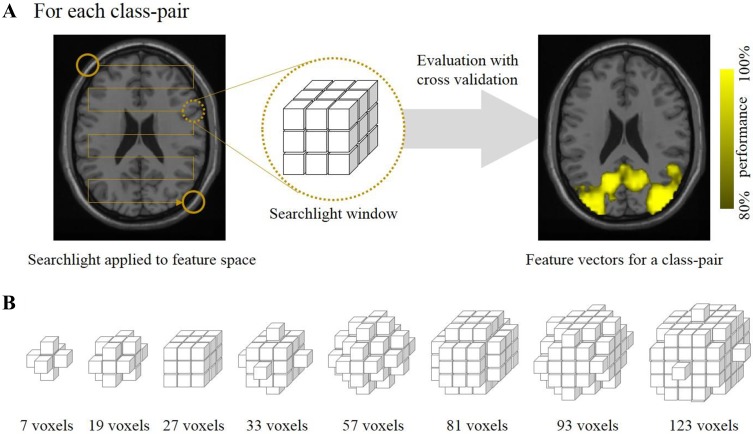
In fMRI pattern analysis, the pattern information distributed over multiple voxels was analyzed using a feature vector for the classification. Each classification had its own optimal feature set containing critical features for high classification performance. For each class-pair, the selected regions in the feature space were evaluated with the searchlight approach, detecting the informative feature set for the pairwise classification (Fig. 2A). In the searchlight analysis, the selected voxels in the feature space were used as center points of the searchlight windows. The spatial pattern of the voxels in the searchlight window was treated as a feature vector of multiple voxels. There can be a number of regions providing feature vectors that could be useful for the classification, and the proposed method was designed to employ all useful feature vectors. The performance of the classifier was defined as a ratio of the correct classification. Leave-one-trial-out cross-validation was performed using the training data with multiple trials, and the reliability of each feature vector was estimated as the classification performance. The optimal size of the searchlight window depends on the spatial size of the pattern [32], and the proposed method adaptively determined the window size to extract a detailed pattern. In this study, the radius of the searchlight window had a value between one and three voxels. The searchlight size showing the highest classification performance was selected at each location. Figure 2B shows the searchlight windows with various sizes.

Fig. 2.

Selection of feature vector using the searchlight approach. A Illustration of the feature vector evaluation. Highlighted voxels indicate the informative regions (center of the searchlight window) for the class-pair of faces and houses. B Candidate shapes of searchlight windows and numbers of voxels included in the windows.

The number of useful feature vectors, which can be different for each classification, is important for maximizing performance. At the same time, using an excessive number of feature vectors should be avoided because it may cause over-fitting and add noise to the classifier. Thus, the proposed method adaptively estimated the optimal number of useful feature vectors. In this paper, the number of useful feature vectors for a class-pair of i and j classes (CP _ij) was denoted as M _ij. For estimation of the optimum number of feature vectors for each class-pair, leave-two-trial-out cross-validation was performed. For selection of the optimal M _ij, a number of binary classifications were conducted using the training data of classes i and j with various numbers of feature vectors. For each classification, the most reliable feature vectors were selected based on the searchlight analysis. The number of feature vectors with the best performance for a class-pair C _ij was assigned to M _ij. In the case that the feature vectors had the same performances, the feature vectors were randomly ordered. When two or more feature vectors produced the same and best performance, the largest value was assigned to M _ij since the ensemble of many classifiers is more robust to noise.

As a result, the locations, spatial sizes, and number of useful feature vectors were determined for the binary classification.

Construction of the Sub-classifiers

A sub-classifier was constructed for each selected feature vector. Each sub-classifier took into account the information of the two classes of interest.

A linear SVM classifier was used as the sub-classifier because of its simplicity and robust performance [19, 20], and the decision boundary was determined using the training data of two classes of interest. Each class-pair consisted of multiple sub-classifiers having their own optimized feature vectors.

Test Phase

After the training phase, each class-pair consisted of a number of sub-classifiers. When a pair of classes i and j (CP _ij) had a number of feature vectors of M _ij, the class-pair had M _ij sub-classifiers of {SC _ij,1, SC _ij,2, …, SC _ij,Mij} (Fig. 3A). The test data of an unknown class were applied to all pairwise sub-classifiers. In the sub-classifier SC _ij,k of a class-pair CP _ij, the probabilities of class interests, P _ij,i,k and P _ij,j,k, were estimated from the signed distances of the feature vectors from the decision boundary. The probability was calculated by taking the probability density function (PDF) into account. The PDFs of the signed distance of each class of CP _ij from the decision boundary were estimated from the training data. The distances between the training data and the decision boundary were applied to a kernel density estimation (KDE) [33, 34] to estimate the PDF for each class. The KDE is a non-parametric method to estimate the underlying PDF of a random variable from its histogram and kernel function. The kernel function for the KDE is a Gaussian function, and the standard deviation of the kernel function is chosen by approximation of the normal distribution [35]. Each class-pair had a different number of sub-classifiers because the number of useful feature vectors depends on the class-pair. Thus, normalization using the number of sub-classifiers was required. Therefore, the voting values of V _ij,i and V _ij,j were defined by normalizing the probability as follows:

$$V_{ij,i}=\sum _{k=1}^{M_{ij}}{P}_{ij,i,k}/M_{ij},V_{ij,j}=\sum _{k=1}^{M_{ij}}{P}_{ij,j,k}/M_{ij}$$ 1

Fig. 3.

Voting in the test phase. A Calculation of voting values of a class-pair. B Calculation of the classification result.

The voting values were obtained from every class-pair, as shown in Fig. 3B. Finally, the proposed classifier selected the class with the largest sum of voting values from the related class-pairs as follows:

$$\text{Estimated}\text{class}=arg\underset{k}{max}{\sum }_{\{(i,j)|i=k\text{or}j=k,i<j\}}{V}_{ij,k}$$ 2

where the preceding subscript number is always smaller than the following one (e.g. i < j in CP _ij).

Experiment

The proposed classifier was compared to widely used classifiers, such as SVMs with one-against-all and pairwise environments, adaptive boosting (AdaBoost), bagging, random forest, random subspace ensemble, and logistic regression (LR) with elastic net regularization [36, 37]. We used the standardized Weka software [38] and default parameters: a complexity of 1 for the SVM, a weight threshold of 100 for the AdaBoost, a size of each bag of 100% for the bagging, and a size of a subspace of 0.5 for the random subspace ensemble. Exceptionally, the number of base classifiers was set to 1000 for all tested ensemble classifiers to boost performance. The experiments showed that the performances were saturated at an ensemble of 1000 classifiers in all cases. Linear SVM classifiers were used as the base classifiers for the classifier ensembles. For the LR classifier with elastic net regularization, we used the implemented package glmnet (http://www.stanford.edu/~hastie/glmnet_matlab/). The parameters of elastic net regularization were selected to have the highest performance in grid searches. The parameter α was a tradeoff parameter between lasso and ridge penalties, which was selected from a range of [0, 0.1, 0.2, …, 1]. The parameter λ was a Lagrange multiplier, which was selected from a range of [0, 0.001, 0.002, …, 1].

Simulation

In fMRI classification, the pattern information is analyzed for classification. A simulation was performed to assess the properties of the proposed method on the simulated images, where locations of the pattern information and its contrast-to-noise ratio (CNR) were known. The simulation contained different conditions including ten levels of CNR and two settings of pattern information overlapping to show the performance of the proposed method in comparison to the previous classification methods.

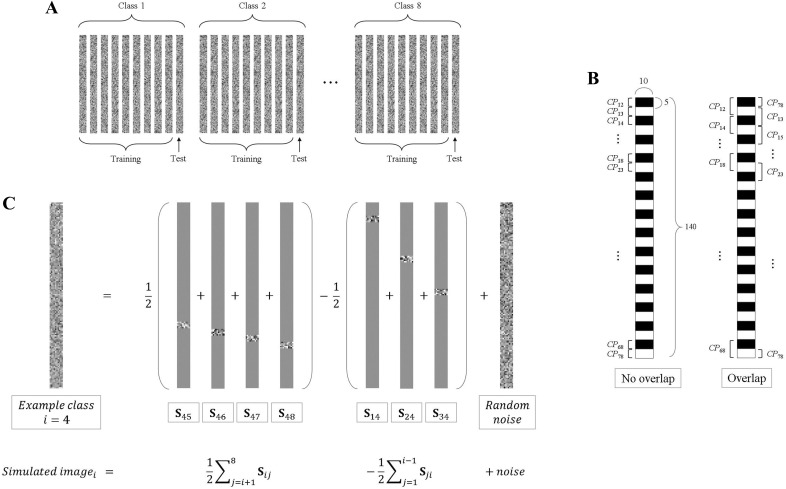
For each simulation, there were eight classes and each class had ten simulated images. Nine images of each class were used as training data and the other one was used as testing data (Fig. 4A). The simulated images were generated as follows:

1. Noise images of 140 × 10 were randomly generated with a zero mean and a standard deviation of ${\mathit{\sigma }}_N$. The noise images were different for every simulated image.

2. The pattern information in the brain could have arbitrary values for each class-pair and region, so the value of each voxel was randomly generated to generalize the pattern information by selecting voxel values from a normal distribution with a zero mean [39]. The standard deviation of the pattern information was adjusted so that its CNR could be a value of [0.1, 0.2, …, 1.0], which was defined as follows:

   $$\text{CNR}=\frac{{\mathit{\sigma }}_S}{{\mathit{\sigma }}_N}$$ 3

   where ${\mathit{\sigma }}_S$ is the standard deviation of the pattern information.

3. The locations of the pattern information in the simulated images were different according to class-pairs as shown in Fig. 4B. A simulated pairwise signal S _ij of 140 × 10 for a class-pair CP _ij included pattern information (as specified in B) on the pre-allocated region in Fig. 4B, and all zeros in the other regions. In the first no-overlap setting, the pattern information that was useful to classify each class-pair was localized separately, so that each class-pair had pattern information of a 5 × 10 region exclusively. On the other hand, in the second overlap setting, each class-pair had 10 × 10 pattern information and every region had overlapped pattern information which could distinguish two class-pairs.

4. The simulated image for class i was generated by adding the simulated pairwise signal to the noise image (Fig. 4C) as follows:

   $$\text{Simulated}{\text{image}}_i=\frac{1}{2}\sum _{j=i+1}^8{\mathbf{S}}_{ij}-\frac{1}{2}\sum _{j=1}^{i-1}{\mathbf{S}}_{ji}+\text{noise}$$ 4

   The simulated pairwise signal S _ij was divided and distributed to two related classes i and j with opposite signs. While S _ij was the optimal signal for the classification of classes i and j, other regions could contribute slightly to distinguishing classes i and j.

5. The signal intensity of each voxel in the simulated image was normalized to have zero mean and unit variance for multiple trials and various classes.

Fig. 4.

Simulation settings. A Composition of the whole simulated dataset. B Location of the pattern information in the simulated image according to class-pairs with two settings of the simulation. C Example of the construction of a simulated image for class i.

For each CNR and overlapping setting, ten repetitions of simulations were performed to evaluate the performance of the proposed method in comparison with the other classifiers. The individual performance could be caused to fluctuate by the randomness. However, the simulation was performed multiple times on images with a number of voxels that were adjusted to have intended CNRs. From the multiple simulations, the performance tendencies of the classifiers could be validated with respect to CNR. For analysis of the simulated data, all voxels were used as the feature space.

fMRI Dataset

Actual fMRI datasets were used for training and testing of the proposed method for verification. We used an open-source fMRI dataset of Haxby’s experiment [9]. All the data in the set were acquired from seven subjects. The first subject’s data are available as an example of the MVPA MATLAB Toolbox (http://code.google.com/p/princeton-mvpa-toolbox/) and the data of the other six subjects can be downloaded from the PyMVPA.org Data Server (http://data.pymvpa.org/datasets/haxby2001/). The fMRI data were acquired while visual stimuli were presented to the subjects. The experiment consisted of multiple runs: 10 runs for subject 1, 11 for subject 6, and 12 for each of the rest. Note that the ninth run of the fifth subject from the PyMVPA.org data server (subject 6 in this paper) was not included in the analysis because the data have been reported to be corrupted. Each run consisted of eight blocks of visual stimuli in eight classes: faces, houses, cats, bottles, scissors, shoes, chairs, and scrambled pictures, where the scrambled pictures were composed of random textures. The order of the class blocks were randomized across runs. Whole-volume images of brain activity containing 64 × 64 × 40 voxels were acquired during each period of repetition (TR) of 2500 ms. Each class block contained 9 TRs. Thus, each run had 72 volume images (8 class blocks × 9 volumes/block).

The entire dataset was preprocessed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8) for motion correction, removal of low-frequency drift, and registration to align the different subject images into the same space with isotropic voxels of 3.5 × 3.5 × 3.5 mm³. The spatial registration was performed with 12 linear affine transformation and non-linear transformation of SPM8. The signal intensity of each voxel was normalized to have zero mean and unit variance for multiple trials and various classes. The hemodynamic delay was considered to be 5 s [40]. In the analysis, it was not appropriate to take each volume image for training or testing because the multiple volume images within the same block were highly correlated. Therefore, the training and the test processes were performed on an average of nine volume images in each class block. The number of voxels in the feature space was around 10000–30000 for the whole brain analysis, 300–700 for the VTC mask, and 1000 for the other feature space selection methods.

The analyses were performed in intra- and inter-subject experiments. In the intra-subject experiment, the data of each subject were analyzed independently. For each subject, the classifiers were trained with all runs except one, and the excepted run was used as the test signal. Every run was used as test data (as with the jackknife method). The inter-subject analysis was performed to verify that subject-invariant pattern information could be extracted using the proposed method. In the inter-subject analysis, the classifiers were trained with signals from all subjects except one, and the signals from the excepted subject were used for testing. Every subject was used as a test subject, in succession.

Results

Simulation

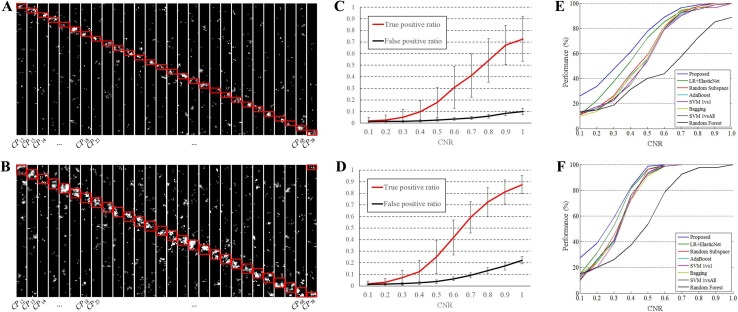
An example of the informative regions detected by the proposed method for pairwise classification from the training phase of both settings is shown in Fig. 5A and B. This typical example is from one of ten repetitions of simulation. For each class-pair, centers of the searchlight windows that had significant classification performances (>90%) are highlighted. The highlighted regions were highly correlated with the locations of the pairwise pattern information in both settings of the simulations. The CNR of the simulated pattern information was 0.6 for Fig. 5A and B. Figure 5C and D show the correctness of the proposed method in selection of the feature vector. True positive ratio and false positive ratio represent the proportions of the selected feature vectors in the red boxes and the other sections, respectively. Mean and standard deviation were measured across all repetitions of simulation for each CNR. The correlation between the highlighted regions and pattern information was well preserved for various CNRs. The result showed that the proposed method can detect informative regions. Figure 5E and F show the performance of the proposed method in comparison with the other classifiers in both settings of the simulations. The classification performances of eight classes in ten trials were averaged. The results showed that the proposed method had the highest performance in all conditions, suggesting that the proposed method is robust over a wide range of CNR and information overlapping. For all tested classifiers, the performances improved as CNR became large. When CNR decreased, the performance differences between the proposed method and the other methods increased since the proposed method adaptively searches for an informative feature set.

Fig. 5.

Results of the simulation. For each class-pair, informative regions analyzed by the proposed method are highlighted while the locations of the pairwise pattern information are displayed by red boxes in both settings of the simulation; (A) no overlap and (B) overlaps exist in pairwise informative regions. The correctness of the proposed method in selection of the feature vector for (C) no overlap and (D) overlapped settings. The classification performances for (E) no overlap and (F) overlapped settings with respect to CNR.

A Wilcoxon signed-rank test was performed to verify the significance of the performance difference [41, 42]. The test was performed for all CNR with a null hypothesis of PER _proposed ≤ PER _conventional, where PER denoted the performance. The statistical analysis showed that the proposed method outperformed the compared classifiers (Tables 1 and 2).

Table 1.

P values from Wilcoxon signed-rank test in the non-overlap setting

Classifier	CNR
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
SVM 1vsAll	0.0090**	0.0083**	0.0865	0.0059**	0.0064**	0.0641*	0.2004	0.1367	0.1587	–
SVM 1vs1	0.0139**	0.0213**	0.0125**	0.0054**	0.0076**	0.0315*	0.0579*	0.1807	0.0899	–
AdaBoost	0.0090**	0.0083**	0.0125**	0.0216**	0.0038**	0.0641*	0.1468	0.2113	0.1587	–
Bagging	0.0059**	0.0104**	0.0178**	0.0150**	0.0054**	0.0467*	0.3766	0.1807	0.1587	–
Random Forest	0.0429*	0.0076**	0.0038**	0.0064**	0.0059**	0.0038**	0.0038**	0.0059**	0.0059**	0.0139**
Random SubSpace	0.0090**	0.0142**	0.0090**	0.0178**	0.0142**	0.0641*	0.1990	0.2965	–	–
LR + ElasticNet	0.0090**	0.0542*	0.1468	0.0776	0.2234	0.1727	0.2771	0.3274	–	–

The P values were acquired with the null hypothesis of PER _proposed ≤ PER _conventional. En dashes in the table indicate that the statistical test was not available since both results showed 100% performance. Multiple comparison correction was performed by controlling the false discovery rate (FDR) < q.

* q < 0.1, ** q < 0.05.

Table 2.

P values from Wilcoxon signed-rank test in the overlap setting

Classifier	CNR
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
SVM 1vsAll	0.0122**	0.1302	0.0693*	0.1244	0.0339*	0.1587	–	–	–	–
SVM 1vs1	0.0464*	0.0213**	0.0150**	0.1184	0.0888	–	–	–	–	–
AdaBoost	0.0260**	0.1068	0.0253**	0.0865	0.0339*	0.1587	–	–	–	–
Bagging	0.0260**	0.0917	0.0250**	0.0711*	0.0294*	0.1587	–	–	–	–
Random Forest	0.0296*	0.0372*	0.0025*	0.0025**	0.0025**	0.0059**	0.0216**	0.0899	0.0899	–
Random SubSpace	0.0332*	0.0807	0.0618*	0.0641*	0.1807	0.1587	–	–	–	–
LR + ElasticNet	0.0549*	0.0881	0.2643	0.4583	0.1807	–	–	–	–	–

The P values were acquired with the null hypothesis of PER _proposed ≤ PER _conventional. En dashes in the table indicate that the statistical test was not available since both results showed 100% performance. Multiple comparison correction was performed by controlling the false discovery rate (FDR) < q.

* q < 0.1, ** q < 0.05.

fMRI Dataset

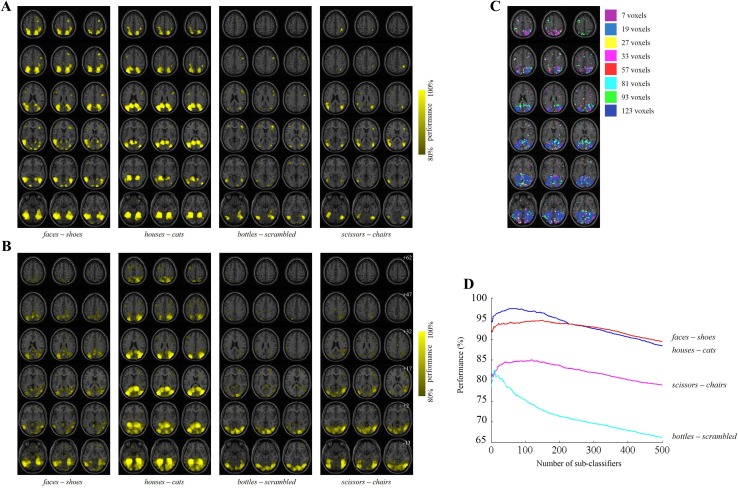
Examples of searchlight analysis across the whole brain are shown in Fig. 6A and B, in which regions that have reliable information for pairwise classification in the intra- and inter-subject analyses are highlighted. Four class-pairs were selected as examples among all 28 class-pairs from eight classes. In both experiments, some class-pairs shared common regions such as the VTC region, which is known to be responsible for the classification of visually-presented objects. However, different patterns for each class-pair reflected that each class-pair had specific informative feature set. In the intra-subject analysis (Fig. 6A), there was subject-specific information that produced a relatively high performance. On the other hand, the outcome of the inter-subject analysis (Fig. 6B) showed that useful subject-invariant pattern information can be detected by the proposed method. The adaptive searchlight window sizes showing the highest performance were different for locations (Fig. 6C), since the spatial size of the useful pattern information depends on locations. Therefore, the adaptive searchlight window size can improve the classification performance. The analyzed results were overlaid onto a high-resolution Colin brain template [43].

Fig. 6.

Examples of analyzed feature vectors. A and B show the informative regions that were analyzed by the searchlight analysis according to different class-pairs; A intra-subject and B inter-subject analyses. The center locations of the feature vectors whose performance was higher than a threshold are highlighted. The thresholds for the intra- and inter-subject analyses were 80% and 70%, respectively. In the intra-subject example, the analyzed regions of the first subject are displayed. The z-coordinate is indicated in the MNI coordinate system. C Adaptive searchlight window sizes for class-pair of houses and cats in the inter-subject analysis as an example. The test subject was the first subject. D Examples of the classification performances of a pairwise ensemble classifier with respect to the number of the feature vector. The selected class-pairs are the same as in (A) and (B). The results under 500 feature vectors are displayed for readability.

The number of useful feature vectors for each class-pair was estimated adaptively. Examples of the inter-subject classification accuracy according to the number of feature vectors are shown in Fig. 6D. The accuracies were averaged for all the test subjects. As the number of feature vectors increased, the accuracy improved at first but then gradually decreased because less informative features were added. The result showed that each class-pair had its own optimal number of feature vectors.

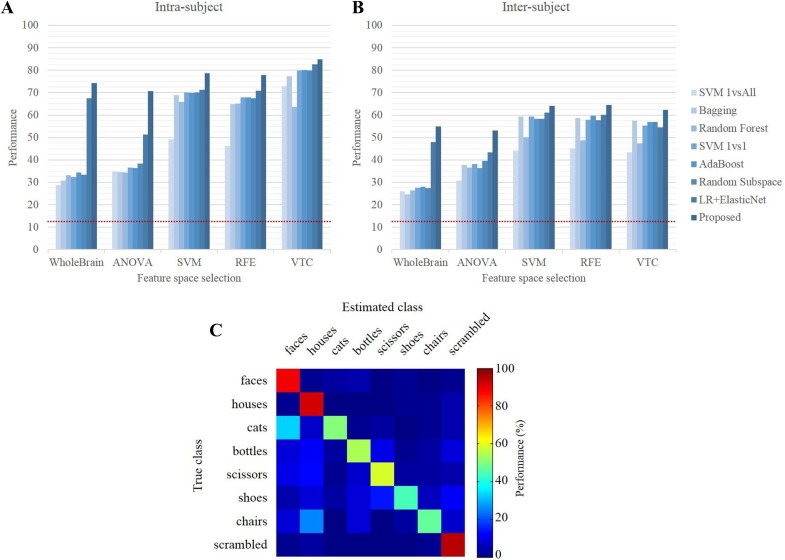
The intra-subject classification accuracies from various classifiers using the five feature selection methods for each subject are shown in Fig. 7A. The performances of each subject are averaged (see Fig. S1 for detailed performances of individual subjects), and the proposed method had the best performance in all cases. Classification performance is known to be degraded by over-fitting when there are many irrelevant features [11]. Because fMRI analysis usually deals with a huge number of voxels, adequate selection of informative voxels can improve the classification performance [44]. Unlike the previous classifiers which have low performance when all voxels in the brain are considered in the classification because of the inclusion of less informative voxels, the proposed method had relatively high performance because it searched for an informative feature set of each class-pair.

Fig. 7.

The classification performance of all tested classifiers for each subject; A intra-subject and B inter-subject analyses. The dotted lines refer to the chance level of 12.5% for eight classes. C Confusion matrix of the proposed method in the inter-subject analysis.

The result of inter-subject analysis exhibited a tendency similar to that of the intra-subject analysis (Fig. 7B). The proposed method showed robust performance using all five feature selection methods and worked successfully for inter-subject classification. The confusion matrix of the proposed method for inter-subject analysis revealed that some classes were more difficult to discriminate than others, such as the faces-cats pair in the experiments (Fig. 7C).

A statistical test was performed to show the significance of the performance differences on the fMRI experiment. For each feature space selection method, all results from all classifiers were collected to perform statistical analysis using the Wilcoxon signed-rank test with the null hypothesis of PER _proposed ≤ PER _conventional. Table 3 shows the P-values of the analysis. The results showed that the performance differences between the proposed and compared classifiers were statistically significant.

Table 3.

P values from Wilcoxon signed-rank test of the fMRI experiment for each feature space selection method.

Classifier	Feature selection
	Whole brain	ANOVA	SVM	RFE	VTC
SVM 1vsAll	0.0059**	0.0059**	0.0059**	0.0059**	0.0059**
SVM 1vs1	0.0059**	0.0059**	0.0059**	0.0059**	0.0464*
AdaBoost	0.0059**	0.0059**	0.0059**	0.0086**	0.0617*
Bagging	0.0059**	0.0059**	0.0059**	0.0059**	0.0059**
Random forest	0.0059**	0.0059**	0.0059**	0.0059**	0.0059**
Random SubSpace	0.0059**	0.0059**	0.0059**	0.0059**	0.0344*
LR + ElasticNet	0.0125**	0.0059**	0.0086**	0.0086**	0.0213**

The P values were acquired with the null hypothesis of PER _proposed ≤ PER _conventional. Multiple comparison correction was performed by controlling the false discovery rate (FDR) < q.

* q < 0.1, ** q < 0.05.

Discussion

In this study, we proposed a binary classifier ensemble for the analysis of fMRI data, where every binary classifier was optimized by customized searchlight analysis and all binary classifiers were combined to acquire a robust performance. The proposed method optimized sizes, locations, and number of feature vectors for every binary classification, and multiclass classification was achieved by the ensemble of binary classifications. A similar idea was suggested by Kuncheva et al. [13], that the spatial relationship between voxels could be considered in the random subspace ensemble classifier. The proposed method constructed sub-classifiers in an information-based process rather than a random-based method, adaptively taking optimum values of the locations, spatial sizes, and number of useful feature vectors. The proposed method can be applied to both of binary and multiclass classification problems. When it is applied to the binary classification, the classification procedure is treated as if there is one class-pair. In this paper, the multiclass classification problem was adopted to verify the proposed method.

We analyzed the computational cost for the proposed method. It took 247.73 min for the training and 9.02 min for the intra-subject analysis of an fMRI dataset with the SVM-based feature space, which had 10 runs, 23127 voxels in the brain, 1000 voxels in the feature space, and 28 class-pairs from 8 classes. The computational cost depended on the experimental environment, such as the size of the dataset and the number of classes. The computation times were measured using an Intel^® Core™ i7-3930 k CPU and the analysis was performed using MATLAB. Due to its pairwise-adaptive characteristics, the training process of the proposed method has a high computational cost. Once the training is performed, the test can be performed in a relatively short time.

The searchlight analysis with the adaptive window size was used to detect both the detailed information in small regions and the general tendency over broad regions. Therefore, it was suitable for intra-subject analysis and showed robust performance even in the inter-subject environment. To further improve the inter-subject analysis, it could be considered that the proposed method could use sub-classifiers devoted to the inter-subject fMRI analysis such as graph-based pattern analysis [45].

The proposed method used surrounding voxels of the selected feature voxels, so it could be performed using more voxels than the compared classifiers. To verify the effect of an increased number of voxels, the compared classifiers underwent the analyses with a wide range of feature space sizes [1000, 2000, …, 10000]. The intra-subject experiment with the first subject was tested and the feature space was analyzed by the SVM-based selection method. The experiment results showed that the excessive voxels degraded the performance because they had less information for classification.

To assure a fair comparison between the proposed and the previous classification methods, we performed grid searches for the number of key parameters of the compared classifiers, such as the complex parameter of the SVM classifier in a range of [0.0001, 0.001, …, 10000], the weight threshold parameter of the AdaBoost classifier in a range of [0, 10, 20, …, 200], the size of each bag parameter of the bagging classifier in a range of [10%, 20%, …, 100%], and the size of each subspace of the random subspace ensemble classifier in a range of [0.1, 0.2, …, 1]. All analyses were performed using Weka on the simulation with the non-overlapping setting. The results showed that the classification performance was less sensitive to the parameters in the tested environment and the default parameters used in the experiments showed the highest performances.

In conclusion, the proposed classifier ensemble method was developed to improve the classification performance of the fMRI data, where multiple sub-classifiers were optimized by customized searchlight analysis. The proposed method provides a pairwise classifier ensemble framework for multiclass classification, which took adaptive feature vectors for each binary classification. We showed robust performance of the proposed method applied to real fMRI analyses for simulation and actual fMRI data including intra- and inter-subject cases, in comparison with the previous classifiers including single and ensemble classifiers. The proposed method is expected to be applicable to multiclass fMRI pattern analysis.

Electronic supplementary material

Below is the link to the electronic supplementary material.