TomoMiner and TomoMinerCloud: A software platform for large-scale subtomogram structural analysis

SUMMARY

Cryo-electron tomography (cryoET) captures the 3D electron density distribution of macromolecular complexes in close to native state. With the rapid advance of cryoET acquisition technologies, it is possible to generate large numbers (>100,000) of subtomograms, each containing a macromolecular complex. Often, these subtomograms represent a heterogeneous sample due to variations in structure and composition of a complex in situ form or because particles are a mixture of different complexes. In this case subtomograms must be classified. However, classification of large numbers of subtomograms is a time-intensive task and often a limiting bottleneck. This paper introduces an open source software platform, TomoMiner, for large-scale subtomogram classification, template matching, subtomogram averaging, and alignment. Its scalable and robust parallel processing allows efficient classification of tens to hundreds of thousands of subtomograms. Additionally, TomoMiner provides a pre-configured TomoMinerCloud computing service permitting users without sufficient computing resources instant access to TomoMiners high-performance features.

INTRODUCTION

Cryo-electron tomography (CryoET) captures the density distributions of macromolecular complexes and pleomorphic objects at nanometer resolution (e.g. (Asano et al., 2015; Briggs, 2013; Lučić et al., 2013; Mahamid et al., 2016; Milne et al., 2013; Pfeffer et al., 2015; Tocheva et al., 2014)). CryoET has provided important insights into the ultra-structures of entire bacterial cells, and revealed the structures of numerous macromolecular complexes.

Several factors complicate the analysis of cryo-electron tomograms to determine structures of macromolecular complexes; these factors include the relatively low and non-isotropic resolution and distortions due to electron optical effects and missing data (Förster et al., 2008). For example, unavoidable systematic distortions are caused by variations in the Contrast Transfer Function (CTF) in individual electron micrographs (Briggs, 2013). Orientation-specific distortions can result from the missing-wedge effect, which arises from the restricted range of tilt-angles when collecting the micrographs (typically between −60 to +60 degrees). This limitation in data coverage means that Fourier space structure factors are missing from a wedge-shaped region, causing non-isotropic resolution and other image artifacts, which depend on the orientation and shape of the object relative to the tilt axis (Bartesaghi et al., 2008; Förster et al., 2008; Xu et al., 2012).

The nominal resolution of tomography images can be increased by aligning and averaging multiple subtomograms containing the same structure (Briggs, 2013). Typically, for a given complex of interest sub-volumes (i.e., the subtomograms) are extracted from a tomogram containing distinct examples of the complex, which are typically aligned and their signals averaged to generate a density map with increased nominal resolution. But if the subtomograms represent a heterogeneous sample (a mixture of different complexes, or multiple conformational or compositional states of the target complex) it is necessary to first group them into homogeneous sets in an unbiased manner, using reference-free classification methods. This classification or clustering step is a common subtask in subtomogram analysis. It often costs significantly more computation than subtomogram averaging and therefore requires fast and accurate subtomogram alignments. We recently introduced an efficient alignment algorithm designed for use with reference-free subtomogram classification ((Xu et al., 2012), STAR Methods Section). The method relies on fast rotational alignment and uses the Fourier space equivalent form of a constrained correlation measure (Förster et al., 2008) that accounts for missing wedge effects and density variances in the subtomograms. The fast rotational search is based on 3D volumetric matching (Kovacs and Wriggers, 2002). We have also proposed a fast real space alignment method (Xu and Alber, 2013) and a gradient-based local search method for alignment refinement to increase the alignment precision (Xu and Alber, 2012). However, all our methods were implemented only as prototype MATLAB codes and were not optimized to be executed on computer clusters.

Having a larger number of subtomograms increases the accuracy of classification, which in turn improves the resolution of the resulting averaged structures (e.g. (Bartesaghi et al., 2008; Chen et al., 2014; Xu et al., 2012)). With the rapid advance of cryoET acquisition technologies (Morado et al., 2016), it has become easy to acquire a large number (> 10, 000) of instances of macromolecular complexes. Offsetting the clear advantage in accuracy is the high computational cost of 3D image processing. To take advantage of the available data, the field therefore needs efficient high-throughput computational methods for processing large numbers of subtomograms, in particular for subtomogram classifications. To our knowledge, currently only a few alignment algorithms (e.g. (Bartesaghi et al., 2008; Chen et al., 2013; Xu and Alber, 2013; Xu et al., 2012)) have the scalability to process large subtomogram data sets. A performance comparison of algorithms of (Bartesaghi et al., 2008; Chen et al., 2013; Xu et al., 2012)) can be found in (Chen et al., 2013).

Here, we describe the Python/C++ software package TomoMiner, which was developed with particular focus for scalability and therefore the ability to process a large number of subtomograms (> 100, 000). TomoMiner includes a high-performance implementation of several of our previously developed methods, including reference-free subtomogram classification (Xu et al., 2012), template matching, and both Fourier space (Xu et al., 2012) and real space (Xu and Alber, 2013) fast subtomogram alignment. All these methods are implemented in a parallel-computation framework designed to be highly scalable, efficient, robust, and flexible. The software can run on a single personal computer or in parallel on a computer cluster, in order to quickly process large numbers (> 100,000) of subtomograms. Additionally, TomoMiner provides an open source platform for users to implement their own tomographic structural analysis algorithms within the parallel-computation framework of the TomoMiner framework. Although many methods have been proposed for the structural analysis of macromolecular complexes from cryoET subtomograms, only a few software packages are currently available to the research community. These include, but are not limited to, the TOM Toolbox (Nickell et al., 2005), PyTOM (Hrabe, 2015; Hrabe et al., 2012), AV3 (Förster et al., 2005; Nickell et al., 2005), Dynamo (Castaño-Díez et al., 2012), EMAN2 (Galaz-Montoya et al., 2015; Tang et al., 2007), PEET (Nicastro et al., 2006), Bsoft (Heymann et al., 2008), and RELION (Bharat et al., 2015; Scheres, 2012). TomoMiner complements existing software solutions because it focuses on large-scale data processing and implementing proven algorithms and tools in parallel form, so that researchers can process tens or even hundreds of thousands of subtomograms.

TomoMiner has been designed to run on computer clusters, and scales to hundreds of processors. Some components, such as the data storage interface, have been abstracted, so are easily replaced with different implementations on different cluster computing platform architectures. In addition, we provide a cloud computing version of TomoMiner on Amazon’s Web Services (AWS, http://aws.amazon.com). Those research labs without access to substantial computational capacity, or the ability to adapt, install and maintain TomoMiner on existing computer clusters can use the cloud computing version immediately by paying for resources as they go.

Our results show that TomoMiner is able to achieve a close to linear scaling with increasing amount of input data. Here, we show that TomoMiner is able to efficiently and accurately average 100,000 subtomograms, and classify 100,000 subtomograms of a heterogeneous mixture of 5 different complexes. In addition, TomoMinerCloud is able to perform large scale averaging and classification with affordable cost on cloud computing services.

RESULTS

Software Implementation

The TomoMiner package contains a suite of programs covering a variety of important tasks in subtomogram analysis, including among others (i) fast and accurate subtomogram alignment which accounts for missing wedge effect; (ii) large-scale, reference-free subtomogram averaging and classification; (iii) reference-based subtomogram classification; and (iv) template matching for detecting complexes in large tomograms.

TomoMiner is optimized for processing large numbers (≈100,000) of subtomograms. It is designed to be scalable, robust, computationally efficient and flexible. This is accomplished through modular design and parallel computing architecture. The programs function by breaking computations into smaller independent tasks, which can be computed in parallel by individual CPU cores on a computer cluster.

Software design and modular architecture for parallel processing

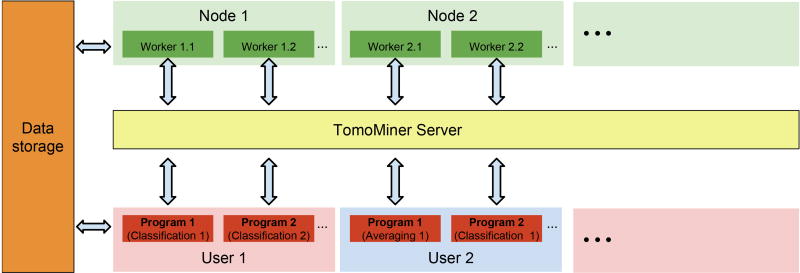
TomoMiner’s parallel processing system consists of three major components (Figure 1): 1) the analysis programs, such as the subtomogram classification, averaging and template matching; 2) the TomoMiner server, which manages the execution of tasks generated by the analysis programs and passes the results of each task back to its requesting program; and 3) the workers, which process the tasks.

Figure 1.

Parallel processing architecture.

Each analysis program breaks its computations down into small independent tasks, which are submitted to the TomoMiner server. The server distributes the tasks to workers for execution, monitors worker processes, and passes results from the workers back to the analysis program. Workers and analysis programs communicate with the server over a network, allowing all of these components to run on separate computers. Since workers are single-threaded, we usually run one worker per CPU core. The workers connect to the server and request tasks for execution. When a task is finished, the worker sends the result to the server and requests a new task. The results of all completed tasks are collected by the analysis program. Importantly, several independent analysis programs from different users can submit their tasks to the same TomoMiner server and worker pool at the same time. This design allows for maximum utilization of cluster resources. For example, an analysis program may stop running as it awaits the completion of a non-parallelizable task or a set of parallel tasks. Typically, some parallel tasks finish earlier than others, so if only one analysis program is using the server then many workers will remain idle when the number of unfinished tasks is smaller than the number of workers. We can decrease the idle time on the available cluster nodes by running two or more analysis programs communicating with the same TomoMiner server. Idle nodes can then receive tasks from a second program, and total node utilization will be higher. This design is particularly useful when programs are submitted in a shared cluster environment that limits the number of submitted jobs and the assigned cluster time per user.

The TomoMiner software system can run the analysis and server programs and the workers layer on a single desktop computer, or run each component independently on separate computers within a cluster. For example, we frequently use TomoMiner with 256 workers running on different machines.

To reduce the communication load on the server, both the tasks and the results that pass through the server are limited to small messages. Large results or inputs, such as the subtomograms themselves, are kept on shared data storage (Figure 1), where they can be easily retrieved by workers and analysis programs as needed. A task passed to a worker only needs the path to the data, not the data object itself.

Software robustness

Component failures are inevitable when using distributed computer systems; these must be handled without causing the failure of other system components and without terminating the analysis process. TomoMiner components are designed to be robust to intermittent network and remote failures. When a task is sent to a worker, the TomoMiner server monitors its progress. If the task takes longer than expected, or the connection to the worker is lost, the server re-assigned the task to another worker. If a task fails, the worker passes the failure notification to the server. The server can then take an action, such as rescheduling, or pass the notification back to the analysis program for handling. All tasks are carefully tracked, and an uncompleted task can be attempted by multiple workers when computational resources are available. As soon as one of these attempts succeeds, the server can cancel remaining instances of the same task, so that the freed workers can request new tasks. A worker processes each task by launching an independent subprocess, so that the worker program cannot be crashed by bugs in the analysis code. If the subprocess crashes, the worker notifies the server of the failure, but remains on-line.

Each task can also be assigned properties to control how it is executed. For example, one can specify the maximum run time, after which the task will be considered lost and the server will send the task to another worker. One can also set up an upper limit on the number of times a task can be re-assigned to a new worker after loss or failure. All these features provide the foundation for a robust parallel processing system. Because subtomogram analysis is usually an iterative process, we have also added checkpointing so that the can resume from the last iteration if the program is terminated unexpectedly.

Software flexibility

TomoMiner is designed to run multiple analysis programs connected to the same TomoMiner server with the same pool of workers (Figure 1). Multiple users can run multiple analysis programs concurrently. The server will manage tasks for multiple programs on the same pool of workers. Such design enables our system to simultaneously perform different types of calculations, for example replicate calculations with different initializations and/or different parameter settings. In addition, the same pool of workers and the same TomoMiner server can act as a shared service used by multiple users, multiple research labs, or even multiple research institutions. Moreover, developing new subtomogram analysis programs does not require knowledge of the internal parallel worker implementation, only a way to match the parallel interface to the functions processed by the tasks.

Software components and dependencies

The TomoMiner code consists of several components. The core is a library of basic functions dealing with (i) data input and output, (ii) subtomogram processing, such as fast rotational and translational alignment of subtomograms and averaging, and (iii) calculations of subtomogram correlations. This core is written in C++ to maximize computational efficiency.

This core has been wrapped into a Python module. All TomoMiner top-level programs are implemented as Python programs. These include analysis programs such as the reference-free subtomogram classification routine, parallel processing programs such as the TomoMiner server, and utility programs such as FSC (Fourier Shell Correlation) calculator. The choice of languages allows for fast prototyping of new algorithms and interoperability with other software. Python is more accessible for novice programmers. TomoMiner provides the advantages of developing software in a high-level language without sacrificing performance, because all numerically intensive calculations are carried out by the wrapped C++ functions.

The C++ code is built on top of several existing libraries. The open source Armadillo (Sanderson, 2010) library is used to represent volumes, masks, matrices, and vectors. Fast Fourier Transforms are provided by FFTW (Frigo and Johnson, 2005). The C++ core is wrapped using Cython (Behnel et al., 2011). This library enables a user to call core functions written in C++ directly from Python programs, using Python data structures as arguments. A number of auxiliary routines from Scipy (Oliphant, 2007), and scikit-learn (Pedregosa et al., 2011) are also used by the classification code.

Cloud Computing Setup

Due to the computationally intensive nature of 3D image processing of large numbers of subtomograms, analysis software needs to scale well and support parallel computation environments to achieve high performance. TomoMiner was designed to meet these criteria, and can be installed on computer clusters. However, many research labs do not have access to a computer cluster with sufficient computational resources. Also, the hardware and software architectures of computer clusters can vary substantially and the installation and configuration of specialized software is often non-trivial, and may introduce conflicts with the previously installed software and libraries. Therefore, it may be impractical for labs who may only occasionally perform subtomogram analysis tasks to invest money and/or labor in setting up and maintaining the required software and hardware.

Here, we provide a pre-installed and pre-configured TomoMiner system (TomoMinerCloud) in the form of a cloud computing service to those labs without access to high-performance computing. TomoMinerCloud is a system image that can be used on publically available cloud computing platforms, such as AWS. Cloud platforms allow computational capacity to be purchased as a service, where users are charged based on the amount of computational resources used (Cianfrocco and Leschziner, 2015). They provide the flexibility to run large computations or analyses using a pool of Virtual Machines (VMs), without the burdens of owning and maintaining hardware or installing cluster management software.

We have built a publicly available virtual machine image and installed our software into the image to provide cloud services. The service allows users to immediately use the TomoMiner software for large-scale subtomogram analysis, at an affordable cost and with very little configuration or maintenance burden. The amount of computational resources can be determined dynamically as a function of the data size and budget. Currently TomoMinerCloud is available on Amazon Web Services (AWS). TomoMinerCloud is designed so that researchers can set up a high-performance parallel data analysis environment with little informatics expertise. Inside a Virtual Private Cloud (VPC), the VM used to run the analysis program can be started and accessed from the users own computer. The same VM can also host the server layer and shared data storage. A large number of workers (hundreds or thousands) can be executed in the cloud, each running on its own VM.

Therefore, an end-user only needs a computer with Internet access, a web browser, and a secure shell (SSH) client. No specialized software is required. TomoMinerCloud can be instantiated using the web console of AWS. SSH can be used to transfer data and launch the jobs on the VMs.

An additional advantage of TomoMinerCloud is that snapshots can be taken to record the current status of the VM, TomoMiner program, and data. The snapshot mechanism can be used to verify the reproducibility of computational experiments, record exact parameter settings and configuration details, measure the effect of bug fixes or algorithmic changes, and share analysis between collaborators. Detailed procedures for using TomoMinerCloud are described in the documentation available from the main TomoMiner website.

TomoMiner Analysis programs

TomoMiner includes the high-performance, parallel software implementation of several of our previously described and new methods, which include: 1) fast subtomogram alignment; 2) reference-free and reference-based large-scale subtomogram averaging and classification and 3) template matching applications. In the next section we describe the reference-free classification program.

Reference-free Classification

TomoMiner contains a program for large-scale reference-free subtomogram classification. The software is based on a previously published method (Xu et al., 2012), and includes modifications for processing large data sets. The program does not rely on template structures; the only input is a large set of subtomograms that are randomly oriented at the beginning of the iterative process. The outputs are a classification of the subtomograms into individual complexes, a rigid transformation for each subtomogram, and a density map generated by averaging all the aligned subtomograms within each class. In comparison with our previously published method (Xu et al., 2012), which is a variant of alignment-through-classification method (Bartesaghi et al., 2008), this software implementation has several adaptations to parallelize the algorithm and improve efficiency and scalability. The reference-free classification is an iterative process. Each iteration consists of the following steps:

• Step 1: Dimension Reduction: The similarity between subtomograms is measured in a reduced dimension space to focus on the features most relevant for discrimination. For each voxel and its neighbors, this step calculates the average covariance of the voxel intensities across all subtomograms in a similar way as (Xu et al., 2012). The voxels with the largest covariance are selected as the most informative features, and each subtomogram is represented by a high-dimension feature vector (see (Xu et al., 2012) for details). To account for missing wedge effects, the covariances and feature vectors are calculated on missing wedge-masked difference maps (Heumann et al., 2011). In contrast to our previous work (Xu et al., 2012), we use feature extraction to further reduce the number of dimensions in order to reduce the computational costs in the clustering step. To do so, principal component analysis (PCA) is used to project the high-dimension feature vectors into a low-dimension space. In practice, EM-PCA (Bailey, 2012) is used for its scalability and speed when one only extracts a small number of principal components.

• Step 2: Clustering: K-means clustering is performed based on the Euclidean distance of the low-dimension feature vectors generated in step 1. The value of the K parameter is specified by the user and should be chosen to over-partition the data set. This is because clusters leading to similar averaged tomograms are easily identified and the corresponding subtomograms merged into one cluster later in the analysis. In our previous method, we used hierarchical clustering (Xu et al., 2012) but K-means clustering results in a more efficient and scalable algorithm. Finally, the class labels of all subtomograms are assigned according to the clustering.

• Step 3: Generate cluster averages: The subtomograms within each cluster are averaged to generate density maps, which are used as cluster representatives.

• Step 4: Alignment of cluster averages: All the averaged density maps resulting from step 3 are grouped using hierarchical clustering, based on the pairwise optimal alignment scores of the cluster averages (Xu et al., 2012). A silhouette (Rousseeuw, 1987) score determines the optimal cutoff to cluster all averaged density maps into classes. Within each hierarchical class, the map that was generated from the largest number of subtomograms is chosen as a reference. Then all other maps in the hierarchical class are aligned relative to this reference.

• Step 5: Alignment of subtomograms: All of the original subtomograms are aligned to each of the cluster averages generated in step 4. To allow high-throughput processing, we implemented a fast computationally efficient alignment algorithm based on fast rotational matching (Xu et al., 2012). For each subtomogram the rigid transform with the highest scoring alignment is used as input for the next iteration.

The iterative process (step 1 to 5) can either be executed for a fixed number of iterations, or terminated when the amount of changes in subtomogram class labels or changes in the cluster averages between two iterations is small.

Reference-based classification

If template structures are provided as a reference, the classification process can use these alongside the averaged density maps of each cluster as cluster representatives.

Subtomogram alignment by fast rotational matching

TomoMiner contains a program for fast alignment ((Xu et al., 2012), STAR Methods Section). This method increases the computational efficiency of subtomogram alignments by at least three orders of magnitude (Xu et al., 2012) compared to exhaustive search methods (Förster et al., 2008), while at the same time accounting for missing wedge effects when calculating the correlations between the tomograms. This approach allows subtomogram alignments on a single CPU core to achieve comparable speeds to exhaustive search based alignment methods accelerated GPU usage. The missing wedge constrained fast alignment is implemented as a C++ library. This new C++ implementation has been thoroughly tested, and is at least 6 times faster than our previous MATLAB prototype used in (Xu et al., 2012). In addition, TomoMiner implements our previously proposed real space fast subtomogram alignment method (Xu and Alber, 2013).

Template-matching

TomoMiner also provides an efficient template matching protocol. Given a set of templates with known structures, and a set of candidate subtomograms with unknown structures extracted through template-free particle picking (e.g. (Langlois et al., 2011; Voss et al., 2009), TomoMiner can perform fast alignment (Xu et al., 2012) to compute which structures are most similar to the unknown subtomograms in terms of the alignment score.

Data scalability, worker scalability, and efficiency

Scalability is an important measure of performance for parallel software. We evaluate it using two measures: data scalability and strong scalability. Data scalability measures the performance of TomoMiner when the number of subtomgrams increases while the number of workers is held constant. Strong scalability measures performance when the number of workers increases for a data set of fixed size.

Whether we change the number of processors or the number of subtomograms, we are most interested in the time required to process a single subtomogram. This is captured by the efficiency, defined as the ratio of the observed rate (total time / subtomogram number) to the expected linear rate. As a reference point for both performance measures (data scalability and strong scalability) we use the highest observed rate among all the calculations as the linear expected rate to represent the ideal scenario. A relative efficiency of 100% corresponds to perfect linear scaling, while a relative efficiency of 50% indicates that the program took twice as long as the ideal scenario.

Data scalability and strong scalability are assessed for a single iteration of the reference-free subtomogram alignment and averaging process: averaging all subtomograms and aligning them against a single average. The subtomograms are cubes (463 voxels) containing a single randomly oriented complex (PDBID: 2AWB). They were generated following the simulation procedure described in the STAR Methods Section using a signal to noise ratio of 0.01 and a tilt angle range of ±60°.

Data scalability

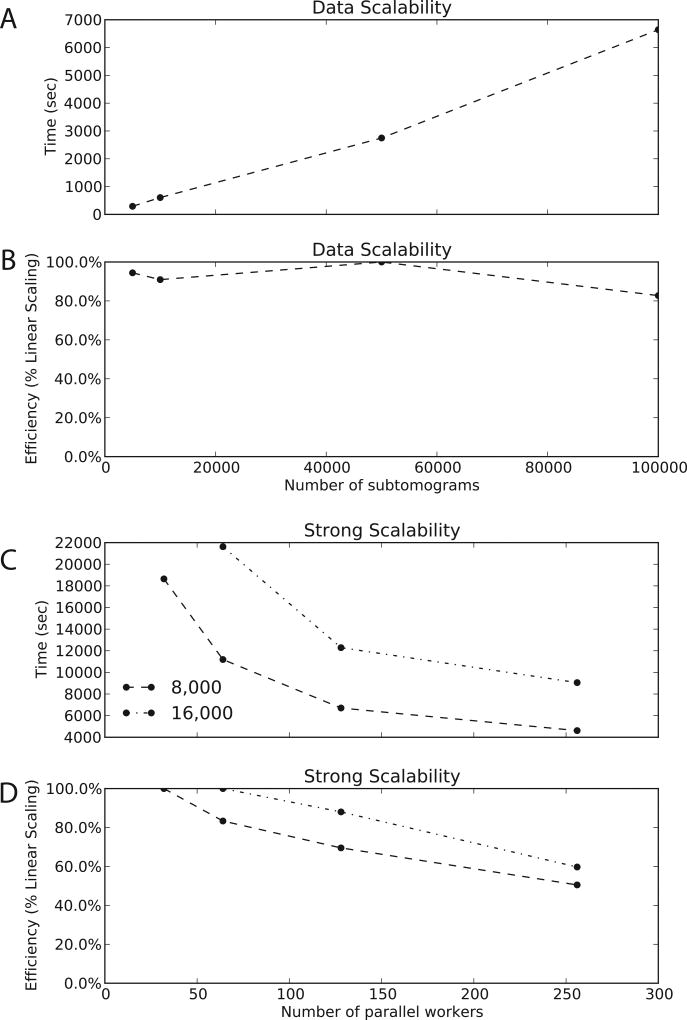
TomoMiner makes effective use of computational resources. When using a constant 256 workers, the computational time increases nearly linearly with increasing numbers of subtomograms (5000 to 100,000 subtomograms, see Figure 2A). The software aligns and averages 100,000 subtomograms in under 2 hours using 256 workers (Figure 2A). For all data sets with more than 5000 subtomograms, the efficiency remains above 80% (Figure 2B). TomoMiner scales very well with increasing data and is an efficient platform for data analysis.

Figure 2.

Efficiency and Scalability (A) The time required for a single round of alignment and averaging as a function of subtomogram number, for a constant 256 workers. The curve is close to linear across the entire range of data. (B) The relative efficiency of the data scalability when additional data is added, for a constant 256 workers. The rate of processing is very stable across several orders of magnitude. (C) The time required for a single round of alignment and averaging for two different data sets, with 8,000 and 16,000 subtomograms. The number of workers varies from 32 to 256. For a relatively small number of subtomograms, there are not enough subproblems generated to occupy 256 workers, so some are idle, creating the plateau seen in the graphs. (D) The relative efficiency of strong scalability. For these problem sizes TomoMiner scales well, with very little overhead for the increased communication and coordination load of additional workers. There is a clear loss of efficiency when using too many workers for a given problem size, but this demonstrates that even for medium-sized data sets (10,000+ subtomgorams) TomoMiner is far away from reaching its computational limits.

Strong Scalability

When increasing the number of workers for a fixed number of subtomograms, the computing time decreases (Figure 2C). For example, for a data set containing 16000 subtomograms, the computing time dramatically decreases when increasing the number of workers from 32 to 128 (Figure 2CD). Increasing the number of workers further results in less pronounced gains, because the worker pool is not fully utilized. When using 256 workers for 8000 subtomograms, for example, many of the workers are idle at any given moment so the processing rate is lower than the expected linear rate leading to a decreased efficiency (Figure 2D). Interestingly, we find optimal performance at about 100 subtomograms/workers. To further validate our observations, we have also simulated subtomograms at 3Å voxel spacing, and achieved similar linear scaling (STAR Methods Section, Figure S1).

In summary, we can demonstrate that TomoMiner makes effective use of computational resources and is able to process very large number of subtomograms in an effective manner.

Performance of reference-free subtomogram classification

We previously presented a reference-free subtomogram classification method (Xu et al., 2012). We implemented this pipeline in TomoMiner and adapted it to increase its scalability. To test the performance of this program, we classified 100,000 subtomograms, divided into five groups of 20,000, each group depicting a different complex (Figure 3A). Each subtomogram is a cube with sides of 41 voxels. The complexes are generated with a SNR of 0.01, and tilt angles in the range of ±60°. The complexes were randomly rotated, and given a random offset from the tomogram center up to 7 voxels in each dimension. The classification program requires a user-defined number of clusters, which should be chosen to over-partition the data as described earlier. In our example, the initial number of clusters was set to 10 to demonstrate the performance with the expected overpartition of the data.

Figure 3.

Reference-free classification of 100,000 subtomograms. 20,000 subtomograms are generated for each of five different structures, using the procedure defined in the STAR Methods Section. The subtomograms were simulated using a signal to noise ratio of 0.01 and a tilt angle of ±60°. The clusters converged after 10 iterations of reference-free subtomogram classification, using a cluster number of 10. (A) After 10 iterations, the averaged subtomograms in each cluster converged to structures close to the ground truth. Since there are more clusters than structures, some clusters have converged to the same structure. (B) Pairwise correlations between the averaged density maps of all ten clusters. Clusters corresponding to the same complex are easily identified by their high correlation values, then can be combined into a single cluster. (C) The number of subtomograms in each cluster (top). Each cluster is dominated by a single complex. The percentages of subtomograms generated from the dominant complex are 96.2%, 97.8%, 99.9%, 100%, 95.6%, 98.5%, 97.7%, 90.7%, 89.4%, 99.9% for clusters 1 to 10, respectively. Cluster IDs are shown on the horizontal axis. Since the numbers are arbitrary labels, they have been arranged so that similar clusters are adjacent. The correlations between the true structures (bottom), and the averaged density maps demonstrate that the clustering is accurate.

After 10 iterations the reference-free classification process converged and all the subtomograms were successfully classified. Because we have access to the true subtomograms used to generate the data, we can compare the cluster averages to the corresponding true structures for validation. The classification performance is assessed as described in the STAR Methods section ‘Assessment of classification accuracy’ The resulting cluster averages are accurate reconstructions of the true complexes, with Pearson correlation values between cluster averages and the ground truth > 0.9 (Figure 3A,C). The over-partition leads to several clusters containing identical complexes, which can easily be identified based on the high correlation score between the aligned cluster averages (Figure 3B). Subtomograms within a cluster overwhelmingly depict only a single complex. The fraction of subtomograms from the same complex ranges between 89.4% and 99.9% (Figure 3C) for the ten clusters.

When using 256 workers, TomoMiner required an average of 207 minutes per iteration to classify the hundred thousand subtomograms without a reference structure.

Accuracy increases with larger data sets

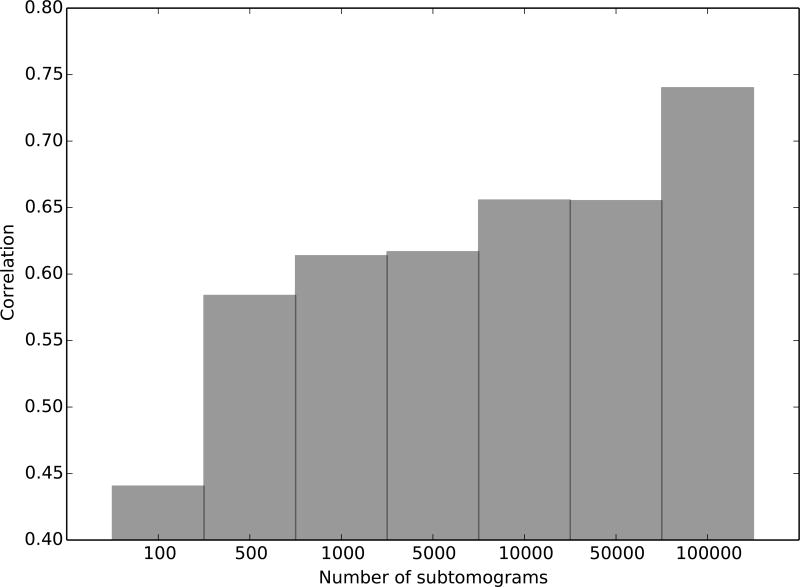
Next, we demonstrate the benefit of very large data sets for reference-free subtomogram averaging. We generated 100,000 subtomograms of the 50S subunit of the E. coli ribosome (PDB ID: 2AWB) with SNR 0.005 and tilt angle range ±60°. Each subtomogram is a cube with a side length of 33 voxels. Our reference-free iterative alignment and averaging pipeline is able to recover the underlying structure. TomoMiner required an average of 37 minutes per iteration for alignment and averaging using 256 workers. Figure 4 shows the correlation score after 20 iterations, when different numbers of subtomograms are given as the input dataset. Using a very large number of subtomograms increases the accuracy of the generated model, demonstrating the advantage of using high-performance parallel analysis software. To further validate our observations, we have also simulated subtomograms at 3Å voxel spacing. Similar to our previous tests, the accuracy of averaging increases with the number of subtomograms (STAR Methods Section, Figure S2).

Figure 4.

Accuracy of the averaged density maps generated from reference-free alignment and averaging. The accuracy is measured as the Pearson correlation between the generated averages and the template of the true structure. Several correlations are shown, for averages generated with an increasing number of subtomograms in the dataset. We generated 100,000 subtomograms of a randomly oriented complex (PDBID: 2AWB) using the procedure described in the STAR Methods Section, with a signal to noise ratio of 0.005 and a tilt angle range of ±60°. The computed average is more accurate when using more subtomograms. TomoMiner’s ability to handle large numbers of subtomograms therefore efficiently allows for accurate reconstructions and classifications of structures from noisy data, given sufficiently large datasets.

Reference-free classification of GroEL and GroEL/GroES subtomograms

Next we demonstrate the use of our reference-free classification method on a set of publicly available experimental subtomograms of purified GroEL and GroEL/GroES complexes previously published in (Förster et al., 2008) and frequently used for testing of subtomogram classification methods (Xu et al., 2012). The dataset consists of two sets of subtomograms: 214 obtained from 13 cryo-electron tomograms of purified GroEL complexes, and 572 obtained from 11 cryo-electron tomograms containing GroEL/GroES complexes. The differences between the subtomograms of the two different complexes are subtle, so their classification is a challenging test case.

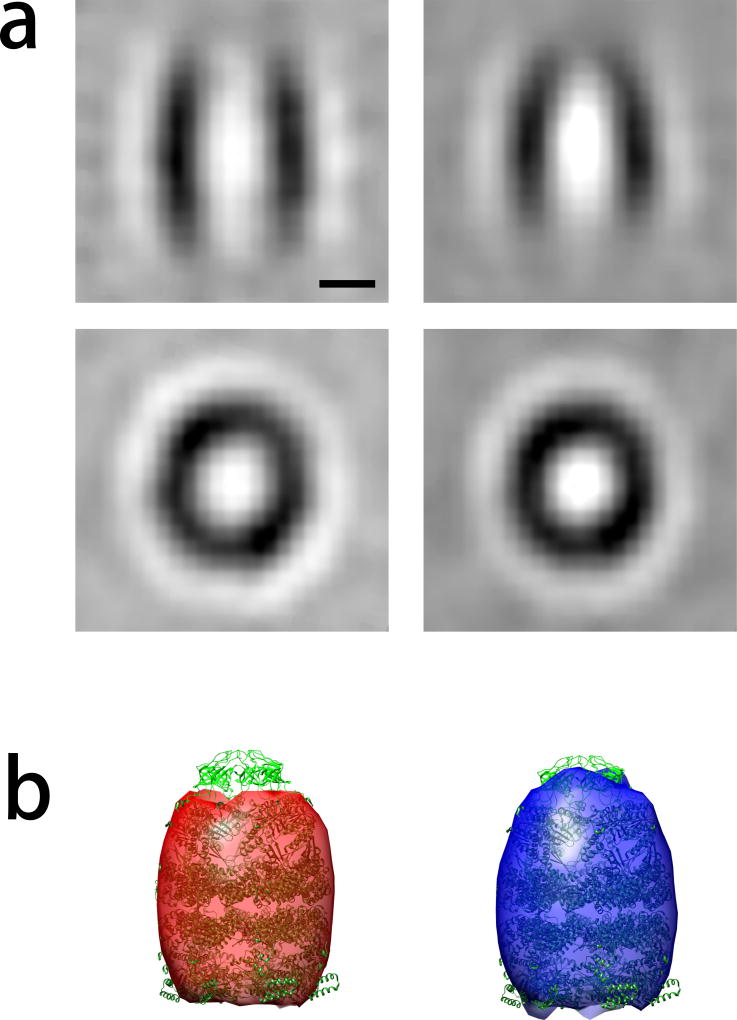
Because the total number of subtomograms is small (786), the classification can be easily performed on a single computer with multiple CPU cores. The test was carried out on a workstation with 8 CPU cores and 12 GB memory. When using 8 parallel workers, and setting the number of classes to K=2, 5 iterations of classification only took 140 minutes. Both major classes of structures GroEL and GroEL/GroEL were well recovered (Figure 5).

Figure 5.

Reference-free classification of 886 experimental subtomograms containing the GroEL and GroEL/GroES complexes taken from (Förster et al., 2008). Convergence was reached after 5 iterative rounds of reference-free classification. (a) Slice through the resulting cluster averages. The scale bar indicates 5nm. (b) Cluster averages depicted by isosurface rendering. The atomic structure of the GroEL/GroES complex is fitted into both cluster averages for comparison.

Cost analysis of cloud computing

We have implemented and made TomoMinerCloud publicly available on the AWS cloud. The AWS cloud infrastructure can be accessed worldwide, and there are data centers in many regions of the world. Researchers without access to local computing clusters are now able to leverage Amazon’s cloud computing infrastructure to perform large-scale data analysis, at low cost.

Current prices for renting an analysis program and server VM with 2 cores and 15GB memory (instance type r3.large) start from $0.175 (USD) per hour, based on AWS pricing (http://aws.amazon.com/ec2/pricing). Renting a worker VM with 36 core and 60GB memory (instance type c4.8×large) can cost as little as $1.763 (USD) per hour. Each such VM can host 36 workers, therefore the cost per worker per hour is $0.049(USD). The design of our task distribution also conveniently enables one to rent spot instances, which use unused AWS capacity at a significantly lower price. Renting solid-state storage costs $0.10 USD per GB per month. Uploading data is free of charge. Downloading analysis results is nearly free of charge, because the generated results consist of only a small amount of data, namely the rigid transformations of each subtomogram and the class averages. Inter-communication among VMs inside the VPC is also free of charge. Given such pricing, the total cost for the reference-free classification example of 100,000 subtomograms depicted in Figure 3 is estimated to be below $500. Therefore TomoMinerCloud is an affordable and efficient solution for high-performance subtomogram analysis for tomography laboratories that will not maintain a large computer cluster or need additional computing resources to perform the calculations.

We also estimated the time cost for uploading data. The transfer of a compressed file containing 100 subtomograms (volume 36nm³, voxel spacing 3Å) to AWS North California region took 8.61 seconds at a speed of around 76MB/s. In such case the transfer of 100,000 subtomograms would be estimated to take 2.4 hours.

In addition, we performed a simple averaging test of the Tobacco Mosaic Virus (TMV) subtomograms (Kunz et al., 2015) using TomoMinerCloud, following a similar procedure as in (Kunz et al., 2015). The total cost for the averaging is below $50. The results for the TMV averaging are summarized in the STAR Methods Section and Figure S3.

DISCUSSION

With current developments in cryo electron tomography it is possible to acquire cryoET 3D images of large numbers of particles. Processing large numbers of subtomograms is a bottleneck in structural analysis, so high-performance subtomogram analysis software is an increasingly important part of the toolkit used for the structural analysis of macromolecular complexes.

TomoMiner is a software for high-performance parallelized cryoET structural analysis. It is able to handle very large numbers of subtomograms, which is necessary for handling structural heterogeneity and increasing the quality and resolution of macromolecular complex structures from cryoET applications. TomoMiner provides a scalable architecture with respect to computational resources and can handle huge numbers of subtomograms. The platform provides both reference-based and reference-free subtomogram classification methods, and perform averaging and template matching based on subtomogram alignment methods.

We intend to transfer the TomoMiner into a community-centered, collaborative development project, with publication of the initial source code and programs as the first step. Our framework will be available through a distributed source code repository, which makes it easy for developers to participate in the project, modify TomoMiner to suit their own needs, and build their own tools on the platform. Additionally, the TomoMiner core library can be easily integrated into other tomogram analysis systems, especially those written in Python or C++. As an example, the core library and distributed processing components of TomoMiner have recently been used for supporting De Novo Visual Proteomics analysis (Xu, 2015).

In TomoMiner, various components such as the data storage interface have been abstracted, allowing for fast adaptation to novel computing environments. Further, different implementations of these components can be used on different high-performance computing clusters.

TomoMinerCloud provides an instant solution for users who do not have access to, or do not want to maintain, a high-performance computing cluster. Virtual Machines (VMs) running on cloud computing platforms are a useful alternative to local infrastructure, requiring minimal setup and no up-front hardware costs. Renting VMs allows smaller research laboratories to avoid the costs of hardware and maintaining a data center, while still benefitting from large-scale computational methods. Currently, the cloud computing solution only runs on Amazon AWS. We expect future releases to support other cloud computing providers, such as Google Cloud (https://cloud.google.com) and Rackspace (http://www.rackspace.com).

In summary, TomoMiner provides several high-performance, scalable solutions for large-scale subtomogram analysis. We believe that TomoMiner will be an important and efficient tool for the cryoET community, and it complements existing tools in the community.

STAR Methods

METHOD DETAILS

Fast subtomogram alignment based on fast rotational matching

Subtomograms are 3D volumes defined as 3D arrays of real numbers representing the intensity values at each voxel position. The voxel intensities are the result of a discretization of the density function f : ℝ³ → ℝ.

A tomogram is subject to orientation specific distortions as a result of the missing-wedge effect. This effect is a consequence of the data collection being limited to tilt angle ranges when collecting individual micrographs (with a maximum tilt range of θ ± 70°). As a result, in Fourier space structure factors are missing in a characteristic wedge shaped region. This missing data leads to anisotropic resolution and distortion artifacts that depend on the structure of the object and its orientation with respect to the tilt-axis.

To accurately calculate the similarity between two subtomograms, we have recently introduced a Fourier space equivalent form (Xu et al., 2012) of a popular constrained correlation score (Förster et al., 2008) that accounts for missing wedge effects. It is based on a subtomogram transform that eliminates the Fourier coefficients located in the missing wedge regions of any of the two subtomograms. For each subtomogram (f), a missing wedge mask function ℳ_f : ℝ³ → {0,1} defines valid and missing Fourier coefficients in Fourier space.

To allow for missing wedge corrections in our analysis procedures, a series of missing wedge masks can be given as input information together with the subtomograms.

The search for the optimal subtomogram alignments is performed through rigid transformations with rotational and translational components. A transformed subtomogram can be represented as:

$${\tau }_a{\mathrm{\Lambda }}_{R}f(x)=f(R^{-1}(a-a))$$ equation (1)

where f is a subtomogram, Λ_R is a transformation operator which applies the rotation given by rotation matrix R. τ_a is a transformation operator applying a shift by vector a ∈ ℝ.

The previously developed correlation score (Xu et al., 2012) for subtomograms f and g, where g has been rotated by Λ_R, the correlation is defined as

$$c=Re\left(\frac{\int (ℱf\mathrm{\Omega })\overline{ℱ{\tau }_a{\mathrm{\Lambda }}_{R}g\mathrm{\Omega }}}{\sqrt{(ℱf)\mathrm{\Omega }\overline{ℱf\mathrm{\Omega }}}\sqrt{(ℱ{\tau }_a{\mathrm{\Lambda }}_{R}g)\mathrm{\Omega }\overline{ℱ{\tau }_a{\mathrm{\Lambda }}_{R}g\mathrm{\Omega }}}}\right)$$ equation (2)

Here ℱ is the Fourier transform and Ω ≔ ℳ_fΛ_Rgℳ_g. The optimal rotational alignment R and translation a are found by maximizing this correlation.

The above formulation allowed us to design a fast alignment procedure (Xu et al., 2012). Summarizing, we first form a translation invariant approximation score defined by keeping only the magnitudes of the Fourier coefficients of the subtomograms. This score can be decomposed into three rotational correlation functions. After representing the values in a spherical harmonics expansion of the magnitude values these rotational correlation functions can be efficiently and simultaneously calculated over all rotation angles (Kovacs and Wriggers, 2002) using the FFT after representing the values in Spherical Harmonics expansion of the magnitude values. Therefore a small number of local maxima of the approximation score can be collected, representing a set of rotation angle candidates. Given each candidate rotation, a fast translation search can be performed to obtain optimal translations to determine a. The overall optimal alignment can then be obtained. This procedure is detailed in Equations 7–9 of (Xu et al., 2012).

In our software implementation, the volume rotation method for rotating the volumes uses cubic interpolation. Mask rotations use linear interpolation. In rotational searches, we re-sample the volume in spherical coordinates using cubic interpolation.

Generating a benchmark set of cryo-electron subtomograms

We tested the performance of TomoMiner with realistically simulated subtomograms as ground truth. This benchmark set of tomograms contains five known protein complexes (Table 2). For a reliable assessment of the software, the subtomograms must be generated by simulating the actual tomographic image reconstruction process, including the applications of noise, distortions due to the missing wedge effect, and electron optical factors, such as the Contrast Transfer Function (CTF) and Modulation Transfer Function (MTF). We follow a previously described methodology for realistic simulation of the tomographic image reconstruction process (Beck et al., 2009; Förster et al., 2008; Nickell et al., 2005; Xu et al., 2011). Macromolecular complexes have an electron optical density proportional to the electrostatic potential. The PDB2VOL program from the Situs (Wriggers et al., 1999) package has been used to generate volumes with a 4 nm or 3Å resolution, with a voxel spacing of 1nm or 3Å. The volumes are cubes, whose length dimension can be chosen depending on the experiment. The density maps are used to simulate electron micrograph images through a set of tilt-angles. The angles are chosen to represent the experimental conditions of cryo electron tomography, and to have a missing wedge angle similar to experimental data. For this paper we use a typical tilt-angle range of ±60°. Noise is added to achieve the desired SNR value (Förster et al., 2008). Next the images are convoluted with the CTF and MTF to simulate optical artifacts (Frank, 1996; Nickell et al., 2005). The acquisition parameters used are typical of those found in experimental tomograms (Beck et al., 2009); voxel grid length of 1 nm, spherical aberration of 2 × 10⁻³ m, defocus of −4 × 10⁻⁶m, and voltage of 300kV. The MTF is defined as sinc(πω/2) where ω is the fraction of the Nyquist frequency, corresponding to a realistic detector ((McMullan et al., 2009). Finally a backprojection algorithm (Nickell et al., 2005) is used to produce subtomogram from the tilt series.

Table 2.

To assess the methods we used five different macromolecular complexes selected from the PDB and used previously as a test set (Berman et al., 2000).

PDB ID	Description
1BXR	Carbamoyl phosphate synthetase complexed with the ATP analog AMPPNP
1KP8	GroEL-KMgATP
1W6T	Octameric enolase from S. pneumoniae
1YG6	ClpP
2AWB	50s subunit of E. coli ribosome.

QUANTIFICATION AND STATISTICAL ANALYSIS

Assessment of classification accuracy

We assessed the reference-free subtomogram classification performance with simulated data, by comparing the results with the ground truth. The accuracy is measured as the number of true positives. To compare the computed class labels with the ground truth, we construct a confusion matrix where each row corresponds to a known class, and each column to a predicted class label. The matrix elements are the number of subtomograms belonging to each class of a given class label. A maximum-weight matching (Munkres, 1957) is computed to determine the best correspondence between ground truth classes and detected clusters. That is, we determine the labeling of ground truth classes to class labels, which maximizes the number of true positives of the confusion matrix. In the event that we have more generated clusters than true classes, we do not require a one-to-one matching, and allow for multiple clusters to map to the same ground truth class. The accuracy of the generated subtomogram cluster averages is determined by comparison with templates of the ground truth protein complexes. The Pearson correlation score between the two structures is used to quantify the similarity.

Averaging subtomograms of 3Å voxel spacing

We also simulated ribosome subtomograms with a voxel size of 3Å, resolution 3Å, SNR 0.03, and tilt angle range ±60° and performed the averaging tests. The test was performed to demonstrate the computational efficiency of the parallel implementation with respect to the scaling of the computational efficiency with respect to the number of subtomograms and cluster nodes. When using the simulated subtomograms at 3Å voxel size we can show almost identical linear scaling behavior in comparison to tests with maps using 1 nm voxel size. The following figures describe the results for subtomograms at 3Å voxel size.

Figure S1A shows that the required computation time increases close to linear with respect to the number of tomograms analyzed. Figure S1B shows that when the number of subtomograms increases the computation time per subtomogram per iterative round decreases. The plateau at 10,000 subtomograms indicates that the scaling converges on a constant speed. Figure S2 shows the increase of the structural accuracy of averages with the increase of the number of subtomograms.

Structural reconstruction of the Tobacco Mosaic Virus (TMV) using TomoMinerCloud

We also demonstrated the performance of TomoMinerCloud on the amazon cloud computing services using a recent data set. We performed a reference-free iterative alignment and averaging for the Tobacco Mosaic Virus (TMV) using TomoMinerCloud. The 2743 TMV subtomograms were provided by the Frangakis lab and the reconstruction followed a similar procedure as in (Kunz et al., 2015). As shown in Figure S3, we were able to reconstruct the structure and characteristic features of the TMV virus, including its helical symmetry. The resolution of the subtomogram average is 10.4Å measured by FSC (with 0.5 cutoff) between two half-set averages. The reference-free iterative alignment and averaging was performed on amazon cloud. Uploading of the subtomograms took about 1 hour. The amazon cloud application was performed on 3 nodes each running 36 workers. A single iteration took about 30 minutes. The total cost for the iterative process using TomoMinerCloud is below $50 US Dollars. These results demonstrate the applicability of our program on direct detector data and also the feasibility to use TomominerCloud without the use of a high performance-computing cluster.

DATA AND SOFTWARE AVAILABILITY

The TomoMiner and TomoMinerCloud source code and user guide are available at http://web.cmb.usc.edu/people/alber/Software/tomominer

Table 1.

The various executables included in the TomoMiner software package.

Parallel processing programs	Description
tm_server	Run a server
tm_worker	Run a worker which will process subproblems
tm_watch	Report progress and statistics on the server
Utility programs	Description
tm_align	Calculate optimal alignment between two subtomograms using fast rotational matching
tm_fsc	Calculate the Fourier Shell Correlation(FSC) between two aligned structures
tm_corr	Calculate the correlation score of the best alignment between two subtomograms
Analysis programs	Description
tm_classify	Reference-free or reference-based subtomogram classification
tm_average	Reference-free or reference-based subtomogram alignment and global averaging
tm_match	Template matching

Highlights.

1. TomoMiner allows large-scale subtomogram classification, alignment and averaging.

2. TomoMinerCloud permits users instant access to cloud-based high-performance features.

3. Software for template matching, subtomogram classification and averaging.

4. TomoMiner is scalable and allows robust parallel processing.