Visualizing redox orbitals and their potentials in advanced lithium-ion battery materials using high-resolution x-ray Compton scattering

A spectroscopic descriptor of the link between lattice distortion and voltage in Li battery materials.

Abstract

Reduction-oxidation (redox) reactions are the key processes that underlie the batteries powering smartphones, laptops, and electric cars. A redox process involves transfer of electrons between two species. For example, in a lithium-ion battery, current is generated when conduction electrons from the lithium anode are transferred to the redox orbitals of the cathode material. The ability to visualize or image the redox orbitals and how these orbitals evolve under lithiation and delithiation processes is thus of great fundamental and practical interest for understanding the workings of battery materials. We show that inelastic scattering spectroscopy using high-energy x-ray photons (Compton scattering) can yield faithful momentum space images of the redox orbitals by considering lithium iron phosphate (LiFePO₄ or LFP) as an exemplar cathode battery material. Our analysis reveals a new link between voltage and the localization of transition metal 3d orbitals and provides insight into the puzzling mechanism of potential shift and how it is connected to the modification of the bond between the transition metal and oxygen atoms. Our study thus opens a novel spectroscopic pathway for improving the performance of battery materials.

INTRODUCTION

Lithium iron phosphate (LFP) (1), a member of the olivine family, has been a surprising candidate in the search for safe, high-performance cathode materials (2, 3), despite some unfavorable properties. For example, the band gap of LFP is quite large (4). Moreover, delithiation in LFP is a two-phase process that leads to microscopic phase separation in equilibrium (5, 6). LFP also carries one-dimensional (1D) lithium diffusion channels (7, 8), which could be blocked by impurities and defects. LFP thus challenges conventional wisdom for developing high-performance cathode materials (9).

Recent research (6, 10, 11) aimed at studying LFP has combined x-ray absorption spectroscopy (XAS), theoretical modeling, and materials synthesis efforts to monitor the evolution of the redox orbitals in nanoparticles and single-crystal LFP cathodes under different lithiation levels. The sensitivity and high resolution of XAS enable identification of spectroscopic signatures of the lithiation process and information on phase transformations, valence and spin states, and local structural distortions. Thus, XAS allows a handle on the interplay between lithiation and electronic structure evolution, shedding light on the lithium diffusion mechanism in LFP cathodes. Note that although XAS probes unoccupied electronic states, complementary information on occupied states can be obtained via x-ray emission spectroscopy (XES) (12). However, XAS and XES can only access the energy dependencies of the electronic states and the associated spectral functions. It is here that the role of x-ray Compton scattering becomes crucially important because Compton scattering is uniquely capable of accessing the momentum characteristics of the correlated ground-state wave functions, which are beyond the reach of XAS and XES (13–19). In particular, the experimentally measured Compton profile is directly related to a simple 2D integral of the electron momentum density (EMD) (20), which can also be obtained by positron annihilation experiments (21). Because the EMD is given by an energy integral of the spectral function over all occupied states, the spectral function and its momentum dependence near the Fermi level can be obtained via an energy derivative of the EMD. That is, characteristics of the evolution of redox orbitals with lithiation/delitihiation in the battery materials can be unraveled by monitoring changes in Compton profiles with Li content.

The redox reaction in pristine LFP has been well characterized via previous soft x-ray experiments (10, 12, 22). It is for this reason that we focus here on LFP for the purpose of testing the efficacy of the new method discussed in this study for gaining a spectroscopic handle on the redox orbitals in battery materials more generally (23). It should be noted that orbitals can be “visualized” in momentum space, much like the more familiar images of the orbitals illustrating symmetries and spatial distributions of the associated real-space charge densities (24). For example, Sakurai et al. (25) show how signatures of the dopant orbitals in cuprate high-temperature superconductors can be adduced from the doping dependencies of the Compton spectra and the related 2D EMDs.

RESULTS

Compton profile differences of lithiated and delithiated LFP

Our analysis is simplified by the fact that as a cathode material, LFP only exists in two distinct phases (10): the fully lithiated form LFP and the delithiated compound FePO₄. Figure 1 shows the theoretical and experimental Compton profile differences ΔJ between these two limiting cases. To understand various contributions to ΔJ, we keep the structure of LFP fixed and consider three different simulations for the Compton profile of FePO₄ as follows: (i) rigid band model in which the band structure of FePO₄ is assumed to be the same as that of LFP but the band occupation is adjusted to account for the correct number of electrons per unit cell; (ii) rigid octahedron model, where the FeO₆ octahedron of FePO₄ is identical to the one of LFP; and (iii) relaxed octahedron model, where the FeO₆ octahedron of FePO₄ distorts with a smaller volume than that of LFP. The inset to Fig. 1 gives a schematic representation of the density of states (DOS) in LFP and FePO₄. The rigid band model captures the removal of electrons upon delithiation. Because the removed electrons are in the minority Fe 3d states of LFP, the resulting profile ΔJ is flat at low momenta and decays slowly with momentum, consistent with earlier models of ΔJ associated to 3d atomic orbitals (13). Here, however, the rigid band scheme deviates significantly from the experimental ΔJ, indicating its shortcomings as shown in Fig. 1. On the other hand, the rigid octahedron model produces a trend similar to that seen in the experiment at high momenta but fails in the low momentum region. Thus, this model yields insight into the role of octahedral distortions, as we shall discuss further below. Finally, we see that good agreement between theory and experiment is obtained over the entire momentum range in Fig. 1, when the FeO₆ octahedron is allowed to relax during delithiation because Fe²⁺ ions are oxidized to Fe³⁺ and the Fe–O bond is modified. The relaxation produces a smaller Fe–O interatomic distance and a smaller FeO₆ octahedron in FePO₄ compared to that in LFP (see inset to Fig. 4). The effect of distortion can be highlighted by considering the distortion profile (26) D(p), which is obtained by taking the difference between ΔJ profiles for rigid and relaxed octahedron models (solid blue line in Fig. 1).

Fig. 1. Differences between the Compton profiles of LFP and FePO_4, $\mathrm{\Delta }\mathit{J}(\mathit{p})={\mathit{J}}_{\text{LiFeP}{\mathrm{O}}_4}(\mathit{p})-{\mathit{J}}_{\text{FeP}{\mathrm{O}}_4}(\mathit{p})$.

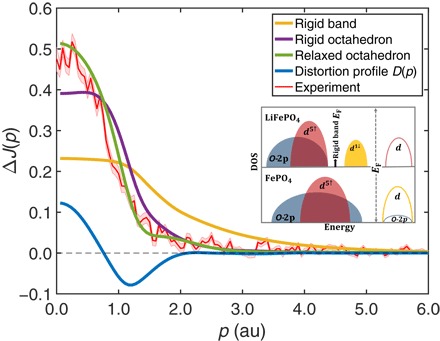
Theoretical results based on three different models of the electronic structure of FePO₄ are considered: rigid band model (gold line), rigid octahedron model (purple line), and relaxed octahedron model (green line). The electronic structure and the Compton profile for LFP, ${\mathit{J}}_{\text{LiFeP}{\mathrm{O}}_4}(\mathit{p}),$ remains fixed for all three models, whereas the Compton profiles of FePO₄, ${\mathit{J}}_{\text{FeP}{\mathrm{O}}_4}(\mathit{p})$, are different. The inset shows a sketch of the DOS of LFP and FePO₄. During the charge-discharge process, electrons are transferred from the highest occupied d states of LFP (yellow shaded area) to the lowest unoccupied d states of FePO₄. Thus, in the rigid band model, FePO₄ electronic structure is approximated similarly as LFP, but the Fermi level is adjusted below the highest occupied states as shown by the energy position of the arrow in the DOS of LFP. In the rigid octahedron model, FePO₄ experiences the same FeO₆ octahedral environment as LFP, whereas in the relaxed octahedron model, FePO₄ structure is fully relaxed, which produces a distortion and a smaller volume in FeO₆ octahedron. The experimental difference profile (red line) is seen to be well reproduced by the relaxed octahedron model. Pink shading gives the experimental error bars. Effect of the distortion of the FeO₆ octahedron in FePO₄ is highlighted by considering the distortion profile D(p), which is defined as the difference in Compton profiles between the relaxed (green line) and rigid octahedron (purple line) models.

Fig. 4. Distortion profiles D(p) for various olivine battery materials.

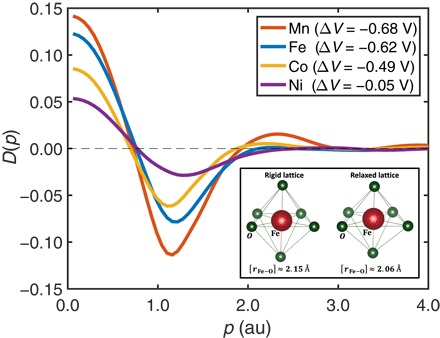
Distortion profile, D(p), highlights the effect of distortion of the metal-oxygen octahedron. D(p) is defined as the difference in Compton profiles between the relaxed and rigid octahedron models, $\mathit{D}(\mathit{p})=\mathrm{\Delta }{\mathit{J}}_{\text{rigid}}(\mathit{p})-\mathrm{\Delta }{\mathit{J}}_{\text{relaxed}}(\mathit{p})={\mathit{J}}_{\mathit{M}\mathrm{P}{\mathrm{O}}_4}^{\text{relaxed}}(\mathit{p})-{\mathit{J}}_{\mathit{M}\mathrm{P}{\mathrm{O}}_4}^{\text{rigid}}(\mathit{p})$. Results for MPO₄ (M = Mn, Fe, Co, and Ni) are shown. The amplitude of D(p) is seen to increase systematically in going from Ni to Co to Fe to Mn. The increasing amplitude of D(p) is also reflected in a corresponding loss in the redox potential (potential shift) due to distortion of the metal-oxygen octahedron. The inset shows the rigid and relaxed structures of FePO₄. The metal-oxygen octahedron FeO₆ in the rigid octahedron model is assumed to be the same as that in LFP. In the relaxed octahedron model, the FeO₆ octahedron experiences a strong distortion during delithiation and produces a smaller average Fe–O interatomic distance (〈r〉 = 2.06 Å) than that of the rigid structure (〈r〉= 2.15 Å).

Kinetic energy and voltage

It is well known that there are significant errors in the redox energies obtained through first-principles total energy computations based on either the commonly used local density approximation (LDA) or the generalized gradient approximation (GGA) (8). In this connection, Ceder et al. (4) report that the use of a self-interaction correction U within the density functional theory (DFT) + U scheme yields an improved agreement with experiments and provides a tool for accurately estimating the average Li intercalation voltage V of the battery in terms of the single parameter U. They also showed that V varies linearly with U (see inset to Fig. 2). To gain a new handle on the parameter U, we recall that the Compton profile difference ΔJ can be viewed as a probability distribution of the redox orbitals to obtain their characteristic kinetic energy ΔK given by the second moment (27) of the distribution ΔJ. Figure 2 demonstrates that kinetic energy ΔK computed in this way is proportional to U. It is clear then that ΔK provides a direct descriptor for monitoring the value of the parameter U. The value of ΔK obtained from the experimental ΔJ profile is 1.09 atomic units (au) with an error of about 0.10 au, whereas the corresponding theoretical value obtained from our relaxed octahedron model with U = 4.3 eV is ΔK = 1.04 au, with a related voltage of 3.48 V.

Fig. 2. Kinetic energy ΔK and voltage as a function of Hubbard parameter U.

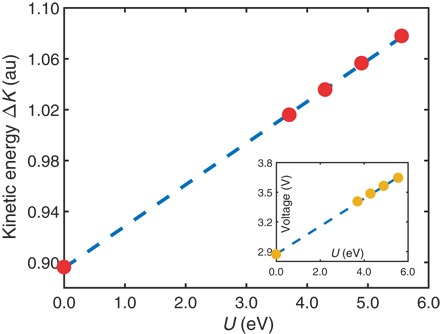
The main figure gives the kinetic energy ΔK for several different values of U (red dots; dashed blue line is drawn to connect the dots), where ΔK is computed by taking the second moment of the difference Compton profile ΔJ. Inset shows the average Li insertion voltage as a function of U (gold dots; dashed blue line is drawn to connect the dots), where the voltage is calculated from the total energies of LFP, FePO₄, and body-centered cubic lithium, as discussed in the text. The voltage calculated with U = 4.3 eV is 3.48V, which agrees well with the experimental value of 3.5 V.

Visualization of the redox orbitals

Figure 3 presents several theoretical 2D EMD differences between LFP and FePO₄ obtained by integrating the 3D EMDs along the a axis. These maps show the extent to which the 3d Fe orbitals are modified by the chemical bond and help clarify the link between voltage shift and the modification of the bond between the transition metal and oxygen atoms. Experimentally, the 2D EMD map can be obtained by measuring Compton profiles for a number of different directions of the x-ray scattering vector, which can then be used to reconstruct (25) the 2D EMD differences between LFP and FePO₄. Three different theoretical maps are simulated to delineate the nature of the redox orbitals. We emphasize that various electronic orbitals carry their own angular dependencies, which facilitates the identification of their presence in the EMD. In fact, the EMD, which is the squared modulus of the momentum-space wave function (summed over all occupied states), has the same point group symmetry as the charge density in real space. The EMD shape in Fig. 3A is consistent with the minority 3d states of iron, which show a considerable delocalization in momentum space (or localization in real space), as expected from the ΔJ profile of the rigid band model in Fig. 1. Looking at Fig. 3B, we see that this delocalization effect is reduced in the rigid octahedron model, although the angular dependence of the EMD appears to have peaks at high momenta along the p_z direction, and it is, therefore, still dominated by its 3d character. However, the results of Fig. 3C show that FeO₆ octahedral distortion (see right-hand side inset in Fig. 4) significantly modifies the EMD by bringing in new contributions at low momenta, which imply an increased localization of states in momentum space compared to the two previous cases, and emphasizes the key role of octahedral distortions in the delithiation process. XAS experiments (10) have also provided information on the octahedral distortion in LFP during the charge-discharge cycle.

Fig. 3. Momentum maps of the redox orbital.

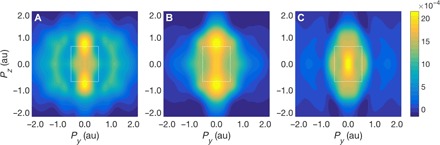
The difference of the 2D EMDs of LFP and FePO₄ provides a visualization of the wave function of the redox orbital in momentum space for the three models considered in Fig. 1: (A) rigid band model; (B) rigid octahedron model; and (C) relaxed octahedron model. The white rectangular box marks the boundary of the first Brillouin zone. P_y and P_z axes are parallel to the [010] and [001] directions, respectively. Amplitudes of the maps in (A) and (B) have been rescaled by factors of 3.3 and 1.7, respectively, to highlight the symmetry of the orbital without the masking effect of a decreasing amplitude due to the delocalization of the state.

Distortion profile and potential shift

The distortion profile D(p), shown in Fig. 1, gives complementary information about the nature of the FeO₆ octahedral deformation. This profile appears as a modulation in the momentum space and represents a significant correction to the Compton profile in the lithiation/delithiation process. It monitors modifications of wave functions and changes in the Fe–O bond. The profile D(p) also reveals loss in redox potential or potential shift ΔV generated by the octahedral distortion, which, as already discussed, can be described in terms of the associated kinetic energy ΔK. In the rigid octahedron model, we compute ΔK to be 1.30 au and the corresponding voltage V to be 4.10 V. On the other hand, in the relaxed octahedron model, ΔK and voltage V are 1.04 au and 3.48 V, respectively. The octahedral distortion thus produces a potential shift ΔV = −0.62 V with a related kinetic energy loss of 0.26 au. We have further investigated this remarkable connection between the distortion profile D(p) and the potential shift as well as kinetic energy loss by considering several different olivine compounds, as shown in Fig. 4. When Fe is substituted by Mn, Co, or Ni, the resulting higher amplitude of D(p) seen in Fig. 4 for Mn would indicate a larger potential shift, which is consistent with a study of potential shift in mixed olivine systems via tensile strain (28). It is clear that potential shift in LFP can be reduced by substituting Fe with other transition metals such as Co and Ni, notwithstanding the challenges of other contributing factors such as degradation of Li-ion electrolytes (9), and electronic and ionic conductivities (5) of the resulting cathode materials. Hautier et al. (29) discuss the role of crystal structure in driving a substantial spread in voltage around its average value for a given redox couple. These considerations suggest that strains and octahedral distortions in olivine phosphate compounds produced by iron atom substitution (28) could be used to improve the limited energy density of the pristine LFP (11). In this context, the deformation profiles introduced in this study would provide a unique spectroscopic descriptor for monitoring the shifts in the redox potentials of olivine in the quest to optimize the energy density of the cathodes.

DISCUSSION

Our analysis reveals an exciting new link between voltage and the localization of transition metal 3d orbitals and provides insight into the puzzling mechanism of potential shift. In fact, by taking Compton profile differences and extracting the so-called distortion profile D(p), we have observed modulations in momentum space due to the interference between electron orbitals on neighboring iron and oxygen bonding sites (20). The presence of these interference patterns allows us to monitor and understand the potential shift in cathodes at the molecular and bonding scale because D(p) is connected directly to the modification of the battery voltage, resulting from distortion of transition metal/oxygen atoms octahedra in the olivine cathode materials. This distortion decreases (Mn > Fe > Co > Ni) with increasing number of electrons in the d orbital. This is to be expected because when the minority d-band is filled or almost filled, adding or removing an electron causes a smaller perturbation than when such a band is empty or almost empty. Our method thus correlates with empirical rules for electrochemical potentials of cathode materials (30).

The present study is limited to the spherical average of the experimental Compton profile because the cathode is composed of a powder rather than a single crystal. Therefore, the full reconstruction of the redox orbitals cannot rely on experimental profiles alone as in the case of Sakurai et al. (25), but also needs validation by robust EMD simulations.

In conclusion, we have introduced a general method for delineating the poorly understood link between lattice distortion and potential shifts. Extensions of the present method to consider other cathode families (31–33) and its applications to classic problems, such as the potential change of more than 1 V due to the displacement of Li atoms in Li_xMn₂O₄ systems (34), via Compton experiments would be worthwhile. Our method could also be useful in investigating tunable battery materials (35) for boosting catalytic activity of oxygen reduction reactions (36). Because high-energy x-rays can easily penetrate closed electrochemical cells, our study establishes a spectroscopic basis for monitoring changes in redox orbitals during charging-discharging processes in ex situ, in situ, and in operando (14) setups, and will thus facilitate the design and development of high-performance cathodes for Li batteries.

MATERIALS AND METHODS

Electronic structure calculations

The ground-state electronic structure was obtained within the GGA + U scheme using the projector augmented-wave (PAW) method (37) as implemented in the Vienna Ab initio simulation package (38–40). Because the gradient corrections to the local spin density approximation are important for correctly describing the magnetic properties of transition metals (41), we used the GGA with Perdew-Burke-Ernzerhof functional (42) to account for exchange-correlation effects. The kinetic energy cutoff for the plane-wave expansions was set at 560 eV, and a 6 × 10 × 12 k-point mesh was used so that the total ground-state energy is well converged. Orthorhombic LFP and FePO₄ containing 28 and 24 atoms per unit cell, respectively, were initialized in the antiferromagnetic configuration. Because the standard DFT in either LDA or GGA implementation underestimates the Coulomb interaction for localized d electrons in strongly correlated systems, the Hubbard term U was introduced for calculating Fe 3d states to avoid electron self-interaction errors. Following the work of Zhou et al. (4, 43), the value of U was taken to be 4.3 eV, which improves the accuracy of the predicted voltage over the bare LDA or GGA. Experimental lattice parameters were used for LFP (44). The relaxed structure of FePO₄ was obtained by performing a full optimization of ionic positions until the total energy was converged to 0.1 meV per atom. The relaxation was found to produce a strong octahedral distortion and yield an average Fe–O bond length of 2.06 Å (see inset in Fig. 4), which is in good accord with the experimentally observed distortion of FeO₆ octahedron in FePO₄ with an average Fe–O bond length of 2.04 Å (1, 44). Similar computations were also carried for the other three olivine compounds LiMPO₄, where M = Mn, Co, and Ni, using U values of 4.5, 5.7, and 6.1 eV, respectively (4, 43).

The voltage was calculated from the total energies of LFP, FePO₄, and body-centered cubic Li using the formula (4)

$$\mathit{V}=-\frac{1}{\mathit{e}}[\mathit{E}({\text{LiFePO}}_4)-\mathit{E}({\text{FePO}}_4)-\mathit{E}(\text{Li})]$$

where e denotes electron charge.

The potential shift is defined as the difference of voltages corresponding to relaxed and rigid FePO₄ structures

$$\mathrm{\Delta }\mathit{V}={\mathit{V}}_{{({\text{FePO}}_4)}_{\text{relaxed}}}-{\mathit{V}}_{{({\text{FePO}}_4)}_{\text{rigid}}}=-\frac{1}{\mathit{e}}[\mathit{E}{({\text{FePO}}_4)}_{\text{rigid}}-\mathit{E}{({\text{FePO}}_4)}_{\text{relaxed}}]$$

Compton profile calculation

We calculated the EMD and the Compton profiles of the valence electrons from the PAW Kohn-Sham orbitals along the lines of Makkonen et al. (45). The PAW correction was needed to describe the high-momentum Fourier components of the valence wave functions. The Compton profile J(p_z) is a 1D projection of the 3D EMD, ρ(p), and it can be extracted from the Compton scattering cross section within the impulse approximation (19, 20). Thus, J(p_z) was obtained by performing the double integral of ρ(p)

$$\mathit{J}({\mathit{p}}_{\mathit{z}})={\displaystyle \iint }\mathrm{\rho }(\mathbf{p})\mathit{d}{\mathit{p}}_{\mathit{x}}\mathit{d}{\mathit{p}}_{\mathit{y}}$$

where p = (p_x, p_y, p_z) denotes electron momentum and p_z was taken to lie along the direction of the scattering vector. The momentum density can be expressed as (46, 47)

$$\mathrm{\rho }(\mathbf{p})={\displaystyle \sum _{\mathit{j}}}{\mathit{n}}_{\mathit{j}}{|{\displaystyle \int }{\mathrm{\Psi }}_{\mathit{j}}(\mathbf{r})\text{exp}(-\mathit{i}\mathbf{p}\mathbf{\times }\mathbf{r})\mathit{d}\mathit{r}|}^2$$

where Ψ_j(r) is the wavefunction of the electron in state j, and n_j is the corresponding occupation number. The 3D EMD was first calculated over a uniform k-point mesh, which was chosen to be dense enough to accurately capture the fine structure in the momentum density. The Compton profile was then obtained by performing the 2D momentum integrals.

The expectation value of the electron kinetic energy can be calculated from spherically averaged Compton profiles. As pointed out by Epstein (27), the variation of kinetic energy can be related to the Compton profile difference ΔJ(p) as

$${\mathit{E}}_{\text{KE}}(\mathit{p})=3{\displaystyle {\int }_0^{\mathit{p}}}{\mathit{q}}^2\mathrm{\Delta }\mathit{J}(\mathit{q})\mathit{d}\mathit{q}$$

Here, the parameter ΔK is defined as ΔK = E_KE (p = 3 au), where p = 3 au is a momentum cutoff introduced to minimize the effects of statistical errors in the experimental ΔK.

Compton scattering measurement and sample preparation

Compton measurements were performed using a Cauchois-type x-ray spectrometer on the BL08W beamline at the SPring-8 (48–50). Incident x-rays emitted from a multipole wiggler were monochromatized to 115 keV by a bent-type Si (400) crystal. The size of the incident x-ray beam was 2.5 mm in height and 5 mm in width at the sample position. The scattering angle was fixed at 165°. The Compton-scattered x-rays were measured by a 2D position-sensitive detector. Energy distribution of the Compton-scattered x-rays was centered at 80 keV. The Compton profiles were corrected for absorption, analyzer and detector efficiencies, scattering cross section, possible double-scattering contributions, and x-ray background (20). The overall momentum resolution in the present measurements is 0.1 au. The measurements were performed under vacuum and room temperature conditions. The area under the Compton profile was normalized to the total number of valence electrons after subtracting the contribution of core electrons. LFP powder was prepared by the solid-state method through the reaction of stoichiometric quantities of Li₂CO₃ (Kojundo Chemical Laboratory, 99.99%), FeC₂O₄·2H₂O (Wako, 99.6%), and (NH₄)₂HPO₄ (Wako, 98.0%). Starting materials were ball-milled with ethanol for 12 hours and dried for more than 12 hours. The precursor was remixed with 10 weight % of carbon black using a ball mill with a rotation speed of 400 rpm. LFP was delithiated by chemical oxidation of LFP using nitronium tetrafluoroborate (NO₂BF₄) as an oxidizing agent. NO₂BF₄ was dissolved in acetonitrile, and then the LFP powder was stirred in the solution for 48 hours. The mixture was filtered and washed with acetonitrile. Synthesized LFP pellets were then used for Compton scattering measurements.