A simple statistical approach to model the time-dependent response of polymers with reversible cross-links

Abstract

A new class of polymers characterized by dynamic cross-links is analyzed from a mechanical point of view. A thermodynamically consistent model is developed within the Lagrangian framework for polymers that can rearrange their internal cross-links. Such a class of polymers has the capability to reset their internal microstructure and the microscopic remodeling mechanism leads to a behavior similar to that of an elastic fluid. These materials can potentially be used in several fields, such as in biomechanics, smart materials, morphing materials to cite e few. However, a comprehensive understanding is necessary before we can predict their behavior and perform material design for advanced technologies. The proposed formulation–following a statistical approach adapted from classical rubber elasticitye is based on the evolution of the molecular chains’ end-to-end distance distribution function. This distribution is allowed here to evolve with time, starting from an initial stress-free state and depending on the deformation history and the cross-link attachment/detachment kinetics. Some simple examples are finally presented and discussed to illustrate the capability and generality of the developed approach.

1. Introduction

A class of soft materials, such as gels, elastomers or biological tissues, can either be characterized as solid or liquids, depending on the time scale of applications. This peculiar response arises from the fact that these materials have the capacity to internally remodel and evolve their microstructure in time, yielding a time-dependent behavior that resembles to that of viscoelastic solids. From a modeling perspective, these materials present a significant challenge since theory typically separates the concepts of Lagrangian mechanics (for solids) and Eulerian mechanics (for fluids) [1–4]. We propose here to address this problem by focusing on a relatively new family of polymers whose cross-links can actively attach and detach in time following controllable kinetics [5–7]. This family may include, for instance, double network gels that have a system of stable background cross-links and a secondary lightly cross-linked pattern that can easily fail and reform under external actions. Polymer with reversible cross-links are also ubiquitous in living matters [11,12] and a proper understanding of their mechanical response will have impact in biomechanics and mechanobiology but also in the design of bio-inspired synthetic materials whose internal can evolve with their environment. Environment responsive materials can further be developed by leveraging the sensitivity of dynamic cross-links to external forces, strain, chemistry, heat, light and pH [10]. In this context it was recently shown that the use of the so-called click nucleic acid (CNA) polymers can enable the design of gels with highly controllable reversible physical cross-links [8]. The dynamic nature of the chains’ cross-links enables a rearrangement of the polymer network, leading to stress relaxation and irreversible deformations [9]. Such characteristics open the way for a new class of materials [13–16] that are capable of adapting to applied loads without failing, tuning their shape to minimize stresses or self-healing by reattaching two surfaces that are close enough. Such a remodeling feature depends on both the bond detachment-attachment balance as well as on the bond density in the equilibrium state of the material.

A key to understand, quantify and eventually predict the response of these complex materials resides in establishing a link between the physico-chemistry of cross-link attachment/detachment and the overall time dependent mechanical response of the material. Moving in this direction, a number of experimental studies were performed to characterize these polymers via stress-relaxation and creep tests [17–20]. Several theoretical models have been also proposed to complement and explain experimental observations [21–25], while in Ref. [26] a comprehensive review on reorganizable polymers with dynamic covalent bonds is presented. In Refs. [21,22] a thermodynamically consistent constitutive models is proposed to account for thermal-chemical and mechanical behavior of network polymers with thermally reversible linkages in which phases are formed, continuously in time, in a stress-free state and without any deformation in their appearance configuration; in Refs. [23–25] a finite deformation model is developed, based on the strain energy evolution evaluated by accounting for the contribution of the chains that break and reform at different instants during the loading history, according to a proper decaying function of time. A comprehensive review on materials (whose properties are based on reversible chemistry, i.e. reversible breaking and reformation of covalent and non-covalent bonds) with the ability to reversibly adapt to the environmental stimuli can be found in Ref. [27].

In the present paper we propose to develop a simple mechanical model that clearly connects the distribution of cross-links in the material and the evolution of its macroscopic mechanical properties; we treat here a polymer as a nano-composite made up of two phases: a polymeric network and dynamic cross-links. The interaction of the two above ‘constituents’ provides a material with unique features that can be usefully exploited in real macroscopic applications. The proposed approach is based on the extension of the classical concept of entropic elasticity that connects the internal forces in polymer chains to their end-to-end distance distribution. The continuous detachment and attachment of cross-links affects the time evolution of the point-wise statistical distribution of the chains’ end-to-end distance, and hence its stored mechanical energy. This feature, in turns, affects the redistribution of stress and strain in the materials eventually leading to stress relaxation. We show that this approach enables a relatively simple and effective description of the mechanical behavior of polymeric materials with an evolving microstructure without the need to keep track of the deformation history. We also show that in the limit case of static cross-links, the model degenerates to classical rubber elasticity, while increasing the rate of cross-link detachment yields the behavior of an elastic viscous fluid. The model is finally implemented with the finite element method and predictions of simple relaxation tests are analyzed and compared with the literature. This is complemented by additional parametric analyses that aim to demonstrate the versatility and capability of the approach for polymer with active cross-links.

2. General concepts

The general concept relating the evolving nature of covalent bonds in the presence of heat to the overall behaviors of polymers has been firstly introduced by Rowan [28]. In a cross-linked elastomer, polymer chains constantly undergo dynamic fluctuations under finite temperature. The energy associated with this thermal motion is not only responsible for the material’s stiffness, but also for its ability to evolve its structure if cross-links are reversible. At the nano-scale, the energy stored in a chain can be related to its end-to-end distance via the framework of flexible polymer chains. At the macroscopic level, however, it is convenient to describe the structure in terms of the chain density, as well as the statistical distribution of the end-to-end distance. In the case of reversible cross-linked polymer, we further refine the description by considering the chains in either a detached (inactive) or attached (active) state. In the case of reversible cross-links, this end-to-end distribution evolves from two mechanisms: (a) chain stretch due to the imposition of an external stress and (b) a change in chain connectivity due to the detachment and re-attachment of active cross-links. These mechanisms strongly depends on the strain rate and the rate of detachment (k_off, fraction of cross-links that detaches in a unit time) and re-attachment (k_on, fraction of cross-links that reattaches in a unit time). At the macroscale, this translates to a material whose stress-free configuration is continuously updated as the microstructure changes. (Fig. 1).

Fig. 1.

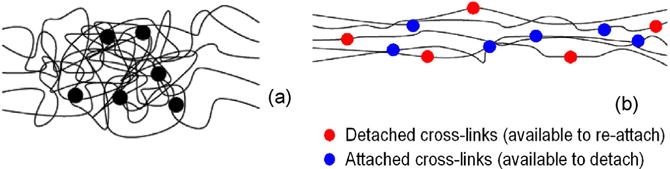
Scheme of the polymeric network (a). Activable (k_on mechanism) and de-activable (k_off mechanism) cross-links in the stretched material (b).

From a mechanical prospective the above observation is justified by the fact that initially stretched polymer chain (Fig. 2) have the possibility to detach from the network and reattach in a lower energy state (smaller stretch). The rearranging mechanism corresponds yields an overall energy dissipation: before the detachment the chain has a certain amount of stored energy, while such an energy is lost due to the links reverse, typically occurring with an increase of the material temperature. The formation of a new cross-link between two previously relaxed chains, induce an increase in stored mechanical energy of the system. This phenomenon can also be thought of as a healing mechanism; if the deformation rate is not too fast with respect to the cross-links rearrangement speed, it can prevent macroscopic failure or the formation of macro cracks, with the beneficial effect of providing a more stretchable material capable of smooth out the stresses and strains peaks.

Fig. 2.

Scheme of three 2-D chains in their reference state (a, b, c) and the corresponding configurations after deformation acting along the x-direction quantified by the stretch λ (a1, b1, c1).

3. Evolution of cross-link density

Let us now assume that the concentration of the cross-linked chains is at equilibrium during the whole stretch history and that evolves according to the well-known mass action law [29–31]:

$${\dot{c}}_A=c_D·k_{on}-c_A·k_{\mathit{off}}$$ (1a)

where c_A, c_D, k_on, k_off are concentrations of detached and attached chains per unit volume and the number of re-attachments and detachments rate per unit volume, respectively; at steady state, the time variation of the active cross links vanish and we obtain:

$${\dot{c}}_A=(c-c_A)·k_{on}-c_A·k_{\mathit{off}}=0$$ (1b)

where c = c_A + c_D is a constant. The above relation states that the rate of change of active cross-links is equal to zero when the steady equilibrium is fulfilled and that such a rate is the sum of the new formed cross-links (proportional to the actual detached cross-links density, c_D = c − c_A, through the re-attachment rate parameter k_on) minus the lost cross-links (proportional to the actual existing links density c_A through the detachment rate parameter k_off); although in general the rate of detachment is likely to increase with stress, we assume here, for simplicity, that the strain does not affect the rates of attachment and detachment. From relation (1b) we deduce that at equilibrium, the concentration of active (or attached) links is:

$$c_A=\frac{c·k_{on}}{k_{on}+k_{\mathit{off}}}$$ (2a)

Considering that the polymer is initially at equilibrium, the initial concentration is also given by Eq. (2a). This concentration can also be related to the equilibrium density function ϕ₀(r) of end-to-end distance r by:

$$c_{A,0}={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\varphi }_0(\mathbf{r})d\mathbf{r}}$$ (2b)

Note here that the variation of the active cross-links, governed by Eq. (1a), reflects the macroscopic mechanical properties of the elastomer since the amount of stored energy in the material depends on the current active cross-links.

4. Mechanical model for dynamically cross-linked polymers

In the present section we develop the mechanical model for polymers with reversible cross-links via a proper description of the end-to-end chain length statistical distribution evolution of the polymer.

4.1. Statistical model

According to the standard theory of elastomers (rubber elasticity, [29–34]) where a constant cross-link density is assumed (fixed cross-links network), the distribution of the chains’ end-to-end vector r at a given time instant t, can be described through the classical Gaussian function written in the following form [29,32–34]:

$${\phi }_t(\mathbf{r},t)={\phi }_0(\mathbf{r},t=0)={\overline{\phi }}_0·P_0(\mathbf{r})={\left(\frac{3}{2\pi N{b}^2}\right)}^{3/2}·\exp \left(-\frac{3\langle {\mathbf{r}}^2\rangle }{2N{b}^2}\right)$$ (3)

where 〈r²〉 = 〈x² + y² + z²〉,N, b represent the average value of the squared end-to-end vector length, the number of segments in one polymeric chain and its length, respectively, and ${\overline{\varphi }}_0$ is the initial cross-links density distributed according to the Gaussian function P₀(r). According to the statistical mechanics approach, the amount of energy stored in the unit volume of the material at a given time, can be evaluated by adding up all the contributions of the single stretched chains as:

$${\Psi }_V(\mathbf{r},t)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\varphi }_t(\mathbf{r},t)·U(\mathbf{r})d\mathbf{r},}\text{with}U(r)=\frac{3kT}{2N{b}^2}{r}^2$$ (4)

where the integral ${\displaystyle {\int }_{-\infty }^{+\infty }{\varphi }_t(\mathbf{r},t)}d\mathbf{r}$ is the number density of chains per unit volume of material in its current configuration and U(r) represents the elastic energy in one single chain [29]. The notation (●)_V in Eq. (4) indicates that the quantity (●) is evaluated per unit volume. At equilibrium, the stored elastic energy is thus ${\Psi }_V(\mathbf{r},0)={\displaystyle {\int }_{-\infty }^{+\infty }{\varphi }_0(\mathbf{r})U(\mathbf{r})}d\mathbf{r}$. Polymer chain statistics is a useful tool to describe the mechanical behavior of elastomeric materials (such as rubbers, polymers, gels, etc.), whose microstructure is based on a complex entangled network of long linear chains joined together in several points [30–34]. On the other hand such a complex microstructural layout can be found also in others materials, such as in polymeric matrix fibrous composites [35] and in particulate filled elastomers [36] whose mechanical response can be conveniently described through a chains network approach.

In our formulation, we choose to describe the elastic energy function ΔΨ_V(r, t) as the difference between the stored elastic energy time t and the stored elastic energy in the equilibrium condition. This reads:

$$\Delta {\Psi }_V(\mathbf{r},t)={\Psi }_V(\mathbf{r},t)-{\Psi }_V(\mathbf{r},0)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}[{\varphi }_t(\mathbf{r},t)-{\varphi }_0(\mathbf{r})]}U(\mathbf{r})d\mathbf{r}$$ (5)

This definition ensures that the energy vanishes at equilibrium. Substituting (4) into (5), we find that [29]:

$$\Delta {\Psi }_V(\mathbf{r},t)=\frac{3kT}{2N{b}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}[{\varphi }_t(\mathbf{r},t)-{\varphi }_0(\mathbf{r})]}{\mathbf{r}}^{2}d\mathbf{r}$$ (6a)

Note: In the particular case of static cross-links (standard rubber elasticity), the distribution of the end-to-end vector r can be taken in the reference state (Lagrangian view). In this case, the elastic energy becomes:

$${\Psi }_V(\mathbf{r},t)=\frac{3kT}{2N{b}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\varphi }_t}(\mathbf{r},t){\mathbf{r}}^{2}d\mathbf{r}=\frac{3kT}{2N{b}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\varphi }_0}(\mathbf{r}){\left(\mathbf{F}{\mathbf{r}}_0\right)}^{2}d{\mathbf{r}}_0\mathrm{i}.\mathrm{e}.\Delta {\Psi }_V(\mathbf{r},t)=\frac{3kT}{2N{b}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\varphi }_0}(\mathbf{r})\left({\mathbf{F}}^T\mathbf{F}-\mathbf{I}\right){\mathbf{r}}_0^{2}d{\mathbf{r}}_0=\frac{\mathit{nkT}}{2}\left[\text{tr}({\mathbf{F}}^T\mathbf{F})-3\right]$$ (6b)

which is consistent with conventional rubber elasticity. Here, n is the number of linked chains per unit volume (with n = E·(3kT)⁻¹, [29]) and its is assumed that the distribution function remains Gaussian irrespectively of the applied strain state. For an incompressible material, the deformation energy provided by Eq. (5) must be enriched with an extra term that enforces the incompressibility condition. Using the Lagrange multiplier method, and denoting p as the Lagrange multiplier that enforces the condition J = 1, the increment of energy per unit volume can be rewritten as:

$$\Delta {\Psi }_V(\mathbf{r},t)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\mathrm{\Delta }\varphi (\mathbf{r},t)U(\mathbf{r})d\mathbf{r}+p(J-1)}$$ (7)

We note that p is to be interpreted as the hydrostatic pressure (p = tr(P)/3). From the above discussion it appears that in order to formulate the macroscopic mechanical model in terms of the energy (6a), a knowledge of the evolution of the distribution function ϕ(r,t) is required.

For the sake of illustration, let us first consider a unit material volume undergoing a stretched deformation represented by the scalar λ = x₁/X₁, where x₁ and X₁ are the lengths of the domain in its underformed and deformed configurations (Fig. 2). In this case, the distribution function under a given stretch, the end-to-end distance is represented by a scalar r = 〈r〉 and the distribution function ϕ(<r>,t) is now a scalar function of the variable r. When this volume undergoes a stretch λ, the length l₀ of the initial end-to-end vector becomes l = λ·l₀. At the level of the distribution, this implies that the initial Gaussian curve (Fig. 3a) modifies its shape, i.e. a new distribution ϕ(<r>,t) is obtained as shown in Fig. 3b. Now allowing the cross-link to be reversible, we consider that during a small time interval, existing links detach while others reattach in a different configuration. We here assume that the reattachment process occurs in the reference Gaussian distribution (curve (2) in Fig. 3b). The distribution ϕ(<r>,t) (labeled (1) in Fig. 3b) that represents a generic stretched state at the time instant t, therefore evolves and – after a small time increment dt− the distribution of the end-to-end distance of the stretched chains is represented by the curve (2) in Fig. 3b (at the time instant t + dt), which tends to evolve in time to the initial one (0).

Fig. 3.

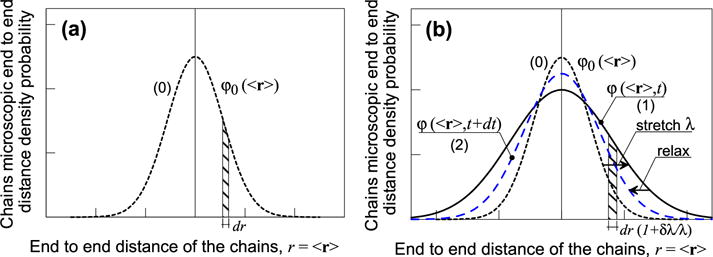
Gaussian distribution of the initial chains’ length density (0) vs the corresponding microscopic chains length in the reference configuration (a); evolution of the chains’ density length distribution after applying an external macroscopic stretch (1) (b).

To mathematically represent the above processes, we now propose to derive an evolution law of the form:

$$\delta {\varphi }_t(\mathbf{r},t)=\delta {\varphi }_t(\mathbf{r},t){|}_{xl}+\delta {\varphi }_t(\mathbf{r},t){|}_{\mathbf{F}}=[{\dot{\varphi }}_t(\mathbf{r},t){|}_{xl}+{\dot{\varphi }}_t(\mathbf{r},t){|}_{\mathbf{F}}]dt$$ (8)

where the term ${\dot{\varphi }}_t(\mathbf{r},t){|}_{xl}$ represents the time derivative of ϕ_t(r,t) at fixed active cross-link density, while δϕ_t(r,t)|_F = ∂ϕ_t(r,t)/∂t|_F is the time derivative of ϕ_t(r,t) for a fixed macroscopic deformation tensor F. The two above contributions, namely ${\dot{\varphi }}_t(\mathbf{r},t){|}_{xl}$, ${\dot{\varphi }}_t(\mathbf{r},t){|}_{\mathbf{F}}$, can be explicitly written as follows. The first contribution is obtained by performing a power series expansions of ϕ(r + δr) to obtain:

$${\dot{\varphi }}_t(\mathbf{r},t){|}_{xl}=-\frac{\partial {\varphi }_t(\mathbf{r})}{\partial \mathbf{r}}\left(\delta \dot{\mathbf{F}}{\mathbf{F}}^{-1}\mathbf{r}\right)-{\varphi }_t(\mathbf{r})\text{tr}\left(\delta \dot{\mathbf{F}}{\mathbf{F}}^{-1}\right)$$ (9)

where $\delta \dot{\mathbf{F}}$ is a time increment of the macroscopic deformation gradient. The second contribution follows from the kinetic law [37];

$${\dot{\phi }}_t(\mathbf{r},t){|}_{\mathbf{F}}=-k_{\mathit{off}}·{\phi }_t(\mathbf{r},t)+k_{on}·{\overline{\phi }}_t(\mathbf{r},t)$$

where

$${\overline{\phi }}_t(\mathbf{r},t)=\frac{(c-c_A)}{c_{A,0}}{P}_0(\mathbf{r})$$ (10)

${\overline{\varphi }}_t(\mathbf{r},t)$ being the current density of the detached cross-links that can potentially reattach and $c_A={\displaystyle {\int }_{-\infty }^{+\infty }{\varphi }_t(\mathbf{r},t)}d\mathbf{r}$. Eq. (10) expresses the variation of ${\dot{\varphi }}_t(\mathbf{r},t){|}_{\mathbf{F}}$ with time, as the amount of the new created links. The latter is proportional to the difference between the concentration of detached cross-links $c-{\displaystyle {\int }_{-\infty }^{+\infty }{\varphi }_t(\mathbf{r},t)}d\mathbf{r}$ and the number of detached links. The final expression for the rate of change of the distribution function at time t is therefore:

$$\delta {\varphi }_t(\mathbf{r},t)={\dot{\varphi }}_t(\mathbf{r},t)dt=\left\{\frac{\partial {\varphi }_t(\mathbf{r},t)}{\partial \mathbf{F}}\dot{\mathbf{F}}-{\overbrace{k_{\mathit{off}}·{\varphi }_t(\mathbf{r},t)}}^{{\dot{\varphi }}_{\mathit{off}}(\mathbf{r},t)}+{\overbrace{k_{on}·{\overline{\varphi }}_t(\mathbf{r},t)}}^{{\dot{\varphi }}_{on}(\mathbf{r},t)}\right\}\mathit{dt}$$ (11)

where it can be appreciated that the evolution of the distribution function depends on the dynamic nature of cross-links through the terms ${\dot{\varphi }}_{\mathit{off}}(\mathbf{r},t)$, ${\dot{\varphi }}_{on}(\mathbf{r},t)$; these latter terms are assumed by the model to be independent by the strain and strain rate applied to the material.

Note that since expression (11) provides the variation of the distribution function in the current state (ϕ(r,t)), it corresponds to an updated Lagrangian formulation. This is different from the standard theory of rubber elasticity, which takes a total Lagrangian approach.

4.2. Thermodynamical model

For a volume of material – considered as a thermodynamical system – the balance of energy rate per unit volume reads:

$$\dot{\mathrm{K}}(t)+\underset{{\dot{\mathbf{F}}}_{\mathrm{int}}(t)}{\underbrace{\mathbf{P}:\dot{\mathbf{F}}-\nabla \mathbf{q}}}=\underset{{\dot{\mathbf{F}}}_{\text{ext}}(t)}{\underbrace{\mathbf{b}·\mathbf{v}+{\displaystyle \underset{\Gamma }{\int }\mathbf{t}·\mathbf{v}ds}}}$$ (12)

where $\dot{\mathrm{K}}(t)=\raisebox{1ex}{$\mathit{1}$}\!\left/ \!\raisebox{-1ex}{$\mathit{2}$}\right.d\rho {\mathbf{v}}^2/dt$ is the rate of change of kinetic energy, q is the production rate of internal energy, b is the vector of body forces and the last integral represents the power of the surface tractions acting on the boundary Γ of the unit volume of material, while v is the velocity field vector. Hereafter the deformation process will be assumed to be over-damped (i.e. without any inertial effect) and with negligible production of internal energy (q = 0). Moreover the entropy inequality (second law of thermodynamics) evaluated for a generic portion of matter occupying the volume Ω, is:

$$\gamma (t)=\dot{S}(t)-\overline{Q}(t)\ge 0,\text{with}S(t)={\displaystyle \underset{\Omega }{\int }\eta (\mathbf{x},t)}d\Omega$$ (13)

which states that the entropy production γ(t) per unit time, must remain positive. In the above expression η(x,t) is the entropy per unit volume and $\overline{Q}(t)=-{\displaystyle {\int }_{\Gamma }\mathbf{h}·\mathbf{n}\mathrm{d}s}+{\displaystyle {\int }_{\Omega }\overline{\zeta }\mathrm{d}\Omega }$ is the rate of entropy input with h and $\overline{\zeta }=\zeta /T$ the rates of boundary and volume entropy sources, respectively. The Helmoltz free energy per unit volume can be finally written as [38]:

$$-{\dot{\Psi }}_V(\mathbf{F},t)-\eta \dot{T}+\mathbf{P}:\dot{\mathbf{F}}-\frac{1}{T}\mathbf{q}\nabla T+\zeta \ge 0$$ (14)

where the time derivative of the elastic energy Ψ_V(F,t) can be explicitly written, using the chain rule, as:

$${\dot{\Psi }}_V=\frac{\partial {\Psi }_V}{\partial {\varphi }_t}{\dot{\varphi }}_t+\frac{\partial {\Psi }_V}{\partial T}\dot{T}=\frac{\partial {\Psi }_V}{\partial \varphi }\left(\frac{\partial {\varphi }_t}{\partial \mathbf{F}}\dot{\mathbf{F}}+{\dot{\varphi }}_t{|}_{\mathbf{F}}\right)+\frac{\partial {\Psi }_V}{\partial T}\dot{T}=\frac{\partial {\Psi }_V}{\partial {\varphi }_t}·\left[\frac{\partial {\varphi }_t}{\partial \mathbf{F}}\dot{\mathbf{F}}+{\dot{\varphi }}_{on}(\mathbf{r},t)-{\dot{\varphi }}_{\mathit{off}}(\mathbf{r},t)\right]+\frac{\partial {\Psi }_V}{\partial T}\dot{T}$$ (15)

In Eq. (15) the term ${\dot{\varphi }}_{on}(\mathbf{r},t)$ represents the (positive) contribution to the energy rate due the new formed links, while ${\dot{\varphi }}_{\mathit{off}}(\mathbf{r},t)$ is the (negative) contribution from link detachment; finally the latter term in Eq. (15) represents the change of energy density with temperature. The energy increment with respect to the initial state expressed by Eq. (5), can be evaluated once the current distribution function ϕ_t(r,t), evaluated through the evolution law given by (11), is known.

4.3. Determination of the stress state

Making use of Eqs (4), (5) and (16), the variation of Helmoltz free energy can be also expressed as:

$$\Delta {\dot{\Psi }}_V=\frac{\partial \Delta {\Psi }_V}{\partial \Delta \varphi }\left(\frac{\partial \varphi }{\partial \mathbf{F}}\dot{\mathbf{F}}+{\dot{\varphi }}_t{|}_{\mathbf{F}}\right)-pJ{\mathbf{F}}^{-T}\dot{\mathbf{F}}+\frac{\partial \Delta {\Psi }_V}{\partial T}\dot{T}={{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\left(\frac{\partial \varphi (\mathbf{r},t)}{\partial \mathbf{F}}\dot{\mathbf{F}}\right)}U(\mathbf{r})d\mathbf{r}+\frac{\partial \Delta {\Psi }_V}{\partial \Delta \varphi }{\dot{\varphi }}_t|}_{\mathbf{F}}-pJ{\mathbf{F}}^{-T}\dot{\mathbf{F}}+\frac{\partial \Delta {\Psi }_V}{\partial T}\dot{T}={\frac{3kT}{2N{b}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\left(\frac{\partial \varphi (\mathbf{r},t)}{\partial \mathbf{F}}\dot{\mathbf{F}}\right){\mathbf{r}}^{2}d\mathbf{r}+\frac{\partial \Delta {\Psi }_V}{\partial \Delta \varphi }}{\dot{\varphi }}_t|}_{\mathbf{F}}-pJ{\mathbf{F}}^{-T}\dot{\mathbf{F}}+\frac{\partial \Delta {\Psi }_V}{\partial T}\dot{T}$$ (16)

Taking into account the above expression, the free energy variation inequality (14) becomes:

$$\left[\mathbf{P}-\left({\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\frac{\partial \varphi (\mathbf{r},t)}{\partial \mathbf{F}}}U(\mathbf{r})d\mathbf{r}-pJ{\mathbf{F}}^{-T}\right)\right]\dot{\mathbf{F}}-\left(\eta +\frac{\partial {\Psi }_V}{\partial T}\right)\dot{T}-\frac{\partial {\Psi }_V}{\partial \Delta \varphi }{\dot{\varphi }}_t{|}_{\mathbf{F}}-\frac{1}{T}\mathbf{q}\nabla T+\zeta \ge 0$$ (17)

Further assuming that the energy is minimized under any arbitrary process, we find that

$$\mathbf{P}(\mathbf{F},t)=\frac{\partial \Delta {\Psi }_V}{\partial \mathbf{F}}=\frac{\partial \Delta {\Psi }_V}{\partial \Delta \varphi }\frac{\partial \varphi (\mathbf{r},t)}{\partial \mathbf{F}}-pJ{\mathbf{F}}^{-T}={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}-\left[\frac{\partial \varphi (\mathbf{r},t)}{\partial \mathbf{r}}\otimes {\mathbf{F}}^{-1}\mathbf{r}+\varphi (\mathbf{r},t){\mathbf{F}}^{-T}\right]}U(\mathbf{r})\mathrm{d}\mathbf{r}-pJ{\mathbf{F}}^{-T}$$ (18)

while the Cauchy stress can be obtained through the standard relation σ = P(F,t) F^T/J. The remaining terms in the inequality expressed by Eq. (14) provide the following relationships:

$$\eta =\frac{\partial {\Psi }_V}{\partial T},-\frac{1}{T}\mathbf{q}\nabla T+\zeta \ge 0,\frac{\partial \Delta {\Psi }_V}{\partial \varphi }·[{\dot{\varphi }}_{\mathbf{r},on}(\mathbf{r},t)-{\dot{\varphi }}_{\mathbf{r},\mathit{off}}(\mathbf{r},t)]\ge 0$$ (19)

As expected, the first term indicates that the entropy is the derivative of the internal work with respect to temperature, the second implies that the heat flux is related to the temperature gradient, and the last corresponds to the dissipated energy produced by the attachment/detachment of polymer chains in time.

5. Numerical examples

In this section, a few example problems are presented and discussed in order to verify the capability of the proposed formulation, implemented in a non-linear 2D finite element code (where both mechanical and geometrical - i.e. large displacements - nonlinearities are considered), to capture the response of elastomers characterized by an evolving interval microstructure.

5.1. Stress relaxation simulation

The case of stress relaxation, i.e. the analysis of the stress history for a constant applied stretch, is herein considered [24]. The specimen is loaded in tension at a given strain rate of 0.2 s⁻¹ to t = 1 s and subsequently the nominal strain is held constant at λ = 1.2. The initial elastic modulus of the material is assumed equal to about 0.8E + 5 Pa. The nominal stress vs time from Ref. [24] and that obtained with the present model is plotted in Fig. 4; a best fit of the first portion of the experimental curve (0s ≤ t ≤ 5s) provides the values k_on = 0.02; k_off = 0.3 for the dynamic cross-link model.

Fig. 4.

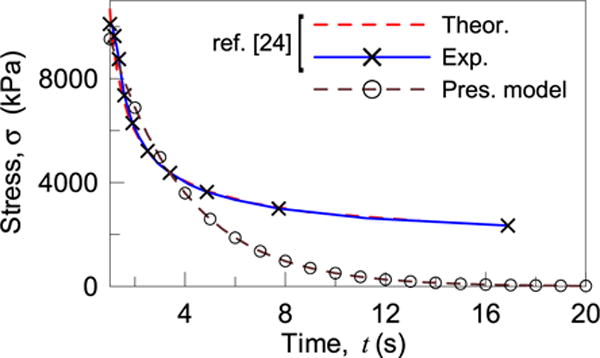
Relaxation test under a prescribed nominal stretch λ = 1.2.

Since in the proposed model the material has only dynamic cross-links – i.e. no permanent cross-links are assumed to exist e it tends to return spontaneously to its initial free stress state; on the other hand from the experimental outcomes it appears that a certain residual stress remains even for longer times, probably because of the existence of a fraction of permanent cross-links.

5.2. Parametric study

In order to show the macroscopic mechanical behavior of polymer with reversible cross-links, we consider some simple cases in which the main parameters are varied. In the following section a tensile tests with different material remodeling parameters will be considered. In the second example, we investigate the bending of a cantilever beam under prescribed displacements boundary conditions, for different material reversible cross-links parameters. The third last example considers the bending of a circular plate under a uniform pressure history for different material reversible cross-links parameters. As has been discussed above, the statistical model can take into account for the microstructure rearrangement of the polymer only through the k_on, k_off parameters that quantify the number of newly activated and deactivated physical cross-links per unit time in the reference volume of material.

5.2.1. Tensile relaxation test

In the present example, an element under tension is considered (Fig. 5a); a positive stretch equal to λ = 1.0025 is progressively applied according to the time law of the displacement factor f and subsequently is kept constant (Fig. 5b); the material is assumed simple elastic (Young modulus 7 MPa, Poisson’s ratio ~ 0.45) and with reversible cross-links; in this latter case different values of the k_on, k_off parameters are assumed as shown in Fig. 6a and b. Two different factor rates, $\dot{f}=1÷2$, are assumed in order to study the effect of the strain velocity on the material mechanical response.

Fig. 5.

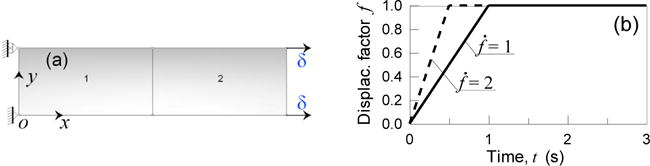
Relaxation test under tension: 2D mesh (a). Histories of the displacement factor (b).

Fig. 6.

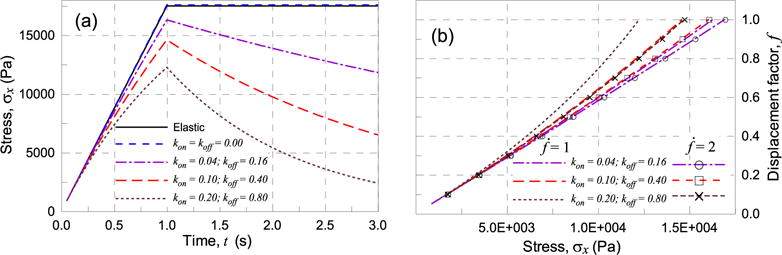
Evolution of the stress σ_x in time for different values of the k_on, k_off parameters of the material for factor rate $\dot{f}=1$ (a). Effect of the factor rate on the stress during loading (b).

It can be observed (Fig. 6a) that the elastic behavior is recovered for the simple case of static cross-links (k_on = k_off = 0), while a nonlinear softening behavior during loading and a stress relaxation during the phase λ = const. can be observed when different degrees of cross-links evolution is accounted for.

Finally, the factor rate effect on the mechanical response of the material is considered; in the slower loading rate case $\left(\dot{f}=1\right)$ the material has enough time to re-arrange its microstructure, as much as higher is the k_off/k_on ratio. On the other hand for the faster rate $\left(\dot{f}=2\right)$ the stress evolution during loading is less influenced by the k_on − k_off mechanism and the response in term of stress is only slightly affected by the microstructural internal remodeling of the material.

5.2.2. Cantilever beam under a free-end displacement history

The present example considers the bending of a cantilever beam (Fig. 7a) with a Young modulus of 10 MPa, (Poisson’s ratio ~0.45); a prescribed displacement history is imposed to the beam’s free end as shown in Fig. 6b; a maximum downward displacement equal to δ = 0.1 m is reached in 1s while an unloading step is subsequently considered during which the beam’s tip is brought back to its initial location and maintained at such a value during the rest of the simulation. The beam is assumed in a plane stress condition, having a small thickness equal to s = 0.1 m.

Fig. 7.

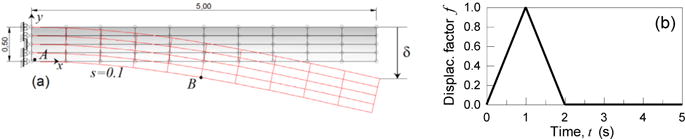
Cantilever beam (dimensions in m) under a prescribed displacement history applied at its free end (a). History of the adopted displacement factor (b).

In Fig. 8a1, the stress history at point A (Fig. 7a) is shown for the elastic case as well as for three different cases characterized by different dynamic cross-links parameters. An increasing time-dependent response is observed as the rates of attachment/detachment are increased. In Fig. 8a2 the history of the vertical displacement at point B (Fig. 7a) after the free-end displacement has been returned to zero (t ≥ 2s) is shown.

Fig. 8.

Evolution of the stress σ_x in time at point A (a1) and the vertical displacement at point B (a2) for different values of the k_on, k_off parameters of the material (a1). Stress field σ_x (in Pa) at t = 5s for the case k_on = 0.2, k_off = 0.2 (b), k_on = 0.2, k_off = 0.4 (c) and k_on = 0.2, k_off = 0.8 (d); stress patterns along the clamped cross-section of the beam at t = 2s(e) and t = 5s(f).

In Fig. 8b,c,d the tensile stress σ_x contours in the beam at t = 5s are shown: materials with high k_off/k_on values present the highest stress reversal just after δ returns to zero (λ = 1.0), while subsequently, after a given time, the stress state becomes lower than for the cases with lower k_off/k_on values. The σ_x stress pattern along the clamped cross-section x = 0 of the beam, for the same three different dynamic cross-links cases, is also shown at t = 2s (Fig. 8e) and at t = 5s (Fig. 8f).

5.2.3. Circular plate under a uniform pressure history

The last example deals with the bending of a simply supported circular plate under a uniform pressure variable in time, characterized by a Young modulus equal to 10 MPa and (Poisson’s ratio ~0.45); an axisymmetric model of the plate is considered (Fig. 9a). The pressure load varies according to the equation q = q₀·f(t), where q₀ = 10Pa is the base pressure and f(t) is the load factor history (Fig. 9b). As can be noted the load is increased up to its final maximum value, it’s kept constant for 2 s and then it is brought to zero and maintained at such a value in the following instants. The vertical displacement and the radial stress at point A (Fig. 9a) is monitored. The plate’s material is assumed to be elastic as well as with reversible cross-links characterized by different values of the k_on, k_off parameters (Fig. 10).

Fig. 9.

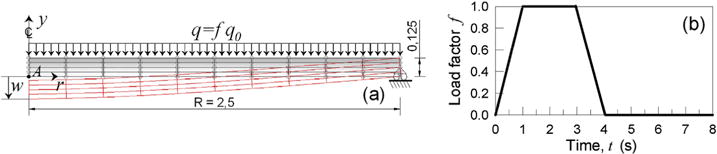
Axisymmetric FE model of the circular plate (a) (dimensions in m) and load factor history, f(t) adopted (b).

Fig. 10.

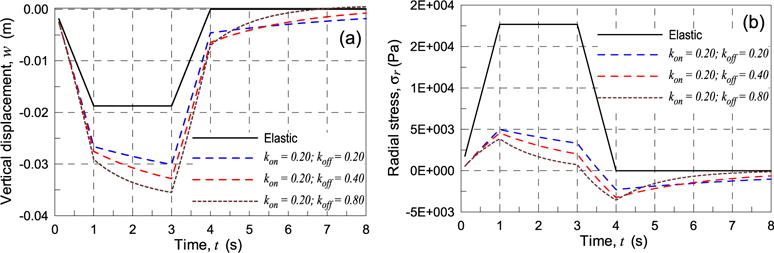
Vertical displacement (a) and history of the radial stress (b) at point A vs time, for different values of the k_on, k_off parameters of the material and for the elastic case.

In cases of dynamic cross-links the vertical displacement during loading (0 ≤ t ≤ 1s) is greater than in the linear case, particularly in cases with greater k_off/k_on ratio; by keeping constant the applied pressure (1s ≤ t ≤ 3s) the displacement continues to growth for the materials having dynamic cross-links and, after completely removing the load (t > 4s) a residual vertical displacement still exist in the plate and it tends subsequently to zero as the time increases; the speed of the plate to return to its initial configuration is more pronounced for higher k_off/k_on ratios (Fig. 10a).

The radial stress at point A increases meanwhile the load reaches its maximum value but in a softening fashion for the material with reversible cross-links; during the constant load phase the stress decreases if k_on ≠ 0, k_off ≠ 0 and reverses the sign as soon as the load is completely removed. Subsequently the stress tends to zero in time, with a faster rate for higher values of the k_off/k_on ratios (Fig. 10b), indicating that, according to the formulated model, the material tends to go back to its initial free-stress state, irrespectively of the applied stress or strain values.

In Fig. 11 the stress field σ_r in the radial cross-section of the plate is displayed at t = 3s, i.e. at the last instant before the applied pressure load starts to decrease; a progressively relaxed stress distribution in the plate can be observed by increasing the k_off/k_on ratio (Fig. 11b, c, d), characterized by values well below those corresponding to the elastic material (Fig. 11a).

Fig. 11.

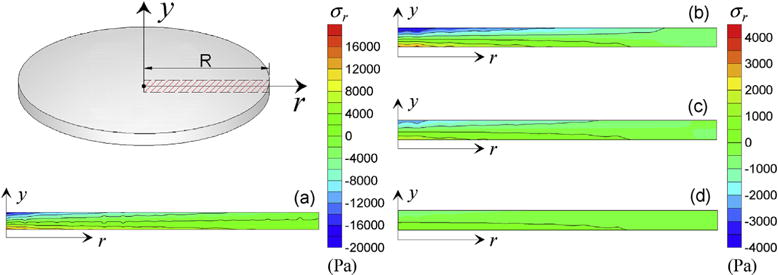
Stress field σ_r in the radial cross-section of the circular plate (in Pa) at t = 3s for the elastic case (a) and for material with dynamic cross-links with k_on = 0.2, k_off = 0.2 (b), k_on = 0.2, k_off = 0.4 (c) and k_on = 0.2, k_off = 0.8 (d).

6. Conclusions

In the present paper a new class of polymers with reversible cross-links has been considered; these materials have the capability to reset their internal microstructure thanks to a microscopic remodeling mechanism that leads to a behavior similar to that of an elastic fluid. A thermodynamically consistent model has been proposed – following a similar approach as the statistical theory adopted for rubber elasticity – on the basis of the evolution of the molecular chains’ end-to-end distance distribution function. By allowing this distribution to evolve in time (depending on the deformation history and on the internal remodeling parameters), the free energy and the stress state of the material can be evaluated during a generic stretch history. Some simple examples are finally presented and discussed to illustrate the capability and generality of the developed approach.

Nomenclature

b

Average chain’s segment length

c = c_A + c_D = const

Maximum potential number of link concentration in the polymer

c_A0, c_A, c_D,

Link concentration of the attached cross-links in the initial state and at a generic time and detached links in the polymer, respectively

F, F_ij = ∂x_i/∂X_j

Macroscopic deformation gradient tensor

$\dot{\mathbf{F}}$

Macroscopic deformation rate tensor

J = detF

Determinant of the deformation gradient

k

Boltzman’s constant

k_off, k_on

Rate of lost links density and rate of new formed links density, respectively

n, N

Number of linked chains in the unit volume of material and number of chains’ segments, respectively

P

First Piola-Kirchhoff stress tensor

P₀(r)

Standard Gaussian distribution (referred to the material’s initial free-stress state)

r₀, r

End-to-end vector of a chain in the initial and in a generic state, respectively

T

Absolute temperature

U(r)

Energy stored in a single chain having an end-to-end vector r

γ(t)

Rate of entropy production

δϕ(r, t)

Total variation of the chains’ end-to-end vector r distribution function at the time

ϕ_t(r, t)

Distribution of the chains’ end-to-end vector r density at a generic time t

${\varphi }_0(\mathbf{r})={\overline{\varphi }}_0·P_0(\mathbf{r})$

Distribution of the chains’ end-to-end vector r density in the initial stress-free state

φ(r, t) = φ_t(r,t) − φ₀(r)

Distribution difference of the chains’ end-to-end vector r density in the current and in the stress-free state

${\dot{\varphi }}_{on}(\mathbf{r},t),{\dot{\varphi }}_{\mathit{off}}(\mathbf{r},t)$

Positive and negative contributions rate to the stretch distribution function rates, respectively

${\overline{\varphi }}_0$

Density of attached cross-links at equilibrium

λ

Macroscopic stretch of the polymer

σ

Cauchy stress tensor

Ψ_V, ΔΨ_V

Strain energy density (unit volume) contained in a stretched elastomer and its increment, respectively