Percent mammographic density prediction: development of a model in the Nurses’ Health Studies

Abstract

Purpose

To develop a model to predict percent mammographic density (MD) using questionnaire data and mammograms from controls in the Nurses’ Health Studies’ nested breast cancer case-control studies. Further, we assessed the association between both measured and predicted percent MD and breast cancer risk.

Methods

Using data from 2955 controls, we assessed several variables as potential predictors. We randomly divided our dataset into a training dataset (two-thirds of the dataset) and a testing dataset (one-third of the dataset). We used stepwise linear regression to identify the subset of variables that were most predictive. Next, we examined the correlation between measured and predicted percent MD in the testing dataset and computed the r² in the total dataset. We used logistic regression to examine the association between measured and predicted percent MD and breast cancer risk.

Results

In the training dataset, several variables were selected for inclusion, including age, body mass index, and parity, among others. In the testing dataset, the Spearman correlation coefficient between predicted and measured percent MD was 0.61. As the prediction model performed well in the testing dataset, we developed the final model in the total dataset. The final prediction model explained 41% of the variability in percent MD. Both measured and predicted percent MD were similarly associated with breast cancer risk adjusting for age, menopausal status, and hormone use (OR per 5 unit increase=1.09 for both).

Conclusion

These results suggest that predicted percent MD may be useful for research studies in which mammograms are unavailable.

Introduction

Percent mammographic density (MD), or the percent of dense breast tissue on a mammogram, is a strong, consistent predictor of subsequent breast cancer risk. Women with over 75 percent dense tissue on a mammogram have approximately 4–6 times the risk of developing breast cancer compared to women with very little dense tissue.[1] Interestingly, percent MD has been consistently associated with several anthropometric, reproductive and lifestyle factors, including age, early life body size, body mass index (BMI), parity, menopause, and postmenopausal hormone therapy (HT) use, among others. [2–7]

While percent MD is one of the strongest risk factors for breast cancer, few large-scale epidemiologic studies have collected mammograms or measured percent MD in the majority of their participants due to monetary and/or time constraints. For example, in the Nurses’ Health Study (NHS) and NHSII, we have collected mammograms only on a subset of our participants in nested case-control studies of breast cancer. Therefore, our goal was to develop a model to predict percent MD using questionnaire data and mammograms collected from a subset of controls in the NHS/NHSII nested case-control studies of breast cancer. Further, we examined the association between both measured and predicted percent MD and breast cancer risk in the NHS/NHSII nested case-control studies.

Materials and Methods

Mammography collection

Mammograms were collected from women in the NHS/NHSII breast cancer case-control studies nested in the blood and cheek collection sub-cohorts. Mammograms conducted as close as possible to the date of blood collection (or 1997 for participants in the cheek cell collection) were obtained for cases (and their matched controls) diagnosed after collection, but before June 1, 2004 (NHS) or June 1, 2009 (NHSII). Controls were matched to cases on age, menopausal status at blood draw and diagnosis, current postmenopausal hormone therapy (HT) use, month, time of day, fasting status at time of blood collection, and luteal day (NHSII timed samples only). In total, mammograms were collected from 2,062 breast cancer cases and 4,194 matched controls.

Mammographic density measurement

A Lumysis 85 laser film scanner was used to digitize the craniocaudal views of both breasts for all mammograms in the NHS and for the first two batches of mammograms in the NHSII. The third batch of mammograms in the NHSII was scanned using a VIDAR CAD PRO Advantage scanner (VIDAR Systems Corporation; Herndon, VA) using comparable resolution of 150 dots per inch and 12 bit depth. We measured absolute dense area as well as the total area and calculated percent MD as the dense area divided by the total area using the Cumulus software for computer-assisted thresholding. Next, we averaged the percent MD of both breasts. In a sample of 50 mammograms digitized with both scanners, the correlation between percent MD measurements from the digitized images from each scanner was 0.88; the mean difference was 2.3 percentage points. In NHSII, a single observer read the mammograms in three batches (batches 1 and 2 were read three years apart, batches 2 and 3 were read three years apart). A small number of mammograms were included in all three NHSII batches. While there was high reproducibility within each batch, there was evidence of between batch variability in the NHSII. Therefore, for the overall NHSII breast cancer case-control mammography dataset, we used multivariable linear regression models to estimate the effect of batch on density measurements, controlling for age, menopausal status, BMI, and case-control status.[8] We then adjusted density measurements in the second and third NHSII batches by subtracting the coefficient for each mammogram batch from the raw value to estimate the measurements that would have been obtained if the mammogram had been included in the first batch. For all batches, readers were blinded to case-control status.

Candidate predictors

Candidate predictors were selected based on prior research of predictors of percent MD in the NHS and other studies.[2, 9–13] The following variables were evaluated as potential predictors of percent MD: age (continuous, centered at 53), adolescent somatotype (continuous), body mass index (BMI) at age 18 (continuous, centered at 21), current BMI (continuous, centered at 25), age at menarche (continuous, centered at 12), nulliparity (no, yes), parity (continuous), age at first birth (continuous, centered at 25), height (continuous inches, centered at 65), family history of breast cancer (no, yes), personal history of benign breast disease (BBD) confirmed by biopsy (no, yes), BBD not confirmed or biopsy status unknown (no, yes), alcohol use (grams/day continuous), menopausal status (premenopausal, postmenopausal), HT use (postmenopausal only: never, past, current), and duration of menopause (postmenopausal only: continuous). In addition, we evaluated interaction terms for each of the candidate predictors and menopausal status (premenopausal, postmenopausal); therefore, menopausal status was forced into the stepwise regression model discussed below. In addition, nulliparity was forced into the model to allow for the assessment of age at first birth during the stepwise procedure. For all variables, we used the information collected on the biennial questionnaire closest in time preceding the date of the mammogram.

Exclusions

Women with unknown menopausal status were excluded (N=496). Postmenopausal women whose type of menopause was not either a) natural or b) due to bilateral oophorectomy (e.g., due to radiation, unknown type of menopause) were excluded from the analysis (N=481). We further excluded women with missing data on any of the candidate predictor variables: adolescent somatotype (N=156), current BMI (N=97), BMI at age 18 (n=143), parity (n=37), age at first birth (N=4), age at menarche (n=20), alcohol use (N=269), hormone therapy (HT) use (n=62, postmenopausal only), and duration of menopause (N=15, postmenopausal only). Next, we excluded women with outlying values based on the generalized extreme studentized deviate many-outlier detection approach [14] for the following variables: adolescent somatotype (N=1), BMI (N=14), BMI at age 18 (N=16), age at first birth (N=6), height (N=1), age at menarche (N=2), alcohol use (N=41), and duration of menopause (N=4). The nested case-control sample included 1436 cases and 2955 controls.

Statistical analysis

In our primary analysis, we developed the percent MD prediction model among the 2955 controls only. We randomly divided our dataset into a training dataset with two-thirds of the observations (N=1962 controls) and into a testing dataset with the remaining one-third of the dataset (N=993 controls). As the distribution of percent MD was right-skewed, we square-root transformed percent density. We used stepwise linear regression (p<0.15 for selection into the model and p<0.15 to remain in the model) to identify the subset of candidate variables that were most predictive of square-root transformed percent MD in the training dataset and computed the r² for the final model in the training dataset. We then used the estimates from the prediction model developed in the training dataset to calculate predicted square-root transformed percent MD in the testing dataset. We then back-transformed predicted percent MD. The Spearman correlation coefficient was calculated to assess the agreement between the predicted and measured percent MD in the testing dataset. We also performed a paired t-test to examine the mean difference between the measured and predicted percent MD. We plotted measured percent MD by predicted percent MD as well as examined mean levels of measured percent MD according to decile of predicted percent MD. We developed the final prediction model in the total dataset using the variables identified in the training dataset and computed the r² and root mean square error (RMSE) for the final model.

Next, we used multivariable logistic regression to assess the association between measured percent MD, predicted percent MD, and breast cancer risk using data from the 1436 cases and 2955 controls. As cases and controls were matched on age, menopausal status, and HT use, we adjusted our logistic models for these variables. As a sensitivity analysis, we derived predicted percent MD among both the cases and controls using the same methods described above, with the addition of a case-control indicator forced into the model. All statistical tests were two-sided and analyses were performed using SAS version 9.4 for UNIX (SAS Institute Inc., Cary NC).

Results

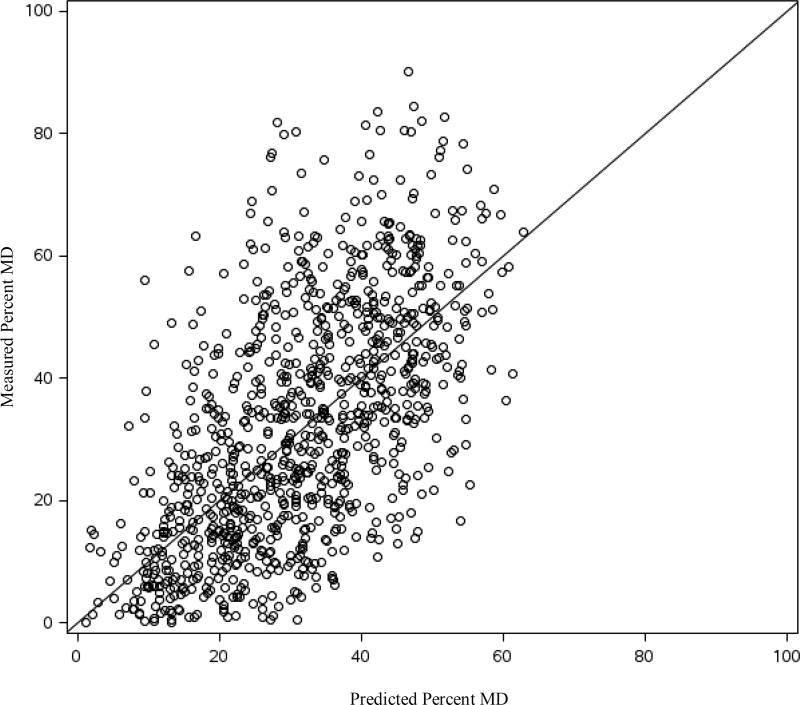
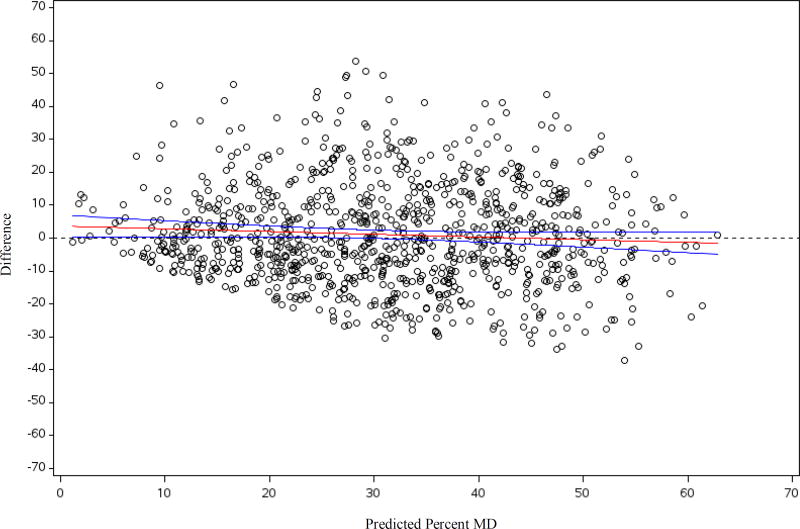
The distribution of candidate predictor variables by menopausal status and percent MD among controls in the total dataset is presented in Table 1. Age-adjusted differences in percent MD by the candidate predictors among the controls are presented in Supplemental Table 1. In both premenopausal and postmenopausal women, women with denser breasts were younger, had a lower BMI at age 18 and at mammogram, were more like to be nulliparous, and were more likely to have a history of BBD. Further, among postmenopausal women, those with denser breasts were more likely to be current HT users. In the initial stepwise-regression in the training dataset, the following variables were selected for inclusion (in addition to menopausal status and nulliparity): age, current BMI, BMI at age 18, HT use, biopsy confirmed BBD, unconfirmed BBD, adolescent somatotype, parity, and age at first birth as well as the interaction term between menopausal status and age at first birth (Table 2). The final prediction model explained 42% of the total variability in square-root transformed percent MD in the training dataset. Using the regression coefficients estimated in the training dataset, we calculated predicted square-root transformed percent MD for women in the testing dataset and back transformed to predicted percent MD. The Spearman correlation coefficient between the predicted and the measured percent MD in the testing dataset was 0.61 (95%CI: 0.57, 0.65). The mean difference between the measured and predicted percent MD was 1.06 percentage points (p=0.03). Measured percent MD increased with increasing predicted percent MD (Figure 1 and Supplemental Figure 1). The difference between measured and predicted percent MD by predicted percent MD is presented in Figure 2. The difference in mean measured percent MD between extreme deciles of predicted percent MD was 38.5. As the prediction model performed well in the testing dataset, we used the total dataset to develop the regression estimates for the final prediction model. Regression estimates for the selected predictor variables and the R-square for the prediction model were very similar in the training dataset, the testing dataset, and the total dataset (Table 2). The final prediction model explained 41% of the total variability in square-root transformed percent density in the total dataset. Next, we examined the association between both predicted and measured percent MD and breast cancer risk in the total dataset. The odds ratio (OR) for breast cancer per 5 unit increase in measured percent MD adjusted for matching factors (i.e., age, menopausal status, and HT use) was 1.09 (95%CI: 1.07, 1.11). The association with breast cancer risk was the same for predicted percent MD (OR per 5 unit increase=1.09, 95%CI: 1.05, 1.13). When we predicted percent MD in both the cases and controls, the same variables were selected for inclusion into the model in the training dataset (Supplemental table 2). The coefficients in the training and total dataset were similar to those from the model including only controls. When derived using both the cases and controls, the final prediction model explained 42% of the total variability in square-root transformed percent density in the total dataset.

Table 1.

Candidate predictors by quartiles of percent mammographic density and menopausal status among controls in the total dataset, NHS/NHSII

	Premenopausal				Postmenopausal
	Quartile 1 (<25) N=403	Quartile 2 (25-<39) N=403	Quartile 3 (39-<54) N=403	Quartile 4 (54+) N=404	Quartile 1 (<11) N=335	Quartile 2 (11-<22) N=336	Quartile 3 (22-<36) N=335	Quartile 4 (36+) N=336
Mean (SD)
Age (y)	46.8(4.3)	46(4.4)	45.7(4.2)	45(4.2)	61.4(6.4)	59.7(7.5)	59.1(7.7)	56.5(7.6)
BMI (kg/m2)	29.3(5.5)	25.6(4.6)	24.3(4.2)	22.5(3.1)	29(5.4)	26.5(4.7)	24.9(4.2)	23.4(3.6)
Adolescent somatotype	3.4(1.1)	2.9(1.0)	2.7(1.0)	2.6(0.9)	3.2(1.3)	2.7(1.2)	2.5(1.2)	2.5(1.0)
BMI at age 18 (kg/m2)	22.7(3.1)	21.1(2.6)	20.5(2.4)	20(1.9)	22.4(3.1)	21.2(2.6)	20.7(2.4)	20.3(2.0)
Age at menarche (y)	12.1(1.3)	12.3(1.4)	12.6(1.4)	12.7(1.5)	12.5(1.4)	12.4(1.3)	12.6(1.4)	12.6(1.3)
Parity (among parous)	2.6(1.1)	2.5(1.0)	2.5(1.0)	2.3(0.8)	3.4(1.5)	3.2(1.6)	3.1(1.5)	2.8(1.4)
Age at first birth (among parous)	25.1(4.1)	26.2(3.9)	26.3(4)	26.4(4.1)	25.2(3.1)	25(3.5)	25.2(3.7)	25.8(3.9)
Height (inches)	64.7(2.5)	64.7(2.7)	65(2.5)	65(2.3)	64.7(2.4)	64.4(2.3)	64.7(2.5)	64.8(2.4)
Alcohol use (g/day)	3.4(5.3)	4.1(6.5)	4.6(6.5)	4.7(6.8)	5.3(8.9)	3.8(6.3)	4.4(7.4)	5.6(7.9)
Age at menopause					49(5.0)	48.9(4.8)	48(5.2)	47.2(5.4)
N (Percent)
Nulliparous	39(9.7)	51(12.7)	56(13.9)	74(18.3)	22(6.6)	17(5.1)	33(9.9)	42(12.5)
BBD (biopsy confirmed)	48(11.9)	52(12.9)	68(16.9)	92(22.8)	50(14.9)	73(21.7)	92(27.5)	86(25.6)
BBD (unconfirmed)	113(28.0)	127(31.5)	131(32.5)	148(36.6)	60(17.9)	93(27.7)	78(23.3)	116(34.5)
Family history of breast cancer	26(6.5)	43(10.7)	36(8.9)	36(8.9)	35(10.4)	44(13.1)	47(14)	41(12.2)
Postmenopausal HT Use
Never					166(49.6)	131(39.0)	91(27.2)	73(21.7)
Past					77(23.0)	66(19.6)	84(25.1)	43(12.8)
Current					92(27.5)	139(41.4)	160(47.8)	220(65.5)

NHS=Nurses’ Health Study, SD=standard deviation, BMI=body mass index, BBD=benign breast disease, HT use=hormone therapy use

Table 2.

Percent mammographic density (square-root transformed) model in the training dataset and the total dataset, NHS/NHSII among controls

		Training dataset (Controls=1962)			Testing dataset (Controls=993)			Total dataset (Controls=2955)
		Beta	SE	p- value	Beta	SE	p-value	Beta	SE	p-value
Intercept		6.192	0.153	<0.01	5.906	0.226	<0.01	6.087	0.127	<0.01
Age (per year)^		−0.049	0.006	<0.01	−0.034	0.009	<0.01	−0.045	0.005	<0.01
Adolescent somatotype (per 1 unit)		−0.154	0.037	<0.01	−0.069	0.056	0.22	−0.125	0.031	<0.01
BMI at age 18 (per kg/m2)^		−0.048	0.017	<0.01	−0.046	0.025	0.06	−0.047	0.014	<0.01
Current BMI (per kg/m2)^		−0.125	0.008	<0.01	−0.142	0.011	<0.01	−0.131	0.006	<0.01
Nulliparous		0.234	0.130	0.07	0.103	0.190	0.59	0.185	0.107	0.09
Parity (per child among parous)		−0.068	0.030	0.02	−0.077	0.044	0.08	−0.070	0.025	<0.01
Age at first birth (per year)^		0.015	0.012	0.21	0.046	0.017	<0.01	0.025	0.010	0.01
Age at first birth*postmenopausal		0.036	0.018	0.05	−0.010	0.027	0.71	0.023	0.015	0.13
BBD history (biopsy confirmed)		0.511	0.087	<0.01	0.426	0.131	<0.01	0.497	0.072	<0.01
BBD history (unconfirmed)		0.311	0.077	<0.01	0.409	0.108	<0.01	0.342	0.062	<0.01
Postmenopausal status		−1.087	0.128	<0.01	−1.087	0.184	<0.01	−1.079	0.105	<0.01
Past HT user (vs never)		0.242	0.138	0.08	0.446	0.192	0.02	0.318	0.112	<0.01
Current HT user (vs never)		0.681	0.113	<0.01	0.594	0.165	<0.01	0.647	0.093	<0.01
Root mean square error		1.434			1.458			1.443
R-square		0.42			0.40			0.41

NHS=Nurses’ Health Study, SE=standard error, BMI=body mass index, BBD=benign breast disease, HT use=hormone therapy use

^{^}Age centered at 53, BMI at age 18 centered at 21, current BMI centered at 25, age at first birth centered at 25

Figure 1.

Measured percent mammographic density by predicted percent mammographic density in the testing dataset among controls, NHS/NHSII

Figure 2.

The difference between measured percent mammographic density and predicted percent mammographic density by predicted percent mammographic density in the testing dataset among controls with regression line and 95% confidence interval, NHS/NHSII

Discussion

Using mammograms and questionnaire data from controls on the NHS nested case-control studies of breast cancer, we derived predicted percent MD using a number of anthropometric, reproductive, and lifestyle factors which have been previously associated with breast density. Our final prediction model explained 41% of the total variability in percent MD. When we assessed the association between measured and predicted percent MD and breast cancer risk, the association was the same for the two measures (OR per 5 unit increase=1.09).

Percent MD has been consistently associated with breast cancer risk and is one of the strongest predictors of subsequent risk. [1, 15–22] However, most large-scale epidemiologic studies do not collect information on percent MD for the majority of participants. While automated measures of percent MD have been developed, it is very time consuming and costly to both collect mammograms and measure percent MD in large studies. Therefore, some studies have collected mammograms from a subset of participants, such as in nested case-control or case-cohort studies of breast cancer. Predicted percent MD models, such as the model outlined here, are advantageous in that predicted values can be estimated for most women in large-scale cohort analyses. This is a highly cost-effective approach that may be especially useful for older cohort studies in which it is not feasible to obtain mammograms from participants. Further, in prospective cohorts with updated data collection, predicted percent MD can be derived for each data collection cycle, allowing for changes over time. As percent MD is a strong risk factor for breast cancer, the inclusion of predicted percent MD may be particularly useful for the development and expansion of breast cancer risk prediction models in populations for which measured percent MD is unavailable. Recent work suggests that adding data on mammographic density to established breast cancer prediction models, such as the Gail and Tyrer-Cuzick models, can significantly improve risk prediction. [23–27] For example, in an analysis in the International Breast Cancer Intervention Study I, adding breast density to the Tyrer-Cuzick model improved the AUC by 0.11.[26] However, for the percent MD prediction model to be used in other study populations, data on several risk factors would need to be collected. For example, several studies have not collected information on early life body size even though it is strongly associated with both percent MD and breast cancer risk. Studies considering predicting percent MD in their populations would need to collect information on body size across the lifecourse as well as on other anthropometric, reproductive, and lifestyle factors included in the model.

Our final percent MD prediction model explained 41% of the total variability in percent MD, which is greater than the percent of variability explained for some other biomarker prediction models developed in large-scale epidemiologic studies. For example, in the NHS, NHSII, and the Health Professionals Follow-up Study, we developed a model to predict plasma 25-hydroxyvitamin D [25(OH)D] in which the r² for each cohort ranged from 0.25 to 0.33, generally consistent with the r² from 25(OH)D prediction models derived in other studies.[28–30] Though these models explained only a proportion of the variability in 25(OH)D, predicted 25(OH)D has been inversely associated with several chronic diseases including colorectal cancer,[31] renal cell cancer,[32] and type 2 diabetes[29] among others, highlighting the utility of biomarker prediction models.

There are some limitations to our analysis. While the final model r² of 0.41 is greater than some prior biomarker prediction models, it does indicate that there is a substantial amount of unexplained variability in percent MD. This unexplained variability may be due to measurement error in the self-reported anthropometric, reproductive, and lifestyle factors, measurement error in percent MD, as well as lack of information on (or availability of) additional predictors of percent MD, such as genetic contributors.[33] As a result, predicted MD values cannot be interpreted as direct measurements of percent MD. However, the high correlation between measured and predicted values in the testing dataset indicates that women likely are appropriately ranked with respect to their percent MD values. Mammograms collected in this study were film whereas increasingly mammograms administered in the US are digital. However, much of the research which demonstrated that percent MD is a risk factor for breast cancer is based on data from film mammograms.[22, 34] Further, studies which have assessed percent MD from digital mammograms and risk of breast cancer demonstrated that MD as assessed from digital mammography was valid and had similar association with breast cancer risk as was seen with film mammograms.[35] Additionally, recently published work from the International Pooling Project of Mammographic Density observed that in 128 paired images “MD differences between screen-film [mammograms] and processed digital [mammograms] on the subsequent screening round were consistent with expected time-related MD declines.”[36] Another limitation is that NHS and NHSII participants are predominantly Caucasian and are more similar to each other in various characteristics (e.g., education) than the general population, potentially limiting generalizability. Additional validation of the prediction model would be useful, especially in diverse populations. Strengths of this analysis include the standardized review of mammograms and measurement of percent MD, detailed data on several anthropometric, reproductive, and lifestyle factors, and a relatively large sample of pre-diagnostic screening mammograms.

Overall, our results suggest that the model developed to predict percent MD may be useful in large-scale epidemiologic analyses where the collection of mammograms for the majority of participants is not feasible.