Abstract
Models to assess mediation in the pretest-posttest control group design are understudied in the behavioral sciences even though it is the design of choice for evaluating experimental manipulations. The paper provides analytical comparisons of the four most commonly used models used to estimate the mediated effect in this design: Analysis of Covariance (ANCOVA), difference score, residualized change score, and cross-sectional model. Each of these models are fitted using a Latent Change Score specification and a simulation study assessed bias, Type I error, power, and confidence interval coverage of the four models. All but the ANCOVA model make stringent assumptions about the stability and cross-lagged relations of the mediator and outcome that may not be plausible in real-world applications. When these assumptions do not hold, Type I error and statistical power results suggest that only the ANCOVA model has good performance. The four models are applied to an empirical example.
Keywords: longitudinal mediation, two-waves, pretest, posttest design, mediation
Introduction
The cross-sectional single mediator model has been widely applied to test mediational theory in psychology and many areas of social science. Statistical and methodological aspects of the cross-sectional single mediator model have been studied extensively including significance testing (MacKinnon, Lockwood, Hoffmann, West, & Sheets, 2002; Shrout & Bolger, 2002, Valente, Gonzalez, Miočević, & MacKinnon, 2016), confidence limit estimation (Cheung 2007, 2009; MacKinnon, Lockwood, & Williams 2004; MacKinnon, Warsi, & Dwyer, 1995), effect size (Preacher & Kelly, 2011; Wen & Fan, 2015), influence of omitted variables (Cox, Kisbu-Sakarya, Miočević, & MacKinnon, 2014; James, 1980; Jo, 2008; MacKinnon & Pirlott, 2015), and causal estimation (Imai, Keele, & Tingley 2010; Jo, Stuart, MacKinnon, & Vinokur, 2011; MacKinnon, Krull, & Lockwood, 2000; Valeri & VanderWeele 2013; VanderWeele & Vansteelandt, 2009). The limitations of cross-sectional mediation analysis for assessing longitudinal mediation have been described in several articles (Cheong, MacKinnon, & Khoo, 2003; Cole & Maxwell, 2003; Fritz, 2014; Gollob & Reichardt, 1991; Kraemer, Stice, Kazdin, Offord, & Kupfer, 2001; MacKinnon, 1994, 2008; Maxwell & Cole, 2007; Maxwell, Cole, & Mitchell, 2011; Tein, Sandler, MacKinnon, & Wolchik, 2004).
None of this work has addressed statistical and methodological aspects of the simplest longitudinal model and most common experimental design, the pretest-posttest control group design (Shadish, Cook, & Campbell, 2002). Therefore there is little information regarding the best statistical model for estimating the mediated effect in this design. Jang, Kim, and Reeve (2012) specifically mentioned this lack of methodological information for estimating multi-wave mediation effects “…described well-known procedures to test for mediation with cross-sectional research designs, similar procedures to test for mediation with multi-wave longitudinal research designs have not yet been developed” (p. 1181). The purpose of this article is to demonstrate both analytically and empirically how four common statistical models used to estimate the mediated effect in the pretest-posttest control group design compare, and the additional complexity that occurs with the addition of pretest measures of a mediating and outcome variable.
Statistical Mediation
Statistical mediation is represented by three linear regression equations and allows researchers to test indirect effects of an independent variable on a dependent variable through the independent variable’s effect on the mediating variable (Lazarsfeld, 1955; MacKinnon, 2008; MacKinnon & Dwyer, 1993; Sobel 1990). Equation 1 represents the total effect of X on Y (c coefficient), Equation 2 represents the effect of X on M (a coefficient), and Equation 3 represents the effect of X on Y adjusted for M (c′ coefficient) and the effect of M on Y adjusted for X (b coefficient). An interaction between X and M provides a test of whether the relation between the mediator and the dependent variable differs across levels of X but is not included in the equations below and is not a focus of this study. Computing the product of a and b coefficients from Equation 2 and Equation 3, respectively, represents the mediated effect of X on Y through M (ab).
| (1) |
| (2) |
| (3) |
These three linear regression equations used to assess statistical mediation in crosssectional experimental designs, are extended in this paper for the pretest-posttest control group design.
As noted by many researchers, mediation models are inherently longitudinal and researchers should take time into account when assessing mediated effects (Cheong, et al., 2003; Cole & Maxwell, 2003; Fritz, 2014; Gollob & Reichardt, 1991; Kraemer, et al., 2001, MacKinnon, 1994, 2008; Maxwell & Cole, 2007; Tein, et al., 2004). That is, mediation is a type of third variable effect such that a mediating variable is both a dependent variable and an independent variable in a causal sequence (Lazarsfeld, 1955; MacKinnon, 2008, Sobel, 1990). Mediating variables are intermediate in a causal sequence such that an event, X, occurs which has a causal effect on a mediating variable, M, which then has a causal effect on a dependent variable, Y. Given the temporal nature of the causal sequence, longitudinal data (i.e., data collected over time) is needed to accurately assess mediated effects (Cole & Maxwell, 2003; Gollob & Reichardt, 1991; MacKinnon, 1994, 2008; Maxwell & Cole, 2007; Maxwell, Cole, & Mitchell, 2011). Maxwell and Cole (2007) and Maxwell et al (2011) noted the lack of research on the performance of the cross-sectional model for estimating mediated effects in a longitudinal model where X represents an experimental manipulation.
Pretest-Posttest Control Group Design
The pretest-posttest control group design consists of randomly assigning units to either a treatment or a control group, measuring theoretically relevant variables prior to randomization (i.e., pretest measures) and measuring theoretically relevant variables again after randomization (i.e., posttest measures) (Bonate, 2000; Shadish et al., 2002). The simplest case consists of an independent variable that represents treatment assignment (X) and a dependent variable (Y). In this case, a pretest measure of Y is obtained prior to treatment assignment and incorporated into the estimation of the treatment effect of X on Y at posttest. This design allows researchers to take into account nuisance variation in the outcome variable subsequently leading to more powerful inferential test statistics, narrower and more precise confidence intervals, and increased internal validity (Maxwell & Delaney, 2004; Shadish et al., 2002).
In the case of a randomized experiment, there are numerous ways to adjust for these pretest scores to increase the precision of the treatment effect estimate including difference scores, residualized change scores, and Analysis of Covariance (ANCOVA). The benefits of adjusting for pretest scores in longitudinal experimental designs can be extended to designs that include a mediating variable. In the pretest-posttest control group design with a mediating variable, there are pretest scores for both the mediating variable and the outcome variable and the same adjustment techniques for the pretest scores can be applied to both the mediating variable and the outcome variable.
When a mediating variable (M) is involved, pretest measures of M and of Y can be used in the estimation of the mediated effect of X on Y through M at posttest. The pretest-posttest design with a mediating variable can be used to estimate a longitudinal mediated effect when only two waves (e.g., pretest and posttest) of data are collected and is sometimes referred to as a half-longitudinal mediation model (Cole & Maxwell, 2003). Because X is an experimental manipulation which we assume marks the beginning of the mediational chain for all units, we argue that the longitudinal mediated effect in this design is the mediated effect of X on posttest outcome through its effect on w for the M2 – Y2 relation to be free of any time-invariant third variable effects on the mediator outcome relation and can be considered a causal effect assuming no time-varying confounding (derivation of causal mediated effects using the potential outcome framework can be obtained from the second author’s website, https://psychology.clas.asu.edu/research/labs/research-prevention-laboratory-mackinnon, and there is further discussion of this point later in the paper).
Pretest-Posttest Control Group Design with a Mediating Variable
When X is a randomized experimental manipulation, a common way to assess the mediated effect is by estimating a series of linear regression equations (or simultaneously estimating the equations in a structural equation model) similar to those used to assess the mediated effect in cross-sectional data (as shown in Figure 1). Equation 4 represents the effect of X on the mediator measured at posttest (M2) adjusted for pretest mediator (M1) (am2x coefficient; a path) and the pretest outcome variable (Y1), the effect of M1 on M2 is the stability of the mediator (Sm2m1 coefficient) adjusted for X and Y1, and the effect of Y1 on M2 is the M2 cross-lagged relation (bm2y1 coefficient) adjusted for X and M1. Equation 5 represents the effect of X on the outcome variable measured at posttest (Y2) (c′y2x coefficient; c′ path) adjusted for the other variables in the equation, the effect of Y1 on Y2 is the stability of the dependent variable (Sy2y1 coefficient) adjusted for the other variables in the equation, the effect of M1 on Y2 is the Y2 cross-lagged relation (by2m1 coefficient) adjusted for the other variables in the equation, and the effect of M2 on Y2 (by2m2 coefficient; b path) adjusted for the other variables in the equation. In addition to these parameters, the model includes a pretest covariance between the mediator and the outcome (σm1y1) (see Figure 1).
| (4) |
| (5) |
The mediated effect of X on Y2 through M2 in the pretest-posttest design is assessed by taking the product of am2x coefficient in Equation 4 and by2m2 coefficient in Equation 5 (am2xby2m2) and represents the mediated effect estimate in the ANCOVA model.
Figure 1.
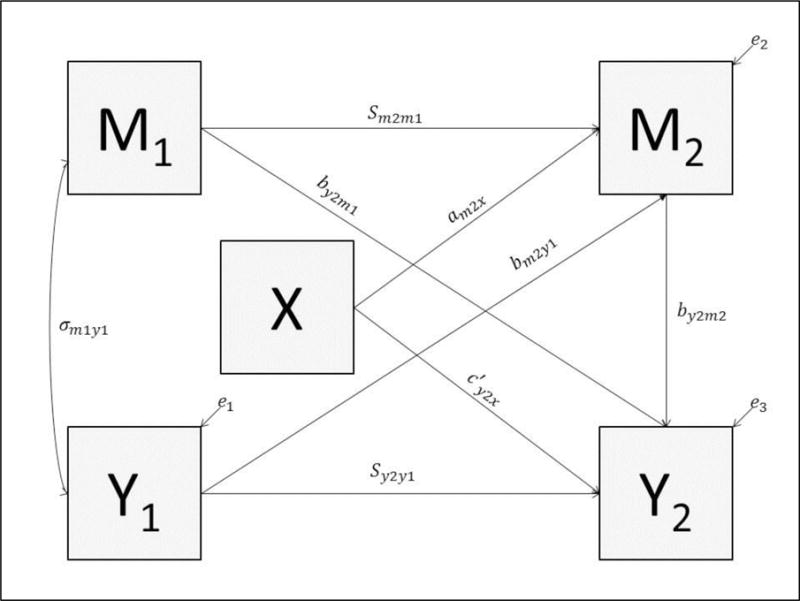
Path diagram of pretest posttest control group design with mediating variable. Diagram includes pretest correlation between mediator and dependent variable ρy1m1, stability of mediator (sm2m1) and stability of dependent variable (sy2y1), Y2 cross-lag (by2m1), M2 cross-lag (bm2y1), effect of X on M2 (am2x), effect of X on Y2 (c′y2x), and effect of M2 on Y2 (by2m2).
Prior research has investigated the limitations of the cross-sectional model for investigating longitudinal mediated effects, but has not investigated the performance of various longitudinal models for investigating the longitudinal mediated effect in the pretest-posttest design. Four statistical models can be used to investigate the mediated effect: the cross – sectional model, the difference score model (Jansen, et al., 2013; MacKinnon et al., 1991), the residualized change score model (Miller, Trost, & Brown, 2002; Reid & Aiken, 2013), the Analysis of Covariance (ANCOVA) model (Jang et al., 2012; Schmiege, Broaddus, Levin, & Bryan, 2009). Alternatively, the parameters of the ANCOVA model can be estimated simultaneously via path analysis (MacKinnon, 1994, 2008; MacKinnon, et al., 2001).
Although each of these models address different questions about change from pretest to posttest, researchers use each of them to address questions regarding longitudinal mediation. Little is known about the accuracy of these different mediated effect estimators because of the pretest-posttest relations between the mediator and the outcome that are a consequence of adding a mediating variable to the traditional pretest-posttest control group design. Therefore, the purpose of this article is fourfold. First, we discuss model assumptions and compare the four models discussed earlier in this paper and show how the mediated effect estimate for each of these models relates to the mediated effect estimate in the ANCOVA model. Second, we demonstrate how the difference score, residualized change score, and cross-sectional models are hierarchically nested within the ANCOVA model using a Latent Change Score specification (e.g., McArdle, 2009). Third, we conduct a simulation study investigating the relative bias, Type 1 error rates, confidence interval coverage, and power to detect the mediated effect for each of the four models. Fourth, we apply these models to an empirical example.
Analysis of Change in Mediation Models and Model Assumptions
Assuming there is successful randomization of units to the control group and treatment group so that these groups do not differ systematically at pretest, any observed change in a unit from the treatment group from pretest to posttest would not have occurred had that unit been assigned to the control group (Van Breukelen, 2006, 2013). Researchers have explored the results of violating these assumptions using ANCOVA and difference score models outside the context of mediation (Jamieson, 1999; Kisbu-Sakarya, MacKinnon, & Aiken, 2013; Van Breukelen, 2006, 2013; Wright, 2006). For the application of mediation, VanderWeele and Vansteelandt (2009) describe the four assumptions necessary for identification of a mediated effect:
No unmeasured confounders of the relation between X and Y.
No unmeasured confounders of the relation between M and Y.
No unmeasured confounders of the relation between X and M.
No measured or unmeasured confounders of M and Y that have been affected by treatment.
Because X is an experimental manipulation, assumptions one and three outlined by VanderWeele and Vansteelandt (2009) will hold true in the pretest- posttest control group design. That is, the randomization of X will help to ensure an equivalent balance across all measured and unmeasured variables, in expectation, that may theoretically affect X and M2. This also holds for the relation between X and Y2 not adjusted for M2. For this article, we assume that there are no unmeasured confounders of the relation between M1 and Y1 or M2 and Y2 although using the pretest scores from two-waves of data adjusts for time invariant confounders in a randomized experiment (James, 1980, Judd & Kenny, 1981) and there are some potential alternatives to address confounding of the M to Y relation (MacKinnon & Pirlott, 2015). We also assume there are no measured or unmeasured confounders of the M2 to Y2 relation that are affected by X and all variables are measured without error. A full list of assumptions for the single mediator model can be found in MacKinnon (2008) and VanderWeele and Vansteelandt (2009). We will address how violating these assumptions may affect results and approaches to improving inference in these situations in the Discussion section of this article.
Cross-sectional model
The cross-sectional model is the simplest model because it does not take into account the pretest measures of the mediator and dependent variable and therefore does not address a question of change across time. Equation 6 represents the relation between the treatment variable and the posttest mediator (am2x) and Equation 7 represents the relation between the treatment variable and the posttest dependent variable (c′y2x) adjusted for the posttest mediator and the relation between the posttest mediator and the posttest dependent variable (by2m2) adjusted for the treatment.
| (6) |
| (7) |
The cross-sectional mediated effect is estimated by computing the product of am2x coefficient from Equation 6 and by2m2 coefficient from Equation 7 (am2xby2m2) which is the effect of X on Y2 through its effect on M2 not adjusted for pretest measures, M1 and Y1.
The performance of the cross-sectional model has been investigated for estimating mediated effects when the true underlying model is a longitudinal model with repeated measures of X, M, and Y (Cole & Maxwell, 2003; Gollob & Reichardt, 1991; Maxwell & Cole, 2007; Maxwell, et al., 2011). The cross-sectional estimate of the mediated effect when there is a true underlying longitudinal model is biased and this bias has been shown in Maxwell and Cole (2007) and Maxwell et al (2011). However, what has not been demonstrated in this prior research, was the Type 1 error rate, confidence interval coverage, and power for cross-sectional estimates when the true longitudinal model corresponds to a pretest-posttest control group design.
Difference score model
The difference score model is unconditional on pretest scores (Cronbach & Furby, 1970; Dwyer, 1983; McArdle, 2009) and assumes that the unstandardized regression coefficient between the prestest and posttest measure (stability) is 1.0 (Bonate, 2000; Campbell & Kenny, 1999; Cronbach & Furby, 1970; Laird, 1983) (see Table 1). Equation 8 represents the difference score that would be calculated for a mediator variable where Δm represents scores on the mediator variable measured at pretest subtracted from scores on the mediator variable measured at posttest. Equation 9 represents the difference scores calculated for the dependent variable where Δy represents scores on the dependent variable measured at pretest subtracted from scores on the dependent variable measured at posttest.
| (8) |
| (9) |
Equations 10 and 11 represent regression equations using difference scores for the mediator variable and dependent variable, respectively.
| (10) |
| (11) |
The mediated effect is estimated by computing the product of aΔ coefficient from Equation 10 and bΔ coefficient from Equation 11 (aΔbΔ) which is the effect of X on change in Y through its effect on change in M.
Table 1.
Hierarchy of Two-wave Mediation Models as a Function of Parameter Constraints
| Model | Parameters | ||||
|---|---|---|---|---|---|
|
| |||||
| M1<->Y1 |
M1->M2 Y1->Y2 |
M1->Y2 | Y1->M2 | DFs | |
| ANCOVA (Autoregressive) | Free | Free | Free | Free | 0 |
| Difference Score | Free | Constrained to 1 | Constrained to 0 | Constrained to 0 | 4 |
| Residualized Change Score | Free | Constrained to OLS or ML estimate of Posttest on Pretest regression | Constrained to 0 | Constrained to 0 | 4 |
| Cross-sectional | Free | Constrained to 0 | Constrained to 0 | Constrained to 0 | 6 |
Note. The ANCOVA (autoregressive) model may have the M1->Y2 or Y1->M2 or both parameters constrained to zero resulting in a model with 1 or 2 DFs, respectively.
Residualized change score model
Residualized change scores are computed by regressing posttest scores on pretest scores and then computing the difference between observed posttest scores and predicted posttest scores (i.e., residual; Cronbach & Furby, 1970). No treatment group variable is included in the regression of posttest scores on pretest scores which means posttest scores for units in both treatment groups are adjusted for pretest scores based on an aggregate of pretest scores across both treatment groups (e.g., Cronbach & Furby, 1970; Kisbu-Sakarya et al., 2013) which may lead to erroneous inference regarding group differences in some cases (Maxwell, Delaney, & Manheimer, 1985).
Residualized change scores are conditional on pretest scores and are the part of the posttest score that is not predictable from the pretest score (Cronbach & Furby, 1970; Rogosa, 1988). Equation 12 represents residualized change scores calculated for the mediator variable, where Rm indicates change in predicted scores on the mediator variable measured at posttest subtracted from observed scores on the mediator variable measured at posttest. Equation 13 represents residualized change scores calculated for the dependent variable, where Ry indicates change in predicted scores on the dependent variable measured at posttest subtracted from observed scores on the dependent variable at posttest.
| (12) |
| (13) |
Equations 14 and 15 represent regression equations using residualized change scores for the mediator variable and the dependent variable, respectively.
| (14) |
| (15) |
The mediated effect is estimated by computing the product of ar coefficient from Equation 14 and br coefficient from Equation 15 (arbr) which is the effect of X on the residual change in Y through its effect on the residual change in M.
ANCOVA
ANCOVA is used to assess change by using pretest scores as a covariate when predicting posttest scores (Bonate, 2000; Campbell & Kenny, 1999; Laird, 1983). ANCOVA removes the influence of pretest scores on posttest scores by computing a within-group regression coefficient of posttest scores on pretest scores for each treatment and control group, separately. Next, these within group regression coefficients are pooled to form a single regression coefficient by which posttest scores are adjusted for pretest scores. ANCOVA is conditional on pretest scores and is considered a base-free measure of change (Cronbach & Furby, 1970; McArdle, 2009). The ANCOVA model assumes that within group regression coefficients are homogenous, there is no interaction of the covariate (e.g., pretest scores) and the treatment group, and that the covariate is measured without error (Maxwell & Delaney, 2004). Equations 16 and 17 represent regression equations using ANCOVA to adjust for pretest scores for the mediator and the dependent variable, respectively.
| (16) |
| (17) |
Sm2m1 in Equation 16 represents the relation of pretest scores measured on the mediator to posttest scores measured on the mediator within each treatment and control group and then pooled across both groups. Sy2y1 in Equation 17 represents the relation of pretest scores measured on the dependent variable to posttest scores measured on the dependent variable within each treatment and control group and then pooled across both groups. The mediated effect is estimated by computing the product of am2x coefficient from Equation 16 and by2m2 coefficient from Equation 17 (am2xby2m2) which is the effect of experimental manipulation on Y2 through its effect on M2 adjusted for M1 and Y1.
In summary, each of these four models provide a different estimate of the mediated effect. The mediated effect estimates across these four models can be compared analytically to determine under what conditions researchers would expect to observe differences in these mediated effect estimates. The following section provides analytical derivations of the differences in the b path component (i.e., relation of the mediator to the outcome adjusted for X) of the mediated effect estimate as this is the component of the mediated effect that differs across the four models discussed earlier.
Comparing Models of Change
The four models for two waves of data for estimating the mediated effect adjusted for pretest measures differ from one another in the assumptions they make regarding the relation of pretest measures to posttest measures. Of particular interest is how the path coefficients involved in estimating the mediated effect are similar across models. The paths of interest are the paths relating X to M2 (a path) and the path relating M2 to Y2 adjusted for X(b path). The unstandardized relation of X to M2 in the pretest-posttest control group design is equivalent in expectation across all models because the covariances of X and M2, X and Δm, and X and Rm are equivalent when the covariance between X and M1 and X and Y1 are zero (i.e., assuming successful randomization of units to levels of X). Therefore no analytical comparisons are needed for this component of the mediated effect.
The unstandardized relation of M2 to Y2 adjusted for X varies across the four different models depending on a number of factors and will be referred to as the b path throughout this paper. The difference in the b path across models can be thought of as an unmeasured confounder problem by applying results from Clark (2005) and Hanushek and Jackson (1977). That is, assuming the data-generating model is the ANCOVA model, the predicted ΔY using the difference score model will not explain all the variance in ΔY and therefore there will be a residual of this prediction. Any relation of the predictor ΔM with this residual will capture the difference in the b path across the two models (full derivations of the differences in the b path from the ANCOVA versus the difference score model, the ANCOVA versus the residualized change score model, and the ANCOVA versus the cross-sectional model can be obtained from the second author’s website, https://psychology.clas.asu.edu/research/labs/research-prevention-laboratory-mackinnon). For brevity, only the final solutions for each model comparison are presented below. The unstandardized b path from the difference score model can be characterized with the following equations:
| (18) |
| (19) |
| (20) |
The term is the covariance between the mediator variable for the difference score model and the residual of prediction of the outcome variable for the difference score model from the true difference score outcome variable assuming the ANCOVA model is the population model. The term is the variance of this residual of prediction, the term is the variance of the mediator variable for the difference score model, and the term is the squared correlation between X and the mediator variable for the difference score model. When the term is equal to zero, the b path in the difference score model (bΔ)will equal the b path in the ANCOVA model (bY2M2). The unstandardized b path from the residualized change score model can be characterized with the following equations:
| (21) |
| (22) |
| (23) |
The terms represented in Equations 21–23 for the residualized change score model are analogous to the terms described in Equations 18–20 for the difference score model. When the term is equal to zero, the b path in the residualized change score model (bR)will equal the b path in the ANCOVA model (bY2M2). The unstandardized b path from the cross-sectional model can be characterized with the following equations:
| (24) |
| (25) |
| (26) |
The terms represented in Equations 24–26 for the cross-sectional model are analogous to the terms described in Equations 18–20 for the difference score model. Therefore, when the term is equal to zero, the b path in the cross-sectional model (b)will equal the b path in the ANCOVA model (bY2M2).
In summary, the mediated effect estimate for difference score, residualized change score, and cross-sectional models will not generally equal the mediated effect estimate for the ANCOVA model because of differences in the b path component of the mediated effect. Generally speaking, the mediated effect estimates for the non-ANCOVA (i.e., difference score, residualized change score, and cross-sectional) models will differ from the mediated effect estimate of the ANCOVA model as a function of the pretest correlation, stabilities, and cross-lagged paths. The following section demonstrates how all of these models can be fitted in a general structural equation modeling approach using a Latent Change Score specification. The latent change score specification of these models is useful for providing evidence of model fit, which can be used to assess the adequacy of the each of these four models.
Latent Change Score Specification
The latent change score (LCS) specification is a Structural Equation Modeling (SEM) approach to modeling longitudinal data that can represent simple and dynamic change over time with either manifest or latent measures of a time-dependent outcome (McArdle, 2001, 2009). With two waves of data measured for both the mediating and outcome variable a variety of models can be fitted to the data to assess the mediated effect. Assuming random assignment to two groups and the two waves represent pretest measure (M1, Y1) and posttest measures (M2, Y2), all four two wave models previously mentioned can be fitted with the LCS specification. Because these models can all be fitted with the LCS specification, we can view the difference score, residualized change score, and cross-sectional models nested within the ANCOVA model to which they can be compared using traditional (SEM) fit indices (See Table 1).
ANCOVA
The ANCOVA model can be estimated in the LCS specification as in Figure 2a. We now have the second wave of the mediator and the outcome as a unit-weighted function of pretest and a new unobserved change variable (ΔM and ΔY) to mimic subtracting pretest scores from posttest scores on the respective variables. The fit of this model will be identical to the fit of the traditional ANCOVA model1 (i.e., saturated, 0 dfs). The mediated effect is estimated as the effect of experimental manipulation, X, on ΔY through its effect on ΔM (ab) and is equivalent to the estimate of the mediated effect in the traditional ANCOVA model although some of the parameters in the LCS specification are re-parameterizations of the traditional ANCOVA parameters. The ANCOVA parameters can be recovered from the LCS framework by applying the following equations (McArdle, 2009) with the asterisked quantities representing quantities from the LCS specification: Sm2m1 = S*m2m1 + 1 and Sy2y1 = S*y2y1 + 1 and by2m1 =b *y2m1 − by2m2.
Figure 2.
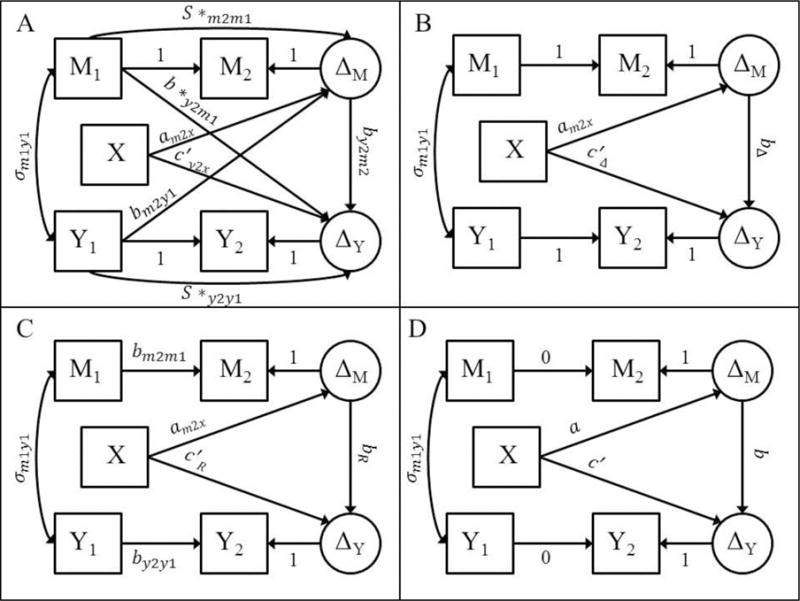
The top left panel displays the ANCOVA equivalent pretest-posttest control group design with a mediating variable. The S *m2m1, S *y2y1, b *y2m1, parameters are re-parameterized versions of Sm2m1, Sy2y1, by2m1, in the traditional ANCOVA model. The top right panel displays the difference score model for estimating the mediated effect. The cross-lagged paths are excluded and the stabilities are constrained to one. The bottom left panel displays the residualized change score model for estimating the mediated effect. The cross-lagged paths are excluded, the stability of the mediator is constrained to bm2m1 which is the relation of posttest mediator on pretest mediator with no group information or pretest outcome information included, and the stability of the outcome is constrained to by2y1 which is the relation of posttest outcome on pretest outcome with no group information or pretest mediator information included. The bottom right panel displays the cross-sectional model for estimating the mediated effect. The cross-lagged paths are excluded and the stabilities are constrained to zero.
Difference score model
The difference score model and can be estimated in the LCS specification as in Figure 2b. The following constraints are made on the ANCOVA model to estimate the LCS resulting in a model with four degrees of freedom: Cross-lagged paths areconstrained to zero and Pretest effects on Δ′s are constrained to zero.
Residualized change score model
The residualized change score model can be estimated in the LCS specification as in Figure 2c. The following constraints are made to the LCS model to estimate the residualized change score model resulting in a model with four degrees of freedom. The residualized change score and the difference score models cannot be compared based on a chi-square difference test because they have the same degrees of freedom. These two models represent change in different ways. Recall, in the LCS specification, change is defined as the part of posttest scores that is not identical to pretest scores. For residualized change, change is defined as the part of posttest scores that is not predictable from pretest scores (i.e., base-free). To get the residualized change score estimates from the LCS framework two constraints are needed: (1) Fix stability of the mediator to the simple regression estimate of posttest mediator on pretest mediator and (2) fix the stability of the outcome to the simple regression estimate of the posttest outcome on the pretest outcome. This requires a two-step procedure where the simple regression estimate is first computed of posttest scores on pretest scores for both the mediator (bm2m1) and the outcome (by2yl) separately. These estimates are then used as the constraints in the LCS specification in place of the traditional constraint of 1 that is used for the difference score model.
Cross-sectional model
The cross-sectional model can be estimated in the LCS specification as in Figure 2d. The following constraints are made to estimate the crosssectional model resulting in a model with four degrees of freedom. The cross-sectional model implies that there is no stability of scores across time. This also implies that if the true generating model is longitudinal in nature (e.g., there are stable individual differences across time) the cross-sectional model will result in biased estimation of the mediated effect (Cole & Maxwell, 2003; Maxwell & Cole, 2007; Maxwell et al., 2011). To get the cross-sectional model estimates from the LCS specification, constrain the stability coefficients zero.
Summary of Model Assumptions and Comparisons
In summary, there are four models for estimating the mediated effect with two waves of data. Those models include: the cross-sectional model, the difference score model, the residualized change score model, and the ANCOVA model. Assuming the pretest-correlation is present, the b path from the difference score model differs from the b path from the ANCOVA model because the stabilities of the mediator and outcome are not equal to one and the cross-lagged paths are not exactly zero. This relation is implied by examining Equation 20. The b path from the residualized change score model differs from the b path from the ANCOVA model because the simple regression relating M2 to M1 and Y2 to Y1 are not equivalent to the stabilities estimated in the ANCOVA model and the cross-lagged paths are non-zero. This relation is implied by examining Equation 23. The b path from the cross-sectional model differs from the b path from the ANCOVA model because the stabilities are non-zero and the cross-lagged paths are non-zero. This relation is implied by examining Equation 26. Because four different models could be fitted to any two-wave data with a mediating variable, it is important to understand the statistical properties of the various estimators of the mediated effect.
Overview of Simulation Study
The purpose of the simulation study was to provide researchers with information regarding the performance of four statistical models for estimating the mediated effect in the pretest-posttest control group design. The primary focus of our comparison was Type 1 error rates, confidence interval coverage, relative bias, and statistical power of each model. We predicted that the ANCOVA model would perform the best in terms of our criteria. The difference score and residualized change score model would be unbiased when compared to their respective population true values but not as powerful as the ANCOVA model when assumptions of the difference score and residualized change score models regardingthe stabilities and cross-lagged relations do not hold because there will be unexplained variability not accounted for by either model when these assumptions do not hold. It was hypothesized the cross-sectional model would be biased when compared to the population true value adjusted for pretest measures (i.e., to reflect a longitudinal mediated effect value) when there is a pretest correlation between the mediator and the dependent variable in the population and when cross-lagged paths are present in the population. It was hypothesized that conditions which led to increased bias in the cross-sectional model would lead to more power than the ANCOVA model. The overall goal of the simulation was to provide information to researchers regarding the options for assessing mediation in the pretest-posttest control group design.
Method
Data-Generating Model
The SAS 9.3 programming language was used to conduct a Monte Carlo simulation. The following equations represent the data-generating model and correspond to the ANCOVA model in the Monte Carlo simulation where x is an observed value of random variable X and is the sample median.
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
In the Monte Carlo simulation the following factors were varied: sample size (N = 50, 100, 200, 500), effect size of the a (am2x) (0 .14, .39, .59), b(by2m2) (0 .14, .39, .59), and c′ (c′y2x) (0 and .39) paths, effect size of the Y2 cross-lag (by2m1 path) (0 and .50), effect size of the M2 cross-lag (bm2y1 path) (0 and .50), stability of the mediator variable (Sm2m1) and the dependent variable (Sy2y1) (.3 and .7), and the correlation between M1 and Y1 (0 and 0.5). The by1m1 coefficient in Equation 29 was simulated to be equivalent to a correlation (ρy1m1) of 0 or .5. Thirty-two combinations of effect sizes for the a (am2x), b (by2m2), and c′ (c′y2x) path were studied. The effect sizes were chosen to reflect approximately small, medium, and large effect sizes, respectively (Cohen, 1988). There were 2048 conditions defined by 32 effect size combinations, 4 sample sizes, 2 effect sizes of Y2 cross-lag, 2 effect sizes of M2 cross-lag, 2 stabilities of the mediator variable and dependent variable, and 2 correlations between M1 and Y1. This resulted in a complete factorial design with all factors being fully crossed with one another. A total of 1,000 replications of each condition was conducted. The focus of this simulation study was to evaluate estimator characteristics of the mediated effect (am2x by2m2) for the four data analysis models: ANCOVA, difference score, residualized change score, and crosssectional models.
Bias of Parameter Estimates
Relative bias was computed for the parameter estimates of the mediated effect by subtracting the true value of the parameter from the parameter estimate and then dividing the bias of the parameter estimate by the true value of the parameter across replications. An estimator of the mediated effect was considered acceptable in terms of bias if the absolute value of relative bias was less than .10 (Flora & Curran, 2004). Other measures of bias, absolute bias and standardized bias, led to similar conclusions as reported below.
Significance Testing
Distribution of a product
The PRODCLIN program was used to compute asymmetric confidence intervals based on the non-normal distribution of the product of two regression coefficients (e.g., ab; MacKinnon, Fritz, Williams, & Lockwood, 2007). The PRODCLIN program was used to compute the 95% asymmetric confidence interval for each estimate of the mediated effect for each replication.
Type 1 error rates were the proportion of times across the 1000 replications per condition an estimate of the mediated effect was statistically significant at the 0.05 alpha level when the true value of the parameter estimate was equal to zero. Bradley’s (1978) liberal criterion was used to evaluate the performance of the methods in terms of Type 1 error rates. That is, Type 1 error rates were deemed acceptable if they fell within the range of [0.025, 0.075]. Power was the proportion of times across the 1000 replications per condition an estimate of the mediated effect was statistically significant at the 0.05 alpha level when the true value of the parameter was not equal to zero. The best performing estimator in terms of statistical power had the highest statistical power given the effect size and sample size generated for a given simulation condition. Coverage was the proportion of times the true value of the mediated effect fell within the asymmetric confidence intervals. Confidence intervals were deemed acceptable if the interval contained the true value of the mediated effect within the range of [0.925, 0.975].
Results
Organization
The results section is organized in the following way. Type 1 error rates are discussed first followed by bias, confidence interval coverage, and then power results. All Type 1error, confidence interval coverage, and power results are reported using the distribution of a product method. The distribution of a product method results were reported because they perform better than normal theory results and they perform similarly to the percentile bootstrap results when detecting the mediated effect in this study and in prior research (MacKinnon, Lockwood, & Williams, 2004). The raw data were analyzed using Analysis of Variance. For example, for one set of parameter combinations, N = 200, and 1,000 replications, the dataset analyzed consisted of 200,000 observations. Because of the large sample size and number of factors involved in this simulation study, only the highest order interaction and main effects for each model with semi-partial eta-squared values of 0.01 (i.e., small effect) or greater were reported in this article.
Type 1 Error Rates
The mediated effect in this article is tested by taking the product of two regression coefficients. Because the mediated effect is the product of two quantities, the mediated effect can equal zero in three separate cases. First, the mediated effect can equal zero if the a path is equal to zero. Second, the mediated effect can equal zero if the b path is equal to zero. Third, the mediated effect can equal zero if both the a and the b path are equal to zero. The Type I error rates only exceeded the robustness interval when the a path was non-zero and the b path was zero therefore only these results were presented.
Type 1 Error Rates – b Path Equal To Zero
Type 1 error rates were investigated for true values of a equal to 0 – .59 when the true value of b was equal to 0. The Type 1 error rates for the ANCOVA model never exceeded the robustness interval so these results were not reported. There were main effects of true value of a , sample size , M2 cross-lag , and Y2 cross-lag on Type 1 error rates for the difference score, residualized change score, and the cross-sectional models. As these factors increased, the Type 1 error rates for these models increased and exceeded the top-end of the robustness interval. There was a significant three-way interaction of pretest correlation by M2 cross-lag by Y2 cross-lag on Type 1 error rate for the difference score model such that Type 1 error rates exceeded the top-end of the robustness interval when either the M2 cross-lag was equal to 0.50 or the Y2 cross-lag was equal to 0.50 but was the highest when both the M2 cross-lag and Y2 cross-lag were equal to 0.50. The Type 1 error rates for the difference score model were within the robustness interval when both the M2 cross-lag and Y2 cross-lag were equal to zero except for when the pretest correlation was equal to 0.50 (see Table 2).
Table 2.
Type 1 error rates for tests of the mediated effect for difference score (Diff), residualized change score (Res), and cross-sectional model (Cross) when b is equal to zero and for all values of pretest correlation, M2 cross-lag, and Y2 cross-lag.
| M2 cross-lag | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | |||||||||||||
| Y2 cross-lag | Y2 cross-lag | |||||||||||||
| 0 | 0.5 | 0 | 0.5 | |||||||||||
| Diff | Res | Cross | Diff | Res | Cross | Diff | Res | Cross | Diff | Res | Cross | |||
| Pretest Correlation | Sample Size | a | ||||||||||||
| 0 | 50 | 0.00 | 0.002 | 0.001 | 0.001 | 0.016 | 0.000 | 0.027 | 0.009 | 0.002 | 0.011 | 0.027 | 0.000 | 0.038 |
| 0.14 | 0.006 | 0.009 | 0.006 | 0.050 | 0.003 | 0.061 | 0.029 | 0.002 | 0.024 | 0.057 | 0.002 | 0.083 | ||
| 0.39 | 0.038 | 0.039 | 0.027 | 0.231 | 0.018 | 0.314 | 0.151 | 0.022 | 0.131 | 0.298 | 0.010 | 0.379 | ||
| 0.59 | 0.051 | 0.056 | 0.058 | 0.354 | 0.037 | 0.536 | 0.252 | 0.025 | 0.256 | 0.501 | 0.021 | 0.690 | ||
| 100 | 0.00 | 0.002 | 0.002 | 0.002 | 0.023 | 0.001 | 0.037 | 0.018 | 0.001 | 0.018 | 0.030 | 0.000 | 0.046 | |
| 0.14 | 0.007 | 0.010 | 0.007 | 0.103 | 0.003 | 0.145 | 0.071 | 0.004 | 0.071 | 0.104 | 0.001 | 0.157 | ||
| 0.39 | 0.047 | 0.046 | 0.046 | 0.452 | 0.018 | 0.657 | 0.378 | 0.028 | 0.377 | 0.482 | 0.011 | 0.745 | ||
| 0.59 | 0.058 | 0.059 | 0.059 | 0.494 | 0.034 | 0.737 | 0.431 | 0.033 | 0.466 | 0.555 | 0.024 | 0.883 | ||
| 200 | 0.00 | 0.002 | 0.001 | 0.001 | 0.022 | 0.000 | 0.041 | 0.025 | 0.001 | 0.026 | 0.032 | 0.000 | 0.053 | |
| 0.14 | 0.019 | 0.022 | 0.017 | 0.199 | 0.006 | 0.323 | 0.170 | 0.007 | 0.188 | 0.190 | 0.003 | 0.327 | ||
| 0.39 | 0.043 | 0.045 | 0.050 | 0.518 | 0.013 | 0.895 | 0.562 | 0.028 | 0.683 | 0.576 | 0.013 | 0.966 | ||
| 0.59 | 0.055 | 0.053 | 0.055 | 0.525 | 0.028 | 0.897 | 0.573 | 0.027 | 0.694 | 0.580 | 0.020 | 0.986 | ||
| 500 | 0.00 | 0.002 | 0.001 | 0.001 | 0.027 | 0.001 | 0.050 | 0.034 | 0.000 | 0.043 | 0.029 | 0.001 | 0.052 | |
| 0.14 | 0.038 | 0.044 | 0.035 | 0.403 | 0.008 | 0.740 | 0.465 | 0.018 | 0.580 | 0.434 | 0.005 | 0.669 | ||
| 0.39 | 0.049 | 0.048 | 0.049 | 0.521 | 0.013 | 0.997 | 0.699 | 0.028 | 0.909 | 0.669 | 0.016 | 1.000 | ||
| 0.59 | 0.048 | 0.053 | 0.053 | 0.529 | 0.028 | 0.996 | 0.700 | 0.026 | 0.917 | 0.654 | 0.021 | 1.000 | ||
| 0.5 | 50 | 0.00 | 0.005 | 0.002 | 0.011 | 0.004 | 0.001 | 0.032 | 0.005 | 0.001 | 0.029 | 0.019 | 0.003 | 0.045 |
| 0.14 | 0.015 | 0.008 | 0.023 | 0.020 | 0.002 | 0.072 | 0.013 | 0.003 | 0.056 | 0.053 | 0.014 | 0.094 | ||
| 0.39 | 0.101 | 0.040 | 0.123 | 0.115 | 0.025 | 0.392 | 0.107 | 0.021 | 0.240 | 0.274 | 0.090 | 0.439 | ||
| 0.59 | 0.152 | 0.054 | 0.234 | 0.172 | 0.042 | 0.616 | 0.169 | 0.032 | 0.510 | 0.432 | 0.155 | 0.854 | ||
| 10 | 0.00 | 0.008 | 0.001 | 0.011 | 0.010 | 0.001 | 0.035 | 0.010 | 0.001 | 0.037 | 0.025 | 0.008 | 0.057 | |
| 0.14 | 0.046 | 0.012 | 0.061 | 0.051 | 0.005 | 0.147 | 0.045 | 0.004 | 0.104 | 0.110 | 0.049 | 0.165 | ||
| 0.39 | 0.232 | 0.052 | 0.323 | 0.242 | 0.026 | 0.696 | 0.256 | 0.029 | 0.537 | 0.525 | 0.271 | 0.776 | ||
| 0.59 | 0.254 | 0.048 | 0.388 | 0.297 | 0.038 | 0.789 | 0.286 | 0.032 | 0.728 | 0.567 | 0.294 | 0.989 | ||
| 200 | 0.00 | 0.017 | 0.001 | 0.026 | 0.019 | 0.001 | 0.048 | 0.017 | 0.001 | 0.042 | 0.032 | 0.022 | 0.055 | |
| 0.14 | 0.134 | 0.018 | 0.150 | 0.147 | 0.008 | 0.337 | 0.156 | 0.009 | 0.222 | 0.240 | 0.203 | 0.274 | ||
| 0.39 | 0.392 | 0.051 | 0.511 | 0.424 | 0.030 | 0.923 | 0.478 | 0.031 | 0.848 | 0.655 | 0.568 | 0.960 | ||
| 0.59 | 0.385 | 0.053 | 0.522 | 0.431 | 0.039 | 0.928 | 0.478 | 0.032 | 0.883 | 0.653 | 0.578 | 1.000 | ||
| 500 | 0.00 | 0.027 | 0.001 | 0.028 | 0.024 | 0.000 | 0.049 | 0.031 | 0.001 | 0.048 | 0.037 | 0.043 | 0.054 | |
| 0.14 | 0.380 | 0.041 | 0.369 | 0.391 | 0.016 | 0.740 | 0.563 | 0.021 | 0.545 | 0.605 | 0.752 | 0.565 | ||
| 0.39 | 0.515 | 0.052 | 0.581 | 0.531 | 0.027 | 1.000 | 0.772 | 0.030 | 0.994 | 0.817 | 0.956 | 1.000 | ||
| 0.59 | 0.515 | 0.046 | 0.590 | 0.525 | 0.032 | 0.999 | 0.777 | 0.036 | 0.995 | 0.823 | 0.947 | 1.000 | ||
Note. Type 1 error rates outside of the robustness interval (i.e., > 0.075) are underlined. Pretest correlation refers to the correlation between M1 and Y1. M2 cross-lag refers to the relation between Y1 and M2. Y2 cross-lag refers to the relation between M1 and Y2.
In addition to the main effects for the difference score, residualized change score, and cross-sectional models, there was also a main effect of pretest correlation on the Type 1 error rates for the residualized change score model. The Type 1 error rates were above the top-end of the robustness interval when the pretest correlation was equal to 0.50 compared to when the pretest correlation was equal to zero. There was also a three-way interaction of pretest correlation by M2 cross-lag by Y2 cross-lag on the Type 1 error rate for the residualized change score model. The Type 1 error rates for the residualized change score model were above the top-end of the robustness interval except when both the M2 cross-lag and the Y2 cross-lag were equal to 0.00.
There were additional main effects of pretest correlation and stability on the Type 1 error rates for the cross-sectional model. Although there was not a three-way interaction of pretest correlation by M2 cross-lag by Y2 cross-lag there was however a three-way interaction of sample size by M2 cross-lag by Y2 cross-lag on Type 1 error rates for the cross-sectional score model. The pattern of results for the Type 1 error rates for the cross-sectional model were similar to the pattern of results for the difference score model but with generally higher values of Type 1 errors.
Relative Bias and Confidence Interval Coverage Results
There were no significant predictors of relative bias for either the ANCOVA, difference score, or residualized change score model. Therefore, the relative bias for these models is not presented here. Because the confidence interval coverage results for the cross-sectional model were nearly identical to the relative bias results for the crosssectional model, only the relative bias results are presented but the coverage results are available upon request. There were main effects of true value of the Mediated Effect , pretest correlation , M2 cross-lag , and Y2 cross-lag on the relative bias for the cross-sectional model. Relative bias was outside the boundaries (≤ −0.10 or ≥ 0.10) for the cross-sectional models as the true value of the mediated effect decreased and when either the pretest correlation, M2 cross-lag, or the Y2 cross-lag was equal to 0.50. There was an additional main effect of stability on the relative bias of the cross-sectional model, a two-way interaction of true value of the mediated effect by stability and a two-way interaction of true value of the mediated effect by Y2 cross-lag (see Figures 3 – 4). The relative bias of the cross-sectional model was quite substantial for all conditions (relative bias > .4) except when pretest correlation, M2 cross-lag, and Y2 cross-lag were all equal to zero.
Figure 3.
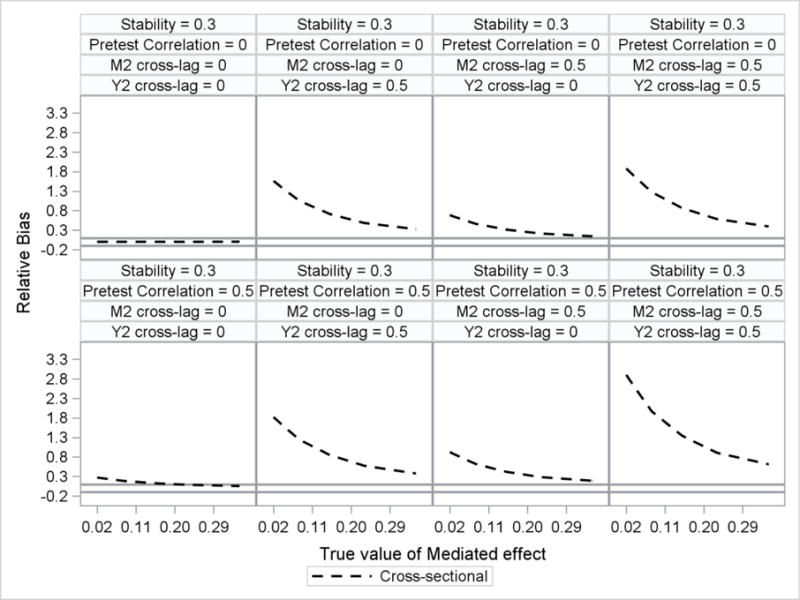
Relative bias of the mediated effect for the cross-sectional model plotted by the true value of the mediated effect. Reference lines are included at values of −0.10 and +0.10 to illustrate boundaries of acceptable relative bias. The top row contains results for pretest correlation equal to zero and stability equal to 0.30. The bottom row contains results for pretest correlation equal to 0.50 and stability equal to 0.30.
Figure 4.
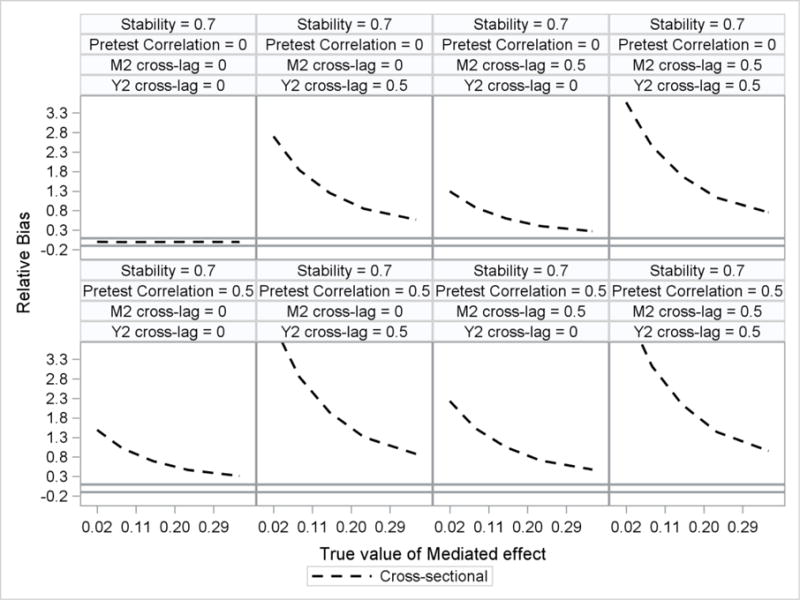
Relative bias of the mediated effect for the cross-sectional model plotted by the true value of the mediated effect. Reference lines are included at values of −0.10 and +0.10 to illustrate boundaries of acceptable relative bias. The top row contains results for pretest correlation equal to zero and stability equal to 0.70. The bottom row contains results for pretest correlation equal to 0.50 and stability equal to 0.70.
Power Results
For every model there was a significant true value of the mediated effect by sample size two-way interaction and main effects of sample size and true value of the mediated effect on the power to detect the mediated effect. There were no additional predictors of power for the ANCOVA model or for the cross-sectional model (see Figure 5). The power to detect the mediated effect for both the ANCOVA model and the cross-sectional model were very similar. Power to detect the mediated effect was greater than 0.80 for each sample size for medium to large true values of the mediated effect and was greater than 0.80 for all true values of the mediated effect when the sample size was equal to 500. When sample size was 50, 100, or 200, the cross-sectional model had more power to detect the mediated effect than the ANCOVA model for small to medium true values of the mediated effect. This difference went away when the sample size was equal to 500.
Figure 5.
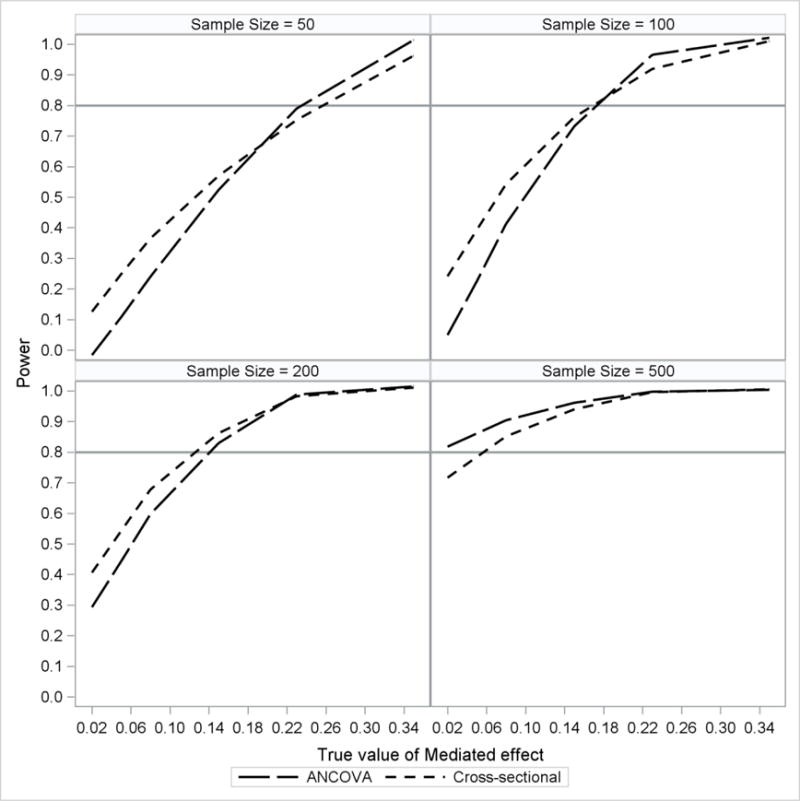
Power to detect the mediated effect for the ANCOVA model and the crosssectional model plotted by sample size and true value of the mediated effect. ANCOVA results are represented by the long dashed line. Cross-sectional results are represented by the short dashed line. A reference line was included at 0.80 to illustrate a nominal boundary of statistical power.
In addition to the main effects of sample size and true value of the mediated effect, there were main effects of stability and Y2 cross-lag on the power to detect the mediated effect with the difference score model. Power for the difference score model was lower when either stability was equal to 0.30 compared to 0.70 or Y2 cross-lag was equal to 0.50 compared to zero. There was also a three-way interaction of pretest correlation by stability by Y2 cross-lag and a three-way interaction of true value of the mediated effect by stability by Y2 cross-lag for the power of the difference score model. Power was lowest when stability was equal to 0.30, pretest correlation was equal to 0.50, and when the Y2 cross-lag was equal to 0.50 (see Figure 6).
Figure 6.
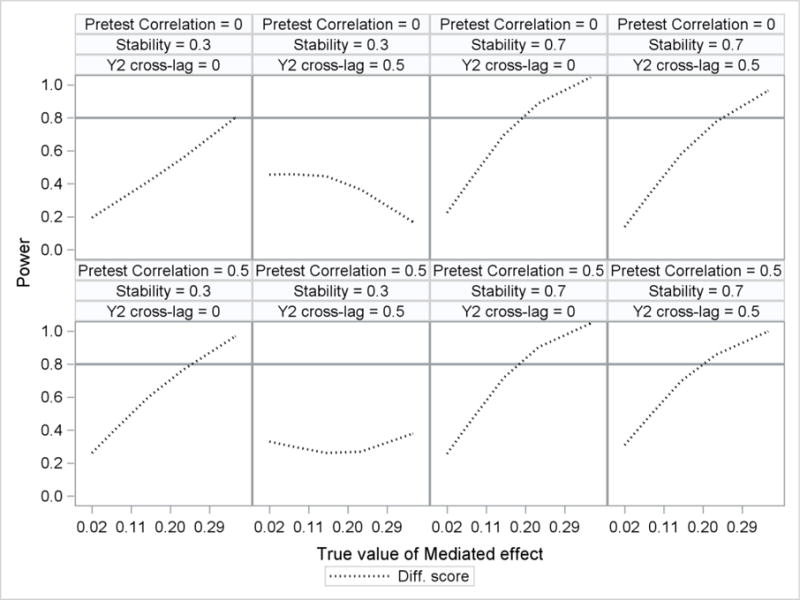
Power to detect the mediated effect for the difference score model plotted by true value of the mediated effect. A reference line was included at 0.80 to illustrate a nominal boundary of statistical power. The top row contains results for pretest correlation equal to zero. The bottom row contains results for pretest correlation equal to 0.50.
For the residualized change score model, in addition to the main effects of sample size and true value of the mediated effect there were main effects of M2 cross-lag and Y2 cross-lag . Power to detect the mediated effect for the residualized change score model was lower when either the M2 cross-lag or the Y2 cross-lag were equal to 0.50 as compared to when they were equal to zero. There was also a two-way interaction of pretest correlation by M2 cross-lag . Power to detect the mediated effect with the residualized change score model was lowest when the pretest correlation, M2 cross-lag, and Y2 cross-lag were equal to 0.50 (see Figure 7).
Figure 7.
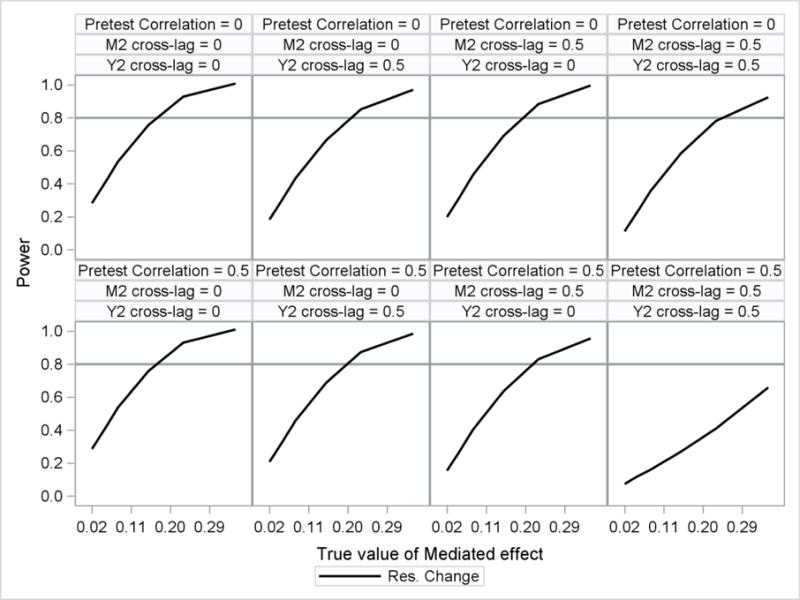
Power to detect the mediated effect for the residualized change score model plotted by true value of the mediated effect. A reference line was included at 0.80 to illustrate a nominal boundary of statistical power. The top row contains results for pretest correlation equal to zero. The bottom row contains results for pretest correlation equal to 0.50.
Summary of Simulation Results
In summary, all models produced an unbiased estimate of the longitudinal mediated effect except for the cross-sectional model, as was expected. The only condition for which the cross-sectional model produced an unbiased estimate of the longitudinal mediated effect was when the pretest correlation and cross-lagged paths were zero. The ANCOVA model was the only model that did not have elevated Type 1 error rates for the case when by2m2 was zero but am2x was greater than zero. The statistical power for the ANCOVA model was unaffected by the predictors in the simulation study and was higher than the cross-sectional model except for a few conditions.
Empirical Example
In order to demonstrate and compare the mediated effect estimates using the LCS specification, we present an empirical example. The data for the empirical example come from the Athletes Training and Learning to Avoid Steroids (ATLAS; Goldberg et al., 1996) study, which was a program designed to reduce high school football players’ use of anabolic steroids by engaging students in healthy nutrition and strength training alternatives. MacKinnon et al. (2001) investigated 12 mediating mechanisms of the ATLAS program on three different outcomes: intentions to use anabolic steroids, nutrition behaviors, and strength training self-efficacy. In the current example, the model tested students’ perception of their high school football team as an information source at posttest as the mediating variable of the ATLAS program on strength training self-efficacy at posttest.
Method
The variables included pretest measures of the mediator, perception of team as information source at pretest (M1) which included items such as “Being on the football team has improved my health” and the outcome, strength training self-efficacy at pretest (Y1) which included items such as “I know how to train with weights to become stronger”. Both the mediator and the outcome were measured immediately after the ATLAS programmed was administered (i.e., units randomly assigned to experimental conditions) and constitute the posttest measures of these variables, respectively (M2 and Y2). There were 1,144 observations used in this example after listwise deletion of the original 1,506 observations. The empirical example is used to demonstrate how to apply the LCS specification and substantive interpretation of model results should be approached with caution.
Results
All models were fitted using Mplus version 7.11 (Muthén & Muthén, 1998–2012) (See Appendix A for Mplus syntax for the latent change score specification of each of these models for a user-specified dataset). Table 3 displays the parameter estimates of the four models that were fitted to the data, relative fit indices, chi-square test of fit, and when applicable, chi-square difference test. Because of the large sample size, most estimates were statistically significant, therefore no discussion of statistical significance is warranted. The mediated effect estimate ranged from 0.181 (SE= 0.032) under the difference score model to 0.254 (SE = 0.037) under the cross-sectional model. The mediated effect estimate under the ANCOVA and residualized change score models were the most similar. The mediated effect estimate under the ANCOVA model was 0.237 (SE= 0.033) and the mediated effect estimate under the residualized change score model was 0.222 (SE = 0.032).
Table 3.
Mediated effect estimates and model fit indices for ANCOVA. Diff Score. Res Change. and Cross-sectional mediation models
| a path | b path | c′ path | Med Effect | Pretest Cov. | Y1 –M2 | M1- Y2 | M Stab | Y Stab | Δχ2 (df) | CFI | RMSEA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANCOVA | 0.572+ (0.063) |
0.415+ (0.035) |
0.131+ (0.054) |
0.237* (0.033) |
0.498+ (0.045) |
0.104+ (0.034) |
−0.061 (0.037) |
0.436+ (0.037) |
0.290+ (0.036) |
N/A | 1.000 | 0.000 |
| Diff Score | 0.538+ (0.071) |
0.337+ (0.041) |
0.353+ (0.068) |
0.181* (0.032) |
0.498+ (0.045) |
0.000 | 0.000 | 1.000 | 1.000 | 855.026+ (4) |
0.000 | 0.431 |
| Res Change | 0.545+ (0.062) |
0.408+ (0.035) |
0.156+ (0.053) |
0.222* (0.032) |
0.498+ (0.045) |
0.000 | 0.000 | 0.480+ (0.029) |
0.366+ (0.028) |
38.769+ (4) |
0.956 | 0.087 |
| Cross-sec | 0.552+ (0.069) |
0.460+ (0.030) |
0.034 (0.055) |
0.254* (0.037) |
0.498+ (0.045) |
0.000 | 0.000 | 0.000 | 0.000 | 387.234+ (4) |
0.515 | 0.289 |
indicates 0 was not in the percentile bootstrap confidence interval.
indicates p < 0.05
All the chi-square difference tests were statistically significant when comparing the respective models to the ANCOVA model. The residualized change score model performed the best in terms of the relative fit indices (CFI = 0.956, RMSEA = 0.087) although there is room for improvement.
Summary of Empirical Example
There was not sufficient evidence to suggest that the difference score, residualized change score, or the cross-sectional model fit the data better than did the ANCOVA model. That is, each of these models made strict assumptions about stabilities and cross-lagged relations of the pretest-posttest model that were not supported by the data. The residualized change score model had the most similar estimate of the mediated effect as the ANCOVA model which is supported by the fact the estimated stabilities across these models were similar and the cross-lagged relations were not large in magnitude.
Additionally, the mediated effect estimates for the difference score and residualized change score model were both smaller in magnitude than the mediated effect estimate for the ANCOVA model. This supports the simulation results that suggests these models may be underpowered compared to the ANCOVA model when there is some combination of pretest covariance and non-zero cross-lagged paths. The mediated effect estimate for the cross-sectional model was larger in magnitude than the mediated effect estimate for the ANCOVA model, again supporting the simulation results. It is important to note, however, if the pretest covariance or cross-lagged paths were large in magnitude and negative, the opposite pattern of results could occur when comparing the difference score, residualized change score, and cross-sectional mediated effect estimates to the ANCOVA mediated effect estimate.
Discussion
The four models discussed in this article each estimate the mediated effect and each address different questions of change. The ANCOVA and residualized change score models are each base-free measures of change while the difference score model is not a base-free measure of change and the cross-sectional model does not directly address a question of change unless strict assumptions are made (Gollob & Reichardt, 1991). Regardless of these differences, a researcher may be interested in investigating mediation using one or many of the models investigated in this article. Because the difference score, residualized change score, and cross-sectional models were all affected by either the pretest correlation, M2 cross-lag, Y2 cross-lag, or all three, if these models are used it is important for researchers to investigate whether or not these relations exist in their longitudinal mediation model. Using the LCS specification as outlined earlier in this paper, it becomes apparent the relation between these four models for assessing the mediated effect in the pretest – posttest control group design and provides a hierarchy for testing the differences between the difference score, residualized change score, and cross-sectional models and the ANCOVA model based on standard SEM fit indices.
Overall, the ANCOVA model performed the best for estimating the mediated effect in terms of Type 1 error rates, bias, confidence interval coverage, and power. Although the difference score, residualized change score, and cross-sectional models had elevated Type 1 error rates (i.e., a > 0.05) for conditions when the b path was zero but the a path varied, this may not be problematic from a substantive perspective. Recall the focus of this article was to investigate the mediated effect in the pretest-posttest control group design which consists of pretest measures of the mediating variable and the dependent variable, an experimental manipulation, and posttest measures of the mediating variable and the dependent variable. Typically when mediation hypotheses are tested and the independent variable is an experimental manipulation like in the pretest – posttest control group design, the experimental manipulation is designed to affect the outcome through the mediating variable because evidence exists a priori that suggests the mediator and outcome variable are related.
This framework for assessing mediation is referred to as mediation for design and within this framework mediating variables are typically chosen prior to the experiment because these mediating variables are related to the outcome (i.e., they are correlated; MacKinnon, 2008). Using this framework, it is unlikely either the relation between the mediating variable and the dependent variable at pretest (i.e., the pretest correlation) is equal to zero, or the relation between the mediating variable and the dependent variable at posttest (i.e., the b path) is equal to zero. Therefore, it is important to emphasize the simulation conditions where the pretest relation of mediating and dependent variables at baseline was zero, but the relation at posttest was nonzero would be unlikely situations with real data and it is not surprising that the difference score, residualized change score, and cross-sectional models were less accurate in these conditions. The by2m2 path in the ANCOVA model is a function of the pretest correlation, cross-lagged paths, and the effects of the experimental manipulation on both the mediator (am2x) and the outcome (cy2x). Therefore, it is very unlikely that the by2m2 path estimated with the difference score, residualized change score, or cross-sectional models will be zero when any of combination of these paths are non-zero.
The power to detect the mediated effect for the difference score, residualized change score, and cross-sectional models were all affected by the factors outlined above in the model comparisons section. When the assumptions of these models (i.e., assumptions about stabilities and cross-lagged paths) did not hold, the power to detect the mediated effect decreased whereas the power to detect the mediated effect with the ANCOVA and cross-sectional models did not decrease as a function of these factors. Additionally, the reason the power to detect the mediated effect with the cross-sectional model was as high as or higher than the power to detect the mediated effect with the ANCOVA model in some conditions was that the cross-sectional model estimate was positively biased across many conditions. It is a note of caution to use the difference score, residualized change score, and cross-sectional models to estimate the mediated effect because of the sometimes implausible assumptions they make regarding the relation of pretest measures to posttest measures.
Assumptions for Identification of Causal Mediated Effects
VanderWeele and Vansteelandt (2009) have outlined four assumptions necessary for the identification of causal mediated effects (see Imai, Keele, & Yamamoto, 2010 and Pearl, 2014, for alternate assumptions regarding identification of causal mediated effects). Assumptions 1 and 3 are with regard to there being no unmeasured confounders of the X and M relation and no unmeasured confounders of the X and Y relation given pretreatment covariates. These assumptions are generally satisfied with successful randomization of units to the treatment groups. Assumptions 2 and 4 are with regard to the M and Y relation. These assumptions are that there are no unmeasured confounders of the M to Y relation given pretreatment covariates and no unmeasured confounders of the M to Y relation that are affected by X (Assumption 4 can be replaced by a no XM interaction assumption).
The pretest-posttest control group design is particularly well suited for estimating causal mediated effects because it will satisfy Assumptions 1 and 3 because X is randomized and potentially satisfy Assumption 2 and 4 assuming there are no time varying covariates. One of the benefits of adjusting for pretest scores is that when an adjustment on pretest scores is done, any time invariant confounders of the pretest scores will be adjusted for as a consequence of adjusting for the pretest scores themselves. Subsequently, if there are any time invariant covariates (i.e., stable individual differences) such as genetic background, the treatment will not be able to affect these time invariant covariates thus making Assumption 4 plausible. If any of these assumptions are violated or not plausible, however, the mediated effect estimate will not be interpretable as a causal effect. That is, there will be non-causal associations between X and Y2 adjusting for M2 rendering the mediated effect a function of some causal effect of X on Y2 through M2 and some non-causal associations.
Sensitivity analyses are an option for assessing both the potential effects of unmeasured confounders of the M2 – Y2 relation and the potential effects of a pretest correlation, cross-lagged paths, or varying stability if only cross-sectional data are available. Similar to how sensitivity analyses are performed to assess the potential effects of unmeasured confounders on the M to Y relation in the single mediator model (Cox, et al., 2014; Imai, et al., 2010; Mauro, 1990; VanderWeele, 2010), sensitivity analyses can be used to assess the potential effect of an unmeasured pretest correlation between M and Y, unmeasured cross-lagged relations, and varying effects of unmeasured stability of M and Y. This can be done following Gollob and Reichardt (1991) by fitting the analysis of covariance model in this article and assessing the impact of incremental changes in the fixed values of the pretest correlation, cross-lags, or stability on mediated effect estimates(SAS syntax is available to carry out this sensitivity analysis upon request from the first author).
Implications
Researchers can apply several different models when assessing the mediated effect in the pretest – posttest control group design including the cross-sectional model, the difference score model, the residualized change score model, and ANCOVA. These models can all be estimated using the LCS specification as described in this paper and the non-ANCOVA models can be compared to the ANCOVA model using standard SEM fit indices.
Given the findings of this study, when researchers use the cross-sectional model, the difference score model (Jansen et al., 2012; MacKinnon et al., 1991), or the residualized change score model (Miller, et al., 2002; Reid & Aiken, 2013) they are making assumptions about the conditions that need to be met regarding the stability of the mediator and outcome and any cross-lagged paths. All four models investigated place different constraints on these quantities. When these constraints are unrealistic, for example, there are cross-lagged paths in the population but these are not modeled in the difference score model, statistical properties of the model will be affected (e.g., Type 1 error or model fit).
As demonstrated with Equations 18 – 20, the difference score model makes a number of assumptions regarding the stability of both the mediator and outcome as well as the cross-lagged paths from pretest to posttest. Assuming the mediator and outcome are related at pretest, the difference score model assumes the stabilities of both the mediator and the outcome are exactly equal to one and it assumes the cross-lagged paths are exactly equal to zero. These are strong assumptions to make because it is unlikely that the stabilities are exactly equal to one and the cross-lagged paths are exactly equal to zero. If the stabilities are close to one and the cross-lagged paths are close to zero, then the difference score model would fit approximately as well as the ANCOVA model and the estimate of the mediated effect across both models would be very similar.
Equations 21 – 23 highlight the difference between the residualized change score model and the ANCOVA model. Assuming the mediator and outcome are related at pretest, the residualized change score model assumes the cross-lagged paths are equal to zero and the stabilities of the mediator and outcome are equal to the simple regression of posttest scores on pretest scores for the mediator and outcome, respectively. The stability of the mediator will not equal the simple regression of the posttest score on the pretest score unless the cross-lagged path from pretest outcome to posttest mediator is zero and the mediator and outcome are not related at pretest. The stability of the outcome will not equal the simple regression of the posttest score on the pretest score unless both the cross-lagged paths are zero and the mediator and outcome are not related at pretest which we already established as being unlikely.
Previous research has explored the limitations of using cross-sectional data to estimate mediated effects (Gollob & Reichardt, 1991; Maxwell & Cole, 2007; Maxwell, et al., 2011). Cross-sectional estimates of mediated effects will often be biased because they do not allow for mediating variables (M) to exert their influence on dependent variables (Y), which presumably occurs over a specific period of time. As time interval varies, so do estimates of mediated effects because estimates of mediated effects depend on the time interval during which they are assessed. This study confirms the general findings of previous literature regarding the bias of the cross-sectional mediated effect as an estimate of a longitudinal mediated effect. The implications of the findings of this study is that there are some conditions for which the cross-sectional estimate of the mediated effect is unbiased (i.e., when there are no cross-lagged relations and when the stabilities are zero, see Equations 24 – 26). These implications build on previous research and provide a more detailed picture of when the cross-sectional model will result in biased estimates of longitudinal mediated effects, how this affects Type 1 error rates, confidence interval coverage, power, and how the cross-sectional model specifically performs when the independent variable, X, represents an experimental manipulation.
Some general results and recommendations can be made based on the simulation results. First, the cross-sectional model performs the worst in terms to Type 1 error and bias. The increased power of the cross-sectional model comes at the cost of a biased estimate of the mediated effect. Second, the difference score model was unbiased and had lower statistical power than the ANCOVA model when the stabilities were low. Although there were some conditions for which the difference score model produced elevated Type 1 error rates, these conditions are not very likely to occur in practice. Third, the residualized change score model was unbiased and had similar power as the ANCOVA model with one exception. When there was a pretest correlation and both cross-lagged paths were non-zero, the power of the residualized change score model was much lower than that of the ANCOVA model. This particular combination of conditions leads to a smaller estimate of the mediated effect than when either one of the cross-lagged paths are present separately (See Equations 21 – 23). The residualized change score model had elevated Type 1 error rates which were highest when the pretest correlation and both cross-lagged paths were present (See Equations 21 – 23) although these conditions may not happen often in practice. Overall, we recommended that researchers use the ANCOVA model to test the mediated effect in the pretest-posttest control group design.
The benefit, however, of some of these models of change, in particular the difference score and residualized change score models is that they reduce the pretest and posttest mediator and dependent variable scores to a single score for M and a single score for Y, respectively, which allows for methods developed for a single mediator and single dependent variable to be easily applied. If researchers use the cross-sectional, difference score, or residualized change score model, they may be inadvertently missing the true mediated effect that is present and they may be reporting biased estimates of the true mediated effect. The LCS specification can be used to compare the non-ANCOVA models to the ANCOVA model and test the assumptions the non-ANCOVA models make regarding the pretest correlation, stabilities, and cross-lagged paths. Using the LCS specification and conducting model comparisons may provide empirical evidence of the adequacy of one of the non-ANCOVA models compared to the ANCOVA model but it is generally recommended that researchers use the ANCOVA model when estimating the mediated effect in this design.
Limitations and Future Directions
Recall, the pretest-posttest control group design involves the random assignment of units to either a treatment or a control group. Successful randomization of units to groups in this experimental design ensures that any pre-existing differences between the units in the treatment and control groups are due to chance and do not reflect systematic differences. In the case of non-randomized or observational studies, adjusting for pretest scores require more careful consideration in order to ensure accurate estimation of treatment effects (Morgan & Winship, 2014). It is known from previous research that ANCOVA and difference score models can lead to very different results regarding change across two-waves of data and represent different theoretical models of change (Jamieson, 1999; Kisbu-Sakarya, et al., 2013; Lord, 1967; Wright, 2006) but further work is needed in order to examine which of the four longitudinal models discussed in this article would perform the best for estimating the mediated effect when systematic preexisting differences exist.
Further, it was assumed the mediator and outcome were measured perfectly at pretest and posttest. Unreliable measures of the mediator and dependent variables can substantially bias estimates of the mediated effect in most cases but the pattern of results can be complicated and even counter-intuitive in some cases (Fritz, Kenny, & MacKinnon, 2016; Hoyle & Kenny, 1999). In general, measurement error in the mediator leads to a reduced mediated effect and consequently an inflated direct effect in the single mediator model with linear relations. With the addition of pretest measures of the mediator and outcome that may not be measured perfectly reliably, the impact of measurement error on the estimate of the mediated effect may be more complicated than in the single mediator model.
It is possible to extend the pretest – posttest control group design to more than two waves of data (e.g., 3 or more waves of data) and have mediation effects across all waves. The addition of more waves of data may complicate the estimation of mediation effects but provides longitudinal estimation of the X to M relation and longitudinal estimation of the M to Y relation (Cole & Maxwell, 2003; MacKinnon, 1994; 2008). That is, all the assumptions and effects regarding stability, timing of effects, and cross-lagged relations across two waves of data will now apply across three or more waves of data. Similar to how the difference score and residualized change score models were used in the pretest – posttest control group design to reduce the number of waves from two to one, these models could be used in a design consisting of three waves of data to reduce the number of waves from 3 to 2.
Finally, the longitudinal models discussed in this project all handled the pretest information on the mediator and dependent variable in different ways (e.g., condition on it or remove it via difference scores). It is possible to handle the pretest information on the mediator and the dependent variable by treating this information as prior information in a Bayesian analysis (Miočević, MacKinnon, & Levy, 2015) or by using new methods derived from the potential outcomes framework for causal inference (MacKinnon & Valente, 2015). These are promising areas for bolstering the precision and causal interpretation of mediated effect estimates, respectively.
The pretest-posttest control design improves on cross-sectional mediation analysis by generating information on the relation of a randomized experiment on the change in M and the change in Y. This article provided insight into the best model to estimate the mediated effect in this design and how the mediated effect estimates of the difference score, residualized change score, and cross-sectional models relate to the mediated effect estimate of the ANCOVA model and the assumptions each model makes in doing so. Additional research is needed on this simple longitudinal mediation model following the now extensive work done for the cross-sectional mediation model. Ultimately, if researchers are planning future pretest-posttest research designs with mediating variables, the ANCOVA model should be used to estimate the mediated effect.
Acknowledgments
The authors would like to acknowledge Leona Aiken, Craig Enders, and Stephen West for their invaluable feedback on the ideas presented in this manuscript.
This research was supported in part by the National Institute on Drug Abuse grant number R37 DA09757.
Appendix A
This Appendix contains the Mplus syntax used to estimate the ANCOVA, difference score, residualized change score, and cross-sectional models using the latent change score specification. All syntax is annotated. The percentile bootstrap procedure is used to test the significance of the mediated effect across all four models.
Mplus Syntax for ANCOVA Model
TITLE: Two wave ANCOVA;
DATA: FILE=;
VARIABLE:
NAMES =
id x m1 m2 y1 y2;
IDVARIABLE=id;
USEVAR = x m1 m2 y1 y2;
ANALYSIS:
estimator=ml;
type=general;
bootstrap=1000;
MODEL:
!Defining change in M as a function of M1 and M2;
deltam BY m2@1;
deltam;
[deltam];
m2 on m1@1;
m2 with m1@0;
m2@0;
[m2@0 m1];
!Defining the change is Y as a function of Y1 and Y2;
deltay BY y2@1;
deltay;
[deltay];
y2 on y1@1;
y2 with y1@0;
y2@0;
[y2@0 y1];
!Estimating the Pretest correlation between M1 and Y1 and Variance of X;
m1 with y1;
!Regression of change in M on X and pretest measures;
!The inclusion of pretest measures makes this equivalent to ANCOVA;
deltam on x (am2x)
m1(sm1) !Labeling the stability of M for use in Model constraints;
y1;
!Regression of change in Y on X, change in M, and pretest measures;
!The inclusion of pretest measures makes this equivalent to ANCOVA;
deltay on x
deltam (by2m2) !Labeling path of change in M on change in Y for use in Model Constraints;
m1(b) !Labeling the path of pretest M on change in Y for use in Model constraints;
y1(sy1); !Labeling the stability of Y for use in Model constraints;
Model constraint:
NEW(sm,sy,by2m1,med); !Making constraints to match estimates to ANCOVA;
sm=sm1+1; !Estimate of effect of M1 on M2 in ANCOVA;
sy=sy1+1; !Estimate of effect of Y1 on Y2 in ANCOVA;
by2m1=b-by2m2; !Estimate of effect of M1 on Y2 in ANCOVA;
med=am2x*by2m2; !Estimate of mediated effect;
OUTPUT: SAMPSTAT STANDARDIZED CINTERVAL(Bootstrap) TECH1 TECH4;
Mplus Syntax for difference score Model
TITLE: Two wave diff score;
DATA: FILE=;
VARIABLE:
NAMES =
id x m1 m2 y1 y2;
IDVARIABLE=id;
USEVAR = x m1 m2 y1 y2;
ANALYSIS:
estimator=ml;
type=general;
bootstrap=1000;
MODEL:
!Defining change in M as a function of M1 and M2;
deltam BY m2@1;
deltam;
[deltam];
m2 on m1@1;
m2 with m1@0;
m2@0;
[m2@0 m1];
!Defining the change is Y as a function of Y1 and Y2;
deltay BY y2@1;
deltay;
[deltay];
y2 on y1@1;
y2 with y1@0;
y2@0;
[y2@0 y1];
m1 with y1;
!Regression of change in M on X;
deltam on x (a);
!Regression of change in Y on change in M and X;
deltay on x
deltam (b);
Model constraint:
NEW(med); !Making constraints to match estimates to ANCOVA;
med=a*b; !Estimate of mediated effect;
OUTPUT: SAMPSTAT STANDARDIZED CINTERVAL(BOOTSTRAP) TECH1;
Mplus Syntax for simple regression of posttest scores on pretest scores for use in the residualized change score Model
TITLE: Two wave res score simple prediction;
!Use this model to get the estimates of the simple regression of M2 on M1 and;
!the simple regression of Y2 on Y1 for use in the residualized change score model;
DATA: FILE=;
VARIABLE:
NAMES =
id x m1 m2 y1 y2;
IDVARIABLE=id;
USEVAR = m1 m2 y1 y2;
ANALYSIS:
estimator=ml;
type=general;
MODEL:
deltam BY m2@1;
deltam@0;
[deltam];
m2 on m1;
m2;
[m2@0 m1];
deltay BY y2@1;
deltay@0;
[deltay];
y2 on y1;
y2;
[y2@0 y1];
m2 with y2@0;
m1 with y1; m1 with deltam@0;
m1 with deltay @0;
y1 with deltam@0;
y1 with deltay @0;
deltay with deltam@0;
OUTPUT: SAMPSTAT STANDARDIZED TECH1 TECH3;
Mplus Syntax for residualized change score Model
TITLE: Two wave res score;
DATA: FILE=;
VARIABLE:
NAMES =
id x m1 m2 y1 y2;
IDVARIABLE=id;
USEVAR = x m1 m2 y1 y2;
ANALYSIS:
estimator=ml;
type=general;
bootstrap=1000;
MODEL:
deltam BY m2@1;
deltam;
[deltam];
!@0.189 is the estimate of the simple regression of M2 on M1;
m2 on m1@0.189;
m2 with m1@0;
m2@0;
[m2@0 m1];
deltay BY y2@1;
deltay;
[deltay];
!@0.418 is the estimate of the simple regression of Y2 on Y1;
y2 on y1@0.418;
y2 with y1@0;
y2@0;
[y2@0 y1];
!Regressing Mchange on X. Equivalent to Res change;
deltam on x (a);
!Regressing Ychange on Mchange and X. Equivalent to Res change;
deltay on x
deltam (b);
m1 with y1;
Model constraint:
NEW(med);
med=a*b; !Estimate of mediated effect;
OUTPUT: SAMPSTAT STANDARDIZED CINTERVAL(BOOTSTRAP) TECH1;
Mplus Syntax for cross-sectional Model
TITLE: Two wave cross;
DATA: FILE=;
VARIABLE:
NAMES =
id x m1 m2 y1 y2;
IDVARIABLE=id;
USEVAR = x m1 m2 y1 y2;
ANALYSIS:
estimator=ml;
type=general;
bootstrap=1000;
MODEL:
deltam BY m2@1;
deltam;
[deltam];
!Constraining the stability of M to 0;
m2 on m1@0;
m2 with m1@0;
m2@0;
[m2@0 m1];
deltay BY y2@1;
deltay;
[deltay];
!Constraining the stability of Y to 0;
y2 on y1@0;
y2 with y1@0;
y2@0;
[y2@0 y1];
!Regressing Ychange on Mchange and X. Equivalent to Cross model;
deltam on x (a);
!Regressing Ychange on Mchange and X. Equivalent to Cross model;
deltay on x
deltam (b);
!The pretest correlation only affects the fit.
m1 with y1;
Model constraint:
NEW(med);
med=a*b; !Estimate of mediated effect;
OUTPUT: SAMPSTAT STANDARDIZED CINTERVAL(BOOTSTRAP) TECH1;
Footnotes
Additionally, an ANCOVA model could be fitted that constrains either the bm2y1 or by2m1 or both to zero. These constraints can be made and the fit of these alternative models can be compared to the saturated ANCOVA model. If a model with either or both of these paths constrained to zero fit the data well, the following difference score, residualized change score, and cross-sectional models can be compared to this unsaturated ANCOVA model as opposed to the saturated ANCOVA model.
References
- Bonate PL. Analysis of pretest-posttest designs. Boca Raton, FL: CRC Press; 2000. [Google Scholar]
- Bradley JV. Robustness? British Journal of Mathematical and Statistical Psychology. 1978;31(2):144–152. doi: 10.1111/j.2044-8317.1978.tb00587.x. [DOI] [PubMed] [Google Scholar]
- Campbell DT, Kenny DA. A primer on regression artifacts. New York, NY: Guilford Press; 1999. [Google Scholar]
- Cheong J, MacKinnon DP, Khoo ST. Investigation of mediational processes using parallel process latent growth curve modeling. Structural Equation Modeling. 2003;10(2):238–262. doi: 10.1207/S15328007SEM1002_5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung MW. Comparison of approaches to constructing confidence intervals for mediating effects using structural equation models. Structural Equation Modeling. 2007;14(2):227–246. [Google Scholar]
- Cheung MW. Comparison of methods for constructing confidence intervals of standardized indirect effects. Behavior Research Methods. 2009;41(2):425–438. doi: 10.3758/BRM.41.2.425. [DOI] [PubMed] [Google Scholar]
- Clark KA. The phantom menace: Omitted variable bias in econometric research. Conflict Management and Peace Science. 2005;22:341–353. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112(4):558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Cox MG, Kisbu-Sakarya Y, Miočević M, MacKinnon DP. Sensitivity plots for confounder bias in the single mediator model. Evaluation Review. 2013;37(5):405–431. doi: 10.1177/0193841X14524576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cronbach LJ, Furby L. How we should measure “change”: Or should we? Psychological Bulletin. 1970;74(1):68–80. [Google Scholar]
- Dwyer JH. Statistical models for the social and behavioral sciences. New York, NY: Oxford University Press; 1983. [Google Scholar]
- Flora DB, Curran PJ. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological Methods. 2004;9(4):466–491. doi: 10.1037/1082-989X.9.4.466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz MS. An exponential decay model for mediation. Prevention Science. 2014;15(5):611–622. doi: 10.1007/s11121-013-0390-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritz MS, Kenny DA, MacKinnon DP. The opposing effects of simultaneously ignoring measurement error and omitting confounders in a single mediator model. Multivariate Behavioral Research. 2016 doi: 10.1080/00273171.2016.1224154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg L, Elliot D, Clarke GN, MacKinnon DP, Moe E, Zoref L, Lapin A. Effects of a multidimensional anabolic steroid prevention intervention: The Adolescents Training and Learning to Avoid Steroids (ATLAS) Program. JAMA. 1996;276(19):1555–1562. [PubMed] [Google Scholar]
- Gollob HF, Reichardt CS. Best Methods for the Analysis of Change: Recent Advances, Unanswered Questions, Future Directions. American Psychological Association; Washington, DC: 1991. Interpreting and estimating indirect effects assuming time lags really matter. doi: http://dx.doi.org/10.1037/10099-015. [Google Scholar]
- Hanushek EA, Jackson JE. Statistical methods for the social scientists. New York, NY: Academic Press; 1977. [Google Scholar]
- Hoyle RH, Kenny DA. Sample size, reliability, and tests of statistical mediation. Statistical Strategies for Small Sample Research. 1999;1:195–222. [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010;15(4):309. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science. 2010;25(1):51–71. [Google Scholar]
- James LR. The unmeasured variables problem in path analysis. Journal of Applied Psychology. 1980;65(4):415–421. [Google Scholar]
- Jamieson J. Dealing with baseline differences: Two principles and two dilemmas. International Journal of Psychophysiology. 1999;31(2):155–161. doi: 10.1016/s0167-8760(98)00048-8. [DOI] [PubMed] [Google Scholar]
- Jang H, Kim EJ, Reeve J. Longitudinal test of self-determination theory’s motivation mediation model in a naturally occurring classroom context. Journal of Educational Psychology. 2012;104(4):1175–1188. [Google Scholar]
- Jansen BRJ, Louwerse J, Straatemeier M, Van d V, Klinkenberg S, Van d M The influence of experiencing success in math on math anxiety, perceived math competence, and math performance. Learning and Individual Differences. 2013;24:190–197. [Google Scholar]
- Jo B. Causal inference in randomized experiments with mediational processes. Psychological Methods. 2008;13(4):314–336. doi: 10.1037/a0014207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo B, Stuart EA, MacKinnon DP, Vinokur AD. The use of propensity scores in mediation analysis. Multivariate Behavioral Research. 2011;46(3):425–452. doi: 10.1080/00273171.2011.576624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judd CM, Kenny DA. Estimating the effects of social interventions. New York, NY: Cambridge University Press; 1981. [Google Scholar]
- Kisbu-Sakarya Y, MacKinnon DP, Aiken LS. A monte carlo comparison study of the power of the analysis of covariance, simple difference, and residual change scores in testing two-wave data. Educational and Psychological Measurement. 2013;73(1):47–62. doi: 10.1177/0013164412450574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer HC, Stice E, Kazdin A, Offord D, Kupfer D. How do risk factors work together? mediators, moderators, and independent, overlapping, and proxy risk factors. The American Journal of Psychiatry. 2001;158(6):848–856. doi: 10.1176/appi.ajp.158.6.848. [DOI] [PubMed] [Google Scholar]
- Laird N. Further comparative analyses of pretest-posttest research designs. The American Statistician. 1983;37(4a):329–330. [Google Scholar]
- Lazarsfeld PF. Interpretation of statistical relations as a research operation. In: Lazarsfeld PF, Rosenburg M, editors. The language of social research: A reader in the methodology of social research. Glencoe, IL: Free Press; 1955. pp. 115–125. [Google Scholar]
- Lord FM. A paradox in the interpretation of group comparisons. Psychological Bulletin. 1967;68(5):304–305. doi: 10.1037/h0025105. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP. Analysis of mediating variables in prevention and intervention research. In: Cazares A, Beatty LA, editors. Scientific methods for prevention/intervention research. Washington DC: U. S. Department of Health and Human Services; 1994. pp. 127–153. (NIDA Research Monograph Series 139, DHHS). Pub 94–3631. [PubMed] [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Mahwah, NJ: Lawrence Erlbaum Associates; 2008. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17(2):144–158. [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PRODLIN. Behavior Research Methods. 2007;39(3):384–389. doi: 10.3758/bf03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Goldberg L, Clarke GN, Elliot DL, Cheong J, Lapin A, Moe EL, Krull JL. Mediating mechanisms in a program to reduce intentions to use anabolic steroids and improve exercise self-efficacy and dietary behavior. Prevention Science. 2001;2(1):15–28. doi: 10.1023/a:1010082828000. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP, Johnson CA, Pentz MA, Dwyer JH, Hansen WB, Flay BR, Wang EY. Mediating mechanisms in a school-based drug prevention program: First-year effects of the midwestern prevention project. Health Psychology. 1991;10(3):164–172. doi: 10.1037//0278-6133.10.3.164. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7(1):83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivariate Behavioral Research. 2004;39(1):99–128. doi: 10.1207/s15327906mbr3901_4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Pirlott AG. Statistical approaches for enhancing causal interpretation of the M to Y relation in mediation analysis. Personality and Social Psychology Review. 2015;19(1):30–43. doi: 10.1177/1088868314542878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Valente MJ. Causal Mediation Approaches for the Pretest-Posttest Control Group Design in Prevention Research. Presentation at the 23rd annual meeting of the Society for Prevention Research; Washington, DC. 2015. May, [Google Scholar]
- MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivariate Behavioral Research. 1995;30(1):41–62. doi: 10.1207/s15327906mbr3001_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauro R. Understanding L. O. V. E. (left out variables error): A method for estimating the effects of omitted variables. Psychological Bulletin. 1990;108(2):314–329. [Google Scholar]
- Maxwell SE, Cole DA. Bias in cross-sectional analyses of longitudinal mediation. Psychological Methods. 2007;12(1):23–44. doi: 10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- Maxwell SE, Cole DA, Mitchell MA. Bias in cross-sectional analyses of longitudinal mediation: Partial and complete mediation under an autoregressive model. Multivariate Behavioral Research. 2011;46(5):816–841. doi: 10.1080/00273171.2011.606716. [DOI] [PubMed] [Google Scholar]
- Maxwell SE, Delaney HD. Designing experiments and analyzing data: A model comparison perspective. 2nd. MahWah, NJ: Lawrence Erlbaum Associates; 2004. [Google Scholar]
- Maxwell SE, Delaney HD, Manheimer JM. ANOVA of residuals and ANCOVA: Correcting an illusion by using model comparisons and graphs. Journal of Educational and Behavioral Statistics. 1985;10(3):197–209. [Google Scholar]
- McArdle JJ. A latent difference score approach to longitudinal dynamic structure analysis. In: Cudeck R, du Toit S, Sorbom D, editors. Structural equation modeling: Present and future A Festschrift in honor of Karl Jöreskog. Washington, DC: American Psychological Association; 2001. pp. 341–380. [Google Scholar]
- McArdle JJ. Latent variable modeling of differences and changes with longitudinal data. Annual Review of Psychology. 2009;60:577–605. doi: 10.1146/annurev.psych.60.110707.163612. [DOI] [PubMed] [Google Scholar]
- Miller YD, Trost SG, Brown WJ. Mediators of physical activity behavior change among women with young children. American Journal of Preventive Medicine. 2002;23(2):98–103. doi: 10.1016/s0749-3797(02)00484-1. [DOI] [PubMed] [Google Scholar]
- Miočević M, MacKinnon DP, Levy R. Bayesian Longitudinal Mediation for Stable Processes. Poster presented at O-Bayes workshop; Valencia, Spain. 2015. Jun, [Google Scholar]
- Morgan SL, Winship C. Counterfactuals and causal inference. New York, NY: Cambridge University Press; 2014. [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. Seventh. Los Angeles, CA: Muthén & Muthén; 1998–2012. [Google Scholar]
- Pearl J. Interpretation and identification of causal mediation. Psychological Methods. 2014;19(4):459–481. doi: 10.1037/a0036434. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Kelley K. Effect size measures for mediation models: Quantitative strategies for communicating indirect effects. Psychological Methods. 2011;16(2):93–115. doi: 10.1037/a0022658. [DOI] [PubMed] [Google Scholar]
- Reid AE, Aiken LS. Correcting injunctive norm misperceptions motivates behavior change: A randomized controlled sun protection intervention. Health Psychology. 2013;32(5):551–560. doi: 10.1037/a0028140. [DOI] [PubMed] [Google Scholar]
- Rogosa D. Myths about longitudinal research. In: Schaie KW, Campbell RT, Meredith W, editors. Methodological issues in aging research. New York, NY: Springer Publishing Co; 1988. pp. 171–209. [Google Scholar]
- Schmiege SJ, Broaddus MR, Levin M, Bryan AD. Randomized trial of group interventions to reduce HIV/STD risk and change theoretical mediators among detained adolescents. Journal of Consulting and Clinical Psychology. 2009;77(1):38–50. doi: 10.1037/a0014513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadish WR, Cook TD, Campbell DT. Experimental and quasiexperimental designs for generalized causal inference. Boston, MA: Houghton, Mifflin and Company; 2002. [Google Scholar]
- Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: New procedures and recommendations. Psychological Methods. 2002;7(4):422–445. [PubMed] [Google Scholar]
- Sobel ME. Effect analysis and causation in linear structural equation models. Psychometrika. 1990;55(3):495–515. [Google Scholar]
- Tein J, Sandler IN, MacKinnon DP, Wolchik SA. How did it work? who did it work for? mediation in the context of a moderated prevention effect for children of divorce. Journal of Consulting and Clinical Psychology. 2004;72(4):617–624. doi: 10.1037/0022-006X.72.4.617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valente MJ, Gonzalez O, Miočević M, MacKinnon DP. A note on testing mediated effects in structural equation models: Reconciliing past and current research of the test of joint significance. Educational and Psychological Measurement. 2016;76(6):889–911. doi: 10.1177/0013164415618992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valeri L, VanderWeele TJ. Mediation analysis allowing for exposure-mediator interactions and causal interpretation: Theoretical assumptions and implementation with SAS and SPSS macros. Psychological Methods. 2013;18(2):137–150. doi: 10.1037/a0031034. http://dx.doi.org/10.1037/a0031034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Breukelen GJP. ANCOVA versus change from baseline: More power in randomized studies, more bias in nonrandomized studies. Journal of Clinical Epidemiology. 2006;59(9):920–925. doi: 10.1016/j.jclinepi.2006.02.007. [DOI] [PubMed] [Google Scholar]
- Van Breukelen GJP. ANCOVA versus CHANGE from baseline in nonrandomized studies: The difference. Multivariate Behavioral Research. 2013;48(6):895–922. doi: 10.1080/00273171.2013.831743. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology (Cambridge, Mass) 2010;21(4):540–551. doi: 10.1097/EDE.0b013e3181df191c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T, Vansteelandt S. Conceptual issues concerning mediation, interventions and composition. Statistics and its Interface. 2009;2(4):457–468. [Google Scholar]
- Wen Z, Fan X. Monotonicity of effect sizes: Questioning kappa-squared as mediation effect size measure. Psychological Methods. 2015;20(2):193–203. doi: 10.1037/met0000029. [DOI] [PubMed] [Google Scholar]
- Wright DB. Comparing groups in a before-after design: When t test and ANCOVA produce different results. British Journal of Educational Psychology. 2006;76(3):663–675. doi: 10.1348/000709905X52210. [DOI] [PubMed] [Google Scholar]


