Brownian ratchet mechanisms of ParA-mediated partitioning

The faithful segregation of DNA, coordinated with cell division, assures genetic inheritance for all organisms. Bacteria are single-celled organisms that lack nuclei. Bacterial genomic DNA is condensed along with associated proteins into a nucleoid structure. Many bacterial strains also carry plasmids, which are autonomously replicating and segregating DNA entities. Chromosome segregation via a mitotic spindle apparatus has been established in eukaryotes. In prokaryotes, however, the mechanisms governing the partition of genetic material remain under debate. For high-copy-number small plasmids, random diffusion is sufficient to ensure both daughter cells inherit at least one plasmid copy following cell division. However, for most low-copy-number large plasmids and bacterial chromosomes, active partitioning is required. Active partitioning is predominantly carried out by a conserved tripartite partition system comprising a ParA-type ATPase, its stimulator protein ParB, and a centromere-like site, parS, on the plasmid or the chromosome, to which ParB specifically binds. Many key aspects of the biochemistry of ParA-type systems have been experimentally defined (1), but the underlying operational principle for this important DNA segregation machinery remains largely unknown. Defining the inner workings of ParA-mediated partition will not only shed light on the general mechanism of chromosome segregation, but also bridge the gap in our understanding of how evolution shapes these key processes throughout all kingdoms of life.

Recent progress in in vitro reconstitution experiments (2–4), in parallel with super-resolution microscopy approaches (5, 6), have provided new mechanistic insights into the inner workings of ParA-mediated partitioning that challenge established filament-based models. Collectively, these experiments show that, in contrast to eukaryotic mitosis, ParA-type partition machinery drives the directed movement of DNA without the formation of filamentous structures. These studies have converged upon a new proposal in which ParA-type partitioning is driven by a Brownian ratchet-driven motility even though the precise mechanistic underpinnings of these ratchet models remains under debate. In this short essay, we provide an overview of the ParA-mediated Brownian ratchets and compare the different implementations of this general framework that have recently been proposed.

1. What is a Brownian ratchet?

Without delving into the rigor of thermodynamics and statistical physics (7–9), let us illustrate the concept of a Brownian ratchet via an intuitive example that demonstrates how useful work can be extracted from thermal fluctuations. Here, we borrow from the seminal paper by George Oster and colleagues (10). Consider a particle diffusing in one dimension that is divided into intervals. Suppose that each boundary of these intervals is a “ratchet”. That is, the particle can pass freely through a boundary from the left, but it cannot go back once having passed the boundary. Due to the irreversibility imposed by the ratchet, the diffusing particle undergoes direct movement to the right, even if the particle intrinsically diffuses in both directions. Directed motion certainly requires the input of energy; but rather than directly powering a “power stroke” per se, the input of energy can serve to establish the ratchets and thereby rectify Brownian motion to produce biased motion. Importantly, this does not violate thermodynamics, but provides an alternative mechanism of generating directed motion commonly found in, or proposed for, many motor proteins (e.g., (11–13)). As you see from the above picture, ratcheting requires two essential conditions: an environmental asymmetry that itself requires energy input and dictates the direction of motion, and random diffusion of the object that “rides” on this asymmetry, perpetuating the directed movement.

2. Common features shared by ParA-mediated burnt-bridge Brownian ratchets

The conceptual underpinning of different ParA-mediated Brownian ratchet models, including the “DNA-relay model” (6), “hitch-hiking model” (5), and our mechanochemical coupling-mediated Brownian ratchet model (3, 4, 14–16), is essentially the same. All three can be considered as burnt-bridge Brownian ratchets, as originally proposed in (3, 4, 15). The movement of the ParB-bound cargo “burns the ParA bridge”, creating a path of no return and establishing the requisite environmental asymmetry. More specifically, cargo-bound ParB binds to and stimulates the ATPase activity of DNA-bound ParA, which triggers the dissociation of ParA from the DNA substrate surface. The slow rate of dissociated ParA resetting its DNA-binding capability maintains a ParA-depleted zone behind the moving cargo (17). Restricted diffusion of ParA dimers on the DNA substrate due to inter-segmental transfer, or “hopping”, also plays a role in the delayed rebinding behind the cargo (2, 18). The asymmetric ParA distribution, either pre-existing or resulting from cargo movement, perpetuates the forward movement of the cargo.

There are two interpretations of the action driven by this asymmetric ParA distribution, reflecting two aspects of the same coin. From the perspective of energy, this asymmetric ParA distribution presents an effective chemical potential gradient for the ParB–bound cargo. As proposed by our original ParA-mediated Brownian ratchet model (3, 4, 15), this free energy gradient results in a so-called “chemophoresis” force (energy descent/distance) (19) that could direct the cargo movement (3, 4, 15). From the standpoint of chemical bonds, this asymmetric distribution of the ParA–ParB bonds bridging the cargo with the substrate provides a net force that pulls the cargo forward (6, 14, 16). Regardless of the mode of driving force, all the ParA-mediated Brownian ratchet models agree that the asymmetric ParA distribution is necessary for directed and persistent cargo movement (3–6, 14–16), as originally proposed (3, 4, 15). The differences among these models lie in the details concerning exactly how this asymmetry in ParA distribution emerges and is harnessed to drive directed cargo movements, the dimensionality over which ratcheting takes place, and the effect of ParA-ParB bonds on the diffusive mobility of the cargo. These differences matter when it comes to understanding the mechanism of ParA-mediated partitioning and the exact role of the players involved. We will dedicate the rest of the essay to explain these differences (Figure 1 and Table 1).

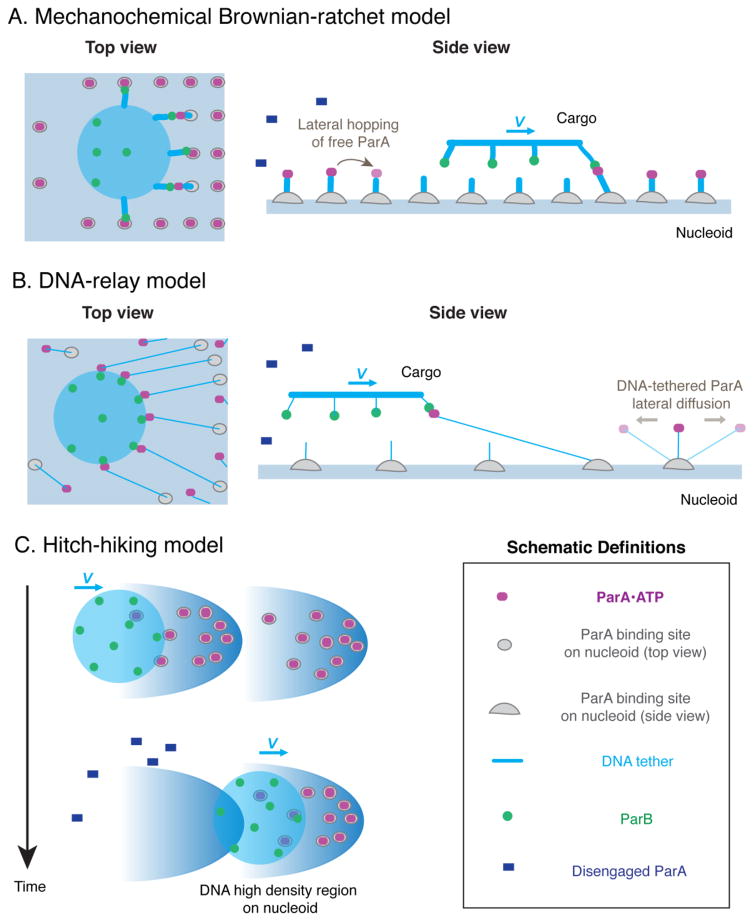
Figure 1.

Schematic comparisons between different Brownian ratchet models for the ParA-mediated partition mechanism. (A). Mechanochemical Brownian ratchet model. (B) DNA-relay model. (C) Hitch-hiking model. For (A) and (B), the thickness of the DNA tether qualitatively scales with the stiffness of the spring. For (C), ParA molecules assemble in small patches in high DNA density regions within the nucleoid, and the partition complex is suggested to move to these high-density regions through a biased Brownian motion.

Table 1.

Comparisons between different ParA-mediated Brownian ratchet models

	Mechanochemical Brownian ratchet	DNA-relay model	Hitch-hiking model
Originally proposed cargo	Plasmid	Chromosome	Plasmid and chromosome
Proposed substrate	Nucleoid	Nucleoid	Nucleoid
Substrate dimension	2D (*)	2D (*)	>2D
Does it entail the time-delay for ParA rebinding?	Yes	Yes	Yes
Does it invoke ParA-ParB bond elasticity?	Yes	Yes	N/A
Does it describe the intrinsic cargo diffusion?	Yes	No	N/A
Does bond tethering quench cargo diffusion?	Yes	No	N/A
Does the DNA-tethered ParA diffuse extensively?	No	Yes	No
Can the ParA without being bound to DNA laterally diffuse along nucleoid?	Yes	No	Yes
Does it require pre-existing ParA gradient?	No	Yes	N/A

^(*)Although both the mechanochemical Brownian ratchet model and the DNA-relay model were originally designated for a cargo moving on a two-dimensional substrate, it remains to be tested whether and how they support directed and persistent movement along substrates of higher dimensionality.

3. Differences among ParA-mediated Brownian ratchet models

Both the mechanochemical Brownian ratchet model (14, 16) and the DNA-relay model (6) invoke chemical bond-mediated tethering to exert mechanical forces that direct persistent movement. The chemical bond herein refers to DNA-ParA-ParB-cargo linkage, which, for brevity, we refer as a ParA-ParB bond thereafter. Thermal fluctuation renders each newly formed DNA-ParA-ParB-cargo bond in a pre-stretched state, thus “loading the spring”. There are more bonds forming at the front than at the rear of the moving cargo because of the ParA depletion zone in the cargo’s wake. Overall, the loaded springs drive the cargo forward, and keep it moving in the same direction.

The key difference between these two models hinges on the exact mechanistic role of the chemical bond-based tethering, which embodies the fundamental mechanochemical nature of ParA-ParB interaction, much of which is still unknown. In perspective, every biological process must harness chemical energy to do useful mechanical work. The coupling between mechanics and chemistry dictates function. There are two important realizations that apply to almost every cellular process. First, because long-range electrostatic interaction is largely screened out in the high-salt environment inside a cell, pair-wise interaction is always short-ranged, which is essentially a physical contact in nature. Second, the cytoplasm is highly viscous and is thus in low-Reynolds-number limit. That is, the moment that the cargo loses contact with a tether, i.e., the chemical bond bridging the cargo to the substrate breaks, the momentum of the cargo drops to zero almost immediately. As such, inertia is negligibly small compared to the viscous drag. To drive the motion of the cargo, the partition machine must be in contact with the cargo at all times. This physical contact reciprocally introduces the effects of tethering, i.e., the chemical bonding provides an effective additional viscous drag in addition to the driving force. A reasonable estimate for the effective additional viscous drag coefficient can be obtained from the bond elasticity multiplied by the bond lifetime. It is a generic property of any chemical bond. In this sense, one expects the apparent diffusive motion of the cargo to be quenched for chemical bond-directed movement, and hence is slower than the intrinsic diffusion of the cargo.

In our mechanochemical Brownian ratchet model, tethering and driving are by default two inseparable aspects of the same ParA-ParB bond (Figure 1A). In connection with our original proposals (3, 4, 15), this model shows that the free energy gradient arising from the asymmetric ParA distribution presents an interesting two-dimensional energy landscape (14). On one hand, the energy potential descends in the forward direction of the moving cargo, providing a forward driving force, akin to the proposed chemophoresis force (3, 4, 15, 19). On the other hand, the energy potential ascends in the traverse directions, presenting an energy barrier that quenches the intrinsic lateral diffusive motion of the cargo. That is, the chemical bond-mediated tethering not only drives forward movement of the cargo, but also quenches its diffusive motion in orthogonal directions (14), thus yielding remarkably directed and persistent movement as observed in experiments (3).

In contrast, the DNA-relay model, which was developed for the chromosome partition system of C. crescentus, the role of the ParA-ParB bond is only to drive cargo movement (Figure 1B), rather than both driving directed and persistent movement and simultaneously quenching the lateral diffusions as that in the mechanochemical Brownian ratchet model. Instead, the DNA-relay model simply takes the apparent diffusion constant of the cargo as the intrinsic diffusion constant (6). Conceptually, this is problematic, because it essentially conflates the effect of bond tethering while artificially diminishing the effect of diffusion on Brownian ratcheting-mediated directed movements. Certainly, the quenching of cargo diffusion due to bond tethering hinges on bond elasticity: If the bond tether stiffness is insufficient to quench cargo diffusion, as assumed in the DNA-relay model, then it will be equally incapable of maintaining directed and persistent cargo movement. The corresponding movement trajectories would be much more diffusive (6), as opposed to relatively straight lines (3, 14, 16).

On the other hand, the same DNA tether associates with ParA dimers in the DNA-relay model. For the resulting DNA-tethered ParA dimers, which is essential for the “relay”, their lateral diffusion constant is assumed to be ~ 0.01 μm²/sec at the time resolution of 1 millisecond (6), or measured to be ~ 0.001 μm²/sec (18). If the DNA tether in the DNA-relay model is too weak to impact the intrinsic diffusive mobility of its cargo, i.e., the chromosome loci, then it will not quench the lateral diffusion constant of the ParA dimer, as the ParA dimer is much smaller in size and hence more diffusive than chromosome loci. However, experiments from the same group of researchers show that the intrinsic diffusion of ParA dimers, while not binding to DNA, is ~ 3 μm²/sec (18); 300 – 3000 fold faster than that of the DNA-tethered ParA dimers (6, 18). This suggests that the DNA tether is in fact much more stiffer than that assumed in the DNA-relay model, and can effectively quench cargo diffusion, as predicted in the mechanochemical Brownian ratchet model (14, 16). Alternatively, this inconsistency within the DNA-relay model itself might point to some unknown mechanisms of DNA-ParA interactions, which will be interesting to explore in the future.

Moreover, given the soft DNA tether assumed in the DNA-relay model, the DNA-bound ParA dimers can diffuse extensively from their corresponding equilibrium positions (~ 100s nm) (6). Consequently, as the cargo moves forward, it not only leaves behind a ParA-depletion zone, but also attracts and significantly accumulates the DNA-bound ParA dimers from far away to its frontal rim (6) (Figure 1B). In comparison, in the mechanochemical Brownian ratchet model, the ParA lateral diffusion along the nucleoid simply reflects two-dimensional hopping of the molecules that are not tethered by the DNA (16), whereas the DNA-bound ParA dimers – due to the much stiffer DNA tether – are highly localized around equilibrium positions (~ nm) (14, 16). As a result, ParA dimers are not significantly attracted to the rim of the cargo (Figure 1A).

The second difference concerns the identity of the cargo. In both cases (6, 14, 16), the nucleoid is the substrate along which the cargo undergoes ratcheting. The cargo, on the other hand, is a plasmid in the mechanochemical Brownian ratchet model (14, 16), and the chromosome itself in the DNA-relay model (6). In other words, the cargo is also the substrate in the DNA-relay model. It is possible that the intrinsic diffusion of chromosomal loci is slower than typical plasmids. But exactly how the chromosome remodels in response to partition complex movement and how such chromosomal remodeling impacts the diffusion of chromosomal loci remain to be examined. What is certain is that for the purpose of quantitative modeling, the observed apparent diffusion cannot be simply assumed as the intrinsic diffusion of the cargo in the absence of tethering.

A third difference is that a pre-existing ParA concentration gradient is assumed in the DNA-relay model (6). However, ParA diffusion along the DNA matrix is reasonably fast relative to the mobility of the cargo itself (2). Consequently, within minutes, the pre-existing ParA concentration gradient would be smoothed out by diffusion. The ParA concentration gradient would have to be maintained by some additional unspecified process not explicitly described in the DNA-relay model. The ParA concentration gradient in the mechanochemical Brownian ratchet model, on the other hand, arises as a natural consequence of symmetry breaking, wherein ParA is depleted at the trailing end of the cargo.

Arguably, some of these differences between the DNA-relay model and our mechanochemical model might be system-specific. The DNA partition system in C. crescentus might be an atypical case, as it has been shown to function with much fewer ParA molecules inside the cell compared to typical plasmid DNA partition systems (6, 20–22). Furthermore, a uni-polar ParA concentration gradient in C. crescentus is present at the onset of segregation (6). In this system, additional proteins localized to the two poles of the cell appear to orchestrate the partition process. PopZ, localized at the old pole might help hold one of the daughter partition complexes there, whereas TipN localized at the new pole perhaps helps in shaping the ParA concentration gradient, together with ParB molecules concentrated at the partition complex (23). Thus, one daughter partition complex travels from the old pole to the new pole uni-directionally only once prior to cell division.

Putting these distinct features of C. crescentus into perspective, however, we suspect that the ParA-mediated partition machinery in that system might operate in a sub-regime of the general picture predicted by the mechanochemical Brownian ratchet model (14). According to our predictions, fewer ParA–ParB bonds require a much slower diffusion of the cargo to maintain directed and persistent movement (14). But, on a substrate with sparsely and uniformly distributed ParA, it will take a slow-diffusing cargo a long time (if not forever) to break symmetry that sets off the directed movement (14, 16). This “dilemma” necessitates the pre-existing ParA distribution to speed up the partition process in the first place. That is, the somewhat atypical behavior of the partition complex in C. crescentus might be reminiscent of the same mechanochemical Brownian ratchet under a distinct physiological condition. In line with this insight, when ParA is over-expressed, the C. crescentus partition complex exhibits similar oscillatory motion as those typically observed with plasmid partition complexes in other systems (23–26).

The “hitch-hiking” model (5) also posits that depletion of nucleoid-bound ParA by ATP hydrolysis weakens the linkage between the partition complex and the nucleoid, which is coupled to motion of the partition complex. The cargo “hitch-hikes” on high DNA-density regions of the nucleoid, hopping from one such region to another (Figure 1C). Whereas this model incorporates the fact that the DNA density distribution within a nucleoid in vivo is complex, with many local peaks and valleys, it is not immediately clear how non-random, directed cargo motion, or how multiple partition complexes are properly positioned within the context of the proposed model. In this regard, the hitch-hiking model remains a conceptual model; it is no different from a generic Brownian ratchet, which entails simple cargo diffusion and an asymmetric environment. However, it does not invoke ParA-ParB bond elasticity as the mechanical driving force for cargo movement. Until a quantitative model based on the hitch-hiking concept is put forward, it is difficult to make a full comparison with the other two more fully elaborated models.

The data from which the hitch-hiking model was conceived are interesting. Chief among these is the finding that partition complexes move within the interior of the nucleoid, rather than on the surface of the nucleoid as has been assumed based on previous measurements in addition to physical arguments based on the size and translocation rate of the partition complex and the sheer density of the nucleoid itself. One consideration is that while the same Brownian ratchet mechanism will work for mini-partition complexes, the smaller size of the mini-plasmid could allow it to penetrate into the nucleoid, at least partially. Related, the nucleoid is known to be arranged in a collapsed toroid configuration often adopting a helical geometry (27); a geometry that was not resolved in the paper proposing the hitch-hiking model. If partition complexes follow these helical grooves, they may appear to be inside the nucleoid volume even though they are not actually penetrating into the high DNA density regions of the nucleoid. Finally, whereas the super-resolution 3-D SIM approaches used to obtain the three-dimensional distributions of ParB and the nucleoid envelope are powerful and have the potential to reveal hitherto obscured cellular organization and dynamics, they can be plagued by artifacts including those arising from motion during acquisition and anisotropic spatial resolution. Given the novelty of the technique applied to the highly dynamic partitioning process and the counterintuitive findings of this study, additional follow-up confirmatory experiments are needed to settle the important questions raised by this work. Nevertheless, this interesting data beg the question as to how the dimensionality of the substrate influences a Brownian ratchet as elaborated above. For cargo moving along a two-dimensional substrate, the mechanochemical Brownian ratchet model is capable of supporting directed and persistent movement (14, 16). It remains to be tested whether and how the same mechanism plays out in higher dimensions.

4. Future outlook

To properly put these Brownian ratchet models to the test in vivo, one requires more detailed measurements of the biochemistry of ParA-type partition systems, high-resolution data on the spatial and temporal patterns of ParA, and the trajectories of the ParB-associated cargos.

Currently, the biochemical steps involved in ParA ATPase activation by ParB have not been investigated in detail. Whereas some of the reaction rate parameters have been experimentally estimated, many remain unconstrained. Future studies are aimed at establishing useful constraints on the models to better understand these systems and refine the models. In current modeling efforts, diffusional properties of DNA-interacting proteins and DNA sites are typically oversimplified by necessity. Treating these processes with a simple diffusion constant may need to be revised as the experimental data and modeling efforts continue to be refined. Furthermore, the nature of “DNA elasticity” at high DNA concentrations is likely more complex than currently considered in the modeling exercises. Incorporating these considerations in future modeling efforts will help advance our understanding of these complex dynamic systems. Comparison of multiple closely related systems that exhibit significantly different system behaviors will also continue to improve our understanding.

Equally importantly, super-resolution live cell imaging approaches will be invaluable in defining the distributions and dynamics of the partition complex machinery. These super-resolution measurements will provide more detailed spatial-temporal dynamics of ParA, ParB, the nucleoid, and plasmids, which permit distinguishing among different models, and further refining of validated models. Furthermore, it is of great interest to investigate how the ParA-mediated Brownian ratchet plays out in a more realistic geometric setting, and how chromosome remodeling is coupled to plasmid partition as well as its own segregation processes.

In summary, the basics of ParA-mediated Brownian ratcheting of low-copy-number plasmid partition has been firmly established, while the details are still under debate. Synergy between new biochemical characterizations of the ParA-type system and super-resolution microscopy data will help iron out the remaining wrinkles of the mechanistic model. This more refined model will provide a unified mechanism not only for low-copy-number plasmid partitioning but also for chromosome segregation in bacteria.

Highlights.

• Recent investigations have converged upon a new model in which ParA-type partitions as a Brownian ratchet.

• Several models are proposed and all share the same biochemistry of ParA-system; but they differ in mechanical aspects.

• We review the different implementations of the ParA-mediated Brownian ratchets.