Patterned disordered cell motion ensures vertebral column symmetry

Summary

The biomechanics of posterior embryonic growth must be dynamically regulated to ensure bilateral symmetry of the spinal column. Throughout vertebrate trunk elongation, motile mesodermal progenitors undergo an order to disorder transition via EMT and sort symmetrically into the left and right paraxial mesoderm. We combine theoretical modeling of cell migration in a tailbud-like geometry with experimental data analysis to assess the importance of ordered and disordered cell motion. We find that increasing order in cell motion causes a phase transition from symmetric to asymmetric body elongation. In silico and in vivo, overly ordered cell motion converts normal anisotropic fluxes into stable vortices near the posterior tailbud, contributing to asymmetric cell sorting. Thus, disorder is a physical mechanism that ensures the bilateral symmetry of the spinal column. These physical properties of the tissue connect across scales such that patterned disorder at the cellular level leads to the emergence of organism-level order.

eTOC Blurb

Das et al. find that localized disorder in cell motion can function as a central component of a pattern forming mechanism. This disorder is a physical mechanism that ensures the bilateral symmetry of the spinal column. Thus, patterned disorder at the cellular level leads to the emergence of organism-level order.

Introduction

Organisms have evolved precise pattern formation mechanisms to ensure the emergence of the correct species-specific form. In accordance with this pattern, cells born in one location often migrate over long distances, and in the process, changes at the cellular level manifest as physical changes in the local mechanical environment that shape organism morphology. Here, we examine how regulated local disorder in cell motion can function as a central component of a pattern forming mechanism.

Bilaterally symmetric elongation of the trunk is a critical process during vertebrate development as normal spinal column morphology is required for optimal biomechanics and mobility. Trunk elongation involves the collective movement and proliferation of cells within the posterior edge of the embryo in a structure called the tailbud (Kanki and Ho, 1997; Lawton et al., 2013; McMillen and Holley, 2015; Quesada-Hernandez et al., 2010; Steventon et al., 2016; Wilson et al., 2009; Zhang et al., 2008) (Figure 1A, highlighted region). Throughout trunk elongation in the mouse, zebrafish and chick, a subset of prospective mesodermal cells undergo epithelial-to-mesenchymal transition (EMT) joining a pool of disordered mesenchymal progenitors that sort symmetrically into the paraxial mesoderm, which later develops into the skeletal muscle and vertebral column (Goto et al., 2017; Manning and Kimelman, 2015; Ohta et al., 2007; Wilson and Beddington, 1996). In zebrafish, this is a two-step EMT, with the first step regulated by Wnt signaling, and the second step regulated by Fgf signaling (Goto et al., 2017; Manning and Kimelman, 2015).

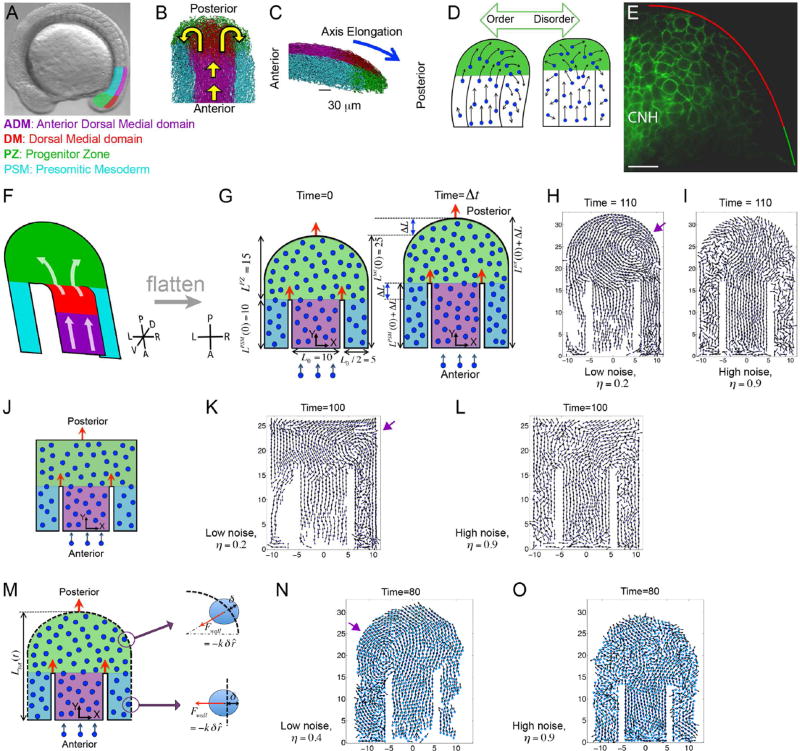
Figure 1. An order to disorder transition in in vivo and in silico tailbuds.

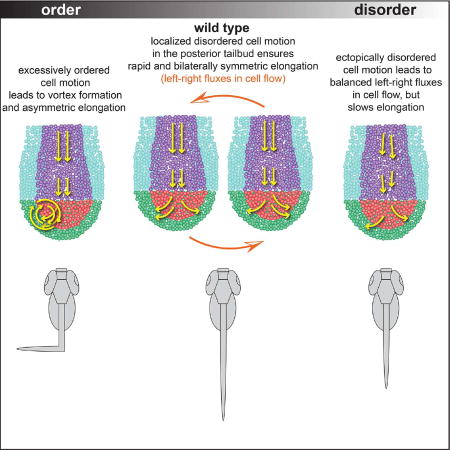
(A) A zebrafish embryo with four tailbud domains highlighted: ADM (magenta), DM (red), PZ (green) and PSM (cyan). (B–C) Dorsal (B) and lateral (C) views of experimental cell tracks within the tailbud. Yellow arrows in B indicate the overall flow direction, while the blue arrow in C denotes the direction of posterior elongation. (D) A schematic posing our hypothesis that overly ordered motion in the PZ breaks axial symmetry. (E) A mid-sagittal view of Cadherin 2-GFP localization along the boundary between the DM and PZ. Anterior is to the left. The chordoneural hinge (CNH) expresses very high levels of Cadherin 2. Posterior to the CNH, Cadherin 2 levels are substantially higher in the DM (red) than in the PZ (green). n= 9 embryos. Scale bar equals 20 microns. (F) The general flow of cells in the tailbud represented as a folded 2D surface. Our computer model is a flattened version of this flow pattern. (G) A diagram of our 2D model involving self-propelled particles within a horseshoe geometry with rigid boundaries. The dimensions reflect the in vivo data, and domains are colored as in panels A-C, but the ADM and DM are merged into a single domain (purple). Left: The tailbud at the initial time t = 0. The widths of the ADM and PSM, and the initial length are shown. Right: The tailbud at a later time Δt. After time Δt, the lengths incrementally increase by an amount ΔL. Orange arrows indicate the posterior movements of the boundaries. New particles are introduced at a fixed rate into the ADM. In simulations (Movie S1), vortices emerge (purple arrow) at low noise (H), and PZ cells sort asymmetrically creating left/right population differences. (I) At high noise cells sort symmetrically. (J) An idealized model of the tailbud with rectangular PZ. (K, L) Snapshots of simulated cell dynamics at low (K) and high noise (L). Note the vortex in K (purple arrow). (M) A variation of our 2D model of tailbud with an elastic outer boundary (dashed lines). (N, O) The elastic forces on a cell penetrating the boundary are shown on the right. Simulation snapshots of the cell dynamics at a low noise (N) and at high noise (O) in the presence of elastic boundaries. Note the vortex in N (purple arrow). The times are in units of 36 in silico iterations. Parameters are specified in Methods. See also Movie S1.

This domain of disordered cell motion is observed in the posterior tailbud of zebrafish and chick (Benazeraf et al., 2010; Delfini et al., 2005; Dray et al., 2013; Kanki and Ho, 1997; Lawton et al., 2013; Mara et al., 2007). Recently, cell-tracking experiments have quantified this motion within the zebrafish tailbud (Dray et al., 2013; Lawton et al., 2013). An ordered stream of cells enters the tailbud through the Anterior Dorsal Medial domain, which will largely contribute to the spinal cord (ADM, Figure 1B and 1C; magenta). The Dorsal Medial zone contains both neural and mesodermal progenitors as well as bipotential neural/mesodermal progenitors (DM, Figure 1B and 1C; red), and prospective mesodermal cells move ventrally into the disordered Progenitor Zone (PZ, Figure 1B and 1C; green)(Martin and Kimelman, 2012; Row et al., 2016). The PZ cells then symmetrically sort into two bilateral columns of the presomitic mesoderm (PSM, Figure 1B and 1C; cyan), which grows posteriorly as cells coalesce with diminishing speed and assemble a Fibronectin matrix on the tissue surface (Fior et al., 2012; Jülich et al., 2015; Jülich et al., 2009).

Conservation of the localized disordered cell motion in the posterior tailbud across vertebrates suggests its maintenance by natural selection and its significance in proper body axis formation. It was proposed that this disordered motion of paraxial mesoderm progenitors aids the synchronization of the segmentation clock (Uriu et al., 2010). Here, we explore the complementary hypothesis that disordered motion in the posterior tailbud is necessary for left-right axial symmetry (Figure 1D). With excessive order, we find that small left-right fluxes in cell flow can become self-sustaining, leading to asymmetric sorting of paraxial mesoderm progenitors and causing axial deformation.

Results

Cadherin 2 turnover at the order to disorder transition

We previously found that cell motion is more disordered in cadherin 2 mutant embryos with the DM being more strongly affected than the PZ (Lawton et al., 2013). To examine Cadherin 2 protein at the DM to PZ transition, we used zebrafish embryos that express a fluorescently tagged Cadherin 2 under the control of the endogenous promoter in a BAC transgene (Revenu et al., 2014). We observed a sharp down-regulation of cell surface Cadherin 2 in the PZ relative to the DM (Figure 1E). In situ hybridization data imply that this regulation of Cadherin 2 is post-transcriptional (Bitzur et al., 1994; Warga and Kane, 2007).

These data indicate that downregulation of Cadherin 2 mediated adhesion during EMT affects the order to disorder transition in the posterior tailbud.

An in silico model of tailbud elongation

To test the hypothesis that disorder helps maintain symmetry, we theoretically model cell migration in a simple horseshoe geometry mimicking a 2D projection of the tailbud (Figure 1F and 1G). The upper part of the horseshoe represents the PZ, the central channel is the ADM and DM, and the two side-arms are the left/right PSM. Following a coarse-grain methodology (Basan et al., 2013; Baskaran and Marchetti, 2009; Bialek et al., 2012; Couzin et al., 2002; Gregoire and Chate, 2004; Szabó et al., 2006; Vicsek and Zafeiris, 2012), we represent cells as self-propelled soft particles that interact via adhesion-repulsion forces and tend to align with the motion of their neighbors.

Our simulations use only the most basic physical parameters to describe cell flow inside the zebrafish tailbud. This model provides a quantitative framework to analyze regulation of motile behavior at the individual cell level using three dimensionless model parameters. Two parameters are the maximum dimensionless adhesive and repulsive forces (F_adh, F_rep ) between cells (see the equations of motion in Methods). Cell adhesion represents cell-cell binding via proteins such as Cadherins. Repulsion represents 'excluded volume' interactions such that two cells cannot occupy the same position in space. High adhesion promotes ordered motion, while high repulsion promotes disordered motion. The third parameter is the variability in the direction of motion of individual cells modeled as 'angular noise' and represented by the dimensionless noise strength η (Gregoire and Chate, 2004; Szabó et al., 2006; Vicsek and Zafeiris, 2012). When η = 0, cells effectively align their motion with their neighbors and ordered motion quickly emerges. At maximum noise (η = 1) the motion is completely random as cells cannot align their motion with the neighboring cells.

We simulated cell motion inside reflecting rigid boundaries starting with closely packed cells and maintained a fixed rate of cell influx through the ADM (Figure 1G; see Methods for details). The dimensions of the 2D tailbud as well as its growth rate, both measured in cell diameters, mirror the in vivo dimensions and elongation rate. We systematically varied η, F_rep and F_adh to explore their impact on the symmetry of trunk elongation.

Effects of overly ordered cell motion in silico

Our simulations showed that at low noise, vortices emerge and significant differences in cell number arise on either side of the axis, indicating left-right symmetry breaking (Figure 1H; Movie S1). In contrast, at high noise, both sides of the PSM populate evenly, and vortices are absent (Figure 1I; Movie S1). Abnormal bending in an elongating trunk could thus originate from asymmetric cell sorting due to excessively ordered cell motion in the posterior tailbud. Changing some details of our model, for example choosing a rectangular geometry for PZ (Figure 1J–1L), or adding an elastic outer boundary instead of a rigid one (Figures 1M–1O; Movie S1) also demonstrated that low noise promotes asymmetry. Hereafter, we focus on the circular PZ geometry with a rigid outer boundary (Figure 1G).

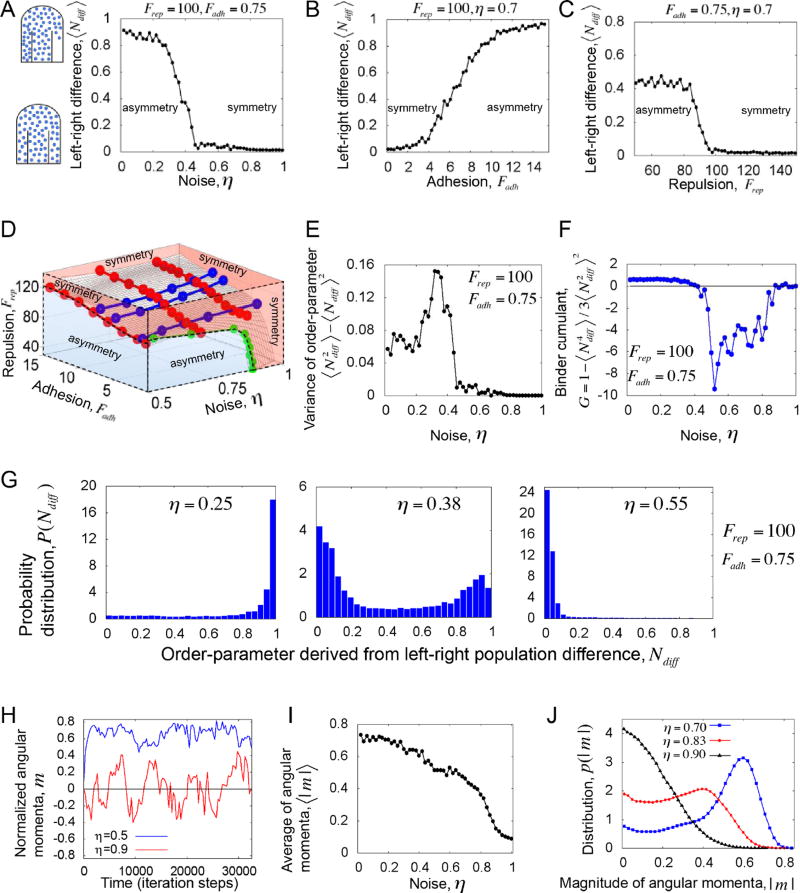
Symmetry breaking generally manifests in a phase transition (see Box 1 for definition of 'phase transition' in this context), where tuning of a parameter dramatically alters the macroscopic state of the system (Vicsek and Zafeiris, 2012). Therefore, we asked if there is a threshold of angular noise that separates the symmetric and asymmetric 'phases' of trunk elongation. We defined an order-parameter, the 'left-right population difference' N_diff (see Box 1 for definition), to quantify the degree of asymmetry in the system. At a high level of noise (η), the order parameter is nearly zero ⟨N_diff⟩ ≈ 0, which signifies bilateral symmetry with equal numbers of cells populating the left and right PSM on average (Figure 2A) (Here, ⟨ ⟩ denotes average). The plots showing the transitions were made by averaging the order-parameter over 100 simulations of growing tailbuds for each parameter value, and over a finite time-window comparable to the developmental timescale (excluding a few initial time-steps). At fixed values of adhesion and repulsion parameters ( F_adh, F_rep ), decreasing noise (η) results in an increase in the order parameter, revealing a sharp transition from symmetry to asymmetry (Figure 2A). Hence, above a threshold noise, cells segregate symmetrically. Next, keeping fixed η and F_rep, we observed a transition from symmetry to asymmetry with increasing adhesion (Figure 2B). At fixed η and F_adh, the system again makes a transition from asymmetry to symmetry with increasing repulsion (Figure 2C). The simulations suggest that the system undergoes a transition from symmetric to asymmetric phases of elongation with increasing order in cell motion, where high noise and high repulsion destroys order, and high adhesion promotes order.

Box 1. Definitions.

Definitions of biophysical concepts

• Ordered and disordered cell motion: Ordered motion means that cells have high degree of directional correlation, i.e. all cells in a group move in the same direction. Disordered motion refers to low directional correlation, where each individual cell moves randomly, independent of its neighbors.

• Symmetric and asymmetric 'phases' of body elongation: In vivo, cells from the medial PZ domain bilaterally sort into the left and right sides of the PSM. This left/right sorting is symmetric for wild-type embryos, i.e. on average a similar number of cells enter both in left and right sides of PSM. This state of elongation is called the 'symmetric phase' of elongation. By contrast, in the 'asymmetric phase' of elongation more cells distribute to either the left or right PSM.

• Phase transition: By phase transition, we specifically refer to the non-equilibrium transition from symmetric to asymmetric phases of elongation, which is effectively tuned by the local order. Since the transition occurs inside the geometry of the tailbud, it is not a 'true' phase transition as found in equilibrium thermodynamic systems of infinite size. This non-equilibrium system has finite size and body elongation is confined to a finite time-window. The transition that we describe bears an essential similarity to 1st order transitions as found in the literature of active matter physics (Chate et al., 2008; Ginelli and Chate, 2010) (see Figure 2E–2G).

Definitions of the in silico and in vivo quantitative metrics

• Left-right population difference: Left-right population difference is a parameter that demarcates the symmetric and asymmetric phases of elongation in our theoretical model. It is defined as N_diff = |N_L –N_R| /(N_L + N_R), where N_L and N_R are the cell numbers in the left and right boxes, respectively (box-size = (L₀ × L₀ /2), see Fig. 1G) inside the PSM. ⟨N_diff⟩ ≈ 0 signifies the bilaterally symmetric phase.

• Average angular momentum per particle: This metric quantifies the leftward and rightward motion in the posterior tailbud. Mathematically it is defined as $\overrightarrow{m}=\sum _{i=1}^N[({\overrightarrow{r}}_i^{\prime }/|{\overrightarrow{r}}_i^{\prime }|)\times ({\overrightarrow{\nu }}_i^{\prime }/|{\overrightarrow{\nu }}_i^{\prime }|)]/N$ summed over all PZ cells about their center of mass (Couzin et al., 2002). Here, ${\overrightarrow{r}}_i^{\prime }={\overrightarrow{r}}_i-{\overrightarrow{R}}_{\mathit{\text{CM}}}^{’}$ and ${\overrightarrow{\nu }}_i^{\prime }={\overrightarrow{\nu }}_i-{\overrightarrow{V}}_{\mathit{\text{CM}}}$ are respectively the positions and velocities of PZ cells relative to the center of mass of the PZ, normalized by their respective magnitudes. In 2 dimensions, m⃗ points perpendicular to the plane of motion (along the Z-axis), i.e. m⃗ = m ẑ(−1≤ m ≤ 1). While in 3 dimensions, m⃗ has three components: the dorsal-ventral component (z-component), the medial-lateral component (y-component) and anterior-posterior component (x-component). We use the z-component as an in vivo metric for symmetric (m_z = 0) and asymmetric (m_z ≠ 0) phases of elongation.

• Alignment angle: For each i-th cell within the PZ, we define the 'alignment angle' as ${\theta }_i={\text{cos}}^{-1}[({\overrightarrow{\nu }}_i/|{\overrightarrow{\nu }}_i|)•({\overrightarrow{V}}_{\mathit{\text{Ri}}}/|{\overrightarrow{V}}_{\mathit{\text{Ri}}}|)]$. Here, i-th cell has a velocity ${\overrightarrow{\nu }}_i$, and the local mean is ${\overrightarrow{V}}_{\mathit{\text{Ri}}}=(\sum _{i=1\in R}^N{\overrightarrow{\nu }}_i)/N$ averaged over the cells (including cell i) that lie within a sphere of radius R centering on cell i. We choose R = 20µm (average cell diameter ~ 10µm), though our results are consistent for different R (Figure S2). Here, θ_i ≈ 0 implies local order.

• Average anterior-posterior velocity per cell: To quantify the motion inside the ADM, we defined the net anterior-posterior velocity (Y-component) per cell as $V_y=\sum _{i=1}^N{({\overrightarrow{\nu }}_i)}_y/N$, where N is the number of cells inside the ADM.

Figure 2. Increasing order leads to a phase transition from symmetric to asymmetric elongation in silico.

We use an order parameter that quantifies the bilaterally symmetric/asymmetric distribution of cells into the left and right PSM. (A) The average order-parameter, left-right population difference ⟨N_diff⟩ plotted versus noise (η) at fixed repulsion and adhesion parameters. (B) ⟨N_diff⟩ plotted versus adhesion F_adh, at fixed noise and repulsion. (C) ⟨N_diff⟩ plotted versus repulsion F_rep, at fixed noise and adhesion. Increasing the model parameters “angular noise” and “repulsion” increases disorder while increasing the model parameter “adhesion” increases order. The simulations show that regardless of the specific parameter that is varied, disordered motion correlates with symmetry and ordered motion correlates with asymmetry. (D) The phase boundaries between the symmetric and asymmetric phases of elongation, which are tuned by three dimensionless parameters (noise, adhesion and repulsion), are organized into a 3D phase diagram. Red lines on the surface correspond to 'constant-noise' contours, the blue lines correspond to 'constant-repulsion' contours, and the green line corresponds to a 'constant-adhesion' contour. (E) The variance of order-parameter versus noise. (F) The Binder cumulant G versus noise. Panels E and F correspond to the transition cure in panel A. The sharp minimum in the Binder cumulant near the transition point implies a 1st order transition. (G) The distribution of the order-parameter across the transition. Left: Below the threshold noise; Middle: around the threshold noise; Right: above the threshold noise. Note that near the transition point the distribution is bimodal showing coexistence of phases, which is a signature of a 1st order transition. (H) The normalized angular momentum per particle m quantifies the leftward (>0) or rightward (<0) bias in cell flow in the posterior tailbud. Time traces of m show that with disordered motion the cell flow switches between leftward and rightward flow (red), but with ordered motion anisotropic flow is persistent (blue). (I) The average angular momentum per particle⟨|m|⟩ decreases with increasing noise. These data indicate that flow approaches symmetry as disorder increases. (J) The probability distribution of angular momentum p(|m|). These data suggest that the system exists in two phases: asymmetric flow (caused by ordered motion) or symmetric flow (caused by disordered motion). In panels H–J the adhesion and repulsion parameters are F_adh = 0.75, F_rep = 30 . Other parameters are specified in Methods.

The phase transitions are sharp, analogous to a 1st order transition in physical systems, which are manifested in a sharp peak and a dip respectively in the variance and cumulant of the order-parameter (Figures 2E–2F; also see Methods for a detailed discussion of the transition behavior ). Thus, away from the transition-boundary there is an entire parameter space, where the axial symmetry can be maintained without fine regulation of parameters. At low noise, the probability distribution of the order-parameter, P(N_diff ) peaks at one, while at high noise P(N_diff ) peaks at zero (Figure 2G). Interestingly, around the transition-point, P(N_diff ) is bimodal, implying phase-coexistence (both N_diff ≈ 0 and N_diff ≈ 1 ), typical of a 1^st order transition (Figure 2G). Though the transitions (Figures 2A–2C) qualitatively represent the same crossover from symmetric to asymmetric phases of elongation, the transition points are nevertheless different. A series of such transition points define the phase boundaries, which are tuned by three dimensionless model parameters (noise, adhesion and repulsion). To examine how the transition depends on these three parameters, in addition to the 1D projections (Figures 2A–2C), we visualized the transition in three-dimensions (Figure 2D). We see that the transition-boundary is a surface that divides the parameter space into symmetric (red) and asymmetric phases (blue). Where the surface is relatively flat the transition primarily depends on two independent combinations of our 3 non-dimensional parameters. The 3D phase diagram provides a quantitative prediction for how the macroscopic state of the elongation depends on individual cellular properties.

We investigated how tissue vortices originate by quantifying the average angular momentum per particle (see Box 1 for mathematical definition) (Couzin et al., 2002). The magnitude of the angular momentum m differentiates between the directions of motion. Specifically, m < 0 and m > 0 indicate clockwise and counterclockwise rotational motion, respectively. When seen from a dorsal perspective, a clockwise rotation is a rightward flow while a counterclockwise rotation is a leftward flow. At low noise, time traces of angular momenta m are almost always nonzero, implying stable leftward or rightward motion (Figure 2H). A vortex will be reflected in a stable nonzero m. At high noise, m has smaller magnitude and frequently crosses zero, indicating no stable rotation in either direction. The continuous sign reversal of m represents left-right turns of cell collectives that are too small to create a vortex throughout the PZ. These small fluxes cancel each other out over time, leading to equal populations of cells sorting to the left and right PSM. The average magnitude of the angular momentum (⟨|m|⟩) also makes a transition with increasing noise (Figure 2I). Correspondingly, the probability distribution of angular momentum p(|m|) changes its form across the transition-point. p(|m|)peaks at a nonzero value at low noise, while at high noise p(|m|) peaks at zero (Figure 2J). These data suggest that normal left-right fluxes in the posterior tailbud are short-lived in a disordered cell motion regime, as the disorder disrupts the directional flow. By contrast, a random left-right flux is stabilized and amplified by highly ordered cell motion. In theory, over an infinite time-scale, a leftward flux would eventually reverse to a rightward flux (or vice versa) even in an ordered cell motion regime. However, over the finite timescale of embryonic body elongation, ordered cell motion would be predicted to produce stable leftward or rightward asymmetry of the axis.

Effects of overly ordered cell motion in vivo

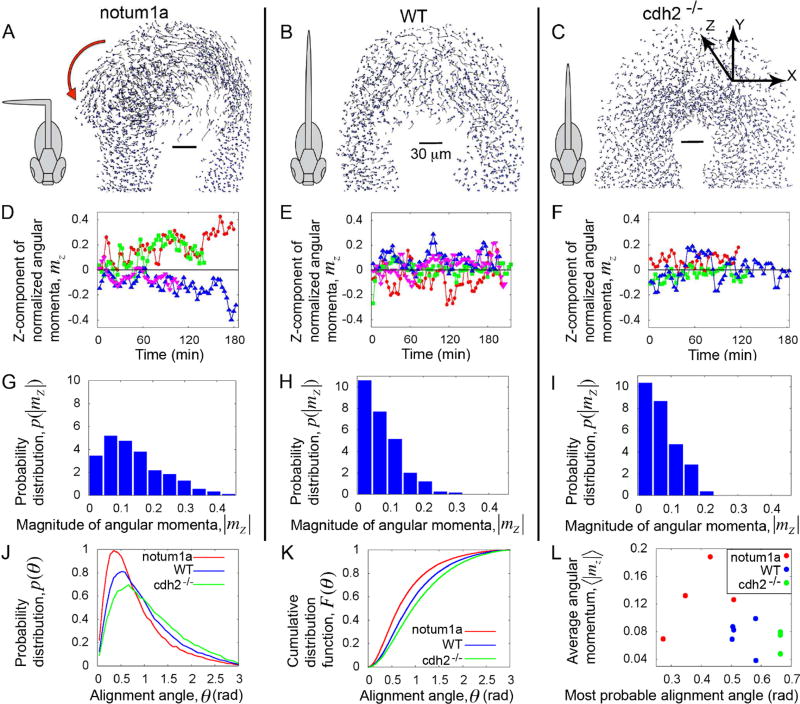
We next tested the theoretical predictions by analyzing published experimental data of in vivo cell motion within the zebrafish tailbud (Dray et al., 2013; Lawton et al., 2013). We compared the datasets in 4 different conditions (Figure 3A–3C): wild type (WT), mutants for the adhesion protein cadherin 2 (cdh2^−/−) and embryos with reduced Fgf signaling (SU5402-treated, Figure S1A–S1F) both of which exhibit stunted elongation, and embryos with reduced Wnt signaling (overexpressing notum1a) which exhibit bent body axes.

Figure 3. Localized disordered cell motion in vivo ensures symmetric elongation.

(A–C) Snapshots of cell-tracking analysis of experimental timelapses (Movie S2) show the cell tracks from the last few time-points. The ADM is omitted for visual clarity. Schematics of the corresponding body phenotypes are shown. Red arrow in A indicates the direction of a swirl. (D–F) Time traces of the Z-components (dorsal-ventral components) of the angular momentum per cell, m_z. (G–I) Probability distributions of angular momenta p(|m_z |). The cell flow in the PZ domain of WT and cdh2^−/− frequently switches between leftward and rightward biases and averaged over time the flow is symmetric. By contrast, the cell flow in the PZ domain of notum1a overexpressing embryos is asymmetric. (J) Probability distributions of the alignment angle, p(θ). (K) Cumulative distribution function F(θ) showing distinct state of cellular order for different phenotypes. These data show that notum1a overexpressing embryos have the most ordered cell motion and that cdh2^−/− is the least ordered. (L) Average z-component of the angular momentum in the PZ versus most probable values of the alignment angle for each individual embryo. Here, the Y-axis is a proxy for increasing asymmetry, and the X-axis represents increasing local disorder in cell motion. All results are based on the data of 5 wild-type embryos (B, E, H), 3 cdh2^−/− mutants (C, F, I) and 4 notum1a overexpressing embryos (A, D, G). These three experimental conditions represent distinct regimes with notum1a overexpressing embryos having ordered cell motion in the PZ and asymmetric cell flow, cdh2^−/− having the most disordered cell motion in the PZ and symmetric cell flow, and wild type having disordered cell motion in the PZ and symmetric cell flow. For further analysis see Figures S1, S2 and Movie S2.

To qualitatively compare our 2D model predictions with 3D in vivo cell motion, we first examined the z-components of the angular momenta m_z (see Box 1), which describe the leftward and rightward fluxes in cell flow in the PZ. The time traces of m_z for notum1a overexpressing embryos are mostly non-zero, while m_z crosses zero more frequently for WT and cdh2^−/− embryos (Figure 3D–3F). Accordingly, for notum1a overexpressing embryos, the probability distribution p(| m_z |) is much broader and peaks at a nonzero m_z (Figure 3G–3I). Similar to our simulation at low noise (Figure 1H and Movie S1), we observed stable vortices in the tailbuds of notum1a overexpressing embryos (Figure 3A and Movie S2). These data correlate with the left or right bending of the body axis in notum1a overexpressing embryos (Figure 3A) (Lawton et al., 2013). By contrast, in WT and cdh2^−/− embryos, p(| m_z |) are narrower and peak at zero, and their body axes are bilaterally symmetric (Figure 3B, 3C, 3H and 3I) (Lawton et al., 2013).

The presence of vortices in the posterior tailbud of notum1a expressing embryos indicates high directional correlation and suggests that their PZ cells will be more ordered than in WT and cdh2^−/− embryos. We quantified the local order of cell motion by measuring how cell velocities are aligned with the local mean of their neighbors. For each i-th cell within the PZ, we define the 'local alignment angle' θ_i, which quantifies the angular deviation of an individual cell velocity from the local average velocity (see Box 1 for mathematical definition). To measure a local average velocity, we needed to define a neighborhood with a radius R around a cell. We show the data for R = 20 µm (average cell diameter ~ 10 µm), though the results are consistent for different values of R (Figure S2). Here, θ_i ≈ 0 implies local order. We plotted the distribution p(θ_i), collecting all θ_i values for each phenotype (Figure 3J). p(θ_i) for notum1a overexpressing embryos is the narrowest distribution with a mode closest to zero (Figure S2C). Hence, we find that cell motion in the notum1a overexpression embryos is more ordered. Similarly, the cumulative distribution function (CDF) F(θ_i) for notum1a overexpressing embryos lies above the other two phenotypes, indicating θ_i~ 0 to be more probable, thus signifying highest local order (Figure 3K and Figure S1E).

The p(θ_i) for cdh2 mutants exhibits the widest distribution (Figure 3J) and the CDF lies below all other phenotypes (Figure 3K), indicating that abrogating cell adhesion reduces order in cell motion. Accordingly, cell flow in the PZ of both WT and cdh2^−/− embryos is bilaterally symmetric, while cell flow in notum1a overexpressing embryos is asymmetric (Figure 3A–3C; Movie S2) (Lawton et al., 2013). This is consistent with our theoretical prediction that diminishing adhesion maintains axial symmetry (Figure 2B).

To explore the relationship between axial symmetry breaking and local order in cell motion, we plotted the average z-component of angular momentum in the PZ, ⟨|m_z|⟩ versus the most probable value of the alignment angle for each embryo, i.e. the mode of the distribution p(θ_i) (see Figure 3L). A high average angular momentum in the PZ signifies a lower degree of symmetry maintenance, while higher most probable values of the alignment angle represents less ordered cell motion. This plot reveals that notum1a overexpressing embryos, WT embryos and cdh2 mutants map to different locations in a phase diagram. Thus, these three experimental conditions represent three different regimes in the phase diagram defined by the local order of cell motion in the posterior tailbud and the global state of bilateral symmetry. notum1a overexpressing embryos cluster towards an asymmetric and ordered cell motion regime, whereas cdh2 mutants cluster around a symmetric and disordered cell motion regime. WT embryos cluster in an intermediate domain (Figure 3L). All together, the data suggest that trunk elongation is poised near a phase transition from symmetric to asymmetric elongation as a function of the local order of cell motion in the posterior tailbud.

Effects of overly disordered cell motion in silico

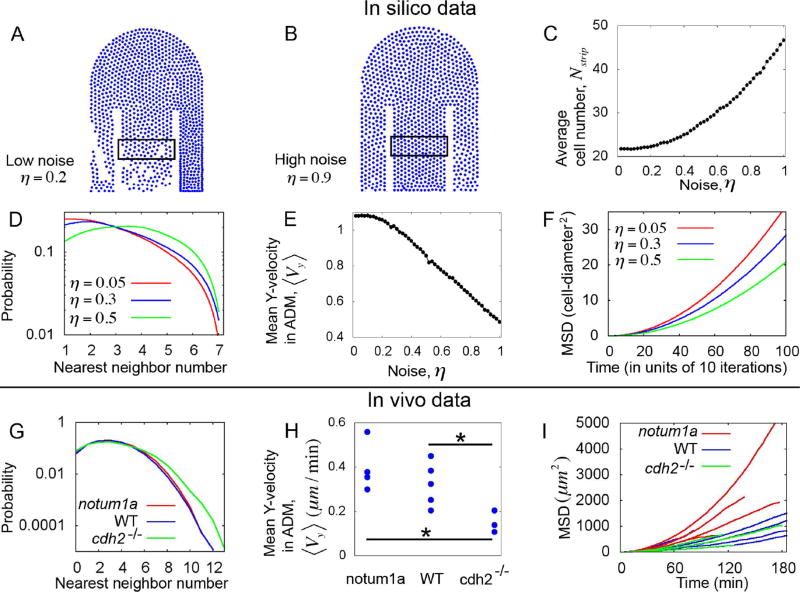
Having observed that too much order in cell motion breaks axial symmetry, we asked if excessive disorder in cell motion entailed any cost. In our simulations, at high directional noise, the cell density inside the ADM becomes higher than at low noise (Figure 4A and 4B). The cell number ( N_strip ) inside a thin strip within the ADM increases with noise, which indicates congested flow (Figure 4C). To further quantify this congestion of flow in the ADM, we counted the number of nearest neighbors for each cell, which is defined as the number of cells that are present within a distance of 1 cell-diameter from a given cell center. The probability distribution of nearest neighbors has more weight towards a large number of neighbors at high noise (Figure 4D). Such an increase in neighbor density in a highly disordered motion regime may slow the posterior flow of cells. Indeed, we found that the net anterior-posterior velocity (Y-component) per cell (defined by $V_y=\sum _{i=1}^N{({\overrightarrow{\nu }}_i)}_y/N$) decreases as noise increases (Figure 4E).

Figure 4. Excessive disorder in cell motion retards elongation.

(A–B) Simulation snapshots showing low cell density within the ADM at low noise (A), and high cell density at high noise (B). We quantified the cell number (N_strip) inside the rectangular strips shown in figures A and B. (C) N_strip increases with noise, indicating congestion. (D) In silico probability distribution of nearest neighbors inside the ADM for different values of noise parameters. (E) Average Y-velocities (posterior-components) per particle within the ADM. ⟨V_y⟩ decreases with increasing noise. (F) Mean square displacement (MSD) versus lag time (as calculated from the simulated tracks inside the ADM) for different values of noise. These simulations indicate that increasing disordered cell motion increases congestion and reduces effective posterior migration. In panels A-F the adhesion and repulsion parameters are F_adh =0.75, F_rep =30, and a fixed rate of cell influx is maintained in the anterior ADM. Other parameters are as specified in the Experimental Procedures. (G) In vivo probability distribution of nearest neighbors for different phenotypes. These data show congestion in cdh2^−/−. (H) Average posterior-components of velocities per cell. ⟨V_y⟩ shows the slowest ADM cell movement in cdh2^−/−. Here, “*” denotes p-value <0.05 (T-test). (I) In vivo MSD (calculated from the cell tracks within the ADM) versus lag-time for each embryo of different phenotypes. These data show that disordered cell motion in the ADM of cdh2^−/− leads to congestion and reduction of posterior cell movement. See also Figure S3.

To better understand this decrease in posterior cell motion at high noise, we calculated the mean square displacement (MSD) of the cells within a fixed box inside the ADM. To calculate the MSD, the displacements were measured with respect to the center-of-mass of the ADM, which is equivalent to subtracting the posterior drift of the ADM cells. The MSD curves have lower slopes at comparatively higher noise (Figure 4F). The MSD curves were fitted with power law functions to infer the nature of the flow and to extract the values of diffusion constants (see Figure S3A, and the corresponding discussion in the Methods). We found that the motion inside the ADM is super-diffusive, and the diffusion constant decreases with increasing noise (Figure S3B). Such a decrease in diffusion constant can be interpreted as an increase of impeded cell motion within a crowded environment (Lappala et al., 2013). In other words, the cells cannot efficiently transit the confined geometry of the ADM when the motion is overly disordered. As a result, the net outflow from the ADM decreases relative to the inflow creating a condition that resembles automobile traffic congestion (Bain et al., 2016). These simulations thus suggest that overly disordered cell motion slows trunk elongation.

The phenomenon of congestion in the narrow 'channel' of the ADM can be intuited by noting that there is a competition between two characteristic timescales: the timescale of cell influx into the channel, and the diffusion timescale of cells through the channel. The influx timescale is the time-interval after which a cell is inserted at the entrance. On the other hand, the diffusion time-scale is the average time taken by an individual cell to reach the other end of the channel (mean first passage time). So, there can be two regimes: a diffusion-dominated regime (when diffusion timescale is greater than influx timescale), and an impediment-dominated regime (when influx timescale is greater than diffusion timescale). The impediment-dominated regime can be achieved in two ways: either by increasing the rate of influx at a fixed state of disorder in cell motion, or by increasing the disorder in motion at a fixed rate of influx. In both these cases, there is a crossover to a congested flow due to the enhanced impediment to cellular motion, which results in a decreasing diffusion constant. In simulations, we maintained a fixed influx rate, but enhanced the state of disorder in the motion by increasing the angular noise to observe the congestion.

Effects of overly disordered cell motion in vivo

We next tested these predictions in vivo. Since cdh2^−/− embryos showed higher disorder than the WT and notum1a overexpressing embryos, we first checked whether the cell flow in the ADM is congested for the cdh2^−/− embryos. We indeed found that the nearest neighbor distribution in the ADM of cdh2 mutants has more weight at higher number of neighbors than WT and notum1a expressing embryos (Figure 4G). The tail of the nearest neighbor distribution for cdh2 mutants is distinct from the other phenotypes. The fraction of cells in the ADM having more than 8 neighbors is higher in cdh2 mutants than other phenotypes. This congestion in cdh2 mutants could be due to changes in the relative levels of order of cell motion and flux into the ADM. In other words, an increase in either disorder or flux into the ADM could cause congestion. We quantified flux in the anterior ADM and found no significant difference in flux in the three experimental conditions (Figure S1H). Thus, the congestion in the cell flow of the ADM of cdh2 mutants is likely due to disordered cell motion.

The in vivo evidence of congestion leads to another prediction of the model; i.e. disordered motion should lead to slower posterior migration in cdh2^−/− embryos (Figure 4E). As in our simulation, we calculated the net anterior-posterior components of velocities per cell ( $V_y=\sum _{i=1}^N{({\overrightarrow{\nu }}_i)}_y/N$) from the in vivo data. We calculated the velocities with respect to the center of mass of the anterior 50 microns of the PSM, which sets the reference frame for this context (Lawton et al., 2013). cdh2^−/− embryos indeed display a significantly lower average ⟨V_y⟩ than the other phenotypes (Figure 4H) and also exhibit stunted body elongation (Harrington et al., 2007; Lawton et al., 2013; Lele et al., 2002). Following the model prediction for MSD (Figure 4F), we then tested whether the cdh2 mutants show higher hindrance in cell flow than notum1a overexpressing embryos, since notum1a overexpressing embryos displayed much higher order in motion than cdh2 mutants (Figure 3J and 3K). We computed the in vivo MSD inside the ADM (with respect to its center of mass) for each embryo, and found that the MSD curves for notum1a embryos generally have higher slopes than the WT and cdh2^−/− embryos (Figure 4I). In fact, the cdh2 mutants displayed significant lower values of the diffusion constant (as obtained by fitting the MSD curves to power-law functions) than WT and notum overexpressing embryos (see Figure S3C–S3E). Altogether, the theory and in vivo data indicate that the trade-off for ectopically disordered cell motion is a decrease in the effective posterior flow of cells and a corresponding slowing of body elongation.

Discussion

Our theoretical study and experimental data analysis demonstrate that localized disordered cell motion in the posterior tailbud ensures an ordered, i.e. linear, spinal column. Importantly the different scales of the system are causally connected. The parameters at the 'microscopic scale' (adhesion, repulsion, noise) tune the local order at the 'mesoscopic scale'. The mesoscopic scale can be thought to be spread over a few cell-diameters. The mesoscopic level of order among neighboring cells further determines the macroscopic effect of symmetry breaking at the level of entire body axis.

An intriguing finding is that elongation appears poised near a phase transition that separates symmetric and asymmetric trunk elongation. The wild-type embryo exhibits short-lived left-right anisotropies that would become a stable asymmetric flow in a more ordered regime. The benefit of operating near this phase transition is that the rate of elongation is maximized while also maintaining symmetry. Wild-type embryos achieve this Goldilocks coupling via localized high order to facilitate rapid elongation and localized low order to maintain bilateral symmetry. Loss of either localized disorder or order may create abnormalities, such as a bilaterally asymmetric body axis as in notum1a overexpressing embryos or retarded body elongation as in cdh2 mutants.

A similar cell flow pattern is common to zebrafish, mice and chick tailbuds: some fraction of prospective mesodermal cells arrive at the posterior tailbud during trunk elongation as an epithelium and undergo EMT (Manning and Kimelman, 2015; Ohta et al., 2007; Wilson and Beddington, 1996). The EMT creates a pool of disorganized mesodermal progenitors in the medial tailbud that then segregate in a bilaterally symmetric manner into the paraxial mesoderm. In zebrafish, Wnt signaling regulates the first step in this EMT (Goto et al., 2017). Thus, over-expression of the Wnt inhibitor notum1a likely increases ordered cell motion by abrogating this EMT. By contrast, since Cadherin 2 levels are normally reduced at the EMT, the cadherin 2 mutant approximates a precocious reduction of order. Our study suggests that a function of the EMT is to create a regulated transition from local intercellular order to disorder to facilitate efficient and bilaterally symmetric vertebrate trunk elongation (Figure S1G). In other words, embryonic patterning creates a localized domain of intercellular disorder that in turn ensures maintenance of organism-level symmetry.

The localized domain of disorder contrasts not only with the ordered influx of cells into the tailbud, but also with the more sessile bilateral columns of paraxial mesoderm that emerge from the tailbud (Benazeraf et al., 2010; Delfini et al., 2005; Dray et al., 2013; Kanki and Ho, 1997; Lawton et al., 2013; Mara et al., 2007). As cells join the posteriorly advancing paraxial mesoderm, they decrease their cell motion and assemble a cortex of extracellular matrix that mechanically couples the paraxial mesoderm to the notochord and overlying epidermis (Dray et al., 2013; Jülich et al., 2015). Based on the cell motion analysis and the observation that the Xenopus paraxial mesoderm stiffens more than the adjacent tissues, we proposed that the assembly of the PSM from the PZ represents a transition from a viscoelastic fluid to a viscoelastic solid (McMillen and Holley, 2015; Zhou et al., 2009). This hypothesis is supported by recent in vivo measurements in zebrafish using oil microdroplets. This study found the PSM is more viscous and has a higher elastic modulus than the PZ (Serwane et al., 2017). Importantly, the solidifying columns of paraxial mesoderm are responsible for advancing the posterior growth of the embryo (Dray et al., 2013; Zhou et al., 2009; Zhou et al., 2010; Zhou et al., 2015). Here, our data indicate that the localized domain of disordered motion in the PZ guides elongation by ensuring bilaterally symmetric sorting of cells into the paraxial mesoderm.

Using only the most basic physical parameters to describe cell flow inside the zebrafish tailbud, our model successfully explains the origin of different phenotypes. In doing so, the model provides a quantitative framework to analyze the relationship between the regulation of motile behavior at the individual cell level, such as adhesion, repulsion (e.g. cytoskeletal contractility) and angular noise (e.g. polarity), and higher-level properties such as rate of elongation and axial symmetry. We find that the decisive switch to disordered motion is mediated in part by a sharp reduction of Cadherin 2 on the cell surface. Future experiments examining other cell adhesion molecules, cell polarity and cytoskeletal tension will determine whether these cell biological properties are regulated at this transition and how these local cell biological processes give rise to tissue biomechanics. For example, quantification of in vivo tissue viscosity found that PZ domain is more fluid in cadherin 2 mutants (Serwane et al., 2017). More broadly, symmetry maintenance entails the cross-scale emergence of organism-level order from regulated disorder at the cellular level.

The model presented here was built to have the minimum possible number of parameters and to focus on the most basic and general aspects of the physics at play during trunk elongation. At the cellular level, the model abstracts out all molecular details into two simple ingredients: an adhesion-repulsion potential and a noisy tendency to align the direction of motion with the neighbors. Another important aspect of the model is the horse-shoe-like epithelial geometry that forces the migrating cells from the DM to sort at the PZ into two PSMs. In our model, we fixed the influx of cells into the anterior ADM since we did not observe any significant difference in this flux among the experimental conditions (Figure S1H). Moreover, the relationship between symmetric and asymmetric elongation and disordered and ordered cell motion, respectively, is maintained in 3D simulations (data not shown).

Our results highlight the need for developing tissues to dynamically control their physical properties to accommodate the ever-changing underlying geometry of the developing embryo. They also demonstrate how the physics of active granular materials imposes general constraints on the process of vertebrate trunk development. An important aspect of such constraints is that they link the microscopic behavior of individual cells to the macroscopic physical properties of the entire tissue. There is a reciprocal relationship in which macroscopic morphological features emerge from local cellular processes, while macroscopic morphology constrains the parameter space within which cellular processes must operate. Indeed, after initial symmetry breaking, morphological asymmetry or left-right displacement of cell signaling domains may stabilize the asymmetry. In summary, these results provide a guide for the future experimental investigation of both the molecular mechanisms that enable the developing embryo to satisfy such physical constraints, as well as how genetic changes alter biomechanics during disease (like scoliosis) and the evolution of new morphologies.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Scott Holley (scott.hollev@yale.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Zebrafish were raised according to standard protocols (Nüsslein-Volhard and Dahm, 2002) and approved by the Yale Institutional Animal Care and Use Committee. The TL wild-type strain was used. The pac^tm101B allele of cdh2 was used (Lele et al., 2002). The Cadherin 2 transgenic line expresses Cdh2-tFT via a BAC transgenic (tg-cdh2:Cdh2-tFT) created using homologous recombination to attach the tFT to the c-terminus of Cadherin 2 (Revenu et al., 2014). Embryos were collected from pair-wise natural matings. Sex-specific data were not collected as zebrafish do not have a strictly genetic sex determination mechanism, and sex is determined after the first 36 hours of development studied here (Wilson et al., 2014). Imaging was performed on 10–12 somite stage embryos. Each embryo examined by timelapse was derived from a distinct mating on different days.

METHOD DETAILS

Confocal Imaging

In this paper, we reanalyzed the published cell tracking data of 5 wild-type embryos, 4 notum1a overexpression embryos, 3 cadherin2 mutants and 3 SU5402-treated embryos (Dray et al., 2013; Lawton et al., 2013). Here, we recap the original experimental methods. One-cell-stage wild-type embryos were injected with nuclear localization signal red fluorescent protein (nlsRFP) mRNA (70 ng/µl) or both nlsRFP (70 ng/µl) and notum1a (100 ng/µl) mRNAs. At the 10–12 somite stage, embryos were mounted in low-melt agarose and imaged using a Zeiss LSM 510 confocal microscope. All time-lapses were taken at 18°C using a Linkam Scientific PE100 stage. Image stacks were taken with an interval of 2.5–3.5 minutes. The experimental datasets were analyzed using Imaris software (Bitplane) to track the 3D motion of nuclei and extract the data of nuclear positions and velocities. The anterior 50 microns of the PSM was used as a reference frame to account for growth and/or shifting of the embryo during the timelapse.

Simulation Methods

The code for the simulations is available at: https://github.com/Dipjyoti-das/zebrafish-cell-motion Based on a study of 2D cell migration by (Szabó et al., 2006), we model each cell, _i, as a self-propelled soft particle with a radius a_i and instantaneous position ${\overrightarrow{r}}_i$, moving in a well-defined direction n̂_i with a constant speed ν₀(Figure 1G). The overdamped dynamics of the ith cell is described by

$$\frac{d{\overrightarrow{r}}_i}{\mathit{\text{dt}}}={\nu }_0{\widehat{n}}_i+\mu \sum _j\overrightarrow{f}({\overrightarrow{r}}_i,{\overrightarrow{r}}_j)$$ (1)

Here, µ is the mobility parameter, and $\overrightarrow{f}({\overrightarrow{r}}_i,{\overrightarrow{r}}_j)$ is an intercellular force between the ith and jth cells. The intercellular force is summed over all the nearest neighbors. Thus, the instantaneous velocity of ith cell ( $d{\overrightarrow{r}}_i/\mathit{\text{dt}}={\dot{\overrightarrow{r}}}_i$) has two parts --- one is the cellular self-propelling velocity ν_on̂_i stemming from an active force, and the other is proportional to the net intercellular force exerted by its neighbors.

To model the emergence of collective order, an 'alignment rule' is assumed for the self-propulsion unit vector n̂_i defined by the angle θ_i with respect to the X-axis (or the medial-lateral axis). The direction of cellular self-propulsion attempts to align itself to the direction of instantaneous velocity ( ${\widehat{\dot{r}}}_i={\dot{\overrightarrow{r}}}_i/|{\dot{\overrightarrow{r}}}_i|$) with a relaxation time τ in response to the net acting force. This is described by

$$\frac{d{\theta }_i}{\mathit{\text{dt}}}=\frac{1}{\tau }{\text{sin}}^{-1}[({\widehat{n}}_i\times {\widehat{\dot{r}}}_i).\widehat{z}]+\overline{\eta }{\xi }_i(t)$$ (2)

Within this framework, the local directional variability of a group of self-propelled particles is commonly modeled in a coarse-grained manner as angular noise (Szabó et al., 2006; Vicsek and Zafeiris, 2012). Here ξ_i(t) is a delta-correlated white noise chosen from a uniform distribution (ξ_i ∊ [−π, π]), and the Z-axis is perpendicular to the plane of motion. η̄ is the strength of the angular noise. It controls the tendency of the individual cell to follow the average direction of its neighbors. When the angular noise strength is η̄ = 0, ordered motion quickly emerges if cell density is large enough. At maximum noise (η̄ = 1) the motion is completely random.

The intercellular force is modeled as a short-ranged and piece-wise linear function of intercellular distance $r_{\mathit{\text{ij}}}=|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j|$. This force is repulsive for distances smaller than R_eq, while attractive for distances R_eq ≤ R_ij ≤ R₀, and zero if cells are farther apart than R₀:

$$\begin{array}{cc}\overrightarrow{f}({\overrightarrow{r}}_i,{\overrightarrow{r}}_j)\hfill & ={\widehat{r}}_{\mathit{\text{ij}}}{f}_{\mathit{\text{rep}}}\frac{(R_{\mathit{\text{eq}}}-r_{\mathit{\text{ij}}})}{R_{\mathit{\text{eq}}}},r_{\mathit{\text{ij}}}<R_{\mathit{\text{eq}}}\hfill \\ \hfill & ={\widehat{r}}_{\mathit{\text{ij}}}{f}_{\mathit{\text{adh}}}\frac{(R_{\mathit{\text{eq}}}-r_{\mathit{\text{ij}}})}{(R_0-R_{\mathit{\text{eq}}})},R_{\mathit{\text{eq}}}\le r_{\mathit{\text{ij}}}\le R_0\hfill \\ \hfill & =0,r_{\mathit{\text{ij}}}>R_0\hfill \end{array}$$

Here, f_rep and f_adh are the maximum repulsive and adhesive forces, and ${\widehat{r}}_{\mathit{\text{ij}}}=({\overrightarrow{r}}_i-{\overrightarrow{r}}_j)/|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j|$. Note that repulsive forces represent 'excluded volume' interactions between cells, as two cells cannot occupy the same position due to their definite volumes. The adhesive forces result from the cell-cell interactions via proteins like Cadherins. We set f_rep >>f_adh to avoid any clustering (or crystallization) of cells (Lawton et al., 2013; Vicsek and Zafeiris, 2012), which was never observed experimentally. The equilibrium distance between two cells is taken to be R_eq = (a_i+ a_j), i.e. sum of the corresponding radii. We assigned the individual cellular radius as a_i ∊[a₀ – δ, a₀ + δ], which are uniformly distributed over an average radius a₀ with δ = 0.05.

We simulated the cell motion by numerically integrating Eqs. (1) and (2) using the Euler method with a time step Δt = 0.005, and assuming a perfectly reflecting boundary condition (rigid boundaries). We start with random initial positions and self-propulsion directions of the cells, which are put together with a high packing fraction (0.95), as cells are closely packed inside the tailbud. The lateral dimension of the horseshoe structure was chosen in order to align with the experimental datasets (see Figure 1G). The ADM is roughly L₀ /2a₀ =N₀ ~12 cells wide, while the width of the PSM is about half of the ADM. Note that L₀ is the width of the ADM and a₀ is the average cell radius.

To make the tailbud grow in time, particles are introduced in the ADM at a constant rate from the lower boundary (Figure 1G). This approximates the posterior flow of cells in the embryo partly due to convergent extension (Roszko et al., 2009; Steventon et al., 2016). We introduce a particle in every (γ/(N₀ν_o Δt)) iteration steps, where γ is a parameter that controls the influx. In response to the increase in cell number, we simultaneously slide the upper curved boundary of PZ and the boundaries between the ADM and PSM in the posterior direction (see the bold red arrows in Figure 1G). The barriers between ADM and PSM represent the extra-cellular matrix (ECM) that progressively forms over time and binds the cells to the epidermis. To estimate the increase in the length of the horseshoe structure we assume that the global cell density is constant, i.e.

$$\frac{N(t)}{A(t)}=\frac{N(t+\mathrm{\Delta }t)}{A(t+\mathrm{\Delta }t)}\mathit{\text{or}},\mathrm{\Delta }A=\mathrm{\Delta }N\frac{A(t)}{N(t)}$$ (3)

Here, N(t) is the total cell number inside the tailbud, and A(t) is the net area of the horseshoe-shaped tailbud at a time t . The increase in area ΔA = A(t + Δt)- A(t) can be calculated from the increase in cell number ΔN = N(t + Δt)−N(t). From Eq. S3, ΔA gives the corresponding length increment ΔL, by which amount the boundaries need to be moved forward, preserving the shape of the horseshoe structure (see Figure 1G). Thus, we increase the length as below:

$$L_{\mathit{\text{tot}}}(t+\mathrm{\Delta }t)=L_{\mathit{\text{tot}}}(t)+\mathrm{\Delta }L,\mathit{\text{ and }}{L}_{\mathit{\text{PSM}}}(t+\mathrm{\Delta }t)=L_{\mathit{\text{PSM}}}(t)+\mathrm{\Delta }L.$$ (4)

Here, L_tot is the overall length and L_PSM is the length of the PSM (Figure 1G). Note that the overall length is L_tot = L_PSM + L_PZ. The length of the PZ, L_PZ is kept fixed; while the length of the PSM, L_PSM increases according to Eqs (3) and (4).

By choosing the unit of time as t̃=t/τ and the unit of length as ${\tilde{\overrightarrow{r}}}_i={\overrightarrow{r}}_i/{\nu }_0\tau$, we can transform the Eqs (1) and (2) into the dimensionless forms:

$$\frac{d{\overrightarrow{\tilde{r}}}_i}{d\tilde{t}}={\widehat{n}}_i+\sum _j\overrightarrow{F}({\tilde{\overrightarrow{r}}}_i,{\tilde{\overrightarrow{r}}}_j)$$ (5)

$$\frac{d{\theta }_i}{d\tilde{t}}={\text{sin}}^{-1}[({\widehat{n}}_i\times {\widehat{\dot{\tilde{r}}}}_i).\widehat{z}]+\eta {\tilde{\xi }}_i(\tilde{t})$$ (6)

Here, dimensionless noise strength is $\eta =\sqrt{\tau }\overline{\eta }$ and dimensionless forces are $\overrightarrow{F}=\mu \overrightarrow{f}/{\nu }_0$. The original white noise ξ_i(t) transforms into ${\tilde{\xi }}_i(\tilde{t})=\sqrt{\tau }{\xi }_i(t/\tau )$. In our model, there are five free parameters after non-dimensionalization: noise strength (η), maximum values of the dimensionless adhesive and repulsive forces (F_adh = µf_adh /ν₀ and F_rep = µf_rep /ν₀), maximum cut-off of the cell-cell interaction (R̃₀), and the influx parameter (γ). Thus, without losing generality we fixed other parameters ν₀ = µ = τ = 1 . In the main text, we varied the basic parameters of interest η, F_adh and F_rep (assuming fixed R̃₀ and γ).

Parameters values

Unless otherwise specified, in the simulation we used L₀ = 10, ν₀ = 1, µ = 1, τ = 1, γ = 1, 2a₀ = 5/6 F_adh = 0.75, F_rep = 30 and R₀ = 1.2 R_eq, consistent with earlier theories (Vicsek and Zafeiris, 2012). We also used the lengths L^PSM(0) = 10, and L^PZ = 15 (Figure 1G). However, our qualitative conclusions are not sensitive to these parameter choices. We systematically varied η, F_rep and F_adh in the main text.

Analysis of phase transition-like behaviors

In the main text, we defined the order-parameter N_diff = N_L−N_R/(N_L+ N_R), where N_L and N_R are respectively the cell numbers within a fixed box in the left and right sides of PSM. The average ⟨N_diff⟩ showed symmetry breaking transitions with the variation of the angular noise η. The variance of order-parameter signifies the response function of the system (analogous to susceptibility) and it showed a sharp peak near the transition point (Figure 2E). To further explore the nature of this phase transition, a well-known technique is the calculation of the Binder cumulant, defined as $G=1-\langle N_{\mathit{\text{diff}}}^4\rangle /3{\langle N_{\mathit{\text{diff}}}^2\rangle }^2$ (Gregoire and Chate, 2004). This ratio of moments was constructed in such a way that it sharply drops to negative values at the threshold of a 1st order transition. We found a sharp minimum in the Binder cumulant (Figure 2F). This minimum in Binder cumulant is due to the simultaneous contribution of two phases (⟨N_diff⟩ ≈ 1 and ⟨N_diff⟩ ≈ 0) coexisting at the 1st order transition point. We indeed found a bimodal distribution of the order-parameter, P(N_diff) which shows the phase coexistence (Figure 2G). Thus, our model shows a 1st order transition within the parameter range studied. A 1st order transition implies a sharp (discontinuous) transition in the limit of a very large system-size. An advantage of such a sharp transition could be that away from the transition boundary there is an entire parameter space where the system can maintain the bilateral symmetry without the need to finely regulate the parameters.

The positions of the minima of the Binder cumulant can be taken as the values of the threshold. Monitoring these threshold parameter values for the transitions, we have also constructed a phase diagram for our model (Figure 2D). This phase diagram indicates the feasible parameter regimes where bilateral symmetry of trunk elongation is maintained.

Different variations of our model

We checked if our predicted phenomenon of the left-right symmetry breaking is robust against different variations of our model. We first idealized a rectangular PZ (Figure 1J). We consistently found that at low noise left-right population difference arises in the PSM and a vortex forms in the PZ (Figure 1K).

Next, we made our existing 2D model more realistic by incorporating two new features. First, we made the external periderm layer elastic instead of rigid (Figure 1M). The boundary cells experience an opposing (radially inward) elastic force ${\overrightarrow{f}}_{\mathit{\text{elastic}}}=-k\delta \widehat{r}$, where k is the elastic constant and δ is the distance by which the cell penetrates within the boundary. Secondly, we made the cellular self-propulsion speed diminishing in the PSM, since experimentally the PSM exhibited much lower average speed than the ADM, DM and PZ (Lawton et al., 2013). We assumed that the self-propulsion speed in the PSM linearly drops in the anterior direction from a value ν₀ to its fraction ν₀/n. The speed inside the PSM is calculated from a function ν_PSM(y) = (ν₀/n) + ν₀[(n–1)/n](y/L_PSM), where L_PSM is the length of the PSM, and we used n = 4. The speed is ν₀, if the cell is outside of the PSM. We further constructed a different mechanism to grow the tailbud in time. We no longer assumed the global cell density to be constant; rather we increased the length in response to the total force exerted by the posterior boundary cells along the +Y axis. Note that the force exerted by the cells in the posterior boundary of the PZ is the same magnitude of elastic force experienced by the cells due to the boundary, but in an opposite direction. So, we used the following overdamped growth law for the length:

$$\frac{d{L}_{\mathit{\text{tot}}}}{\mathit{\text{dt}}}=\frac{1}{\Gamma }{(\sum _i-f_{\mathit{\text{elastic}}}^i)}_y.$$

Here, Г is the drag coefficient that signifies the resisting force felt by the embryo during its posterior movement as it was mounted in low-melt agarose during imaging. The summation is taken over all posterior cells close to the boundary inside the PZ. We only consider here the Y-components (posterior components) of the elastic forces that drive the increase in length. The length of the PSM, L_PSM follows the same equation as above. For the simulation, we used the drag coefficient Г =150 and elastic constant k = 1, while other parameters were as specified above. The general phenomenon of symmetry breaking was again observed in such a detailed model. At low values of noise strength, we found the emergence of left-right population differences in the PSM and vortex formation in the PZ (Figure 1N).

Analysis of SU5402 treated embryos

In the main text, we presented the analysis of the data for wild-type (WT) embryos, notum1a overexpression embryos and cdh2 mutants. Here, we present the analysis of the data for SU5402-treated embryos (Figure S1A–S1F). Firstly, we did not find any signature of stable vortex formation in the PZ (Figure S1A–S1C). We then analyzed the statistics of the alignment angle in the PZ. Consistent with our theory, we found that the cellular order in SU5402-treated embryos is lower than notum1a overexpression embryos and WT but similar to the cdh2 mutants (Figure S1D and S1E). Finally, we found that the ADM cells in SU5402-treated embryos display much slower anterior-to-posterior movements (similar to cdh2 mutants), as predicted in our theory (Figure S1F).

Comparison of the local order in cell motion

We showed that the cellular order in the PZ of notum1a overexpression embryos is much higher than WT and cdh2 mutants. Here, we compare the local order of cell motion in the ADM and PZ (Figure S1G). For all three phenotypes (WT, cdh2 mutants and notum1a overexpression), the ADM cells are more ordered than the PZ cells showing that epithelium is more ordered than mesenchyme. Nonetheless, notum1a overexpression embryos show higher order both in the ADM and PZ compared to other phenotypes, and cdh2 mutants consistently exhibit lower order everywhere compared to the other experimental conditions.

Analysis of flux into the ADM

Using the Imaris software package (version 8.1), we counted the number of nuclear 'spots' that passed through a fixed transverse plane 50 microns from the anterior end of ADM during each timelapse. From this analysis, we calculated the flux into the ADM (i.e. number of cells passing per unit area per unit time). We did not observe any significant difference of fluxes among the experimental conditions (Figure S1H). Thus, we maintained a fixed rate of cell influx in the simulations.

Consistency in the statistics of local alignment

In the main text, we calculated the cumulative distribution functions (CDFs) of the alignment angles for each phenotype, by accumulating all the data corresponding to that phenotype from different embryos. The assumption is that one phenotype constitutes one ensemble, i.e. there exists an empirical distribution corresponding to each phenotype. Here, in an alternative approach, we present the distributions for each embryo (Figure S2A and S2B). Interestingly, the CDFs of individual WT embryos closely fall on top of each other, pointing the fine regulation of local order (Figure S2B). To check if the distributions are significantly distinct from each other, we first looked at their modes or most-probable values of the alignment angles (Figure S2C). Lower modes (closer to zero) indicate higher local order. The modes of the notum1a overexpression embryos are significantly lower than the cdh2 mutants. Next, to check the difference between the full CDFs, we calculated the area under the curves (AUC) for the CDFs. The idea is that distinct CDFs correspond to different values of AUCs, thus helping us to differentiate among them. Note that the CDF that more steeply rises to 1 corresponds to a higher value of AUC and also indicates higher cellular order (Figure S2B and S2D). We indeed find that notum1a overexpression embryos exhibit significantly higher values of AUCs than others, and cdh2 mutants display lower AUCs than WT and notum1a overexpression embryos (Figure S2D).

To determine the alignment angles, we implicitly assumed an interaction radius R surrounding each cell. The choice of R is subjective, but we varied it to check the consistency of our results. We used R = 10µm, 20µm, 30µm corresponding to one, two and three neighboring cells respectively. Irrespective of the choice of R, notum1a overexpression embryos consistently exhibited highest order and cdh2 mutants exhibited lowest order in the PZ (Figure S2E–S2H).

Analysis of mean square displacement

To understand the nature of the diffusive motion inside the ADM, we plotted the MSD curves in a log-log plot, where the slopes of the curves revealed that the motion is super-diffusive (Figure S3A). The MSD exponent (~1.88) did not vary with different levels of noise. To determine the variation in diffusivity, we fitted the long-time regime of the MSD curves by a power-law ~ 4Δt^α, where D is the diffusion constant and α is the MSD exponent. We found that D decreases with increasing noise (Figure S3B).

The in vivo data of cell motion inside the ADM were also analyzed by fitting the MSD curves by a power-law ~ 6Δt^α, appropriate for 3-dimensions (Figure S3C). We found that cdh2 mutants have significantly lower diffusion constants (Figure S3D). The MSD exponents are similar for all of the phenotypes (greater than 1), implying super-diffusive motion inside the ADM for all phenotypes (Figure S3E).

QUANTIFICATION AND STATISTICAL ANALYSIS

Analysis of Simulation data

The codes for model simulations were written in FORTRAN 90. The outputs of the program were averaged over 100 simulations of the tailbud to prepare the panels in Figure 2.

Experimental data analysis

Experimental timelapse datasets were analyzed in two steps. The timelapse data were first processed by the Imaris software, which created 'spots' in the position of each nucleus and tracked spot displacement between time intervals. This analysis thus provided the data of positions and velocities of all nuclear spots in the tailbud. The nuclear tracks were then segmented manually to locate the tracks within each domain of the tailbud (PZ, DM, ADM and PSM). The data extracted from Imaris were analyzed further to calculate angular momentum, local order, net posterior velocity, distribution of nearest neighbors, flux, and MSD. These metrics were calculated using custom codes written in Matlab. We analyzed the position and velocity data of labeled nuclei from 4 notum1a overexpressing embryos, 5 wild-type embryos, 3 cadherin 2 mutants, and 3 SU5402-treated embryos.

Significance test

To establish if there is any significant difference between samples in a metric, we used a two-sample T-test provided by the Matlab function 'ttest2'. Significance was defined as p< 0.05.

Supplementary Material

2. Movie S1. in silco models of tailbud cell motion with different boundary conditions. Related to Figure 1.

The first two simulations have rigid boundary conditions while the second two simulations have elastic boundary conditions. The adhesion and repulsion strengths are F_adh = 0.75, F_rep = 30 in all simulations, but we performed simulations with high or low angular noise under each boundary condition. Other parameters are as specified in the Methods. Each simulation starts from a random initial configuration. The times are in units of 36 in silico iterations. (A) With rigid boundaries at a high value of noise strength η = 0.9, cells sort symmetrically from the PZ and evenly populate the left and right sides of the PSM. Note that the cell motion in the PZ is disordered. By contrast, at low noise, cells sort asymmetrically from the PZ, and a significant population difference emerges between the left and right sides of the PSM. Also note that a vortex forms inside the PZ, indicated by an arrow. (B) (23 seconds from the start) In an elastic boundary model, at high noise, cells sort symmetrically from the PZ and evenly populate the left and right sides of the PSM. Similar to the rigid boundary model, at low noise, cells sort asymmetrically from the PZ, and a significant population difference emerges between the left and right sides of the PSM. Also note that a vortex forms inside the PZ, indicated by an arrow.

3. Movie S2. Experimental timelapses of cell motion in a wild-type tailbud, a notum1a overexpression tailbud and a cadherin2 mutant tailbud. Related to Figure 3.

The circular dots denote the nuclei, and the trails represent the nuclear trajectory over the last few time-points as visualized using the Imaris software. The ADM domain is omitted for visual clarity. (1) (21 seconds from the start) In the wild-type tailbud, the motion inside the PZ is disordered, similar to our simulation at high noise. (2) In the notum1a overexpression tailbud, a vortex forms inside the PZ (denoted by arrow), similar to our simulation at low noise. (3) (43 seconds from the start) In the cadherin2 mutant tailbud, the motion inside the PZ is disordered, similar to our simulation at high noise.

Highlights.

• A domain of disordered cell motion is created in the vertebrate tail bud via EMT

• During body elongation, there are random left-right fluxes in cell flow

• Disordered cell motion ensures that left-right fluxes balance over time

• Excessively ordered cell motion leads to asymmetric elongation