Reactivation of emergent task-related ensembles during slow-wave sleep after neuroprosthetic learning

Abstract

Brain-Machine Interfaces can allow neural control over assistive devices. They also provide an important platform to study neural plasticity. Recent studies indicate that optimal engagement of learning is essential for robust neuroprosthetic control. However, little is known about the neural processes that may consolidate a neuroprosthetic skill. Based on the growing body of evidence linking slow-wave activity (SWA) during sleep to consolidation, we examined if there is ‘offline’ processing after neuroprosthetic learning. Using a rodent model, here we show that after successful learning, task-related units specifically experienced increased locking and coherency to SWA during sleep. Moreover, spike-spike coherence among these units was significantly enhanced. These changes were not present with poor skill acquisition or after control awake periods, demonstrating specificity of our observations to learning. Interestingly, time spent in SWA predicted performance gains. Thus, SWA appears to play a role in offline processing after neuroprosthetic learning.

INTRODUCTION

Brain-machine interfaces (BMIs) have the potential to seamlessly merge the computational power of the motor system with that of artificial electronic systems. Research into the development of BMIs has flourished over the past decade, leading to impressive demonstrations of rodents^1–3, non-human primates^4–10, and humans controlling prosthetic devices^11–13 in real-time through modulation of neural signals. This body of work has also identified that adaptive processes, both in the motor system and in the algorithms that transform neural activity into prosthetic control signals (i.e. ‘decoders’), are essential for achieving stable neuroprosthetic control^{3,6, 8, 9, 14,15}. For example, practicing neuroprosthetic control over multiple sessions in the setting of a fixed decoder is known to result in persistent improvements in performance¹⁴. Moreover, long-term adaptation of decoders at a rate that is seemingly concordant with neural learning rates can be essential for long-term stable performance¹⁵. Together, these studies underscore the importance of optimal engagement of long-term neural learning mechanisms^{9, 14, 15}. However, the specific neural process that stabilizes a newly acquired prosthetic skill remains incompletely understood.

Based on the growing body of literature indicating that cortical slow-wave activity (SWA) is associated with ‘offline’ processing^16–19, we hypothesized that such processing facilitates direct cortical control of an artificial actuator. Studies in humans indicate that offline processing during overnight sleep^20–23 as well as during daytime naps²⁴ facilitates memory consolidation. Motor task performance is also known to improve after sleep versus an equivalent amount of wakefulness^21–25. While SWA is also directly implicated in the consolidation of motor skills^26–30, it remains poorly understood how neural ensembles in motor cortex are precisely modified during SWA after skill acquisition. While most theories suggest that reactivation of cortical neurons during SWA is important for consolidation³¹, to our knowledge there is little experimental support of this for procedural memory formation. In this context, BMIs offer a powerful tool to directly modulate single units, thereby allowing precise characterization of how both task-related (tr) and task-unrelated (tu) cortical units are differentially processed in motor cortex during SWA. In these experiments, rats were trained to control the angular velocity of a feeding tube via direct modulation of cortical units through operant conditioning. We hypothesized that after neuroprosthetic skill acquisition, tr units would be differentially processed from tu units during SWA.

RESULTS

After implantation of microelectrodes in M1, we trained six rats to exert direct neural control of the angular velocity of a mechanical actuator that could also deliver water (Fig. 1a). A linear decoder with randomized weights typically converted the firing rates of two randomly selected units (hereafter direct units) into the angular velocity of the actuator (see Supplementary Fig. 1 and 2 and Methods for discussion of unit sorting using microwire arrays versus silicon probes in a tetrode configuration). We also recorded multiple other units that were not causally linked to actuator movements (hereafter indirect units). The decoder weights were held constant during the session in order to exclusively rely on neural learning mechanisms. Each trial started with the simultaneous delivery of an auditory tone and the opening of a door to allow access to the tube (Fig. 1a,b). At the start of each trial the angular position of the tube was set to 0° (P₁). If the angular position of the tube was held for > 300 ms at position P₂ (90°), a defined amount of water was delivered (i.e. successful trial). A trial was stopped if this was not achieved within 15 seconds (i.e. unsuccessful trial). At the end of a trial, the door was closed and the actuator returned to position P₁.

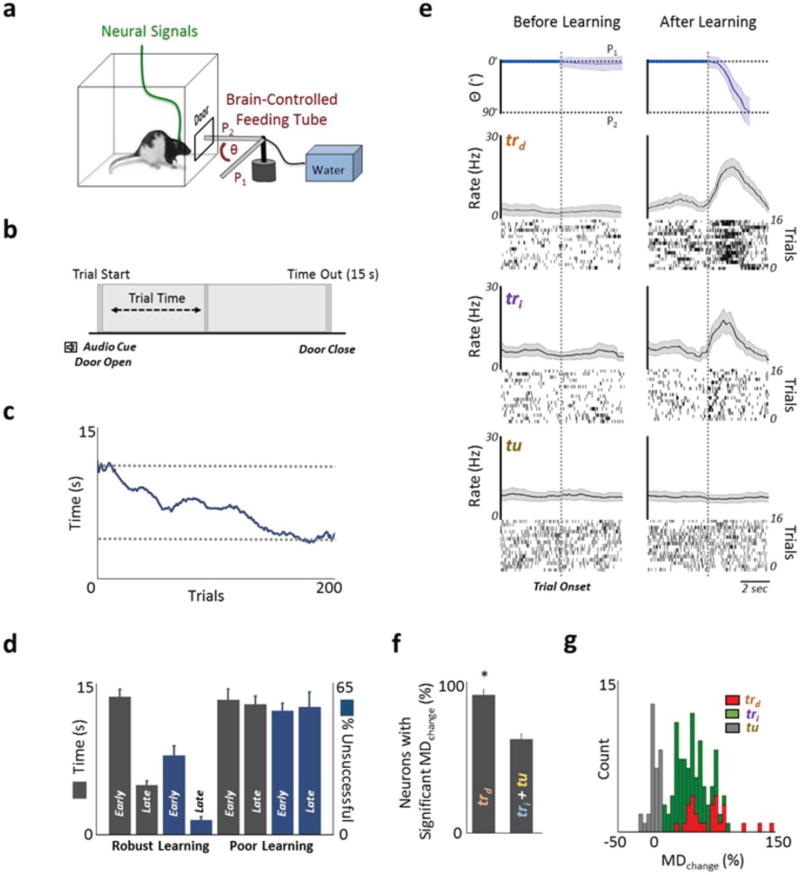
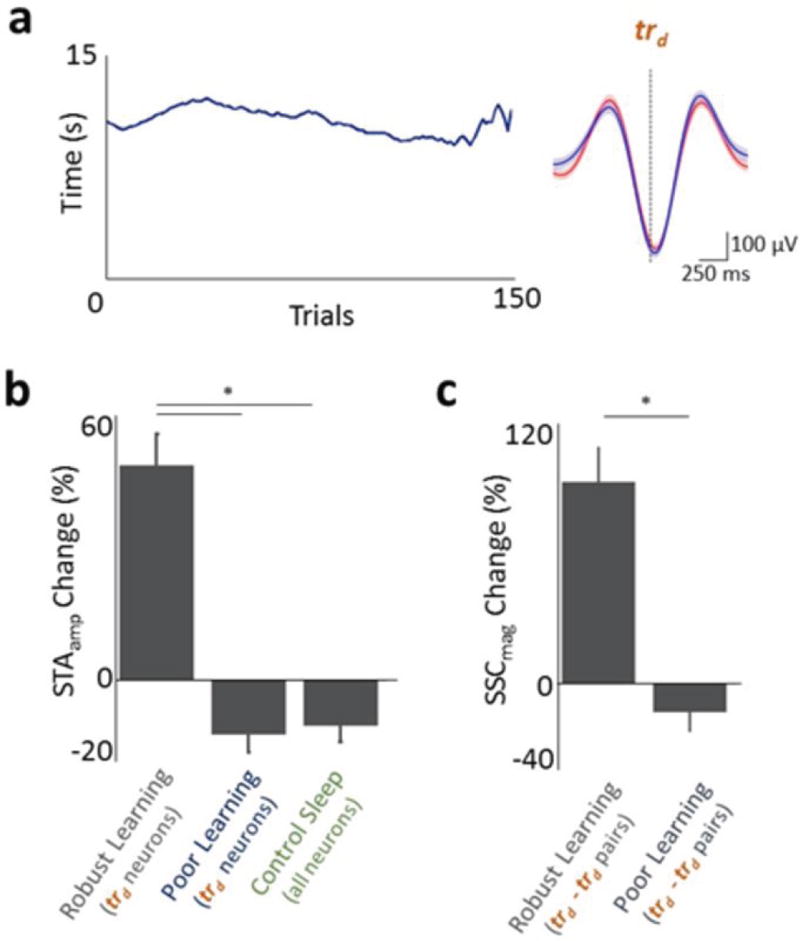
Figure 1. Direct control of motor cortex units.

a, Direct neural control of a feeding tube (θ = angular position). Each trial started with the tube at P1. b, Trial started with an audio tone cue and opening of the door. A successful trial required movement of the tube to P₂ within 15 seconds. c, Change in task completion time as a function of trial number (line shows moving average of 20 trials). d, Comparison of time to trial completion and change in percentage of unsuccessful trials for ‘robust learning’ and ‘poor learning’ sessions. e, Angular position of the tube is shown from a single session (mean ± s.e.m.). Peri-event histogram (PETH) from early and late trials from a single session are shown in left and right panels respectively. tr_d task-related direct units, tri: task-related indirect units and tu: task-unrelated units. f, Comparison of the percentage of units that experienced a significant change in modulation depth. * = p < 0.001. g, Histogram of percentage change in modulation depth (MD_change) for each of the three category of units.

Over the course of a typical two-hour practice session, animals showed improvements in task performance, with a significant reduction in the time to successful trial completion and a decrease in the number of unsuccessful trials (Fig. 1c, d). Specifically, out of 19 such training sessions, there were 15 ‘robust learning’ sessions with significant reductions for both metrics (Fig. 1d, n=15 sessions; ‘early’ completion time: 13.49 ± 0.75 seconds; ‘late’ completion time: 4.83 ± 0.42 mean ± s.e.m., p < 0.0001, one tailed t-test). Moreover, the percentage of unsuccessful trials significantly decreased from 33.56 ± 4.04% to 6.00 ± 1.51%. (p < 0.0001, one tailed t-test). For the remaining four sessions these values did not improve with training (i.e. ‘poor learning’). In the robust learning sessions, we also found that the path of the actuator taken from position P₁ to P₂ became direct (Fig. 1e).

As also illustrated in Figure 1f, for direct units that were causally linked to actuator movements via the decoder (i.e. task-related direct or tr_d), nearly all experienced significant changes in task-related modulation at the end of session (96 % of 27 tr_d units with a significant increase in modulation depth). As outlined in the methods, we assigned weights in the decoder that ranged from +1 to −1. While we did not see suppression of activity relative to the baseline, there was a significantly greater modulation of the units assigned positive weights (i.e. tr_d⁺) than negative weights (i.e. tr_d⁻) (Supplementary Fig. 3). Direct units were also significantly more likely to experience a change in modulation in comparison to indirect units (Fig. 1f, n=15 sessions; direct: 96.7% ± 3.5%; indirect: 65.7 ± 3.7%, p <0.001, t-test). However, based on the growing notion that subsets of indirect units likely contribute to neuroprosthetic control^32–34, we further sub-classified such units as either task-related (tr_i) or task-unrelated (tu) based on changes in modulation depth with learning. A unit was assigned as task-related if its post-learning change in firing rate was 2.5 standard deviation above the baseline firing rate (see Methods for details). Moreover, we did not find a preponderance of particular cell types in either category as determined by the width of the record spike (Supplementary Fig. 1b,c, and d). For subsequent analysis we respectively used 27 tr_d, 108 tr_i, and 39 tu units in 15 BMI training sessions (see Supplementary Table 1 for details). Figure 1g illustrates the distribution of changes in modulation depth for each of the three categories. Interestingly, after learning, the temporal profiles of activation (i.e. Fig. 1e for single examples) for tr_d and tr_i were not significantly different (time to peak firing, direct 3.1 ± 0.2 and tr_i 3.3± 0.1 seconds, p=0.24, t-test), suggesting that these two distinct groups of task-related units became functionally and temporally coupled with learning and successful task performance. We also saw evidence for changes in the spike-triggered local field potential (LFP) for task-related units that was not present for the task unrelated units (Supplementary Fig. 4).

Increased locking to SWA after learning

Because of the literature indicating a link between slow-wave sleep (SWS) and motor learning^16–18, we first examined whether the spike-field relationship during SWS is altered after robust learning sessions. To look for signatures of offline processing, we first assessed whether individual units (tr_d, tr_i and tu) experienced changes when comparing the pre- and post-SWS around a successful training session (hereafter SWS_pre and SWS_post; see Methods and Supplementary Fig. 5 for identification of SWS epochs). Specifically, we used spike-triggered averaging (STA) to quantify the relationship between spiking and SWA. The STA provides an intuitive estimate of how neural spiking is modulated by cortical oscillations. In order to match SWS durations, we used the first 10 minutes of SWS_pre and SWS_post for this analysis (see Methods). Interestingly, we found that tr_d and tr_i units consistently experienced a significant increase in the peak-to-peak amplitude of the STA in comparison to tu units even in the absence of any changes in the LFP power (Fig. 2). This appeared to be the result of a greater likelihood of spikes occurring at a specific phase of the SWA (Fig. 2a). While tr_d and tr_i units experienced respective 48.87 ± 7.23 % and 54.37 ± 8.46 % increases in STA amplitude, tu units experienced a significant net −11.68 ± 4.89 % reduction (Fig. 2c, p < 0.0001, one-way ANOVA for overall, post hoc t-test for tr_d and tu; and tr_i and tu ). In contrast, we did not find any significant differences when we calculated the STA for spindle (8 – 20Hz) and ripple (100 – 300 Hz) frequency bands (p>0.05, one-way ANOVA, Supplementary Fig. 6). We next assessed whether changes in the power or frequency of SWS or firing properties of units could account for our observations. There were no significant changes in either the SWA power (average change of 3.11 ± 6.48 %, p=0.79 on paired t-test of absolute values, Fig. 2e and Supplementary Fig. 7), density of delta waves in SWS (11.82 ± 5.67 waves min⁻¹ vs. 12.86 ± 6.09 delta waves min⁻¹, p=0.16, Supplementary Fig. 8c), firing rate (6.42 ± 0.43 Hz vs. 7.01 ± 0.34 Hz, p = 0.270, Supplementary Fig. 1e,f and g), or changes in bursting properties (Supplementary Fig. 8a, b). We also did not find any evidence for a significant relationship between the changes in the firing rates of individual units and changes in STA amplitude (linear regression R² = 0.01, p=0.29; Supplementary Fig. 1e also shows plots of the firing rate in SWS_pre versus SWS_post) or changes in the LFP power relative to change in STA amplitude (linear regression R²= 0.033, p= 0.64). Moreover, we did not find evidence for spatiotemporal changes in the occurrence and rate of SWA (Supplementary Fig. 9).

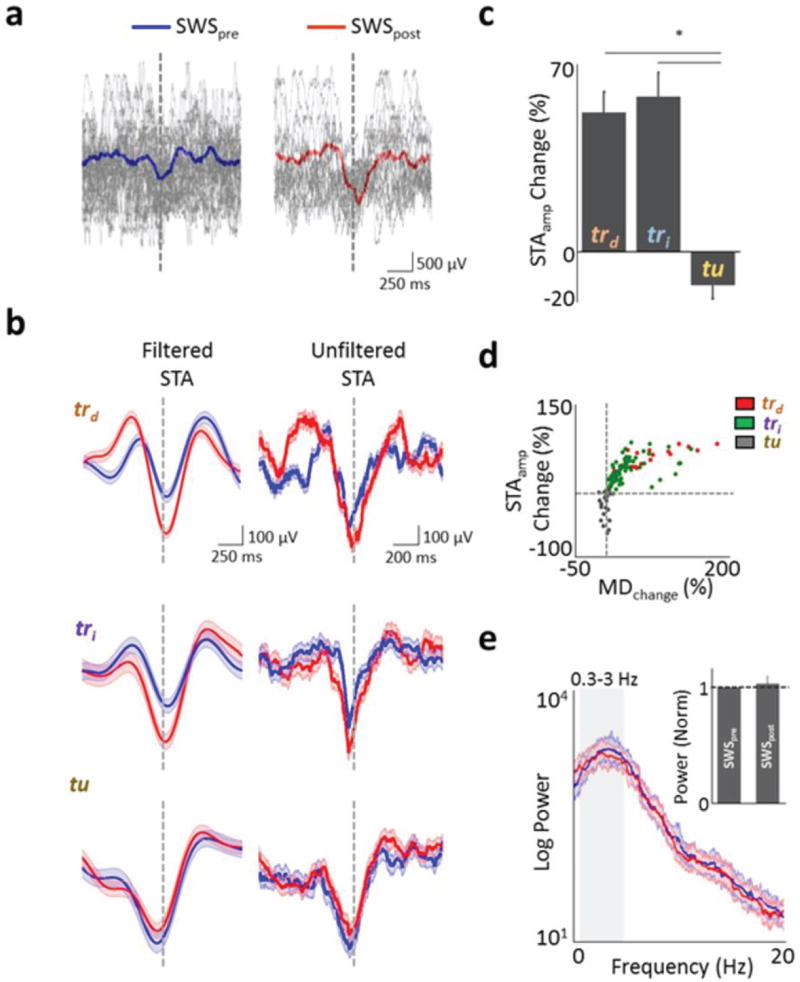
Figure 2. Changes in phase-locking and coherent spiking during SWS after learning.

a, Examples of fifty raw LFP traces during SWS_pre and SWS_post for a task-related direct neuron. Superimposed is the mean trace from an SWS epoch. Each trace was aligned to time of spike (dotted line). b, Filtered (0.3–3Hz) and unfiltered spike-triggered averages (STA) during SWS before and after successful acquisition of neuroprosthetic skill. c, Percent change in STA amplitude for each of the three categories of units in 15 sessions (mean ± s.e.m., * p < 0.001). d, Scatter plot showing relationship of depth of modulation during task performance to change in STA amplitude (R=0.85, Spearman correlation; p < 0.05). Color code represents each class of neuron. Dotted lines are the 0 values for the × and y-axes. e, Comparison of the power spectra from 10 minutes of SWS_pre and SWS_post from a single experiment. Inset compares the power in the 0.3–3 Hz band for multiple experiments (n=15, normalized to SWS_pre for each experiment).

To further establish a link between the task-dependent modulation that emerges after learning and the change in phase-locking to SWA we examined the relationship between the extent of task-dependent modulation and the percent changes in the STA amplitude. Interestingly, we found that the degree of task-related firing rate modulation significantly predicted the extent of increased STA amplitude during the subsequent slow-wave sleep (Fig. 2d, R = 0.85, P < 0.05, Spearman correlation). The non-linear nature of the curve is likely the result of the significant reduction in STA amplitude without a mirror symmetric reduction in depth of modulation for tu units. Also consistent with the notion of a link between the extent of task-dependent modulation and the change in STA amplitude was the finding that tr_d⁺ units experienced a significantly greater change in the STA amplitude than tr_d⁻ units (Supplementary Fig. 3d). Together, these results suggest that after successful learning of direct cortical control there is greater locking of the task-related cortical spiking to SWA.

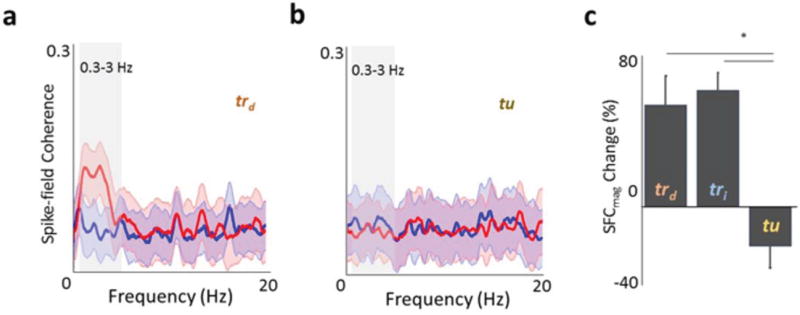
To further confirm that changes in STA amplitude reflect greater phase-locking of tr_d and tr_i units, we used spike-field coherence (SFC) to measure coherence in the 0.3–3Hz band between the spiking activity and the local field potential (LFP). The SFC measure complements the STA analysis in that it is not sensitive to changes in power and can readily assess all frequencies. The magnitude of SFC, which varies as a function of frequency and yields a value between 0 and 1, showed a similar trend of enhanced SFC for tr_d and tr_i units in the SWA frequency range (Fig. 3 and Supplementary Fig. 10 for the full spectrum and phase analysis). Consistent with the STA results in the spindle/ripple bands, there were no significant differences for other frequency bands (i.e multitaper method using jackknife-based confidence intervals). The three groups tr_d, tr_i and tu respectively experienced a change in SFC magnitude of 53.24 ± 15.02%, 60.95 ± 8.89% and −20.39 ± 11.42%. Thus, task-related units (i.e. both tr_d and tri) showed a significant increase in SFC magnitude compared to tu units (p < 0.0001, one-way ANOVA for overall, post hoc t-test for tr_d and tu; and tr_i and tu). There were no significant changes in SFC phases of the task-related units between SWS_pre and SWS_post (0.18 ± 0.14 radians, mean ± s.e.m., net change in phase and p=0.44, Watson-Williams circular t-test for comparison of phases pre- and post-learning, Supplementary Fig. 10). Together with the findings from the STA analysis, these results confirm that tr units, in contrast to tu units, were significantly more phase-locked to SWA after successful learning.

Figure 3. Changes in spike-filed coherence (SFC) after learning.

a, Example plot of SFC as a function of frequency before (blue) and after (red) skill acquisition for a direct pair. The lighter band is the jackknife error. The box highlights the 0.3–3Hz band. b, Task-unrelated SFC. c, Mean changes in SFC for the various categories of units. Lines marked by an ‘*’ indicate comparisons that showed significant differences (one-way ANOVA for overall, post hoc t-test with p < 0.001).

Increased spike-spike coherence after learning

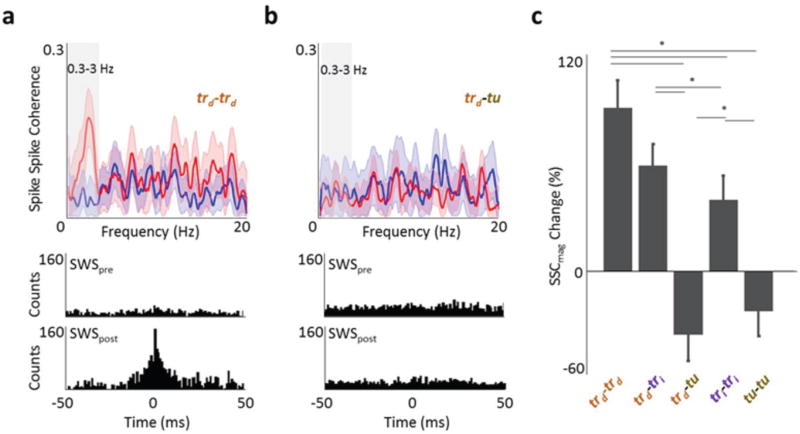
We subsequently assessed whether there are changes in the functional connectivity among the recorded M1 neural ensembles during SWS_post. We calculated the magnitude of spike-spike coherence (SSC) for both SWS_post and SWS_pre for direct units (tr_d) relative to all other units (i.e. tr_d - tr_d, tr_d - tr_i, and tr_d - tu neuronal pairs). We used a ‘shuffling’ method to assess significant SSC increases in SWS_post in comparison to SWS_pre. For example in Figure 4a, only the SWS_post SSC curves showed a significant increase in the 0.3–3 Hz band (i.e. SWA). In Figure 4b, however, both SSC curves were not significantly greater than chance. We found surprisingly robust increases in SSC (0.3–3 Hz range) for task-related pairs (i.e. tr_d - tr_d and tr_d - tr_i) after successful learning (Fig. 4c, 92.65 ± 15.55 % increase for 12 tr_d - tr_d pairs and 59.84 ± 12.04 % increase for 108 tr_d - tr_i pairs). In comparison, the change in SSC for the tr_d -tu pairs was −35.96 ± 15.55 % (Fig. 4c, p<0.001, one-way ANOVA for overall three groups; post-hoc t-test for tr_d - tr_d, and tr_d - tu pairs; and tr_d - tr_i, and tr_d - tu pairs). When we used cross-correlation analysis, we also found similar results (Fig. 4 a, b shows single examples and summary statistics of p<0.001 in Supplementary Fig. 11). This indicates that task-related units are significantly more likely to fire synchronously when compared with task-unrelated units during SWS_post.

Figure 4. Changes in spike-spike coherence (SSC) after learning.

a, Example plot of SSC as a function of frequency before (blue) and after (red) skill acquisition for a direct pair. The lighter band is the jackknife error. The box highlights the 0.3–3Hz band. Below are the respective cross-correlograms from SWS_pre and SWS_post b, Spike-spike coherence of a task-unrelated pair. c, Mean changes in SSC for the various categories of neuron pairs. Lines above with an ‘*’ indicate comparisons that showed significant differences (one-way ANOVA for overall, post hoc t-test with p < 0.001).

Lack of changes after poor learning

We next determined whether these changes in STA, SFC and SSC are specific to successful learning. We thus analyzed four sessions in which animals performed the BMI task but did not demonstrate robust learning (Fig. 1d, Fig. 5a). During these sessions many of the trials ended because the 15 second timeout was reached. As shown in Figure 1d, the respective time to completion were 13.19 ± 1.10 seconds for early trials versus 12.76 ± 0.80 seconds for late trials (p = 0.72, one tailed t-test); and the percentage of unsuccessful trials remained unchanged (52.50 ± 3.29 % early versus 54.17 ± 6.36 %, for late; P = 0.68, one tailed t-test). In these sessions, tr units did not experience an increase in STA amplitude (Fig. 5a, b). The mean STA amplitude change for tr_d units was −12.24 ± 4.24 % (n=8 units). In addition, the SSC between tr_d-tr_d pairs did not increase in a manner similar to that during robust learning sessions (Fig. 5c, −12.67 ± 8.78 %, n=4 pairs). These were significantly different from the corresponding values in robust learning sessions (p < 0.001, t-test). Moreover, we also performed control experiments in which rodents were placed in the BMI chamber but did not perform any task (i.e. “control sleep” in Fig. 5b). Instead, they received an equivalent amount of water reward over a time period that matched a typical practice session. The STA before and after these control sessions did not show any increase. The overall change was significantly different from tr_d units from robust learning sessions (n=3 sessions with 32 units, −10.23 ± 3.76% STA change, p<0.01; t-test, see Fig. 5b). This suggests that factors such as sustained attention, reward and attempts at execution without evidence of learning are not sufficient to trigger increased coherent activation during the SWA_post. Together, this further supports a conclusion that enhanced locking occurs only for task-related ensembles linked to learning.

Figure 5. Lack of increase in coherent spiking with poor learning and in control sleep.

a, Plot of trial times versus trial number. Right panel shows the STA before and after. b, Mean changes in direct unit STA for robust learning (reproduced from Fig. 2c) and poor learning sessions. Also shown are units from ‘control awake’ periods. c, Changes in SSC for robust learning (reproduced from Fig. 2e) and poor learning for task-related pairs.

Reactivation of emergent task-related ensembles

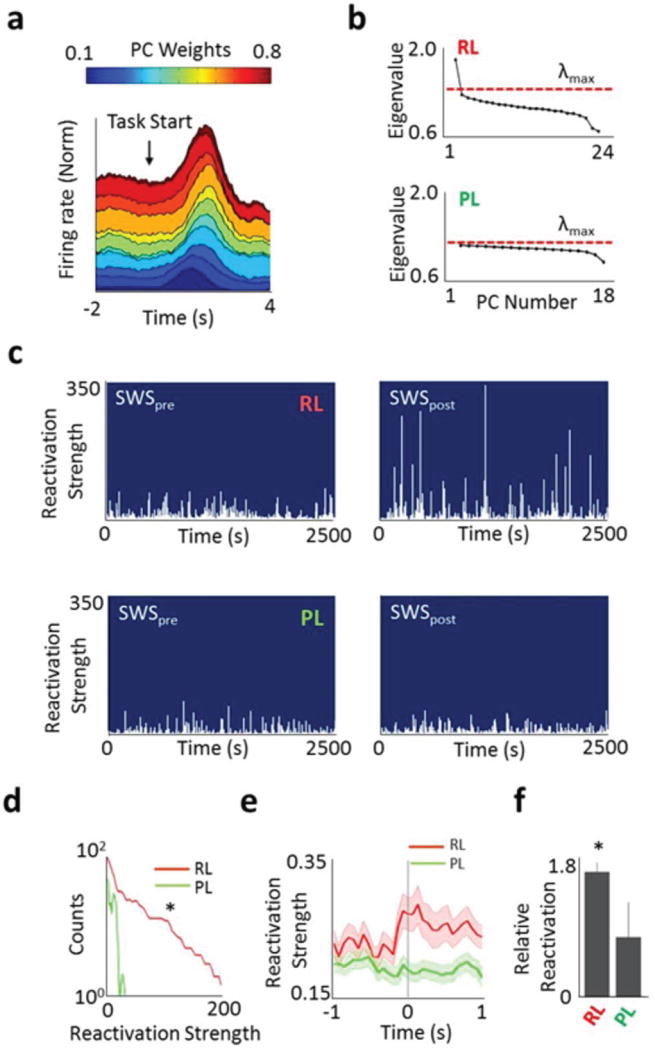
The analysis presented above examined changes in spike-field relationships and pairwise interactions among task related units after robust and poor learning. We next used a method previously developed to identify task-related neuronal cell assemblies and their coordinated reactivation^35–37. This method uses principal components analysis (PCA, see Methods) to identify significant ‘signal components’, or ensembles of neurons that become temporally correlated during learning and task performance. The output of this analysis are principle components (PCs), consisting of an array of weights assigned to each unit in the identified ensemble, and the eigenvalue, a numerical value that represents the extent of total variance that is captured by a given PC; PCs with the largest eigenvalues capture the most variance (Fig. 6a,b). Whether a calculated PC represents a significant temporally correlated pattern of activity is determined by λ_max, i.e. the highest eigenvalue that arises out of an equivalently sized random matrix based on the Marchenko-Pastur law ^35–37 (Fig. 6b). Thus, PCs with eigenvalues greater than λ_max were considered ‘signal components’ whereas those below λ_max were considered as arising from chance interactions. We started by estimating the signal components (i.e. ensemble patterns of activity) linked to successful learning (Fig. 6a, b). Interestingly, we found evidence for significant signals only for robust learning sessions (Fig. 6b). In contrast, poor-learning sessions generated PCs that were never greater than λ_max.

Figure 6. Changes in reactivation strength after learning.

a, Peri-event firing rate modulation of units from a single session. Only task related units are shown and sorted by weights in the first principle component (PC). b, Correlation matrix eigenvalues calculated from activity during task performance (RL = Robust Learning; PL = Poor Learning). Dotted line is the signal threshold (λ_max), defined as the theoretical upper bound for a randomized spike train. c, Reactivation strength during SWS_pre and SWS_post for RL and PL. d, Mean population differences between SWS_pre and SWS_post distributions of reactivation strengths for RL (n=15 sessions) and PL (n=4 sessions). * p < 0.05 logrank test. e, Event triggered average of reactivation strength centered on maximum delta wave negativity (time = 0) for SWS_post. * p < 0.01 t-test. f, Comparison of relative ratio of reactivation during baseline period and at time of maximum delta negativity (i.e. at time 0 in e). * p<0.001, t-test.

We then examined if there was a change in the ‘reactivation strength’ during SWS_post by calculating the instantaneous reactivation strength of signal components^35–37. The reactivation strength is an instantaneous measure of how similar the ensemble activity during the SWS epoch is to that identified during the awake period using the PCA analysis. Importantly, by comparing the SWS_pre and the SWS_post epochs we can identify changes that are specifically linked to learning control. After robust learning sessions, the observed strength of reactivation of the signal component was greatly enhanced in comparison to SWS_pre (Fig. 6c,d illustrate the significant increase in the incidence of high reactivation strength events). Moreover, this was not evident during the awake spontaneous periods prior to the onset of SWS (n=15, logrank, Supplementary Fig. 12). Across multiple sessions, the reactivation strength of the task-related ensemble during SWS_post was significantly greater after robust learning in comparison to poor learning (Fig. 6d, logrank test, p <0.05). We also examined the specific relationship between instantaneous reactivation and SWA. We thus performed a delta-wave triggered averaging of reactivation strength. As shown in Figure 6 e,f, cell assembly reactivation events occurred in concert with maximum delta wave negativity. The ratio of peak reactivation at the time of maximum delta negativity to the baseline reactivation strength was significantly greater after robust learning than either after poor learning (Fig. 6e, f) or during spontaneous awake-periods after robust learning (p<0.0001, unpaired t-test, Supplementary Fig. 12c, d).

Improvements in task performance

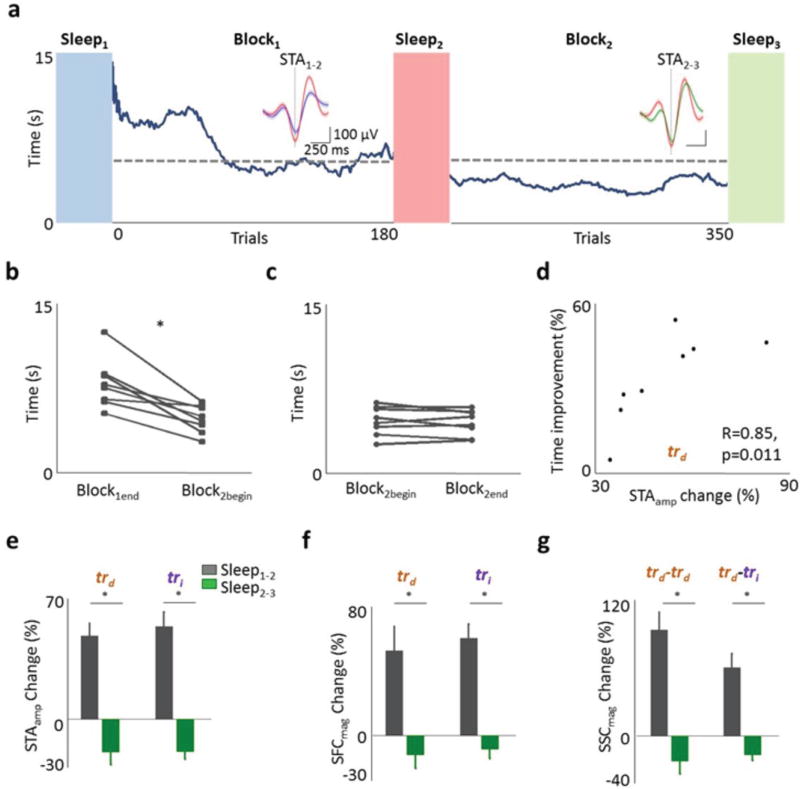
We also conducted experiments in which the animals performed the task during two sessions (hereafter Block1 and Block₂) using the same decoder but separated by a period of spontaneous activity and sleep (Fig. 7a). Interestingly, we found that task performance consistently improved at the start of Block₂ (Fig. 7b, p<0.05 for each of the eight individual comparisons of the last 30 trials from Block₁ and the first 30 trials from Block₂, paired t-test). Such improvements were also evident if we compared the best performance at the end of Block₁ with that of early Block₂ (p<0.05, paired t-test, Supplementary Fig. 13). That increased motivation after rest does not account for this finding is supported by the lack of significant performance changes during Block₂ itself (Fig. 7c, p > 0.05 for each of the eight comparisons). Moreover, even while the total period was the same between the two blocks, the time-spent in SWS after Block₁ was positively correlated with the extent of improvement at the beginning of Block₂ (R=0.67, p<0.05, Spearman Correlation). Interestingly, the extent of improvement was also positively correlated with the mean change in STA amplitude between Sleep_1–2 for tr_d units (Fig 7d; R=0.85, P=0.01, Spearman correlation).

Figure 7. Continued task performance after sleep.

a, Plot of time to task completion versus trial number. Conventions same as in Fig. 1c. Trace inset shows the STA from the respective sleep for a task-related neuron. STA scales are the same. b, Average time to reward at the end of first training session (Block_1end) compared to the beginning of second session (Block_2begin). * p<0.05 for all eight comparisons. c, Average trial time at the beginning of second session (Block_2begin) compared to its end (Block_2end). d, Relationship between mean change in STA amplitude for tr_d units and the improvement in performance. Also noted are the correlation coefficient and p value for the Spearman test. e, Relative changes in STA amplitude for tr_d and tr_i units between sleep_1–2 and sleep_2–3f, Relative change in SFC magnitude. g, Relative change in SSC magnitude.

Changes with continued task performance

We first compared the STA amplitude and SFC magnitude changes for tr_d and tr_i units (n=8 experiments, 15 tr_d and 47 tr_i units for Sleep_1–2 and Sleep_2–3). With continued execution of the task there was no further increase in coherent spiking for task-related units (Fig. 7a, e-g). As shown in Figure 7, STA amplitude changes were −19.06 ± 7.55 % for tr_d units and −18.85 ± 4.62 for tr_i units, whereas SFC magnitude changes were −12.06 ± 8.42 % for tr_d units and −8.54 ± 6.09 for tr_i units, after the second training session (for Sleep₂-₃). We also examined SSC magnitude changes for task-related pairs (i.e. tr_d -tr_d and tr_d-tr_i). The changes in SSC magnitude were −21.92 ± 11.22 % for tr_d - tr_d pairs (n=7) and −16.36 ± 5.01 for tr_d - tr_i pairs (Fig. 7g, n=47 pairs). The small changes observed between Sleep₂ and Sleep₃ (i.e. Fig. 7 e–g, STA_amp and SSC_mag) were not significantly different from the absolute changes seen during poor learning sessions (p = 0.23 and 0.20 respectively for STA_amp changes for comparisons of tr_d and tr_i units; and p=0.14 and 0.07 respectively for SSC_mag changes for tr_d - tr_d pairs and tr_d - tr_i pairs). Together, this indicates that the continued execution of the task in the absence of new learning is not sufficient to trigger further increases in phase-locking and coherent spiking.

DISCUSSION

In summary, here we show that successful learning of direct neural control of an actuator is linked to enhanced phase-locking and coherent activation of emergent task-related activity, both direct and indirect, during the post-learning SWS. During the process of learning, these two sets of task-related units became increasingly activated with similar temporal profiles. Interestingly, we found strong evidence for coherent reactivation of these newly functionally coupled ensembles during SWA. In contrast, task-unrelated activity either remained unchanged or experienced a reduction in phase-locking and coherent activation. For control sleep sessions, poor-learning sessions, and second sessions without evidence of new performance gains, we did not find evidence of increased phase-locking to SWA or coherent activation, indicating specificity of our observed findings to new learning and skill acquisition. Interestingly, we found a positive correlation between both time spent in SWS and the extent of STA amplitude change and improvements in task performance upon awakening.

Processing of an emergent task-related ensemble

Learning was associated with the emergence of a novel task-related ensemble of both direct and indirect units. In our experiments, randomly chosen pairs of direct units were conditioned through feedback to be volitionally modulated in order to move an actuator. Consistent with a growing body of literature^{3, 33,34}, modulation of direct units was accompanied by similar task-related firing rate changes in a subset of indirect units (i.e. tr). As shown in Figure 1 and outlined in the results section, nearly all direct and a subset of indirect units became increasingly modulated in a task-dependent manner with practice. The emergent functional coupling between these units appeared to be a consequence of learning and successful completion of the neuroprosthetic task. Because direct units are embedded in highly connected M1 cortical networks, it is possible that such modulation of adjacent indirect activity is important for precise cortical control.

During the post-learning SWS there was significantly higher coincident activation of the emergent task-related ensemble. We also found that the extent of firing rate modulation during task performance predicted the strength of the modifications evident during SWS (Fig 2d). In the absence of learning or new performance gains this was not present. This strongly suggests that the functional co-activation of units during successful learning is directly linked to the modified functional connectivity and coherent reactivation detected during SWS. We also noted a positive correlation between time spent in SWS and subsequent improvements in task performance. This observed performance gain is consistent with past studies suggesting that even brief periods of sleep can improve motor performance^20–24. It remains unclear if our observed offline processing during SWA is sufficient and necessary to trigger performance gains upon awakening; there may be other processes recruited during SWS that could also contribute to task improvements^17,38.

Broader link to sleep and memory

A growing body of literature has linked offline processing during sleep to memory consolidation^{17, 18}. Memory formation in the hippocampal system is the most widely studied^19,39–41. In general, after an initial encoding phase, hippocampus-based memories appear to undergo a process of consolidation in which its representation is stabilized to neocortical systems. While the precise mechanisms underlying such consolidation are incompletely understood, sleep-dependent interactions between hippocampal and cortical circuits have been linked to this process of consolidation. Spontaneous reactivation of neurons reflecting previous experiences have been found during both non-REM (i.e. including SWA) and REM sleep in both the hippocampus and cortex¹⁹. Recent studies have also suggested that both disruption of hippocampal circuits with electrical stimulation as well as sensory cue dependent facilitation of memory formations can respectively impede and facilitate memory formation, suggesting a direct link between the offline processing and the consolidation of episodic memories^42,43.

Sleep, in general, and SWS, in particular, also appear to be important for the consolidation of procedural memories^21–25. For example, after learning a new motor skill, offline processing during overnight sleep^20–23 or brief daytime naps²⁴ can facilitate consolidation. Local changes in SWA are also associated with motor learning and performance^26–29. After new motor learning or sensory stimulation there appear to be local increases of SWA in specific cortical areas or hemispheres^26,44. In contrast, disuse and inactivity can locally decrease SWA and also deteriorate task performance²⁸. It remains incompletely understood, however, how neural ensembles in motor cortex are precisely modified during SWA after skill acquisition. In this context, BMIs offer a powerful tool to directly modulate neurons in motor cortex, thereby allowing precise characterization of how both task-related and task-unrelated ensembles are differentially processed in motor cortex during SWA. While the exact link between neuroprosthetic learning and general procedural learning remains unclear, our results suggest that the emergent task-related ensembles could be also processed in a similar manner after natural motor learning.

Implications for neuroprosthetic control

An important goal of the field of BMIs is to allow stable control of complex devices over long periods of time. While decoder adaptation can speed the overall rate of skill acquisition, adaptation of neural circuits and neural plasticity over longer periods of time may be essential for stable skill acquisition. This may be especially important for skilled control over complex devices that resemble our natural control of limbs. For example, a recent study highlighted that optimal recruitment of long-term neural plasticity is essential for achieving flexible control that resembles our natural abilities¹⁴. The study illustrated that long-term neural plasticity (i.e. across multiple sessions) is essential for achieving BMI control that can readily switch between two control schemes without interference. Specifically, only after long-term stabilization of a single control scheme, was simultaneous acquisition of a second control scheme possible. Based on the parallels between motor and neuroprosthetic control, a reasonable hypothesis is that consolidation of ‘prosthetic memory’ is essential for such apparent resistance to interference. Our observed phenomenon of offline processing during SWS may consolidate such a prosthetic memory.

Conclusion

We provide direct evidence that an emergent group of task-related units, which were increasingly functionally coupled with learning and task performance, experienced coherent reactivation during SWS_post. Knowledge about this phenomenon should help better account for mechanisms of neural plasticity and further the goal of achieving stable long-lasting neuroprosthetic control that resembles natural motor control.

FULL METHODS

Animals/Surgery

Experiments were approved by the Institutional Animal Care and Use Committee at the San Francisco VA Medical Center. We used six adult Long-Evans male rats. Animals were kept under controlled temperature and a 12-hour light: 12-hour dark cycle with lights on at 06:00 AM. Probes were implanted during a recovery surgery performed under isofluorane (1–3%) anesthesia following induction with ketamine (2mg/kg body weight or b.w.) and xylazine (1 mg/kg b.w.). Atropine sulfate was also administered prior to anesthesia (0.02 mg/kg b.w.) The post-operative recovery regimen included administration of buprenorphine at 0.02 mg/kg b.w and meloxicam at 0.2mg/kg b.w. Dexamethasone at 0.5 mg/kg b.w. and Trimethoprim sulfadiazine at 15 mg/kg b.w. were also administered post-operatively for five days. We used 32-channel microwire arrays (33 µm polyimide coated tungsten microwire arrays) in four rats. We also used 32-channel silicon probe arrays in a tetrode configuration in two rats. Arrays were lowered down to 1400–1800 µm in the primary motor cortex (M1) in the upper limb area (1–3 mm anterior to bregma and 2–4 mm lateral from midline). The reference wire was wrapped around a screw inserted in the midline over the cerebellum. Final localization of depth was based on quality of recordings across the array at the time of implantation. In one rat we implanted electromyogram (EMG) wires into neck muscles. Specifically, pairs of Teflon-coated stainless steel wires (AM Systems) were inserted in neck muscles and tunneled subcutaneously to a connector on the cap. All animals were allowed to recover for 1-week prior to start of experiments.

Electrophysiology

We recorded extracellular neural activity using tungsten microwire electrode arrays (MEAs, n=4 rats, Tucker-Davis Technologies or TDT, FL) or silicon probes in a tetrode configuration (n=2 rats, Neuronexus Technologies, MI). We recorded spike and LFP activity using a 128-channel TDT-RZ2 system (Tucker-Davies Technologies). Spike data was sampled at 24414 Hz and LFP data at 1018 Hz. ZIF-clip based analog headstages with a unity gain and high impedance (~1 GΩ) were used. Differential EMG was also recorded at 1018 Hz and high-pass filtered with low-frequency cut off at 100 Hz. Only clearly identifiable units with good waveforms and high signal-to-noise were used. The remaining neural data was recorded for offline analysis. Behavior related timestamps (i.e. trial onset, trial completion) were sent to the RZ2 analog input channel using an Arduino digital board and synchronized to neural data.

We have used the term ‘unit’ to refer to the sorted spike recordings from both the MEA and tetrode recordings. For both, we initially used an online sorting program (SpikePac, TDT) for neuroprosthetic control (i.e. either in single channel or tetrode mode). We then conducted offline sorting. We sorted the MEA recordings using standard offline cluster cutting methods in TDT’s OpenSorter software. We subsequently used waveform shape and the presence of an absolute/relative refractory period in the interspike interval (ISI) to judge quality of isolation (Supplementary Fig. 1)¹⁴. Offline tetrode sorting was performed using a method described previously (Supplementary Fig. 2)^45,46. Specifically, a voltage-based threshold was set based on visual inspection for each channel that allowed for best separation between putative spikes and noise; typically this threshold was at least 4 standard deviation (SD) away from the mean. Events were time-stamped and waveforms for each event were peak aligned. K-means clustering was then performed across the entire data matrix of waveforms (30 samples/ch × 4 chs × # of waveforms). Automated sorting was performed by: (1) first over-clustering wave-forms using a K-means algorithm (i.e. split into many mini-clusters), (2) followed by a calculation of interface energy (a nonlinear similarity metric that allows for an automated decision of whether mini-clusters are actually part of the same cluster), and (3) followed by aggregation of similar clusters. Such aggregation allows for a reduction in the total numbers of clusters that need to be manually inspected. Automated sorting was followed by manual inspection and sorting of spikes (including both merging and splitting clusters further, and removing significant outliers based on Gaussian distribution), using feature space, autocorrelations, cross-correlations and linear discriminant analysis to determine which clusters represent single units and to prevent over-sorting. Supplementary Fig. 1 and 2 illustrates examples of sorting achieved with the MEA and silicon probe tetrode recordings.

Behavior

After recovery, animals were typically gentled for several days prior to the start of experimental sessions. Animals acclimated to a custom plexiglass behavioral box (Fig. 1a) during this period. The box was equipped with a slit (covered with a door at one end) that served as a drinking zone. Initially, water delivery from the actuator was not introduced to the rats and they were just acclimatized to the box. Towards the end of the acclimation period, the rats typically fell asleep while in the box. Animals were then water scheduled such that water (from the feeding tube illustrated in Fig. 1a) was available in a randomized fashion while in the behavioral box. We monitored body weights on a daily basis to ensure that the weight did not drop below 95% of the initial weight.

Behavioral sessions were typically conducted in the morning, with second sessions conducted in the afternoon. Two single learning sessions were conducted in the afternoon. We found the same results for these experiments. We recorded neural data from the rats for 2 hours prior to start of BMI training. The rats were then allowed to perform the task over a 2-hour session. Recorded neural data was entered in real-time to custom routines in Matlab. These then served as control signals for the angular velocity of the feeding tube. The rats typically performed ~180–200 trials for robust learning sessions (e.g. Fig. 1c, Fig. 6a). Following this, we recorded neural data from animals for a 2-hour period. For the two session experiments, the animals then continued with another 2-hour training session followed by another spontaneous activity recording. Sorted units at the beginning of the recording were checked for maintenance throughout the second training session. We also collected ‘control sleep’ data in a subset of animals. After an initial spontaneous activity period with sleep, we delivered random automatic water rewards over a period to match a typical time period for task performance. We then recorded spontaneous activity and sleep.

Neural control of the feeding tube

During the BMI training sessions, we typically selected two well-isolated units as ‘direct’ and allowed their neural activity to control the angular velocity of the feeding tube (Fig. 1c). In three of the 15 sessions, there was only one neuron selected as the direct unit. These units maintained their stability throughout the recording as evidenced by stability of waveform shape and interspike-interval histograms¹⁴. We binned the spiking activity into 100 ms bins. We then established a mean firing rate for each neuron over a 3–5 minute baseline period. The mean firing rate was then subtracted from its current firing rate at all times. The specific transform that we used was:

$${\mathbf{\Theta }}_{\mathrm{v}}=C^{\ast }[{G_1}^{\ast }r1(i)+{G_2}^{\ast }r2(i)]$$

where Θ_v was the angular velocity of the feeding tube, r1(i) and r2(i) were firing rates of the direct units. G₁ and G₂ were randomized coefficients that ranged from +1 to −1 and were held constant after initialization. C was a fixed constant that scaled the firing rates to angular velocity. The animals were then allowed to control the feeding tube via modulation of neural activity. The tube started at the same position at the start of each trial (P₁ in Fig. 1a). The calculated angular velocity was added to the previous angular position at each time step (100 ms). During each trial, the angular position could range from −45 to +180 degrees. If the tube stayed in the ‘target zone’ (P₂ in Fig. 1a; spanned 10° area) for a period of 300 ms a water reward was delivered. In the beginning of a session, most rats were unsuccessful at bringing the feeding tube to position P₂. Most rats steadily improved control and reduced the time to completion of the task during the first session. In some cases, animals did not improve control (i.e. poor learning shown in Figure 4). In subsequent sessions these animals did demonstrate that they could learn the task. As shown in Supplementary Table 1, multiple learning sessions were obtained from each animal. These sessions were typically 1 week apart in order to ensure that new units were recorded. Consistent with past studies, we also found that incorporation of new units into the control scheme required new learning^8,14,15. In many sessions we videotaped the rat during the BMI training blocks. Consistent with multiple reports we did not observe movements that systematically predicted feeding tube movements^2,15,32. Specifically, we analyzed whether limb movements measured using the video recording (i.e. markers manually assigned to the head, torso and each limb using image processing software) co-varied with movements of the feeding tube. Across multiple sessions we did not find evidence for significant co-variation (data not shown). This is likely due to the fact that non-movement related random weights were assigned to the direct units.

Data Analysis

Sessions and changes in performance

Analysis was performed in Matlab (Mathworks, Natick, MA) with custom-written routines. A total of 19 training sessions recorded from 6 rats were used for our initial analysis. Fifteen of these sessions had ‘robust learning’ (i.e. > 3 SD drop in time to completion in the last 1/3 of trials or ‘late’ trials in comparison to the first 1/3 of trials or ‘early’ trials). Eight of these 15 sessions also had a second follow-up training session (i.e. Fig. 7). Four additional sessions were classified as ‘poor learning’ (i.e. no significant improvement in time to task completion). Supplementary Table 1 summarizes the Session details. In addition we analyzed three separate ‘control sleep’ sessions. As outlined above, during these experiments we matched the time awake using a randomized reward schedule that did not require learning. For Figure 7b and c we compared changes in task performance between and across sessions. Specifically, we compared the performance change between Block₁ and Block₂ by calculating the mean and standard deviation of the time to completion during the last 30 trials in Block1 and the first 30 trials Block₂ (Fig. 7b). We also compared the first and last 30 trials within Block₂. Furthermore, we also compared the best performance in Block1 (30 trials with the shortest time to reward) and the first 30 trials Block₂ (Supplementary Fig. 13). We used a paired t-test to assess statistical significance.

Task-related activity

The distinction between tr_d, tr_i and tu units was based on whether significant modulation of baseline firing activity after the ‘Go cue’ was present (i.e. peak of modulation at the time > 2.5 SD above the baseline period). For the correlation between task-related modulation and changes in amplitude of the STA, the percentage change in modulation was calculated for firing rates during the first four seconds after the ‘Go Cue’ relative to 3 seconds of the baseline segment (i.e. prior to the Go Cue).

Putative cell-type identification

This was performed by comparing the widths between the first trough in the negatively-detected spikes and the first peak after that on the mean waveforms (Supplementary Fig 1b–d).

Identification of NREM oscillations

Identification of pre and post-SWS epochs was performed by combined visual assessment of low-frequency, high amplitude slow-wave oscillations as well as a 3 SD threshold of the filtered data (0.3 – 3 Hz)^47,48. If there was a sustained reduction > 1.5 seconds in the amplitude of the SWA below threshold during a continuous epoch we excluded these segments. For the analysis of STA’s and coherence we matched the SWS time periods used for each (first 600 seconds). For subsequent analysis (i.e. Spearman correlation below) we used the entire time spent in SWS per session. Delta waves were detected directly from a filtered, z-scored SWS in the ‘median LFP channel’ in each animal (i.e. median value of z-scored LFP from all channels). After identification, only waves that contained a negativity larger than 80 µV (i.e. in the raw LFP) were included⁴⁸. These criteria resulted in reproducible and specific detection of high-amplitude delta waves in pre and post SWS epochs. We classified SWS using video analysis in 5 rats and EMG recordings/video analysis in 1 rat. We used the EMG recordings to confirm SWS (Supplementary Fig. 5). The video recordings were processed using MATLAB (Image Processing Toolbox) to detect any movements. We specifically subtracted a baseline image of the cage environment from each frame, converted the difference into a black and white image, filtered the resulting image for large objects, and then used segmentation analysis to identify the rodent’s body/head. We found that the previously described ‘40 second rule’ ⁴⁹ was a reliable indicator of sleep in comparison to EMG recordings. There were no significant differences between the duration of SWS (p=0.98, paired t-test) in the SWS_pre and SWS_post blocks (Supplementary Fig. 5). Moreover, we also examined if there are changes in the frequency and temporal lags between channels with a tr_d and those with ‘distant’ tu’s (i.e. greater than 2 electrodes apart). We did not find any differences in the temporal latencies (p=0.76, unpaired t-test, Supplementary Fig. 9b) and the OFF period density (p=0.77, unpaired t-test, Supplementary Fig. 9c).

Spike-triggered average

We first calculated the STA to measure how spikes locked to the SWA. For the SWS, we used both the filtered (0.3–3Hz) and the unfiltered LFP. Given the predominance of high amplitude low-frequencies these were not significantly different (Figure 2b). For the filtering we used a zero-phase distortion filter in MATLAB⁴⁸. While we used 600 sec for comparing the changes shown in the figure, we found that effects were similar even if all recorded SWS durations were used (data not shown). However, for subsequent analysis in the spindle (8–20 Hz) and ripple (100–300 Hz range) bands we used filtered data to minimize contamination from other bands⁴⁸. During the task, we found that the task related STA changed only in the ‘beta’ range (i.e. 12–40Hz band but not in other bands, p<0.0001, one-way ANOVA, Supplementary Fig. 4). We used the first 5 seconds after the start of the trial to calculate these STAs. We also used the LFP from a neighboring channel at a distance ranging from 150–250 µm (depending on if it was a MEA or silicon probe). For a subset of the data we also ensured that coherent spiking did not contribute to our results. Thus, we excised LFP data around the spike times (in the neighboring channel) and linearly interpolated the excised segment using neighboring data points. Our results were identical both with and without this procedure.

Coherency measures

We used the Chronux toolbox to calculate both the spike-spike coherence (SSC) and spike-field coherence (SFC)⁵⁰ (available online at : http://chronux.org/). The magnitude of both is a function of frequency and takes values between 0 and 1. We segmented the pre and post-SWS into 20-second segments and then averaged the coherency measures across segments. For the multitaper analysis we used a time-bandwidth (TW) product of 10 with 19 tapers. To compare coherences across groups, a z-score was calculated using the programs available in the Chronux Toolkit. Coherence between activity in two regions was calculated and defined as:

$$\mathit{\text{Cxy}}=\frac{\left|\mathit{\text{Rxy}}\right|}{\sqrt{\left|\mathit{\text{Rxx}}\right|}\sqrt{\left|\mathit{\text{Ryy}}\right|}}$$

where R_xx and R_yy are the power spectra and R_xy is the cross-spectrum. Spectral analysis were calculated in segmented SWS epochs and averaged across these epochs across animals. Mean coherence in the slow-wave band was calculated for the 0.3 – 3 Hz band. Significance testing on coherence estimates was performed on mean slow-wave band estimates across spike-field and spike-spike pairs using one-way ANOVA and independent samples t-tests for multiple comparisons. Circular statistics were used for comparing phases of the different cell types before and after learning. Specifically, Raleigh test for homogeneity was used to check the presence of a uniform distribution of the phases and Watson-Williams circular t-test was used to compare changes in phase. The change of magnitude for SFC and SSC were analyzed between the 0.3 and 3 Hz frequency band. For SSC analysis, task-related direct unit with greatest depth modulation was used to calculate SSC for every other unit. For tu - tu and tr_i - tr_i pairs, the least modulated unrelated unit and greatest modulated indirect unit were chosen respectively. The power-spectrum of the LFP channels used in the coherence calculation as well as for overall SWA power change in pre and post SWS was also determined using the multitaper method (Supplementary Fig. 7).

Spike cross-correlation

We computed the cross-correlation histogram (CCH) for the same tr_d – tr_d, tr_d -tr_i and tu - tu pairs that were evaluated during the SSC analyses. The spike counts were equalized in pre and post SWS and the pairwise coincident firing was quantified by taking the ratio of the peak (within a time period of ±5 ms) in the center with tail on side (time period of ±10–20ms; see Supplementary Fig 11). For a subset of data we also constructed pseudo random spike train CCH with identical spike counts, mean firing rate and duration to the experimental data. Such simulations were run 200 times (Monte Carlo Simulations). Significant CCH in these cases were the ones with higher central peaks than 99% of the simulated data. Only task related neuronal pairs were found to have significant CCHs.

Ensemble Reactivation Analyses

Reactivation analysis characterized the neural activity patterns in SWS_pre and SWS_post using a template that was created during task execution in the awake period^35–37. We computed a pairwise unit activity correlation matrix as described in Peyrache et al, 2010 for SWS_pre, awake and SWS_post. The eigenvector with the largest eigenvalue in the awake correlation matrix served as the learning-related cell assembly. For all epochs, spike trains were binned (Δt_bin = 50ms). The obtained spike counts for each cell [sⁱ (t), i = 1:n, t= 1:B, where n is the number of cells and B is the number of time bins in the epoch] were z transformed, obtaining the Q matrix

$$Q_{\mathit{\text{it}}}=\frac{s^i(t)-<s^i>}{{\sigma }_{s^i}}$$

where < sⁱ > is the mean and is σ_sⁱ the standard deviation.

The pairwise cell activity correlation matrix can be presented in following equation (1):

$$C=\frac{1}{B}{\mathit{\text{QQ}}}^t$$

We thus obtained three spike count matrices, Q_SWSpre, Q_awake and Q_SWSpost, and the three correlation matrices, C_SWSpre, C_awake and C_SWSpost. For quantification of the instantaneous match of activity during SWS to learning related activity during awake periods, we established a C^template (i.e. awake) and C^match (i.e. SWS_pre and SWS_post). As outlined in Peyrache et. al, we also calculated a measure of similarity, M, using the elements of C^template and C^match:

$$M^{\mathit{\text{template}}-\mathit{\text{match}}}={\sum }_{i,j,i<j}{C}_{\mathit{\text{ij}}}^{\mathit{\text{match}}}{C}_{\mathit{\text{ij}}}^{\mathit{\text{template}}}$$

$$=\frac{1}{2B^{\mathit{\text{match}}}}\sum _{t=1}^{B^{\mathit{\text{match}}}}{\sum }_{i,j,i\ne j}{Q}_{\mathit{\text{ij}}}^{\mathit{\text{match}}}{C}_{\mathit{\text{ij}}}^{\mathit{\text{template}}}{Q}_{\mathit{\text{jt}}}^{\mathit{\text{match}}}$$

To distinguish among groups, we calculated the eigenvectors of C^template, namely p^(l) (with p(¹) associated with the largest eigenvalue λ₁). We then decomposed C^template into projectors, P^(l), defined by the outer products of the eigenvectors with themselves.

$$C^{\mathit{\text{template}}}=\sum _l{\mathrm{\lambda }}_l{P}^{(l)}=\sum _l{\mathrm{\lambda }}_l{p}^{(l)}{(p^{(l)})}^T$$

We also generated a time series R_l^match (t) that measured the instantaneous match of the l-th template, corresponding to the eigenvectors described below. Put another way, this value is the ‘reactivation strength’ or the instantaneous measure of how similar the ensemble activity during SWS_pre and SWS_post is to that identified during the awake period.

$$M^{\mathit{\text{template}}-\mathit{\text{match}}}=\frac{1}{2B^{\mathit{\text{match}}}}{\sum }_l{\mathrm{\lambda }}_l\sum _{t=1}^{B^{\mathit{\text{match}}}}\sum _{i,j,i\ne j}{Q}_{\mathit{\text{ij}}}^{\mathit{\text{match}}}{P}^{(l)}{Q}_{\mathit{\text{jt}}}^{\mathit{\text{match}}}$$

$$=\frac{1}{2B^{\mathit{\text{match}}}}{\sum }_l{\mathrm{\lambda }}_l\sum _{t=1}^{B^{\mathit{\text{match}}}}{R}_l^{\mathit{\text{match}}}(t)$$

with

$$R_l^{\mathit{\text{match}}}(t)=\sum _{i,j,i\ne j}{Q}_{\mathit{\text{ij}}}^{\mathit{\text{match}}}{P}^{(l)}{Q}_{\mathit{\text{jt}}}^{\mathit{\text{match}}}$$

Q_ij^match is a vector of the multi-cell counts at time point t. Peyrache et. al further proposed the use of the Marcenko-Pastur distribution as the null hypothesis for the existence of cell assemblies. It was demonstrated that eigenvalues of the correlation matrix of a normal random matrix R with statistically independent rows follows a probability distribution described.

$$\mathrm{p}(\mathrm{\lambda })=\frac{q}{2\mathrm{\pi }{\mathrm{\sigma }}^2}\frac{\sqrt{({\mathrm{\lambda }}_{\mathit{\text{max}}}-\mathrm{\lambda })(\mathrm{\lambda }-{\mathrm{\lambda }}_{\text{min}}}}{\mathrm{\lambda }}$$

where

$${\mathrm{\lambda }}_{\mathit{\text{min}}}^{\mathit{\text{max}}}={\sigma }^2{(1\pm \sqrt{1/q})}^2$$

And σ² is the variance of the elements of the random matrix R, which is 1 here (due to z scoring), and q = R_columns/R_rows ≥ 1. Under the null hypothesis of an uncorrelated matrix, the correlations between spike trains are determined only by random fluctuations and the eigenvalues of template awake matrix must lie between λ_min and λ_max. Eigenvalues greater than λ_max are therefore a sign of nonrandom correlations in the matrix, and for this reason we refer to these principal components as signal. A reactivation time series (i.e. Figure 6c) measured the instantaneous match of this cell assembly to the ongoing activity³⁵.

Statistical analysis

We performed one-way ANOVA with multiple comparisons wherever significance assessment was required (Fig. 2c,3c,4c,5b,c; Supp. Fig 1d,f,g, 4b 6a,b, and 11). We also used a paired t-test for comparisons between early and late trials and features of SWS_pre and SWS_post and other relevant comparisons(e.g. time to reward and proportion of unsuccessful trials in and early and late trials, and time to reward comparison between block1 and block₂ for second sleep dataset; delta wave density, PSD amplitude changes, duration changes, etc in SWS_pre and SWS_post; change in firing rate of units, reactivation strengths in post awake and SWS epochs, etc). Unpaired t-test were also used for several comparisons namely, proportion of cells with significant MD_change in direct and indirect unit pools, STA_amp change for units recorded with silicon probes versus multielectrode arrays, delta-triggered reactivation strength comparison in SWS_post from robust and poor learning sessions, etc. We also used linear regression to evaluate trends between firing rate change of individual units versus STA amplitude and PSD amplitude versus STA amplitude. Kolmogorov-Smirnov test was used for comparing burst distribution in ISI distributions from SWS_pre and SWS_post. We used the spearman correlation between time spent in SWS and improvements in task performance because the distribution of SWS durations were not normal. For similar reasons, we used spearman correlation between the firing rate modulation and STA effect size. Logrank test was used to determine probability of higher strength reactivation strength in SWS_post after robust or poor learning and also in SWS_post versus post awake epochs after robust learning. If there was higher likelihood of greater reactivation strength in comparison to SWS_pre, the difference of counts of reactivations strengths of higher magnitude would show right skewed histogram and logrank test can test if such right-skewed curves are different from each other.