Understanding the Origin of Species with Genome-Scale Data: the Role of Gene Flow

Abstract

As it becomes easier to sequence multiple genomes from closely related species, evolutionary biologists working on speciation are struggling to get the most out of very large population-genomic data sets. Such data hold the potential to resolve evolutionary biology’s long-standing questions about the role of gene exchange in species formation. In principle the new population genomic data can be used to disentangle the conflicting roles of natural selection and gene flow during the divergence process. However there are great challenges in taking full advantage of such data, especially with regard to including recombination in genetic models of the divergence process. Current data, models, methods and the potential pitfalls in using them will be considered here.

Introduction

One of the many doors that open when a species’ genome is first sequenced is to the world of population genomics and to the unparalleled study of the evolutionary divergence of closely related populations and species. Ever since Darwin developed his model of how one species splits into two (his principle of divergence described in Chapter four of “The Origin of Species”)¹ the field of evolutionary biology has been divided on the question of whether Darwin’s model is correct. With growing access to very large amounts of genome data, from multiple individuals of a species, it becomes increasingly likely that we will resolve this long-standing question. Recent next-generation sequencing (NGS) technologies and assembly tools, including restriction-site-associated DNA sequencing (RAD-tag) ², now make it possible to affordably obtain genome-scale data from multiple individuals ^{3, 4}. When individuals are sampled from multiple populations of a species, as has been done for humans e.g. ^{5, 6, 7}, as well as stickleback fish e.g. ² and dogs ⁸, or from closely related species as has been done with Heliconius butterflies ⁹ and orangutans ¹⁰, we gain an exceptional view, not only the variation within populations and species, but also the variation that lies between. Data sets like these include millions of variable SNPs and other kinds of polymorphisms and hold the promise of finally revealing the secrets of how species have formed.

However a flood of new data may not lead directly to a commensurate gain in knowledge; and today, as new population genomic data sets are emerging, our skills of analysis and interpretation are partly overwhelmed. With the rise of large NGS datasets, that reveal complex patterns of variation across species’ genomes, we find that our best models and tools for explaining patterns of variation were designed for a simpler time, with smaller data sets. In the first place NGS datasets present unique challenges, apart from their size, that result from the way they are generated. For example, it is common to use a reference genome to align additional genomes and yet this introduces a form of ascertainment bias that can affect one’s findings. Secondly most models and methods available to analyze NGS data have limitations that prevent using all of the information in the data that bears on the processes of interest.

In this review we survey the state of the art of population divergence models and inference methods, with regard to population genomics data sets. We do not examine in detail the technical challenges related with NGS for correcting sequencing, assembly and SNP calling errors, as these have been recently reviewed elsewhere ^{3, 11, 12}. Rather we focus on models of population divergence and on methods to detect and quantify gene flow, as well as methods to distinguish alternative modes of speciation. We discuss the limitations of these methods and provide examples of their application to recently available genome-wide datasets.

Models s of species formation

Speciation in the absence of gene flow

When two populations become allopatric (i.e. completely geographically separated) they can diverge without mixing genes and eventually become reproductively isolated ¹³. Compared to divergence in the presence of gene exchange this is a comparatively simple process; and this simplicity, together with clear biogeographic evidence, such as the finding that in island archipelagos it is common to find different species on different islands, convinced many that this was how nearly all new species formed ^13–18. For much of the 20th century, this allopatric mode of speciation was thought to explain nearly all speciation events, at least in animals.

Speciation in the presence of gene flow

Darwin supposed that species could form even without having geographically separated populations. Rather he envisioned that natural selection can act in disparate ways over a species range to pull a species in different directions and eventually split it, first into different varieties and finally into separate species. However Darwin’s model of what has come to be called ‘sympatric speciation’ was considered by many to be unlikely. The reason is that researchers realized that gene exchange across a species range, which would occur in Darwin’s scenario, would be a strong homogenizing force counteracting divergence via natural selection. More recently genetic data (e.g. mtDNA sequences and microsatellites) together with biogeographic circumstances have provided compelling evidence that sympatric speciation has occurred in a number of contexts ^19–21.

At the genetic level Darwin’s model raises complexities, for it predicts that divergence in the presence of gene flow can cause different genes to experience very different histories. Diversifying selection favors different alleles in different parts of a species range (and at one or more loci). However, the movement of all genes across the range of the species as the normal result of organisms reproducing and dispersing will regularly move alleles that are affected by the diversifying selection into the “wrong” part of the species range. It will also cause the species to appear to be homogenous when examined for patterns of variation at genes not targeted by diversifying selection. For example, it is possible for diversifying selection to be driving divergence at just a few genes, while gene flow maintains relative uniformity across the species range for most of the genome^{22, 23}. Finding the genomic regions of divergence – so-called “islands of speciation” – typically requires a genomic approach ²⁴.

An additional major player in the divergence process, particularly when gene-flow is occurring, is recombination, the breaking and re-joining of chromosomes that happens during meiosis every generation, and that allows different parts of the genome to have different histories. Because of recombination, an allele favored by selection and increasing in frequency will carry with it, in its trajectory towards fixation, only those flanking regions to which it is most tightly linked ^{25, 26}. Also, it is possible for alleles at neutral loci to move by the action of gene flow across the species range, and to co-occur in the very same population of genomes where there are loci diverging by the action of diversifying selection ²⁷. Recombination thus allows a species to have a population of genomes with a split personality – to resemble two diverging gene pools at loci affected by diversifying selection, and to resemble a single gene pool at loci that are not under selection in this way. Evidence of this kind of genomic schism has come from a diversity of systems in recent years, based on DNA Sanger sequence and microsatellite data ²³ and more recently from NGS data in stickleback fishes ² and Heliconius butterflies ⁹.

Modeling Population Divergence

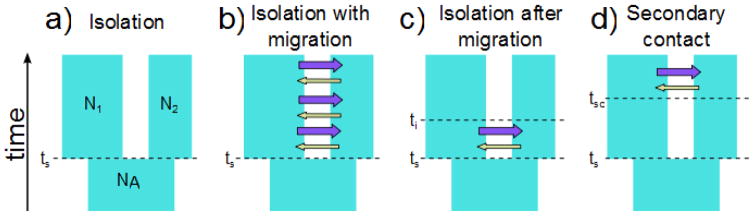
A widely used theoretical framework for studying speciation using genetic data is the “isolation with migration” (IM) model, so named because it includes both the separation of two populations (isolation) following a splitting event from their common ancestral population as well as migration between populations ^28–30. Figure 1 shows a series of IM models of increasing complexity that are relevant when studying speciation. At one extreme is a simple isolation model, where the migration rate is zero in both directions, which corresponds to an allopatric divergence scenario (Fig. 1A). Other models include isolation with migration (Fig 1B), isolation after migration (Fig 1C) and secondary contact (Fig 1D). Models like those in Figure 1 have been the focus of a great deal of research in recent years, and it has been shown that patterns of genetic variation in samples from two closely related populations or species can be used to distinguish a pure isolation model (Fig. 1A) from a model with migration (Fig. 1B–D) ^{28, 29}. The growing evidence of persistent gene exchange between closely related species means that divergence often arises in the midst of conflicting evolutionary processes ²³. Given evidence of diversifying selection together with gene flow, the next question is often “when did the gene flow occur?”. Has it been continuous (model 1B), or has it stopped (model 1C), or did it start anew with secondary contact after the populations had already diverged (model 1D).

Figure 1. Alternative modes of divergence.

All models assume that an ancestral population of size N_A splits into two populations at time t_s (time of split). The two present day populations have effective sizes N₁ and N₂, respectively. In model A) the migration rate is zero in both directions, which corresponds to an allopatric divergence scenario. B–D) Alternative models in which populations have been exchanging migrants. B) Gene flow at constant rates since the split from the ancestral population. Migration rates are assumed constant through time but gene flow can be asymmetric, i.e. one migration rate for each direction. C) Scenario in which populations begin diverging in the presence of gene flow but experience a cessation of gene flow after some time t_i (time since isolation). If the lack of current gene flow in this model is due to reproductive isolation then this represents a history in which divergence occurred to the point of speciation in the presence of gene flow. In D) we consider the alternative migration history where populations were isolated and diverged for a period of time in the absence of gene flow, followed by secondary contact at t_sc (time of secondary contact), and the introgression of alleles from the other population by gene flow.

Inferring the history of divergence

With enormous information content, NGS data from multiple individuals offer the promise of disentangling the complex interplay between selection, gene flow and recombination that occurs during speciation with gene flow. First, by having information for essentially all parts of the genome, we can gain a more detailed and accurate picture of the demography of populations ^{31, 32}. Second, it becomes possible to ask whether some parts of the genome have been exchanging genes more than others. Significant variation in gene flow levels across the genome constitutes clear, albeit indirect evidence that selection is acting against gene flow to a greater degree in some genome regions than others ^{33, 34}. Third, NGS data allow us to get better estimates of recombination rates and linkage disequilibrium (LD) patterns along the genome ^{35, 36} and this can in principle be used to infer the timing and magnitude of gene flow. Finally, polymorphism and LD along the genome also bear information about selective sweeps and genes that are the targets of diversifying selection reviewed in ^{37, 38}). However, all of these inferences depend on having a theoretical framework that connects patterns of variation to an explicit model.

Historical gene flow and LD patterns

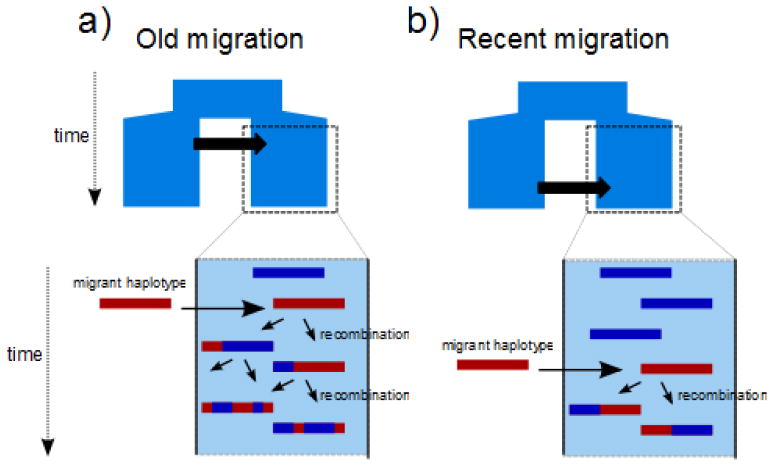
Population geneticists have long known that the movement of genes into a population can create strong patterns of LD in the regions of the genome experiencing that gene flow ^{36, 39, 40}. However it remains a challenge to take advantage of this phenomenon to infer the history of gene flow ^40–42. One approach to disentangle alternative divergence models, such as the ones shown in Fig. 1, is based on the distribution of haplotype block lengths ^{43, 44}. The principle is that when a migrant enters a population it carries a set of chromosomes that, as time goes by, are broken into smaller fragments due to recombination (Fig. 3).

Figure 3. Distinguishing migration events based on LD block structure.

Schematic representation of the expected distribution of the haplotype block lengths for A) an old migration event, and B) a recent migration event. For simplicity, we assumed that all individuals share the same haplotype in the destination population (blue haplotype), i.e. this haplotype has reached fixation. When a migrant haplotype enters a population, as times goes by, recombination breaks it into smaller fragments. Thus, blocks are expected to be shorter following an old migration event (a), than right after a recent migration event, for which blocks are expected to be larger.

The distribution of block lengths depends not only on the recombination rate but also on the frequency at which a given population receives immigrants and the older the migration event the shorter the blocks are expected to be. Thus, the distribution of block lengths should allow disentangling alternative scenarios. A similar idea has been recently used to separate a scenario of admixture from ancestral population structure in the case of Neanderthals and modern humans ⁴⁵. In this study LD patterns in present day European genomes data supported a model with gene flow from Neanderthals, estimated to have occurred between 37 and 86 KYA.

Genome Scans using Indicators of Divergence

Depending on an investigator’s question, it can sometimes be useful to take a fairly simple approach that does not use models with lots of parameters to study the levels of divergence between populations. This is achieved by tailoring analyses to a specific component of the divergence process, and scanning across the genome while calculating statistics that are expected to be sensitive to that feature. In particular, there has been lots of interest in detecting “islands of differentiation” that are those regions of the genome that are different between species, potentially as a result of the action of selection, by looking at the distribution of summary statistics that measure genetic differentiation, such as F_ST ⁴⁶. For example, in the first study using RAD-tag sequencing, the differentiation of 45,000 SNPs along the genome between oceanic and freshwater populations of threespine sticklebacks (Gasterosteus aculeatus) showed, overall, reduced levels of differentiation (F_ST values close to zero) ². However, when taking a sliding window approach, in comparisons between the freshwater and oceanic populations the authors found evidence for genomic regions characterized by very high F_ST values (>0.35), potentially harboring genes under selection in freshwater environment. Interestingly, the same genomic regions were found in the different freshwater populations, suggesting parallel adaptation to the freshwater environment. These results are in agreement with a larger study comprising seven pairs of closely related marine and freshwater populations comprising 5,897,368 SNPs ⁴⁷.

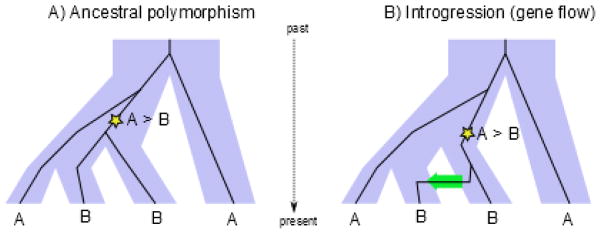
Another type of genome scan that is targeted to identify recent admixture relies upon comparing the population tree (assumed to be known) with the gene trees inferred at a specific site. Incongruences between the population tree and the gene tree can be due to lineage sorting (shared ancestral polymorphism) or to gene flow. One statistic, called “D”, that was specifically designed to detect introgression from one population to another is shown in Fig. 4 ⁴⁸. Computing D requires a genome from each of two sister populations, a genome from a third population (potential source of introgressed genes) and a fourth outgroup genome to identify the ancestral state (identified as A). Focusing on SNPs where the candidate source population has the derived allele (B) and the two sister genomes have different alleles, there are two possible configurations, either ABBA or BABA. Under the hypothesis of shared ancestral polymorphism the number of tree topologies of ABBA and BABA are expected to be equal and the expected D will be zero. Deviations from that expectation are interpreted as evidence of introgression. As with F_ST genome scans, investigators can look at the distribution of D along the genome given an arbitrary window size, but when using D the aim is to find genomic regions that specifically experienced introgression, whereas in the case of F_ST, the goal is to identify regions of high differentiation, regardless of the cause.

Figure 4. Disentangling ancestral polymorphism from gene flow (ABBA/BABA statistic).

The pattern ABBA can occurs due to A) ancestral polymorphism, i.e. coalescent of lineage from population 2 with lineage from population 3 in the ancestral population, or B) gene flow from population 3 to population 2. Mutation from ancestral state (A) to derived (B) shown as a star. Under a model with no gene flow, we expect that the pattern ABBA is as frequent as BABA, due to the fact that there is 50% chance that either the lineage from population 1 or from population 2 coalesce with lineage from population 3.

Genome scans using D were used to detect admixture between archaic and modern humans ^{49, 50}, and to study the patterns of introgression in Heliconius butterflies ⁹. In the case of modern and archaic humans unidirectional introgression from Neanderthals to non-African humans was estimated to have occurred for 1–4% of the genome ⁴⁹. Similarly, in the case of archaic Denisovans and present-day humans at 642,690 SNPs point to 4–6% of the present day Melanesian genomes being derived from admixture with Denisovans ⁵⁰. In the application of this approach to Heliconius butterflies a very interesting example of introgression driven by positive selection was identified ^{9, 51}. Using RAD-tag sequencing of 4% of the genome (~12 Mb), it was possible to detect introgression from the sympatric H. timareta to H. melpomene amaryllis (2–5% admixture), which are species exhibiting the same wing color patterns. Interestingly, only a few regions exhibited significant values of the D statistic, including genes known to contain the mimicry loci B/D and N/Yb. Despite the lack of an explicit test of positive selection, the fact that these regions harbor genes involved in mimicry is in agreement with an active role of selection promoting introgression at these regions. In both cases of humans and Heliconius there was evidence of regions exchanged between populations that were already differentiated, pointing to the importance of secondary contact in the recent evolutionary history of these species. In these species, the patterns of differentiation along the genome suggest a case where most of the genome is differentiated, consistent with a model of allopatric divergence (Fig. 1A) or divergence with limited gene flow (Fig. 1B), whereas other regions show evidence of secondary contact and uni- or by-directional introgression of genes from one population (species) to the other (Fig. 1C).

Likelihood and Model-Based Methods

As useful as genome scans with indicator variables can be to identify components of the divergence process, they fall short of providing a full portrait of divergence unless they are combined with other analyses. In this light, the goal for many investigators is to be able to calculate the likelihood of the data under a rich divergence model. For some model of divergence M, with a parameter set Θ, the likelihood is the probability, under that model, of the data given the parameters, i.e. Pr_M (Data|Θ)Having a likelihood function at hand allows estimating the most likely parameters of a given model either with frequentist or Bayesian approaches ⁵². Also, comparing the likelihood of the data under alternative divergence models opens the door to model choice approaches to infer the most probably divergence model. Currently there are two main families of likelihood-based approaches to studying divergence: one based on the Allele Frequency Spectrum (AFS), and a second based on sampling genealogies for short portions of the genome (BOX 1).

Box 1. Contrasting the AFS with genealogy sampling approaches.

AFS

In two populations, the AFS corresponds to a multidimensional matrix X, where each x_i,jentry gives the number of SNPs with an observed derived allele count of iin population1, and jin population 2. The likelihood of the observed AFS is easily computed given the AFS expected under a given evolutionary model. Each entry in the expected AFS reflects the probability of a given SNP falling into that cell. Assuming all SNPs are independent (i.e. assuming free recombination between SNPs), these probabilities can be obtained given the distribution of allele frequencies across populations, which are found with diffusion approximations to the evolutionary processes or with the coalescent. Once the expected AFS is obtained under a given model, it is easy to compute the likelihood for an arbitrarily large number of SNPs, making this a method applicable to the analysis of genomic data.

Genealogy sampling

Coalescent-based models aim at extracting information about relevant selective and demographic events from gene trees relating homologous DNA sequences (haplotypes) sampled from multiple populations. Each locus may contain several SNPs, and hence haplotype data contains an extra layer of information when compared with AFS approaches. Most methods assume no recombination within each locus, and free recombination among loci. Coalescent-based methods are usually based on samplers that collect genealogies from the posterior distribution. However, exploring the genealogical space can be extremely complex and relies on highly computationally intensive Monte Carlo algorithms, such as MCMC, that do not easily extend to large genomic multilocus datasets.

	AFS	Coalescent-based
Type of data	SNPs (biallelic markers)	Phased DNA segment (haplotype)
Assumptions about recombination	Free recombination among SNPs (all SNPs independent)	Free recombination among loci, and complete linkage within loci
Assumptions about mutation	Mutation rates equal for all SNP	Mutation rates vary across loci
Likelihood	Diffusion-based or Coalescent-based	Coalescent-based
Methods	Composite -likelihoods. Relatively fast and able to deal with millions of SNPs.	Monte Carlo methods based on genealogy samplers (MCMC, Importance Sampling, etc.) or based on approximate methods (ABC, PAC). Usually slow and computationally intensive, compromising their application to large genomic datasets.

Likelihoods using the Allele Frequency Spectrum

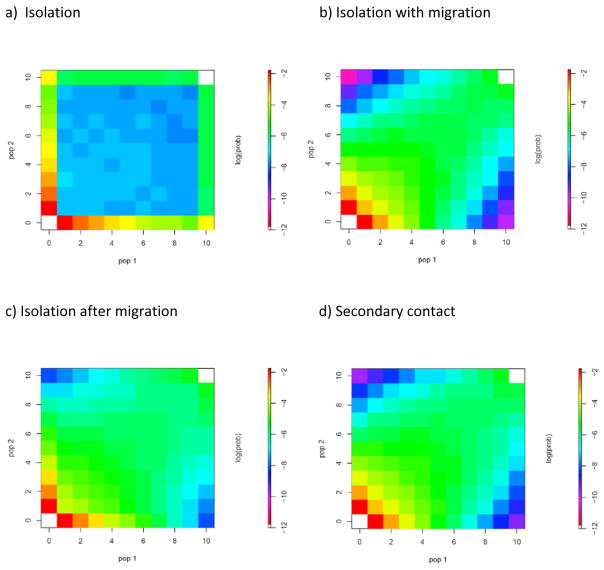
For a single SNP sampled in each of two populations, considered together with the base that is present in an outgroup genome, the data can be summarized as the number of copies of the derived allele in each of the two populations. For a large number of SNPs these counts fill a discrete distribution, the allele frequency spectrum (AFS) in two dimensions (one for each sampled population), which can be represented in graphical form (see Figure 3). A population genomic data set that is reduced to an AFS contains no information on LD, and thus discards much of the signal of gene flow. Nevertheless this approach has seen renewed interest as large SNP data sets have become more common ^53–55. Fig. 2 shows how the AFS can vary considerably for the different IM models shown in Fig. 1, particularly how simple isolation differs from models with gene flow. In the absence of gene flow (Fig 2A) the frequencies of SNPs found in only one population are different from the SNPs in the other population because genetic drift drives different alleles to fixation in each population. In contrast, in models with gene flow, the cells along the diagonal exhibit a higher density (Fig. 2B) because there are many SNPs with similar frequencies in the two populations. However, as exemplified in these AFSs, it is difficult to separate alternative scenarios with gene flow, as these tend to be similar (Fig. 2B–D).

Figure 2. Allele frequency spectrum under alternative divergence models. Each entry in the matrix (x,y) correspond to the probability of observing a SNP with frequency of derived allele x in pop 1 and y in pop 2.

The colors represent the log of the expected probability for each cell of the AFS. The white color corresponds to –Inf, i.e. to cells with an expected probability of zero. These AFS are conditional on polymorphic SNPs, hence the cells (0,0) and (10,10) have zero probability. The likelihood of an observed AFS can be computed by comparing it with these expected AFS. A) Isolation model. B) Isolation with migration. C) Isolation after migration. D) Secondary contact. The joint allele frequency spectrums for the different scenarios were obtained with coalescent simulations performed with ms (Hudson 2002). All scenarios were simulated assuming all populations share the same effective sizes (N=10,000), a time of split t_s=20,000 generations ago (T/4N=0.5), symmetric migration rate (2N₁m₁₂=5, 2N₂m₂₁=5, for scenarios b, c and d), for scenario c) a time of isolation of t_i=2000 generations ago (Ti/4N=0.05) and, for scenario d) a time of secondary contact of t_sc=6000 generations ago (Tsc/4N=0.15).

Given an AFS calculated from a data set, it is necessary then to be able to generate an expected AFS given a model of speciation and a set of parameter values. Although the expected AFS can be generated by simulations ^{41, 53, 56}, the expected AFS is also the focus of a famous body of population genetic theory in which differential equations describe the diffusion of allele frequencies in populations ^{57, 58}. In recent years the diffusion equation approach has been reawakened for the study of the AFS under IM models, such as the ones shown in Fig. 1, from genomic data ^{55, 59, 60}. If it is assumed that the SNPs segregate independently, then given both an observed and an expected AFS for a model of interest, the likelihood can be calculated directly using a multinomial distribution. One difficulty is that in reality most data sets comprise SNPs close enough on the genome that the assumption of independence does not apply. Still, the same likelihood calculation can be applied (now identified as a “composite likelihood” ⁵⁵) without introducing bias to the parameter estimates, albeit with limited access to confidence intervals and other analyses for which a likelihood is often used⁶¹.

AFS-based analyses on population genomic data sets have so far been conducted mostly on human data humans ^{44, 55, 60}, but the same approach can be used to study the divergence of closely related species. A nice example of this is the study of the divergence of Sumatran (Pongo abelii) and Bornean (Pongo pygmaeus) orangutans ¹⁰. Low coverage (8x) Illumina sequencing of 10 individuals from each species yielded a total of 12.74 million SNPS, and an AFS analysis lead to an estimated speciation time of 400,000 years with a low level of gene exchange between the species ¹⁰.

The AFS approach has also been applied to more complex models with more than two populations or species. One example comes from the analysis of human data from the 1000 Genomes Project under a three population IM model with gene flow and population expansions ⁶². By considering only SNPs at synonymous sites, and by modeling explicitly genotype calling errors, these authors estimated a time for expansion out of Africa around 51 KYA, a split between Europeans and East Asians around 23 KYA, recent population expansion in both Europeans and East Asians, and significant but reduced gene flow among all populations.

Likelihoods by Sampling Genealogies

If the recombination rate is low, such that it is unlikely to have occurred in the time since the common ancestor of a sample of sequences from one or various populations, as can be the case over a short region of the genome, the history of a sample of sequences can be described by a gene tree or genealogy (Box 2). The depth and structure of such genealogies have been described by coalescent theory for a diversity of models, including the models shown in Fig 1. ^63–65, and this coalescent modeling has made it possible to calculate the likelihood for data sets with multiple sequences of a short genomic region sampled from one or more populations. The key parameters in this approach do not include the actual genealogy for the sequences, but rather include the demographic parameters, like those in an IM model. Rather than focusing on the best gene tree (as is often the case in phylogenetics), the likelihood that is the target of this kind of population genetic research is obtained by integrating over all possible genealogies ⁶⁶. However because this integration cannot be solved analytically except for small sample sizes, likelihoods calculated using these approaches rely on computationally intensive methods ^{67, 68}. The general principle of these methods is to sample a set of genealogies consistent with the data to calculate the likelihood ^{68, 69}, which may in turn be used to obtain a posterior probability in a Bayesian approach ⁵². These methods have seen tremendous advances in recent decades, making it possible to estimate effective population sizes, migration rates, admixture contributions, dates of population declines, etc.^{32, 67}. Moreover, through likelihood ratio tests ⁶⁹ or through marginal likelihoods ⁷⁰, it has become possible to assess the fit of alternative models of divergence.

Box 2. Challenges of computing likelihoods with recombination.

If there is free recombination among sites, the likelihood of the data under most models is simply the product of the likelihoods of each site. This is the assumption underlying the AFS based methods. At the other extreme, when all sites are fully linked, the ancestry of a sample is fully captured by a gene tree shared by all sites. This is the realm of coalescent-based methods and of most genealogy sampling approaches. However the reality for most portions of most genomes lies in between these two extremes, and it is for intermediate levels of recombination, when two portions of the genome are neither completely linked, not completely unlinked, that the calculation of the likelihood becomes very difficult.

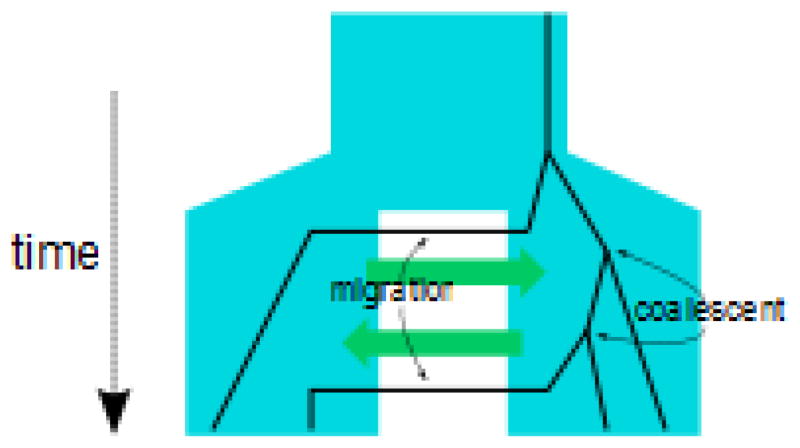
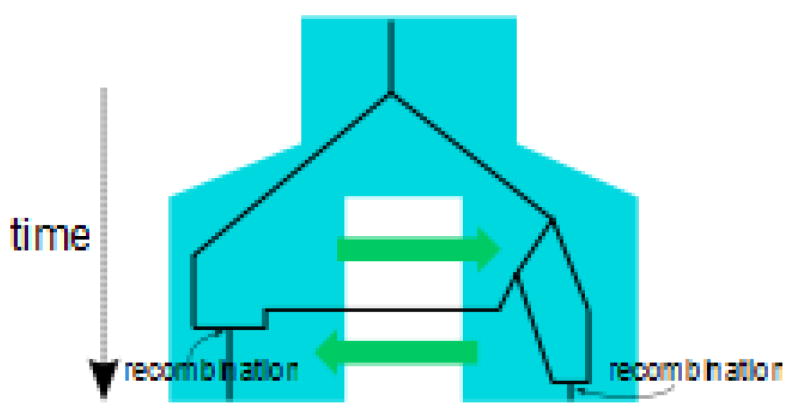
In a genealogy sampling method, likelihoods are computed by integrating over the genealogy space. Under a model characterized by a set of parameters Θ given data from L loci, X = (X₁,..., X_L), and its underlying gene trees, G = (G₁,..., G_L), where X_i and G_i represent the data and gene trees of the i^th locus (i = 1,..., L), respectively, the likelihood is found as a product over loci:

$$f(X\mid \mathrm{\Theta })=\int f(G\mid \mathrm{\Theta })\prod _{i=1}^{L}f(X_i\mid G_i)dG$$

where f(G|Θ) is the probability of the genealogies given the parameters Θ, and f(X_i|G_i) is the probability of the data at the i^th locus given its genealogy. The ancestral relationships between sequences are described by a gene tree with coalescent and migration events (Fig a). Recombination causes different parts of the genome to have different genealogical histories, and so the ancestry of a set of sequences is best pictured as a graph known as the Ancestral Recombination Graph (ARG) with joining events (coalescent events) and the splitting of gene copies into two parental copies (recombination events) ^{64, 74, 95, 96} (Fig b). Each recombination event corresponds to a split of the sequence into two sub-sequences that carry different ancestral segments. Interestingly, given the ARG, denoted A, we can look at the marginal gene trees for each site along the sequence, and compute the likelihood as a product over those marginal genealogies G_i as

$$f(X\mid \mathrm{\Theta })=\int f(A\mid \mathit{\Theta })\prod _{i=1}^{S}f(X\mid G_i)f(G_i\mid A)dA$$

where S is the number of sites, and f(G_i|A) is the probability of the marginal genealogy of i^th site given the ARG, which is by definition 1. The marginal distribution of genealogies can be obtained given the ARG, but the ARG cannot be obtained given the marginal genealogies. This is at the core of the difficulties of dealing with recombination. First, in comparison with gene trees, the ARG is dramatically more complex making the search through the ARG space intractable for population divergence models. Second, data typically contains diffuse information about which ARGs are more likely.

Figure a.

No recombination - gene tree

Figure b.

Recombination - ancestral graph

A genealogy-sampling approach to the likelihood can easily be extended to multiple loci if each has not had recombination, and if free recombination is assumed between loci. Under these assumptions the overall likelihood is the product of that for each locus (BOX 2). Thus, in principle, a genealogy sampling approach can be extended to a genome scale, if the computational power is available to handle many thousands of genome segments. For small sample sizes it is possible to obtain analytic solutions for the likelihood. This has been found for a two population IM model with constant gene flow for the special case of two sampled genomes ⁷¹. When applied to the divergence between Drosophila melanogaster and D. simulans, in a dataset with 30,323 genomic segments (average length of 405bp), a divergence time of 3.04 MYA and a non-zero migration rate from D. simulans to D. melanogaster was inferred ⁷¹. An alternative approach to computing the likelihood for larger sample sizes consists of computing the likelihood under IM models using generating functions, which so far has been shown to be possible for up to samples of three gene copies ^{72, 73}.

The largest dataset analyzed so far using a genealogy sampling approach consists of six genomes (each divided into 35,574 1kb segments), with one from each of six human populations. The data were examined assuming an isolation model with five populations and migration between one single pair of populations ⁶. Significant migration was estimated between two pairs of African populations, namely between San and Bantu and San and Yoruba. Surprisingly, the estimates for the times of split pointed to a very old divergence between these African populations (108–157 KYA), suggesting an ancient and complex population structure in that continent.

Likelihoods for Models with Recombination

Our ability to extract the information contained in linkage disequilibrium patterns about migration and admixture relies on an explicit model of the process of recombination. However, obtaining likelihoods under such models implies complex expressions that are difficult to solve or approximate (BOX 2). Full-likelihood methods that jointly estimate demography and recombination rates that have been developed so far use a model with just a single population ^74–76. Because of the difficulties of explicitly including intermediate levels of recombination (i.e. neither zero recombination nor effectively free recombination) most likelihood methods are limited to small segments of the data, as is typicall with genealogy samplers. Alternatively recombination may be ignored as in the composite likelihood approaches ^{77, 78}, as represented by most AFS-based applications with concomitant limitations ⁶¹.

Among approaches that are being developed to include recombination in likelihood calculations, are those based on the approximations of conditional likelihoods^79–81. These methods seems promising, as these conditional distributions can be used to generate genealogies and ancestral recombination graphs (ARGs) consistent with the data, which in turn can be used to compute likelihoods via importance sampling ⁸². Another promising approach that can be used to obtain the likelihood under a model with recombination for data from a small number of individuals (i.e. three), but large numbers of loci, is based on generating functions ⁷².

Another family of approaches treats recombination as a spatial process along the genome ^{83, 84}. In this framework the ancestry of each site is modeled by a gene tree that changes at points of recombination as one moves along the genome, as a function of the recombination rates and of some underlying demographic model. The recombination rate is treated as a parameter of the model and hence can be fixed by the researcher (assumed to be known) or can be estimated based on the data. This has been implemented in Hidden Markov Models to estimate divergence times and ancestral effective sizes ^{85, 86}, and to estimate population size changes⁸⁷.

Finally, another promising avenue for further research is based on the distribution of haplotype block lengths as a function of immigration timing and rates ⁴³. This approach has been recently extended to infer changes in migration rates through time ⁶², and was applied to infer changes in historical gene flow rates from Europe using admixed African-American HapMap data. Other variations on the this idea are methods that use summary statistics sensitive to LD have also been proposed ^{45, 88}, and methods to detect tracts of identity by descent (IBD) for informing on rates of migration ⁸⁹.

Technical challenges of NGS data for population genomic questions

In addition to the current theoretical and methodological limitations described above, there are also technical challenges in generating the data. An ideal sequencing technology, perhaps someday in the not too distant future, will output high quality reads of lengths greater than the size of duplicated regions in the target genome. The current crop of technologies that are in wide use fall short of these ideals, particularly in that they generate sequences of short lengths (generally less than 500 bp and often less than 100bp) ^{3, 4}. Even with very many reads and with paired-end libraries, assembly into a genome facsimile generally requires the aid of a previously sequenced reference genome. Two of the main difficulties with this protocol are Reference Genome Bias and Phase Uncertainty ¹¹ Other challenges with NGS have been recently reviewed elsewhere ^{3, 4, 11}.

Reference Genome Bias

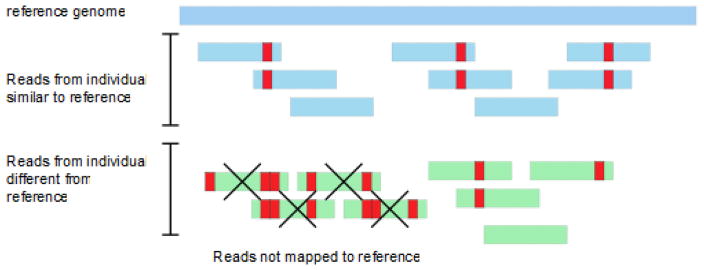
When a set of short sequences are assembled with the aid of a guide or reference genome, there arises a tendency for the resulting assembly to resemble the reference genome. This is a form of Ascertainment Bias which occurs whenever new data is obtained conditional on data previously ascertained ^{90, 91}. NGS reads that are different from their homologous location in the reference genome at polymorphic sites will tend to be misassembled, and overall there will be a tendency to underestimate differences between the new data and the reference genome to which it is aligned (Fig. 5)¹¹. This is particularly true for insertions and deletions, but also occurs for SNPs. Very high levels of sequence coverage will diminish this, as will de novo genome assembly.

Figure 5. Reference genome as a source of ascertainment bias.

Reads from two different individuals are mapped into a reference genome. Reads from individual 1 are similar to the reference genome (differences shown in red), and hence are easily aligned. However, reads from individual 2 contain several differences (shown in red - single point mutations or indels) in one of the regions. Given that these reads contain several differences it becomes difficult to align them with the reference genome. This introduces a source of ascertainment bias, as the allele frequencies in our sample depends on the reference genome, and hence on how it was constructed.

Phase Uncertainty

With diploid genome samples two genomes are sequenced simultaneously and the investigator typically does not know whether any pair of reads came from the same genome in the sample or from different genomes. This issue does not affect the identification of heterozygous positions, but this phase uncertainty greatly hinders the assembly of two genomes from one diploid sample and it complicates considerably the assessment of LD over longer distances. Use of pair-ended reads can extend the lengths of regions over which two separate sequences can be resolved, beyond the length of the actual reads ⁹². If data are available from an individual as well as both of its parents (a so-called “trio”), then it is possible to infer both chromosomes of the individual⁵. Alternatively a population genetic statistical approach can be used to estimate phase when there are data from multiple individuals⁹³. In the future, technology developments that allow for long reads from each chromosome are likely to reduce the problem of phase uncertainty ⁹⁴.

Conclusions

Notwithstanding the difficulties of reference genome bias, and phase uncertainty, population genomic data sets generated using NGS technologies offer tremendous potential for discerning the speciation process. However, in the quest to better understand population divergence and speciation, we wish to have theory and statistical methods that accommodate very large data sets and that connect the observed genomic patterns with relevant historical events for complex models of divergence. Currently the available tools do not take full advantage of population genomic data sets, although there are sophisticated methods for taking a genome scan approach for particular aspects of the divergence process that come into their own when population genomic data is available.

Going forward the greatest challenges on the theoretical and statistical side are to develop ways to fully include recombination in the analyses. Currently AFS and genealogy sampling approaches assume that different SNPs or loci are segregating independently, and other methods that take fuller account of recombination are restricted to smaller portions of the genome. NGS data has not yet changed our main paradigm of how populations diverge, but it has confirmed that natural selection is sometimes in conflict with gene exchange during the divergence process, and that gene flow is a widespread process. We envision that great advances in population genomic inference will be achieved as comprehensive methods emerge for fully including recombination in our divergence models, as these will allow investigators to use all of the relevant information in their NGS data.

Glossary

Allopatric divergence

The process of divergence between populations or species that are geographically separated, in the absence of gene flow.

Sympatric divergence

The process of divergence between populations or species occupying the same geographical area and in presence of gene flow.

Genetic Drift

Stochastic changes in gene frequency due to finite size of populations, resulting from the random sampling of gametes from the parents at each generation.

Neutral Genes

Genes whose genetic patterns are mostly affected by mutation and demographic factors, such as genetic drift and migration.

Haplotype

DNA sequence that is inherited as a single unit in absence of recombination.

Single Nucleotide Polymorphism (SNP)

Site in the DNA where there is variation across the genomes in a population, usually comprising two alleles that correspond to two different nucleotides.

F_ST

Proportion of the total genetic variability occurring among populations, typically used as a measure of the level of population genetic differentiation.

Allele Frequency Spectrum (AFS)

Distribution of the counts of SNPs with a given observed frequency in a single or multiple populations.

Ascertainment bias

Systematic bias introduced by the sampling design (e.g. criteria used to select individuals and/or genetic markers) that induces a nonrandom sample of observations

Linkage Disequilibrium

The non-random association of alleles at different sites or loci.

Islands of Differentiation

Genomic regions of elevated differentiation due to the action of natural selection.

Gene tree

Bifurcating tree representing the ancestral relationships of homologous haplotypes sampled from a single or multiple populations. A gene tree includes coalescent events and, in models with gene flow, migration events. A gene tree is characterized by a topology, branch lengths, coalescent times and migration times.

Ancestral Recombination Graph (ARG)

Graph representing the ancestral relationship of homologous DNA sequences sampled from a single or multiple populations. In models with gene flow, and ARG includes coalescent, migration and recombination events.

Diversifying Selection

natural selection acting towards different alleles (or phenotypes) being favored in different regions within a single or among multiple connected populations.

Coalescent Theory

Theory describing the distribution of gene trees (and ARGs) under a given demographic model that can be used to compute the probability of a given gene tree.

Bayesian Inference

Statistical framework where the parameters of the models are treated as random variables, allowing expressing the probability of parameters given the data – posterior. The posterior probability is obtained via Bayes rule and it is proportional to the likelihood times the prior.

Generating functions

Statistical technique used to obtain the distribution of sums of random variables, as required in computation of the probability of genealogies given the parameters of an underlying model.

Paired-end libraries

Sequencing from each end of the fragments in a library. The two sequenced ends are typically separated by a gap.

Identity by descent (IBD)

Two haplotypes are identical by descent if they are identical copies of a haplotype that are shared between individuals within families, and hence are assumed to be identical by descent.