Abstract
Delineation of large-scale functional networks (FNs) from resting state functional MRI data has become a standard tool to explore the functional brain organization in neuroscience. However, existing methods sacrifice subject specific variation in order to maintain the across-subject correspondence necessary for group-level analyses. In order to obtain subject specific FNs that are comparable across subjects, existing brain decomposition techniques typically adopt heuristic strategies or assume a specific statistical distribution for the FNs across subjects, and therefore might yield biased results. Here we present a novel data-driven method for detecting subject specific FNs while establishing group level correspondence. Our method simultaneously computes subject specific FNs for a group of subjects regularized by group sparsity, to generate subject specific FNs that are spatially sparse and share common spatial patterns across subjects. Our method is built upon non-negative matrix decomposition techniques, enhanced by a data locality regularization term that makes the decomposition robust to imaging noise and improves spatial smoothness and functional coherences of the subject specific FNs. Our method also adopts automatic relevance determination techniques to eliminate redundant FNs in order to generate a compact set of informative sparse FNs. We have validated our method based on simulated, task fMRI, and resting state fMRI datasets. The experimental results have demonstrated our method could obtain subject specific, sparse, non-negative FNs with improved functional coherence, providing enhanced ability for characterizing the functional brain of individual subjects.
Keywords: Functional networks, subject-specific networks, collaborative decomposition, inter-subject correspondence
Introduction
Resting state fMRI (rsfMRI) has been a powerful tool for investigating functional connecitivty patterns of the human brain. Among funtional connectivity modeling methods, decomposing the brain into spatially overlapping components is favored for modeling many-to-many mapping between brain regions and functions (Smith et al., 2009, Power et al., 2011, Calhoun et al., 2012, Smith et al., 2012, Park and Friston, 2013, Pessoa, 2014). The brain decomposition methods typically build upon matrix factorization techniques to decompose the functional imaging data into a set of spatial components, referred to as functional networks (FNs) or functional modes (Calhoun et al., 2001b, Beckmann et al., 2005, Calhoun et al., 2009, Du and Fan, 2011, Lee et al., 2011a, Varoquaux et al., 2011, Yeo et al., 2011, Smith et al., 2012, Abraham et al., 2013, Du and Fan, 2013, Varoquaux et al., 2013, Yeo et al., 2014, Harrison et al., 2015), such as Default Mode Network (DMN). The most common brain decomposition methods are built upon spatial or temporal independent component analysis (ICA) (McKeown and Sejnowski, 1998, Calhoun et al., 2001b, Beckmann et al., 2005, Smith et al., 2009, Smith et al., 2012). Several methods have also been proposed to compute FNs from rsfMRI data with non-independence assumptions (Lee et al., 2011a, Lee et al., 2011b, Varoquaux et al., 2011, Yeo et al., 2011, Abraham et al., 2013, Lv et al., 2013, Hjelm et al., 2014, Yeo et al., 2014, Harrison et al., 2015).
Recent work has demonstrated important subject specific variation in the functional neuroanatomy of large-scale brain networks (Poldrack et al., 2015, Satterthwaite and Davatzikos, 2015), emphasizing the need for tools which can flexibly adapt to individual variation while simultaneously maintaining correspondence for group-level analyses. Most of the brain decomposition methods are applicable to rsfMRI data of individual subjects. However, they are more robust when applied to pooled data of a group of subjects. For instance, group ICA is more robust (Calhoun et al., 2009) than ICA computation for each subject separately followed by establishing correspondence of independent components (ICs) across subjects (McKeown et al., 1998, Calhoun et al., 2001a, Moritz et al., 2003, Esposito et al., 2005, De Martino et al., 2007, Yang et al., 2008) since ICA computations applied to data of different subjects may generate ICs without direct correspondence (McKeown et al., 1998). It is a difficult task to compute subject specific ICs from the group ICA results, and heuristic techniques are often adopted, such as back-reconstruction (Calhoun et al., 2009) and dual regression (Smith et al., 2012). In order to robustly compute subject specific ICs from fMRI data of individual subjects while facilitating groupwise inference in fMRI studies, independent vector analysis (IVA) (Lee et al., 2008) and group-information guided ICA (GIGICA) (Du and Fan, 2013) methods have been proposed. Similar to IVA and GIGICA, multi-subject dictionary learning methods also directly work on fMRI data of individual subjects and simultaneously enforce correspondence across FNs of different subjects by assuming that corresponding FNs of different subjects follow Gaussian (Varoquaux et al., 2011, Abraham et al., 2013, Varoquaux et al., 2013) or delta-Gaussian (Harrison et al., 2015) distributions. However, these methods may yield subject specific FNs biased to the group level information since the assumptions about the statistical distribution of FNs are not necessarily valid.
Excepting those with nonnegative constraints (Lee et al., 2011a), most existing methods tend to produce FNs with mixed positive and negative loadings that typically correspond to anti-correlated signals. Since time courses associated with FNs are projection results of the original fMRI time series onto the FNs, this hampers interpretability, as it is difficult to interpret the biological meaning of time courses of an FN with mixed positive and negative loadings. Furthermore, potentially relevant information regarding anti-correlation of component timecourses can be lost due to inaccurate assignment of negative loadings.
Aiming to overcome these challenges, we propose a brain decomposition method for computing subject specific, sparse function networks (SFNs) without losing comparability across subjects, as schematically illustrated by Fig. 1. In particular, our method is built upon nonnegative matrix factorization techniques (Lee and Seung, 1999) with following enhancements: 1) an inter-subject group sparsity regularization term is adopted to enforce subject specific SFNs to have common spatial patterns across subjects; 2) a data locality regularization term (Cai et al., 2011) is applied to the brain decomposition of individual subjects to obtain subject specific SFNs with enhanced spatial smoothness and functional coherence; and 3) a parsimonious regularization term is adopted to eliminate redundant SFNs in a data-driven way using automatic relevance determination techniques (M. Morup and Hansen, 2009). In the current study, we validate the proposed method with respect to its parameters, based on a simulated dataset, a dataset with both task fMRI (tfMRI) and rsfMRI scans obtained from the Human Connectome Project (HCP) (Glasser et al., 2013), and an rsfMRI dataset obtained from the Philadelphia Neurodevelopmental Cohort (PNC) (Satterthwaite et al., 2014). The experimental results have demonstrated that our method could obtain sparse, non-negative subject specific FNs with improved functional coherence, providing enhanced ability for characterizing the functional brain of individual subjects. Preliminary results of this work has been reported in (Li et al., 2016).
Fig. 1.
Schematic diagram of the proposed method. The rsfMRI data of each individual subject are arranged as a matrix with each row for one time point and each column for one voxel. The rsfMRI data of a group of subjects are simultaneously decomposed into non-negative subject specific FNs with their corresponding time courses in a collaborative setting with 3 regularization terms: 1) a voxel-wise group sparsity regularization term is adopted as an inter-subject consensus prior so that spatial correspondence and variations of FNs of different subjects are preserved simultaneously; 2) a data locality regularization term is adopted to enhance both functional coherence and spatial proximity of voxels so that spatially continuous and functionally coherent voxels are encouraged to reside in the same FN; and 3) an intra-subject parsimonious regularization term is adopted to eliminate redundant FNs with similar functional profiles using automatic relevance determination techniques.
Methods
Nonnegative decomposition model for rsfMRI data
Given a group of n subjects, each having rsfMRI data Xi ∈ RT×S, i = 1, …, n, consisting of S voxels and T time points, we aim to find K nonnegative FNs and their corresponding nonnegative time courses for each subject, such that
| (1) |
where (Vi)′ is the transpose of Vi, and Ei is additional noise with a Gaussian distribution of N(0,σI). Both Ui and Vi are constrained to be non-negative so that each FN does not contain any anti-correlated functional units (Lee and Seung, 1999).
Group sparsity and data locality regularization terms
To identify subject specific FNs that are comparable across subjects, FNs of all subjects are computed collaboratively with an inter-subject group sparsity regularization term that enforces FNs of different subjects to have common spatial structures. Particularly, the consensus prior is a scale-invariant group sparsity regularization term on each column of Vi, i = 1, …, n:
| (2) |
The group sparsity regularization term enforces corresponding FNs of different subjects to have common structures in the spatial domain, i.e., corresponding FNs of different subjects having non-zero elements at the same spatial locations. Different from existing methods that typically assume that corresponding FNs of different subjects follow a Gaussian/Delta-Gaussian distribution in the spatial domain (Lee et al., 2008, Abraham et al., 2013, Du and Fan, 2013, Harrison et al., 2015), our consensus prior does not constrain elements of corresponding FNs of different subjects to be close to the group mean FNs directly, therefore the subject specific FNs will be less biased to the group mean FNs. Moreover, the group sparsity regularization term also encourages the spatial locality of the functional networks due to its sparsity preference.
Besides the inter-subject consensus prior, we also adopt a data locality regularization term to encourage spatial smoothness and functional coherence of the FNs using graph regularization techniques (Deng et al., 2011). Such a data locality regularization term is formulated as
| (3) |
where is a Laplacian matrix for subject i, is a pairwise affinity matrix to measure spatial closeness or functional similarity between different voxels, and is its corresponding degree matrix. Particularly, the affinity matrix could encode both spatial proximity and functional affinity, with the assumption that spatially neighboring voxels or voxels that have similar functional profiles would reside in the same FN. Therefore, the decomposition would respect the intrinsic manifold structure of the functional data, and yield FNs with improved spatial continuity and functional consistency. In the current study, the affinity between each pair of spatially connected voxels is calculated as , where is the Pearson correlation coefficient between their rsfMRI signals, and others are set to be zero so that had a sparse structure.
Parsimonious regularization term for compact decomposition
Since no independence or orthogonality constraints are applied to SFNs, the nonnegative decomposition method may yield redundant FNs with large spatial overlap. In order to obtain compact representations of FNs, we adopt a parsimonious regularization term to prune redundant ones at the subject level with automatic relevance determination (ARD) techniques (M. Morup and Hansen, 2009, Tan and Fevotte, 2013) by minimizing
| (4) |
where , and is hyper-parameters, indicating the relevance of FNs with respect to the data decomposition. As time course reflects the functional dynamic of the corresponding FN, redundant FNs would have similar time courses. The parsimonious prior imposes a sparsity preference on time courses of FNs, which helps remove redundant FNs with similar time courses in the decomposition. Non-informative priors on are adopted, which allow us to tune the degree of sparsity preference by updating in a data driven fashion (M. Morup and Hansen, 2009).
Optimization of the joint brain decomposition model
We identify subject specific FNs by optimizing a joint model with integrated data fitting and regularization terms formulated by Eqns. (1–4)
| (5) |
where and are used to balance the data fitting, group sparsity, and data locality regularization terms, and n is the number of subjects, T is the number of time points, K is the number of FNs, nM is the number of neighboring voxels, α and β are two free parameters. It is worth noting that our method is directly applicable to single subject dataset, while the group sparsity regularization term degenerates to be an ordinary spatial sparsity regularization term. Moreover, it is applicable to both surface and volumetric data, as the graph based locality regularization term can handle different topologies from different data types, and other terms are free of the data topologies.
As the objective function is not convex with respect to and together, an iterative procedure is proposed to solve the optimization problem by updating and alternatively.
Given , we have
| (6) |
and is updated as
| (7) |
where T is the number of time points of the functional data.
Given , we have
| (8) |
| (9) |
| (10) |
| (11) |
Specifically, is normalized by its maximum value so that all its entries have values in [0, 1] after each iteration step. The objective function would monotonically decrease with this alternatively multiplicative update strategy (M. Morup and Hansen, 2009, Tan and Fevotte, 2013). The updating procedure is illustrated in table 1. The objective function typically converges in less than 50 iteration steps at the population level based on our observations on both the simulated and real functional datasets.
Table 1.
Alternative optimization of the joint brain decomposition model
| 1. | Input: Xi, i = 1,2,…,n: functional data of n subjects |
| α: group sparsity parameter, β: data locality parameter, K: number of FNs | |
| R: number of iterations at the population level, L: number of iterations at subject level | |
| 2. | Output: Vi and Ui for each subject |
| 3. | Initialize Vi and Ui as described in the Robust initialization section |
| 4. | Alternative updates |
| for r = 1,2,…,R | |
| for i = 1,2,…,n: | |
| for j = 1,2,…,L: (subscripts for voxels/time points and FNs were omitted for clarity) | |
| Update Vi as in eqn.8 | |
| Update Ui as in eqn.6 | |
| Update λi as in eqn.7 | |
| end j | |
| end i | |
| if ; break; end if; (obj calculated as in eqn.5) | |
| end r |
Robust initialization of the joint decomposition framework
We apply our method to pooled group data as a single subject to obtain an initialization result for our method. In particular, the functional data of a group of subjects are concatenated temporally, and our method with an ordinary spatial sparsity regularization term is used to get group-level FNs that are used to initialize the simultaneous decomposition at the subject-level. At the group level decomposition, a random nonnegative initialization is used (Lee and Seung, 1999). A bootstrap strategy is utilized to perform the group-level decomposition multiple times on a subset of randomly selected subjects, and the resulting multiple decomposition results are fused to obtain one robust initialization that is highly reproducible, using a strategy similar to ICASSO (Himberg et al., 2004). Particularly, all the decomposed FNs across different runs are pooled together and clustered into groups using normalized cuts (Shi and Malik, 2000), where the inter-FN similarity is calculated as
| (12) |
where dij = 1 − corr(ICNi,ICNj), corr(ICNi,ICNj) is Pearson correlation coefficient between ICNi and ICNj, and σ is the median of dij across all possible pairs of FNs. The number of clusters is set to be the number of FNs for each single run. For each cluster, the FN with the highest overall similarity with all other FNs within the same cluster is selected as the group FN and used to initialize the subject specific brain decomposition. In the current study, we computed group FNs with 50 random runs. The number of FNs of a fMRI dataset can be estimated using methods such as Laplace approximation, Bayesian information criterion (BIC), Akaike information criterion (AIC), and Minimum description length (MDL) (Beckmann and Smith, 2004, Li et al., 2007). In the current study, we use the Laplace approximation by MELODIC of FSL (Jenkinson et al., 2012).
In order to make the decomposition robust to rsfMRI data that may have different numbers of time points and make preprocessed rsfMRI data to have nonnegative values, a voxel-wise normalization procedure can be applied to each subject’s rsfMRI data before the decomposition. Particularly, time course of each voxel is first shifted linearly to make all time points to have positive values if necessary, and then the time course is normalized by its maximum value so that all the time points have values in [0, 1].
Choices of parameters
Our method has two free parameters, i.e., α and β, which balance the data fitting, group sparsity, and data locality regularization terms in the decomposition. As no ground truth is available for a decomposition of real fMRI data, we use a simulated dataset to tune these parameters. In particular, different combinations of α ∈ {0.01, 0.05, 0.1, 0.5, 1, 2, 5, 10} and β ∈ {0.01, 0.05, 0.1, 0.5, 1, 2, 5, 10, 20, 50, 100} are used in the experiment, and their corresponding decomposition results are evaluated with spatial accuracy and temporal accuracy of FNs. These parameters can also be adopted to analyze real fMRI datasets.
Validation and evaluation experiments
We evaluate the proposed method based on both simulated and real fMRI datasets, including real tfMRI and rsfMRI datasets. We compared our method with group ICA and GIGICA (Beckmann et al., 2005, Du and Fan, 2013). For group ICA, MELODIC of FSL (Jenkinson et al., 2012) was adopted to obtain the group level ICs. Then, dual regression and GIGICA were used to compute subject specific ICs based on the group ICs. The subject specific ICs obtained with the dual regression are referred to as results of group ICA. Default parameters were adopted for group ICA (Beckmann et al., 2005) and GIGICA (Du and Fan, 2013).
Evaluation based on simulated datasets
We generated 2 simulated functional datasets using the SimTB toolbox (Erhardt et al., 2012), one for tuning the parameters (sim_training dataset) and the other for evaluating our method’s performance (sim_eval dataset). In particular, each of the dataset consisted of simulated data of 20 subjects, and every subject had 150 2D images with 100×100 voxels, generated by linear combinations of 25 distinct FNs. Inter-subject variability was introduced by spatial variability in translation, rotation, and spread during the data generation (Erhardt et al., 2012). In addition to the inter-subject variability, Rician noise was added to the simulated images with random contrast-to-noise ratios (CNR) ranging from 0.65 to 1.0 for different subjects.
To estimate FNs based on the simulated data, the number of FNs was set to be 35 for all the methods under comparison, and estimated FNs were matched with the ground truth FNs using the Hungarian algorithm (Carpaneto and Toth, 1980). For FNs obtained by our method, we obtained group level FNs based on average FNs of all subjects after they were transfer to z-scores, and every pixel was assigned to an FN if its average z-score had the largest value on the pixel. These FNs were evaluated based on spatial and temporal accuracy measures. Particularly, the spatial accuracy of an individual FN was measured by Pearson correlation coefficient between the estimated FN and its corresponding ground truth FN, and the temporal accuracy of an FN was measured by Pearson correlation coefficient between its associated time courses and its corresponding ground truth time course. An overall accuracy measure for each subject was obtained by averaging accuracy measures of all individual FNs that were matched with the ground truth FNs.
Evaluation based on the Human Connectome Project (HCP) dataset
Our method was also validated based on fMRI data of 40 unrelated subjects of the Human Connectome Project (HCP) (Glasser et al., 2013), aiming to evaluate the consistency between task-evoked activation responses and FNs estimated by the brain decomposition methods from both the task and resting state fMRI scans. Similar evaluation strategies have been adopted in studies of cortical parcellation based on rsfMRI data (Wang et al., 2015, Gordon et al., 2016, Parisot et al., 2016), and the resting state FNs have demonstrated promising performance for predicting task-evoked brain activation (Tavor et al., 2016).
In the current study, we focused on motor task. The motor-task fMRI scans were obtained under 6 events, including 5 movement events, namely left foot (LF), left hand (LH), right foot (RF), right hand (RH), tongue (T), and additionally 1 cue event (CUE) prior to each movement event. The fMRI data acquisition and task paradigm were detailed in (Barch et al., 2013). Task-evoked activation maps corresponding to the aforementioned 6 events were also obtained as part of the released data, and these maps were converted to z-scores so that task-invoked activation regions can be determined according to p values (Barch et al., 2013). Specifically, we identified task-evoked activation regions by thresholding z-score maps at 1.64, 1.96, and 2.57, corresponding to p-values of 0.1, 0.05, and 0.01 respectively.
The brain decomposition methods under comparison were applied to minimal-preprocessed, cortical gray-coordinates based motor-task fMRI data, smoothed with a 4 mm full width at half maximal (FWHM) kernel (Barch et al., 2013). The number of FNs of this dataset estimated by MELODIC was 83. From the FNs identified by each brain decomposition method, we identified task specific FNs as those whose time courses had the highest correlation coefficients with the task event paradigms. Then, spatial correlation coefficients between activation maps and their corresponding FNs were computed to measure their consistency. Moreover, all these decomposition methods under comparison were also applied to the minimal-preprocessed, cortical gray-coordinates based resting-state fMRI data, to investigate the consistency between the identified FNs and the task-evoked activation regions. The number of FNs of the resting-state dataset estimated by MELODIC was 90. The task-corresponding FNs was identified as those having the highest spatial correlation coefficients with the task-evoked regions. Specifically, the spatial correlation coefficients were computed within task-evoked activation regions, corresponding to p-values of 0.1, 0.05, and 0.01 respectively.
Evaluation based on a resting-state fMRI dataset
We further validated our method based on a rsfMRI dataset obtained from the PNC (Satterthwaite et al., 2014, Satterthwaite et al., 2016), consisting of rsfMRI scans of 50 younger subjects (8~13 years old, 11.4 ± 1.29 years) and 50 older subjects (19~22 years old, 20.71 ± 0.75) years) with mean relative displacement (MRD) less than 0.05mm (Satterthwaite et al., 2013a). Wilcoxon rank sum test indicated that these two groups had similar head motion (MRD, 0.037 ± 0.007 versus 0.034 ± 0.009, p = 0.145). For each subject, a T1 scan was acquired prior to an rsfMRI scan with 124 time-points. The T1 images were processed using Freesurfer and registered to the FreeSurfer fsaverage5 cortical template. Each rsfMRI scan was first registered to its corresponding T1 image using boundary based registration in FSL, and then was projected to the fsaverage surface space using FreeSurfer after preprocessing using an optimized confound regression procedure, including removal of the first four volumes, slice time correction, 36-parameter confound regression, and band-pass filtering (Satterthwaite et al., 2013a). These rsfMRI scans were preprocessed in a study of functional parcellation of the cortex (Honnorat et al., 2015). The number of FNs of this dataset estimated by MELODIC was 50.
As no ground truth of FNs for the rsfMRI dataset is available, we evaluated the FNs using a functional coherence measure. For each FN, the coherence measure was calculated as the weighted sum of the correlation coefficients between the time courses of all the voxels within the FN and the its centroid time course, which was calculated as the weighted mean time course within the FN. The median value of FN-wise coherence measures was adopted as the coherence measure at subject level.
Besides functional coherence, we also evaluated our method with a classification task, i.e., distinguishing the younger subjects from the older subjects based on their functional network connectivity (FNC) measures between FNs. The FNC measures between FNs were estimated as Pearson correlation coefficients between their corresponding time courses, and then were converted to z-scores as features to be used in the pattern classification. We adopted a sparse linear support vector machine (SVM) model to build classifiers (Fan et al., 2008). In particularly, we used LIBLINEAR (Fan et al., 2008) to build sparse linear SVM classifiers. The performance of the classifiers was estimated with a 10-fold cross-validation setting, and the classifiers’ sparsity parameter was automatically optimized with a nested 10-fold cross-validation procedure based on the training data.
Results
Decomposition results for the simulated data
Fig. 2 shows FN maps of a randomly selected subject from the sim_eval dataset and quantitative evaluation results. In particular, Fig. 2A shows FNs of the selected subject, computed by the brain decomposition methods under comparison. The FNs obtained by each method are illustrated with an FN map that was obtained by assigning each voxel to an FN according the highest z-score of the loadings across all FNs. These results demonstrated that all the methods under comparison were able to identify FNs similar to the ground truth. ICA and GIGICA identified all 25 real components. However, noise and spatial blurring was evident in both ICA and GIGICA results, which degraded both spatial and temporal accuracy. In contrast, the FNs identified by our method were relatively clean, and had similar appearance as the ground truth FNs. Not surprisingly, the difference between the ground truth and group level FNs was larger than the difference between the ground truth and the subject specific FNs.
Fig. 2.
FN maps of a selected subject from the sim_eval dataset, and spatial and temporal accuracy of FNs obtained by different methods. (A) Ground truth FN map, and FN maps identified by ICA, GIGICA, the proposed method, group level FNs obtained by our method (Prop-grp), and its degraded version without the data locality regularization (Degraded). (B) Boxplots show spatial and temporal accuracy measures of the FNs from all the simulated subjects obtained by different methods. For the boxplots, the central mark is the median, the edges of the box are the 25th and 75th percentiles, and whiskers extend from each edge of the box to the extreme values within 1.5 times the interquartile range.
The data locality regularization could improve our method’s robustness to imaging noise, as demonstrated by the results obtained by a degraded version of our method, i.e., without the data locality regularization. As shown in Fig. 2B, the FNs obtained by our method had better spatial and temporal accuracy than those obtained by ICA and GIGICA (p = 4.78 × 10−5, 4.78 × 10−5 for spatial accuracy respectively, and p = 4.78 × 10−5, 4.78 × 10−5 for temporal accuracy respectively, by Wilcoxon signed rank test). The subject specific FNs had better accuracy than the group level FNs (p = 4.78 × 10−5 for spatial accuracy, and p = 4.78 × 10−5 for temporal accuracy, by Wilcoxon signed rank test), indicating that the proposed method could better capture the subject specific information than the group level results.
Nonnegative and compact decomposition results
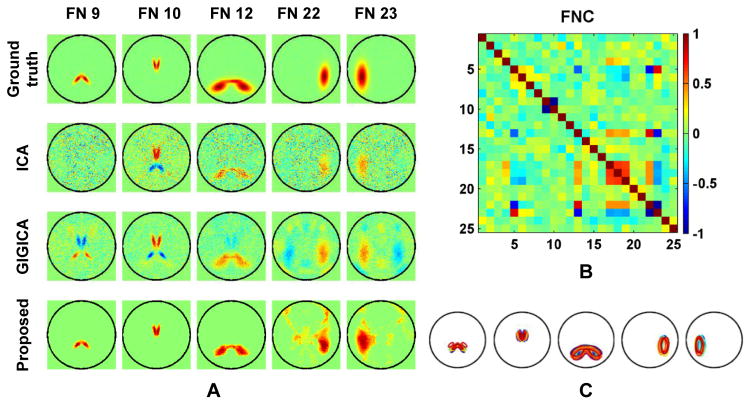
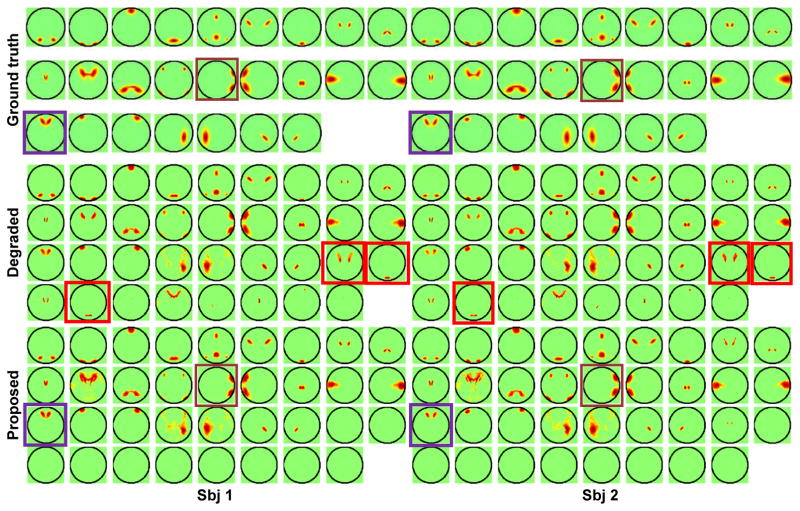
One important feature of the proposed method is the non-negativity constraint that forces all FNs to have only nonnegative loadings. As illustrated by the FNs of the selected subject shown in Fig. 3A, the subject specific FNs identified by ICA were noisy, with mixed positive and negative loadings (FNs 9 and 10). The results obtained by GIGICA also had FNs with mixed positive and negative loadings (FNs 9, 10, 22, and 23). As expected, due to the non-negativity constraint, our method obtained FNs without anti-correlated loadings. These results were consistent with temporal correlation coefficients of these FNs measured by the ground truth functional signals, as shown in Fig. 3B. Particularly, FNs 9 and 10 had anti-correlated functional signals, so did FNs 22 and 23. The inter-subject variations of these 5 FNs are illustrated by varying boundaries in different colors in Fig. 3C. Such variations are also clearly shown in Fig. 4, as highlighted by the purple and brown boxes, illustrating that the corresponding FNs across subjects vary in both location and spatial extent.
Fig. 3.
Five FNs of the same subject as shown in Fig. 3A. (A) Ground truth FNs, and FNs identified by different methods. Warm colors indicate positive loadings while cool colors indicate negative ones. (B) inter-FN correlation measures calculated as Pearson correlation between time courses of different ground truth FNs. No thresholding was applied to any of the FNs. (C) Inter-subject variations of these 5 FNs. Contours in different colors indicate the ground truth FN boundaries of different subjects.
Fig. 4.
FNs of two randomly selected subject obtained by the proposed method and its degraded version without the parsimonious regularization. The red boxes indicate examples of redundant FNs, purple and brown boxes indicate examples of inter-subject FN variations. No thresholding was applied to any of the FNs.
Our method also adopts a parsimonious regularization that encourages compact decomposition results, alleviates data over-fitting, and improves the interpretability of the decomposition results. As illustrated by the results shown in Fig. 4, the parsimonious regularization could help remove redundant FNs with large spatial overlap and similar time courses in the decomposition. Without the parsimonious regularization, the resulting FNs contained redundant ones.
Choices of parameters
Fig. 5 shows how the spatial and temporal accuracy measures changed with β for different α based on the sim_training dataset, indicating that with appropriate consensus regularization and graph regularization, better decomposition results could be obtained. A small regularization would be insufficient against the noise and a large regularization would eliminate inter-subject variability. The results indicated that the best performance could be obtained by setting α = 2 and β = 10. This setting was adopted to compute decomposition results for both the simulated and the real fMRI datasets.
Fig. 5.
Spatial accuracy (A) and temporal accuracy (B) on the sim_training dataset under different parameter settings, x-axis shows the values of β, and error bars in different colors correspond to different values of α.
Subject specific, task related FNs identified from task fMRI data
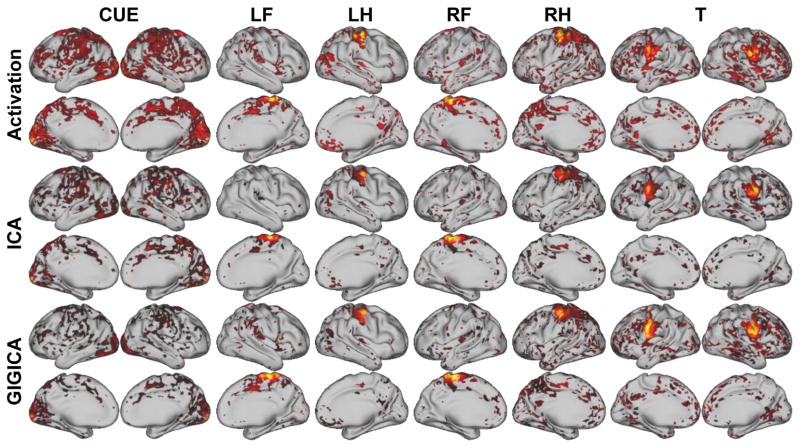
As a next step, we validated our method based on a well-characterized motor-task fMRI dataset from the HCP (Glasser et al., 2013). Fig. 6 shows the activation maps and their corresponding FNs from one randomly selected subject. Although all the decomposition methods could identify the task-related FNs, the FNs obtained by the proposed method were more spatially localized, and had better spatial correspondence to the activation peaks of the tasks, such as those related to events of LF, RF, and RH. The activation maps and identified FNs of another subject are illustrated in Fig. S2.
Fig. 6.
Task-evoked activation maps and task-related FNs identified by different methods of one randomly selected subject (subject 100307). The z-score activation maps were thresholded at 1.64, and the activation region masks were applied to their corresponding FN maps. (LF: left foot, LH: left hand, RF: right foot, RH: right hand, T: tongue, CUE: cue).
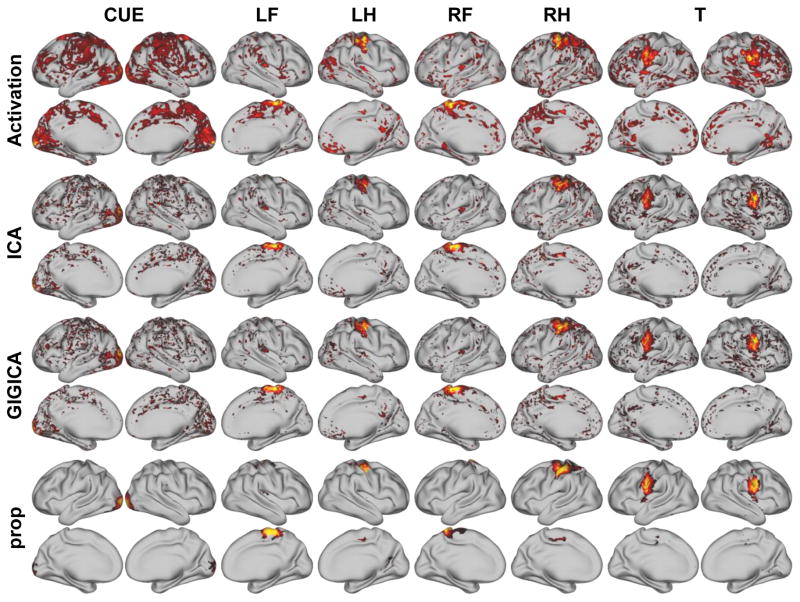
Fig. 7 shows the activation maps and their corresponding FNs identified based on the resting-state fMRI data from the same subject as shown in Fig. 6. Similar to that based on the task fMRI data, all the decomposition methods could identify the task-related FNs, the FNs obtained by the proposed method were more spatially localized, and had better spatial correspondence to the activation peaks of the tasks, such as those related to events of RF, RH, and T. The activation maps and identified FNs of another subject are illustrated in Fig. S3.
Fig. 7.
Task-evoked activation maps and resting-state FNs identified by different methods of the same subject as shown in Fig. 6. The z-score activation maps were thresholded at 1.64, and the activation region masks were applied to their corresponding FN maps. (LF: left foot, LH: left hand, RF: right foot, RH: right hand, T: tongue, CUE: cue).
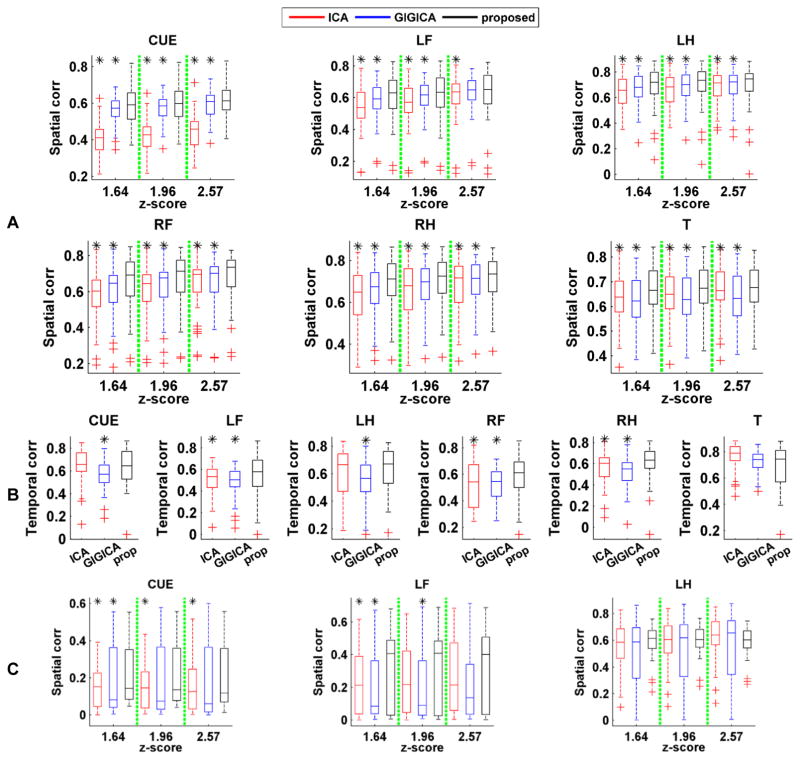
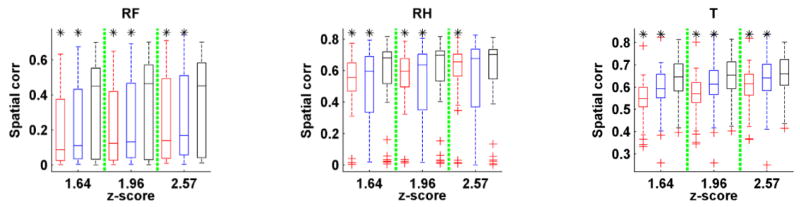
The average spatial correlation and temporal correlation measures with respect to different task events across all subjects are illustrated in Fig. 8. The quantitative results indicated that the FNs obtained by the proposed method had higher spatial consistency with the activation maps than those identified by ICA and GIGICA, while the temporal consistency were comparable or better than those identified by ICA and GIGICA based on the task fMRI data. Moreover, the FNs identified by the proposed method based on resting-state fMRI data also had comparable or higher spatial consistency than those identified by ICA and GIGICA.
Fig. 8.
Spatial and temporal consistency between the task-related FNs identified by different methods and their corresponding task-evoked response. (A) Spatial correlation coefficients between identified FNs based on task fMRI and the task-evoked activations with different threshold values. (B) Temporal correlation coefficients between time course of identified FNs based on task fMRI and the task paradigms. (C) Spatial correlation coefficients between identified FNs based on resting-state fMRI and the task-evoked activations with different threshold values (LF: left foot, LH: left hand, RF: right foot, RH: right hand, T: tongue, CUE: cue). Results of the methods under comparison are shown in different colors (red: ICA, blue: GIGICA, black: proposed), and asterisk indicates that the proposed method performed significantly better than the alternatives (p < 0.05, by Wilcoxon signed rank test).
Subject specific, groupwise comparable FNs identified from rsfMRI data
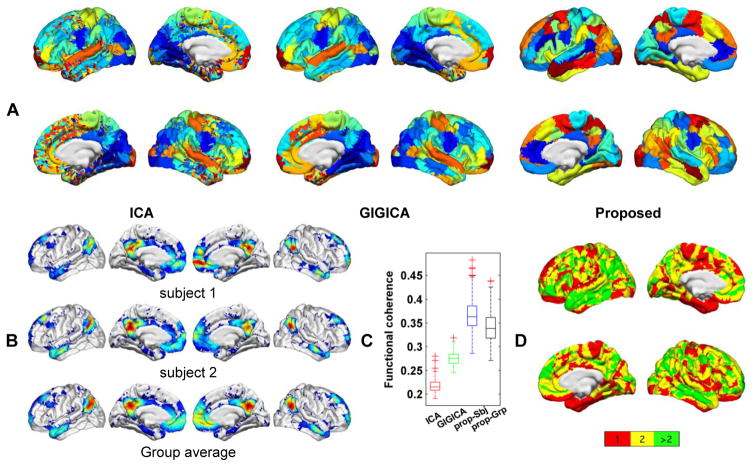
Finally, we validated our method on a rsfMRI dataset from the PNC (Satterthwaite et al., 2014, Satterthwaite et al., 2016). The FNs obtained by each method under comparison are illustrated with a group level FN map that was obtained on average FNs of all subjects after they were transformed to z-scores, and each vertex was assigned to an FN if its average z-score had the largest value on the vertex. Individual group average FNs obtained by our method are shown in Fig. S1. Fig. 9A shows group level FNs maps obtained by different methods. These results demonstrated that all the methods could identify FNs commonly reported in the literature, such as DMN, visual network, and sensorimotor network. The FNs identified by our method are spatially localized. Fig. 9B shows the DMN of two randomly selected subjects and the average DMN of all subjects, obtained by our method. The subject specific DMNs share similar spatial layout while preserving their own coefficient distribution. Furthermore, as FNs represent brain networks with functionally synchronized voxels, we also evaluated intra-FN functional coherence of FNs identified by different methods. The quantitative results shown in Fig. 9C indicated that the FNs obtained by our method had higher functional coherence than those identified by group level FNs as well as both ICA and GIGICA (p = 1.98 × 10−18, 1.98 × 10−18, 1.98 × 10−18 respectively, by Wilcoxon signed rank test). Fig. 9D shows a spatial map of overlap between FNs obtained by the proposed method, indicating that certain brain regions might play multiple roles in the brain networks, especially higher-order association cortex within the frontal and temporal lobes (Pessoa, 2014).
Fig. 9.
Brain decomposition results containing 50 FNs. (A) Group map with 50 FNs obtained by group ICA, GIGICA, and the proposed method. Colors indicate different FNs, the same color indicates corresponding FNs for the ICA and GIGICA results, but the same color does not indicate correspondence for FNs obtained by the proposed method and those obtained by ICA and GIGICA. (B) Subject-specific DMN of two randomly selected subjects and average DMN of all subjects, obtained by the proposed method. (C) Intra-FN functional coherence measures of decomposition results under comparison. (D) Spatial overlap between FNs obtained by the proposed method, with colors encoding the number of FNs in which each vertex was involved.
Younger versus Older group classification using inter-FN functional connectivity
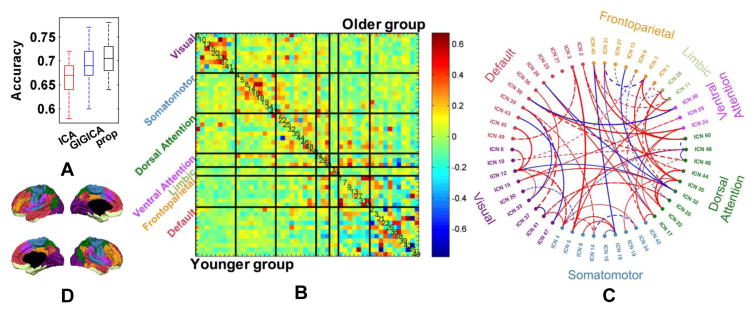
Based on the FNs identified by different decomposition methods, we further performed a classification study to distinguish younger subjects from older ones based on their inter-FN connectivity measures, aiming to investigate the FNs’ ability of characterizing the functional brain development. The ten-fold validation procedure was repeated 50 times, the mean classification accuracy based on FNs obtained by ICA, GIGICA, and the proposed method was 0.666, 0.694, and 0.704 respectively, with standard deviation 0.034, 0.032, and 0.034. The overall classification results were illustrated in Fig. 10A, indicating that the FNs obtained by our method might better capture subject-specific functional connectivity patterns of the brain development (p = 1.42 × 10−7, 0.02 compared with GICA and GIGICA respectively, by Wilcoxon signed rank test. The power of paired tests might be overestimated as different runs of the cross-validation are not truly independent samples).
Fig. 10.
Younger versus Older classification using FNC measures between FNs based on 50 FNs. (A) Classification accuracy of 50 runs of 10-fold cross-validation. (B) Mean FNC pattern of younger (lower triangular part) and older group (upper triangular part). The FNs are grouped into visual, somatomotor, dorsal attention, ventral attention, limbic, frontoparietal, and default networks, as shown in (D), and their FN IDs are shown in the diagonal elements. (C) Top 5% (61) FNC measures selected by the classification models according to their average weights from 50 runs. Colored text indicates the FN IDs, red/blue lines indicate FNC measures increase/decrease from younger to older group, solid/dashed lines indicate positive/negative average FNC measures, and line thickness indicates their average weights in the classification models.
Fig. 10B shows average FNC measures for the younger group and the old group respectively obtained by the proposed decomposition method, and Fig. 10C shows the top 5% (61) functional connections that were selected by the classification models according to their average weights of 50 runs. To facilitate the interpretability of the FNC connections selected, the FNs were assigned to different cognitive systems according to the Yeo’s 7-network atlas (Yeo et al., 2011), namely visual network, somatomotor network, dorsal attention network, ventral attention network, limbic network, frontoparietal network, and default network (Yeo et al., 2011), as shown in Fig. 10D. In particular, the group average FNs were matched with the 7-network atlas and assigned to the network with the highest spatial overlap measure. The spatial overlap measure is defined as , where is the coefficient for vertex i in our j-th FN, and is the membership (0 or 1) in Yeo’s k-th network. Notably, FNC connections within cognitive systems tended to increase with age; this was particularly prominent in visual, somatomotor, and dorsal attention systems. In contrast, connections between cognitive systems weakened with the brain development; this was notable in connections between the default mode system and “task-positive” networks (Fox et al., 2005). This is consistent with a process of developmental network segregation, whereby connections within cognitive systems becomes stronger, whereas between-network connections become weaker (Dosenbach et al., 2010, Satterthwaite et al., 2013b, Gu et al., 2015).
Discussion
Decomposition-based techniques to identify FNs have been widely adopted to study functional network organization of the human brain. For group-level analyses across subjects, FNs identified must be comparable across subjects. However, recent data emphasize the importance of retaining individual level variability in the spatial distribution of FNs (Poldrack et al., 2015, Satterthwaite and Davatzikos, 2015, Wang et al., 2015). ICA based methods have been the most commonly used tool for computing FNs, and several strategies are currently available to compute subject specific ICs with inter-subject comparability (McKeown and Sejnowski, 1998, Calhoun et al., 2001b, Beckmann et al., 2005, Lee et al., 2008, Smith et al., 2009, Smith et al., 2012, Du and Fan, 2013). Such network-based techniques should be distinguished from whole-brain parcellation techniques which seek to define finer-grained functional regions (Gordon et al., 2015, Laumann et al., 2015, Glasser et al., 2016), which often require multi-modality data or very long time series acquisitions. However, the independence assumption adopted in these techniques is under debate (Daubechies et al., 2009, Varoquaux et al., 2010, Calhoun et al., 2013). Other than the independence assumption, efforts have been made to discover sparse FNs (Lee et al., 2011a, Lee et al., 2011b, Varoquaux et al., 2011, Yeo et al., 2011, Abraham et al., 2013, Lv et al., 2013, Varoquaux et al., 2013, Yeo et al., 2014, Harrison et al., 2015), and some of them also directly work on individual subject fMRI data and simultaneously enforce correspondence across FNs of different subjects. To make the FNs of different subjects directly comparable, the existing methods typically force subject specific FNs to have loadings not far away from their group representations. Instead of formulating the discrepancy between subject specific spatial FNs and their group representations explicitly, the group sparsity regularization adopted in our method enforces FNs of different subjects to have common spatial structures, and does not penalize the FNs’ loadings at the subject level. The group sparsity regularization would be more robust to the inter-subject heterogeneity, compared with those minimizing difference between the group and subject specific representations (Du and Fan, 2011, Varoquaux et al., 2011, Abraham et al., 2013, Du and Fan, 2013, Varoquaux et al., 2013, Harrison et al., 2015). Beyond the regularization of inter-subject correspondence, it also simultaneously encourages spatial locality of the FNs.
Besides the group sparsity regularization term, our method also adopts a data locality regularization term and a parsimonious regularization term for FNs. In particular, the data locality regularization term is applied to the brain decomposition of individual subjects to obtain subject specific FNs with spatial smoothness and functional coherence. The parsimonious regularization is adopted to prune redundant FNs in a data-driven way using automatic relevance determination techniques (M. Morup and Hansen, 2009). The regularization does not enhance the spatial independence of FNs in an ICA fashion, but the spatial/temporal sparsity in an automatic relevance determination (ARD) fashion. It could preserve the potential spatial overlaps between FNs, while the spatial independence would eliminate the spatial overlaps (spatial overlaps increase the spatial correlation). The non-negative matrix decomposition may yield components with duplicated information that better fit the data. Such duplicated FNs can be successfully suppressed by the adopted parsimonious regularization in our method.
FNs with mixed positive and negative loadings may reflect competing interactions between different functional regions (Fox et al., 2005, Kelly et al., 2008), although it is under debate whether such interactions result from the neural origin or data manipulation (Murphy et al., 2009, Chai et al., 2012, Keller et al., 2013, Power et al., 2014). However, it is non-trivial to interpret the biological meaning of time courses of an FN with both positive and negative loadings. Most importantly, the anti-correlation information is lost in functional connectivity measures if an FN with both positive and negative loadings is not split properly. Our method adopts a non-negativity constraint that could facilitate easy interpretation of FNC analyses of FNs. From the perspective of data decomposition, it was shown that the non-negative constraint may favor sparse representation of the data (Lee and Seung, 1999), which further encourages the spatial locality of the FNs.
The choices of parameters used in the decomposition framework need to be further optimized. It is nontrivial to identify the optimal parameter setting for real fMRI data due to the lack of ground truth. In this study, we optimized the regularization parameters of our method based on the simulated dataset and adopted these parameters for the decomposition of real fMRI data, as detailed in the Methods section. However, a better strategy is needed to further optimize the decomposition performance for specific applications. One feasible way is to tune the parameter in a cross-validation manner that splits the dataset into halves, and select the parameters that lead to better reproducibility between brain decomposition results of different halves. Though the proposed method has been applied to tfMRI and rsfMRI datasets with different lengths of time series, it is still not clear how the time series length would affect the decomposition performance. Future work will be devoted to investigation with respect to this by examining reproducibility and functional coherence of FNs obtained from data segments of different lengths.
Conclusions
In this paper, we propose a novel method for identifying comparable, subject specific FNs from rsfMRI data. Our method collaboratively identifies subject specific FNs with a group sparsity regularization term, which enforces subject specific FNs to have common spatial structures while preserving their inter-subject variations and enforcing their spatial locality. Our method is further enhanced by data locality and parsimonious regularization terms that encourage spatially localized, functionally coherent, and compact representation of FNs. We have evaluated this collaborative decomposition method based on a simulated functional dataset, a cohort of task fMRI data, and a developmental cohort of rsfMRI data, and compared it with widely used ICA techniques. The experimental results have demonstrated that our method could obtain FNs with better spatial and temporal accuracy on both the simulated data and the task fMRI dataset, and was also more sensitive to detection of developmental change on the real rsfMRI data. Moreover, FNs identified by our method based on resting-state fMRI data also had better spatial correspondence with the task activation maps of the same individuals.
Supplementary Material
Highlights.
A collaborative decomposition method is proposed to compute subject specific FNs
The method yields non-negative, spatially sparse, and functionally coherent FNs
Subject specific FNs better characterize the functional brain of individual subjects
Acknowledgments
This work was supported in part by NIH grants: EB022573, CA189523, MH107703, DA039215, and DA039002.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abraham A, Dohmatob E, Thirion B, Samaras D, Varoquaux G. Extracting brain regions from rest fMRI with total-variation constrained dictionary learning. Med Image Comput Comput Assist Interv. 2013;16:607–615. doi: 10.1007/978-3-642-40763-5_75. [DOI] [PubMed] [Google Scholar]
- Barch DM, Burgess GC, Harms MP, Petersen SE, Schlaggar BL, Corbetta M, Glasser MF, Curtiss S, Dixit S, Feldt C, Nolan D, Bryant E, Hartley T, Footer O, Bjork JM, Poldrack R, Smith S, Johansen-Berg H, Snyder AZ, Van Essen DC Consortium WU-MH. Function in the human connectome: task-fMRI and individual differences in behavior. NeuroImage. 2013;80:169–189. doi: 10.1016/j.neuroimage.2013.05.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. 2005 doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans Med Imaging. 2004;23:137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Cai D, He X, Han J, Huang TS. Graph Regularized Nonnegative Matrix Factorization for Data Representation. IEEE Trans Pattern Anal Mach Intell. 2011;33:1548–1560. doi: 10.1109/TPAMI.2010.231. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, McGinty VB, Pekar JJ, Watson TD, Pearlson GD. fMRI activation in a visual-perception task: Network of areas detected using the general linear model and independent components analysis. NeuroImage. 2001a;14:1080–1088. doi: 10.1006/nimg.2001.0921. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional mri data using independent component analysis. Human Brain Mapping. 2001b;14:140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Eichelel T, Adali T, Allen EA. Decomposing the brain: components and modes, networks and nodes. Trends Cogn Sci. 2012;16:255–256. doi: 10.1016/j.tics.2012.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Liu J, Adali T. A review of group ICA for fMRI data and ICA for joint inference of imaging, genetic, and ERP data. NeuroImage. 2009;45:S163–S172. doi: 10.1016/j.neuroimage.2008.10.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Potluru VK, Phlypo R, Silva RF, Pearlmutter BA, Caprihan A, Plis SM, Adali T. Independent Component Analysis for Brain fMRI Does Indeed Select for Maximal Independence. Plos One. 2013:8. doi: 10.1371/journal.pone.0073309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpaneto G, Toth P. Algorithm 548: Solution of the Assignment Problem [H] ACM Trans Math Softw. 1980;6:104–111. [Google Scholar]
- Chai XJ, Castanon AN, Ongur D, Whitfield-Gabrieli S. Anticorrelations in resting state networks without global signal regression. NeuroImage. 2012;59:1420–1428. doi: 10.1016/j.neuroimage.2011.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daubechies I, Roussos E, Takerkart S, Benharrosh M, Golden C, D’Ardenne K, Richter W, Cohen JD, Haxby J. Independent component analysis for brain fMRI does not select for independence. P Natl Acad Sci USA. 2009;106:10415–10422. doi: 10.1073/pnas.0903525106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino F, Gentile F, Esposito F, Balsi M, Di Salle F, Goebel R, Formisano E. Classification of fMRI independent components using IC-fingerprints and support vector machine classifiers. NeuroImage. 2007;34:177–194. doi: 10.1016/j.neuroimage.2006.08.041. [DOI] [PubMed] [Google Scholar]
- Deng C, Xiaofei H, Jiawei H, Huang TS. Graph Regularized Nonnegative Matrix Factorization for Data Representation. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2011;33:1548–1560. doi: 10.1109/TPAMI.2010.231. [DOI] [PubMed] [Google Scholar]
- Dosenbach NUF, Nardos B, Cohen AL, Fair DA, Power JD, Church JA, Nelson SM, Wig GS, Vogel AC, Lessov-Schlaggar CN, Barnes KA, Dubis JW, Feczko E, Coalson RS, Pruett JR, Barch DM, Petersen SE, Schlaggar BL. Prediction of Individual Brain Maturity Using fMRI. Science. 2010;329:1358–1361. doi: 10.1126/science.1194144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Y, Fan Y. Group information guided ICA for analysis of multi-subject fMRI data. 17th Annual Meeting of the Organization for Human Brain Mapping; Quebec City, Canada. 2011. [Google Scholar]
- Du YH, Fan Y. Group information guided ICA for fMRI data analysis. NeuroImage. 2013;69:157–197. doi: 10.1016/j.neuroimage.2012.11.008. [DOI] [PubMed] [Google Scholar]
- Erhardt EB, Allen EA, Wei Y, Eichele T, Calhoun VD. SimTB, a simulation toolbox for fMRI data under a model of spatiotemporal separability. Neuroimage. 2012;59:4160–4167. doi: 10.1016/j.neuroimage.2011.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esposito F, Scarabino T, Hyvarinen A, Himberg J, Formisano E, Comani S, Tedeschi G, Goebel R, Seifritz E, Di Salle F. Independent component analysis of fMRI group studies by self-organizing clustering. NeuroImage. 2005;25:193–205. doi: 10.1016/j.neuroimage.2004.10.042. [DOI] [PubMed] [Google Scholar]
- Fan RE, Chang KW, Hsieh CJ, Wang XR, Lin CJ. LIBLINEAR: A Library for Large Linear Classification. J Mach Learn Res. 2008;9:1871–1874. [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, Smith SM, Van Essen DC. A multi-modal parcellation of human cerebral cortex. Nature. 2016;536:171–178. doi: 10.1038/nature18933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M Consortium WU-MH. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage. 2013;80:105–124. doi: 10.1016/j.neuroimage.2013.04.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE. Generation and Evaluation of a Cortical Area Parcellation from Resting-State Correlations. Cereb Cortex. 2016;26:288–303. doi: 10.1093/cercor/bhu239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Petersen SE. Individual Variability of the System-Level Organization of the Human Brain. Cereb Cortex. 2015 doi: 10.1093/cercor/bhv239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu S, Satterthwaite TD, Medaglia JD, Yang M, Gur RE, Gur RC, Bassett DS. Emergence of system roles in normative neurodevelopment. Proc Natl Acad Sci U S A. 2015;112:13681–13686. doi: 10.1073/pnas.1502829112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison SJ, Woolrich MW, Robinson EC, Glasser MF, Beckmann CF, Jenkinson M, Smith SM. Large-scale probabilistic functional modes from resting state fMRI. NeuroImage. 2015;109:217–231. doi: 10.1016/j.neuroimage.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himberg J, Hyvarinen A, Esposito F. Validating the independent components of neuroimaging time series via clustering and visualization. NeuroImage. 2004;22:1214–1222. doi: 10.1016/j.neuroimage.2004.03.027. [DOI] [PubMed] [Google Scholar]
- Hjelm RD, Calhoun VD, Salakhutdinov R, Allen EA, Adali T, Plis SM. Restricted Boltzmann machines for neuroimaging: an application in identifying intrinsic networks. NeuroImage. 2014;96:245–260. doi: 10.1016/j.neuroimage.2014.03.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honnorat N, Eavani H, Satterthwaite TD, Gur RE, Gur RC, Davatzikos C. GraSP: Geodesic Graph-based Segmentation with Shape Priors for the functional parcellation of the cortex. NeuroImage. 2015;106:207–221. doi: 10.1016/j.neuroimage.2014.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl. NeuroImage. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Keller CJ, Bickel S, Honey CJ, Groppe DM, Entz L, Craddock RC, Lado FA, Kelly C, Milham M, Mehta AD. Neurophysiological investigation of spontaneous correlated and anticorrelated fluctuations of the BOLD signal. J Neurosci. 2013;33:6333–6342. doi: 10.1523/JNEUROSCI.4837-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly AM, Uddin LQ, Biswal BB, Castellanos FX, Milham MP. Competition between functional brain networks mediates behavioral variability. NeuroImage. 2008;39:527–537. doi: 10.1016/j.neuroimage.2007.08.008. [DOI] [PubMed] [Google Scholar]
- Laumann TO, Gordon EM, Adeyemo B, Snyder AZ, Joo SJ, Chen MY, Gilmore AW, McDermott KB, Nelson SM, Dosenbach NU, Schlaggar BL, Mumford JA, Poldrack RA, Petersen SE. Functional System and Areal Organization of a Highly Sampled Individual Human Brain. Neuron. 2015;87:657–670. doi: 10.1016/j.neuron.2015.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- Lee JH, Hashimoto R, Wible CG, Yoo SS. Investigation of Spectrally Coherent Resting-State Networks Using Non-Negative Matrix Factorization for Functional MRI Data. Int J Imag Syst Tech. 2011a;21:211–222. [Google Scholar]
- Lee JH, Lee TW, Jolesz FA, Yoo SS. Independent vector analysis (IVA): multivariate approach for fMRI group study. NeuroImage. 2008;40:86–109. doi: 10.1016/j.neuroimage.2007.11.019. [DOI] [PubMed] [Google Scholar]
- Lee K, Tak S, Ye JC. A Data-Driven Sparse GLM for fMRI Analysis Using Sparse Dictionary Learning With MDL Criterion. Ieee T Med Imaging. 2011b;30:1076–1089. doi: 10.1109/TMI.2010.2097275. [DOI] [PubMed] [Google Scholar]
- Li H, Satterthwaite T, Fan Y. Identification of subject-specific brain functional networks using a collaborative sparse nonnegative matrix decomposition method. 2016:984–987. [Google Scholar]
- Li YO, Adali T, Calhoun VD. Estimating the number of independent components for functional magnetic resonance imaging data. Hum Brain Mapp. 2007;28:1251–1266. doi: 10.1002/hbm.20359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv J, Li X, Zhu D, Jiang X, Zhang X, Hu X, Zhang T, Guo L, Liu T. Sparse representation of group-wise FMRI signals. Med Image Comput Comput Assist Interv. 2013;16:608–616. doi: 10.1007/978-3-642-40760-4_76. [DOI] [PubMed] [Google Scholar]
- Morup M, Hansen LK. Tuning pruning in sparse non-negative matrix factorization. Signal Processing Conference, 2009 17th European; 2009. pp. 1923–1927. [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ. Analysis of fMRI data by blind separation into independent spatial components. Human Brain Mapping. 1998;6:160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeown MJ, Sejnowski TJ. Independent component analysis of fMRI data: examining the assumptions. Hum Brain Mapp. 1998;6:368–372. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<368::AID-HBM7>3.0.CO;2-E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moritz CH, Rogers BP, Meyerand ME. Power spectrum ranked independent component analysis of a periodic fMRI complex motor paradigm. Human Brain Mapping. 2003;18:111–122. doi: 10.1002/hbm.10081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? NeuroImage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisot S, Arslan S, Passerat-Palmbach J, Wells WM, 3rd, Rueckert D. Group-wise parcellation of the cortex through multi-scale spectral clustering. NeuroImage. 2016;136:68–83. doi: 10.1016/j.neuroimage.2016.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park HJ, Friston KJ. Structural and Functional Brain Networks: From Connections to Cognition. Science. 2013;342:579. doi: 10.1126/science.1238411. [DOI] [PubMed] [Google Scholar]
- Pessoa L. Understanding brain networks and brain organization. Phys Life Rev. 2014;11:400–435. doi: 10.1016/j.plrev.2014.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Laumann TO, Koyejo O, Gregory B, Hover A, Chen MY, Gorgolewski KJ, Luci J, Joo SJ, Boyd RL, Hunicke-Smith S, Simpson ZB, Caven T, Sochat V, Shine JM, Gordon E, Snyder AZ, Adeyemo B, Petersen SE, Glahn DC, Reese Mckay D, Curran JE, Goring HH, Carless MA, Blangero J, Dougherty R, Leemans A, Handwerker DA, Frick L, Marcotte EM, Mumford JA. Long-term neural and physiological phenotyping of a single human. Nature communications. 2015;6:8885. doi: 10.1038/ncomms9885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE. Functional network organization of the human brain. Neuron. 2011;72:665–678. doi: 10.1016/j.neuron.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Petersen SE. Studying brain organization via spontaneous fMRI signal. Neuron. 2014;84:681–696. doi: 10.1016/j.neuron.2014.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Connolly JJ, Ruparel K, Calkins ME, Jackson C, Elliott MA, Roalf DR, Ryan Hopsona KP, Behr M, Qiu H, Mentch FD, Chiavacci R, Sleiman PM, Gur RC, Hakonarson H, Gur RE. The Philadelphia Neurodevelopmental Cohort: A publicly available resource for the study of normal and abnormal brain development in youth. NeuroImage. 2016;124:1115–1119. doi: 10.1016/j.neuroimage.2015.03.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Davatzikos C. Towards an Individualized Delineation of Functional Neuroanatomy. Neuron. 2015;87:471–473. doi: 10.1016/j.neuron.2015.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE, Wolf DH. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. NeuroImage. 2013a;64:240–256. doi: 10.1016/j.neuroimage.2012.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, Mentch FD, Sleiman P, Verma R, Davatzikos C, Hakonarson H, Gur RC, Gur RE. Neuroimaging of the Philadelphia Neurodevelopmental Cohort. NeuroImage. 2014;86:544–553. doi: 10.1016/j.neuroimage.2013.07.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Wolf DH, Ruparel K, Erus G, Elliott MA, Eickhoff SB, Gennatas ED, Jackson C, Prabhakaran K, Smith A, Hakonarson H, Verma R, Davatzikos C, Gur RE, Gur RC. Heterogeneous impact of motion on fundamental patterns of developmental changes in functional connectivity during youth. NeuroImage. 2013b;83:45–57. doi: 10.1016/j.neuroimage.2013.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi JB, Malik J. Normalized cuts and image segmentation. Ieee T Pattern Anal. 2000;22:888–905. [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain’s functional architecture during activation and rest. P Natl Acad Sci USA. 2009;106:13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu JQ, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, Van Essen DC, Feinberg DA, Yacoub ES, Ugurbil K. Temporally-independent functional modes of spontaneous brain activity. P Natl Acad Sci USA. 2012;109:3131–3136. doi: 10.1073/pnas.1121329109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan VYF, Fevotte C. Automatic Relevance Determination in Nonnegative Matrix Factorization with the beta-Divergence. Ieee T Pattern Anal. 2013;35:1592–1605. doi: 10.1109/TPAMI.2012.240. [DOI] [PubMed] [Google Scholar]
- Tavor I, Parker Jones O, Mars RB, Smith SM, Behrens TE, Jbabdi S. Task-free MRI predicts individual differences in brain activity during task performance. Science. 2016;352:216–220. doi: 10.1126/science.aad8127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varoquaux G, Baronnet F, Kleinschmidt A, Fillard P, Thirion B. Detection of brain functional-connectivity difference in post-stroke patients using group-level covariance modeling. Med Image Comput Comput Assist Interv. 2010;13:200–208. doi: 10.1007/978-3-642-15705-9_25. [DOI] [PubMed] [Google Scholar]
- Varoquaux G, Gramfort A, Pedregosa F, Michel V, Thirion B. Multi-subject dictionary learning to segment an atlas of brain spontaneous activity. Information processing in medical imaging: proceedings of the conference. 2011;22:562–573. doi: 10.1007/978-3-642-22092-0_46. [DOI] [PubMed] [Google Scholar]
- Varoquaux G, Schwartz Y, Pinel P, Thirion B. Cohort-level brain mapping: learning cognitive atoms to single out specialized regions. Information processing in medical imaging: proceedings of the conference. 2013;23:438–449. doi: 10.1007/978-3-642-38868-2_37. [DOI] [PubMed] [Google Scholar]
- Wang D, Buckner RL, Fox MD, Holt DJ, Holmes AJ, Stoecklein S, Langs G, Pan R, Qian T, Li K, Baker JT, Stufflebeam SM, Wang K, Wang X, Hong B, Liu H. Parcellating cortical functional networks in individuals. Nat Neurosci. 2015;18:1853–1860. doi: 10.1038/nn.4164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z, LaConte S, Weng XC, Hu XP. Ranking and averaging independent component analysis by reproducibility (RAICAR) Human Brain Mapping. 2008;29:711–725. doi: 10.1002/hbm.20432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BTT, Krienen FM, Chee MWL, Buckner RL. Estimates of segregation and overlap of functional connectivity networks in the human cerebral cortex. NeuroImage. 2014;88:212–227. doi: 10.1016/j.neuroimage.2013.10.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BTT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL, Smoller JW, Zoller L, Polimeni JR, Fischl B, Liu HS, Buckner RL. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.