Abstract
Cardiac arrhythmias have been traditionally simulated using continuous models that assume tissue homogeneity and use a relatively large spatial discretization. However, it is believed that the tissue fibrosis and collagen deposition, which occur on a micron-level, are critical factors in arrhythmogenesis in diseased tissues. Consequently, it remains unclear how well continuous models, which use averaged electrical properties, are able to accurately capture complex conduction behaviors such as re-entry in fibrotic tissues. The objective of this study was to compare re-entrant behavior in discrete microstructural models of fibrosis and in two types of equivalent continuous models, a homogenous continuous model and a hybrid continuous model with distinct heterogeneities. In the discrete model, increasing levels of tissue fibrosis lead to a substantial increase in the re-entrant cycle length which is inadequately reflected in the homogenous continuous models. These cycle length increases appear to be primarily due to increases in the tip path length and to altered restitution behavior, and suggest that it is critical to consider the discrete effects of fibrosis on conduction when studying arrhythmogenesis in fibrotic myocardium. Hybrid models are able to accurately capture some aspects of re-entry and, if carefully tuned, may provide a framework for simulating conduction in diseased tissues with both accuracy and efficiency.
Computational models of cardiac conduction can play an important role in understanding the mechanisms of and developing treatments for fibrosis-induced cardiac arrhythmias. However, most studies investigating the arrhythmogenic role of cardiac fibrosis have modelled the myocardium as a locally homogenous continuum with slowed conduction and increased conduction anisotropy in the areas of fibrosis. While these continuum methods recreate normal conduction in healthy tissues and allow for increased computational efficiency, it remains unclear how effectively they are able to model complex conduction patterns such as re-entry. In this work, we show that continuous models incompletely represent re-entrant behavior because they are unable to capture changes in tip trajectory and restitution. We find that hybrid models, which incorporate discrete heterogeneity into the continuous tissue representation, are able to capture some aspects of complex re-entry and may allow for accurate simulation with preserved computational efficiency.
INTRODUCTION
Understanding the mechanisms of cardiac arrhythmia initiation and perpetuation has proven to be a challenging problem because of the difficulties in studying the dynamics of abnormal cardiac activity in vivo and recapitulating critical features of interest in vitro. Computational modeling of cardiac electrophysiology provides a useful framework for understanding the mechanisms of and developing treatments for arrhythmia because of the ability to carefully control parameters of interest. However, in order to accurately draw conclusions about the nature of pathological conduction, models must be constructed with sufficient fidelity to reproduce the structural components underlying human diseases.
Because cardiac tissue is a discontinuous network of highly connected individual cells, and because conduction is affected by the discrete cellular structure of the tissue,33 cardiac electrical activity has often been modeled using microstructural model systems that can incorporate variation in the cell shape, size and orientation as well as distinct gap junctions between neighboring cells. This type of detailed structural model allows for the study of the effects of alterations in the tissue structure on conduction, including alterations in source-load balance, gap junctional distribution, and fibrosis.17,18,32 However, because these discrete models require subcellular resolution, they are extremely computationally expensive. In order to speed up computation and simulate larger regions of conduction, continuous models with spatial resolutions at the cellular scale and higher are typically used.15 These models provide an idealized representation of the tissue, with homogenized electrical properties that aggregate the effects of tissue structure, connectivity and cellular orientation.14 Continuous models have proven capable of replicating the dynamics of conduction for models of healthy tissues;5,35 however, recent evidence suggests that these models may be less predictive under diseased conditions such as ischemia35 and reduced coupling,5,11 or at the interfaces of regional heterogeneity.16
Recently, the effects of fibrosis on arrhythmogenesis and arrhythmia dynamics have been of growing interest. Cardiac fibrosis is an injury response that involves the remodeling of gap junctions that couple neighboring cells, proliferation of fibroblasts, and deposition of excess collagen that separates and replaces the functional cardiac tissue, decoupling the syncytium that is necessary for normal cardiac conduction. Fibrosis varies in density, distribution and size, and different types of fibrosis (dense, interstitial, diffuse, etc) have varying impacts on conduction.19,20 Marrouche et al. have found that the degree of fibrosis (estimated via delayed enhancement MRI) can be predictive of the likelihood of recurrent arrhythmia after atrial fibrillation ablation.22 As such, fibrosis may be an important target to new biological therapies for arrhythmia.
The best way to represent fibrosis in tissue models is still an open question. Spach et al. introduced interstitial fibrosis in discrete models by representing non-conductive collagenous septa as the decoupling of transverse cellular connections,32 which maintains the electrical effects of fibrosis without occupying space in the tissue domain. In continuous computational models, fibrosis is traditionally incorporated by decreasing conductivity values to reproduce experimentally observed conduction slowing and conduction anisotropy. While this approach reproduces the macroscopic conduction behavior, it may not capture the microscopic effects of fibrosis that could be crucial in arrhythmogenesis. The more recent approach by Costa et al.9,10 of decoupling elements in a coarse mesh to reproduce the effects of interstitial fibrosis is analogous to the approach of Spach et al. in the discrete model, and has shown promise in reproducing microscale conduction. However, it remains unclear how any of these approaches perform in the setting of complex behavior such as re-entrant spiral waves.
In this study, we compare spiral wave behavior in both discrete and two equivalent continuous models of interstitial fibrosis to understand whether continuous computational models that condense structural complexity into reduced conductivity are sufficient to capture the details of re-entry. We explore the potential source of divergence between discrete and uniform continuous models and consider the use of hybrid models that incorporate distinct decoupling septa into a coarse continuous model.
METHODS
Tissue models
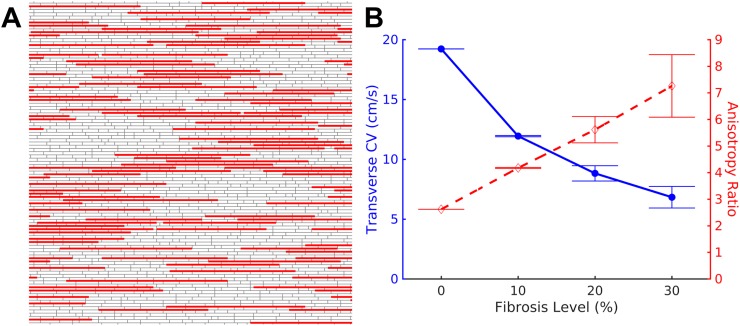
Two-dimensional monodomain microstructural models of anisotropic cardiac monolayers that incorporate discrete, uniformly distributed gap junctions were randomly generated using previously described methods.18 Tissues used were 2 cm × 2 cm, with a spatial discretization of 20 μm. Individual myocytes were an average of 100 μm in length and 20 μm in width, arranged in a brick-wall form and aligned along their length. An intracellular resistivity of 150 Ω·cm and a gap junction conductance of 2.5 μS were used. Collagen septa of variable length (selected from a Poisson distribution with a mean length of 800 μm) were inserted, parallel to cellular orientation, to occupy between 0% and 30% of transverse interfaces between myocytes.18 [Fig. 1(a)]. All transverse junctions between cells separated by collagenous septa were removed to simulate the decoupling effect of collagen deposition. 70% of the remaining combined plicate transverse junctions were decoupled to replicate the adult phenotype of gap junctions concentrated at longitudinal cell junctions.17 Ten distinct microstructural models with random septa placement and transverse decoupling were constructed for each level of fibrosis (0%, 10%, 20%, and 30%).
FIG. 1.
Discrete model of fibrosis. (a) Fibrosis was modeled in the discrete tissue by inserting non-conductive collagen septa (solid) parallel to and between individual cardiac cells (gray). (b) Increasing the percent of transverse cell-to-cell boundaries interrupted by collagenous septa leads to a substantial decrease in the transverse conduction velocity (solid) and an increase in the anisotropy of conduction (dashed).
An equivalent homogenous continuous model with a spatial discretization of 100 μm was produced for each discrete model by adjusting the tissue conductivities to match the conduction velocities (CVs) of transverse and longitudinal conduction measured in the corresponding discrete model. In the presence of fibrosis, the continuous model's mean longitudinal conductivities decreased by 5.7% from 0% to 30% fibrosis (2.82 mS/cm to 2.66 mS/cm), while mean transverse conductivities decreased by 77.2% (0.445 mS/cm to 0.101 mS/cm). Hybrid continuous models were created by inserting longitudinally oriented decoupling septa of mean length of 800 microns into a homogenous continuous model to disrupt between 10% and 50% of transverse coupling between nodes. The electrical conductivities between the tissue nodes were then adjusted such that the combination of decoupling septa and tissue conductivity resulted in conduction velocities equivalent to each discrete model.
Simulation of conduction
In each tissue model, longitudinal and transverse conduction velocities were measured following 2 Hz pacing with a line electrode along the left or top boundary of the tissue. Activation time (time to half-maximal voltage) and action potential duration (APD80, to 80% repolarization) were measured. Conduction velocities were calculated by performing linear regression on activation times.
Re-entry was induced by the application of cross-field S1–S2 stimulation. A planar wave was initiated by a line stimulus along the left boundary of the tissue (S1). A premature second stimulus (S2) was applied in the top left region of the tissue. A stable spiral wave was allowed to form for at least three full revolutions, before the cycle length was measured at several points on the tissue. Tip trajectories were tracked by generating a phase map at 2.5 ms intervals and identifying phase singularities.
Transverse and longitudinal restitution were measured by pacing the tissues in the selected direction at 2 Hz for 5 pulses, followed by application of a premature stimulus of same amplitude. The conduction velocity and action potential duration resulting from the premature stimulus were recorded, and the interval between the final pacing stimulus and the premature stimulus was decreased until the premature stimulus no longer elicited a propagating wave front.
Numerical methods
Cardiac conduction was simulated using the monodomain formulation of electrical propagation. The Wang-Sobie membrane model of the neonatal mouse myocyte40 was used in all simulations because of its relatively short action potential duration and governing ODEs (ordinary differential equations) that are less stiff than the Bondarenko et al. adult mouse model,4,34 reducing the overall computation time. While the model is not ideally suitable to the adult tissue structure, the critical findings of this study were found to be similar to the Bondarenko et al. model used in a preliminary study.13 The governing equations were discretized using finite differences, and propagation was simulated using a semi-implicit Crank-Nicholson scheme with adaptive time steps between 5 μs and 25 μs. A biconjugate gradient stabilized solver with a tridiagonal preconditioner was used at each time-step. Transmembrane potentials and extracellular point electrograms were recorded at intervals of 50 μs at selected points in the domain, as previously described.18 The conductivity of the volume conductor was set to achieve a peak-to-peak electrogram amplitude of approximately 1 mV in the absence of fibrosis. In addition, potentials were recorded at all nodes at intervals of 2.5 ms for tracking tip trajectory and visualization. All simulations were performed across 33 CPUs using the Cardiowave software package28 (available online at cardiowave.duke.edu).
Analytical methods
All discrete model studies were conducted with 10 discrete models at each degree of fibrosis. All continuous and hybrid model studies were conducted in 10 models per degree of fibrosis, with each model tuned to match the behavior of the target discrete model.
All data are presented as mean ± standard deviation, unless otherwise specified. Differences in means between groups are quantified and presented due to concerns regarding the use of statistical tests in model-generated data.27
RESULTS
Propagation in microstructural models and equivalent continuous models
The degree of fibrosis, characterized by the density of collagenous septa, is expected to have an effect on the conduction velocity of wavefronts. Conduction velocity was measured in the discrete microstructural model after applying 2 Hz planar stimulation. As the degree of fibrosis was increased, conduction velocity in the longitudinal direction decreased slightly from 50.39 ± 0.01 cm/s with no fibrosis to 48.65 ± 0.01 cm/s with 30% fibrosis (n = 10 for each case). Transverse conduction velocity slowed substantially with increased fibrosis, from 19.23 ± 0.004 cm/s to 6.83 ± 0.90 cm/s as fibrosis was increased from 0% to 30% [Fig. 1(b), solid], resulting in an increase in the anisotropy ratio from 2.62:1 to 7.26:1 [Fig. 1(b), dashed].
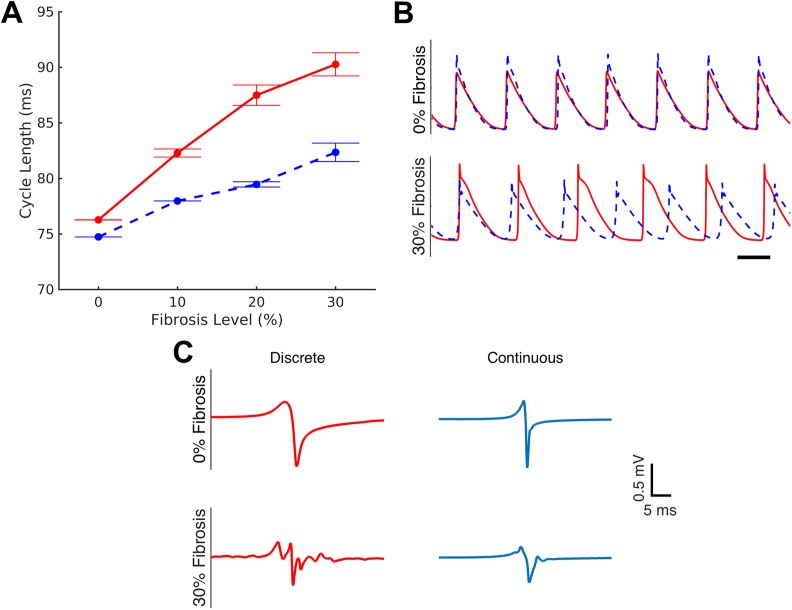
The introduction of septa should affect the trajectory of spiral waves in the discrete tissue. Spiral waves were induced via cross-field stimulation. Increasing fibrosis leads to a prolongation of the mean cycle length from 76.27 ± 0.04 ms in the non-fibrotic tissue to 90.27 ± 3.13 ms in 30% fibrosis, an increase of 18.4% [Fig. 2(a), solid]. In addition, the variability in the cycle length was also observed to increase with increasing fibrosis, with minimal variability between non-fibrotic models and substantial variability between 30% fibrosis models. Unipolar electrograms recorded from point electrodes exhibited increasing complexity and fractionation in discrete tissues with 30% fibrosis. Representative electrograms are shown in Fig. 2(c) (left column).
FIG. 2.
Continuous model fails to capture the details of re-entry. Re-entry was induced in discrete models and their equivalent continuous representations by cross-field stimulation. (a) The discrete model exhibits a substantial increase in the cycle length of re-entry (solid), up to 18.4% in 30% fibrosis that is not captured by the equivalent continuous models (dashed). Cycle lengths are shown as mean ± standard error. (b) Transmembrane potential traces show a clear difference in cycle length between the discrete model (solid) and the homogenous continuous model (dashed) at high degrees of fibrosis (lower panel) that is not seen in the absence of fibrosis (upper panel). Scale bar represents 50 ms. Note that traces were time-shifted to align the first action potential. (c) Electrograms in discrete model simulations exhibit complexity and fractionation in the presence of fibrosis, which is incompletely captured in the equivalent continuous models.
An equivalent continuous model was created for each discrete microstructural model by matching the microstructural model's transverse and longitudinal conduction velocities following 2 Hz pacing, and spiral waves were induced in each continuous model. The non-fibrotic continuous model exhibited cycle lengths similar to those of the discrete non-fibrotic tissue (CL = 74.73 ms vs 76.27 ms). However, at higher degrees of fibrosis, the continuous tissues showed only a modest increase in cycle length, with a maximal increase to 82.24 ± 2.63 ms (10% increase) in 30%-fibrosis-equivalent tissue. As a result, the equivalent continuous model has an 8.9% error in the projected cycle length at 30% fibrosis, which is apparent from transmembrane potential traces from discrete and equivalent continuous simulations [Fig. 2(b)]. In addition, while unipolar electrograms from the equivalent continuous model are qualitatively similar to those of the discrete model in the absence of fibrosis, they fail to exhibit the fractionation seen in electrograms of fibrotic microstructural models [Fig. 2(c)].
Factors affecting the cycle length
To understand what factors lead to the longer cycle length in the discrete model that are not fully captured in the continuous models, the impact of tip trajectory and restitution behaviour was explored. Analysis of tip trajectory in the control (non-fibrotic) case showed that non-fibrotic discrete and continuous models exhibited similar tip trajectories that were hypotrochoid-like in shape, with a mean span of 3.4 mm in length and 0.96 mm in width [Fig. 3(a), left]. In the presence of 30% fibrosis, the tip trajectory in the continuous model remained unchanged in shape, but was significantly flattened, with a mean span of only 0.36 mm in width [Fig. 3(a), right]. However, in the discrete model, the tip trajectory was much longer and thinner (with a mean span of 8.2 mm in length and 0.42 mm in width) [Fig. 3(a), center], suggesting an anatomical rather than functional form of re-entry.
FIG. 3.
Factors contributing to continuous model cycle length error. (a) In the absence of fibrosis, both the discrete (left panel) and continuous (not shown) models exhibit a hypotrochoid-like spiral wave tip trajectory. In the presence of fibrosis, the discrete mode (center panel) transits from functional to anatomical re-entry with a long, linear tip trajectory, while the equivalent continuous model (right panel) continues to exhibit hypotrochoid-like tip trajectory, albeit significantly flattened due to slowed transverse conduction. Note that all figures show only a part of the domain. Scale bar = 2.5 mm. (b) Restitution behavior during longitudinal pacing is nearly equivalent in the discrete (solid) and homogenous continuous (dashed) models, both in the presence and absence of fibrosis. In the transverse direction, the continuous model restitution curve closely matches the discrete model in non-fibrotic tissues, with slight deviation (up to 14.0%) at intervals below 100 ms. In contrast, in fibrotic tissues, the continuous model exhibits significantly faster conduction (up to 43.4% faster) at intervals below 180 ms.
Restitution behavior in the discrete and continuous models with 0% and 20% fibrosis was examined using a standard S1-S2 pacing protocol, in both the longitudinal and transverse directions. In all cases, because the homogenous continuous models were constructed to replicate discrete model CVs at 2 Hz pacing, the CVs are equivalent at longer diastolic intervals (of 500 ms or greater). As the diastolic interval is decreased during longitudinal pacing, the continuous model behavior closely matches that of the discrete model [Fig. 3(b), top row]. Restitution in the continuous model deviates significantly from the discrete model only at intervals under 100 ms (p < 0.05). During transverse pacing of the non-fibrotic tissue, the restitution of the continuous model deviates from the discrete model at intervals below 140 ms, with a maximum error of 14.0% at an S1-S2 interval of 90 ms [Fig. 3(b), bottom left]. A larger deviation is noted in the case of fibrotic tissue [Fig. 3(b), bottom right], where the continuous model significantly underestimates CV slowing at S1-S2 intervals of 180 ms or below, with an error of 43.4% at an interval of 90 ms. As a result, the discrete model CV restitution curve has a maximum slope that is 1.58 times greater than that of the continuous model.
In order to understand how the character of fibrosis affects continuous model estimations of cycle length, the mean length of collagenous septa in the discrete model was adjusted between 0 and 800 μm, and the cycle length was examined in discrete and equivalent continuous models. Because the total amount of fibrosis was maintained at 30% of transverse node-to-node junctions, tissues with shorter fibrosis lengths contained more individual septa. In the absence of fibrosis, the continuous model underestimates the cycle length by 2.1% (1.53 ms). At a mean fibrosis length of 200 μm, there is minimal error between the discrete and equivalent continuous models (0.14% error); however, as fibrosis length is increased further, the continuous model predicts cycle lengths that are significantly shorter than that observed in the discrete model. (Fig. 4).
FIG. 4.
Effect of collagen septa size. Error between the discrete model (solid) and the equivalent continuous models (dashed) is dependent on the size of collagenous septa. Small collagenous septa result in a minimal difference between the discrete and continuous models. In all cases, total septa density was fixed at 30%.
Propagation in hybrid models
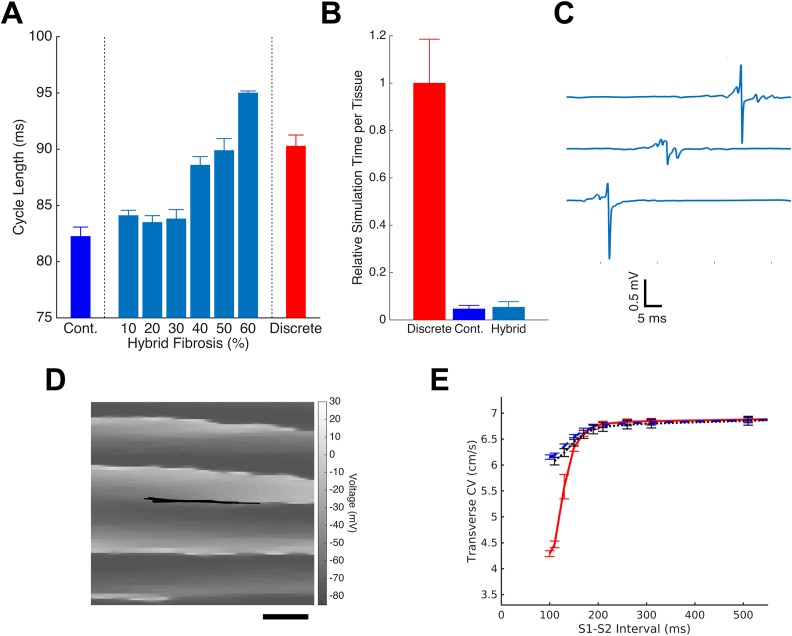
In order to capture the complexity of discrete fibrosis and maintain the computational efficiency of continuous models, we considered the development of hybrid models that incorporate coarse spatial discretization and distinct decoupling septa. Hybrid models were generated to replicate the behavior of 30% fibrotic discrete tissue. The continuous model was modified by disrupting 30% of transverse node-to-node connections with non-conductive septa (mean length 800 μm), and tissue conductivities were adjusted such that the combined effect of septa and conductivity tuning matched the longitudinal and transverse CVs observed in each discrete model. The resulting models exhibited spiral wave behavior with a mean cycle length of 83.9 ms, 1.6 ms longer than that in the homogenous continuous model, but still 6.37 ms shorter than the cycle length of re-entry in the discrete model (Fig. 5). The amount of connection-disrupting collagen in the hybrid models was then altered, and each model was re-tuned to match discrete planer conduction velocities. Increasing the fibrosis density above 30% in the hybrid model resulted in the prolongation of cycle lengths, and models with 50% transverse decoupling closely matched the cycle lengths of the discrete model (mean cycle length, 90.27 ms in 30% fibrotic discrete model vs 89.88 in 50% fibrotic hybrid model). Simulation of 1.5 s of spiral wave activity required substantially less computational time in the hybrid model than in the discrete model, and there was a minimal difference in the simulation time between the continuous and hybrid models [Fig. 5(b); a mean of 4.0 h for discrete model vs 0.19 h for the continuous model and 0.21 h for the hybrid model]. Three representative unipolar electrograms from the hybrid model are shown in Fig. 5(c). Electrograms from the hybrid tissues appear to be qualitatively similar in fractionation and complexity to those obtained from discrete tissues.
FIG. 5.
Hybrid models improve continuous model accuracy. The introduction of discrete heterogeneities (in the form of decoupling septa) in the continuous model allows for accurately replicating discrete model behavior. (a) The degree of fibrosis in the hybrid model was tuned to match discrete model cycle length. For each level of fibrosis, tissue conductivities were first adjusted to match discrete planar conduction velocities. The hybrid model with 50% fibrosis was selected for further use. (b) The hybrid model maintains 18× computational efficiency of the continuous model when each is run with equal computing resources. (c) The selected hybrid model produces electrograms that qualitatively display complexity and fractionation similar to the discrete model. (d) The tip trajectory in the hybrid model is similar to that of the discrete model with a long and narrow path. Note that this panel shows only a part of the domain. Scale bar = 2.5 mm. (e) The transverse restitution behavior of the hybrid tissue (dotted) remains the same as that of the continuous model (dashed) rather than that of the discrete model (solid).
In order to understand how the hybrid model re-creates discrete model behavior, we examined hybrid model restitution and tip trajectory. The tip trajectory profile of the spiral wave in the hybrid model follows a path very similar to the discrete model. The trajectory is thin and long (span of 7.3 mm in length and 0.35 mm in width) and appears to be anatomical in nature rather than functional [Fig. 5(e)]. However, the transverse restitution profile of the hybrid model closely matches that of the homogenous continuous model rather than the discrete model [Fig. 5(d)], indicating that the hybrid model's ability to replicate discrete cycle lengths is primarily due to tip trajectory rather than dynamic variation in conduction velocity.
DISCUSSION
In this study, we examined simulated re-entry in continuous models of cardiac propagation and considered whether continuous models of cardiac propagation are able to accurately capture the details of re-entry in fibrotic myocardium. We showed that (i) continuous models fail to fully capture the increases in the cycle length of re-entry observed in microstructural discrete models of interstitial fibrosis, (ii) differences between discrete and continuous models are due to differences in tip trajectory and restitution behavior, and (iii) hybrid models that incorporate distinct edge-decoupling on coarse discretization are able to, to some degree, recapitulate discrete model behavior without compromising the computational efficiency.
Using a discrete model of cardiac tissue, we first showed that increasing the interstitial fibrosis density in discrete, microstructural models of cardiac tissue causes transverse conduction velocity to decrease at a decreasing rate, and longitudinal velocity to be minimally decreased, as previously described.18 The resulting anisotropy ratios fall within that range previously described experimentally.31,32 When spiral waves are induced in these tissues, we observed that as the degree of fibrosis is increased, the cycle length of re-entry increases, similar to previous findings in models of diffuse fibrosis.38 In addition, as the degree of fibrosis was increased, the variability in the planar conduction velocity and the cycle length increased as well, suggesting that the spatial arrangement of fibrosis grows in importance at higher fibrosis densities.
Because several groups have modeled fibrosis in large tissue or organ models as a homogenous decrease in conductivity to match experimental CVs (for example, Refs. 21 and 42), we used the same approach in developing equivalent continuous models for each discrete tissue model. Despite the fact that the continuous models each closely match the conduction behavior of discrete models during 2 Hz linear pacing, when re-entry was induced at higher densities of fibrosis, the resulting cycle lengths were significantly shorter than those in the discrete models [Fig. 2(a)]. This finding suggests that homogenized models are inadequate to fully capture the details of cardiac re-entry in the diseased tissue. The impact of this discrepancy in the context of whole atrial or ventricular models remains unclear. While the absolute error in the cycle length is relatively modest (8.9% of the discrete cycle length), an error on this magnitude could have a significant impact on the determination of spiral wave stability or instability.8 In addition, previous studies have used computational models to develop tools for interpretation of electrograms, but discrepancy in the complexity of electrograms in the discrete and continuous models suggests that continuous models do not produce electrograms that capture the complexity of the underlying substrate.
In order to understand this difference between continuous and discrete cycle lengths, we examined the differences in restitution behavior in these models. Even though the discrete fibrotic model and the equivalent continuous model have been calibrated to have an equal conduction velocity in response to 2 Hz planar pacing, propagation at different rates or of a premature stimulus may draw out differences between the models. Because spiral waves in the discrete tissues do not cycle at exactly 2 Hz, differences in restitution could affect the cycle length of re-entry. A comparison of non-fibrotic discrete and continuous tissues revealed a small difference in restitution behavior at very short coupling intervals [Fig. 3(b), left column]. These differences, possibly caused by source-load mismatches at cell-to-cell gap junctions due to decreased sodium excitability, may result in the small difference in the cycle length between discrete and continuous models in the absence of fibrosis. In comparison to non-fibrotic tissues, fibrotic tissues exhibited a larger difference in transverse restitution between discrete and continuous models [Fig. 3(b), bottom right]. The additional slowing seen in the discrete model is likely due to source-load mismatches at regions where multiple nearby septa result in tissue expansions, which have been shown to lead to local conduction slowing.30 The resulting difference in restitution, previously described in models of diffuse fibrosis,12 contributes to the prolongation of the cycle length in highly fibrotic tissues that is not captured by the continuous model. Restitution behavior plays a critical role in the initiation and maintenance of arrhythmia.3,29 As such, it is vital for computational models to accurately capture restitution beyond just the effects on cycle length. Variation in the slope of the CV restitution curve has specifically been linked to the formation of alternans, a precursor to re-entry,7 and in the presence of fibrosis, the steepness of the discrete model's transverse CV restitution curve is poorly recapitulated by the continuous model. Taken together, these differences represent significant deficiencies in the continuous model under conditions where the cycle length is not constant, such as during alternans and the initiation of re-entry.
We also studied the path of the spiral wave tip during re-entry in continuous and discrete models and found a substantial prolongation in the path length of re-entry in the fibrotic tissue in the discrete model, but not in the continuous model. This near doubling of the longitudinal tip path length plays a critical role in the prolongation of the spiral wave cycle length. While adjusting conductivities in a continuous model may capture the impact of gap junctional remodeling during fibrosis, the effects of collagen deposition cannot be easily homogenized.
In recognition of potential limitations of using continuous models to replicate the effects of fibrosis, Costa et al. recently described a hybrid method for inserting non-conductive septa into a coarse finite element mesh,9,10 analogous to the insertion of septa into our discrete model.18 This method has recently been used, in combination with simulated junctional remodeling and fibroblast proliferation, in several studies of atrial fibrosis by McDowell et al.23,25,26 Several other methods of incorporating discrete fibrosis into a coarse model have been described. Percolation-based models include randomly distributed decoupled links or fully decoupled sites to reproduce the effects of fibrosis.1,2,39 Studies using link-percolation are functionally equivalent to the introduction of non-conductive septa of a fixed size equal to the discretization of the domain, while site-percolation methods create space-occupying fibrosis that may reproduce functional changes in tissue geometry. The space-fractional model incorporates heterogeneity more abstractly as a deviation from the standard laws of diffusion.6 However, the fidelity of these methods, in comparison to discrete cardiac models, remains unclear. To investigate this, we developed a hybrid model by inserting non-conductive septa into a coarse finite difference mesh. The prevalence of septa was varied and each model was tuned to match planar conduction velocities of the 30%-fibrosis discrete models. We found that 30% transverse decoupling by septa was insufficient to match the discrete cycle length, likely because the coarse discretization of the hybrid model meant that the total length of inserted septa was substantially smaller than in the discrete model. By increasing the number of septa such that they decouple 50% of transverse node-node connections, we were able to closely match the cycle lengths of re-entry observed in the discrete tissue models. While this quantitative 20% difference in septa density is not directly translatable into human fibrotic models because of the inherent limitations of our 2D study, these simulations demonstrate that hybrid models are able to reproduce the macroscale behavior of the discrete model when the nature of the modeled fibrosis is appropriately tuned.
The hybrid model appears to recreate this behavior of the discrete model primarily by capturing the prolonged tip trajectory of the discrete model [Fig. 5(d)]. The presence of discrete heterogeneities in the hybrid model allows for a transition to anatomical re-entry. However, the hybrid model fails to capture the restitution effects of fibrosis in the discrete model. This is potentially because the source-load imbalance that leads to discrete CV slowing at shorter coupling intervals is lost at the hybrid models coarser spatial discretization. Despite this observed difference in restitution behavior, hybrid models show promise in reproducing the aspects of complex behaviors of the discrete model with a substantially reduced computational load, and may prove to be a valuable tool when carefully tuned for their intended purpose.
While homogenization is insufficient in modeling the effects of interstitial fibrosis, our findings suggest that other types of fibrosis, such as diffuse fibrosis, may be adequately represented by altering conductivities of continuous models because of the relatively small size of diffuse collagenous deposits. As such, hybrid models that incorporate both distinct heterogeneities and reduced overall conductivity may be ideally suited to recreate the physiology of conduction in a complex fibrotic substrate. The conductive changes in interstitial fibrosis do not occur in isolation, but rather in concert with a host of other fibrotic changes. Proliferation of myofibroblasts in the myocardium may increase the susceptibility to arrhythmia,24 and the combination of myofibroblast proliferation and gap junctional remodeling is implicated in the initiation of re-entry.26 Models seeking to study the mechanisms of and treatments for arrhythmia must therefore incorporate not only the effects of collagenous deposition, but also an accurate description of the impact of microscale myocyte-myocyte and myocyte-fibroblast coupling.
Limitations
Because of the computational limitations of discrete models, this work was performed in two-dimensional monolayer-like models with idealized cell geometries. While three-dimensional discrete models of cardiac tissue have been previously described,36 they remain extremely computationally expensive. 2D models do not allow for conduction perpendicular to the 2D domain, nor do they incorporate the complexity of native cardiac tissue including the presence of fibers. However, 2D models of cardiac tissue have been used extensively by our group and others37,41 to provide insights into the effects of structural heterogeneity on conduction. They also allow direct comparisons to experiments performed on in vitro monolayers. Another limitation of the study is that the Wang-Sobie membrane model of neonatal mouse cells used in this study has a relatively short action potential duration compared to the human models. The shorter action potential was needed to generate re-entrant propagation in the smaller, finely discretized discrete tissue domains, making the multiple simulations of re-entry in 2D discrete tissues computationally tractable. While the membrane model is more applicable to validation in in vitro monolayers, the structure is more applicable to adult tissues. Hence, the model choices were considered as a compromise. Because of these limitations, the quantitative findings of this study and specifically, the degrees of error between discrete and continuous models will not scale directly to simulations of human disease in the 3D heart model; however, we believe that the general conclusions highlighting the differences between these model types are broadly applicable to more complex computational models in larger domains. We have previously demonstrated qualitatively similar results as Fig. 2(a) (Ref. 13) using the adult mouse Bondarenko model;4 however, as noted, the numerical stiffness of the ODEs underlying this membrane model34 required unreasonably long computation times. The biophysical Wang-Sobie was selected over a simplified model because of its realistic ion channel descriptions. The purpose of this study was to examine whether the effects of fibrosis can be adequately captured in continuous models, and the deviation in behavior between model types in an idealized 2D case suggests that care must be taken in developing models of complex fibrosis, in both 2D and 3D.
CONCLUSIONS
In this study, we examined the ability of continuous cardiac models to capture complex conduction behaviour such as re-entry in the setting of interstitial fibrosis. Our results indicate that the difference in restitution behaviour and spiral tip trajectory leads to modest error in continuous model estimations of cycle length. However, we demonstrate that hybrid models that incorporate non-conductive septa with coarse discretization are able to recapitulate some aspects of complex re-entry, while providing significant computational efficiency. We suggest that it is critical to carefully consider and validate methodologies of incorporating fibrosis in computational tissue models before these models can be used to gain a mechanistic understanding of and devise treatments for clinical arrhythmia.
ACKNOWLEDGMENTS
This work was supported by National Institutes of Health Grant Nos. R01HL093711, R01HL126524, R01HL132389, and 5T32GM007171.
References
- 1. Alonso S. and Bär M., “ Reentry near the percolation threshold in a heterogeneous discrete model for cardiac tissue,” Phys. Rev. Lett. 110, 158101 (2013). 10.1103/PhysRevLett.110.158101 [DOI] [PubMed] [Google Scholar]
- 2. Alonso S., Kapral R., and Bär M., “ Effective medium theory for reaction rates and diffusion coefficients of heterogeneous systems,” Phys. Rev. Lett. 102, 238302 (2009). 10.1103/PhysRevLett.102.238302 [DOI] [PubMed] [Google Scholar]
- 3. Banville I. and Gray R. A., “ Effect of action potential duration and conduction velocity restitution and their spatial dispersion on alternans and the stability of arrhythmias,” J. Cardiovasc. Electrophysiol. 13, 1141–1149 (2002). 10.1046/j.1540-8167.2002.01141.x [DOI] [PubMed] [Google Scholar]
- 4. Bondarenko V. E., “ Computer model of action potential of mouse ventricular myocytes,” AJP, Heart Circ. Physiol. 287, H1378–H1403 (2004). 10.1152/ajpheart.00185.2003 [DOI] [PubMed] [Google Scholar]
- 5. Bruce D., Pathmanathan P., and Whiteley J. P., “ Modelling the effect of gap junctions on tissue-level cardiac electrophysiology,” Bull. Math. Biol. 76, 431–454 (2014). 10.1007/s11538-013-9927-1 [DOI] [PubMed] [Google Scholar]
- 6. Bueno-Orovio A., Kay D., Grau V., Rodriguez B., and Burrage K., “ Fractional diffusion models of cardiac electrical propagation: Role of structural heterogeneity in dispersion of repolarization,” J. R. Soc. Interface 11, 20140352–20140352 (2014). 10.1098/rsif.2014.0352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Cherry E. M., “ Suppression of alternans and conduction blocks despite steep APD restitution: Electrotonic, memory, and conduction velocity restitution effects,” AJP Heart Circ. Physiol. 286, H2332–H2341 (2004). 10.1152/ajpheart.00747.2003 [DOI] [PubMed] [Google Scholar]
- 8. Clayton R. H., Bernus O., Cherry E. M., Dierckx H., Fenton F. H., Mirabella L., Panfilov A. V., Sachse F. B., Seemann G., and Zhang H., “ Models of cardiac tissue electrophysiology: Progress, challenges and open questions,” Prog. Biophys. Mol. Biol. 104, 22–48 (2011). 10.1016/j.pbiomolbio.2010.05.008 [DOI] [PubMed] [Google Scholar]
- 9. Costa C. M., Campos F. O., Prassl A. J., dos Santos R. W., Sánchez-Quintana D., Ahammer H., Hofer E., and Plank G., “ An efficient finite element approach for modeling fibrotic clefts in the heart,” IEEE Trans. Biomed. Eng. 61, 900–910 (2014). 10.1109/TBME.2013.2292320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Costa C. M. C., Campos F. O., Prassl A. J., dos Santos R. W., Sánchez-Quintana D., Hofer E., and Plank G., “ A finite element approach for modeling micro-structural discontinuities in the heart,” Conf. Proc. IEEE Eng. Med. Biol. Soc. 2011, 437–440 (2011). 10.1109/IEMBS.2011.6090059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Costa C. M. and Weber Dos Santos R., “ Limitations of the homogenized cardiac Monodomain model for the case of low gap junctional coupling,” Proc. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2010, 228–231 (2010). 10.1109/IEMBS.2010.5627817 [DOI] [PubMed] [Google Scholar]
- 12. Engelman Z. J., Trew M. L., and Smaill B. H., “ Structural heterogeneity alone is a sufficient substrate for dynamic instability and altered restitution,” Circ. Arrhythmia Electrophysiol. 3, 195–203 (2010). 10.1161/CIRCEP.109.890459 [DOI] [PubMed] [Google Scholar]
- 13. Gokhale T., Medvescek E., and Henriquez C., “ Continuous models fail to capture details of reentry in fibrotic myocardium,” Comput. Cardiol. 2016, 7868706. 10.22489/CinC.2016.052-487 [DOI] [Google Scholar]
- 14. Hand P. E., Griffith B. E., and Peskin C. S., “ Deriving macroscopic myocardial conductivities by homogenization of microscopic models,” Bull. Math. Biol. 71, 1707–1726 (2009). 10.1007/s11538-009-9421-y [DOI] [PubMed] [Google Scholar]
- 15. Henriquez C. S., “ A brief history of tissue models for cardiac electrophysiology,” IEEE Trans. Biomed. Eng. 61, 1457–1465 (2014). 10.1109/TBME.2014.2310515 [DOI] [PubMed] [Google Scholar]
- 16. Hubbard M. L. and Henriquez C. S., “ A microstructural model of reentry arising from focal breakthrough at sites of source-load mismatch in a central region of slow conduction,” Am. J. Physiol. Heart Circ. Physiol. 306, H1341–H1352 (2014). 10.1152/ajpheart.00385.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Hubbard M. L., Ying W., and Henriquez C. S., “ Effect of gap junction distribution on impulse propagation in a monolayer of myocytes: A model study,” Europace 9(Suppl 6), vi20–vi28 (2007). 10.1093/europace/eum203 [DOI] [PubMed] [Google Scholar]
- 18. Jacquemet V. and Henriquez C. S., “ Genesis of complex fractionated atrial electrograms in zones of slow conduction: a computer model of microfibrosis,” Heart Rhythm 6, 803–810 (2009). 10.1016/j.hrthm.2009.02.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. de Jong S., van Veen T. a B., van Rijen H. V. M., and de Bakker J. M. T., “ Fibrosis and cardiac arrhythmias,” J. Cardiovasc. Pharmacol. 57, 630–638 (2011). 10.1097/FJC.0b013e318207a35f [DOI] [PubMed] [Google Scholar]
- 20. Kawara T., Derksen R., de Groot J. R., Coronel R., Tasseron S., Linnenbank a. C., Hauer R. N., Kirkels H., Janse M. J., and de Bakker J. M., “ Activation delay after premature stimulation in chronically diseased human myocardium relates to the architecture of interstitial fibrosis,” Circulation 104, 3069–3075 (2001). 10.1161/hc5001.100833 [DOI] [PubMed] [Google Scholar]
- 21. Krueger M. W., Rhode K. S., O'Neill M. D., Rinaldi C. A., Gill J., Razavi R., Seemann G., and Doessel O., “ Patient-specific modeling of atrial fibrosis increases the accuracy of sinus rhythm simulations and may explain maintenance of atrial fibrillation,” J. Electrocardiol. 47, 324–328 (2014). 10.1016/j.jelectrocard.2013.11.003 [DOI] [PubMed] [Google Scholar]
- 22. Marrouche N. F., Wilber D., Hindricks G., Jais P., Akoum N., Marchlinski F., Kholmovski E., Burgon N., Hu N., Mont L., Deneke T., Duytschaever M., Neumann T., Mansour M., Mahnkopf C., Herweg B., Daoud E., Wissner E., Bansmann P. et al. , “ Association of atrial tissue fibrosis identified by delayed enhancement MRI and atrial fibrillation catheter ablation: The DECAAF study,” JAMA 311, 498–506 (2014). 10.1001/jama.2014.3 [DOI] [PubMed] [Google Scholar]
- 23. McDowell K. S., Zahid S., Vadakkumpadan F., Blauer J., MacLeod R. S., and Trayanova N. A., “ Virtual electrophysiological study of atrial fibrillation in fibrotic remodeling,” PLoS One 10, e0117110 (2015). 10.1371/journal.pone.0117110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. McDowell K. S., Arevalo H. J., Maleckar M. M., and Trayanova N. A., “ Susceptibility to arrhythmia in the infarcted heart depends on myofibroblast density,” Biophys. J. 101, 1307–1315 (2011). 10.1016/j.bpj.2011.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. McDowell K. S., Vadakkumpadan F., Blake R., Blauer J., Plank G., MacLeod R. S., and Trayanova N. A., “ Methodology for patient-specific modeling of atrial fibrosis as a substrate for atrial fibrillation,” J. Electrocardiol. 45, 640–645 (2012). 10.1016/j.jelectrocard.2012.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. McDowell K. S., Vadakkumpadan F., Blake R., Blauer J., Plank G., Macleod R. S., and Trayanova N. A., “ Mechanistic inquiry into the role of tissue remodeling in fibrotic lesions in human atrial fibrillation,” Biophys. J. 104, 2764–2773 (2013). 10.1016/j.bpj.2013.05.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Mistry H. B., “ To the Editor—Misuse of null hypothesis testing: Analysis of biophysical model simulations,” Hear. Rhythm 14, e50 (2017). 10.1016/j.hrthm.2016.12.012 [DOI] [PubMed] [Google Scholar]
- 28. Pormann J., A Modular Simulation System for the Bidomain Equations ( Duke University, 1999). [Google Scholar]
- 29. Qu Z., Weiss J. N., and Garfinkel A., “ Cardiac electrical restitution properties and stability of reentrant spiral waves: a simulation study,” Am. J. Physiol. 276, H269–H283 (1999). [DOI] [PubMed] [Google Scholar]
- 30. Rohr S. and Salzberg B. M., “ Characterization of impulse propagation at the microscopic level across geometrically defined expansions of excitable tissue: Multiple site optical recording of transmembrane voltage (MSORTV) in patterned growth heart cell cultures,” J. Gen. Physiol. 104, 287–309 (1994). 10.1085/jgp.104.2.287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Spach M. S., Dolber P. C., and Heidlage J. F., “ Influence of the passive anisotropic properties on directional differences in propagation following modification of the sodium conductance in human atrial muscle. A model of reentry based on anisotropic discontinuous propagation,” Circ. Res. 62, 811–832 (1988). 10.1161/01.RES.62.4.811 [DOI] [PubMed] [Google Scholar]
- 32. Spach M. S., Heidlage J. F., Dolber P. C., and Barr R. C., “ Mechanism of origin of conduction disturbances in aging human atrial bundles: Experimental and model study,” Hear. Rhythm 4, 175–185 (2007). 10.1016/j.hrthm.2006.10.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Spach M. S., Miller W. T., Geselowitz D. B., Barr R. C., Kootsey J. M., and Johnson E. A., “ The discontinuous nature of propagation in normal canine cardiac muscle. Evidence for recurrent discontinuities of intracellular resistance that affect the membrane currents,” Circ. Res. 48, 39–54 (1981). 10.1161/01.RES.48.1.39 [DOI] [PubMed] [Google Scholar]
- 34. Spiteri R. J. and Dean R. C., “ Stiffness analysis of cardiac electrophysiological models,” Ann. Biomed. Eng. 38, 3592–3604 (2010). 10.1007/s10439-010-0100-9 [DOI] [PubMed] [Google Scholar]
- 35. Stinstra J. G., Henriquez C. S., and Macleod R. S., “ Comparison of microscopic and bidomain models of anisotropic conduction,” Comput. Cardiol. 2010, 657–660 (2009). [Google Scholar]
- 36. Stinstra J., MacLeod R., and Henriquez C., “ Incorporating histology into a 3D microscopic computer model of myocardium to study propagation at a cellular level,” Ann. Biomed. Eng. 38, 1399–1414 (2010). 10.1007/s10439-009-9883-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Toure A. and Cabo C., “ Effect of heterogeneities in the cellular microstructure on propagation of the cardiac action potential,” Med. Biol. Eng. Comput. 50, 813–825 (2012). 10.1007/s11517-012-0934-4 [DOI] [PubMed] [Google Scholar]
- 38. Ten Tusscher K. H. W. J. and Panfilov A. V., “ Influence of diffuse fibrosis on wave propagation in human ventricular tissue,” Europace 9(6), vi38–vi45 (2007). 10.1093/europace/eum206 [DOI] [PubMed] [Google Scholar]
- 39. Vigmond E., Pashaei A., Amraoui S., Cochet H., and Hassaguerre M., “ Percolation as a mechanism to explain atrial fractionated electrograms and reentry in a fibrosis model based on imaging data,” Hear. Rhythm 13, 1536–1543 (2016). 10.1016/j.hrthm.2016.03.019 [DOI] [PubMed] [Google Scholar]
- 40. Wang L. J. and Sobie E. A., “ Mathematical model of the neonatal mouse ventricular action potential,” Am. J. Physiol. Heart Circ. Physiol. 294, H2565–H2575 (2008). 10.1152/ajpheart.01376.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Xie Y., Garfinkel a., Camelliti P., Kohl P., Weiss J. N., and Qu Z., “ Effects of fibroblast-myocyte coupling on cardiac conduction and vulnerability to reentry: A computational study,” Hear. Rhythm 6, 1641–1649 (2009). 10.1016/j.hrthm.2009.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Zahid S., Cochet H., Boyle P. M., Schwarz E. L., Whyte K. N., Vigmond E. J., Dubois R., Hocini M., Haïssaguerre M., Jaïs P., and Trayanova N. A., “ Patient-derived models link re-entrant driver localization in atrial fibrillation to fibrosis spatial pattern,” Cardiovasc. Res. 110, 443–454 (2016). 10.1093/cvr/cvw073 [DOI] [PMC free article] [PubMed] [Google Scholar]