Abstract
Rapid scan electron paramagnetic resonance (RS EPR) is a continuous-wave (CW) method that combines narrowband excitation and broadband detection. Sinusoidal magnetic field scans that span the entire EPR spectrum cause electron spin excitations twice during the scan period. Periodic transient RS signals are digitized and time-averaged. Deconvolution of absorption spectrum from the measured full-cycle signal is an ill-posed problem that does not have a stable solution because the magnetic field passes the same EPR line twice per sinusoidal scan during up- and down-field passages. As a result, RS signals consist of two contributions that need to be separated and postprocessed individually. Deconvolution of either of the contributions is a well-posed problem that has a stable solution. The current version of the RS EPR algorithm solves the separation problem by cutting the full-scan signal into two half-period pieces. This imposes a constraint on the experiment; the EPR signal must completely decay by the end of each half-scan in order to not be truncated. The constraint limits the maximum scan frequency and, therefore, the RS signal-to-noise gain. Faster scans permit the use of higher excitation powers without saturating the spin system, translating into a higher EPR sensitivity. A stable, full-scan algorithm is described in this paper that does not require truncation of the periodic response. This algorithm utilizes the additive property of linear systems: the response to a sum of two inputs is equal the sum of responses to each of the inputs separately. Based on this property, the mathematical model for CW RS EPR can be replaced by that of a sum of two independent full-cycle pulsed field-modulated experiments. In each of these experiments, the excitation power equals to zero during either up- or down-field scan. The full-cycle algorithm permits approaching the upper theoretical scan frequency limit; the transient spin system response must decay within the scan period. Separation of the interfering up- and down-field scan responses remains a challenge for reaching the full potential of this new method. For this reason, only a factor of two increase in the scan rate was achieved, in comparison with the standard half-scan RS EPR algorithm. It is important for practical use that faster scans not necessarily increase the signal bandwidth because acceleration of the Larmor frequency driven by the changing magnetic field changes its sign after passing the inflection points on the scan. The half-scan and full-scan algorithms are compared using a LiNC-BuO spin probe of known line-shape, demonstrating that the new method produces stable solutions when RS signals do not completely decay by the end of each half-scan.
Graphical abstract
1. Introduction
Conventional continuous-wave (CW) spectrometers, which operate on principles developed in the last century, remain major electron paramagnetic resonance (EPR) instruments used worldwide. Magnetic field modulation with an amplitude smaller than the spectral linewidth is used to measure first-derivative spectra. The standard CW experiment is not fully optimized for EPR sensitivity but rather for simplicity of data acquisition and processing, which was an important requirement in the pre-digital era. Only a small fraction of the spins contributes to EPR signal and the resonator bandwidth is often much larger compared to the signal bandwidth. Commercially available fast digitizers and computers have made it possible to reinvent the CW method. The amplitude of the sinusoidal modulation can be increased by one to two orders of magnitude to encompass the entire EPR spectrum. All paramagnetic centers in the sample would contribute to the EPR signal twice during the modulation period, resulting in a signal gain [1]. Because the spin system is not readily saturated in the rapid passage regime, a higher excitation power than in the standard experiment can be used without causing spectral distortions. Improved sensitivity comes with a data processing challenge. In comparison with the standard first-harmonic CW method, periodic response of the spin system to a full-spectrum sweep is a Fourier series of tens to hundreds high-order harmonics of the modulation frequency. Fast magnetic field scans generate transient signals, analogous to free induction decay (FID) responses to an excitation pulse [2]. The mathematical problem of signal-spectrum transformation was solved in the last century for nuclear magnetic resonance [3, 4] and recently for EPR [1] for the special case of a linear scan. The development of an algorithm that permits the use of a sinusoidal magnetic field stimulus was a turning point in the evolution of CW EPR because producing a single harmonic current is much less of an engineering challenge compared to generation of a saw-tooth waveform in a coil [5–7]. The coil inductance can be compensated with a capacitor to make a resonance circuit for a specific frequency. Fast scans that span over wide EPR spectra can be produced [8]. The rapid scan (RS) EPR method of generating and processing transient responses to the sinusoidal magnetic field stimulus was quite a success, producing a multitude of publications [9–25], a patent application [26], and commercialization by Bruker BioSpin [27]. The current version of the RS EPR algorithm solves an ill-posed problem – that the solution is unstable to small variations in the experimental parameters and noise – as two independent well-posed problems. Full-cycle RS signals are divided into two halves for up- and down-field scans [5], and each component is deconvolved separately. The half-scan RS EPR algorithm imposes a restriction on the experiment: transverse magnetization must decay completely by the end of each half-scan to avoid truncation of the signals. This limits the scan frequency and, therefore, the sensitivity. A full scan deconvolution algorithm is proposed in this paper that does not require signal truncation because it utilizes the additive property of linear time-invariant systems, as described in detail in the Theory section of this paper. The new full-cycle algorithm still requires a decoupling of up- and down-field scan contributions to the RS signal. The use of the previously developed background removal procedure [28] permits frequency domain separation of the contributions. The method does not work if up- and down-scan signals overlap. As a result, only a two-fold increase in the scan rate can be achieved, in comparison with the half-scan RS EPR deconvolution algorithm. This limitation will be resolved by the development of new signal separation methods.
2. Theory
Experimentally measured RS signal is an averaged, amplified, and down-converted response of the spin system m(t):
| (1) |
to a stimulus in the form of a sinusoidal magnetic field
| (2) |
in the presence of CW excitation. Bpp is the peak-to-peak amplitude, and fs is the frequency of the alternating field. Because the periodic stimulation B(t) produces a periodic response, then
| (3) |
and measurement of transient EPR coherences that last longer than P can be problematic.
2.1 Linear system approximation
The rapid scan data processing algorithm assumes that the spin system is well-approximated as a linear time-invariant system (LTI). Any LTI system is uniquely characterized by the impulse response function, which is an FID in the case of magnetic resonance. FID is an outcome of an excitation in the form of an infinitely narrow pulse. Within the LTI assumption, an arbitrary pulse, B1(t), produces response m(t):
| (4) |
where ⊗ is the convolution operator. If an input produces an output ma(t) and an input generates an output mb(t), then the sum of the inputs gives the sum of the outputs:
| (5) |
Dependence on time in Eq. (5) is omitted for better readability. An important point of the full scan deconvolution algorithm described below is that Eq. (5) can also be used in reverse. An actual excitation field, B1(t), can be represented as a sum of two arbitrary functions, and the observed in the experiment spin response can also be separated into two contributions corresponding to each of the inputs.
Using the well-known property of Fourier transformation (FT), convolution in Eq. (4) can be changed into multiplication in the frequency domain:
| (6) |
EPR spectrum S(ω) can be found from Eq. (6):
| (7) |
Because both B1(t) and m(t) functions are periodic, FID(t) is also periodic with the same period P. As a result, any spin response signal that lasts longer than P cannot be measured without truncation:
| (8) |
Eq. (8), in which T2* is an observed transverse relaxation time, establishes the upper theoretical limit for the scan frequency fs. The factor N in Eq. (8) can be in the range of three to five, depending on the accepted linewidth broadening. For certain types of experiments lineshape accuracy is not as important as signal intensity.
The spin system is well-approximated as LTI in the conventional CW experiment if the excitation power is below the saturation level. In the rapid scan regime, Eqs. (4–7) are valid at higher compared to the standard method powers. The faster the scan, the larger B1 values can be used without causing spectral distortions. In the extreme case of the scan frequency approaching the limit given by Eq. (8), the RS signal resembles that of an FID in the pulsed EPR experiment. The spins experience a short-duration excitation as B(t) passes through the resonance. Free evolution of the spins in the changing B(t) field is observed after the excitation. In the system of coordinates associated with B(t)-driven Larmor frequency, the spins experience a short frequency modulated pulse (chirp pulse).
2.2 Transformation into reference frame associated with the Larmor frequency
RS EPR is a CW experiment, i.e., the excitation field is time-independent in the frame associated with the excitation source frequency. Direct substitution of a constant B1 value in Eqs. (4–7) does not produce any meaningful results. In addition, there is also no explicit formulation of the scanning field B(t) within the LTI mathematical model. The solution to this problem lies in transformation of the RS signal into a reference frame associated with the Larmor frequency of the spins ωL(t):
| (9) |
To obtain a mathematical expression for the transformation, one should find the phase difference between the laboratory and accelerating frames. The phase gain starting from the beginning of the scan (t = 0) can be found by integration of Eq. (9):
| (10) |
In the frame associated with φ(t), B(t)=0. The transformation into the system of coordinates associated with ωL(t) can be achieved by multiplication:
| (11) |
For an observer in the new system of coordinates, the laboratory frame is accelerating, and the B1 field becomes time-dependent:
| (12) |
Applying Eqs. (11–12) is equivalent to a change of the experiment; field-swept CW is replaced by frequency-swept EPR at a constant external field. The transformation permits Eq. (4) to be rewritten in the form:
| (13) |
Deconvolution of EPR spectrum from RS signals can be done as follows:
| (14) |
The minus sign in front of B in Eq. (14) reflects the fact that field and frequency scans occur in opposite directions. In the up-field scan CW experiment, the spins at a higher local field are observed first. An up-frequency scan at the constant external field excites these spins last.
2.3 Half-cycle deconvolution
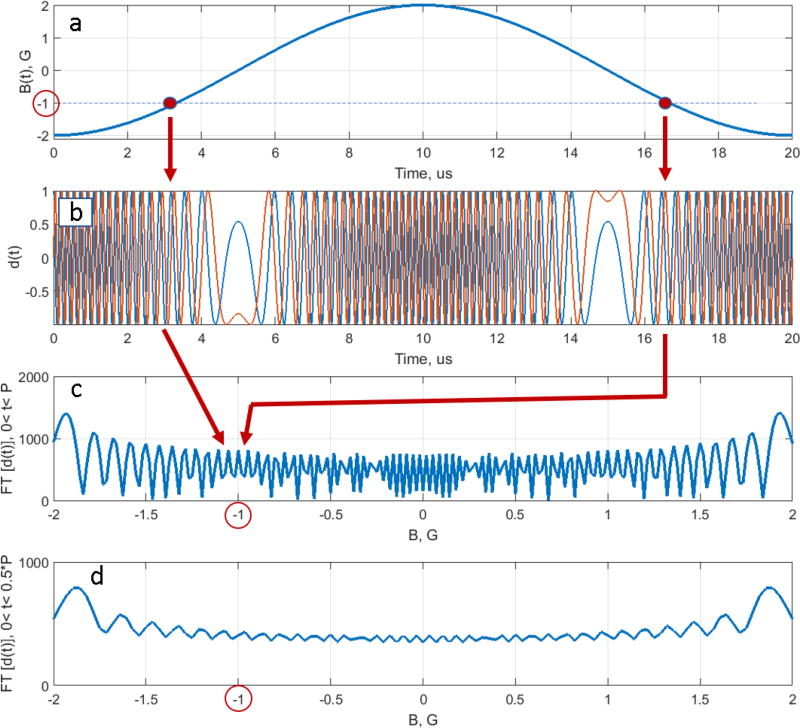
Eq. (14) is a classic example of deconvolution, which is often an ill-posed problem. A unique solution may not exist or/and be unstable, which is the case for RS EPR. The absolute value of the denominator in Eq. (14) is an oscillating function with multiple values approaching zero [5], as shown in Fig. 1c
Fig. 1.
Graphical explanation of the deconvolution problem ill-posedness. (a) Magnetic field passes through a resonance position (−1 G in the example) twice during the scan period in two separate instances of time. (b) Function d(t) oscillates with the Larmor frequency −γ (ca. −2.8 MHz) at these moments. (c) Fourier transformation of d(t) sums two complex contributions corresponding to the same frequency to produce an interference pattern. Depending on the scan frequency and amplitude, the interference can be either constructive or destructive. As a result, FT[d(t)] in the denominator of Eq. (14) causes instability of the deconvolution solution. (d) There is no interference for half-scan d(t), and the solution of Eq. (14) is well-posed.
It happens because B(t) in Fig. 1a passes through the same value of the magnetic field twice during the period (in Fig. 1 B(t)=−1 is chosen as an example). The frequency with which d(t) oscillates (see Fig. 1b) is equal to ωL(t). After FT, two contributions, corresponding to the same frequency but different time instances, are summed. If the contributions are in-phase with each other, there is a constructive interference. If they are 180° out-of-phase, they interfere destructively and FT[d(t)] approaches zero, as shown in Fig. 1c. As a result,, the deconvolution problem in Eq. (14) is ill-posed for two reasons. First, multiple near-zero values of the denominator amplify noise. More importantly, the positions of the zeros strongly depend on the parameters of the scan. Miniscule uncertainty in the estimation of either the experimental scan amplitude and/or phase results is instability of the solution. A stable solution of the deconvolution problem can be found by imposing a restriction on the experiment; transverse magnetization must completely decay by the end of the up- or down-scan, as shown in Fig. 2. In this case, the RS EPR signal can be separated into two halves (see Fig. 2b), and each half-period piece can be deconvolved independently (see Eq. [14]):
| (15.a) |
| (15.b) |
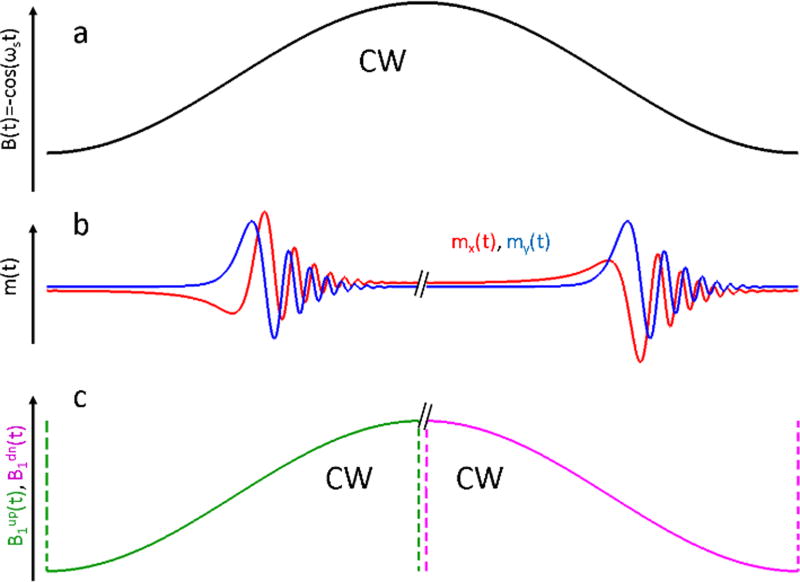
Fig. 2.
Changing the scan model from a full-cycle scan (a) to a half-scan (c) helps to find stable solutions for the deconvolution problem. If the RS signal completely decays before it reaches the inflection points of B(t), up- and down-scan contributions can be separated (b). Bup(t) and Bdown(t) scans (c) are periodic, as well as B(t). The period is equal to P/2. In both models, the excitation field B1 is CW.
Because B(t) doesn’t pass through the same field twice, the denominators do not oscillate as much (see Fig. 1d), and the deconvolution problem becomes well-posed.
It is important to note that Eq. (15a, b) describe experiments that are different from the actual one shown in Fig. 2a. These experiments correspond to a situation in which the magnetic field abruptly changes at the end of each half-scan, as shown in Fig. 2c. They are still CW experiments, but the scan periods are equal to P/2. As a result, the theoretical limit for the duration of FID is reduced by a factor of two (see Eq. [8]). As long as m(P/2)=m(P)=0, substitution of the actual full cycle experiment by a half-cycle experimental model is acceptable.
2.4 Full cycle deconvolution
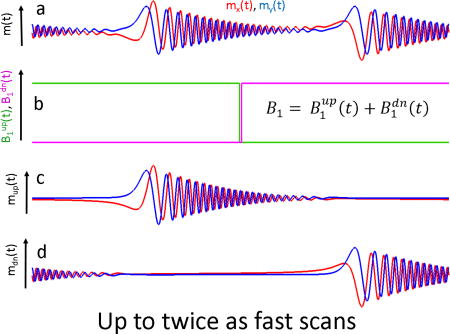
An alternative approach to the deconvolution problem that is based on the property of linear systems described in Eq. (5) is suggested in this paper. It t does not require the restrictive change of the experimental model. A constant B1 amplitude can be represented as a sum of two step functions for up- and down-scans:
| (16) |
shown as blue and red traces in Fig. 3b, respectively.
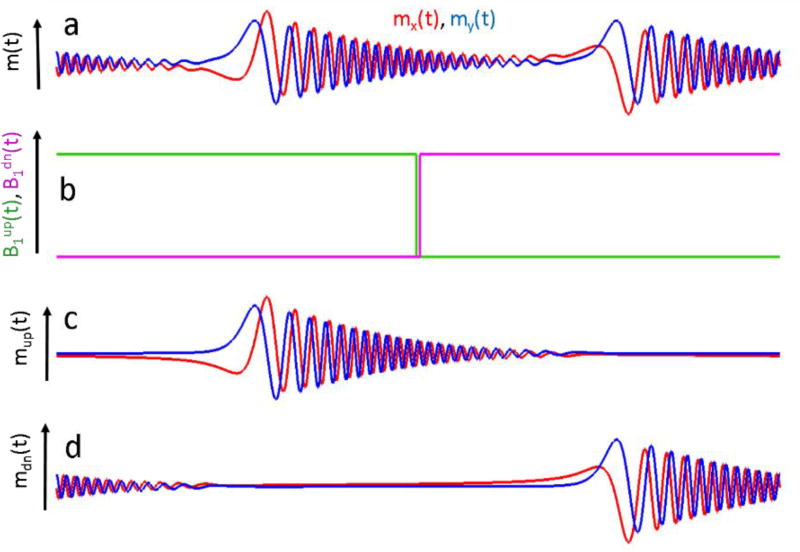
Fig. 3.
A full-scan solution of Eq. (14) that does not limit scan rates. RS signal may not decay by the end of a half-scan (a). Constant B1 can be represented as a sum of up-scan (green) and down-scan (magenta) step-functions (b). Separation of m(t) in (a) into its corresponding excitations responses (c) and (d) permits the stable deconvolution described by Eq. (17).
The exact and stable solution of the full scan deconvolution problem without any restrictions can be found by using Eqs. (5, 13, 14):
| (17.a) |
| (17.b) |
It is because the denominators are well-defined functions. The challenge for the practical use of Eq. (17) is to separate experimental signal m(t) into two components, corresponding to and . The method that was developed for background removal in the half-cycle deconvolution algorithm can be used to accomplish this goal [28]. When a magnetic field passes through the resonance in the up-direction, the precession frequency of the spins increase. Passage in the down-direction is associated with a decrease of the Larmor frequency. As a result, the up-and down-scan EPR signals can be separated in the frequency domain. However, this method has a limitation, which can be demonstrated in the example shown in Fig. 1. After passing the resonance value of B(t) =−1 (first red circle), the precession frequency will continue to increase until it reaches the value of B(t)=2 at the scan extremum. After this point, the Larmor frequency slows down but is still larger than that at the resonance position until it comes to resonance again at B(t)=−1 during the second half-scan. This position is denoted as a red circle as well. The down-scan signal is excited at this point, which can overlap with any residual of the up-scan signal both in the time and frequency domains. The FT-based separation method cannot distinguish these two overlapping signals, imposing restriction of the scan frequency. The RS signal must completely decay between the two re-excitations (between the two red cycles in Fig. 1). This constraint is not as limiting as that imposed by the half-scan algorithm; twice as fast scans can be used with the new algorithm. Further development of the algorithm will permit separation of the overlapping up- and down-field signals that can be achieved, for example, by varying the scan parameters.
Scan rate can also be limited by the bandwidth of the detection resonator, which acts as a band-pass filter for RS signals. In the example of Fig. 1, the transverse magnetization generated at the resonance position B(t)=−1 G will precess with increasing frequency until it reaches the highest point on the scan, B(t)=2 G. At this point, the Larmor frequency will be approximately 9 MHz higher than the excitation frequency. The resonator bandwidth must be large enough to permit an undistorted detection of a 9 MHz component of the signal. As explained above, after passing the maximum field point on the scan, the precession frequency decreases, and the signal bandwidth remains the same. Thus, increasing the frequency for full-cycle deconvolution would not necessarily require reduction of the resonator quality factor, which may be detrimental to EPR sensitivity.
2.5 Sampling interval in the spectral dimension
Any periodic function has a discrete spectrum defined at the integer multipliers of the fundamental frequency. For this reason, FT of m(t) and d(t) are sampled with the interval equal to dω=2πfs in the frequency domain. In the magnetic field domain, EPR spectra are discrete, with the sampling increment equal to:
| (18) |
The number of points in the deconvolved spectrum is equal to
| (19) |
Np is rounded to the closest integer number. Because m(t) and d(t) functions are truncated in the half-scan algorithm, the effecting scan frequency is twice as large so that the sampling interval is equal to 2 ΔB and the number of data points reduces to Np/2. Thus, EPR spectra become under-sampled by a factor of two. This is not a problem if fs is relatively small but may be detrimental for high frequency scans that approach the limit of Eq. (8).
Experiment
3.1 Sample
Locally synthesized Lithium octa-n-butoxy 2,3-naphthalocyanine (LiNc-BuO) microcrystals were used to compare the half-cycle and full-cycle deconvolution algorithms [29, 30]. LiNC-BuO crystals were placed into a 1 mm ID tube, degassed, and flame-sealed. The sample height was approximately 2 mm. LiNC-BuO is used in EPR oximetry, including clinical applications as an oxygen sensitive core of the OxyChip [31]. The spin probe is known to have a Lorentzian line shape, width of which is oxygen dependent.
3.2 Spectrometer
A home-built RS EPR spectrometer/imager was used for the experiments. Even though not all intended pieces of the design have been implemented, the spectrometer is fully functional. Its performance was tested using a variety of samples with the known EPR spectra. A detailed description of the final design will be published elsewhere.
A permanent magnet (Ningbo Jansen NMR Technology Co) was equipped with sweep coils to produce a magnetic field in the range 268 ± 25 G, which corresponds to a frequency span from 680 to 820 MHz. A single loop reflection resonator was manufactured using a previously described design for 300 MHz EPR imaging of rats [32]. The sample was placed into a tubed filled with salted water. The loaded quality factor, Q, was approximately 100 at a 767 MHz operating frequency. Rapid scan coils were locally built using Litz wire wound on a 3D printed plastic support structure that also accommodated a mouse bed, which was not used in the experiments described here. Sinusoidal scans were produced by a Keysight 33622A arbitrary waveform generator (AWG). The AWG output was amplified using an 1800 watt Cerwin-Vega CV-1800 audio amplifier. The RS coils that had Helmholtz configuration were resonated using a series of capacitors. The capacitors were inserted into three breadboards. Two boards were connected to each coil of the Helmholtz pair and the third board was used to insert a current probe capacitor. This design permitted selection of the desired frequencies, which were 29, 72, and 98 kHz in the experiments described below. The phase and amplitude of the current in the coils were measured using a Teledyne AP031 differential probe that was connected to the two terminals of a 100 nF probe capacitor. The waveforms were digitized using an NI PCIe 6363 DAQ card. Measured values were used for deconvolution.. The RF bridge, which was designed and built locally, output a baseband RS signal that was digitized using a Keysight U1084A high-speed digitizer. The card and external field were controlled by SpecMan4EPR software. The digitizer was triggered by the AWG RS signals were post-processed into absorption EPR spectra using locally-written Matlab programs.
3.3 Comparison of half-cycle and full-cycle deconvolution methods
RS data were collected at three scan frequencies: 29, 72, and 98 kHz. The signals were processed using the published half-cycle RS EPR algorithm and the new full-cycle deconvolution method. EPR spectra were fitted with a Lorentzian line-shape function using the Matlab Curve Fitting Tool (CFT). The CFT output the fitting results together with the confidence bounds at a level of 95% and root mean square errors (RMSE) of the fitting. The results are summarized in Table 1.
Table 1.
Comparison of EPR line fitting results for half-cycle and full-cycle RS deconvolution algorithms. EPR spectra obtained at 98 kHz were interpolated.
| Half-cycle algorithm | Full-cycle algorithm | |||
|---|---|---|---|---|
| Scan frequency | FWHM [mG] | RMSE *1e4 | FWHM [mG] | RMSE*1e4 |
| 29 kHz | 123±2 | 62 | 123±1 | 46 |
| 72 kHz | 131±5 | 133 | 127±1 | 51 |
| 98 kHz | 134±9 | 182 | 130±2 | 74 |
| 98 kHz (interpolated) | 135±4 | 160 | 129±1 | 65 |
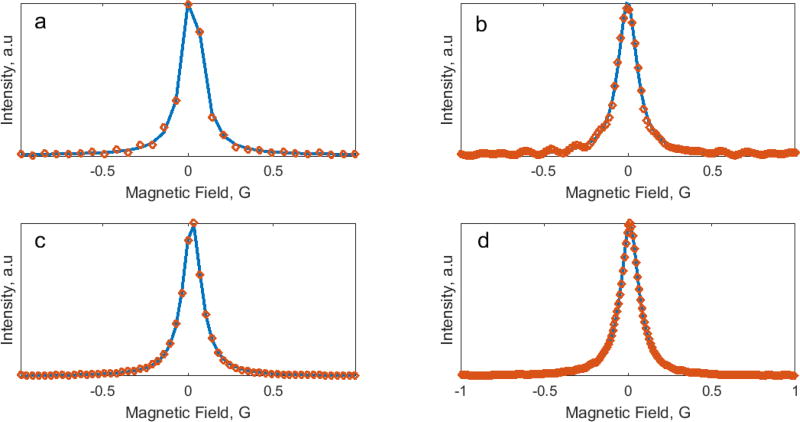
At the lowest frequency of 29 kHz, the scan rate is relatively slow, and RS signals decay completely by the end of each half-scan. Both algorithms give similar half-magnitude (FWHM) linewidth estimations of 123 mG within narrow confidence intervals and low root mean square error (RMSE). The measured linewidth of the deoxygenated sample was confirmed by an independent measurement using a Bruker X-band EPR spectrometer. At higher scan frequencies, both algorithms show increases in FWHM. The fitting results of the spectra deconvolved using the half-cycle method demonstrate larger linewidth broadening, increased confidence intervals, and RSME. The uncertainty caused by under-sampling (see Eqs. 18, 19) can be partially reduced by interpolation using the Matlab routine interpft. Fig. 4 demonstrates EPR spectra obtained using the two algorithms before (Fig. 4a, c) and after (Fig. 4b, d) interpolation. EPR spectra in Fig. 4a, b demonstrate oscillations that is the result of RS signal truncation.
Fig. 4.
EPR spectra (discrete points) obtained using half-cycle (a) and full-cycle (c) RS deconvolution methods. The sampling rate for (c) is twice as large. Fourier interpolation increases the sampling rate for (a) and (c) to give (b) and (d), respectively. Solid blue lines are the fitting functions of Lorentzian shape. Scan frequency and scan rate were 98 kHz and 920 kG/s, respectively.
4. Results and Discussion
A sinusoidal magnetic field scan, B(t), passes through the same EPR line twice during the scan period. Periodic RS signal is a response to two consequent spin system excitations. Recovery of the EPR spectrum from a transient signal is an ill-posed problem. However, in linear system approximations, periodic m(t) can be represented as a sum of the responses to two excitations that occur during up- and down-field scans. Based on this assumption, a half-scan deconvolution algorithm was developed that requires complete decay of the transverse magnetization by the end of each half-scan (see Fig. 2). The RS signal m(t) is split into two equal pieces for 0<t<P/2 and P/2<t<P that are post-processed individually. The algorithm imposes an upper limit of the scan frequency and may generate under-sampled EPR spectra, as shown in Fig. 4 a. The full-scan deconvolution algorithm described in this paper does not require truncation of the signal. Provided that the responses for up-field and down-field scans can be separated from m(t), the algorithm outputs stable solutions with no restrictions beyond those imposed by the spin system itself. The restrictions include a requirement for linearity (see Eq. 5) and the relaxation time limit expressed in Eq. (8). Previously developed background removal was used for the separation of the up- and down-scan contributions. This method can be used if there is no overlap between mup(t) and mdn(t) contributions, as shown in Fig. (3). As a result, the current version of the full-scan algorithm permits only a two-fold increase of the scan frequency, compared to the half-scan method. Further developments will make it possible to reach the theoretical limit given by Eq. (8). It is important to note that a scan rate increase does not necessarily affect the signal bandwidth. RS EPR is a narrowband excitation and broadband detection method that is in comparison with the standard CW (pure narrowbanded) and pulsed (pure broadbanded) methods. The highest signal-to-noise ratio can be achieved when the signal bandwidth matches that of the detection resonator. Very small spectral broadening in the data presented in Table 1 is the result of the resonator bandwidth being slightly smaller than the signal bandwidth. No statistically significant line broadening was observed between the results obtained at 72 and 98 kHz. This is because the Larmor frequency reaches its maximum (or minimum) at the inflection points of the scan. The new full-cycle deconvolution algorithm permits a two-fold increase in the scan frequency without increasing the signal bandwidth. As a result, twice as many signal averages per unit time can be performed to additionally improve signal-to-noise. The goal of this paper is to introduce a second-generation RS EPR algorithm and demonstrate its implementation. The use of this algorithm for EPR spectroscopy and imaging using various samples will provide more insight into the advantages of this new deconvolution method and ways to improve its performance.
Highlights.
Deconvolution of full cycle RS signal is an ill-posed problem
Separation of up- and down-field scan signals makes it well-posed
Currently used algorithm divides RS signal to two halves
Half-cycle deconvolution imposes restrictions on the scan rate
New RS EPR algorithm deconvolves two full-cycle signal components
Acknowledgments
The support of this work by NIH/NIBIB R21 EB022775 and NIH/NIGMS U54GM104942 are gratefully acknowledged. The help of Dr. Andrey Bobko and Oxana Tseytlin in preparation of the sample and manuscript editing by Dr. Brandi Talkington is greatly appreciated. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Joshi JP, Ballard JR, Rinard GA, Quine RW, Eaton SS, Eaton GR. Rapid-scan EPR with triangular scans and fourier deconvolution to recover the slow-scan spectrum. Journal of Magnetic Resonance. 2005;175:44–51. doi: 10.1016/j.jmr.2005.03.013. [DOI] [PubMed] [Google Scholar]
- 2.Schweiger A, Jeschke G. Principles of pulse electron paramagnetic resonance. Oxford University Press; Oxford: 2001. [Google Scholar]
- 3.Dadok J, Sprecher RF. Correlation NMR Spectroscopy. J Magn Reson. 1974;13:243–248. [Google Scholar]
- 4.Gupta RK, Ferretti JA, Becker ED. Rapid Scan Fourier Transform NMR Spectroscopy. J Magn Reson. 1974;13:275–290. [Google Scholar]
- 5.Tseitlin M, Rinard GA, Quine RW, Eaton SS, Eaton GR. Deconvolution of sinusoidal rapid EPR scans. J Magn Reson. 2011;208:279–283. doi: 10.1016/j.jmr.2010.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tseitlin M, Mitchell DG, Eaton SS, Eaton GR. Corrections for sinusoidal background and non-orthogonality of signal channels in sinusoidal rapid magnetic field scans. J Magn Reson. 2012;223:80–84. doi: 10.1016/j.jmr.2012.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tseitlin M, Eaton GR, Eaton SS. Computationally Efficient Steady-State Solution of the Bloch Equations for Rapid Sinusoidal Scans Based on Fourier Expansion in Harmonics of the Scan Frequency. Appl Magn Reson. 2013;44:1373–1379. doi: 10.1007/s00723-013-0494-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Quine RW, Mitchell DG, Tseitlin M, Eaton SS, Eaton GR. A resonated coil driver for rapid scan EPR. Concept Magn Reson B. 2012;41B:95–110. [Google Scholar]
- 9.Quine RW, Rinard GA, Eaton SS, Eaton GR. Quantitative Rapid Scan EPR Spectroscopy at 258 MHz. J. Magn. Reson. 2010;205:23–27. doi: 10.1016/j.jmr.2010.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tseitlin M, Quine RW, Rinard GA, Eaton SS, Eaton GR. Combining absorption and dispersion signals to improve signal-to-noise for rapid-scan EPR imaging. J Magn Reson. 2010;203:305–310. doi: 10.1016/j.jmr.2010.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mitchell DG, Quine RW, Tseitlin M, Weber RT, Meyer V, Avery A, Eaton SS, Eaton GR. Electron spin relaxation and heterogeneity of the 1:1 alpha, gamma-bisdiphenylene-beta-phenylallyl (BDPA)/benzene complex. The journal of physical chemistry. B. 2011;115:7986–7990. doi: 10.1021/jp201978w. [DOI] [PubMed] [Google Scholar]
- 12.Mitchell DG, Quine RW, Tseitlin M, Meyer V, Eaton SS, Eaton GR. Comparison of Continuous Wave, Spin Echo, and Rapid Scan EPR of Irradiated Fused Quartz. Radiation measurements. 2011;46:993–996. doi: 10.1016/j.radmeas.2011.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mitchell DG, Quine RW, Tseitlin M, Eaton SS, Eaton GR. X-band rapid-scan EPR of nitroxyl radicals. J Magn Reson. 2012;214:221–226. doi: 10.1016/j.jmr.2011.11.007. [DOI] [PubMed] [Google Scholar]
- 14.Mitchell DG, Rosen GM, Tseitlin M, Symmes B, Eaton SS, Eaton GR. Use of rapid-scan EPR to improve detection sensitivity for spin-trapped radicals. Biophys J. 2013;105:338–342. doi: 10.1016/j.bpj.2013.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mitchell DG, Tseitlin M, Quine RW, Meyer V, Newton ME, Schnegg A, George B, Eaton SS, Eaton GR. X-Band Rapid-scan EPR of Samples with Long Electron Relaxation Times: A Comparison of Continuous Wave, Pulse, and Rapid-scan EPR. Mol. Phys. 2013;111:2664–2673. [Google Scholar]
- 16.Eaton SS, Quine RW, Tseitlin M, Mitchell DG, Rinard GA, Eaton GR. Handbook of Multifrequency Electron Paramagnetic Resonance: Data and Techniques. Wiley-VCH Verlag; 2014. Rapid-Scan Electron Paramagnetic Resonance; pp. 3–67. [Google Scholar]
- 17.Biller JR, Tseitlin M, Quine RQ, Rinard GA, Weismiller HA, Elajaili H, Rosen GM, Kao JPY, Eaton SS, Eaton GR. Imaging of Nitroxides at 250 MHz using Rapid-Scan Electron Paramagnetic Resonance. J. Magn. Reson. 2014;242:162–168. doi: 10.1016/j.jmr.2014.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tseitlin M, Yu Z, Quine RW, Rinard GA, Eaton SS, Eaton GR. Digitally generated excitation and near-baseband quadrature detection of rapid scan EPR signals. J Magn Reson. 2014;249C:126–134. doi: 10.1016/j.jmr.2014.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tseitlin M, Biller JR, Elajaili H, Khramtsov VV, Dhimitruka I, Eaton GR, Eaton SS. New spectral-spatial imaging algorithm for full EPR spectra of multiline nitroxides and pH sensitive trityl radicals. J Magn Reson. 2014;245:150–155. doi: 10.1016/j.jmr.2014.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Biller JR, Tseitlin M, Quine RW, Rinard GA, Weismiller HA, Elajaili H, Rosen GM, Kao JP, Eaton SS, Eaton GR. Imaging of nitroxides at 250MHz using rapid-scan electron paramagnetic resonance. J Magn Reson. 2014;242:162–168. doi: 10.1016/j.jmr.2014.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yu Z, Quine RW, Rinard GA, Tseitlin M, Elajaili H, Kathirvelu V, Clouston LJ, Boratynski PJ, Rajca A, Stein R, McHaourab H, Eaton SS, Eaton GR. Rapid-scan EPR of immobilized nitroxides. J Magn Reson. 2014;247:67–71. doi: 10.1016/j.jmr.2014.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Czechowski T, Chlewicki W, Baranowski M, Jurga K, Szczepanik P, Szulc P, Kedzia P, Szostak M, Malinowski P, Wosinski S, Prukala W, Jurga J. Two-dimensional spectral-spatial EPR imaging with the rapid scan and modulated magnetic field gradient. J Magn Reson. 2014;243:1–7. doi: 10.1016/j.jmr.2014.03.001. [DOI] [PubMed] [Google Scholar]
- 23.Biller JR, Tseitlin M, Mitchell DG, Yu Z, Buchanan LA, Elajaili H, Rosen GM, Kao JP, Eaton SS, Eaton GR. Improved sensitivity for imaging spin trapped hydroxyl radical at 250 MHz. Chemphyschem : a European journal of chemical physics and physical chemistry. 2015;16:528–531. doi: 10.1002/cphc.201402835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Elajaili HB, Biller JR, Tseitlin M, Dhimitruka I, Khramtsov VV, Eaton SS, Eaton GR. Electron spin relaxation times and rapid scan EPR imaging of pH-sensitive amino-substituted trityl radicals. Magnetic resonance in chemistry : MRC. 2015;53:280–284. doi: 10.1002/mrc.4193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Biller JR, Mitchell DG, Tseytlin M, Elajaili H, Rinard GA, Quine RW, Eaton SS, Eaton GR. Rapid Scan Electron Paramagnetic Resonance Opens New Avenues for Imaging Physiologically Important Parameters In Vivo. J Vis Exp. 2016 doi: 10.3791/54068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Eaton GR, Tseitlin M, Quine RQ. Hall probe, epr coil driver and epr rapid scan deconvolution. 2014 Publication # WO 2014043513 A2 ; Application # PCT/US2013/059726, in, USA. [Google Scholar]
- 27.Gromov I. Improving Signal-to-Noise in EPR. Asia-Pacific EPR/ESR Symposium; Lake Baikal, Irkutsk; Russia. 2016. [Google Scholar]
- 28.Tseitlin M, Czechowski T, Quine RW, Eaton SS, Eaton GR. Background removal procedure for rapid scan EPR. J Magn Reson. 2009;196:48–53. doi: 10.1016/j.jmr.2008.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frank J, Gundel D, Drescher S, Thews O, Mader K. Injectable LiNc-BuO loaded microspheres as in vivo EPR oxygen sensors after co-implantation with tumor cells. Free Radic Biol Med. 2015;89:741–749. doi: 10.1016/j.freeradbiomed.2015.10.401. [DOI] [PubMed] [Google Scholar]
- 30.Pandian RP, Parinandi NL, Ilangovan G, Zweier JL, Kuppusamy P. Novel particulate spin probe for targeted determination of oxygen in cells and tissues. Free Radic Biol Med. 2003;35:1138–1148. doi: 10.1016/s0891-5849(03)00496-9. [DOI] [PubMed] [Google Scholar]
- 31.Jarvis LA, Williams BB, Schaner PE, Chen EY, Angeles CV, Hou H, Schreiber W, Wood VA, Flood AB, Swartz HM, Kuppusamy P. Phase 1 Clinical Trial of OxyChip, an Implantable Absolute pO(2) Sensor for Tumor Oximetry. Int J Radiat Oncol. 2016;96:S109–S110. [Google Scholar]
- 32.Hirata H, He G, Deng Y, Salikhov I, Petryakov S, Zweier JL. A loop resonator for slice-selective in vivo EPR imaging in rats. J Magn Reson. 2008;190:124–134. doi: 10.1016/j.jmr.2007.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]