Abstract
Background
Defining mean and reference intervals for glomerular filtration rate (GFR) has been the subject of only a limited number of studies and review articles, with contradicting statements about the mean. Normal measured GFR (mGFR) values of ∼120–130 mL/min/1.73 m2 have long been the referenced values for young adults but seem to be too high according to recent studies. Reference intervals are difficult to define because of the age decline of GFR, which is also observed in healthy subjects. Little data are available for subjects >70 years of age.
Methods
Based on the reference intervals for serum creatinine (SCr) and the recently published full-age spectrum (FAS) equation, we define simple age-dependent equations for the reference limits of GFR. The mGFR of 633 living potential kidney donors was used to validate the new formulae that define the reference interval.
Results
The reference limits for estimated GFR (eGFR), calculated by entering the reference limits for SCr into the FAS equation closely correspond with published reference limits for mGFR. Of the mGFRs of potential living kidney donors, 97.2% lie between the newly defined reference limits for GFR.
Conclusion
SCr reference limits may serve to define age-dependent reference limits for eGFR and mGFR.
Keywords: age-dependent reference intervals, estimated and measured glomerular filtration rate
Introduction
We recently proposed a new full-age spectrum (FAS) estimating glomerular filtration rate (eGFR) equation [1, 2] for which the serum creatinine (SCr)–based version is presented as:
where Q is the mean or median SCr concentration of an age-/sex-specific healthy population. For children, the value of Q linearly increases with age for both males and females. For adolescents, the Q-value increases with age at the same rate as for children in the case of females, but with a greater slope for males. For adult Caucasians, the value of Q is constant and equals 62 µmol/L (0.70 mg/dL) for females and 80 µmol/L (0.90 mg/dL) for males. We have also shown that the same form of the FAS equation can be applied for serum cystatin C (ScysC). The rescaling factor in ScysC/Q′ has been determined as Q′ = 0.82 mg/L for ages up to 70 years and Q′ = 0.95 mg/L beyond that age. The distributions of both rescaled biomarkers have specific properties that hold for all ages and sexes:
The distribution is normal or Gaussian, that is, it has a symmetrical bell-shaped form with a mean of 1 and a standard deviation (SD) of ∼0.1686.
The 2.5th percentile equals 0.67 and the 97.5th percentile equals 1.33, and consequently the reference interval for the rescaled biomarkers is [0.67 − 1.33], independent of age and sex.
Since the mean value of the rescaled biomarkers for the healthy population equals 1, then, from the FAS equation, it is obvious that the corresponding mean eGFR equals 107.3 mL/min/1.73 m2 for children, adolescents and young adults between 2 and 40 years of age. The referenced measured GFR (mGFR) values in white healthy young adults are ∼120–130 mL/min/1.73 m2, but these reference values date back to the 1950–70s [3, 4]. Also, the currently recommended Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) eGFR equation [5] predicts a value of 124 mL/min/1.73 m2 for an 18-year-old male with SCr = 0.90 mg/dL. However, a recent meta-analysis analysing publications on GFR measurements in healthy living potential kidney donors challenged these prior thresholds and confirmed 107 mL/min/1.73 m2 as an acceptable normal reference value [6]. For the older average healthy adult (with SCr/Q = 1), a simple age-dependent decline of eGFR = 107.3 × 0.988(Age−40) is obtained from the FAS equation. Analogously, the lower and upper limit for SCr/Q of 0.67 and 1.33, respectively, can be entered in the above equation and yields age-dependent equations for FAS-eGFR that correspond to the lower and upper limit for SCr/Q.
In this article we present original un published data from Lyon (France), Liège (Belgium) and Leuven (Belgium) for mGFR in healthy potential living kidney donors to confirm our results from the meta-analysis [6]. The goal of this work is to validate the correspondence between the FAS-eGFR reference limits derived from the upper and lower SCr reference limits, with reference limits for mGFR as obtained from the literature. We also want to verify if the mean GFR for healthy young adults is close to 107.3 mL/min/1.73 m2 and not 120–130 mL/min/1.73 m2 as is mostly reported.
Materials and methods
We collected mGFRs of 633 potential living kidney donors from Lyon, France (inulin, n = 514; iohexol, n = 36), Liège, Belgium Iohexol, n = 41) and Leuven, Belgium (51Cr-EDTA, n = 42). All subjects have been consecutively included in this study, although the entry periods in Leuven, Lyon and Liège were not the same. Any disproportion in gender or age is therefore a consequence of pure chance. The inulin measurement in Lyon was based on the continuous infusion method and the collection of timed urine (U) and plasma (P) samples, from which the mGFR is calculated as GFR = [U]×/[P], with [U] and [P] the concentration of inulin (in mg/mL) and the urine production per time interval (in mL/min) [7, 8]. Iohexol measurements in Lyon and Liège were based on the plasma clearance protocol using three and four time points, respectively, to obtain the area under the concentration–time curve (AUC) from the mono-exponential slow compartment decay. The GFR calculated from this AUC was then corrected with the Bröchner–Mortensen formula [9]. 51Cr-EDTA measurements in Leuven were also based on the plasma clearance protocol, but using eight time points to obtain the concentration–time curve and the AUC was obtained from bi-exponential decay (fast and slow compartment). All presented GFR methods have sufficient accuracy compared with the inulin gold standard reference method [10, 11]. Estimating GFR with the FAS equation is based on standardized assays for SCr and ScysC [1, 2]. A general informed consent was obtained from all patients, including the information that their data could be used anonymously in retrospective data analyses.
We also performed an extensive literature study to obtain reference data for mGFR to support our findings. This literature search resulted in 12 publications that have previously been presented in a meta-analysis study [6]. Mean mGFR and standard deviations (SDs) from this meta-analysis study were used to calculate lower (LRL) and upper (URL) reference limits as mean mGFR ± 2×SD. Statistical analysis [descriptive statistics, t-tests, analysis of variance (ANOVA)] was performed with SAS 9.4 (SAS Institute, Cary, NC, USA).
Results
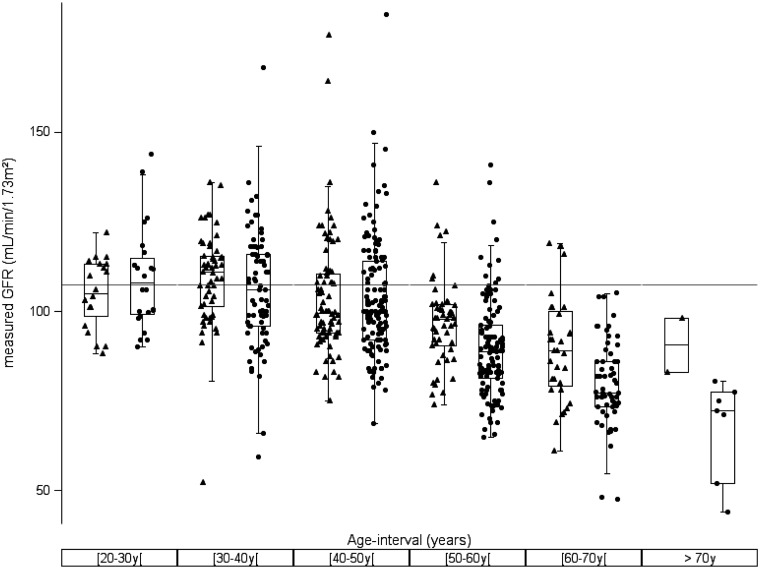
Table 1 and Figure 1 demonstrate the age decline for both male and female potential kidney donors in our dataset (n = 633). No difference was observed between males and females in the defined age groups younger than 50 years of age. However, we noticed a difference between males and females older than 50 years, with a faster decline in females than in males, an observation that we also found in our meta-analysis study [6].
Table 1.
mGFR (mL/min/1.73 m2) in age decades for 633 potential kidney donors
| Males |
Females |
||||||
|---|---|---|---|---|---|---|---|
| Age decade (years) | n | Mean (SD) | 95% CI | n | Mean (SD) | 95% CI | P-value |
| 20–30 | 20 | 105.1 (9.7) | 100.5−109.6 | 24 | 109.1 (14.1) | 103.1−115.1 | 0.2896 |
| 30–40 | 53 | 109.2 (13.3) | 105.6−112.9 | 74 | 106.0 (16.5) | 102.2−109.9 | 0.2297 |
| 40–50 | 76 | 103.7 (16.7) | 99.9−107.5 | 126 | 103.7 (16.5) | 100.7−106.6 | 0.9773 |
| 50–60 | 50 | 96.9 (12.2) | 93.5−100.4 | 111 | 89.5 (13.9) | 86.9−92.2 | 0.0014 |
| 60–70 | 32 | 89.8 (15.0) | 84.4−95.2 | 58 | 79.8 (12.0) | 76.7−83.0 | 0.0008 |
| >70 | 2 | 90.6 (–) | − | 7 | 67.5 (13.9) | 54.7−80.4 | – |
The mean is significantly different from 107.3 mL/min/1.73 m2 when the 95% CI does not contain this value. The P-value (last column) is obtained for testing equality between males and females within each age group.
Fig. 1.
Box plot for mGFR versus age decades for female (filled circles) and male (filled triangles) potential kidney donors (n = 633). A horizontal reference line is drawn at GFR = 107.3 mL/min/1.73 m2.
When combining the mGFR data of males and females in age decades, then, for the decades 20–30 years {mean mGFR = 107.3, [95% confidence interval (CI) 103.5–111.0] (n = 44)}, 30–40 years [mean mGFR = 107.4, (95% CI 104.7–110.1) (n = 127)] and 40–50 years [mean mGFR = 103.7 (95% CI 101.4–106.0) (n = 202)], no difference between the mean mGFRs of these age groups was observed (ANOVA, P = 0.0814) and no difference in the age decades 20–30 years and 30–40 years was observed with a mean value of 107.3 mL/min/1.73 m2, as predicted from the FAS equation. On the other hand, all age groups showed a significant difference from 120 to 130 mL/min/1.73 m2 (P < 0.0001).
Using the LRL (0.67) and URL (1.33) for SCr/Q, we can calculate corresponding eGFR limits as:
URL:
LRL:
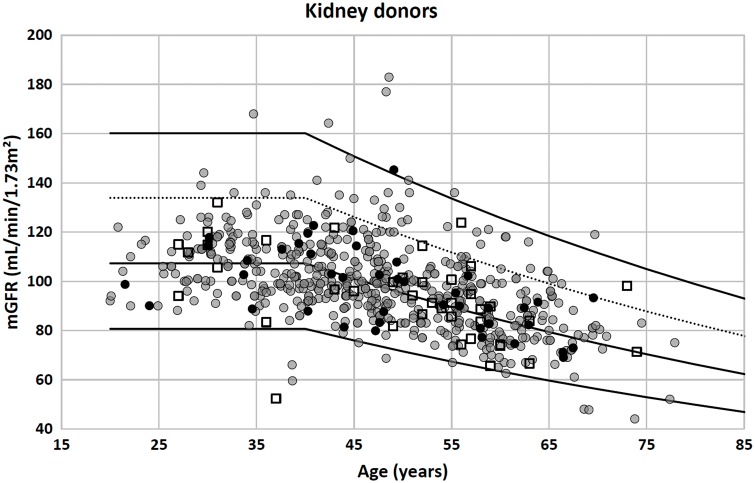
If the correspondence between reference intervals for SCr/Q and GFR is indeed true, then we would expect ∼95% of healthy subjects to have an mGFR between these limits. We therefore plotted the FAS-eGFR reference limits together with the mGFRs of the 633 potential kidney donors in Figure 2, resulting in 97.2% of mGFRs of the kidney donors lying between the limits defined above.
Fig. 2.
Potential (healthy) kideny donors: n = 633 [550, Lyon, France (solid gray circles); 41, Liège, Belgium (open squares); 42, Leuven, Belgium (solid black circles)]. Of mGFR values, 97.2% lie between the upper and lower limit defined by the FAS equation with SCr/Q = 1.33 and SCr/Q = 0.67, respectively (upper and lower solid lines). Of mGFR values, 91.8% lie between the symmetrical upper and lower eGFR limit (lower solid line and dashed line). The middle solid line corresponds with SCr/Q = 1, the average FAS prediction for GFR.
From the meta-analysis table, published previously [6], we calculated 2.5th and 97.5th percentiles for mGFR as mean ± 2× SD for 12 studies (males and females separately) and 6 different age groups. The means of the LRLs and URLs with their SDs obtained from these 12 studies are presented in Table 2.
Table 2.
LRLs and URLs with SDs, obtained from the meta-analysis study for mGFR (in mL/min/1.73 m2)
| Age at mid-point | LRL | SD | FAS-LRL | URL | SD | FAS-URL | FASalt-URL |
|---|---|---|---|---|---|---|---|
| (years) | |||||||
| 25 | 78.1 | 5.5 | 80.7 | 136.0 | 7.6 | 160.1 | 133.9 |
| 35 | 76.8 | 4.6 | 80.7 | 133.8 | 7.1 | 160.1 | 133.9 |
| 45 | 70.1 | 6.0 | 76.0 | 128.5 | 7.0 | 150.8 | 126.1 |
| 55 | 62.1 | 10.5 | 67.3 | 118.6 | 9.7 | 133.6 | 111.7 |
| 65 | 55.3 | 7.4 | 59.7 | 114.0 | 10.0 | 118.4 | 99.0 |
| 75 | 48.6 | 5.3 | 52.9 | 102.8 | 11.3 | 105.0 | 87.8 |
‘Age’ is defined as the mid-point of the age interval. LRL and URL are the means of the lower and upper limits calculated from the meta-analysis data [6]. FAS is the prediction for SCr/Q = 1.33 (LRL) and SCr/Q = 0.67 (URL) at the corresponding age. FASalt-URL is defined as the upper limit symmetrical with the lower limit.
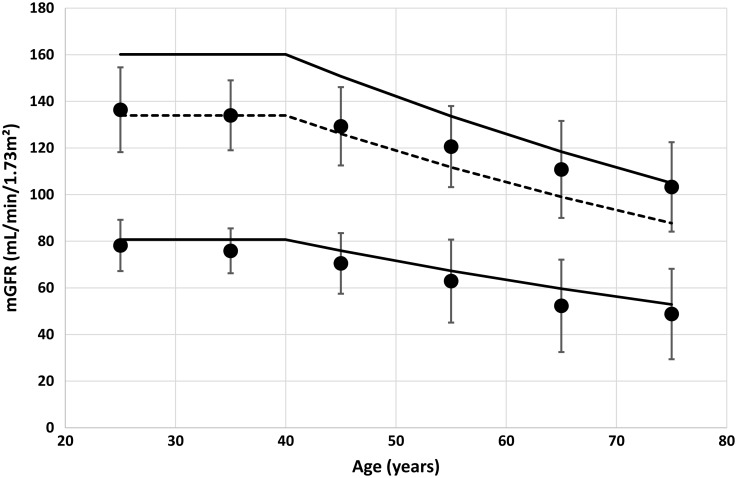
We plotted the results of Table 2 in Figure 3. The lower solid line is the FAS prediction corresponding to SCr/Q = 1.33; the upper solid line is the FAS prediction corresponding to SCr/Q = 0.67. An alternative upper limit for FAS is shown as the dashed line. This alternative upper limit is based on symmetrical properties (normality for mGFR) and defined by using the ΔFAS (i.e. mean FAS prediction – LRL) to define the URL as mean FAS + ΔFAS.
Fig. 3.
Upper and lower limits (solid circles) calculated from the meta-analysis data [6] with error bars (= 2 SD) (Table 2). The solid lines are calculated from the FAS equation with SCr/Q = 1.33 (lower limit) and SCr/Q = 0.67 (upper limit). The dashed line is calculated as mean FAS + ΔFAS.
Discussion
In this study we challenged the mean GFR of 107.3 mL/min/1.73 m2 defined by the new FAS equation for healthy young people, corresponding to a mean SCr/Q of 1. The age/gender subgroup analysis of the mGFRs of a group of 633 potential live kidney donors did not provide evidence to reject the hypothesis that the mean GFR equals 107.3 mL/min/1.73 m2 for individuals up to 50 years of age, but there was statistical evidence to reject the hypothesis that the mean GFR equals 120 mL/min/1.73 m2 in all age groups. This finding is also supported by our recent meta-analysis [6].
The mean value of 107.3 mL/min/1.73 m2 was first introduced by Pottel et al. [12, 13] and was based on non-indexed mean mGFR values in children published by Piepsz et al. [14]. Using Belgian national growth curves for children [15], Pottel et al. indexed these mGFR values for body surface area (BSA) and fitted the obtained results against age, which resulted in the constant mean value for children 2–14 years of age of 107.3 mL/min/1.73 m2. This finding resulted in a very simple height-independent eGFR formula for children [13], which has been extended by Hoste et al. [16] to adolescents and young adults. In two recent publications [1, 2], this simple equation was further extended to adults and older adults and to other biomarkers (cystatin C). The coefficient of 107.3 mL/min/1.73 m2 is obviously the most important value in the equation and it was assigned the interesting property of being the average GFR value for healthy children, adolescents and young adults. The new FAS equation claimed that this value could be maintained up to the age of 40 years, which was defined as age threshold where age-dependent renal decline begins. The findings we have observed here correspond very well with the findings in our recent meta-analysis study [6]: the mean mGFR is ∼107.3 mL/min/1.73 m2 for young adults (up to 40 years of age) and then declines, with an average decline rate of ∼0.92 mL/min/1.73 m2/year between 40 and 100 years of age.
In this study on healthy kidney donors, we did not find a difference between males and females <50 years of age, but beyond 50 years there is a faster renal decline in females compared with males, a finding that we also observed in the meta-analysis study [6].
Poggio et al. [17] found a statistically significant difference between men and women <50 years of age, but the authors underlined that this difference of 3% was not clinically relevant. Rule et al. [18] also presented mean values (2.5th–97.5th percentiles) of mGFR (iothalamate) for 365 healthy potential living kidney donors. In his analysis, Rule et al. did not observe differences between men and women. They implicitly assumed a linear renal decline starting at 18 years of age and regressed the mGFR data over the full age range of 18–71 years, observing a slope or decline of 4.9 mL/min/1.73 m2/decade. The FAS equation would predict a renal decline of 6.3 mL/min/1.73 m2 over the same age range.
Grewal and Blake [19] performed a study on 428 subjects (218 females, 210 males; age range 19–72 years) undergoing assessment as live kidney donors. GFR was evaluated from 51Cr-EDTA plasma clearance and they presented a mean GFR of 103.4 mL/min/1.73 m2 for 187 subjects 19–40 years of age, for whom they also found that the dependence of GFR on age was not statistically significant, a finding that confirms our results. They also found a difference between men and women of 1.3 mL/min/1.73 m2, which was not statistically significant, another finding that was confirmed here. In 241 subjects, 40–72 years of age, they found that GFR decreased by 0.91 mL/min/1.73 m2/year. They presented a model for the decline of GFR with age in which GFR remains constant at 103.4 mL/min/1.73 m2 until the age of 40 years and then declines at a rate of 0.91 mL/min/1.73 m2/year. These reference data have been used as the basis for defining minimal age-dependent GFRs in living donors by the British Transplantation Society [20]. These results are very similar to our findings. Our mean value of 107.3 mL/min/1.73 m2 is 4% higher than the mean value of 103.4 mL/min/1.73 m2 reported by Grewal and Blake, a difference that can be attributed to the difference in measurement method [6]. At the age of 40 years, the FAS equation predicts a mean value of 107.3 mL/min/1.73 m2, and at the age of 100 years the mean value is predicted to be 107.3 × 0.988(100−40) = 52.0 mL/min/1.73 m2, resulting in an average decline rate calculated over 60 years of (107.3–52.0)/60 = 0.92 mL/min/1.73 m2/year, nearly exactly the value reported by Grewal and Blake. The British Transplantation Society also proposes a safety limit of 80 mL/min/1.73 m2 for adults up to the age of 46 years (corresponding with FAS-eGFR = 107.3/1.33 = 81 mL/min/1.73 m2) and declining to 50 mL/min/1.73 m2 at the age of 80 years, which is exactly the value predicted by the FAS equation, corresponding to SCr/Q = 1.33, eGFR = 107.3/1.33×0.988(80−40) = 50 mL/min/1.73 m2. Grewal and Blake presented mean GFR and the upper and lower boundaries were defined as a mean ± 2SD of 103.4 ± 28.9 for individuals <40 years of age (thus ranging from 75 to 132.3 mL/min/1.73 m2) and for those ≥40 years of age, there is an additional decline of 0.91 mL/min/1.73 m2/year.
Hamilton et al. [21] presented mean total plasma clearance values of 51Cr-EDTA in 201 potential kidney donors 16–60 years of age of Saudi Arabian origin, categorized in 10-year groups, showing no decline with age in the 20–50 years age range. He also did not observe a difference between men and women.
Soares et al. [22] measured GFR by the 51Cr-EDTA single-injection method in 285 healthy Brazilian individuals 19–70 years of age. After stratifying data by age decades, they found that GFR starts to decline significantly after 45 years of age. Regression analysis of GFR versus age for subjects <45 years of age did not give a slope significantly different from zero, whereas the slope of the older groups was consistent with a significant decrease in GFR. They defined reference GFR values (mean ± 2SD) ranging from 76 to 148 mL/min/1.73 m2 for individuals <45 years of age and 68 to 128 mL/min/1.73 m2 for subjects >45 years of age. After adjustment for BSA, they also did not find a difference in mean GFR between men and women, <45 years of age (111 ± 18 versus 113 ± 18 mL/min/1.73 m2). For subjects >45 years of age, they observed an age decline in both men and women, but with a trend towards lower GFRs in older women.
Blake et al. [23] presented a non-linear relationship between mean mGFR and age of GFR of 103.9 − 0.0061 × Age2 based on a retrospective study of 904 subjects (468 women, 436 men; age range 18–84 years) undergoing assessment as prospective living kidney donors. GFR was evaluated from 51Cr-EDTA plasma clearance using the slope-intercept method [9]. Their analysis was based on evaluating models of the form mGFR = A – B × Age2, which implicitly assumes that decline starts at the lowest age in the range under study. Blake et al. ’s model and the FAS model are clearly different from a physiological point of view, as the FAS model assumes a decline starting at the age of 40 years. Blake et al. defined the upper and lower limit as ±2SD (±25.8 mL/min/1.73 m2) from the mean (mGFR = 103.9 – 0.0061 × Age2). Although the lower limit defined by Blake et al. is only slightly lower than the lower limit defined by FAS, the upper limit is much higher for FAS than the upper limit defined by Blake et al.
Herein we also used the data from our meta-analysis study [6] to calculate LRLs and URLs and found a very good correspondence between the mGFR – 2 × SD and the FAS lower limit obtained from SCr/Q = 1.33. The upper limit for GFR (mGFR + 2 × SD) is much lower than the FAS prediction corresponding to SCr/Q = 0.67. A possible reason could be that the FAS equation overestimates GFR for low SCr/Q values due to the power coefficient of 1 in the inverse relationship of GFR with SCr/Q. Children with a muscular disorder (e.g. like Duchenne Muscular Dystrophy patients) have extremely low SCr/Q values while still maintaining normal kidney function [24]. Consequently, these subjects have normal mGFR but overestimated (too high) eGFR values (for SCr-based eGFR equations). Thus, too low SCr/Q values may produce incorrect GFR estimates, but the question remains where this threshold lies. However, this is only one possible explanation, as it should also be noted that SCr/Q has a well-established bell-shaped distribution, in other words, it has a Gaussian distribution. Because of the inverse relationship between eGFR and SCr/Q, eGFR can never be distributed in a Gaussian manner when SCr/Q is normally distributed. On the other hand, all studies on kidney donors aimed at defining reference intervals for mGFR assume that the mGFR distribution is Gaussian and thus that mGFR reference intervals can be defined as mean ± 2SD. The value of this assumption is difficult to evaluate since GFR declines with age. Clearly, there is a contradiction here; if there is an inverse relationship between GFR and SCr/Q, GFR and SCr/Q cannot be normally distributed concurrently. Using the symmetrical lower and upper limits from the normal distribution of SCr/Q, that is, SCr/Q = 0.67 and SCr/Q = 1.33, we find upper and lower limits of FAS eGFR of 160.1 and 80.7 mL/min/1.73 m2 for individuals <40 years of age, but these two values are 52.8 and 26.6 mL/min/1.73 m2 away from the mean of 107.3 mL/min/1.73 m2, respectively; nearly twice as far for the upper limit compared with the lower limit. Since the FAS mean and the FAS lower limit are a much closer match to the mean and 2.5th percentile of the literature studies (Table 2), we could propose the difference 107.3 – 80.7 = 26.6 mL/min/1.73 m2 as corresponding to 2 SD and therefore an alternative approximation for the upper GFR limit could be 107.3 + 26.6 = 133.9 mL/min/1.73 m2 for individuals <40 years of age and 133.9 × 0.988(Age−40)mL/min/1.73 m2 for those >40 years.
This upper limit is much closer to the upper limits obtained for mGFR from the meta-analysis for younger adults. When this upper limit is applied to the 633 kidney donors of our dataset, we find 91.8% lying between these reference limits, compared with 97.2% when the SCr-based reference limits are used. The fraction of 5.4% (97.2–91.8%) is completely located between the two upper limits, suggesting a skewed GFR distribution for (normal) healthy subjects.
As limitations to our study, we must emphasize that the presented reference intervals are for Caucasians between 20 and 70 years of age, although we are not aware of differences in GFR due to ethnicity [25]. Possible effects of a protein-rich diet on the mGFR are unknown, as this has not been considered as an exclusion criterion during patient recruitment. We can also not totally rule out a possible selection bias, since donors are mostly relatives of kidney recipients and may therefore have a greater prevalence of subclinical disease [26]. It might also be pointed out that donors, especially in the 30–50 years age group are often mildly obese, have components of metabolic syndrome and may have subclinical insulin resistance. All of this can lead to ‘hyperfiltration’ [27], thus skewing the normal distribution of mGFR, evident from the fraction of high mGFRs in our figures. However, the protocol for the evaluation process for living kidney donors involves obtaining a full medical history, a rigorous clinical examination and investigations (including urinalysis, blood tests, virology, infection screen, etc.). The assessment of GFR occurs subsequently, thus individuals undergoing evaluation of GFR as potential live kidney donors can be regarded as healthy individuals with reasonable certainty and representative of the normal healthy population.
Conclusion
The first coefficient in the FAS equation of 107.3 corresponds to the mean mGFR value for healthy young individuals up to 40 years of age and it is confirmed here that potential live kidney donors have mGFRs that are significantly lower than the referenced value of 120–130 mL/min/1.73 m2. Reference intervals for SCr or ScysC can be used to define eGFR limits, based on the FAS equation, that also correspond with mGFR reference intervals. Clearly, the lower limit (LL) of GFR is the most important reference limit and can be easily expressed as a simple mathematical equation:
Conflict of interest statement
None declared.
References
- 1. Pottel H, Hoste L, Dubourg L. et al. An estimating glomerular filtration rate equation for the full age spectrum. Nephrol Dial Transplant 2016; 31: 798–806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Pottel H, Delanaye P, Schaeffner E. et al. Estimating glomerular filtration rate for the full age spectrum from serum creatinine and cystatin C. Nephrol Dial Transplant 2017. doi:10.1093/ndt/gfw425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Smith H. Comparative physiology of the kidney In: H Smith. (ed). The Kidney: Structure and Function in Health and Disease. New York: Oxford University Press,1951, pp. 520–574 [Google Scholar]
- 4. Wesson L. Physiology of the Human Kidney. New York: Grune & Stratton, 1969 [Google Scholar]
- 5. Levey AS, Stevens LA, Schmid CH. et al. A new equation to estimate glomerular filtration rate. Ann Intern Med 2009; 150: 604–612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Pottel H, Hoste L, Yayo E. et al. Glomerular filtration rate in healthy living potential kidney donors: a meta-analysis supporting the construction of the full age spectrum equation. Nephron 2017; 135: 105–119 [DOI] [PubMed] [Google Scholar]
- 7. Hadj-Aïssa A, Bankir L, Fraysse M. et al. Influence of the level of hydration on the renal response to a protein meal. Kidney Int 1992; 42: 1207–1216 [DOI] [PubMed] [Google Scholar]
- 8. Dubourg L, Hadj-Aïssa A, Ferrier B.. Adaptation of an enzymatic polyfructosan assay to clinical practice. Anal Biochem 2010; 405: 266–268 [DOI] [PubMed] [Google Scholar]
- 9. Bröchner-Mortensen J, Haahr J, Christoffersen J.. A simple method for accurate assessment of the glomerular filtration rate in children. Scand J Clin Lab Invest 1974; 33: 139–143 [PubMed] [Google Scholar]
- 10. Soveri I, Berg UB, Björk J. et al. Measuring GFR: a systematic review. Am J Kidney Dis 2014; 64: 411–424 [DOI] [PubMed] [Google Scholar]
- 11. Delanaye P, Ebert N, Melsom T. et al. Iohexol plasma clearance for measuring glomerular filtration rate in clinical practice and research: a review. Part 1: how to measure glomerular filtration rate with iohexol? Clin Kidney J 2016; 9: 682–699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Pottel H, Mottaghy FM, Zaman Z. et al. On the relationship between glomerular filtration rate and serum creatinine in children. Pediatr Nephrol 2010; 25: 927–934 [DOI] [PubMed] [Google Scholar]
- 13. Pottel H, Hoste L, Martens F.. A simple height-independent equation for estimating glomerular filtration rate in children. Pediatr Nephrol 2012; 27: 973–979 [DOI] [PubMed] [Google Scholar]
- 14. Piepsz A, Tondeur M, Ham H.. Escaping the correction for body surface area when calculating glomerular filtration rate in children. Eur J Nucl Med Mol Imaging 2008; 35: 1669–1672 [DOI] [PubMed] [Google Scholar]
- 15. Roelants M, Hauspie R, Hoppenbrouwers K.. References for growth and pubertal development from birth to 21 years in Flanders, Belgium. Ann Hum Biol 2009; 36: 680–694 [DOI] [PubMed] [Google Scholar]
- 16. Hoste L, Dubourg L, Selistre L. et al. A new equation to estimate the glomerular filtration rate in children, adolescents and young adults. Nephrol Dial Transplant 2013; 29: 944–947 [DOI] [PubMed] [Google Scholar]
- 17. Poggio ED, Rule AD, Tanchanco R. et al. Demographic and clinical characteristics associated with glomerular filtration rates in living kidney donors. Kidney Int 2009; 75: 1079–1087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Rule AD, Gussak HM, Pond GR. et al. Measured and estimated GFR in healthy potential kidney donors. Am J Kidney Dis 2004; 43: 112–119 [DOI] [PubMed] [Google Scholar]
- 19. Grewal GS, Blake GM.. Reference data for 51Cr-EDTA measurements of the glomerular filtration rate derived from live kidney donors. Nucl Med Commun 2005; 26: 61–65 [DOI] [PubMed] [Google Scholar]
- 20. Fleming JS, Zivanovic MA, Blake GM. et al. Guidelines for the measurement of glomerular filtration rate using plasma sampling. Nucl Med Commun 2004; 25: 759–769 [DOI] [PubMed] [Google Scholar]
- 21. Hamilton D, Riley P, Miola U. et al. Total plasma clearance of 51Cr-EDTA: variation with age and sex in normal adults. Nucl Med Commun 2000; 21: 187–192 [DOI] [PubMed] [Google Scholar]
- 22. Soares AA, Prates AB, Weinert LS. et al. Reference values for glomerular filtration rate in healthy Brazilian adults. BMC Nephrol 2013; 14: 54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Blake GM, Sibley-Allen C, Hilton R. et al. Glomerular filtration rate in prospective living kidney donors. Int Urol Nephrol 2013; 45: 1445–1452 [DOI] [PubMed] [Google Scholar]
- 24. Braat E, Hoste L, De Waele L. et al. Renal function in children and adolescents with Duchenne muscular dystrophy. Neuromuscul Disord 2015; 25: 381–387 [DOI] [PubMed] [Google Scholar]
- 25. Inker LA, Shafi T, Okparavero A. et al. Effects of race and sex on measured GFR: the multi-ethnic study of atherosclerosis. Am J Kidney Dis 2016; 68: 743–751 [DOI] [PubMed] [Google Scholar]
- 26. Berg UB. Differences in decline in GFR with age between males and females. Reference data on clearances of inulin and PAH in potential kidney donors. Nephrol Dial Transplant 2006; 21: 2577–2582 [DOI] [PubMed] [Google Scholar]
- 27. Sasson AN, Cherney DZ.. Renal hyperfiltration related to diabetes mellitus and obesity in human disease. World J Diabetes 2012; 3: 1–6 [DOI] [PMC free article] [PubMed] [Google Scholar]