Position Matters: Network Centrality Considerably Impacts Rates of Protein Evolution in the Human Protein–Protein Interaction Network

Abstract

The proteins of any organism evolve at disparate rates. A long list of factors affecting rates of protein evolution have been identified. However, the relative importance of each factor in determining rates of protein evolution remains unresolved. The prevailing view is that evolutionary rates are dominantly determined by gene expression, and that other factors such as network centrality have only a marginal effect, if any. However, this view is largely based on analyses in yeasts, and accurately measuring the importance of the determinants of rates of protein evolution is complicated by the fact that the different factors are often correlated with each other, and by the relatively poor quality of available functional genomics data sets. Here, we use correlation, partial correlation and principal component regression analyses to measure the contributions of several factors to the variability of the rates of evolution of human proteins. For this purpose, we analyzed the entire human protein–protein interaction data set and the human signal transduction network—a network data set of exceptionally high quality, obtained by manual curation, which is expected to be virtually free from false positives. In contrast with the prevailing view, we observe that network centrality (measured as the number of physical and nonphysical interactions, betweenness, and closeness) has a considerable impact on rates of protein evolution. Surprisingly, the impact of centrality on rates of protein evolution seems to be comparable, or even superior according to some analyses, to that of gene expression. Our observations seem to be independent of potentially confounding factors and from the limitations (biases and errors) of interactomic data sets.

Introduction

The rates of evolution of the proteins of any organism vary enormously: some proteins remain virtually unaltered during long evolutionary periods, whereas others tolerate fast accumulation of amino acid changes (Zuckerkandl and Pauling 1965; Dickerson 1971; Li et al. 1985). A long list of factors affecting rates of protein evolution has been identified, including patterns and levels of gene expression (Duret and Mouchiroud 2000; Pál et al. 2001; Drummond et al. 2005), essentiality (Hurst and Smith 1999; Jordan et al. 2002; Rocha and Danchin 2004; Alvarez-Ponce et al. 2016), dispensability (i.e., fitness upon gene knockout; Hirsh and Fraser 2001; Yang et al. 2003; Wall et al. 2005; Zhang and He 2005), functional category (Pál et al. 2001; Rocha and Danchin 2004; Greenberg et al. 2008; Alvarez-Ponce and Fares 2012), number of functions (Wilson et al. 1977; Salathé et al. 2006; Podder et al. 2009), number of protein–protein interactions and other metrics of network centrality (Fraser et al. 2002; Hahn and Kern 2005), protein length (Marais and Duret 2001; Lemos et al. 2005; Ingvarsson 2007), gene compactness (Liao et al. 2006), and duplicability (Lynch and Conery 2000; Van de Peer et al. 2001; Kondrashov et al. 2002; Nembaware et al. 2002; Scannell and Wolfe 2008; Panchin et al. 2010; Pegueroles et al. 2013). However, little is known about what fraction of the variability of rates of evolution is explained by each factor (for review, see Herbeck and Wall 2005; Pál et al. 2006; Rocha 2006; Alvarez-Ponce 2014; Zhang and Yang 2015). Accurately addressing this question is complicated by the facts that 1) the different determinants of rates of protein evolution are often correlated to each other (e.g., Koonin and Wolf 2006), and 2) the available data sets corresponding to the different variables have different quality (i.e., they are not equally noisy; e.g., Plotkin and Fraser 2007).

Initial models, based on theory, predicted that rates of protein evolution should be primarily dictated by the relative importance and functional density of proteins, with more important and/or functionally dense proteins tending to be more evolutionarily constrained (Kimura and Ohta 1974; Zuckerkandl 1976; Wilson et al. 1977). Genomic analyses, however, have lent only limited support to these models (Hurst and Smith 1999; Pál et al. 2003; Wang and Zhang 2009). The current view is that rates of protein evolution are primarily determined by levels of gene expression (and in the case of complex organisms, by expression breadth, i.e., the number of tissues in which a gene is expressed), with all other factors explaining a very small fraction of the variation of rates of protein evolution. For instance, using Principal Component Regression (PCR) analysis (Mandel 1982), Drummond et al. (2006) showed that, in yeasts, one principal component (PC) mostly dominated by surrogates of translation frequency (mRNA abundance, protein abundance and Codon Adaptation Index) accounted for 43% of the variance in rates of evolution, whereas all other PCs accounted for <1%. Analyses in other species, using PCR and other multivariate analysis techniques, have also pointed out to an overarching role of gene expression (e.g., Ingvarsson 2007; Larracuente et al. 2008; Yang and Gaut 2011). However, analyses by Plotkin and Fraser (2007) suggested that this observation was an artifact of the fact that different factors had been measured with different degrees of noise, and that once noise was equalized across the different variables, they all had a comparable contribution to the variability of rates of protein evolution.

Genes and proteins rarely act in isolation. Instead, they tend to work as part of complex networks of interacting molecules. One question that has been subject to intense debate is whether the centrality of proteins within molecular networks significantly impacts rates of protein evolution. Network centrality is typically measured as degree (the number of interactions a protein is involved in), or using more global measures of centrality such as betweenness (the number of shortest paths between all pairs of other proteins that pass throughout a certain protein; Freeman 1977) and closeness (one divided by the average distance between a protein and all other proteins in the network; Bavelas 1950). Pioneers in the field hypothesized that rates of protein evolution should decrease as the number of molecular interactions increases, as interactions impose functional constraints on the involved amino acid residues (Ingram 1961; Dickerson 1971; Wilson et al. 1977). In agreement with this hypothesis, Teichmann (2002) found that proteins that form part of protein complexes tend to evolve particularly slowly, and Fraser et al. (2002) observed a negative correlation between the number of protein–protein interactions in yeast and rates of protein evolution. However, Bloom and Adami (2003) claimed that the correlation between rates of protein evolution and number of interactions observed by Fraser et al. was simply a by-product of the facts that certain techniques used to detect protein interactions systematically detect more interactions for highly abundant proteins, and that abundant proteins tend to be highly constrained. Using partial correlation analysis, Fraser and Hirsh (2004) showed that the correlation between proteins’ rates of evolution and number of interactions was independent of protein abundances. Several subsequent analyses in a range of species have also concluded, using partial correlations, that the correlation between proteins’ rates of evolution and different measures of centrality (including the number of interactions) is independent of confounding factors such as protein abundances (Jordan et al. 2003; Agrafioti et al. 2005; Hahn and Kern 2005; Lemos et al. 2005; Alvarez-Ponce and Fares 2012). However, the correlation is often very weak, and sometimes even nonexistent (Batada et al. 2006; Larracuente et al. 2008; Hahn et al. 2004; see supplementary table S1, Supplementary Material online for a summary of previously reported correlation coefficients). In addition, it has been shown that partial correlation analysis can produce spurious results when applied to noisy data (as functional genomics data usually is), and PCR has been proposed as an alternative (Drummond et al. 2006) (even though this method has limitations as well; Plotkin and Fraser 2007). Using this technique, Drummond et al. (2006) claimed that the effect or the number of protein–protein interactions and betweenness on rates of evolution in yeasts was negligible.

Together, these analyses draw a picture in which the effect of network centrality on rates of protein evolution appears to be very weak, or even negligible, particularly once confounding factors are corrected for. However, it should be noted that most of these analyses have been conducted in yeasts, and none has focused on humans (supplementary table S1, Supplementary Material online). In addition, most analyses have relied on partial correlation analyses and/or on largely incomplete interactomic data sets of poor quality. Currently available interactomic data sets are known to suffer from very high rates of false positives and false negatives, as well as important biases (Bader et al. 2004; Deeds et al. 2006; Hakes et al. 2008; Kelly and Stumpf 2012; Alvarez-Ponce 2017), which may have affected prior analyses.

Here, we use correlation, partial correlation and PCR analyses to assess the relative contributions of several factors to the variability of rates of protein evolution in the human signal transduction network. For that purpose, we use the entire human protein–protein network and a manually curated network data set of exceptionally high quality representing the human signal transduction network (Cui et al. 2007). In sharp contrast with the prevailing view, our analyses show that network centrality has an important effect on rates of protein evolution. Surprisingly, the combined effect of network parameters is comparable, or even stronger according to some analyses, to the combined effect of expression parameters (expression level and breadth, protein abundance and breadth, and Codon Adaptation Index).

Materials and Methods

Interactomic Data Sets

The entire human protein–protein interaction network was derived from the BioGRID database, version 3.4.137 (Chatr-Aryamontri et al. 2015). Only physical interactions among human proteins were considered. After removing redundant interactions, the network consisted of 15,960 proteins and 213,009 nonredundant interactions. The network consists of a giant connected component with 15,928 nodes and 212,992 interactions, and 32 small components (with 2–3 nodes). For each of the 15,960 proteins in the network, we computed their degree as the number of interactions in which they are involved. For the 15,928 proteins in the giant connected component, betweenness and closeness were computed using Pajek 4.05 (Nooy et al. 2005). The yeast, fly, and worm protein–protein interaction networks were derived from the same database and treated in the same manner.

The human signal transduction network was obtained from Cui et al. (2007). This data set consists of a total of 1634 nodes connected by 4665 nonredundant interactions. The data set was obtained by merging multiple manually generated data sets (Ma’ayan et al. 2005; Awan et al. 2007; www.biocarta.com; http://www.ccmi.org/), and by additional manual curation (Cui et al. 2007). We eliminated nodes that do not represent genes/proteins, but signaling molecules of other kinds (e.g., second messengers), resulting in a network with 1,551 nodes and 4,350 interactions. The network consists of a giant connected component with 1,524 nodes and 4,331 interactions, and 11 small components with 2–7 nodes. As for the entire network, degree was computed for all nodes, and betweenness and closeness was computed only for those that were part of the giant connected component. We determined whether each interaction was a physical protein–protein interaction by searching it in the BioGRID database, version 3.4.137 (Chatr-Aryamontri et al. 2015). A total of 1,623 of the 4,350 interactions were deemed physical interactions.

Rates of Protein Evolution

For each of the human genes represented in the network, we identified the most likely mouse ortholog using a best reciprocal hit approach. All human and mouse protein and CDS sequences were retrieved from Ensembl, release 62 (Yates et al. 2016). For each human gene, the longest protein and its encoding CDS were chosen for analysis. The human protein was used in a BLASTP search against the entire mouse proteome, using an E-value cut-off of 10⁻¹⁰. The best hit was used as query in a second BLASTP search against the human proteome. If the best hit recovered in the second BLASTP search was a protein encoded by the original gene, then the corresponding human and mouse genes were considered orthologs. The accuracy of this approach has been demonstrated (Wolf and Koonin 2012; Dalquen and Dessimoz 2013).

For each pair of orthologous genes, the encoded protein sequences were aligned using ProbCons, version 1.12 (Do et al. 2005), and the resulting alignment was used to align the corresponding CDS sequences. For each of the resulting alignments, we estimated the nonsynonymous to synonymous divergence ratio (ω = d_N/d_S) using PAML, version 4.4 (codeml program, M0 model; Yang 2007). The same methods were used to identify and analyze pairs of D. melanogaster–D. yakuba, C. elegans–C. briggsae, and S. cerevisiae–S. paradoxus orthologs.

Gene Expression Data and Additional Information

For each gene, we gathered the following information from different sources:

• Protein abundance: For each human, fly, worm and yeast gene, an estimate of the total abundance of the encoded proteins in the entire body was obtained from the PaxDb database, version 3 (Wang et al. 2012). These estimates were obtained by combining multiple protein abundance data sets.

• Protein expression breadth: For each human gene, protein expression data across six different organs/tissues (brain, heart, liver, lung, plasma, and platelet) were obtained from the PaxDb database, version 3 (Wang et al. 2012). Protein expression breadth was computed as the number of different organs/tissues in which each protein was detected. This number ranged between 0 and 6.

• Messenger RNA abundance: RNA-seq data for a total of 32 human organs/tissues were obtained from the HumanAtlas database (Uhlen et al. 2015). For each human gene, mRNA abundance was estimated as the average across the 32 tissues. Messenger RNA abundance data for D. melanogaster and C. elegans were obtained from the FlyAtlas database (whole adult fly; Chintapalli et al. 2007) and the EBI Expression Atlas (accession number E-MTAB-2812; Petryszak et al. 2015), respectively. S. cerevisiae gene expression data was obtained from Nagalakshmi et al. (2008).

• Messenger RNA expression breadth: For each human gene, mRNA expression breadth was computed as the number of organs/tissues in which the mRNA was detected (with an FPKM value equal to or higher than 1). This number ranged between 0 and 32. For each fly gene, expression breadth was computed as the number of adult tissues in which the gene was expressed according to the FlyAtlas database (ranging from 0 to 16). Genes were considered to be expressed at a certain tissue if they were detectable in at least 3 out of the 4 biological replicates.

• Codon Adaptation Index: For each human, fly, worm and yeast gene, the CAI (Sharp and Li 1987) was computed using the cai program from the EMBOSS package (Rice et al. 2000).

• Protein length: For each human, fly, worm, and yeast gene, the length of the longest encoded protein was considered.

• 5′ and 3′ UTR length: For human, fly, and worm genes, 5′ and 3′ UTR length was derived from the gene structure annotations contained in Ensembl’s BioMart (Kinsella et al. 2011). For yeast genes, average UTR lengths were obtained from Pelechano et al. (2013).

• Average intron length: Intron lengths were derived from the gene structure annotations contained in Ensembl’s BioMart.

• Duplicability: For each human, fly, worm and yeast gene, a list of paralogs in the same genome was obtained from Ensembl’s BioMart. Genes with no paralogs were deemed singletons, and genes with at least one paralog were classified as duplicated.

• Essentiality: For each human gene, phenotypic data for its mouse ortholog was obtained from the Mouse Genome Database (Eppig et al. 2015). If the mouse ortholog was involved in a lethal phenotype, then the human gene was considered essential; otherwise, the human gene was deemed nonessential. Fly and worm essentiality data were derived from the Online Gene Essentiality Database (Chen et al. 2012). Yeast essentiality data were obtained from Giaever et al. (2002).

• Number of publications: For each human gene, the total number of research articles that mention the gene was retrieved from PubMed (ftp://ftp.ncbi.nlm.nih.gov/gene/DATA/gene2pubmed.gz) on November 15, 2016.

• Subcellular location: Human proteins were considered extracellular if classified as such in the MetazSecKB database (categories “curated” or “highly likely”), or membrane if classified as such in the UniProt database (UniProt consortium 2015).

Statistical Analyses

All our correlation, partial correlation and PCR analyses were restricted to genes for which we had both network and evolutionary rate information (i.e., genes that were represented in the network and had detectable orthologs in mouse, D. yakuba, C. briggsae, or S. paradoxus). Our PCR analyses were further restricted to genes for which data were available for all studied variables. Correlation and partial correlation analyses were performed using the functions “cor.test” and “pcor.test” (Kim and Yi 2006) in R (Ihaka and Gentleman 1996), respectively. Data transformation was not required, as we performed nonparametric tests. PCR analyses were performed using the “pls” library (Mevik and Wehrens 2007) for R. Three separate analyses were conducted, using ω, d_N or d_S as response variables. In each analysis, continuous independent variables were log-transformed if that increased the percent of the variance of the dependent variable explained by the model (R²). For those continuous independent variables that included zero values, a small constant (0.0001) was added, in order to allow log-transformation. In all analyses, independent variables were scaled to zero mean and one variance. Essentiality and duplicability were treated as binary variables (essentiality was 0 for nonessential genes and 1 for essential ones; duplicability was 0 for singleton genes and 1 for duplicated ones).

Results

Correlation and Partial Correlation Analysis

We first reconstructed the human protein–protein interaction network from the contents of the BioGRID database (Chatr-Aryamontri et al. 2015). This database contains physical protein–protein interactions determined by thousands of large-scale and small-scale experiments. After filtering (see Materials and Methods), the network consisted of 15,960 genes/proteins and 213,009 nonredundant interactions. For each human gene represented in the network, we identified its most likely ortholog in the mouse genome and inferred the strength of purifying selection acting on the sequence of the encoded protein from the nonsynonymous to synonymous divergence ratio (ω = d_N/d_S). This ratio is expected to be lower than one for genes under purifying selection (with values closer to 0 indicating stronger purifying selection), equal to one for genes evolving neutrally, and higher than one (at least in a subset of codons) for genes under positive selection. Mouse orthologs were identified for a total of 13,576 of the human genes represented in the network. The remaining genes were excluded from all our analyses.

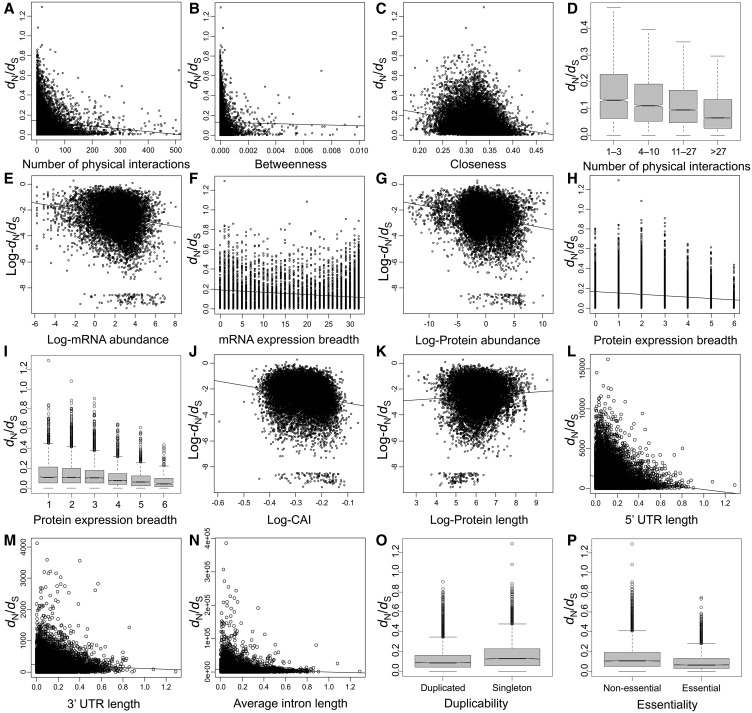
We evaluated the correlation between ω and 14 parameters, including three measures of network centrality (number of physical protein–protein interactions, betweenness, and closeness), five expression parameters (mRNA abundance, mRNA breadth – the number of tissues in which mRNA is present – protein abundance and breadth, and Codon Adaptation Index). four measures of compactness (protein length, 5′ UTR length, 3′ UTR length, and average intron length), and two other parameters (duplicability and essentiality). Essentiality and duplicability were treated as binary variables (essential = 1, nonessential = 0; duplicated = 1, singleton = 0). All parameters negatively correlate with ω, with the only exception of protein length, which exhibits a positive correlation with ω (table 1 and fig. 1). Essential genes evolved slower than nonessential genes (median ω for essential genes: 0.067, median ω for nonessential genes: 0.106; Mann–Whitney U test, P = 2.63 × 10⁻⁹⁶; fig. 1P), and duplicated genes evolved slower than singleton genes (median ω for duplicates: 0.085, median ω for singletons: 0.127; Mann–Whitney U test, P = 6.66 × 10⁻⁷⁸; fig. 1O). This is in agreement with prior observations: even though duplicates evolve faster immediately after gene duplication (Lynch and Conery 2000; Van de Peer et al. 2001; Han et al. 2009; Pegueroles et al. 2013), genes with paralogs are overall more conserved than those without paralogs (Nembaware et al. 2002; Yang et al. 2003; Davis and Petrov 2004; Jordan et al. 2004; Yang and Gaut 2011).

Table 1.

Spearman’s Correlations between ω and 14 Parameters in the Human Protein–Protein Interaction Network

	N	ρ	P Value
Network parameters
Physical protein–protein interactions	13,576	−0.257	1.57 × 10−203***
Betweenness	13,549	−0.237	3.17 × 10−172***
Closeness	13,549	−0.260	1.19 × 10−207***
Expression parameters
mRNA abundance (mean for 32 tissues)	13,576	−0.188	1.39 × 10−107***
mRNA expression breadth	13,576	−0.169	5.07 × 10−88***
Protein abundance (whole body)	12,396	−0.189	2.20 × 10−100***
Protein expression breadth	13,576	−0.158	2.35 × 10−76***
Codon Adaptation Index	13,576	−0.192	2.58 × 10−113***
Compactness parameters
Protein length	13,576	0.024	0.005**
5′ UTR length	13,576	−0.104	3.24 × 10−34***
3′ UTR length	13,576	−0.157	7.84 × 10−76***
Average intron length	13,576	−0.058	1.57 × 10−11***
Other parameters
Duplicability	13,576	−0.160	6.87 × 10−79***
Essentiality	13,038	−0.182	6.70 × 10−98***

^*P < 0.05, **P < 0.01, ***P < 0.001.

Fig. 1.

—Relationship between rates of protein evolution and a number of factors in the human protein–protein interaction network. In panel A, proteins with >500 interactions are not shown. In panel B, proteins with a betweenness higher than 0.1 are not shown. In panels A–C, E–H, and J–N, lines represent regression lines. In panels E and F, outliers are not represented.

Surprisingly, network centrality parameters are stronger correlates of ω (−0.237 ≥ ρ ≥ −0.260) than expression (−0.158 ≥ ρ ≥ −0.192; table 1), compactness (0.024 ≥ ρ ≥ −0.157; table 1) or other parameters (ρ = −0.160 for duplicability and −0.182 for essentiality). We divided proteins into four groups according to the number of interactions (group 1: 1–3 interactions, n = 3101; group 2: 4–10 interactions, n = 3269; group 3: 11–27 interactions, n = 3339; group 4: >27 interactions, n = 3867). The median ω steadily decreased as the number of interaction increased (group 1: 0.131, group 2: 0.110, group 3: 0.094, group 4: 0.064; fig. 1D). Any pair of groups exhibited statistically significant differences (Mann–Whitney’s U test, P ≤ 4.51 × 10⁻⁸).

We next used partial correlation analysis to evaluate whether the correlation between ω and the measures of network centrality was independent of the other 11 factors. We first controlled for each nonnetwork parameter individually. The correlation between ω and the number of interactions, betweenness and closeness was significant in all cases (supplementary table S2, Supplementary Material online). We next evaluated the partial correlations between network centralities and ω, controlling simultaneously for all 11 nonnetwork parameters, also with significant results in all cases (supplementary table S2, Supplementary Material online).

Principal Component Regression Analysis

Partial correlation analysis suffers from at least two problems that limit its applicability to our data set. First, it assumes that the controlling variables are independent of each other; however, many of the variables used in our study are correlated with each other (supplementary table S3, Supplementary Material online). Second, partial correlation analysis can produce spurious results when measurements for some of the variables are noisy (Drummond et al. 2006). PCR has been proposed as a suitable alternative to establish the determinants of rates of protein evolution and their relative contributions (Drummond et al. 2006). This method seems to be less sensitive to noise than partial correlation (but not completely insensitive; Plotkin and Fraser 2007), takes into account the interrelationships among the explanatory variables, and provides information on the relative contribution of several independent variables to the variability of a dependent variable.

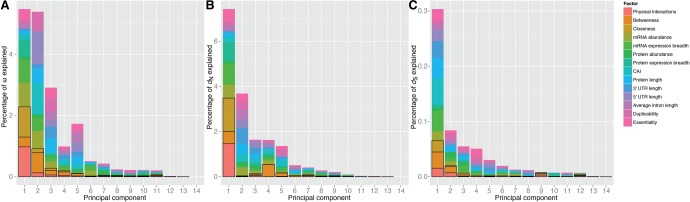
We performed three PCR analyses, using as dependent variable either ω, d_N or d_S (fig. 2). In all analyses, the following variables were used as independent variables: degree, betweenness, closeness, mRNA abundance, protein abundance, mRNA expression breadth, protein expression breadth, Codon Adaptation Index (CAI), protein length, 5′ UTR length, 3′ UTR length, average intron length, duplicability, and essentiality. All analyses were restricted to the 11,593 genes for which data were available for all these variables. The first model explained 18.37% of the variability of ω (fig. 2A), consistent with previous multivariate analyses in complex eukaryotes (Ingvarsson 2007; Yang and Gaut 2011). The first, second, and third PCs explained, respectively, 5.48%, 5.39%, and 2.91% of the variability of ω. The first PC is composed 41.71% of network centrality parameters (number of interactions: 17.85%, betweenness: 5.83%, closeness: 18.03%), 43.41% of expression parameters (mRNA abundance: 14.28%, mRNA breadth: 14.09%, protein abundance: 1.48%, protein breath: 10.16%, CAI: 3.40%), 5.99% of compactness parameters (protein length: 2.01%, 5′ UTR length: 0.03%, 3′ UTR length: 1.11%, average intron length: 2.84%), and 8.89% of other parameters (duplicability: 2.72%, essentiality: 6.18%) (supplementary table S4, Supplementary Material online). The second PC is composed 17.12% of network parameters, 39.67% of expression parameters, 31.88% of compactness parameters, and 11.33% of other parameters. The third PC is composed 9.60% of network parameters, 17.85% of expression parameters, 45.61% of compactness parameters, and 26.95% of other parameters.

Fig. 2.

—Principal component regression analysis on the human protein–protein interaction network. For each principal component (PC), the size of the bar represents the percent of the variability of the response variable explained by the PC. The composition of each component is represented in colors. Network parameters are highlighted within black boxes. This analysis was restricted to the 11,593 genes for which data were available for all variables.

For each variable or kind of variable (network, expression, compactness, and other), we applied the following formula:

$$X_i=\sum _{j=1}^{14}{p}_j{c}_{ij}$$

where i is the variable or group of variables, p_j is the percent of the response variable explained by PC j, and c_ij is the contribution of the variable or group of variables i to PC j. X is the surface of figure 2A–C occupied by each variable or group of variables, and can be taken as an approximation of their explanatory power. X was 4.06% for network parameters, 6.66% for expression parameters, 5.14% for compactness parameters, and 2.51% for other parameters. That is, 4.06/18.37 = 22.08% of the surface of figure 2A is occupied by network parameters, 6.66/18.37 = 36.28% by expression parameters, 5.14/18.37 = 27.98% by compactness parameters and 13.66% by other parameters. Among network parameters, X was 1.33% for the number of interactions, 1.39% for betweenness and 1.33% for closeness.

The second model explained 17.33% of the variability of d_N (fig. 2B), also consistent with previous analyses (Yang and Gaut 2011). The first, second, third, fourth, and fifth PCs explained, respectively, 7.43%, 3.68%, 1.64%, 1.63%, and 1.36% of the variability of d_N. Each of the other PCs explained <1% of this variability. The first PC was composed 46.92% of network parameters, 36.58% of expression parameters, 6.53% of compactness parameters, and 9.98% of other parameters. The second PC was composed 1.12% by network parameters, 26.77% of expression parameters, 52.92% of compactness parameters, and 19.18% of other parameters. The third PC was composed 8.93% of network parameters, 40.42% of expression parameters, 46.63% of compactness parameters, and 4.02% of other parameters. X was 4.65% for network parameters, 6.22% for expression parameters, 4.22% for compactness parameters, and 2.25% for other parameters. Among network parameters, X was 1.63% for the number of interactions, 1.38% for betweenness, and 1.64% for closeness.

In summary, PCR analyses on ω and d_N indicate that the impact of network centralities on rates of protein evolution is far from negligible, and is comparable to that of expression parameters. The third PCR analysis explained only 0.60% of the variability of d_S, consistent with previous analyses (Yang and Gaut 2011). The results of this analysis are summarized in figure 2C and supplementary table S4, Supplementary Material online.

Our Findings Are Not a By-Product of Network Biases

Interactomic data sets are subjected to inspection (or study) bias and technical biases. Inspection bias is due to the fact that, within any proteome, certain proteins (e.g., those of particular biomedical interest) have been better studied than others, and as a result, a higher number of protein–protein interactions involving these proteins has been described (Rual et al. 2005). Indeed, there is a positive correlation between the number of publications mentioning a gene and the number of described interactions involving the encoded products of that gene (Schaefer et al. 2015; Chakraborty and Alvarez-Ponce 2016). Our results might be affected by this kind of bias if 1) more interactions were known for better studied genes, and 2) better studied genes tended to exhibit slower rates of evolution. We found that the number of scientific publications mentioning a certain gene strongly correlates with measures of network centrality (number of physical interactions: ρ = 0.511, P < 10⁻³⁰⁰; betweenness: ρ = 0.509, P < 10⁻³⁰⁰; closeness: ρ = 0.458, P < 10⁻³⁰⁰), indicating strong inspection bias. In addition, a strong correlation was detected between proteins’ rates of evolution and the number of publications mentioning them (ρ = −0.197, P = 5.83 × 10⁻¹¹⁹). However, partial correlation analysis shows that the correlations between centrality measures and ω is not affected by the number of publications (number of physical interactions: ρ = −0.185, P = 9.69 × 10⁻¹⁰⁷; betweenness: ρ = −0.162, P = 4.79 × 10⁻⁸¹; closeness: ρ = −0.194, P = 1.70 × 10⁻¹¹⁷), indicating that our observations are not due to inspection bias.

Another known source of bias is the fact that membrane and secreted proteins are underrepresented in interactomic data sets, due to the technical difficulties that entails working with such proteins (Rual et al. 2005; Wright et al. 2010; Brito and Andrews 2011). It is conceivable that this bias, combined with the fact that membrane and secreted proteins tend to evolve fast (Julenius and Pedersen 2006; Cui et al. 2009; Liao et al. 2010; Nogueira et al. 2012), might be inflating the relationship between centrality and rates of evolution observed here. In addition, the expression level–evolutionary rate anticorrelation is reduced among secreted proteins (Feyertag et al. 2017), which might also be affecting our results. To discard these possibilities, we repeated our correlation and PCR analyses after removing membrane and extracellular proteins. The correlations between ω and network centrality parameters were not affected (number of interactions: ρ = −0.281, P = 5.86 × 10⁻¹⁵¹; betweenness: ρ = −0.266, P = 4.39 × 10⁻¹³⁵; closeness: ρ = −0.282, P = 2.47 × 10⁻¹⁵²), and the results of the PCR analysis were also similar (supplementary table S5, Supplementary Material online).

Finally, tandem affinity purification followed by mass spectrometry (TAP/MS), one of the most used techniques to infer protein interactions, tends to detect more interactions for highly abundant proteins (von Mering et al. 2002; Björklund et al. 2008; Ivanic et al. 2009). It is conceivable that this bias, combined with the fact that highly abundant proteins tend to evolve slowly (Duret and Mouchiroud 2000; Pál et al. 2001; Drummond et al. 2005), may be affecting our results. However, our partial correlation and PCR analyses show that the relationship between ω and centrality is independent from protein abundance (supplementary table S2Supplementary Material online).

Our Findings Are Not a By-Product of the Poor Quality of the Interactomic Data Set: Analysis of a Manually Curated Signal Transduction Network

Large-scale interactomic data sets, such as the one used so far, are known to suffer from very high rates of false positives and false negatives (Bader et al. 2004; Deeds et al. 2006; Hakes et al. 2008; Kelly and Stumpf 2012; Alvarez-Ponce 2017). As a result, our centrality estimates are subjected to a certain amount of noise, which is known to interfere with partial correlation analyses (Drummond et al. 2006). In order to demonstrate that our results are not affected by this noise, we performed two additional analyses. First, we repeated our correlation, partial correlation and PCR analyses after removing 15% of genes randomly chosen, with equivalent results (supplementary tables S6–S8, Supplementary Material online).

Second, we repeated our analyses using a network data set of exceptionally high quality: the human signal transduction network assembled by Cui et al. (2007). This data set was generated by combining multiple manually curated data sets, and by extensive additional manual curation. Therefore, the data set is expected to be virtually free from false positives. The data set is restricted to proteins involved in signal transduction, and contains both physical, direct protein–protein interactions, and other kinds of interactions, including transcriptional activation repression by transcription factors (Cui et al. 2007). After filtering (see Methods), the network consisted of 1,551 genes/proteins and 4,350 nonredundant interactions, including 1,623 physical and 2,727 nonphysical interactions. We restricted our analyses to the 1,443 genes for which mouse orthologs could be identified.

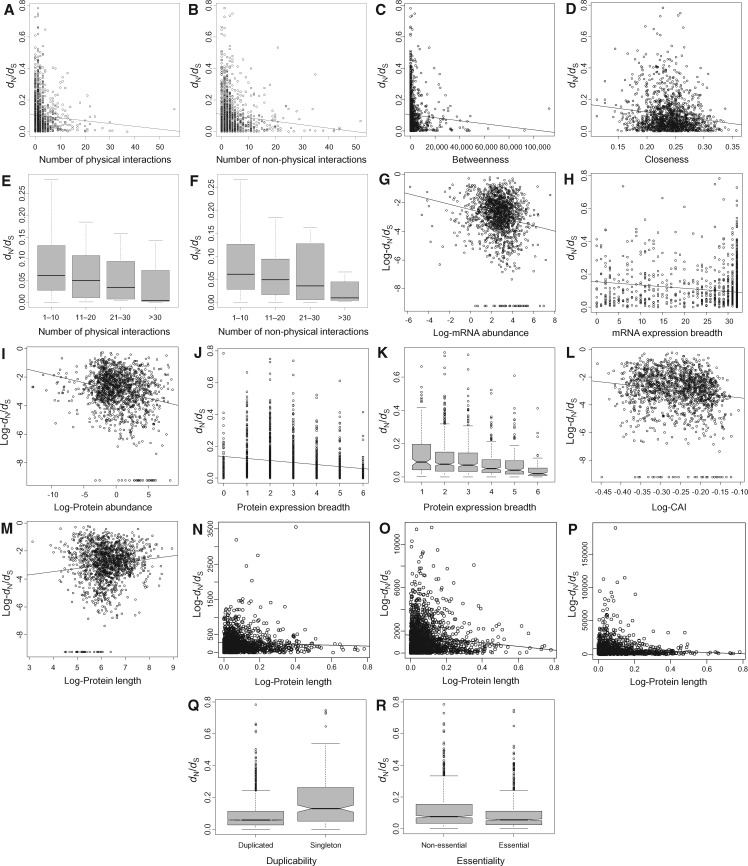
We first evaluated the correlation between ω and 16 parameters, including five measures of network centrality (number of physical protein–protein interactions, number of nonphysical protein interactions, total number of interactions, betweenness, and closeness), and the five expression parameters, four compactness parameters and two other parameters listed above. Results were similar to those for the entire protein–protein interaction network: all parameters exhibit significant negative correlations with ω, except protein length, for which the correlation was not significant (fig. 3 and table 2; supplementary table S9, Supplementary Material online). In general, expression parameters are stronger correlates of ω (−0.171 ≥ ρ ≥ −0.183) than network parameters (−0.065 ≥ ρ ≥ −0.136; fig. 1 and table 2). However, correlation coefficients are somehow comparable between network and expression parameters.

Fig. 3.

—Relationship between rates of protein evolution and a number of factors in the human signal transduction network. In panels A–D, G–J, and L–P, lines represent regression lines. In panels E and F, outliers are not represented.

Table 2.

Spearman’s Correlations between ω and 16 Parameters in the Human Signal Transduction Network

	N	ρ	P Value
Network parameters
Number of interactions	1,443	−0.111	2.44 × 10−5***
Physical protein–protein interactions	1,443	−0.065	0.013*
Nonphysical interactions	1,443	−0.130	7.90 × 10−7***
Betweenness	1,443	−0.083	0.002**
Closeness	1,443	−0.136	2.70 × 10−7***
Expression parameters
mRNA abundance (mean for 32 tissues)	1,443	−0.171	5.75 × 10−11***
mRNA expression breadth	1,443	−0.175	2.26 × 10−11***
Protein abundance (whole body)	1,347	−0.186	5.28 × 10−12***
Protein expression breadth	1,443	−0.175	2.26 × 10−11***
Codon Adaptation Index	1,443	−0.183	2.25 × 10−12***
Compactness parameters
Protein length	1,443	0.040	0.130
5′ UTR length	1,443	−0.096	2.59 × 10−4***
3′ UTR length	1,443	−0.132	5.31 × 10−7***
Average intron length	1,443	−0.002	0.002**
Other parameters
Duplicability	1,443	−0.223	9.36 × 10−18***
Essentiality	1,411	−0.142	7.76 × 10−8***

^*P < 0.05, **P < 0.01, ***P < 0.001.

We divided proteins into four groups according to the number of physical interactions (group 1: 1–10 interactions; group 2: 11–20 interactions; group 3: 21–30 interactions; group 4: >30 interactions). The median ω steadily decreases as the number of interaction increases (group 1: 0.065, group 2: 0.050, group 3: 0.039, group 4: 0.0046; fig. 3E). A similar trend was observed when proteins were classified according to their number of nonphysical interactions (group 1: 0.065, group 2: 0.050, group 3: 0.036, group 4: 0.010; fig. 3F).

The correlation between ω and the number of interactions, number of nonphysical interactions, betweenness, and closeness remains significant when controlling for any of the other 11 variables separately (supplementary table S10, Supplementary Material online). The correlation between ω and the number of physical interactions vanished when controlling for mRNA abundance, mRNA expression breadth, or essentiality, but not when controlling for the other variables (supplementary table S10, Supplementary Material online). When we evaluated the partial correlations between network centralities and ω controlling simultaneously for all 11 nonnetwork parameters, the correlation remained significant for the number of nonphysical interactions and closeness, but not for the number of physical protein–protein interactions, total number of interactions, or betweenness. Nonetheless, correlation coefficients remained negative in all cases (supplementary table S10, Supplementary Material online).

Proteins’ measures of network centrality strongly correlate with the number of scientific publications mentioning them (number of physical interactions: ρ = 0.427, P = 6.70 × 10⁻⁶⁵; number of nonphysical interactions: ρ = 0.138, P = 1.33 × 10⁻⁷; betweenness: ρ = 0.340, P = 1.41 × 10⁻³⁹; closeness: ρ = 0.180, P = 9.16 × 10⁻¹²), indicating strong inspection bias. However, no correlation was detected between proteins’ rates of evolution and the number of publications mentioning them (ρ = −0.013, P = 0.630), and partial correlation analysis shows that the correlations between centrality measures and ω are not affected by the number of publications (number of physical interactions: ρ = −0.066, P = 0.012; number of nonphysical interactions: ρ = −0.129, P = 7.87 × 10⁻⁷; betweenness: ρ = −0.081, P = 0.002; closeness: ρ = −0.134, P = 3.34 × 10⁻⁷), indicating that our observations are not due to inspection bias.

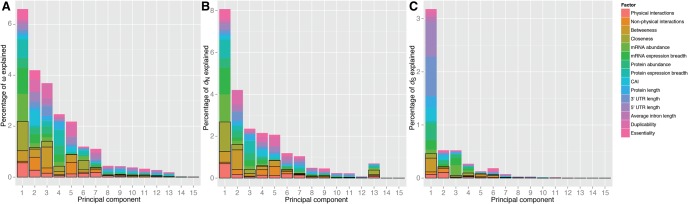
Our PCR analyses explained 23.55% of the variability of ω (fig. 4A), and 23.32% of the variability of d_N (fig. 4B). In the ω analysis, X = 7.58% for network parameters, 8.63% for expression parameters, 4.24% for compactness parameters, and 3.09% for other parameters. In the d_N analysis, X = 7.47% for network parameters, 8.70% for expression parameters, 4.22% for compactness parameters, and 2.94% for other parameters (fig. 4; supplementary table S11, Supplementary Material online). Similar results were obtained when membrane and extracellular proteins were removed from the PCR analyses (supplementary table S12, Supplementary Material online).

Fig. 4.

—Principal component regression analysis on the human signal transduction network. For each principal component (PC), the size of the bar represents the percent of the variability of the response variable explained by the PC. The composition of each component is represented in colors. Network parameters are highlighted within black boxes. This analysis was restricted to the 1,254 genes for which data were available for all variables.

It is in principle conceivable that the correlation between protein rates and evolution and network centralities is particularly strong for signaling proteins, thus biasing the results presented in this section. Indeed, in signal transduction pathways and networks, the relative importance of each protein (and as a result, its rate of evolution) may be particularly linked to its relative position within the network (e.g., Riley et al. 2003; Alvarez-Ponce et al. 2009; Alvarez-Ponce 2012; Song et al. 2012). In order to discard this possibility, we computed the ω-degree, ω-betweenness, and ω-closeness correlations in the entire protein–protein interaction network, separately for signaling proteins (n = 1397) and for the rest of the proteins (n = 12,179). No significant differences were detected between the correlations within each group (supplementary table S13, Supplementary Material online), thus allowing us to discard this possibility.

Analysis of the Drosophila melanogaster, Caenorhabditis elegans, and Saccharomyces cerevisiae Interactomes

We next performed correlation, partial correlation and PCR analyses to ascertain the determinants of rates of protein evolution in the fly Drosophila melanogaster, the worm Caenorhabditis elegans and the yeast Saccharomyces cerevisiae. For each gene, orthologs were identified in Drosophila yakuba, Caenorhabditis briggsae, or Saccharomyces paradoxus, respectively, and a d_N, d_S, as well as the ω ratio was computed. As synonymous sites are under considerable selection in these organisms (Akashi 2001; Hirsh et al. 2005), we focused our analyses on d_N rather than ω (nonetheless, analyses based on ω are presented on supplementary tables S14–S18, Supplementary Material online).

In D. melanogaster, all studied parameters exhibit a significant negative correlation with d_N, except protein length (supplementary tables S15 and S19, Supplementary Material online). The same patterns were observed in S. cerevisiae, except for the facts that protein length positively correlates with d_N and duplicability does not correlate with d_N (supplementary tables S15 and S19, Supplementary Material online). Similar observations were also made in C. elegans, except for the facts that protein length positively correlates with d_N and neither closeness nor the average intron length correlates with d_N (supplementary tables S15 and S19, Supplementary Material online).

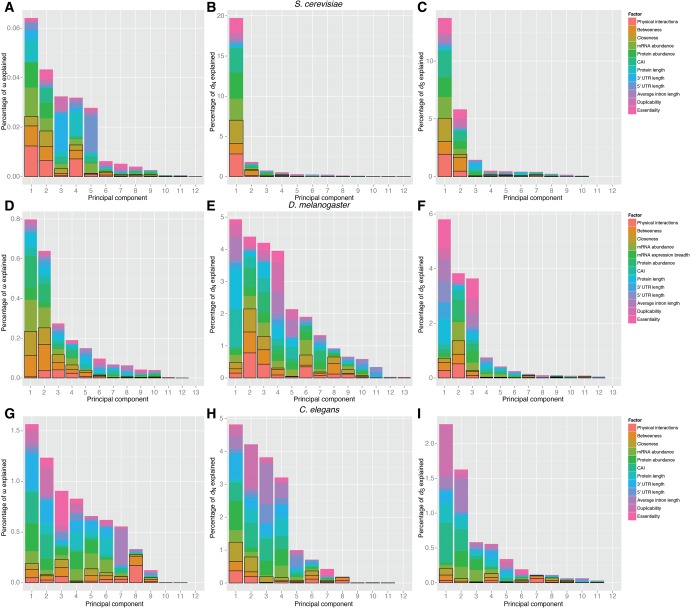
In all three species, expression parameters are better correlates of d_N than network centrality parameters (supplementary table S19, Supplementary Material online). However, our PCR analyses in all three species indicate a comparable effect of network and expression parameters on rates of protein evolution (fig. 5). For D. melanogaster, X = 6.71% for network parameters, 9.25% for expression parameters, 6.93% for compactness parameters, and 3.07% for other parameters (fig. 5; supplementary table S16, Supplementary Material online). For S. cerevisiae, X = 8.48% for network parameters, 10.27% for expression parameters, 2.07% for compactness parameters, and 3.16% for other parameters (fig. 5; supplementary table S17, Supplementary Material online). For C. elegans, X = 3.10% for network parameters, 5.74% for expression parameters, 7.21% for compactness parameters, and 2.39% for other parameters (fig. 5; supplementary table S18, Supplementary Material online). Both d_N and d_S are similarly affected by the studied factors, which might explain why our PCR analyses explain only a small fraction of the variability of ω (fig. 5).

Fig. 5.

—Principal component regression analysis on the yeast, fly, and worm protein–protein interaction networks. For each principal component (PC), the size of the bar represents the percent of the variability of the response variable explained by the PC. The composition of each component is represented in colors. Network parameters are highlighted within black boxes. PCR analyses were restricted to the genes for which data were available for all variables (2,429 for yeast, 3,880 for fly, and 608 for worm).

Discussion

We have conducted a study of the determinants of the rates of evolution of human proteins. For that purpose, we have used two protein–protein interaction network data sets: the entire set of known interactions among human proteins (Chatr-Aryamontri et al. 2015), and a data set of exceptional quality focused on signaling proteins (Cui et al. 2007). Correlation, partial correlation and PCR analyses show that measures of network centrality significantly impact rates of protein evolution, with a contribution that is comparable to that of gene expression, or even superior according to some of our analyses. We show that the impact of network position on rates of protein evolution is independent of a number of confounding factors and network biases.

The fact that similar trends have been observed in the entire network data set and in the manually curated one indicates that our results are not affected by errors and false positives in the network. It should be noted, however, that the manually curated data set (as well as the entire interactome) is expected to contain false negatives (i.e., it is incomplete), as new interactions continue to be discovered constantly. The incompleteness of the network may be still limiting our analyses. Therefore, the actual correlations between proteins’ centralities and rates of evolution are expected to be even stronger than those observed here.

Our results sharply contrast with prior observations suggesting that rates of protein evolution are dominantly determined by gene expression, and that network centrality plays only a minor role, if any (Bloom and Adami 2003; Batada et al. 2006; Drummond et al. 2006; Ingvarsson 2007; Larracuente et al. 2008). This might be due to the fact that prior results have mostly relied on rudimentary interactomic and other “-omic” data sets. Network data sets grow considerably every year (Alvarez-Ponce 2017), and technological advancements are expected to have reduced the error rates of the interactions discovered in the last years. In addition, the human interactome is, by far, the most complete (with more interactions known, followed by the yeast one (Chatr-Aryamontri et al. 2015). Therefore, the strong correlations reported here may have been due to the particularly high quality and/or completeness of the data sets used.

Our PCR analyses in S. cerevisiae and D. melanogaster reveal similar trends in these organisms, with the impact of network and expression parameters on rates of protein evolution being comparable. Therefore, our observations do not represent a peculiarity of the human interactome. Similar analyses in C. elegans suggest a stronger effect of expression parameters, and an even stronger effect of compactness parameters. It should be noted, however, that our knowledge of the C. elegans interactome is far behind that for S. cerevisiae, D. melanogaster, or human. As a result, the number of genes that could be included in our PCR analyses in C. elegans represents just a small fraction of the worm genome (only 608 genes in worm, vs. 2,429 in yeast, 3,880 in fly, and 11,593 in human), and our centrality measures are expected to be poor estimates of the actual ones.

The fraction of the variability of d_N explained by our PCR analyses (23.98% in yeast, 25.42% in fly, 18.44% in worm; fig. 5A, D, G) is in line with the results of prior multivariate analyses in plants (Ingvarsson 2007; Yang and Gaut 2011), but lower than that explained by prior PCR analyses in yeasts (Drummond et al. 2006). It should be noted, however, that the prior analyses were based on a very small fraction of the yeast genome (568 genes; Drummond et al. 2006), and that the quality of the data sets is expected to have increased dramatically in the last decade (e.g., Alvarez-Ponce 2017).

Our analysis of the signal transduction network reveals an unexpected pattern: among the network parameters considered, closeness was the best correlate of ω, followed by the number of nonphysical interactions, betweenness and the number of physical interactions (table 2). Indeed, the correlation between ω and betweenness and particularly the correlation between ω and the number of physical interactions, vanish once confounding factors are corrected for (supplementary table S6, Supplementary Material online). These observations suggest that rates of protein evolution are affected by the global position of proteins within the network, rather than by surface constraints imposed by physical protein–protein interactions. However, our results contrast with previous analyses of entire protein–protein interaction networks showing that ω correlates better with betweenness than with closeness or degree (Hahn and Kern 2005; Alvarez-Ponce and Fares 2012), and that high-betweenness proteins tend to be essential (Yu et al. 2007). A node’s betweenness is directly linked to its potential to connect parts of the network that would otherwise be isolated from each other. In the signal transduction network, where different pathways tend to cross-talk via shared elements (Zielinski et al. 2009; Levy et al. 2010), one would expect betweenness to strongly correlate with protein sequence conservation. Our PCR analysis, nonetheless, suggests a similar effect of the different measures of network centrality on the rates of protein evolution (fig. 4).

Whether or not, and to what extent, essentiality impacts rates of protein evolution has been a source of controversy, and the prevailing view is that it has a minor role (Hurst and Smith 1999; Pál et al. 2003; Drummond et al. 2006; Wang and Zhang 2009; Luisi et al. 2015) (but see Plotkin and Fraser 2007; Alvarez-Ponce et al. 2016). Our analyses, however, indicate that essentiality has a considerable impact on rates of protein evolution. For instance, our PCR analysis using ω as dependent variable shows that the first, second, and third PCs are composed, respectively, 6.18%, 0.03%, and 11.53% by essentiality. Similar results were obtained from our PCR analysis using d_N as dependent variable. Other parameters also seem to play an important role (fig. 2; supplementary table S3, Supplementary Material online).

In summary, our results contradict the prevailing view that rates of protein evolution are almost exclusively determined by gene expression. Instead, our results point out to a different scenario, in which different factors, including both gene expression and network centrality, have an independent impact on rates of protein evolution.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.