Abstract
Ecological networks, both displaying mutualistic or antagonistic interactions, seem to share common structural traits: the presence of nestedness and modularity. A variety of model approaches and hypothesis have been formulated concerning the significance and implications of these properties. In phage-bacteria bipartite infection networks, nestedness seems to be the rule in many different contexts. Modeling the coevolution of a diverse virus–host ensemble is a difficult task, given the dimensionality and multi parametric nature of a standard continuous approximation. Here, we take a different approach, by using a neutral, toy model of host–phage interactions on a spatial lattice. Each individual is represented by a bit string (a digital genome) but all strings in each class (i.e. hosts or phages) share the same sets of parameters. A matching allele model of phage-virus recognition rule is enough to generate a complex, diverse ecosystem with heterogeneous patterns of interaction and nestedness, provided that interactions take place under a spatially constrained setting. It is found that nestedness seems to be an emergent property of the co-evolutionary dynamics. Our results indicate that the enhanced diversity resulting from localized interactions strongly promotes the presence of nested infection matrices.
Keywords: nested networks, coevolution, virus–host interactions, matching allele dynamics
1. Introduction
Our biosphere is a complex adaptive system where flows of energy and matter take place within tangled ecological networks (Montoya et al. 2006). Most of these flows occur at the level of microorganisms, and microbial communities are in turn constantly coevolving with their viruses in highly dynamical ways. One dramatic illustration of the permanent arms race between bacteria and their viral partners is provided by the staggering scale of ecological interactions in marine ecosystems (Suttle 2005, 2007). It has been estimated that 1030 viruses might be present in the entire marine biota, while no less than 1023 phage infections are taking place every second. The impact on population dynamics is no less impressive: bacteriophages might kill around 20% of the total microbial biomass in a single day. This massive turnover happens in an evolutionary context: bacteria and phages constantly (and rapidly) coevolve. Such coevolutionary arms races occur in all known examples, including the gut microbiome or soil ecosystems, and provide a source of both phenotypic and genotypic diversity while affecting community structure (Koskella and Brockhurst 2014).
On a large-scale perspective, the resulting networks of interaction between phages and their host microbes display a number of interesting regularities emerging from the underlying arms race dynamics (Weitz et al. 2013). One pervasive feature of the virus–host infection networks (along with modularity) is the presence of nestedness, namely, the presence of a hierarchical pattern where (ideally) we can order both microorganisms and phages as illustrated in Fig. 1. A nested network is characterized by the tendency of low-degree species to interact with a subset of highly connected species.
Figure 1.
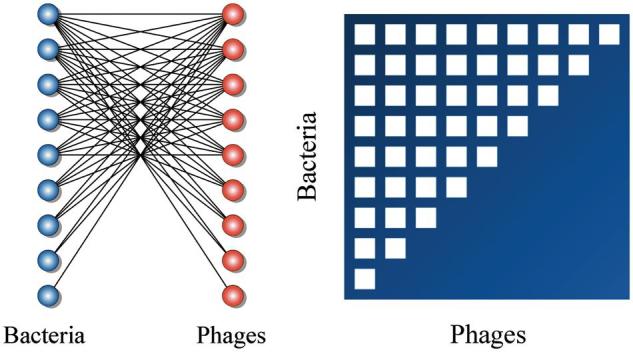
Many ecological networks are characterized by a pattern of nestedness. Our mathematical definitions of nestedness are derived from studies of bipartite networks (or two-mode) networks. A nested network displays a particular pattern of interactions that we can measure and detect. The left panel shows a bipartite network with two set of nodes. For example, one set corresponds to bacteria (blue balls) and the other corresponds to phages (red balls). Links represent interactions (infections) between pairs of dissimilar types. This bipartite network also accepts a matrix representation where rows and columns represent the two types of nodes and the entries of the matrix indicate the presence (white square) or absence (empty square) of pairwise interactions. The right panel shows an example of perfectly nested network, that is, the nonzero elements of each row in the matrix are a subset of the nonzero elements in the subsequent rows.
This type of pattern, which appears widespread in a wide array of contexts, has also been explained under rather different ways, from species-specific approaches grounded in the given community organization to abstract statistical physics models. Some of these studies support the existence of optimization principles that would pervade the nested architecture of ecological webs (Suweis et al. 2013). However, this idea has been challenged by further studies revealing that nested structures are likely to be an inevitable byproduct of other more fundamental properties of these graphs, in particular their heterogeneous character (Jonhson et al. 2013; Feng and Takemoto 2014). What is the origin of nested webs in antagonistic systems?
The nested pattern found in phage-bacteria infection networks has been hypothesized to result from a coevolutionary sequence of adaptations driven by gene-for-gene recognition processes (Flor 1956; Thompson and Burdon 1992; Agrawal and Lively 2002; Weitz et al. 2013). In a dynamic gene-for-gene coevolutionary sequence, new mutations arising in the bacterial genome confer resistance to concurrent phages, while maintaining resistance to phages that were abundant in the past. Likewise, mutations in the concurrent phages result in their ability to infect these newly arose bacterial genotypes while still being able of infecting past bacterial genotypes (Bohannan and Lenski 2000). This process results in bacterial genotypes that are resistant to a subset of all possible phages and phages able of infecting a subset of all bacterial genotypes. In other words, the most infectious phage has access to most bacterial genotypes while the second most infectious phage has only access to a subset of these bacterial genotypes.
From the bacterial perspective, the most resistant bacteria can be only infected by a limited number of phages (usually the most infectious one) while the second most resistant bacteria can be infected a larger number of phages (Fig. 1). According to the gene-for-gene coevolutionary dynamics, fitness costs may appear to limit the phages to broader their host range without limits; bacteria also suffer of fitness costs that limit their capacity to resist all possible phages (Jover et al. 2013, 2015; Ashby and Boots 2017). The gene-for-gene model produces a wide variety of evolutionary outcomes that include stable genetic polymorphisms either within a range of infectivity or defense (Segarra 2005) or across multiple ranges provided direct frequency-dependent selection is on operation (Tellier and Brown 2007), and fluctuating selection between narrow- and broad-range specialists and generalists (Agrawal and Lively 2003).
A popular alternative to the gene-for-gene model is the matching allele model (Agrawal and Lively 2003; Weitz et al. 2013). In this model, bacteria evolve resistance to a single phage genotype and lose resistance to other phages. Likewise, mutations in phage genomes confer the ability to infect new evolved bacterial genotypes while losing the capacity to infect ancestral bacterial genotypes. Henceforth, bacteria attempt to avoid the most common phage while phages seek to match the most common host (Frank 1993). The indirect negative frequency-dependent selection created by the matching allele model leads to fluctuating selection between equally highly specific genotypes. This high specificity between bacterial host and the viruses that can infect them translates into a modular structure in the phage-bacteria infection networks (Weitz et al. 2013). In the extreme case of a one-to-one matching between bacteria and phages, the resulting infection network is call monogamous (Korytowski and Smith 2015).
Most empirical evidences support the idea that variation in hosts and parasites degrees of specialization is in general good agreement with the expectations from the gene-for-gene model. This includes evolution experiments (Bohannan and Lenski 2000; Flores et al. 2011), plants and diverse plant pathogens (Flor 1956; Thompson and Burdon 1992; Hillung et al. 2014), fruit flies and the sigma virus (Bangham et al. 2007), and fishes (Vazquez et al. 2005; Mouillot et al. 2008). Modular infection networks have been also described at higher taxonomic levels, yet with a nested structure within each module (Flores et al. 2013; Roux et al. 2015).
In this paper, we present a neutral model of bacteria–phage interaction that provides a minimal framework to address the problem of what are the requirements for evolving a nested infection network structure. Although other models have been formulated to that goal (Beckett and Williams 2013; Jover et al. 2013; Haerter et al. 2014; Jover et al. 2015; Korytowski and Smith 2015) they rely on a large number of parameters and required some special assumptions concerning the shape of interaction functions. Here we have assumed the smallest amount of complexity by using a quasi-neutral model of bacteria–phage interactions that can account for the emergence of nested webs.
2. Neutral coevolution model
In this section, we define our digital model of host-phage coevolution (all results published in this article are available upon request). Instead of using a model where a diverse repertoire of parameters is associated with each potential phenotype (resulting from a predefined genotype–phenotype mapping) we take the most simplifying assumption, namely, a fully neutral system where all interactions within each species class in a bipartite network have exactly the same weights, irrespective of the underlying digital genomes involved. In the spirit of other theoretical and modeling approaches (Alonso et al. 2006) the species-level idiosyncrasies are ignored in favor of an higher-level of description. By using this toy model approach, we hope to gather insight into the network-level universals.
The model considers two populations of replicators, namely, phages and bacteria, each represented as a ν-dimensional string. Specifically, we indicate as and , respectively the digital genomes (bit strings) associated to the i-th and j-th phage and bacteria genotypes. In other words, we have the strings given by the bit sequences:
| (1) |
| (2) |
with where . Both populations reproduce and evolve on a two-dimensional space where dynamics takes place on the faces of a cube, thus defining a lattice with periodic conditions. By using the appropriate geometric transformation (Tegmark 1996) the resulting dynamics can be displayed on the surface of a sphere, as done here. In Fig. 2, we display the structure of the coupled interaction between phages and bacteria, which will interact under a genome matching rule, defined below. As defined, the resulting matrix of (potential) interactions is a square one. This is of course a limitation of our approach, since it does not take into account the asymmetries resulting from different numbers of species in the bipartite graph. Future extensions of our model should consider these more general cases.
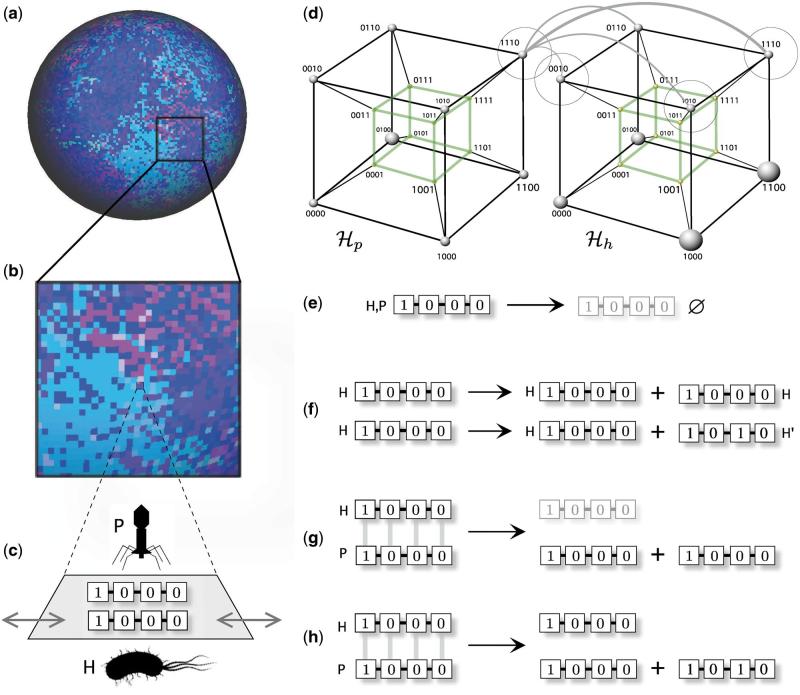
Figure 2.
Coevolution in coupled landscapes associated to a phage-bacteria model based on a digital genomes representation. Each individual is described by means of a digital genome of length ν. The model dynamics is defined on a two-dimensional surface (a) where the color of each site indicates (in this case) the presence of different strings. In (b), an expanded area shows the presence of local patchiness where each site (c) can be occupied by one string of each class. Strings can move randomly to neighboring free sites, as indicated by the grey arrows. From the point of view of the genotype space, we have two coupled sequence hypercubes (here ν = 4) where similarity between phage and bacteria recognition sequences (i.e. the matching allele model or recognition, determines the probability of interaction. Two different hypercubes are shown, one for phages (left) and another (right) for bacteria. One given virus (like 1110) will be able to interact with those bacteria whose genome is closer (the probability of this interaction is indicated by weighted gray lines). The basic rules used in the model are summarized in (e–h). These are: (e) sequence removal (death), (f) replication of host string, which can be accurate H → 2H or inaccurate , for the phage–bacteria interaction.
The model is intended to define a minimal setting of rules including a random death of strings at a given rate, which can be represented as decay reactions, namely,
| (3) |
independent on their specific genome sequence. The bacterial strains are assumed to replicate leading to two identical copies with a probability that depends on the mutation rate, namely,
| (4) |
where is the probability that all the bits are properly copied (no mistakes occur). Any mutation in at least one bit in the string will lead to a different sequence, namely,
| (5) |
where will be usually a one-mutation neighbor in sequence space (provided that mutation rates are small enough) but in general the probability associated to a mutation from to will be
being the Hamming distance between two sequences:
| (6) |
The reproduction of the phage requires the infection of a bacterial cell provided that a genome matching occurs. If the matching is perfect (and thus dH = 0) we assume that the interaction occurs with probability , but if the probability will decay linearly with the Hamming distance (since recognition and matching are less accurate):
| (7) |
Specifically, two strings belonging to a phage and a host will lead to an error-free reaction:
| (8) |
and the alternative scenario with a mutated offspring:
| (9) |
where the term is defined as before.
The final set of rules involves the spatial dynamics of strings on the lattice. Each site in this lattice can be occupied by one string of each class. Host and parasite strings move, independently and randomly, to empty neighbor cells with diffusion probabilities Dh and Dp, respectively. To simplify the analysis, all the simulations were run with maximum diffusion constants , also setting . In this way, we strongly reduce the parameter space, considering the diffusion and decay properties of all strings identical, no matter their precise sequence. This class of models has been shown to display a fluctuating dynamics on a broad range of parameter combinations (Solé and Sardanyes, 2014) resulting from the intrinsic nonlinearities associated to the Red Queen dynamical behavior. As a consequence, fluctuations in both space and time are expected to occur.
The rest of the parameters have been chosen as follows. The mutation rate of the virus must be larger than the one exhibited by the host. Here we use a mutation rate of μ = 10–4 for the phage and μ = 10–5 for the bacteria. Other parameters have been used (avoiding very high rates that can lead to an error catastrophe) and similar results of those reported here have been found. Finally, the replication parameter r of the host strings is fixed to r = 0.8. An important point to be made here is that our genome-independent parameters made our model a highly homogeneous one, that is an effectively neutral model, except for the functional dependence associated to the matching rule. The lattice was randomly inoculated by either bacteria and phage random sequences, starting from an initial condition were 25% of sites are randomly seeded by phages and the same amount (but different random sites) for the bacteria. All initial strings are identical, defined by the sequence 1000. As we can see from this model description, the whole dynamics will lead (if both populations are present and parameters allows) to an arms race that is limited to a constant movements through the sequence hypercube.
3. Spatial dynamics and the emergence of bacteriaphage bipartite nested networks
The degree of interaction among species is not randomly distributed and captures different ecological and evolutionary factors. Disentangling these components requires a combination of empirical measurements and of theoretical models (see below). How do ecological, genetics, and epidemiological processes interact to generate and maintain structural variation? What is the general structure of bacteria–virus infection networks? Empirical and theoretical studies have shown that bipartite networks can be (i) nested, that is, the interactions between nodes can be represented as subsets of each other (Flores et al. 2011), (ii) modular, that is a network composed of densely connected groups of nodes, and (iii) multi-scale, that is, the network shows different features depending on whether the whole or smaller components are under consideration (Flores et al. 2013). In this study, we are particularly interested in how the spatial component influences the emergence of nestedness (see next section).
An infection network involves two disjoint subsets of species, that is, bacterial hosts and viruses. Any pair of species is always related provided that pathogen j can infect host i. The set of links of this network can be described with the (binary) adjacency matrix A = [Aij] in which Aij = 1 (presence) if the nodes i and j are connected or Aij = 0 (absence), otherwise. The degree of a species
is the number of connections attached to this node. Now, assume that hosts are indexed 1,2,.,NH and viruses are labeled where NH is the number of bacterial species, NVis the number of virus species, and is the total number of species in our system. Using this vertex labeling approach, we can show the adjacency matrix has a block off-diagonal form as follows:
| (10) |
where B is the incidence matrix, 0 is the all-zero matrix that reflects the bipartite constraint, that is, we only allow interactions between alike species.
Reliable nestedness measurement takes into account the strength of infections in the bipartite network. For example, previous studies have shown that ubiquitous nestedness of binary adjacency matrices (Flores et al. 2011) is not always reproduced by quantitative studies (Staniczenko et al. 2013). The entries of a quantitative incidence matrix B take values different from 1 or 0, like the number of infected individuals. In both the binary and quantitative cases, an incidence matrix is perfectly nested when its rows and columns can be sorted such that
with and for all and , that is, the set of edges in each row i contains all the edges in row i + 1 while the set of edges in column j contains the set of edges in column j + 1.
The above suggests a costly approach to the maximal nestedness that searches for the optimal arrangement of matrix elements (Atmar and Patterson, 1993). This algorithm has several computational disadvantages and it is, in fact, the basis for many published methods. Different metrics extend the analysis of nestedness to quantitative species preferences. This recognizes the fact that nestedness is a relative value that depends both on the size and the density of interactions. For example, we can define weighted versions of nestedness based on common neighbors (CMNB) (Bastolla et al. 2009), overlap and decreasing fill (WNODF) (Almeida-Neto and Ulrich 2011), and weighted-interaction nestedness estimator (WINE) (Galeano et al. 2009). Here, we use the metric proposed by Allesina and co-workers, which is quantitative measure of nestedness based on the spectral properties of bipartite networks (Staniczenko et al. 2013). The spectral radius ρ(B) (or the dominant eigenvalue) gives a natural scale for nestedness, with higher spectral radius corresponding to more nested configurations. The spectral radius of the incidence matrix has two useful properties: (i) matrix eigenvalues are independent of arbitrary permutations of rows and columns and (ii) this quantity can be derived for both binary and quantitative infection networks.
We now investigate the temporal evolution of nestedness in our model. In our model, the number of species N it is bounded by the fixed genome lengths. On the other hand, link density is a key parameter defined by the network connectance C, or the proportion of possible network connections, that is , where the number of links K is simply . It has been proposed that the stability of dynamical processes constraints the possible values of connectance (May 1972). In our computational simulations, we have observed that connectance reaches an average value C ≈ 0.45 (Fig. 3). A detailed analysis of interactions reveals a highly dynamical system where connections among species are constantly added or removed while keeping the same average connectance.
Figure 3.
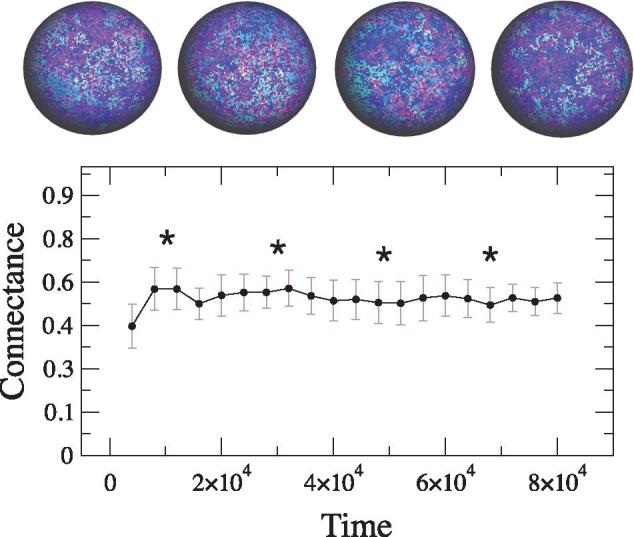
Temporal dynamics of connectance in a typical run of the model. The connectance stabilizes around a well-defined average value C ≈ 0.45. This density of links allows for a high diversity of possible system configurations. From left to right, the snapshots (whose location is pointed with stars in the curve) display an evolving pattern of spatial heterogeneity. Here, we use the same parameters described in the main text.
In general, there is a contribution to the growth of population i from interactions with other species in the system , where xi is the population density of individual species (Staniczenko et al. 2013). We can further divide the interaction between any pair of species (i, j) in two components: the frequency of interactions and the effect of each interaction . Then,
| (11) |
where xixj is a mass action term γi,j indicates the relative probability of interaction compared to mass action. Assuming the mass action hypothesis, the expected number of interactions is proportional to the product of the densities xi and xj of the pair of species. Other factors like the spatial component, consumer search efficiency, or handling time are aggregated in the preference matrix . This matrix measures pairwise interaction preferences: indicates the interaction is more likely to occur than expected, denotes a less favorable interaction and γi,j = 1 is exactly the expectation based on mass action.
When measuring nestedness in our system, we first adjust for the mass action effect (xixj) to isolate interaction preferences. The incidence matrix B is related to the preference matrix by the following: . We compare the nestedness value in the preference matrix with an ensemble of random matrices having similar properties (Beckett and Williams 2013; Weitz et al. 2013). We use the null model proposed by (Staniczenko et al. 2013), which keeps the structural features of the network while swapping the order of weighted links (so-called ‘binary shuffle’) across the binary structure. Among the possible set of null models, this is the adequate when evaluating the statistical significance of weighted nestedness. Specifically, the Z-score defines the statistical significance:
| (12) |
where and are the average value and the standard deviation of the network measure in a random ensemble, respectively. In this study, we will consider that host–phage interactions are significantly nested whenever the corresponding Z > 2 (i.e. P < 0.05 using the Z-test).
Figure 4 shows the statistical significance of nestedness in the γ-matrix tends to a high, well-defined value. In the absence of space, the same model does not tend to a pattern of significant nestedness (Fig. 5). Interestingly, the average connectance is also close to the reported value for the spatial simulation (C ≈ 0.45), and thus suggesting that nestedness is largely a consequence of spatial correlations associated to (transient) similarities between spatially close genomes. This result is consistent with empirical studies of fish-parasite networks suggesting a spatial origin of nestedness (Poulin and Guégan 2000). The main difference is that our model is neutral, that is, it does not consider any of the selection pressures that have influenced the evolution of real fish-parasite networks.
Figure 4.
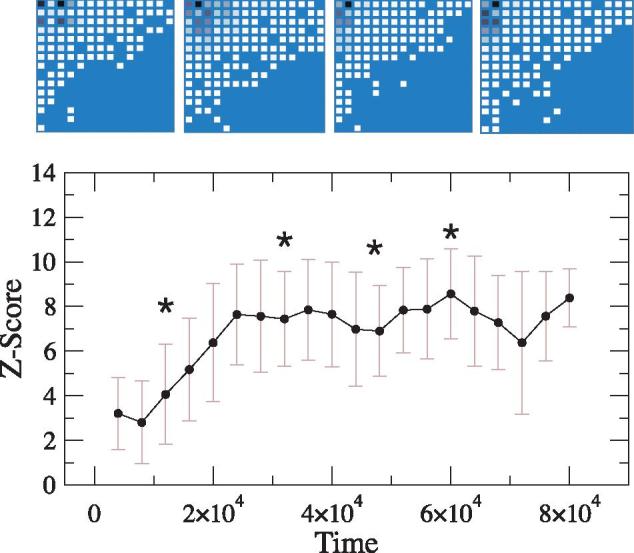
Temporal dynamics of the statistical significance of nestedness. After an initial transient period, the global organization of the γ-matrix settles in stable nested patterns (the average Z ≈ 5). The top row shows several snapshots of the bacteria–phage interaction network taken at different evolutionary stages (whose location is given by stars in the curve). Both the binary structure and the quantitative preference matrix are significantly nested. The matrix at time t has been obtained by first counting the frequency of interactions Bi,j observed in the time period [t– Δt,t] (here Δt = 2000 time steps) and then discarding the mass action term (xixj). In each matrix, darker colors represent higher interaction preferences. Tests for nestedness are based in the null model described in the main text.
Figure 5.
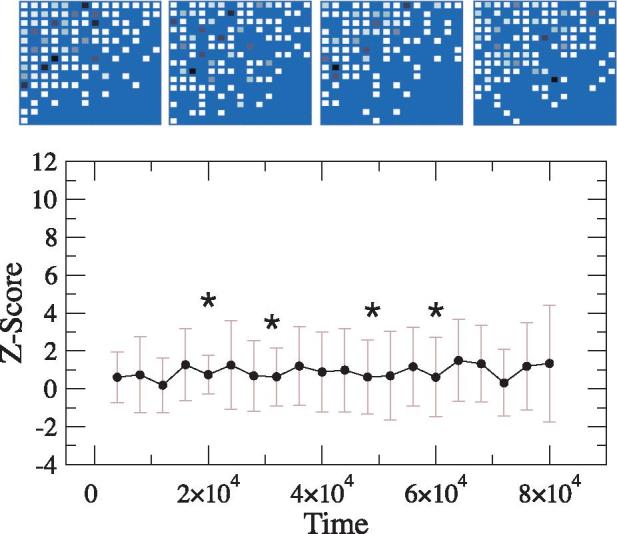
In the absence of space, the model does not tend to a pattern of significant nestedness (the average Z ≈ 0). The top row shows several snapshots of the host–phage interaction network taken at different evolutionary stages (whose location is given by stars in the curve). The binary structure of these matrices is nested but the quantitative preferences are found to be distributed in an anti-nested manner. The matrix at time t has been obtained by aggregating the interactions observed in the time period [t– Δt,t] (here Δt = 2000 time steps). In each matrix, darker colors represent higher preference of interactions. Tests for nestedness are based in the null model described in the main text.
4. Discussion
Host–virus ecological networks are characterized (among other things) by the presence of a nested organization. Since nestedness has been proposed as a key attribute with a relevant role in community stability and diversity, it is especially important to understand its origins. Previous work using available host–phage networks has shown that nestedness appears to be a very common trait in most cases. What is less obvious is to determine the causal origins of this particular feature. A specially elegant piece of work in this context is the study by (Beckett and Williams 2013) on the coevolutionary diversification of bacteria and phage using a lock-and-key model. In their analysis, these authors explored the origins of both nestedness and modularity using a multi-strain chemostat system where the coevolving strains use a single resource. Genotypes were represented by means of a single scalar value, thus lacking our genotype space described by an explicit sequence hypercube. Importantly, the genetic matching was mediated by predefined functional correlations between ‘genotype distance’ and key traits such as adsorption rates of phages on hosts.
In our analysis, we have followed a rather different direction, by introducing a coevolution process where the specific choices of parameters (allowing populations to persist) is not relevant, genotypes are introduced in an explicit way and phenotypes are the same (as described by the kinetic parameters) for all genomes. What is the connection between spatially limited interactions and the enhanced presence of nested structures? In our study, the limited interactions among digital genomes associated to the presence of space play a key role in enhancing correlations and nestedness. We should expect that digital host genomes in a given neighborhood will also be relatively close among them through recent mutation events (in terms of Hamming distance) and exhibit closer ties with their parasites, which will also appear locally correlated. This necessarily helps enforcing the kind of correlations expected for nested graphs. The multiplicative nature of the arms race process necessarily creates spatial correlations that pervade nestedness. The most common string will also be more likely to be the target of a large number of close digital genomes, thus exhibiting a large number of links. Those nearest mutants will have less edges (given their smaller populations) but they are likely to be a subset of the most abundant string. This relationship can be extended to all levels in the cloud of digital genomes, and ultimately explains the observed pattern (a theoretical model will be presented elsewhere).
Despite its limitations, it is remarkable that such a simple set of assumptions recovers the nested organization of these antagonistic systems. As it occurs with other relevant properties, spatial dynamics makes a difference when explicitly included in the description of ecosystem interactions. The loss of nestedness when global mixing is allowed clearly supports our conjecture. Future work should consider different extensions of our model, including spatial heterogeneity (which could lead to modularity) or theoretical developments that might help determine the validity and implications of our neutral approximation. In particular, mean field models using homogeneous parameter sets (and thus effectively neutral couplings) should be studied. Since continuous models implicitly consider very large populations, the potential effects of fluctuations associated to our discrete and finite system could be analyzed.
Acknowledgements
The authors would like to thank the members of the Complex Systems Lab and our colleagues at the Santa Fe Institute for fruitful discussions. This work has been supported by the Botin Foundation by Banco Santander through its Santander Universities Global Division. This work was supported by the grants BFU2015-65037-P (S.F.E.) and FIS2016-77447-R (S.V.) from Spain Ministerio de Economía, Industria y Competitividad, AEI/MINEICO/FEDER and UE. The authors also thank the Santa Fe Institute, where most of this work was done.
Conflict of interest: None declared.
References
- Agrawal A. F., Lively C. M. (2002) ‘Modelling Infection as a Two-Step Process Combining Gene-for-Gene Matching-Allele Genetics’, Proceedings of the Royal Society of London B, 270: 323–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almeida-Neto M., Ulrich W. (2011) ‘A Straightforward Computational Approach for Measuring Nestedness Using Quantitative Matrices’, Environmental Modelling & Software, 26: 173–8. [Google Scholar]
- Alonso D., Etienne R. S., McKane A. J. (2006) ‘The Merits of Neutral Theory’, Trends in Ecology & Evolution, 21: 451–7. [DOI] [PubMed] [Google Scholar]
- Ashby B., Boots M. (2017) ‘Multi-Mode Fluctuating Selection in Host-Parasite Coevolution’, Ecological Letters, 20: 357–65. [DOI] [PubMed] [Google Scholar]
- Atmar W., Patterson B.D. (1993) ‘The measure of order and disorder in the distribution of species in fragmented habitat’, Oecologia, 96: 373–82. [DOI] [PubMed] [Google Scholar]
- Bangham J. et al. (2007) ‘The Age and Evolution of an Antiviral Resistance Mutation in Drosophila melanogaster’, Proceedings of the Royal Society of London B, 274: 2027–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastolla U. et al. (2009) ‘The Architecture of Mutualistic Networks Minimizes Competition and Increases Biodiversity’, Nature, 458: 1018–20. [DOI] [PubMed] [Google Scholar]
- Beckett S. J., Williams H. T. (2013) ‘Coevolutionary Diversification Creates Nested-Modular Structure in Phage-Bacteria Interaction Networks’, Interface Focus, 3/6: 20130033.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohannan B. J. M., Lenski R. E. (2000) ‘Linking Genetic Change to Community Evolution: Insights from Studies of Bacteria and Bacteriophage’, Ecological Letters, 3: 362–77. [Google Scholar]
- Feng W., Takemoto K. (2014) ‘Heterogeneity in Ecological Mutualistic Networks Dominantly Determines Community Stability’, Scientific Reports, 4: 5219.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flor H. H. (1956) ‘The Complementary Genetic Systems in Flax and Flax Rust’, Advances in Genetics, 8: 29–54. [Google Scholar]
- Flores C. O. et al. (2011) ‘Statistical Structure of Host-Phage Interactions’, Proceedings of the National Academy of Sciences of the United States of America, 108: E288–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flores C. O., Valverde S., Weitz J. S. (2013) ‘Multi-Scale Structure and Geographic Drivers of Cross-Infection Within Marine Bacteria And Phages’, The ISME Journal, 7: 520–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank S. A. (1993) ‘Specific Versus Detectable Polymorphism in Host-Parasite Genetics’, Proceedings of the Royal. Society of London B, 254: 191–7. [DOI] [PubMed] [Google Scholar]
- Galeano J., Pastor J. M., Iriondo J. M. (2009) ‘Weighted-Interaction Nestedness Estimator (WINE): A New Estimator to Calculate Over Frequency Matrices’, Environmental Modelling & Software, 24: 1342–6. [Google Scholar]
- Haerter J. O., Mitarai N., Sneppen K. (2014) ‘Phage and Bacteria Support Mutual Diversity in a Narrowing Staircase of Coexistence’, The ISME Journal, 8: 2317–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillung J. et al. (2014) ‘Experimental Evolution of an Emerging Plant Virus in Host Genotypes that Differ in their Susceptibility to Infection’, Evolution, 68: 2467–80. [DOI] [PubMed] [Google Scholar]
- Jonhson S., Dominguez-Garcia V., Munoz M. A. (2013) ‘Factors Determining Nestedness in Complex Networks’, PLos One, 8: e70452.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jover L. F., Cortez M. H., Weitz J. S. (2013) ‘Mechanisms of Multi-Strain Coexistence in Host-Phage Systems with Nested Infection Networks’, Journal of Theoretical Biology, 332: 65–77. [DOI] [PubMed] [Google Scholar]
- Jover L. F. et al. (2015) ‘Multiple Regimes of Robust Patterns Between Network Structure and Biodiversity’, Scientific Reports, 5: 17856.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korytowski D. A., Smith H. L. (2015) ‘How Nested and Monogamous Infection Networks in Host-Phage Communities Come To Be’, Theoretical Ecology, 8: 111–20. [Google Scholar]
- Koskella B., Brockhurst M. A. (2014) ‘Bacteria-Phage Coevolution as a Driver of Ecological and Evolutionary Processes in Microbial Communities’, FEMS Microbiology Reviews, 38: 916–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May R. M. (1972) ‘Will a Large Complex System Be Stable?’, Nature, 238: 413–4. [DOI] [PubMed] [Google Scholar]
- Montoya J. M., Pimm S., Solé R. (2006) ‘Ecological Networks and Their Fragility’, Nature, 442: 259–64. [DOI] [PubMed] [Google Scholar]
- Mouillot D., Krasnov B. R., Poulin R. (2008) ‘High Intervality Explained by Phylogenetic Constraints in Host-Parasite Webs’, Ecology, 89: 2043–51. [DOI] [PubMed] [Google Scholar]
- Poulin R., Guégan J. F. (2000) ‘Nestedness, Anti-Nestedness, and the Relationship Between Prevalence and Intensity in Ectoparasite Assemblages of Marine Fish: A Spatial Model of Species Coexistence’, International Journal of Parasitology, 30: 1147–52. [DOI] [PubMed] [Google Scholar]
- Roux S. et al. (2015) ‘Viral Dark Matter and Virus-Host Interactions Resolved from Publicly Available Microbial Genomes’, eLife, 4: e08490.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segarra J. (2005) ‘Stable Polymorphisms in a Two-Locus Gene-for-Gene System’, Proceedings of the Royal Society of London B, 267: 728–36. [DOI] [PubMed] [Google Scholar]
- Solé R. V., Sardanyes J. (2014). Red Queen Coevolution on Fitness Landscapes In: Recent Advances in the Theory and Application of Fitness Landscapes (pp. 301—38). Berlin Heidelberg: Springer. [Google Scholar]
- Staniczenko P. P., Kopp J. C., Allesina S. (2013) ‘The Ghost of Nestedness in Ecological Networks’, Nature Communications, 4: 1391.. [DOI] [PubMed] [Google Scholar]
- Suttle C. A. (2005) ‘Viruses in the Sea’, Nature, 437: 356–61. [DOI] [PubMed] [Google Scholar]
- Suttle C. A. (2007) ‘Marine Viruses: Major Players in the Global Ecosystem’, Nature Reviews Microbiology, 5: 801–12. [DOI] [PubMed] [Google Scholar]
- Suweis S. et al. (2013) ‘Emergence of Structural and Dynamical Properties of Ecological Mutualistic Networks’, Nature, 500: 449–52. [DOI] [PubMed] [Google Scholar]
- Tegmark M. (1996) ‘An Icosahedron-Based Method for Pixelizing the Celestial Sphere’, Astrophysics Journal, 470: L81–4. [Google Scholar]
- Tellier A., Brown K. M. J. (2007) ‘Stability of Genetic Polymorphisms in Host-Parasite Interactions’, Proceedings of the Royal Society of London B, 274: 809–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson J. N., Burdon J. J. (1992) ‘Gene-for-Gene Coevolution Between Plants and Parasites’, Nature, 360: 121–5. [Google Scholar]
- Vazquez D. P. et al. (2005) ‘Species Abundance and the Distribution of Specialization in Host-Parasite Interaction Networks’, Journal of Animal Ecology, 74: 946–55. [Google Scholar]
- Weitz J. S. et al. (2013) ‘Phage-Bacteria Infection Networks’, Trends in Microbiology, 21: 82–91. [DOI] [PubMed] [Google Scholar]