Comparative Study With New Accuracy Metrics for Target Volume Contouring in PET Image Guided Radiation Therapy

Abstract

The impact of positron emission tomography (PET) on radiation therapy is held back by poor methods of defining functional volumes of interest. Many new software tools are being proposed for contouring target volumes but the different approaches are not adequately compared and their accuracy is poorly evaluated due to the ill-definition of ground truth. This paper compares the largest cohort to date of established, emerging and proposed PET contouring methods, in terms of accuracy and variability. We emphasize spatial accuracy and present a new metric that addresses the lack of unique ground truth. Thirty methods are used at 13 different institutions to contour functional volumes of interest in clinical PET/CT and a custom-built PET phantom representing typical problems in image guided radiotherapy. Contouring methods are grouped according to algorithmic type, level of interactivity and how they exploit structural information in hybrid images. Experiments reveal benefits of high levels of user interaction, as well as simultaneous visualization of CT images and PET gradients to guide interactive procedures. Method-wise evaluation identifies the danger of over-automation and the value of prior knowledge built into an algorithm.

SECTION I. Introduction

Positron emission tomography (PET) with the metabolic tracer ¹⁸F-FDG is in routine use for cancer diagnosis and treatment planning. Target volume contouring for PET image-guided radiotherapy has received much attention in recent years, driven by the combination of PET with computed tomography (CT) for treatment planning [1], unprecedented accuracy of intensity modulated radiation therapy (IMRT) [2], and ongoing debates [3], [4] over the ability of the standardized uptake value (SUV) to define functional volumes of interest (VOIs) by simple thresholding. Many new methods are still threshold-based, but either automate the choice of SUV threshold specific to an image [5], [6] or apply thresholds to a combination (e.g., ratio) of SUV and an image-specific background value [7], [8]. More segmentation algorithms are entering PET oncology from the field of computer vision [9] including the use of image gradients [10], deformable contour models [11], [12], mutual information in hybrid images [13], [14], and histogram mixture models for heterogeneous regions [15], [16]. The explosion of new PET contouring algorithms calls for constraint in order to steer research in the right direction and avoid so-called yapetism (yet another PET image segmentation method) [17]. for this purpose, we identify different approaches and compare their performance.

Previous works to compare contouring methods in PET oncology [18]–[19][20] do not reflect the wide range of proposed and potential algorithms and fall short of measuring spatial accuracy. Nestle et al. [18] compare three threshold-based methods used on PET images of non-small cell lung cancer in terms of the absolute volume of the VOIs, ignoring spatial accuracy of the VOI surface that is important to treatment planning. Greco et al. [19] compare one manual and three threshold-based segmentation schemes performed on PET images of head-and-neck cancer. This comparison also ignores spatial accuracy, being based on absolute volume of the VOI obtained by manual delineation of complementary CT and magnetic resonance imaging (MRI). Vees et al. [20] compare one manual, four threshold-based, one gradient-based and one region-growing method in segmenting PET gliomas and introduce spatial accuracy, measured by volumetric overlap with respect to manual segmentation of complimentary MRI. However, a single manual segmentation can not be considered the unique truth as manual delineation is prone to variability [21], [22].

Outside PET oncology, the society for Medical Image Computing and Computer Assisted Intervention (MICCAI) has run a “challenge” in recent years to compare emerging methods in a range of application areas. Each challenge takes the form of a double-blind experiment, whereby different methods are applied by their developers on common test-data and the results analyzed together objectively. In 2008, two examples of pathological segmentation involved multiple sclerosis lesions in MRI [23] and liver tumors in CT [24]. These tests involved 9 and 10 segmentation algorithms respectively, and evaluated their accuracy using a combination of the Dice similarity coefficient [25] and Hausdorff distance [26] with respect to a single manual delineation of each VOI. in 2009 and 2010, the challenges were to segment the prostate in MRI [27] and parotid in CT [28]. These compared 2 and 10 segmentation methods respectively, each using a combination of various overlap and distance measures to evaluate accuracy with respect to a single manual ground truth per VOI. The MICCAI challenges have had a major impact on segmentation research in their respective application areas, but this type of large-scale, double-blind study has not previously been applied to PET target volume delineation for therapeutic radiation oncology, and the examples above are limited by their dependence upon a single manual delineation to define ground truth of each VOI.

This paper reports on the design and results of a large-scale, multi-center, double-blind experiment to compare the accuracy of 30 established and emerging methods of VOI contouring in PET oncology. The study uses a new, probabilistic accuracy metric [29] that removes the assumption of unique ground truth, along with standard metrics of Dice similarity coefficient, Hausdorff distance and composite metrics. We use both a new tumor phantom [29] and patient images of head-and-neck cancer imaged by hybrid PET/CT. Experiments first validate the new tumor phantom and accuracy metric, then compare conceptual approaches to PET contouring by grouping methods according to how they exploit CT information in hybrid images, the level of user interaction and 10 distinct algorithm types. This grouping leads to conclusions about general approaches to segmentation, also relevant to other tools not tested here. Regarding the role of CT, conflicting reports in the literature further motivate the present experiments: while some authors found that PET tumor discrimination improves when incorporating CT visually [30] or numerically [31], others report on the detrimental effect of visualizing CT on accuracy [32] and inter/intra-observer variability [21], [22]. Further experiments directly evaluate each method in terms of accuracy and, where available, inter−/intra operator variability. Due to the large number of contouring methods, full details of their individual accuracies and all statistically significant differences are provided in the supplementary material and summarized in this paper.

The rest of this paper is organized as follows. Section II describes all contouring algorithms and their groupings. Section III presents the new accuracy metric and describes phantom and patient images and VOIs. Experiments in Section IV evaluate the phantom and accuracy metric and compare segmentation methods as grouped and individually. Section V discusses specific findings about manual practices and the types of automation and prior knowledge built into contouring and Section VI gives conclusions and recommendations for future research in PET-based contouring methodology for image-guided radiation therapy.

SECTION II. Contouring Methods

Thirteen contouring “teams” took part in the experiment. We identify 30 distinct “methods,” where each is a unique combination of team and algorithm. Table I presents the methods along with labels (first column) used to identify them hereafter. Some teams used more than one contouring algorithm and some well-established algorithms such as thresholding were used by more than one team, with different definitions of the quantity and its threshold. Methods are grouped according to algorithm type and distinguished by their level of dependence upon the user (Section II-B) and CT data (Section II-C) in the case of patient images. Contouring by methods MD^b, RG^b, and RG^c was repeated by two users in the respective teams, denoted by subscripts 1 and 2, and the corresponding segmentations are treated separately in our experiments.

Table I.

The 30 Contouring Methods and Their Attributes

method	team	type	interactivity					CT use
			max	high	mid	low	none	high	low	none
PLa	01	PL					▲			■
WSa	02	WS				▲				■
PLb	03	PL			▲				■
PLc					▲				■
PLd					▲				■
T2a		T2					▲			■
MDa	04	MD	▲							■
T4a		T4				▲				■
T4b						▲				■
T4c						▲				■
MDb 1,2	05	MD	▲							■
RGa		RG		▲						■
HB	06	HB				▲		■
WSb	07	WS				▲				■
T1a	08	T1				▲				■
T1b						▲				■
T2b		T2				▲				■
T2c						▲				■
RGb 1,2	09	RG		▲					■
RGc 1,2					▲					■
PLe	10	PL					▲			■
PLf						▲				■
GR	11	GR			▲					■
MDc	12	MD	▲						■
T1c		T1					▲			■
T3a		T3				▲				■
T3b						▲				■
T2d		T2					▲			■
T2e					▲					■
PLg	13	PL					▲			■

Some of the methods are well known for PET segmentation while others are recently proposed. Of the recently proposed methods, some were developed specifically for PET segmentation (e.g., GR,T2^d, and PL^g) while some were adapted and optimized for PET tumor contouring for the purpose of this study. The study actively sought new methods, developed or newly adapted for PET tumors, as their strengths and weaknesses will inform current research that aims to refine or replace state of the art tools, whether those tools are included here or not. Many of the algorithms considered operate on standardized uptake values (SUVs), whereby PET voxel intensity I is rescaled as SUV=I×(β/α_in) to standardize with respect to initial activity α_in of the tracer in Bq ml⁻¹ and patient mass β in grams [33]. The SUV transformation only affects segmentation by fixed thresholding while methods that normalize with respect to a reference value in the image or apply thresholds at a percentage of the maximum value are invariant to the SUV transformation.

A. Method Types and Descriptions

Manual delineation methods (MD) use a computer mouse to delineate a VOI slice-by-slice, and differ by the modes of visualization such as overlaying structural or gradient images and intensity windowing. MD^a is performed by a board certified radiation oncologist and nuclear medicine physician, who has over a decade of research and clinical experience in PET-based radiotherapy planning. MD^b is performed by two independent, experienced physicians viewing only PET image data. for each dataset, the grey-value window and level were manually adjusted. MD^c performed on the PET images by a nuclear medicine physicist who used visual aids derived from the original PET: intensity thresholds, both for the PET and the PET image-gradient, were set interactively for the purpose of visual guidance.

Thresholding methods (T1–T4) are divided into four types according to whether the threshold is applied to signal (T1 and T2) or a combination of signal and background intensity (T3 and T4) and whether the threshold value is chosen a priori, based on recommendations in the literature or the team’s own experience (T1 and T3) or chosen for each image, either automatically according to spatial criteria or visually by the user's judgement (T2 and T4). Without loss of generalization the threshold value may be absolute or percentage (e.g., of peak) intensity or SUV. T1^a and T1^b employ the widely used cutoff values of 2.5 SUV and 40% of the maximum in the VOI, as used for lung tumor segmentation in [34] and [35], respectively. Method T1^a is the only method of all in Table I that is directly affected by the conversion from raw PET intensity to SUVs. The maximum SUV used by method T1^b was taken from inside the VOI defined by T1^a. To calculate SUV for the phantom image, where patient weight β is unavailable, all voxel values were rescaled with respect to a value of unity at one end of the phantom where intensity is near uniform, causing method T1^a to fail for phantom scan 2 as the maximum was below 2.5 for both VOIs. T1^c applies a threshold at 50% of the maximum SUV. Method T2^a is the thresholding scheme of [6], which automatically finds the optimum relative threshold level (RTL) based an estimate of the true absolute volume of the VOI in the image. The RTL is relative to background intensity, where background voxels are first labelled automatically by clustering. An initial VOI is estimated by a threshold of 40% RTL, and its maximum diameter is determined. The RTL is then adjusted iteratively until the absolute volume of the VOI matches that of a sphere of the same diameter, convolved with the point-spread function (PSF) of the imaging device, estimated automatically from the image. Methods T2^b and T2^c automatically define thresholds according to different criteria. They both use the results of method T1^a as an initial VOI, and define local background voxels by dilation. Method T2^b uses two successive dilations and labels the voxels in the second dilation as background. The auto-threshold is then defined as three standard deviations above the mean intensity in this background sample. Method T2^c uses a single dilation to define the background and finds the threshold that minimizes the within-class variance between VOI and background using the optimization technique in [36]. Finally, method T2^c applies a closing operation to eliminate any holes within the VOI, which may also have the effect of smoothing the boundary. Method T2^d finds the RTL using the method of [6] in common with method T2^a but with different parameters and initialization. Method T2^d assumes a PSF of 7 mm full-width at half-maximum (FWHM) rather than estimating this value from the image. The RTL was initialized with background defined by a manual bounding box rather than clustering and foreground defined by method T3^a with a 50% threshold rather than 40% RTL. Adaptive thresholding method T2^e starts with a manually defined bounding box then defines the VOI by the iso-contour at a percentage of the maximum value within the bounding box. Methods T3^a and T3^b are similar to T1^c, but incorporate local background intensity calculated by a method equivalent to that Daisne et al. [7]. A threshold value is then 41% and 50% of the maximum plus background value, respectively. Method T4^a is an automatic SUV-thresholding method implemented in the “Rover” software [37]. After defining a search area that encloses the VOI, the user provides an initial threshold which is adjusted in two steps of an iterative process. The first step estimates background intensity I_b from the average intensity over those voxels that are below the threshold and within a minimum distance of the VOI (above the threshold). The second step redefines the VOI by a new threshold at 39% of the difference I_max−I_b, where I_max is the maximum intensity in the VOI. Methods T4^b and T4^c use the source-to-background algorithm in [8]. The user first defines a background region specific to the given image, then uses parameters a and b to define the threshold t=aµ_VOI + bµ_BG, where µ_VOI + and µ_BG are the mean SUV in the VOI and background respectively. The parameters are found in a calibration procedure by scanning spherical phantom VOIs of known volume. As this calibration was not performed for the particular scanner used in the present experiments (GE Discovery), methods T4^b and T4^c use parameters previously obtained for Gemini and Biograph PET systems respectively.

Region growing methods (RG) use variants of the classical algorithm in [38], which begins at a “seed” voxel in the VOI and agglomerates connected voxels until no more satisfy criteria based on intensity. in RG^a, the user defines a bounding sphere centred on the VOI, defining both the seed at the center of the sphere and a hard constraint at the sphere surface to avoid leakage into other structures. The acceptance criterion is an interactively adjustable threshold and the final VOI is manually modified in individual slices if needed. Methods RG^b and RG^c use the region growing tool in Mirada XD (Mirada Medical, Oxford, U.K.) with seed point location and acceptance threshold defined by the user. in RGb only, the results are manually post-edited using the “adaptive brush” tool available in Mirada XD. This 3-D painting tool adapts in shape to the underlying image. Also in method RG^b only, CT images were fused with PET for visualization and the information used to modify the regions to exclude airways and unaffected bone.

Watershed methods (WS) use variants of the classical algorithm in [39]. The common analogy pictures a gradient-filtered image as a “relief map” and defines a VOI as one or more pools, created and merged by flooding a region with water. Method WS^a, adapted from the algorithm in [40] for segmenting natural color images and remote-sensing images, makes use of the content as well as the location of user-defined markers. A single marker for each VOI (3×3 or 5×5 pixels depending on VOI size) is used along with a background region to train a fuzzy classification procedure where each voxel is described by a texture feature vector. Classification maps are combined with image gradient and the familiar “flooding” procedure is adapted for the case of multiple surfaces. Neither the method nor the user were specialized in medical imaging. Method WS^b, similar way to that in [41], uses two procedures to overcome problems associated with local minima in image gradient. First, viscosity is added to the watershed, which closes gaps in the edge-map. Second, a set of internal and external markers are identified, indicating the VOI and background. After initial markers are identified in one slice by the user, markers are placed automatically in successive slices, terminating when the next slice is deemed no longer to contain the VOI according to a large drop in the “energy,” governed by area and intensity, of the segmented cross section. If necessary, the user interactively overrides the automatic marker placement.

Pipeline methods (PL) are more complex, multi-step algorithms that combine elements of thresholding, region growing, watershed, morphological operations and techniques in [42], [43], [15]. Method PL^a is a deformable contour model adapted from white matter lesion segmentation in brain MRI. The main steps use a region-scalable fitting model [44] and a global standard convex scheme [45] in energy minimization based on the “Split Bregman” technique in [42]. Methods PL^b--PL^d are variants of the “Smart Opening” algorithm, adapted for PET from the tool in [43] for segmenting lung nodules in CT data. in contrast to CT lung lesions, the threshold used in region growing can not be set a priori and is instead obtained from the image interactively. Method PL^b was used by an operator with limited PET experience. The user of method PL^c had more PET experience and, to aid selection of boundary points close to steep PET gradients, also viewed an overlay of local maxima in the edge-map of the PET image. Finally, method PL^d took the results of method PL^c and performed extra processing by dilation, identification of local gradient maxima in the dilated region, and thresholding the gradient at the median of these local maxima. Methods PL^e and PL^f use the so-called “poly-segmentation” algorithm without and with post editing respectively. PL^e is based on a multi-resolution approach, which segments small lesions using recursive thresholding and combines three segmentation algorithms for larger lesions. First, the watershed transform provides an initial segmentation. Second, an iterative procedure improves the segmentation by adaptive thresholding that uses the image statistics. Third, a region growing method based on regional statistics is used. The interactive variant (PL^f) uses a fast interactive tool for watershed-based subregion merging. This intervention is only necessary in at most two slices per VOI. Method PL^g is a new fuzzy segmentation technique for noisy and low resolution oncological PET images. PET images are first smoothed using a nonlinear anisotropic diffusion filter and added as a second input to the fuzzy C-means (FCM) algorithm to incorporate spatial information. Thereafter, the algorithm integrates the à trous wavelet transform in the standard FCM algorithm to handle heterogeneous tracer uptake in lesions [15].

The gradient based method (GR) is the novel edge-finding method in [10], designed to overcome the low signal-to-noise ratio and poor spatial resolution of PET images. As resolution blur distorts image features such as iso-contours and gradient intensity peaks, the method combines edge restoration methods with subsequent edge detection. Edge restoration goes through two successive steps, namely edge-preserving denoising and deblurring with a deconvolution algorithm that takes into account the resolution of a given PET device. Edge-preserving denoising is achieved by bilateral filtering and a variance-stabilizing transform [46]. Segmentation is finally performed by the watershed transform applied after computation of the gradient magnitude. Over-segmentation is addressed with a hierarchical clustering of the watersheds, according to their average tracer uptake. This produces a dendrogram (or tree-diagram) in which the user selects the branch corresponding to the tumor or target. User intervention is usually straightforward, unless the uptake difference between the target and the background is very low.

The Hybrid method (HB) is the multi-spectral algorithm in [14], adapted for PET/CT. This graph-based algorithm exploits the superior contrast of PET and the superior spatial resolution of CT. The algorithm is formulated as a Markov random field (MRF) optimization problem [47]. This incorporates an energy term in the objective function that penalizes the spatial difference between PET and CT segmentation.

B. Level of Interactivity

Levels of interactivity are defined on an ordinal scale of “max,” “high,” “mid,” “low,” and “none,” where “max” and “none” refer to fully manual and fully automatic methods, respectively. Methods with a “high” level involve user initialization, which locates the VOI and/or representative voxels, as well as run-time parameter adjustment and post-editing of the contours. “Mid”-level interactions involve user-initialization and either run-time parameter adjustment or other run-time information such as wrongly included/excluded voxels. “Low”-level interaction refers to initialization or minimal procedures to restart an algorithm with new information such as an additional mouse-click in the VOI.

C. Level of CT Use

We define the levels at which contouring methods exploit CT information in hybrid patient images as “high,” “low,” or “none,” where “high” refers to numerical use of CT together with PET in calculations. The “low” group makes visual use of CT images to guide manual delineation, postediting or other interactions in semi-automatic methods. The “none” group refers to cases where CT is not used, or is viewed incidentally but has no influence on contouring as the algorithm is fully automatic. None of the methods operated on CT images alone.

SECTION III. Experimental Methods

A. Images

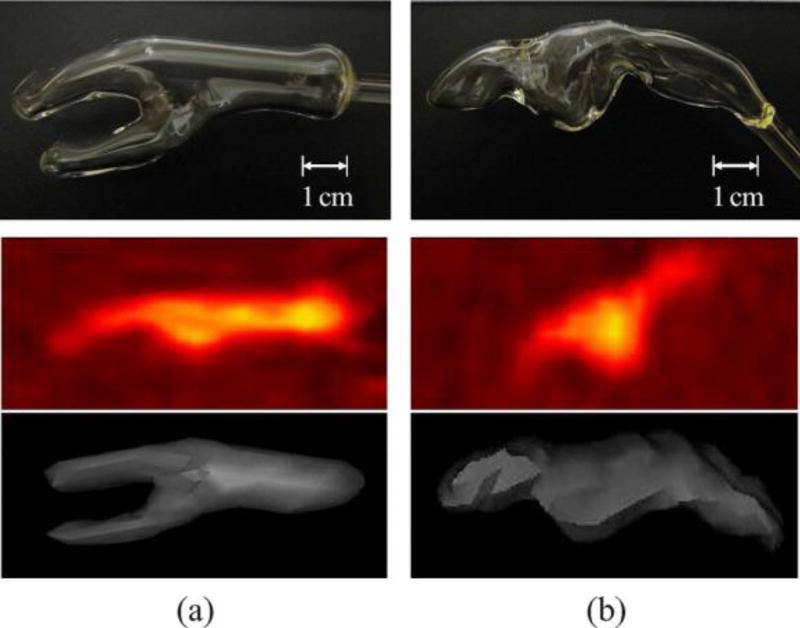
We use two images of a new tumor phantom [29], manufactured for this study and two clinical PET images of different head-and-neck cancer patients. The phantom images are available online [48], along with ground truth sets described in Section III-C. All imaging used the metabolic tracer ¹⁸F-Fluorodeoxyglucose (FDG) and a hybrid PET/CT scanner (GE Discovery), but CT images from phantom scans were omitted from the test set. Table II gives more details of each image type. The tumor phantom contains glass compartments of irregular shapes shown in Fig. 1(top row), mimicking real radiotherapy target volumes. The tumor compartment (a) has branches to recreate the more complex topology of some tumors. This and the nodal chain compartment (b) are based on cancer of the oral cavity and lymph node metastasis respectively, manually segmented from PET images of two head and neck cancer patients and formed by glass blowing. The phantom compartments and surrounding container were filled with low concentrations of FDG and scanned by a hybrid device (1, middle and bottom rows). Four phantom VOIs result from scans 1 and 2, with increasing signal to background ratio achieved by increasing FDG concentration in the VOIs. Details of the four phantom VOIs are given in the first four rows of Table III. Fig. 2 shows the phantom VOIs from scan 1, confirming qualitatively the spatial and radiometric agreement between phantom and patient VOIs.

Table II.

Details of Phantom and Patient PET/CT Images

Image type	PET (18F FDG)					CT
	frame length (min)	width/height (pixels)	depth (slices)	pixel size (mm)	slice depth (mm)	width/height (pixels)	depth (slices)	pixel size (mm)	slice depth (mm)
Phantom	10.0	256	47	1.17×1.17	3.27	512	47	0.59×0.59	3.75
patient	3.0	256	33,37	2.73×2.73	3.27	512	42,47	0.98×0.98	1.37

Figure 1.

(a) Tumor and (b) nodal chain VOIs of the phantom. Top: Digital photographs of glass compartments. Middle: PET images from scan 1 (sagittal view). Bottom: 3-D surface view from an arbitrary threshold of simultaneous CT, lying within the glass wall

Table III.

Properties of VOI and Background (BG) Data (Volumes in cm3 are Estimated as in Section III-C)

VOI	image	Initial activity (kBq ml−1)	Volume (cm3)	source of ground truth
tumour	phantom scan 1	8.7 (VOI) 4.9 (BG)	6.71	thresholds of simultaneous CT image
node			7.45
tumour	phantom scan 2	10.7 (VOI) 2.7 (BG)	6.71
node			7.45
tumour	patient 1	2.4 ×105	35.00	multiple expert delineations
node			2.54
tumour	patient 2	3.6 ×105	2.35

Figure 2.

Axial PET images of phantom and real tumor (top) and lymph node (bottom) VOIs with profile lines traversing each VOI. Plots on the right show the image intensity profiles sampled from each image pair

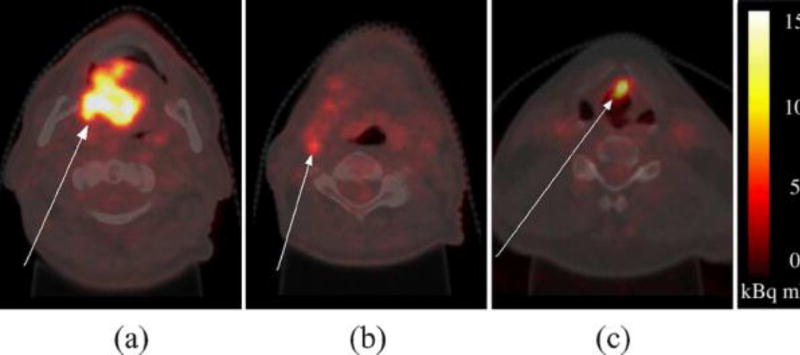
For patient images, head and neck cancer was chosen as it poses particular challenges to PET-based treatment planning due to the many nearby organs at risk (placing extra demand on GTV contouring accuracy), the heterogeneity of tumor tissue and the common occurrence of lymph node metastasis. A large tumor of the oral cavity and a small tumor of the larynx were selected from two different patients, along with a metastatic lymph node in the first patient (Fig. 3). These target volumes were chosen as they were histologically proven and have a range of sizes, anatomical locations/surroundings, and target types (tumor and metastasis). Details of the three patient VOIs are given in the last three rows of Table III.

Figure 3.

Axial neck slices of ¹⁸F-FDG PET images overlain on simultaneous CT. (a) and (b) Oral cavity tumor and lymph node metastasis in patient 1. (c)Laryngeal tumor in patient 2.

B. Contouring

With the exception of the hybrid method (HB) that does not apply to the PET-only phantom data, all methods contoured all seven VOIs. in the case of patient VOIs, participants had the option of using CT as well as PET, and were instructed to contour the gross tumor volume (GTV) and metastatic tissue of tumors and lymph node, respectively. All contouring methods were used at the sites of the respective teams using their own software and workstations. Screen-shots of each VOI were provided in axial, sagittal, and coronal views, with approximate centers indicated by cross-hairs and their voxel coordinates provided to remove any ambiguity regarding the ordering of axes and direction of increasing indexes. No other form of ground truth was provided. Teams were free to refine their algorithms and practice segmentation before accepting final contours. This practicing stage was done without any knowledge of ground truth and is considered normal practice. Any contouring results with sub-voxel precision were down-sampled to the resolution of the PET image grid and any results in millimeters were converted to voxel indexes. Finally, all contouring results were duplicated to represent VOIs first by the voxels on their surface, and second by masks of the solid VOI including the surface voxels. These two representations were used in surface-based and volume-based contour evaluation, respectively.

C. Contouring Evaluation

Accuracy measurement generally compares the contour being evaluated, which we denote C, with some notion of ground truth, denoted GT. We use a new probabilistic metric [29] denoted AUC', as well as a variant of the Hausdorff distance [26] denoted HD' and the standard metric of Dice similarity coefficient [25] (DSC). AUC' and HD' are standardized to the range 0…1 so that they can be easily combined or compared with DSC and other accuracy metrics occupying this range [49]–[50][51]. Treated separately, AUC', HD', and DSC allow performance evaluation with and without the assumption of unique ground truth, and in terms of both volumetric agreement (AUC' and DSC) and surface-displacement (HD') with respect to ground truth.

AUC' is a probabilistic metric based on receiver operating characteristic (ROC) analysis, in a scheme we call inverse-ROC (I-ROC). The I-ROC method removes the assumption of unique ground truth, instead using a set of p arbitrary ground truth definitions {GT_i},i∈{1…p} for each VOI. While uniquely correct ground truth in the space of the PET image would allow deterministic and arguably superior accuracy evaluation, the I-ROC method is proposed for the case here, and perhaps all cases except numerical phantoms, where such truth is not attainable. The theoretical background of I-ROC is given in Appendix A and shows that the area under the curve (AUC) gives a probabilistic measure of accuracy provided that the arbitrary set can be ordered by increasing volume and share the topology and general form of the (unknown) true surface. The power of AUC' as an accuracy metric also relies on the ability to incorporate the best available knowledge of ground truth into the arbitrary set. This is done for phantom and patient VOIs as follows.

For phantom VOIs, the ground truth set is obtained by incrementing a threshold of Hounsfield units (HU) in the CT data from hybrid imaging (Fig. 4). Masks acquired for all CT slices in the following steps.

Figure 4.

(a) 3-D visualization of phantom VOI from CT thresholded at a density near the internal glass surface. (b) Arbitrary ground truth masks of the axial cross section in (a), from 50 thresholds of HU.

1. Reconstruct/down-sample the CT image to the same pixel grid as the PET image.

2. Define a bounding box in the CT image that completely encloses the glass VOI as well as C.

3. Threshold the CT image at a value HU_i.

4. Treat all pixels below this value as being “liquid” and all above it as “glass.”

5. Label all “liquid” pixels that are inside the VOI as positive, but ignore pixels outside the VOI.

6. Repeat for p thresholds HU_i,i∈{1…p} between natural limits HU_min and HU_max.

This ground truth set is guaranteed to pass through the internal surface of the glass compartment and exploits the inherent uncertainty due to partial volume effects in CT. It follows from derivations in Appendix A.2–3 that AUC is equal to the probability that a voxel drawn at random from below the unknown CT threshold at the internal glass surface, lies inside the contour C being evaluated.

For patient VOIs, the ground truth set is the union of an increasing number of expert manual delineations. Experts contoured GTV and node metastasis on PET visualized with co-registered CT. in the absence of histological resection, we assume that the best source of ground truth information is manual PET segmentation by human experts at the imaging site, who have experience of imaging the particular tumor-type and access to extra information such as tumor stage, treatment follow-up and biopsy where available. However, we take the view that no single manual segmentation provides the unique ground truth, which therefore remains unknown. in total, three delineated each VOI on two occasions (denoted N_experts = 3 and N_occasions = 2) with at least a week in between. The resulting set of p=N_experts × N_occasions ground truth estimates were acquired to satisfy the requirements in Appendix A.3 as follows.

1. Define a bounding box in the CT image that completely encloses all N_experts×N_occasions manual segmentations {GT_i} and the contour C being evaluated.

2. Order the segmentations {GT_i} by absolute volume in cm³.

3. Use the smallest segmentation as GT₂.

4. form a new VOI from the union of the smallest and the next largest VOI in the set and use this as GT₃.

5. Repeat until the largest VOI in the set has been used in the union of all N_experts × N_occasions VOIs.

6. Create homogeneous masks for GT₁ and GT_p, having all negative and all positive contents, respectively.

The patient ground truth set encodes uncertainty from inter−/intra-expert variability in manual delineation and AUC is the probability that a voxel drawn at random from the unknown manual contour at the true VOI surface, lies inside the contour C being evaluated. Finally, we rescale AUC to the range {0…1} by

$$\begin{array}{c}\text{AUC}\prime =\frac{\text{AUC}-0.5}{0.5}\\ 0\le \text{AUC}\prime \le 1=\text{maximum accuracy}\end{array}$$ (1)

Reference surfaces that profess to give the unique ground truth are required to measure the Hausdorff distance and Dice similarity. We obtain the “best guess” of the unique ground truth, denoted GT* from the sets of ground truth definitions introduced above. for each phantom VOI we select the CT threshold having the closest internal volume in cm³ to an independent estimate. This estimate is the mean of three repeated measurements of the volume of liquid contained by each glass compartment. for patient VOIs, GT* is the union mask that has the closest absolute volume to the mean of all N_experts × N_occasions raw expert manual delineations.

HD' first uses the reference surface GT* to calculate the Hausdorff distance HD, being the maximum for any point on the surface C of the minimum distances from that point to any point on the surface of GT*. We then normalize HD with respect to a length scale r and subtract the result from 1

$$\begin{array}{c}\text{HD}\prime =\frac{1-\text{min}(\text{HD},\mathrm{r})}{r}\\ 0\le \text{HD}\prime \le 1=\text{maximum accuracy}\end{array}$$ (2)

where $r=\sqrt[3]{\left(\frac{3}{4\pi }\right)\mathit{\text{vol}}(\mathit{\text{GT}}\ast )}$ is the radius of a sphere having the same volume as GT* denoted vol (GT*). Equation (2) transforms HD to the desired range with 1 indicating maximum accuracy.

DSC also uses the reference surface GT* and is calculated by:

$$\begin{array}{c}\mathit{\text{DSC}}=\frac{2N_{c\cap \mathit{\text{GT}}\ast }}{N_C+N_{\mathit{\text{GT}}\ast }}\\ 0\le \text{DSC}\le 1=\text{maximum accuracy}\end{array}$$ (3)

where N_v denotes the number of voxels in volume v defined by contours or their intersect.

Composite metrics are also used. First, we calculate a synthetic accuracy metric from the weighted sum

$$\mathrm{A}\ast =0.5\text{ AUC}\prime +0.25\text{ DSC}+0.25\text{ HD}\prime$$ (4)

which, in the absence of definitive proof of their relative power, assigns equal weighting to the benefits of the probabilistic (AUC′) and deterministic approaches (DSC and HD'). By complementing AUC' with the terms using the best guess of unique ground truth, A* penalizes deviation from the “true” absolute volume, which is measured with greater confidence than spatial truth. Second, we create composite metrics based on the relative accuracy within the set of all methods. Three composite metrics are defined in Table IV and justified as follows. Metric n(n.s.d) favors a segmentation tool that is as good as the most accurate in a statistical sense and, in the presence of false significances due to the multiple comparison effect, gives more conservative rather than falsely high scores.

Table IV.

Composite Accuracy Metrics That Condense Ranking and Significance Information

n(n.s.d): the number between 0 and 4, of accuracy metrics AUC’, DSC, HD and A*, for which a method scores an accuracy of no significant difference (n.s.d) from the best method according to that accuracy

n(>µ+σ): the number between 0 and 4, of accuracy metrics AUC’, DSC, HD and A*, for which a method scores more than one standard deviation (σ) above the mean (µ) of that score achieved by all 32 methods (33 in the case of patient VOIs only)

median rank: the median, calculated over the 4 accuracy metrics, of the ranking of that method in the list of all 32 methods (33 for patient VOIs only) ordered by increasing accuracy

Metric n(>µ+σ) favors the methods in the positive tails of the population, which is irrespective of multiple comparison effects. The rank-based metric is also immune to the multiple comparison effect and we use the median rather than mean rank to avoid misleading results for a method that ranks highly in only one of the metrics AUC', DSC, HD, and A*, considered an outlier.

Intra-operator variability was measured by the raw Hausdorff distance in millimeters between the first and second segmentation result from repeated contouring (no ground truth necessary). However, this was only done for some contouring methods. for fully automatic methods, variability is zero by design and was not explicitly measured. Of the remaining semi-automatic and manual methods, 11 were used twice by the same operator: $\text{MD}\frac{b}{1}\text{MD}\frac{b}{2}$, RG^a, HB, WS^b, $\text{RG}\frac{b}{1}\text{RG}\frac{b}{2}\text{RG}\frac{c}{1}\text{RG}\frac{c}{2}$, GR, and MD^c and for these we measure the intra-operator variability which allows extra, direct comparisons in Section IV-E.

SECTION IV. Experiments

This section motivates the use of the new phantom and accuracy metric (IV-A), then investigates contouring accuracy by comparing the pooled accuracy of methods grouped according to their use of CT data (Section IV-B), level of user interactivity (Section IV-C), and algorithm type (Section IV-D). Section IV-E evaluates methods individually, using condensed accuracy metrics in Table IV. with the inclusion of repeated contouring by methods MD^b, RG^b, and RG^c by a second operator, there are a total of n=33 segmentations of each VOI, with the exception of phantom VOIs where n=32 by the exclusion of method HB. Also, method T1^α failed to recover phantom VOIs in scan 1 as no voxels were above the predefined threshold. in this case a value of zero accuracy is recorded for two out of four phantom VOIs.

A. Phantom and AUC'

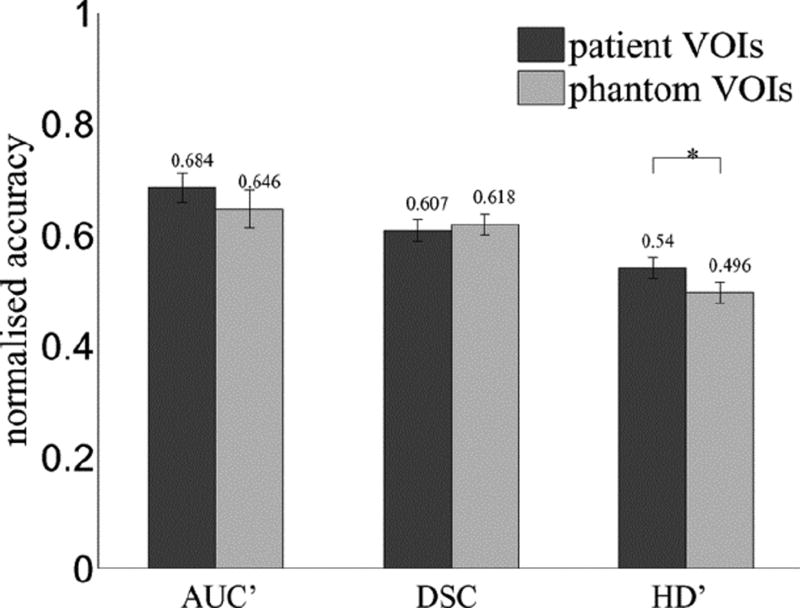
This experiment investigates the ability of the phantom to pose a realistic challenge to PET contouring, by testing the null-hypothesis that both phantom and patient VOIs lead to the same distribution of contouring accuracy across all methods used on both image types. First, we take the mean accuracy over the four phantom VOIs as a single score for each contouring method. Next, we measure the accuracy of the same methods used in patient images and take the mean over the three patient VOIs as a single score for each method. Finally, a paired-samples t-test is used for the difference of means between accuracy scores in each image type, with significant difference defined at a confidence level of p≤0.05. Fig. 5 shows the results separately for accuracy defined by AUC′, DSC, and HD′. There is no significant difference between accuracy in phantom and patient images measured by AUC′ or DSC. A significant difference is seen for HD′, which reflects the sensitivity of HD' to small differences between VOI surfaces. in this case the phantom VOIs are even more difficult to contour accurately than the patient images, which could be explained by the absence of anatomical context in these images, used by operators of manual and semi-automatic contouring methods. A similar experiment found no significant difference between phantom and patient VOIs in terms of intra-operator variability. On the whole we accept the null-hypothesis meaning that the phantom and patient images pose the same challenge to contouring methods in terms of accuracy and variability.

Figure 5.

Contouring accuracy in phantom and patient images, where “┌*┐” indicates significant difference.

Fig. 5 also supports the use of the new metric AUC'. Although values are generally higher than DSC and HD, which may be explained by the involvement of multiple ground truth definitions increasing the likelihood that a contour agrees with anyone in the set, the variance of accuracy scores is greater for AUC' than the other metrics (Table V), which indicates higher sensitivity to small differences in accuracy between any two methods.

Table V.

Variance of AUC′ and Standard Accuracy Metrics Calculated for All Seven VOIs (Second Column), and for the Four and Three VOIs in Phantom and Patient Images, Respectively.

metric	all VOIs	phantom	patient
AUC′	0.028	0.035	0.021
DSC	0.011	0.010	0.012
HD′	0.011	0.010	0.011

B. Role of CT in PET/CT Contouring

For contouring in patient images only, we test the benefit of exploiting CT information in contouring (phantom VOIs are omitted from this experiment as the CT was used for ground truth definitions and not made available during contouring). This information is in the form of anatomical structure in the case of visual CT-guidance (“low” CT use) and higher-level, image texture information in the case of method HB with “high” CT use. The null-hypothesis is that contouring accuracy is not affected by the level of use of CT information.

We compare each pair of groups i and j that differ by CT use, using a t-test for unequal sample sizes n_i and n_j, where the corresponding samples have mean accuracy µ_i and µ_j and standard deviation σ_i and σ_j. for the i_th group containing n_methods contouring methods, each segmenting n_VOIs targets, the sample size n_i=n_methods×n_VOIs and µ_i and σ_j are calculated over all n_methods × n_VOIs accuracy scores. We calculate the significance level from the t-value using the number of degrees of freedom given by the Welch–Satterthwaite formula for unequal sample sizes and sample standard deviations. Significant differences between groups are defined by confidence interval of p≤0.05. for patient images only, n_VOIs =3 and for the grouping according to CT use in Table I, n_methods =1,6 and 26 for the groups with levels of CT use “high,” “low,” and “none,” respectively (methods RG^b in the “low” group and MD^b and RG^c in the “none” group were used twice by different operators in the same team). We repeat for four accuracy metrics AUC′, DSC, HD′ and their weighted sum A*. Fig. 6 shows the results for all groups ordered by level of CT use, in terms of each accuracy metric in turn.

Figure 6.

Effect of CT use on contouring accuracy in patient images, measured by (a) AUC′ , (b) DSC, (c) HD′ , and (d) A*, where “┌*┐” denotes significant difference between two levels of CT use.

With the exception of AUC' the use of CT as a visual guidance (“low”), outperformed the “high” and “none” groups consistently but without significant difference. The fact that the “high” group (method HB only) significantly outperformed the lower groups in terms of AUC' alone indicates that the method had good spatial agreement with one of the union-of-experts masks for any given VOI, but this union mask did not have absolute volume most closely matching the independent estimates used in calculations of DSC and HD'. We conclude that the use of CT images as visual reference (“low” use) generally improves accuracy, as supported by the consistent improvement in three out of four metrics. This is in agreement with experiments in [30] and [31], which found the benefits of adding CT visually and computationally, in manual and automatic tumor delineation and classification, respectively.

C. Role of User Interaction

This experiment investigates the affect of user-interactivity on contouring performance. The null hypothesis is that contouring accuracy is not affected by the level of interactivity in a contouring method. We compare each pair of groups i and j that differ by level of interactivity, using a t-test for unequal sample sizes as above. for the grouping according to level of interactivity in Table I, groups with interactivity level “max,” “high,” “mid,” “low,” and “none” have n_methods =4,3,7,13(12 for phantom images by removal of method HB) and 6, respectively (methods MD^b, RGMD^band RGMD^c in the “max,” “high,” and “mid” groups, respectively, were used twice by different operators in the same team). We repeat for patient images (n_VOIs=3), phantom images (n_VOIs=4), and the combined set (n_VOIs=7) and, as above, for each of the four accuracy metrics. Fig. 7 shows all results for all groups ordered by level of interactivity.

Figure 7.

Effect of user interaction on contouring accuracy measured by top row: AUC′ for (a) phantom, (b) patient, and (c) both VOI types, second row: DSC for (d) phantom, (e) patient, and (f) both image types, third row: HD′ for (g) phantom, (h) patient, and (i) both image types, and bottom row: A* for (j) phantom, (k)patient, and (l) both VOI types. Significant differences between any two levels of user interaction are indicated by “┌*┐.”

The trends for each of phantom, patient and all VOIs are consistent over all metrics. The most accurate methods were those in the “high” and “max” groups for phantom and patient images, respectively. for patient images, the “max” group is significantly more accurate than any other and this trend carries over to the pooled accuracies in both image types despite having less patient VOIs (n=3) than phantom VOIs (n=4). for phantom VOIs, with the exception of HD', there are no significant differences between “high” and “max” groups and these both significantly outperform the “low” and “none” groups in all metrics. for HD' alone, fully manual delineation is significantly less accurate than semi-automatic methods with “high” levels of interaction. This may reflect the lack of anatomical reference in the phantom images, which is present for patient VOIs and guides manual delineation. As high levels of interaction still appear most accurate, the reduced accuracy of fully manual methods is not considered likely to be caused by a bias of manual delineations toward manual ground truth, given the levels of inter-user variability. Overall, we conclude that manual delineation is more accurate than semi- or fully-automatic methods, and that the accuracy of semi-automatic methods improves with the level of interaction built in.

D. Accuracy of Algorithm Types

This experiment compares the accuracy of different algorithm types, defined in Section II-A. The null hypothesis is that contouring accuracy is the same for manual or any numerical method regardless of the general approach they take. We compare each pair of groups i and j that differ by algorithm type, using a t-test for unequal sample sizes as above. for the grouping according to algorithm type in Table I, n_methods=4,3,5,2,3,5,2,1,1 (0 for phantom images by removal of method HB) and 7 for algorithm-types MD, T1, T2, T3, T4, RG, WS, GR, HB, and PL, respectively (methods MD^b in the MD, and RG^b and RG^c in the RG group were used twice by different operators in the same team). As above, we repeat for patient images (n_VOIs=3), phantom images (n_VOIs=4) and the combined set (n_VOIs=7), and for each of the four accuracy metrics. Fig. 8 shows the results separately for all image sets and accuracy metrics.

Figure 8.

Contouring accuracy of all algorithm types measured by top row: AUC′ for (a) phantom, (b) patient, and (c) both VOI types, second row: DSC for (d)phantom, (e) patient, and (f) both image types, third row: HD′ for (g) phantom, (h) patient, and (i) both image types and bottom row: A* for (j) phantom, (k)patient, and (l) both VOI types. Significant differences between any two algorithm types are indicated by “┌*┐.”

Plot (b) reproduces the same anomalous success of the hybrid method (HB) in terms of AUC' alone, as explained above. Manual delineation exhibits higher accuracy than other algorithm types, ranking in the top three for any accuracy metric in phantom images and the top two for any metric in patient images. The pooled results over all images reveal manual delineation as the most accurate in terms of all four metrics. with the exception of T4 in terms of HD' (patient and combined image sets), the improvement of manual delineation over any of the thresholding variants T1–T4 is significant, despite these being the most widely used (semi-)automatic methods. A promising semi-automatic approach is the gradient-based (GR) group (one method), which has the second highest accuracy by all metrics for the combined image set and significant difference from manual delineation. Conversely, the watershed group of methods that also rely on image gradients exhibit consistently low accuracy. This emphasized the problem of poorly-defined edges and noise-induced false edges typical of PET gradient filtering, which in turn suggests that edge-preserving noise reduction by the bilateral filter plays a large part in the success of method GR.

E. Accuracy of Individual Methods

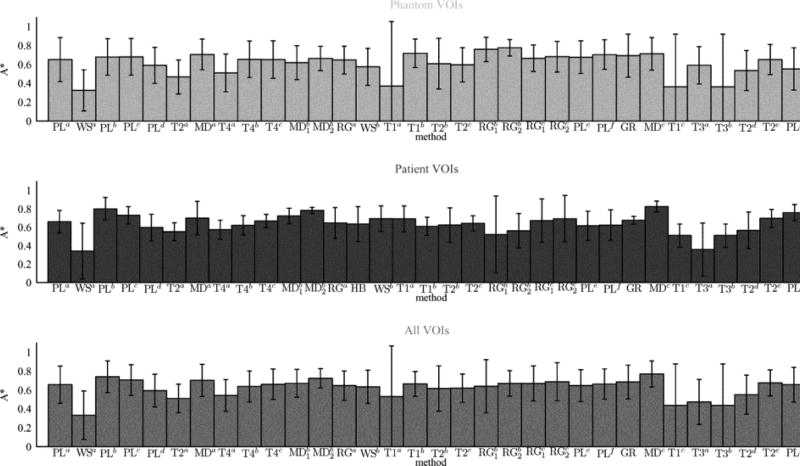
The final experiments directly compare the accuracy of all methods. Where two algorithms have arguably minor difference, as in the case of PL^c and PL^d which differ by an extra processing step applied by PL^d, these are treated as separate methods because the change in contouring results is notable and can be attributed to the addition of the processing step, which is informative. Repeated segmentations by two different users in the cases of methods $\text{MD}\frac{b}{1,2},\text{RG}\frac{b}{1,2},\text{ and RG}\frac{c}{1,2}$ are counted as two individual results so there are a total of n=32 ”methods,” or n=33 for patient VOIs in PET/CT only by inclusion of hybrid method HB. The null hypothesis is that all n cases are equally accurate. We compare each pair of methods i and j that differ by method, using a t-test for equal sample sizes n_i=n_j=n_VOIs, where mean accuracy µ_i and µ_j and standard deviation σ_i and σ_j are calculated over all VOIs and there are 2_nVOIs−2 degrees-of-freedom. As above, we repeat for all image sets and accuracy metrics. Fig. 9 shows the results separately for phantom, patient and combined image sets in terms of A* only. Full results for all metrics and significant differences between methods are given in the supplementary material.

Figure 9.

Mean accuracy measured by A*, of each method used to contour VOIs in phantom (top), patient (middle), and the combined image set (bottom).

The generally low values of A* in Fig. 9 and other metrics in the supplementary material highlight the problem facing accurate PET contouring. These results also reiterate the general finding that manual practices can be more accurate than semi- or fully-automatic contouring. for patient images, and the combined set, the most accurate contours are manually delineated by method MD^c. Also for these image sets the second and third most accurate are another manual method ( $\text{MD}\frac{b}{2}$) and the “smart opening” algorithm (PL^b) with mid-level interactivity.

For phantom VOIs only, methods RG^b and T1^b, with high- and low-level interactivity, out-perform manual method MD^c with no significant difference. Method RG^b is based on SRG with post-editing by the adaptive brush and showed low accuracy for patient VOIs with RGb² being significantly less accurate than the manual method MD^c (see supplementary material). Method T1^b is based on thresholding and showed low accuracy for patient VOIs, being significantly less accurate than the manual methods MD^c and $\text{MD}\frac{b}{2}$ (see supplementary material). Their high accuracy in phantom images alone could be explained by methods T1^b and RG^b being particularly suited to the relative homogeneity of the phantom VOIs.

Methods WS^a, T1^c, and T3^b have the three lowest accuracies by mean A* across all three image sets. The poor performance of method WS^a could be explained by its origins (color photography and remote-sensing) and user having no roots or specialism in medical imaging. Threshold methods T1^c and T3^b give iso-contours at 50% of the local peak intensity without and with adjustment for background intensity, respectively. Their poor performance in all image types highlights the limitations of thresholding.

Table VI presents the composite metrics explained in Section III-C along with intra-operator variability where available (last two columns), measured by the Hausdorff distance in mm between two segmentations of the same VOI, averaged over the three patient or four phantom VOIs. This definition of intra-operator variability gives an anomalously high value if the two segmentations resulting from repeated contouring of the same VOI do not have the same topology, as caused by an internal hole in the first contouring by method $\text{RG}\frac{b}{1}$. Notably, we find no correlation between intra-operator variability and the level of interactivity of the corresponding methods. The same is true for inter-operator variability (not shown) calculated by the Hausdorff distance between segmentations by different users of the same method (applicable to methods MD_b, RG_b, and RG_c). This finding contradicts the general belief that user input should be minimized to reduce variability. Table VI reaffirms the finding that manual delineation is the most accurate method type, with examples MD^c and $\text{MD}\frac{b}{1,2}$ scoring highly in all metrics. The most consistently accurate nonmanual methods are the semi- and fully-automatic methods PL^b and PL^c. More detailed method-wise comparisons are made in the next section.

Table VI.

Summarized Accuracy and Variability of Phantom (ph.) and Patient (pt.) Contouring by All Methods Ordered as in Table I and Using Ranked and Other Composite Accuracy Metrics in Section III-C. Data are not Available (n/a) for Method HB in Phantom Results and Most Methods in Variability Results

method	n(n.s.d)		n(>µ+σ)		median rank		intra-operator HD (mm)
	ph.	pt.	ph.	pt.	ph.	pt.	ph.	pt.
PLa	4	3	0	0	17	19	n/a	n/a
WSa	0	0	0	0	1.5	1.5	n/a	n/a
PLb	4	4	0	3	24	31.5	n/a	n/a
PLc	4	3	1	1	23.5	27	n/a	n/a
PLd	3	2	0	0	10.5	12.5	n/a	n/a
T2a	0	1	0	0	4	7	n/a	n/a
MDa	4	4	2	0	28.5	23	n/a	n/a
T4a	0	0	0	0	6	9	n/a	n/a
T4b	4	1	0	0	18.5	15.5	n/a	n/a
T4c	4	2	0	1	17.5	20.5	n/a	n/a
MDb 1	3	3	0	1	13.5	25.5	3.9±0.9	4.4±1.2
MDb 2	3	3	0	3	20.5	31.5	4.1±1.7	5.6±1.8
RGa	3	3	1	0	14.5	17	3.7±0.6	2.4±0.1
HB	n/a	3	n/a	1	n/a	12	n/a	5.6±0.6
WSb	2	2	0	1	8.5	26	3.3±3.0	7.4±6.7
T1a	2	3	0	1	3	23	n/a	n/a
T1b	4	1	1	0	28.5	11	n/a	n/a
T2b	4	3	0	0	13.5	14	n/a	n/a
T2c	3	1	0	0	11.5	16.5	n/a	n/a
RGb 1	4	3	4	0	31	7	24.0±38.9	18.2±20.8
RGb 2	4	2	4	0	31.5	8	4.5±2.4	3.3±2.0
RGc 1	3	4	0	0	20	20.5	1.5±1.7	1.0±1.5
RGc 2	4	4	0	0	25	22.5	2.6±2.0	2.7=0.4
PLe	4	2	0	0	20	12	n/a	n/a
PLf	4	3	0	0	27.5	14	n/a	n/a
GR	4	0	0	0	25	23	1.2±0.0	2.3±0.7
MDc	4	4	1	4	28.5	32.5	2.9±0.7	3.8±1.2
T1c	4	0	0	0	3	3.5	n/a	n/a
T3a	3	1	0	0	10.5	2	n/a	n/a
T3b	4	0	0	0	4.5	3.5	n/a	n/a
T2d	0	2	0	0	7	7.5	n/a	n/a
T2e	4	3	0	1	18.5	26	n/a	n/a
PLg	3	4	0	3	8.5	29.5	n/a	n/a

SECTION V. Discussion

We have evaluated and compared 30 implementations of PET segmentation methods ranging from fully manual to fully automatic and representing the range from well established to never-before tested on PET data. Region growing and watershed algorithms are well established in other areas of medical image processing, while their use for PET target volume delineation is relatively new. Even more novel approaches are found in the “pipeline” group and the two distinct algorithms of gradient-based and hybrid segmentation. The gradient-based method [10] has already had an impact in the radiation oncology community and the HB method [14] is one of few in the literature to make numerical use of the structural information in fused PET/CT. The multispectral approach is in common with classification experiments in [13] that showed favourable results over PET alone.

A. Manual Delineation

Freehand segmentation produced among the most accurate results, which may be counter-intuitive. One explanation comes from the incorporation of prior knowledge regarding the likely form and extent of pathology. in the case of the patient images alone, bias toward MD may be suspected as the ground-truth set is also built up from manual delineations. However, this does not explain the success of manual methods as they performed better still for phantom VOIs where the ground truth comes from CT thresholds. The use of multiple ground truth estimates by I-ROC may falsely favour manual delineation due to its inherent variability. However, this too does not explain the success of manual methods as they also perform well in terms of DSC and HD' that use a unique, “best-guess” of ground truth (at least one MD is among the five highest DSC and HD for each of the patient phantom VOI sets). These observations challenge the intuition, that manual delineation is less accurate. Although many (semi-)automatic methods outperform freehand delineation in the literature, the inherent bias toward positive results among published work makes this an unfair basis for intuition.

Of the four manual delineations (MD^a $\text{MD}\frac{b}{1},\text{MD}\frac{b}{2}$ and MD^c method MD^c outperformed the rest in all of n(n.s.d), n(>µ+σ), median rank and intra-operator variability where known, with significant improvement over $\text{MD}\frac{b}{1,2}$ in terms of AUC' for patient VOIs (although the multiple comparison effect can mean that one or more of these differences are falsely detected as significant). The obvious difference between these four is the user. It is interesting, and indicative of no bias in terms of user group, that the delineator of MDc was a nuclear medicine physicist while the other users, in common with the experts providing ground truth estimates, were experienced physicians. However, while users of MD^a and $\text{MD}\frac{b}{1,2}$ only viewed the PET images during delineation, the physicist using MD^c also viewed an overlay of the PET gradient magnitude and, in the case of patient images, simultaneous CT. These modes of visual guidance could in part compensate for the relative lack of clinical experience, although no concrete conclusion can be made as clinical sites may disagree on the correct segmentation.

B. Automation versus User Guidance

Two method comparisons provide evidence that too much automation in a semi-automatic algorithm is detrimental to contouring accuracy. First, we compare the accuracy of methods PL^c and PL^d. Method PL^d starts with the same segmentation achieved by PL^c, then performs extra steps in the automatic pipeline intended to improve on the results. However, these extra steps reduce the final accuracy. Second, we compare the accuracy of methods $\text{RG}\frac{b}{1,2},\text{ and RG}\frac{c}{1,2}$ These differ in that $\text{RG}\frac{b}{1,2}$ also employs post-editing by the adaptive brush tool. While the adaptive brush may improve accuracy for phantom VOIs, accuracy is reduced for patient VOIs indicated by n(n.s.d) and median rank. This suggests that, where post-editing by unconstrained manual delineation generally improves accuracy in other methods, the automated component of the adaptive brush may influence the editing procedure, and this influence may be detrimental in cases where underlying image information is less reliable.

Conversely, two comparisons give a clear example of the benefits of user-intervention. First, methods PL^e and PL^f are almost the same with the difference that PL^f employs interactive post-editing by user-defined watershed markers and subregional merging. Method PL^f is consistently more accurate than PL^e over all 12 combinations of accuracy metric and image type. A second example comes from comparing five thresholding schemes used at the same institution (team 13). Methods T^1c, T3^a and T3^b use intensity thresholds of 50% maximum and 41% and 50% of maximum-plus-background, while T2^d and T2^e use thresholds chosen to match an estimate of the VOI's absolute volume and the user's visual judgement of VOI extent, respectively. Of these five, T2^e is most highly influenced by the user and ranks consistently higher than the other four in all 12 combinations of accuracy metric and image set, significantly outperforming T^1c once, T3^b twice, and T3^a three times (notwithstanding the possibility of false significance by the multiple comparison effect).

Fully automated contouring has the potential to reduce the user-time involved, whereas contouring speed is not included in the present evaluation strategy. This study focuses on accuracy, given that even fully automatic results can in principle be edited by medical professionals, who ultimately decide how much time is justified for a given treatment plan as well as just where the final contours should lie. The CPU-time of the more computationally expensive algorithms could be quantified as the subject of further work, but its relevance is debatable given that CPUs have different speeds and large data sets can be processed offline, allowing the medical professional to work on other parts of a treatment in parallel.

C. Building Prior Knowledge into Contouring

As already seen from Fig. 9 method WS^a consistently gave the lowest accuracy. This method was adapted from an algorithm designed for segmenting remote sensing imagery and its user declared no expertise in medical image analysis. Conversely, two methods were adapted for the application of PET oncology, from other areas of medical image segmentation. Method PL^a has origins in white matter lesion segmentation in brain MRI and method PL^b is adapted from segmentation of lung nodules in CT images. These two examples far outperform method WS^a, with method PL^b having the joint second highest median ranking for patient images and no significant difference from the most accurate methods in terms of any metric for any image set.

Some methods were designed for PET oncology, incorporating numerical methods to overcome known challenges. Examples are method GR that overcomes poorly defined gradients around small volumes due in part to partial volume effects, and method PL^g allows for regional heterogeneity that is known to confound PET tumor segmentation. These methods rank reasonably highly, in patient images, ranking similarly to all manual delineations and the semi-automatic “smart opening” algorithm (PL^b), despite neither GR nor PL^g having any user intervention or making any use of simultaneous CT. Method PL^g performs relatively poorly in phantom images, where the problem of tissue heterogeneity is not reproduced.

The benefits of prior knowledge are also revealed by comparing three thresholding schemes T4^a, T4^b, and T4^c used by the same institution (team 04). Of these, method T4^a was considerably less accurate in terms of both n(n.s.d) and median rank. Methods T4^b and T4^c were calibrated using phantom data to build in prior knowledge of the imaging device. Even though the two devices used to calibrate T4^b and T4^c are from different vendors (Siemens and Biograph devices) than the one that acquired the test images (GE Discovery), they are consistently more accurate than method T4^a implemented at the same site, which does not learn from scanner characteristics but instead has an arbitrary parameter (39%). Methods T4^b and T4^c also outperform the majority of the other low-interactivity thresholding schemes, suggesting that the calibration is beneficial and generalizes across imaging devices. This apparent generalization is further evidenced by no significant differences between methods T4^b and T4^c in any individual metric for patient or phantom VOIs.

Finally, the low accuracy of methods T4^a and T4^a may be due to erroneous prior knowledge. These two implementations of the same algorithm [6] inherently approximate the volume of interest as a sphere. Both perform poorly, with median ranking from 4–7 over all four metrics in contouring both phantom and patient VOIs. These low accuracies are likely to arise from the spherical assumption rather than the initialization of the method, as the low accuracies are similar despite different methods of initialization described in Section II.

D. Accuracy Evaluation

Accuracy measurement is fundamentally flawed in many medical image segmentation tasks due to the ill-definition of the true surface of the VOI. It is most common to estimate the ground truth by manual delineation performed by a single expert (e.g., [52], [19], [53]). However, even among experts, inter- and intra-operator variability are inevitable and well documented in PET oncology [21], [22]. The new metric AUC' exploits this variability in a probabilistic framework, and we have also defined a single “best guess” ground truth, for use with traditional metrics of DSC and HD, from the union of a subset of expert contours. for patient VOIs, the I-ROC scheme incorporates knowledge and experience of multiple experts as well as structural and clinical information into accuracy measurement and rewards the ability of an algorithm to derive the same information from image data. The I-ROC method considers all ground truth estimates to be equally valid a priori, and any one estimate can become the operating point on the I-ROC curve built for a given contour under evaluation. This is in common with the simultaneous truth and performance level estimation (STAPLE) algorithm by Warfield et al. [54]. Theirs is also a probabilistic method, which uses maximum likelihood estimation to infer both the accuracy of the segmentation method under investigation and an estimate of the unique ground truth built from the initial set.

Other authors have evaluated segmentation accuracy using phantoms. The most common phantoms used in PET imaging contain simple compartments such as spherical VOIs, attempting to mimick tumors and metastases in head and neck cancer [10], [12], lung nodules [55] and gliomas [20], and cylindrical VOIs, attempting to mimick tumors [7]. The ground truth surface of such VOIs is precisely known due to their geometric form, but many segmentation algorithms are confounded by irregular surfaces and more complex topology such as branching seen in clinical cases and in the new phantom presented here. Another limitation of phantom images including those used here is the difficulty of mimicking heterogeneous or multi-focal tumors as seen in some clinical data.

Digital images of histological resection can in some cases provide unique ground truth, removing the need to combine multiple estimates. A recent example demonstrates this for PET imaging of prostate cancer [56]. While this approach could provide the standard for accuracy evaluation where available, histology-based accuracy measurement is currently limited as described in [57], with errors introduced by deformation of the organ and co-registration of digital images (co-registration in [56] required first registering manually to an intermediate CT image). Furthermore, tumor excision is only appropriate for some applications. for head-and-neck cancer, the location of the disease often calls for noninvasive, in vitro treatment by radiotherapy and in such cases the proposed use of multiple ground truth estimates may provide a new standard.

Neither deterministic metrics with flawed, unique ground truth (DSC and HD) nor probabilistic methods like I-ROC or STAPLE, measure absolute accuracy. However, the relative accuracy of methods or method groups is of interest to our aim of guiding algorithm development. for this purpose, a large and varied cohort of segmentation methods is desirable, and the composite metrics based on method ranking, distributions of accuracy scores n(>µ+σ) and the frequency of having no significant reduction in accuracy with respect to the most accurate n(n.s.d) become more reliable as the number of contouring tools increases. However, without a simultaneous increase in the number of VOIs, significance tests of the difference in accuracy of any one pair of methods becomes less reliable due to multiple comparison effects.

SECTION VI. Conclusion

The multi-center, double-blind comparison of segmentation methods presented here is the largest of its kind completed for VOI contouring in PET oncology. This application has an urgent need for improved software given the demands of modern treatment planning. The number and variety of contouring methods used in this paper alone confirms the need for constraint, if the research is to converge on a small number of contouring solutions for clinical use.

We found that structural images in hybrid PET/CT, now commonly available for treatment planning, should be used for visual reference during semi-automatic contouring while the benefits of high-level CT use by multispectral calculations are revealed only by the new accuracy metric. We also concluded that higher levels of user interaction improves contouring accuracy without increasing intra- or inter-operator variability. Indeed, manual delineation overall outperformed all semi- or fully-automatic methods. However, two methods (T2^b and PL^f) with a low-level of interactivity and two automatic methods (PL^a and PL^g) are characterized by accuracy scores that are frequently not significantly different from those of the best manual method. Contouring research should pursue a semi-automatic method that achieves the same level of accuracy as expert manual delineation, but must strike a balance between 1) guiding manual practices to reduce levels of variability and 2) not overinfluencing the expert or overriding his or her knowledge. To strike this balance, techniques that show promise are 1) visual guidance by both CT and PET-gradient images, 2) model-based handling of heterogeneity and blurred edges that characterize oncological VOIs in PET, and 3) departure from the reliance on the SUV transformation and iso-contours of this parameter or another scalar multiple of PET intensity, given its dependence on the imaging time window and countless other confounding factors.

These results go a long way towards constraining subsequent development of PET contouring methods, by identifying and comparing the distinct components and individual methods used or proposed in research and the clinic. in addition, we provide detailed results and statistical analyses in supplementary material for use by others in retrospective comparisons according to criteria or method groups not attempted here, as well as access to the phantom images and ground truth sets [48] that can be used to evaluate other contouring methods in the future. While our tests focused on head-and-neck oncology, only the fixed threshold method T1a made any assumptions about the tracer or tumor site so results for the remaining methods tested here provide a benchmark for future comparisons. Recently proposed methods in [11], [12], and [58] would be of particular interest to test. However, if the number of tested methods increases without increasing the number of VOIs, the chance of falsely finding significant differences between a pair of methods increases due to the multiple comparison effect so the composite metrics are favoured over pair-wise comparisons for such a benchmark.

Future work using the data from the present study should categorize the 30 methods in terms of user-group and compare segmentation methods in more head and neck VOIs. Future work with a larger set of test data (images and VOIs) is expected to provide more statistically significant findings and should repeat for VOIs outside the realm of FDG in head-and-neck cancer and for images of different signal/background quality. for this purpose the experimental design including phantom, accuracy metrics and the grouping of contemporary segmentation methods, will generalize for other tumor types and PET tracers.